Open Access Article
Open Access ArticleA comparison of the network structure and inner dynamics of homogeneously and heterogeneously crosslinked PNIPAM microgels with high crosslinker content†
Judith
Witte
 *a,
Tetyana
Kyrey
abc,
Jana
Lutzki
a,
Anna Margarethe
Dahl
a,
Judith
Houston
*a,
Tetyana
Kyrey
abc,
Jana
Lutzki
a,
Anna Margarethe
Dahl
a,
Judith
Houston
 b,
Aurel
Radulescu
b,
Vitaliy
Pipich
b,
Laura
Stingaciu
d,
Matthias
Kühnhammer
c,
Marcus U.
Witt
c,
Regine
von Klitzing
c,
Olaf
Holderer
b and
Stefan
Wellert
a
b,
Aurel
Radulescu
b,
Vitaliy
Pipich
b,
Laura
Stingaciu
d,
Matthias
Kühnhammer
c,
Marcus U.
Witt
c,
Regine
von Klitzing
c,
Olaf
Holderer
b and
Stefan
Wellert
a
aInstitute of Chemistry, TU Berlin, Strasse des 17. Juni 124, 10623 Berlin, Germany. E-mail: judith.witte@tu-berlin.de; Fax: +49 30 31426602; Tel: +49 30 31426774
bJülich Centre for Neutron Science JCNS, Forschungszentrum Jülich GmbH, Outstation at MLZ, Lichtenbergstrasse 1, 85747 Garching, Germany
cInstitute of Physics, TU Darmstadt, Alarich-Weiss-Strasse 10, 64287 Darmstadt, Germany
dNScD, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
First published on 21st January 2019
Abstract
Poly(N-isopropylacrylamide) microgel particles were prepared via a “classical” surfactant-free precipitation polymerization and a continuous monomer feeding approach. It is anticipated that this yields microgel particles with different internal structures, namely a dense core with a fluffy shell for the classical approach and a more even crosslink distribution in the case of the continuous monomer feeding approach. A thorough structural investigation of the resulting microgels with dynamic light scattering, atomic force microscopy and small angle neutron scattering was conducted and related to neutron spin echo spectroscopy data. In this way a link between structural and dynamic features of the internal polymer network was made.
1 Introduction
Microgel particles, especially those with responsive properties such as thermoresponsivity, pH-responsivity or responsivity to ionic strength are the object of numerous scientific investigations due to their large potential for applications such as drug delivery,1–3 sensoric applications4–7 or biotechnological applications.8–10N-Isopropylacrylamide (NIPAM) is a widely used monomer for the synthesis of said microgel particles. A lower critical solution temperature (LCST) of the NIPAM monomer of approximately 32 °C leads to a similar volume phase transition temperature (VPTT) for poly(N-isopropylacrylamide) (PNIPAM) microgel particles. Factors that may influence the VPTT are the use of a comonomer with a different LCST11 or the functionalization of the polymer network.12 Those strategies therefore enable the synthesis of microgel particles with a tunable VPTT.N,N′-Methylenebisacrylamide (BIS) is commonly used as a crosslinker in PNIPAM microgels. It was found by Wu et al. that during emulsion polymerization BIS molecules are consumed faster than NIPAM molecules.13 This results in an uneven distribution of crosslinking and hence in a denser core and a fluffier shell.14
To tune the microgel structure towards a more even distribution of crosslinks and polymer, several procedures of introducing the crosslinker and monomers into the network have been tested. For example, semibatch reaction processes were found to lead to a homogeneous morphology.15,16
Beside this, it was demonstrated that droplet based microfluidic templating enables the formation of microgels with different inner homogeneity and sizes of several ten to hundreds of micrometers.17,18 By choosing a monomer feeding approach for the PNIPAM microgel particles it has been attempted to circumvent this problem and achieve an even distribution of crosslinks in sub micrometer sized microgels. Most publications take studies of optical properties such as transparency/turbidity and dynamic light scattering as an evidence for the homogeneous crosslinking of the PNIPAM microgel particles.19,20 Although supporting the conclusion of a homogeneous inner structure, these methods provide no direct access to the inner structural properties. Theoretical considerations and experiments using dielectric spectroscopy21,22 predict an influence of the microstructure of the microgels on their physico-chemical properties, e.g., swelling kinetics23 and desired functionality.24 Besides this, the interaction potential between them, their ability to interpenetrate and their behavior at very dense packing conditions are influenced, e.g., by the microgel softness and the internal crosslinker density distribution.25,26
Hence, a thorough and direct comparison of the internal structure and dynamics of both types of microgels in the often investigated sub micrometer size range is of importance but still missing. In case of inhomogeneity-free macroscopic gels, differences in the network dynamics compared to heterogeneous gels were found in a combined light and neutron scattering study.27
Very recently, it was shown that super-resolution microscopy methods can probe the inner network morphology by indirect or direct labeling. Here, the proportionality between the localization distribution of the probe and the network was used.28,29 Also, photoactivation localization microscopy (PALM) on microgel particles synthesized via precipitation polymerization with the addition of a photochromic diarylethene photoswitch as crosslinker allows a 3D reconstruction of the distribution of crosslinker positions in a microgel in its hydrated state.30 The analysis of the network structure using modern optical methods complements studies without any tracers e.g. scattering experiments.
Small angle neutron scattering (SANS) uses neutron scattering to probe samples on small length scales. Depending on the probed Q-range and the sample dimensions different structural features of an object can be studied. This is especially useful for the study of microgel particles. By choosing larger Q-values it becomes possible to probe properties of the internal polymer network such as correlation length which is related to the mesh size and static inhomogeneities. On the other hand, by choosing smaller Q-values it becomes possible to determine the radius of the microgel particle and by fitting of the scattering length density difference between solvent and sample to gain qualitative insights about the water uptake into the polymer network.14,31 A number of studies discuss the internal structure of heterogeneously crosslinked microgels.14,31–36
The colloidal size of the microgel particles enables the detection of the translational diffusion by dynamic light scattering, but prevents direct access to the inner dynamics. To this end, neutron scattering techniques are well-suited.
Internal dynamics in a microgel particle on a time scale between 1 ps and 1 μs can be studied with neutron spin echo spectroscopy (NSE). This quasielastic neutron scattering technique offers a high energy resolution in the neV range. In principle, internal dynamics from cooperative network diffusion and Zimm-type dynamics, which occur on length scales below the network's mesh size, can be probed with NSE37–40 and was also theoretically elucidated.41 Beside quasi-elastic neutron scattering utilized by NSE also inelastic neutron scattering in combination with PFG-NMR was already used to study the inner dynamics of microgels.42
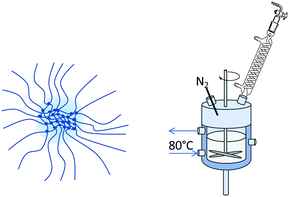
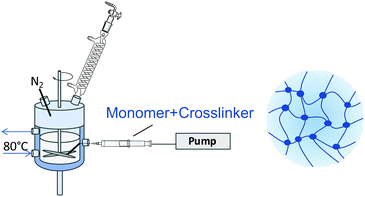
This paper focusses on the inner dynamics of PNIPAM microgel particles prepared via surfactant-free precipitation polymerization and a monomer feeding approach. These different synthesis routes yield the classical heterogeneously crosslinked microgels and microgels with a more homogeneous inner structure.20,43Fig. 1 shows a schematic representation of the anticipated internal structure of both kinds of microgels (Fig. 1–4). Neutron spin echo spectroscopy was used to reveal the local influence of the microgel network structure on its inner dynamics.
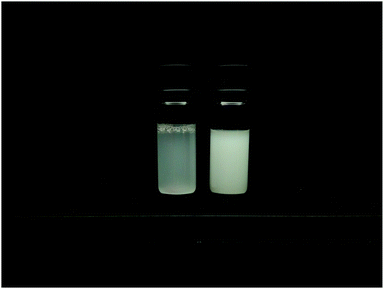 | ||
| Fig. 4 Comparison between the homogeneously (MG10F) (left) and heterogeneously (MG10P) (right) crosslinked microgel particles in suspensions with cMG = 0.5 wt%. The structural heterogeneity of MG10P is clearly visible as a difference between the turbidity of both samples due to stronger multiple light scattering in sample MG10P.20 | ||
For a more thorough investigation of their internal structure neutron scattering experiments were conducted. This results in a first direct comparison of structure and dynamics of both types of microgels. Additionally, a comparison of the dynamics in both types of microgel to the dynamics of a semidilute PNIPAM solution was made to determine the influence of the network structure on the segmental dynamics.
2 Experimental
2.1 Materials
N-Isopropylacrylamide (NIPAM; ≥99%), poly(N-isopropylacrylamide) (PNIPAM; average Mn = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, PDI = 1.5), N,N′-methylenebisacrylamide (BIS; 99%) and 2,2′-azobis(2-methylpropionamidine)dihydrochloride (AAPH; 97%) were purchased from Sigma-Aldrich and used as received. D2O (99.9%) was purchased from Deutero. Water was purified with a MilliQ system (Millipore) with a resistance of 18 MΩ.
000, PDI = 1.5), N,N′-methylenebisacrylamide (BIS; 99%) and 2,2′-azobis(2-methylpropionamidine)dihydrochloride (AAPH; 97%) were purchased from Sigma-Aldrich and used as received. D2O (99.9%) was purchased from Deutero. Water was purified with a MilliQ system (Millipore) with a resistance of 18 MΩ.
2.2 Microgel preparation
Heterogeneously crosslinked microgels were prepared via surfactant-free precipitation polymerization.44 1.527 g NIPAM and 0.232 g BIS (10 mol%) were dissolved in 120 mL water in a 250 mL double walled glass reactor with a PTFE baffle. Under continuous stirring with a PTFE stirrer at 300 rpm, the reaction solution was heated to 80 °C and purged with nitrogen for 60 min for oxygen removal. Afterwards, the stirrer was set to 1000 rpm and 68.7 mg AAPH, dissolved in 1 mL water, was added to initiate the polymerization. After 10 min the turbid microgel dispersion was released into an ice-cooled beaker to quench the reaction.Homogeneously crosslinked microgels were prepared via a continuous monomer feeding approach.19,20,43 100 mL water was filled into a double walled glass reactor and treated as described above. In a separate vessel above mentioned amounts NIPAM and BIS were dissolved in 20 mL water and purged with nitrogen for 60 min. Monomer and crosslinker were filled into a syringe which was mounted onto a pump. Prior to starting the monomer feed, the initiator solution was added into the reactor and the stirrer was set to 1000 rpm. The monomer solution was fed into the reactor at a speed of 2 mL min−1. After 11 min 20 s the reaction was quenched.
To remove unreacted monomer and low molecular weight oligomers the microgel dispersion was dialyzed for 21 days with two solvent (MilliQ water) exchanges per day. The pore size of the dialysis membrane was 14 kDa. Afterwards, the microgel dispersion was freeze-dried at −85 °C and 1 × 10−3 bar.
For readability the microgel with 10 mol% BIS prepared by surfactant free precipitation polymerization is referred to as MG10P and the microgel with 10 mol% BIS prepared by a continuous monomer feeding approach as MG10F in this article.
2.3 Viscosity measurements
Concentration-dependent viscosity measurements in D2O were carried out with a Lauda iVisc glass capillary viscometer in a temperature bath. More precisely micro-Ostwald-viscometers (type I and Ic) suited for different viscosity ranges were used to determine the efflux time t which is directly proportional to the kinematic viscosity ν according to ν = K·t, where K is a calibration factor specific to the viscometer. The kinematic viscosity was then transformed into the dynamic viscosity η according to η = ν·ρ. For temperature equilibration the samples sat in the temperature bath for 10 minutes prior to the measurement. Each viscosity was calculated from a total of five measurements. For the conversion of the kinematic into the dynamic viscosity, the densities of each polymer solution at a given temperature were determined with an Anton Paar DMA 4500 density meter.2.4 Atomic force microscopy
Atomic force microscopy (AFM) images under ambient conditions were recorded with an Asylum Research Cypher AFM (Oxford Instruments, Abington-on-Thames, UK). Imaging was done in the AC mode using an OMCL-AC240TS-R2 cantilever (Olympus) with a spring constant of k = 2 N m−1. Due to the low spring constant these cantilevers are well-suited for the scanning of soft samples. To obtain single particles on the surface, cleaned silicon wavers were dipped into a highly dilute microgel dispersion and were let dry before imaging. Cross sections were analyzed with the Igor Pro software.For the determination of the elastic properties AFM nano-indentation measurements were performed on a MFP-3D AFM (Oxford Instruments, Abington-on-Thames, UK) situated in an acoustic enclosure. At least ten individual force curves of different microgel particles were recorded for every sample at 20 °C and 50 °C. Every force curve was recorded by indenting a CSC-38-A cantilever (Mikromasch) with a spring constant of k = 0.2 N m−1 and a tip radius of Rtip = 8 nm into the center of an individual microgel particle. It is important to probe in the middle of the particles, since they show a lateral stiffness gradient.45 The approach part of the force curves (as shown in Fig. S5, ESI†) was fitted with the Hertz model for spherical indenters.46
 | (1) |
This model links the elastic modulus E of a sample with a Poisson ratio ν with the indentation depth δ and force F exerted by a spherical indenter of radius R. Examples for these fits are shown in the insets in Fig. S5 (ESI†). 20% of the maximum indentation was chosen as the upper fit limit to avoid a contribution of the underlying hard substrate to the deformation of the cantilever.47–49
2.5 Dynamic light scattering
Temperature-dependent dynamic light scattering (DLS) measurements were performed with an ALV/CGS-3 compact goniometer (ALV GmbH, Langen, Germany). Toluene was used as a temperature and refractive index matching bath. The temperature was varied between 18 and 50 °C using a Huber thermostat. The scattering angle was varied between 30 and 100° in steps of 5° at each temperature. H2O was used as a solvent.The setup is equipped with a He–Ne laser (λ = 632.8 nm) with a laser intensity of 35 mW. The acquired raw data was fitted with a second-order cumulant fit in a Python based program (Python Software Foundation, Version 2.7).
2.6 Small angle neutron scattering
Small angle neutron scattering (SANS) experiments were performed on the KWS-2 and KWS-3 instruments of the Jülich Center for Neutron Science (JCNS) at the Heinz Maier-Leibnitz Zentrum (MLZ) (Garching, Germany). KWS-3 measurements covered a Q-range between 3 × 10−4 Å−1 and 2.4 × 10−3 Å−1 and a sample-to-detector distance of 9.5 m was chosen. The instrument KWS-2 covers a Q-range between 1 × 10−4 Å−1 and 0.5 Å−1 at sample-to-detector distances of 2, 8 and 20 m. Thus it is suitable for studies of smaller length scales such as the study of the correlation lengths ξ in differently crosslinked microgel particles. For all SANS measurements Hellma quartz cells with a neutron path way of 2 mm were used. For linear PNIPAM chains a concentration of cPNIPAM = 0.05 g mL−1 and for the microgel particles of cMG = 0.001 g mL−1 were chosen. To ensure that the concentration of the linear PNIPAM solution was in the semidilute regime, concentration dependent viscosity measurements were carried out. For bulk contrast D2O was used as solvent.The data was fitted using SasView (Version 2.2.0) and Igor Pro (WaveMetrics, Version 6.37).
2.7 Neutron spin echo spectroscopy
Neutron spin echo spectroscopy (NSE) experiments were conducted at the SNS-NSE instrument (BL-15) at the spallation neutron source (SNS, Oak Ridge, TN, USA)50 and at the J-NSE instrument (MLZ, Garching, Germany).51 All measurements were carried-out in transmission geometry. At the SNS-NSE two neutron wavelengths (8 and 11 Å) were combined to cover a wide range of Fourier times τ (0.04 ns ≤ τ ≤ 95 ns) in a Q-range between 0.05 Å−1 and 0.20 Å−1. The neutron path way in the Hellma quartz cells was 3 mm. A concentration of cMG = 8 wt% microgel was chosen to suppress center of mass diffusion. For bulk contrast D2O was used as solvent.Linear PNIPAM chains were measured at 15 °C at a concentration of cPNIPAM = 0.05 g mL−1, which is in the semidilute concentration regime.
All microgel samples were measured at 20 °C to ensure the swollen state.
3 Theoretical background
3.1 SANS on linear polymers and microgels
SANS is an elastic scattering technique that can be used to study the structural features of polymers and microgel particles. The scattered intensity I(Q) is measured as a function of the scattering vector Q yielding characteristic scattering curves. The magnitude of the scattering vector Q is related to the scattering angle by52 | (2) |
The probed length scale d depends on the Q-range under investigation and is described by53
 | (3) |
The equation for the scattering intensity of spherically symmetric identical particles is given by
 | (4) |
Here the coherent scattering is the product of the scattering length density difference Δρ between the sample and the solvent, the number of scatterers N, the structure factor S(Q) and the form factor P(Q). As the value for S(Q) depends on interactions between particles, it can be neglected for highly dilute samples (S(Q) = 1). Iinc describes the incoherent scattering due to the background.
| I(Q) = Ipart + Ifluct + IPorod + Iinc. | (5) |
For Ipart a fuzzy sphere model was used for fitting as described by Stieger et al. This model takes into consideration the above mentioned uneven distribution of crosslinks within the microgel particle as follows
 | (6) |
 describes the specific surface area of the sample, Δρ the difference of the scattering length densities of the microgel and the solvent (ρD2O = 6.34 × 10−6 Å−2) and R the radius of the sphere. A thorough display of this model can be found in ref. 14.
describes the specific surface area of the sample, Δρ the difference of the scattering length densities of the microgel and the solvent (ρD2O = 6.34 × 10−6 Å−2) and R the radius of the sphere. A thorough display of this model can be found in ref. 14.
This model accounts for the particle surface's fuzziness by convoluting the radial box profile of the sphere model with a Gaussian. σs is the width of the smeared particle surface, often referred to as the fuzziness of the particle. The overall radius as determined by SANS is RSANS = R + 2σs. The radius of the core is described by the box profile Rbox = R − 2σs.14
At larger Q values the scattering curve can be described by a power law ∼Q−n. For collapsed microgel particles an exponent of n ≈ −4 is observed, which corresponds to a Porod profile. However, at lower temperatures the swollen gels can be fitted with a power law with an exponent n ≤ 4.
A characteristic length in microgel networks is the correlation length ξ, which describes the decay of liquid-like correlations in the polymer network. While ξ is smaller than the mean distance between the chemical crosslinks, it is proportional to it. It can be described by the Ornstein–Zernike equation
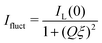 | (7) |
 | (8) |
3.2 Internal dynamics from NSE on microgels
For experiments on the dynamics in bulk systems NSE measurements are carried out in transmission geometry. During an NSE experiment intermediate scattering functions S(Q,τ)/S(Q,0) are measured. These consist of coherent Icoh(Q,τ) and incoherent Iinc(Q,τ) scattering fractions. The coherently scattered neutrons have their spin up. | (9) |
This technique enables the measurement of cooperative density fluctuations of the polymer network at low Q-values and of local polymer segment dynamics for higher Q-values. In the case of semidilute polymer solutions it is expected to observe only the Q3-dependent Zimm dynamics, since there is no crosslinking resulting in cooperative motions of a polymer network. Long range concentration fluctuations and cooperative diffusion in the semidilute regime appear in a shorter Q-range and are rather accessible by DLS56 and fluorescence correlation spectroscopy.57 For microgels on the other hand the observation of cooperative network dynamics of the network breathing, similar to hydrogels,58–60 is expected (Q2-dependent) on larger length scales with a crossover to local segment dynamics (Q3-dependent) on shorter length scales.
 | (10) |
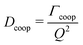 | (11) |
For purely cooperative network dynamics a display of Dcoop against Q should result in a constant value.
From the cooperative diffusion coefficient a dynamic correlation length ξcoop can be calculated from a Stokes–Einstein type relation61
 | (12) |
 | (13) |
 | (14) |
To obtain an apparent solvent viscosity eqn (15) can be used.
 | (15) |
For better comparability the apparent viscosity can be transformed into the specific viscosity. The specific viscosity is a dimensionless number that measures the contribution of a polymer to the solution viscosity and allows a direct comparison between different samples. It is defined as
 | (16) |
4 Results & discussion
4.1 Dynamic light scattering on microgel particles
Temperature-dependent dynamic light scattering measurements were carried out to investigate the thermoresponsive properties of the microgel particles. The hydrodynamic radii, Rh, as a function of the temperature, T, are displayed in Fig. 5.MG10P has a hydrodynamic radius of Rh,swollen = (310 ± 2) nm at 20 °C (PDI = 0.06) and Rh,collapsed = (186 ± 1) nm at 50 °C (PDI = 0.04) MG10F is in a similar size range with a hydrodynamic radius of Rh,swollen = (463 ± 7) nm (PDI = 0.26) and Rh,collapsed = (214 ± 2) nm (PDI = 0.23). This corresponds well to the common observation of low polydispersity in case of microgels synthesized via precipitation polymerization. In contrast to this, MG10F has a moderate size distribution in the swollen and collapsed state. The different sizes in the collapsed state might result from different amounts of incorporated crosslinker and monomer, which limits a quantitative comparison of the swelling ratios (αDLS = Rh,20°C/Rh,50°C, αDLS,MG10P = 1.67, αDLS,MG10F = 2.16). Hence, the difference in the swelling ratios cannot be exclusively attributed to the different inner structures of both microgels.
4.2 Atomic force microscopy
Fig. 6 shows the height profiles of (a) an individual MG10P microgel particle and (b) an individual MG10F microgel particle in the dry state with corresponding cross sections. From the cross sections the height-to-lateral width ratio was determined to be 0.25 for MG10P and 0.08 for MG10F. This illustrates the lower deformation of MG10P in the adsorbed state perpendicular to the substrate. This results from the presence of a densely crosslinked core region. For the microgels resulting from a continuous monomer feeding approach we observe higher deformation, which suggests a more homogeneous distribution of the crosslinks. Due to the high crosslinker content the typical fried egg type structure is not as visible.63 | ||
| Fig. 6 AFM height images of (a) a MG10P microgel particle and (b) a MG10F microgel particle in the dry state with corresponding cross section (height profile, red line). | ||
The lateral dimensions of the microgels in Fig. 6 are similar. Hence, the difference between the heights can most likely be attributed to the difference in the mechanical properties of the microgels and MG10P appears stiffer and more resistant against vertical deformation in the adsorbed state.
In Fig. S5 in the ESI† for both types of microgels a set of force–distance curves is shown for the swollen and the collapsed state. When the tip is in contact with the adsorbed microgel, the force rises at increasing indentation. When indenting into the MG10P and the MG10F sample to the same depth the required force is larger for MG10P than for MG10F. This indicates a softer material of MG10F which agrees to the smaller measured height of MG10F in the dry adsorbed state. In the collapsed state at 50 °C the difference between the force curves reduces and the indentation at a given force reduces compared to the swollen state. All force–distance curves show a steady progression which indicates the absence of discontinuities of the mechanical properties as recently reported for a comparison of the mechanics of adsorbed core–shell and hollow microgels.64 The averaged data was fitted with the Hertz model for spherical indenters as described in Section 2.4. Table 1 summarizes the resulting Young's moduli of both microgel systems in the swollen and collapsed state. The results show that the Young's modulus of MG10P is almost twice the Young's modulus of MG10F in the swollen state. Therefore, the network appears stiffer, which can be explained by the formation of a denser core during classical precipitation polymerization. In the collapsed state the Young's modulus for both microgel systems is the same within the error range. This can be explained with the repulsion of water molecules from the polymer network, which changes the internal structure of the microgel particles. The Young's moduli have the same order of magnitude as previously reported data from neutral PNIPAM microgels of somewhat lower crosslinker content45 and copolymerized ionic PNIPAM microgels.65 They also agree well to the observation of rather small Young's moduli previously reported for much softer PNIPAM microgels with 0.25% BIS corresponding the predictions from scaling theory of polymer gels in good solvents.66
| Microgel | E 20°C [kPa] | E 50°C [kPa] |
|---|---|---|
| MG10P | 312 ± 38 | 1004 ± 67 |
| MG10F | 166 ± 24 | 1070 ± 106 |
4.3 SANS of a semidilute solution of linear PNIPAM chains
SANS measurements of a semidilute solution of linear PNIPAM chains were carried out in a Q-range of 2 × 10−3–0.4 Å−1. The data were fitted according to eqn (8). As a comparison a simple Ornstein–Zernike fit was carried out as well as is displayed in Fig. 7. This however does not sufficiently describe the curve for Q-values below 2 × 10−2 Å−1 where composition fluctuations dominate the scattering signal. A comparison of the results for the different models can be found in the ESI.†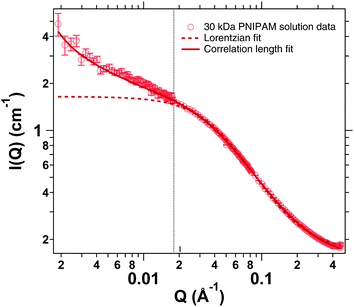 | ||
| Fig. 7 SANS measurements of a semidilute solution of linear PNIPAM chains for higher Q-values. Comparison between a simple Lorentzian (dashed) and a correlation length fit model (solid). | ||
A fit according to eqn (8) yields a correlation length of ξ = (2.40 ± 0.02) nm with the power law exponent n = 1.2 ± 0.01. Meier-Koll et al. investigated PNIPAM chains with a molecular weight of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 and a concentration of 13 wt% and found values for the correlation length below 2 nm at 15 °C. Therefore our value of 2.4 nm at a lower polymer concentration of 4.5 wt% (corresponding to 0.05 g mL−1) and a slightly higher molecular number of 30
000 g mol−1 and a concentration of 13 wt% and found values for the correlation length below 2 nm at 15 °C. Therefore our value of 2.4 nm at a lower polymer concentration of 4.5 wt% (corresponding to 0.05 g mL−1) and a slightly higher molecular number of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 appears reasonable.67
000 g mol−1 appears reasonable.67
4.4 SANS of highly crosslinked PNIPAM microgels
SANS curves of MG10P and MG10F measured at 20 °C at identical experimental conditions are displayed in Fig. 8. The inset shows the scattering curves at small Q-values (2.3 × 10−4 Å−1 ≤ Q ≤ 1.9 × 10−3 Å−1). Here larger length scales are probed and information on the overall radii of the microgel particles is obtained. A fit according to eqn (6) yields RMG10P = (200.0 ± 0.4) nm and RMG10F = (288.7 ± 1.7) nm. These values are in good agreement to the radii of gyration Rg obtained from a Guinier analysis which yields Rg = (176 ± 1) nm for MG10P and Rg = (307 ± 2) nm for MG10F. The comparison to the hydrodynamic radii in the swollen state gives Rg/Rh = 0.57 for MG10P and Rg/Rh = 0.66 for MG10F. Compared to the theoretical ratio of 0.78 for hard spheres, both values indicate the soft nature of the microgels (Table 2). | ||
| Fig. 8 SANS curves for MG10P and MG10F at higher Q-values measured on KWS-2. (I) Fuzzy sphere model,14 (II) Ornstein–Zernike fit. In the intermediate range between (I) and (II) the scattered intensity changes according to a power law. The inset shows the scattering curves at lower Q-values as measured on KWS-3 and fitted with a Fuzzy sphere model. | ||
| Microgel | R h,DLS [nm] | R g [nm] | R SANS [nm] | R box [nm] | σ s [nm] |
|---|---|---|---|---|---|
| 20 °C | |||||
| MG10P | 310 ± 2 | 176 ± 1 | 235 | 200 ± 1 | 17.4 ± 0.3 |
| MG10F | 463 ± 7 | 307 ± 2 | 298 | 289 ± 2 | 4.2 ± 0.5 |
| 50 °C | |||||
| MG10P | 186 ± 1 | 120 ± 1 | 138 | 124 ± 2 | 6.0 ± 0.1 |
| MG10F | 214 ± 2 | 150 ± 1 | 155 | 135 ± 2 | 0.1 ± 1 |
In Fig. 8 the scattering curve is subdivided into two distinct fitting areas denoted (I) and (II). In (I) a fit according to the fuzzy sphere model (eqn (6)) was carried out to determine the fuzziness σs of the spheres. The resulting fuzziness is higher for MG10P (σs,MG10P = 17.4 ± 0.3 nm) compared to MG10F (σs,MG10F = 4.2 ± 0.5 nm). Taking into consideration the overall radii as determined on KWS-3 this accounts for 8.7% for Het10MG and only 1.5% for MG10F. In fit range (II) the scattering curve was fitted with an Ornstein–Zernike equation. The range in between was not perfectly fitted by the superposition of the fuzzy sphere model and the Ornstein–Zernike equation and was therefore omitted. The scattered intensity in this region varies according to a power law I ∝ Q−m. Exponents of −2.5 and −2 for MG10P and MG10F are found respectively. The Ornstein-Zernike fit yields the average correlation length ξOZ-fit. For MG10P we find ξOZ-fit = (2.00 ± 0.04) nm and ξOZ-fit = (3.21 ± 0.05) nm for MG10F. The two fits show major differences in the value for IL(0). While MG10P has a value of IL(0) = (0.090 ± 0.002) cm−1, the value for MG10F is much higher with IL(0) = (0.33 ± 0.01) cm−1. Karg et al. found when analyzing the internal particle morphology of heterogeneously crosslinked microgel particles with different amounts of crosslinker (2, 5 and 10% BIS) that IL(0) decreases with increasing connectivity of the network.32 Therefore the findings show a higher contribution of the fluid like thermal fluctuations to the scattering signal of MG10F. An overview of the resulting fit parameters can be found in Table 3.
| Microgel | I L(0) [cm−1] | ξ OZ-fit [nm] |
|---|---|---|
| MG10P | 0.090 ± 0.002 | 2.00 ± 0.04 |
| MG10F | 0.33 ± 0.01 | 3.21 ± 0.05 |
The SANS data of the collapsed state at 50 °C are shown in the ESI† in Fig. S6. In the medium- and high-Q range the data can be fitted with a Porod decay I(Q) ∝ Q−4. Fits with the fuzzy sphere model in the low-Q range result in RSANS = (138 ± 4) nm for MG10P and RSANS = (155 ± 1) nm for MG10F. The corresponding values of Rg are Rg = (120 ± 2) nm and Rg = (150 ± 5) nm for MG10P and MG10F. For the collapsed state Rg/Rh = 0.65 for MG10P and Rg/Rh = 0.70 for MG10F were obtained. This suggests a decreasing polymer density towards the exterior. So far, the conclusion can be drawn, that in the feeding approach the structural heterogeneity is strongly reduced but remains most probably in the periphery of the particles.
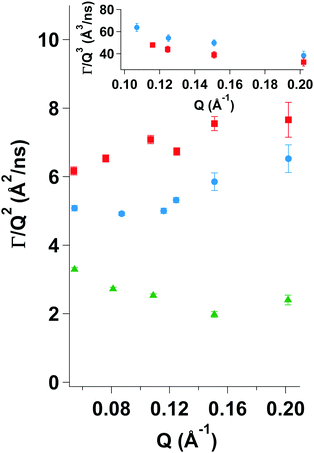
4.5 Internal dynamics from NSE
Fig. 9 clearly shows differences among the three investigated samples. For MG10P Dcoop display a constant value over the entire Q-range. However, for MG10F there is a transition from a constant value to an increase at around 0.11 Å−1. Therefore, it appears that the cooperative network dynamics dominate at lower Q-values, but that Zimm dynamics become observable at higher Q-values. We assume a superposition of both types of dynamics with a gradual change of their amplitudes at increasing Q-values. Dcoop of MG10F was therefore calculated from a linear fit with a slope of zero of the three lowest Q-values in Fig. 9. As might be expected the semidilute linear PNIPAM solution displays a deviation from a constant value over the entire Q-range, since single chain dynamics are observed due to a lack of a crosslinked polymer network. Therefore, NSE data of the semidilute PNIPAM solution was fitted according to eqn (13) with β = 0.85.
We observe that many of the normalized ISFs don't decay to zero. This means that there are elastic contributions to the scattering signal which e.g. hints at the existence of inhomogeneities within the polymer network with very slow to no dynamics. Therefore, the fitting eqn (10) and (13) were extended by an additional term (1 − A) accounting for the elastic contribution (eqn (17)). The values for (1 − A) for both microgels are shown in Tables 5 and 6. As Q increases and hence the observed length scale decreases, the elastic contribution decreases. For the sample MG10F, the elastic contribution vanishes completely at those Q-values corresponding to the Zimm regime. Scherzinger et al. found similar values for the elastic contribution in PDEAAM-core–PNIPAM-shell particles.38
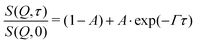 | (17) |
Table 4 lists the cooperative diffusion coefficients for the investigated samples. For the sample prepared by precipitation polymerization the value of Dcoop = (2.69 ± 0.02) × 10−11 m2 s−1 is in agreement with data published by Hellweg et al.,68 who also investigated dynamics of PNIPAM microgel particles with different amounts of crosslinker. For the microgel prepared by a continuous monomer feeding approach the cooperative diffusion coefficient is approximately twice the value of MG10P. This indicates a faster decay of the network fluctuations and thus a less stiff network. This is in agreement with the AFM measurements of Young's moduli on adsorbed microgel particles presented in Section 4.2.
| Sample | T [°C] | D coop [10−11 m2 s−1] | ξ coop [nm] |
|---|---|---|---|
| MG10P | 20 | 2.69 ± 0.02 | 6.4 |
| MG10F | 20 | 4.98 ± 0.04 | 3.4 |
| Q (Å−1) | (1 − A) | Δ(1 − A) |
|---|---|---|
| 0.05 | 0.45907 | 0.0519 |
| 0.08 | 0.37785 | 0.0301 |
| 0.11 | 0.32318 | 0.0169 |
| 0.15 | 0.27728 | 0.0187 |
| 0.20 | 0.20948 | 0.0439 |
| Q (Å−1) | (1 − A) | Δ(1 − A) |
|---|---|---|
| 0.05 | 0.410963 | 0.0212 |
| 0.08 | 0.253 | 0.0146 |
| 0.11 | 0.10076 | 0.0111 |
| 0.15 | −0.035338 | 0.0225 |
| 0.20 | −0.026817 | 0.0266 |
Using ηD2O = 1.251 cP at T = 20 °C eqn (12) yields values of ξcoop = 6.4 nm for MG10P and ξcoop = 3.4 nm for MG10F. This indicates that cooperative network fluctuations in sample MG10P have larger decay lengths. This suggests, that the polymer network of sample MG10F is softer in the size range explored by NSE due to the absence of a dense inner core region. A comparison with data published by Hellweg et al. shows that the dynamics of MG10F behave similar to a microgel prepared via precipitation polymerization with a low crosslinker content.68
Generally, the collective diffusion coefficient Dcoop = E/f relates an elastic modulus to the friction coefficient f which considers the resistance against the relative motion of polymer network and solvent. It measures the relaxation of concentration fluctuations in the network. The elastic modulus of a gel E = K + 4/3G is determined by the osmotic bulk modulus K describing network deformations including volume changes and the shear modulus G accounting for deformations without a volume change.
In previous mechanical measurements of the friction coefficient in macroscopic poly(acrylamide) hydrogels using confocal laser scanning microscopy a decrease of f with increasing crosslinker content and the accompanying increase of structural heterogeneities was observed.69–71 It was argued that the motion in regions of low crosslinker density contributes more to the friction coefficient than the motion in the region of higher polymer and crosslinking density.
In heterogeneously crosslinked microgel particles the size of the dense core region with its higher polymer and crosslinker density increases with increasing crosslinker content and hence, its contribution to the net friction coefficient of the particle increases.
| Sample | T [°C] | D Zimm [Å3 ns−1] | η app [cP] | η sp [cP] |
|---|---|---|---|---|
| MG10P | 20 | — | — | — |
| MG10F | 20 | 42.5 ± 1.5 | 3.7 | 1.96 |
| PNIPAM solution | 15 | 49.2 ± 1.8 | 3.2 | 1.22 |
In Table 7 the apparent and specific viscosities are listed as well. As mentioned above the specific viscosity allows a statement about the contribution of a polymer to the solution viscosity and a comparison between the different samples. We find values of ηsp = 1.96 and 1.22 for MG10F and the semidilute PNIPAM solution respectively. These values show that the polymer has a non-negligible contribution to the viscosity in both samples (Fig. 10).
 | ||
| Fig. 10 Normalized ISFs of MG10P (green symbols) and MG10F (blue symbols) at 20 °C and a semidilute PNIPAM solution at 15 °C (red symbols). MG10P was fitted with eqn (17) over the entire Q-range, MG10F was fitted with eqn (17) for Q = 0.05, 0.08 and 0.11 Å−1 and with eqn (13) for Q = 0.13, 0.15 and 0.20 Å−1. The semidilute PNIPAM solution was fitted with eqn (13). | ||
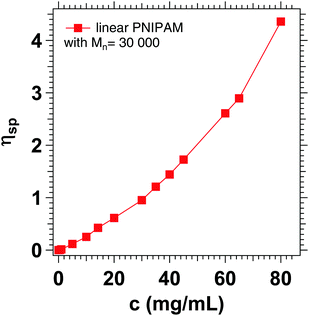
The increased apparent viscosity may be attributed to cooperative hydration, which has been described in the literature for PNIPAM chains and microgels based on PNIPAM.72–75 Due to the formation of hydrophobic isopropyl side groups, there is a positive correlation between neighboring bound water molecules, favoring the formation of further hydrogen bonds. It is assumed that the formation of these hydrogen bonds increases the local viscosity in such polymer systems.76 Concentration dependent viscosity measurements of linear PNIPAM in D2O (Fig. 11) show that the specific viscosity of 1.22 corresponds to a PNIPAM concentration of 35 mg mL−1, which is slightly below the actual concentration of 50 mg mL−1 chosen for the experiment.
Moreover, the analysis of the SANS data presented in Section 4.4 revealed a stronger contribution of fluid like fluctuations in case of MG10F. Possibly larger fluctuation amplitudes of the polymer segments also contribute to the increase of ηapp. A similar behavior was found for microgels during NSE studies of cononsolvency effects on the dynamics of microgels.38–40
Microgels are often discussed as potential carrier medium for nanoparticles, proteins or therapeutic drugs and diagnostic agents. Microgel size, cross-linking density, and network homogeneity are discussed as important influences on the loading capacity and release/uptake kinetics.77 The inner dynamics of the microgel network may also influence the diffusion of probes inside the gel due to hydrodynamic friction between the polymer chains, the solvent and the probes. Therefore, it should also be considered in uptake and release scenarios.
5 Conclusions
Two kinds of PNIPAM based microgel particles with a high crosslinker content were prepared via classical precipitation polymerization (MG10P) and a continuous monomer feeding approach (MG10F). Their structure was investigated with dynamic light scattering and small angle neutron scattering, which revealed clear differences between their inner structure. MG10P displayed a higher fuzziness (σs ≈ 17 nm), compared to MG10F (σs ≈ 4 nm). Furthermore, MG10F has a slightly higher correlation length ξOZ-fit than MG10P. AFM measurements of adsorbed microgels in the dry state of both systems show differences in the particle morphology and the measurement of the Young's moduli indicates a softer network in case of MG10F. Dynamics as investigated by neutron spin echo spectroscopy revealed that in MG10P the presence of a dense core region leads to a dominance of the cooperative dynamics. Zimm-type dynamics could only be observed for MG10F, while a simple Q2 dependence was observed for the dynamics in MG10P in the entire measured Q-range. This corresponds to the results of the AFM indentation measurements. As a comparison to the dynamic properties in both microgels, an aqueous semidilute PNIPAM solution was measured in the same Q-range, which as expected showed a deviation from Q2 dependence, as can be attributed to the observation of Zimm-type dynamics. Interestingly, the pure Zimm-regime was not reached for any sample in the observed Q-range. This leads to the conclusion that higher Q-values would be required to observe pure Zimm-type dynamics. A calculation of the specific viscosity resulted in values 1.2 < ηsp <2.0. Therefore, a contribution of the polymer to the apparent viscosity is observed which in the case of PNIPAM can be attributed to cooperative hydration of the polymer network, which leads to an increased viscosity. Interestingly, MG10P shows a clear elastic contribution over the entire Q-range, while MG10F only shows this contribution at very low Q-values. A comparison with NSE measurements of a lowly crosslinked PNIPAM based microgel revealed that in terms of the cooperative diffusion a high value is measured and a transition to the observation of Zimm-dynamics at a similar Q-value as for MG10F is observed. The presence of the dense inner region of a heterogeneously crosslinked microgel leads to the dominant contribution of cooperative density fluctuations to the observed dynamics.In summary, MG10F synthesized via a monomer feeding method has a more homogeneous inner network structure than MG10P prepared via the classical precipitation polymerization but heterogeneity is still present in the periphery of the particles. The structural differences also clearly affect the dynamic properties. The denser network of MG10P leads to a dominant cooperative dynamics while in case of MG10F also segmental dynamics contributes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The D2O used in the NSE experiments was supplied by the United States Department of Energy Office of Science by Isotope Program in the Office of Nuclear Physics. This work is based upon experiments performed at the KWS-2 and KWS-3 operated by JCNS at Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany. We also thank Malcolm Cochran for technical support during the beam time at SNS-NSE and Piotr A. Zolnierczuk for support with NSE data analysis. S. W. and O. H. gratefully acknowledge the financial support by Deutsche Forschungsgemeinschaft DFG (grant number WE5066/3-1 (S. Wellert) and HO 5488/2-1 (O. Holderer)).Notes and references
- D. Sivakumaran, D. Maitland and T. Hoare, Biomacromolecules, 2011, 12, 4112–4120 CrossRef CAS PubMed.
- T. K. Bronich, S. V. Vinogradov and A. V. Kabanov, Nano Lett., 2001, 1, 535–540 CrossRef CAS.
- D. M. Mock, G. Lankford and P. Horowitz, Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol., 1988, 956, 23–29 CrossRef CAS.
- L. Hu and M. J. Serpe, Chem. Commun., 2013, 49, 2649–2651 RSC.
- M. R. Islam and M. J. Serpe, Chem. Commun., 2013, 49, 2646–2648 RSC.
- Y. Liu, Y. Zhang and Y. Guan, Chem. Commun., 2009, 1867–1869 RSC.
- K. Iwai, Y. Matsumura, S. Uchiyama and A. P. de Silva, J. Mater. Chem., 2005, 15, 2796–2800 RSC.
- C. M. Nolan, C. D. Reyes, J. D. Debord, A. J. Garcia and L. A. Lyon, Biomacromolecules, 2005, 6, 2032–2039 CrossRef CAS PubMed.
- N. Singh, A. W. Bridges, A. J. Garca and L. A. Lyon, Biomacromolecules, 2007, 8, 3271–3275 CrossRef CAS PubMed.
- A. W. Bridges, N. Singh, K. L. Burns, J. E. Babensee, L. A. Lyon and A. J. Garca, Biomaterials, 2008, 29, 4605–4615 CrossRef CAS PubMed.
- J. D. Debord and L. A. Lyon, Langmuir, 2003, 19, 7662–7664 CrossRef CAS.
- Y. Zhang, Y. Guan and S. Zhou, Biomacromolecules, 2006, 7, 3196–3201 CrossRef CAS PubMed.
- X. Wu, R. Pelton, A. Hamielec, D. Woods and W. McPhee, Colloid Polym. Sci., 1994, 272, 467–477 CrossRef CAS.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197–6206 CrossRef CAS PubMed.
- S. Meyer and W. Richtering, Macromolecules, 2005, 38, 1517–1519 CrossRef CAS.
- H. J. M. Wolff, M. Kather, H. Breisig, W. Richtering, A. Rich and M. Wessling, ACS Appl. Mater. Interfaces, 2018, 10, 24799–24806 CrossRef CAS PubMed.
- S. Seiffert, Macromol. Rapid Commun., 2012, 33, 1135–1142 CrossRef CAS PubMed.
- A. Habicht, W. Schmolke, F. Lange, K. Saalwächter and S. Seiffert, Macromol. Chem. Phys., 2014, 215, 1116–1133 CrossRef CAS.
- T. Still, K. Chen, A. M. Alsayed, K. B. Aptowicz and A. Yodh, J. Colloid Interface Sci., 2013, 405, 96–102 CrossRef CAS PubMed.
- R. Acciaro, T. Gilanyi and I. Varga, Langmuir, 2011, 27, 7917–7925 CrossRef CAS PubMed.
- M. Füllbrandt, R. von Klitzing and A. Schönhals, Soft Matter, 2013, 9, 4464–4471 RSC.
- W. Su, K. Zhao, J. Wei and T. Ngai, Soft Matter, 2014, 10, 8711–8723 RSC.
- A. J. Moreno and F. Lo Verso, Soft Matter, 2018, 14, 7083–7096 RSC.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS PubMed.
- P. S. Mohanty, S. Nöjd, K. van Gruijthuijsen, J. J. Crassous, M. Obiols-Rabasa, R. Schweins, A. Stradner and P. Schurtenberger, Sci. Rep., 2017, 7, 1487 CrossRef PubMed.
- J. Mattsson, H. M. Wyss, A. Fernández-Nieves, K. Miyazaki, Z. Hu, D. R. Reichman and D. A. Weitz, Nature, 2009, 462, 83 CrossRef CAS PubMed.
- T. Hiroi, M. Ohl, T. Sakai and M. Shibayama, Macromolecules, 2014, 47, 763–770 CrossRef CAS.
- S. Bergmann, O. Wrede, T. Huser and T. Hellweg, Phys. Chem. Chem. Phys., 2018, 20, 5074–5083 RSC.
- A. P. Gelissen, A. Oppermann, T. Caumanns, P. Hebbeker, S. K. Turnhoff, R. Tiwari, S. Eisold, U. Simon, Y. Lu and J. Mayer, et al. , Nano Lett., 2016, 16, 7295–7301 CrossRef CAS PubMed.
- E. Siemes, O. Nevskyi, D. Sysoiev, S. K. Turnhoff, A. Oppermann, T. Huhn, W. Richtering and D. Wöll, Angew. Chem., Int. Ed., 2018, 57, 12280–12284 CrossRef CAS PubMed.
- S. Höfl, L. Zitzler, T. Hellweg, S. Herminghaus and F. Mugele, Polymer, 2007, 48, 245–254 CrossRef.
- M. Karg, S. Prévost, A. Brandt, D. Wallacher, R. von Klitzing and T. Hellweg, Intelligent Hydrogels, Springer, 2013, vol. 140, pp. 63–76 Search PubMed.
- K. Kratz, T. Hellweg and W. Eimer, Polymer, 2001, 42, 6631–6639 CrossRef CAS.
- K. Kratz, A. Lapp, W. Eimer and T. Hellweg, Colloids Surf., A, 2002, 197, 55–67 CrossRef CAS.
- K. Kratz, A. Lapp, W. Eimer and T. Hellweg, Colloids Surf., A, 2002, 197, 55–67 CrossRef CAS.
- Y. Hertle, M. Zeiser, P. Fouquet, M. Maccarini and T. Hellweg, Z. Phys. Chem., 2014, 228, 1053–1075 CAS.
- T. Hellweg, K. Kratz, S. Pouget and W. Eimer, Colloids Surf., A, 2002, 202, 223–232 CrossRef CAS.
- C. Scherzinger, O. Holderer, D. Richter and W. Richtering, Phys. Chem. Chem. Phys., 2012, 14, 2762–2768 RSC.
- S. Maccarrone, C. Scherzinger, O. Holderer, P. Lindner, M. Sharp, W. Richtering and D. Richter, Macromolecules, 2014, 47, 5982–5988 CrossRef CAS.
- S. Maccarrone, A. Ghavami, O. Holderer, C. Scherzinger, P. Lindner, W. Richtering, D. Richter and R. G. Winkler, Macromolecules, 2016, 49, 3608–3618 CrossRef CAS.
- A. Ghavami, H. Kobayashi and R. G. Winkler, J. Chem. Phys., 2016, 145, 244902 CrossRef PubMed.
- B. Sierra-Martin, J. R. Retama, M. Laurenti, A. Fernandez-Barbero and E. Lopez Cabarcos, Adv. Colloid Interface Sci., 2014, 205, 113–123 CrossRef CAS PubMed.
- M. U. Witt, N. Möller, S. Backes, S. Hinrichs, B. Fischer and R. V. Klitzing, J. Phys. Chem. B Search PubMed , submitted.
- R. H. Pelton and P. Chibante, Colloids Surf., 1986, 20, 247–256 CrossRef CAS.
- S. Schmidt, M. Zeiser, T. Hellweg, C. Duschl, A. Fery and H. Möhwald, Adv. Funct. Mater., 2010, 20, 3235–3243 CrossRef CAS.
- H. Hertz, Reine Angew. Math, 1881, 92, 156–171 Search PubMed.
- V. Tsukruk, A. Sidorenko, V. Gorbunov and S. Chizhik, Langmuir, 2001, 17, 6715–6719 CrossRef CAS.
- M. E. Harmon, D. Kuckling, P. Pareek and C. W. Frank, Langmuir, 2003, 19, 10947–10956 CrossRef CAS.
- J. Wiedemair, M. J. Serpe, J. Kim, J.-F. Masson, L. A. Lyon, B. Mizaikoff and C. Kranz, Langmuir, 2007, 23, 130–137 CrossRef CAS PubMed.
- M. Ohl, M. Monkenbusch, N. Arena, T. Kozielewski, G. Vehres, C. Tiemann, M. Butzek, H. Soltner, U. Giesen, R. Achten, B. Lindenau, A. Budwig, H. Kleines, M. Drochnerd, P. Kaemmerling, M. Wagner, R. Moller, E. B. Iverson, M. Sharp and D. Richter, Nucl. Instrum. Methods Phys. Res., Sect. A, 2012, 696, 85–99 CrossRef CAS.
- O. Holderer, M. Monkenbusch, R. Schätzler, H. Kleines, W. Westerhausen and D. Richter, Meas. Sci. Technol., 2008, 19, 034022 CrossRef.
- P. N. Pusey, in Neutrons, X-rays and Light: Scattering Methods Applied to Soft Condensed Matter, Introduction to Scattering Experiments, ed. P. Lindner and T. Zemb, Elsevier, 2002, pp. 3–21 Search PubMed.
- D. Sivia, Elementary Scattering Theory, Oxford University Press, 2011 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- M. J. Hore, B. Hammouda, Y. Li and H. Cheng, Macromolecules, 2013, 46, 7894–7901 CrossRef CAS.
- G. Yuan, X. Wang, C. C. Han and C. Wu, Macromolecules, 2006, 39, 3642–3647 CrossRef CAS.
- U. Zettl, S. T. Hoffmann, F. Koberlin, G. Krausch, J. Enderlein, L. Harnau and M. Ballauff, Macromolecules, 2009, 42, 9537–9547 CrossRef CAS.
- M. Shibayama, T. Norisuye and S. Nomura, Macromolecules, 1996, 29, 8746–8750 CrossRef CAS.
- M. Shibayama, Macromol. Chem. Phys., 1998, 199, 1–30 CrossRef CAS.
- M. Shibayama, Bull. Chem. Soc. Jpn., 2006, 79, 1799–1819 CrossRef CAS.
- P.-G. de Gennes, Scaling Concepts in Polymer Physics, Dynamics of Gels, Cornell University Press, 1979, pp. 215–217 Search PubMed.
- D. Richter, M. Monkenbusch, A. Arbe and J. Colmenero, Neutron Spin Echo in Polymer Systems, Springer, 2005 Search PubMed.
- A. Mourran, Y. Wu, R. A. Gumerov, A. A. Rudov, I. I. Potemkin, A. Rich and M. Möller, Langmuir, 2016, 32, 723–730 CrossRef CAS PubMed.
- M. F. Schulte, A. Scotti, A. P. Gelissen, W. Richtering and A. Mourran, Langmuir, 2018, 34, 4150–4158 CrossRef CAS PubMed.
- A. Burmistrova, M. Richter, M. Eisele, C. Üzüm and R. von Klitzing, Polymers, 2011, 3, 1575–1590 CrossRef CAS.
- M. Urich and A. R. Denton, Soft Matter, 2016, 12, 9086 RSC.
- A. Meier-Koll, V. Pipich, P. Busch, C. M. Papadakis and P. Müller-Buschbaum, Langmuir, 2012, 28, 8791–8798 CrossRef CAS PubMed.
- T. Hellweg, K. Kratz, S. Pouget and W. Eimer, Colloids Surf., A, 2002, 202, 223–232 CrossRef CAS.
- Y. Doi and M. Tokita, Langmuir, 2005, 21, 9420–9425 CrossRef CAS PubMed.
- M. Tokita and T. Tanaka, J. Chem. Phys., 1991, 95, 4613–4619 CrossRef CAS.
- M. Tokita, Polymers, 2014, 6, 651–666 CrossRef.
- F. Tanaka, T. Koga, H. Kojima and F. M. Winnik, Macromolecules, 2009, 42, 1321–1330 CrossRef CAS.
- H. Kojima, F. Tanaka, C. Scherzinger and W. Richtering, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 1100–1111 CrossRef CAS.
- F. M. Winnik, Macromolecules, 1990, 23, 233–242 CrossRef CAS.
- Y. Ono and T. Shikata, J. Am. Chem. Soc., 2006, 128, 10030–10031 CrossRef CAS PubMed.
- K. Kubota, S. Fujishige and I. Ando, Polym. J., 1990, 22, 15–20 CrossRef CAS.
- M. Malmsten, H. Bysell and P. Hansson, Curr. Opin. Colloid Interface Sci., 2010, 15, 435–444 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm02141d |
| This journal is © The Royal Society of Chemistry 2019 |