Charge transport and glassy dynamics in polymeric ionic liquids as reflected by their inter- and intramolecular interactions

Abstract

Polymeric ionic liquids (PILs) form a novel class of materials in which the extraordinary properties of ionic liquids (ILs) are combined with the mechanical stability of polymeric systems qualifying them for multifold applications. In the present study broadband dielectric spectroscopy (BDS), Fourier transform infrared spectroscopy (FTIR), AC-chip calorimetry (ACC) and differential scanning calorimetry (DSC) are combined in order to unravel the interplay between charge transport and glassy dynamics. Three low molecular weight ILs and their polymeric correspondents are studied with systematic variations of anions and cations. For all examined samples charge transport takes place by glassy dynamics assisted hopping conduction. In contrast to low molecular weight ILs the thermal activation of DC conductivity for the polymeric systems changes from a Vogel–Fulcher–Tammann- to an Arrhenius-dependence at a (sample specific) temperature T_σ0. This temperature has been widely discussed to coincide with the glass transition temperature T_g, a refined analysis, instead, reveals T_σ0 of all PILs under study at up to 80 K higher values. In effect, below the T_σ0 charge transport in PILs becomes more efficient – albeit on a much lower level compared to the low molecular weight pendants – indicating conduction paths along the polymer chain. This is corroborated by analysing the temperature dependence of specific IR-active vibrations showing at T_σ0 distinct changes in the spectral position and the oscillator strength, whereas other molecular units are not affected. This leads to the identification of charge transport responsive (CTR) as well as charge transport irresponsive (CTI) moieties and paves the way to a refined molecular understanding of electrical conduction in PILs.

---

1 Introduction

Polymeric ionic liquids (PILs) have been developed with the primary intention to establish a novel class of potential electrolyte materials for multifold applications, such as power-storage devices or CO₂ absorption appliances.^1–17 With the evolution of these modern materials Hiroyuki Ohno and coworkers pioneered the strategy of incorporating outstanding properties of ILs (e.g. wide electrochemical and thermal window, negligible vapour pressure and non-flammability; but foremost high ionic conductivity) into mechanically stable polymeric systems by polymerization.^18–23 Although those systems have been of deep scientific interest over the last 20 years and the individual components are already used as additives in fuel cells and as battery electrolytes, a satisfying pure PIL candidate for these applications has not been synthesized yet. The most hindering obstacle one faces in that framework are the competing properties of high electrical conductivity and mechanical stability. While the latter is attained by the polymer network, the former is determined by the charge of the individual ionic moieties, their corresponding number density and the mobility of the charge carriers (σ = qnμ). Enlarging the polymeric structure results in a higher stability but, on the other hand, reduces consequently the charge carrier number density. This interrelation is reflected by a characteristic decline in the DC-conductivity σ₀, about 3 to 6 orders of magnitude, for most PILs compared with their low molecular weight counterparts.^19,24–26

In order to compensate or even overcome these competing properties Ohno and coworkers suggested a flexible linker between the polymeric backbone and the ionic moiety which is supposed to maintain the high mobility of the latter.^20,27,28 Colby and coworkers studied a variety of polymerized imidazolium-based ILs with different pendant groups and recommended the attachment of shorter alkyl chains in order to avoid shielding of the charge from the surrounding. As an alternative attached short poly(ethylene glycol) (PEG) chains are expected to ease the accessibility of the counterion to the effective charge which is extended from the imidazolium-ring over the PEG chain.^29,30 Even though the influence of various ion compositions, molecular volumes of certain repeating units and molecular weights have been intensively studied by many groups, one observes – except for one sample material ref. 31 – the general characteristic of conductivity decrease with an increasing degree of polymerization or molecular weight, which has already been addressed by Ohno in 1998.^18,19,23

In contrast to low molecular weight ILs the thermal activation of DC conductivity for all polymeric systems studied so far changes from a Vogel–Fulcher–Tammann- to an Arrhenius-dependence at a (sample specific) temperature T_σ0.^{24–26,32–37} Sangoro and coworkers demonstrated, by combining broadband dielectric spectroscopy (BDS) with pulse-field gradient nuclear magnetic resonance (PFG-NMR), that this transition is caused by tremendous demobilization of the polymeric backbone including the attached ionic species, whereas the counterions are still diffusing through the polymer matrix and thence contributing to σ₀.²⁴ The fact that T_σ0 was found to be close to the calorimetric glass transition temperature T_g of the PILs under study leads to the conjecture of decoupling between charge transport and glassy dynamics.^{24–26,32,33,36,38,39} In the present study such PILs are introduced whose T_σ0 differ as far as 80 K from the calorimetric glass transition temperature. Furthermore, the fact that the mean structural relaxation time τ_α, the charge carrier hopping rate ω_c, and the DC-conductivity σ₀ are proportional to each other (τ_α ∼ ω_c ∼ σ₀) widely below and above the transition temperature T_σ0 demonstrates that the mechanism of charge transport (glassy dynamics assisted hopping conduction) does not change at T_σ0; instead, it becomes more efficient, albeit on a lower level of absolute DC-conductivity.

In order to bridge the gap between the macroscopic characteristics and the underlying microscopic mechanisms broadband dielectric spectroscopy (BDS), differential scanning and AC-chip calorimetry (DSC and ACC) as well as Fourier transform infrared spectroscopy (FTIR) are employed to three polymeric ionic liquids with systematically varied anions and cations as well as to their low molecular weight correspondents. The detailed findings lead to the identification of charge transport responsive (CTR) as well as charge transport irresponsive (CTI) moieties and thence to a refined understanding of electrical conduction in this class of materials.

2 Experimental details

2.1 Synthesis

Materials. Silver nitrate (VWR), lithium bis(trifluoromethylsulfonyl)imide (IoLiTec) and 4,4′-azobisisobutyronitrile (Sigma-Aldrich) were used without further purification. 1-Chlorobutane, 1-iodobutane, 1-methylimidazole, 1-vinylimidazole and 2-(dimethylamino)ethyl methacrylate were purchased from Sigma-Aldrich and purified via distillation: 1-chlorobutane (boiling point (bp) 60 °C, 800 mbar), 1-iodobutane (bp 40 °C, 300 mbar), 1-methylimidazole (bp 98 °C, 30 mbar), 1-vinylimidazole (bp 80 °C, 10 mbar) and 2-(dimethylamino)ethyl methacrylate (bp 70 °C, 50 mbar). The inhibitor (monomethyl ether hydroquinone) was removed from the monomers by adding the monomers dropwise to a column filled with basic aluminium oxide. The organic solvents ethyl acetate, acetonitrile, tert-butyl methyl ether and methanol (purchased from Carl Roth) were also distilled prior to use: ethyl acetate (bp 77 °C), acetonitrile (bp 82 °C), tert-butyl methyl ether (bp 55 °C) and methanol (bp 65 °C).

BMIM-StySu (see Scheme 1): was synthesized according to ref. 40.

Scheme 1 Chemical structures of the examined low molecular weight ionic liquids as well as their polymeric counterparts (PILs).

BVIM-NTf₂ (see Scheme 1): was synthesized according to ref. 41.

BDMAEMA-NTf₂ (see Scheme 1): synthesis of the ionic liquid methacrylate was realized in a two step procedure beginning with alkylation of 2-(dimethylamino)ethyl methacrylate with 1-iodobutane followed by anion exchange with lithium bis(trifluoromethylsulfonyl)imide as described in ref. 42. 2-(Dimethylamino)ethyl methacrylate (110.56 g, 0.703 mol) was dissolved in 100 ml tert-butyl methyl ether and 1-iodobutane (129.41 g, 0.703 mol) was added dropwise to the solution. The reaction mixture was stirred at room temperature for 7 d and N-butyl-N,N-dimethyl-ammonium iodide precipitated as a white solid, which was then isolated and purified as follows: it was dissolved in 50 wt% distilled acetonitrile and precipitated in 80 wt% distilled ethyl acetate.

Lithium bis(trifluoromethylsulfonyl)imide (35.34 g, 0.117 mol) was dissolved in 50 ml water and added dropwise to a solution of N-butyl-N,N-dimethyl-ammonium iodide (40.0 g, 0.123 mol) in 150 ml water. The reaction mixture was stirred at room temperature for 12 h. The water phase was decanted and N-butyl-N,N-dimethyl-ammonium bis(trifluoromethylsulfonyl)imide was washed with fresh water (5 × 50 ml) until no AgI was detected.

P[BMIM-StySu] (see Scheme 1): 1-butyl-3-methylimidazolium styrenesulfonate was polymerized in bulk with 2,2′-azobis(2-methylpropionitrile) (AIBN) as the thermal initiator: 6.4 g (20 mmol) of the monomer was melted at 50 °C prior to addition of AIBN (32.8 mg, 0.2 mmol). The polymerization was carried out at 70 °C for 24 h under an argon atmosphere and stirred as long as possible. To remove the residual monomer the polymer was washed with methanol (3 × 50 ml) and dried at 50 °C for 48 h resulting in 6.4 g of the solid polymer.

P[BVIM-NTf₂] (see Scheme 1): 1-butyl-3-vinylimidazolium bis(trifluoromethylsulfonyl)imide was polymerized in bulk with AIBN as the thermal initiator: 8.63 g of the monomer (20 mmol) was purged with argon for 20 min before addition of AIBN (32.8 mg, 0.2 mmol). The polymerization was carried out at 70 °C for 24 h under an argon atmosphere and stirred as long as possible. The polymer was then dissolved in 20 ml 1-propanol and precipitated in 200 ml acetone in order to remove the residual monomer. Afterwords it was dried at 50 °C for 48 h resulting in 7 g of the solid colourless polymer.

P[BDMAEMA-NTf₂] (see Scheme 1): N-butyl-N,N-dimethyl-ammonium bis(trifluoromethylsulfonyl)imide was polymerized in bulk with AIBN as the thermal initiator: 9.89 g of the monomer (20 mmol) was purged with argon for 20 min before addition of AIBN (32.8 mg, 0.2 mmol). The polymerization was carried out at 70 °C for 24 h under an argon atmosphere and stirred as long as possible. The polymer was then washed with methanol (3 × 50 ml) in order to remove the residual monomer. Afterwards it was dried at 50 °C for 48 h resulting in 9 g of the solid colourless polymer.

2.2 Measurement techniques

Broadband dielectric spectroscopy (BDS) measurements were carried out using a high-resolution α-analyzer from NOVOCONTROL Technologies GmbH & Co. KG in a temperature range of 100–400 K and frequency window of 10⁻²–10⁷ Hz combined with a Quatro temperature controller ensuring absolute thermal stability of ≤1 K. The sample cells for these measurements consist of two polished (mean square roughness ≤1 μm) plane brass electrodes (lower: spectrometer ground plate (d = 40 mm), upper: d = 10 mm) which are separated by 2–3 glass fibre spacers (d = 50 μm) ordered in parallel. To evaporate the remaining solvents (that might act as plasticizer) and water that contributes significantly to the conductivity and several relaxation processes due to its dissociation into H⁺ and OH⁻, the whole arrangement of the upper electrode, spacers and sample material was annealed at 130 °C inside an oil-free vacuum at 10⁻⁶ mbar for 24 h. Subsequently, while still in vacuo, the upper electrode was placed on top of the liquid like sample droplet. The whole annealing and measurement process was carried out in vacuo or in an inert nitrogen or argon atmosphere. Considering the reproducibility each measurement was checked with special care between the cooling and heating run and further repeated after 6 months. All presented data were – within the measurement accuracy – identical. The characteristic temperature T_σ0 at which the DC-conductivity undergoes a transition from a VFT-law to an Arrhenius-dependence was deduced as intersection of the two slopes of the 3-point-derivative of σ₀(1000/T) (see Fig. S19, ESI†). This analysis enabled a more precise determination of T_σ0 compared to the intersection of the VFT- and Arrhenius-fits.

Infrared spectroscopy was performed on a Bio-Rad FTS 6000 FTIR spectrometer equipped with an UMA-500 IR microscope in a spectral range of 700–4000 cm⁻¹. The transmitted radiation of the spin coated sample film (thickness approx. 10 μm) was measured with a resolution of 2 cm⁻¹ (at 4000 cm⁻¹) using a liquid nitrogen cooled mercury cadmium telluride (MCT) detector from Kolmar Technologies Inc, USA. All samples under study were spin-coated and treated before measurement as described in the BDS part. During measurements the samples were kept on a sealed THMS350V stage (Linkam Scientific Instruments, UK) using dry liquid nitrogen as a temperature control agent covering a range between 150 and 400 K. The analysed vibrational bands (see Table 2) were assigned on the basis of results from J. Kiefer and coworkers,⁴³ K. Noack and coworkers,⁴⁴ J. C. Yang and coworkers⁴⁵ as well as quantum chemistry calculations using the ORCA program system, version 3.0^46,47 implementing the B3LYP functional (as implemented in the Gaussian code B3LYP/G) and 6-31G(2d,2p) basis (except for StySu, where the B3LYP functional and 6-31G basis were used).^48–54

AC-chip calorimetry (ACC), employing XEN-39390 chips from Xensor Integration, was conducted using a set-up from the group of Prof. Schick at the University of Rostock as described in ref. 55. The measurements were carried out in a temperature range between 173 and 323 K at the rate of 1 K min⁻¹ in a heating and cooling cycle with operating frequencies in the range of 10⁻¹–10⁴ Hz. The glass transition temperature at a certain frequency was determined as the midpoint of the step of the magnitude of the measured voltage that is proportional to the real part of the complex heat capacity.

Differential scanning calorimetry was conducted using a DSC Q200 from TA Instruments calibrated to the melting temperature of indium (437.65 K). The measurements of the samples under study were carried out for two temperature cycles in a range of 203–373 K and at the temperature rates of 5 K min⁻¹ (low molecular weight ILs) and 10 K min⁻¹ (PILs). The glass transition temperatures were determined as the midpoint of a step in the heat flow of the second heating cycle for all samples under study except BMIM-StySu due to the strong tendency of self-polymerization at elevated temperatures. The latter's T_g was deduced during the first heating cycle.

¹H NMR and ¹³C NMR spectra were were recorded on a Bruker Fourier 300 spectrometer. The deuterated solvents (D₂O, MeOD, CD₃CN and acetone-d₆) comprising tetramethylsilane (TMS) as an internal standard were purchased from ARMAR Chemicals.

Karl Fischer titration was carried out using a coulometer from Metrohm equipped with an oven (Thermoprep) and a dual platinum sensor to determine the water content of the P(ILs) after synthesis. HYDRANAL Coulomat AG water standards from Riedel-de Haën were used for calibration.

3 Results and discussion

3.1 Broadband dielectric spectroscopy

The intermolecular properties of all six (polymeric) ionic liquids (see Scheme 1) under study are investigated by means of broadband dielectric spectroscopy (BDS). A BDS spectrum is characterized by a superposition of the (i) electrode polarization, (ii) charge transport and (iii) molecular dynamics, and to the best analysable in terms of the complex dielectric function (ε* = ε′ − iε′′) as well as the complex conductivity (σ* = σ′ + iσ′′) (Fig. 1). Electrode polarization (i), reflecting the accumulation of mobile (ionic or polaronic) charges at the sample-electrode interface, is observable as a steep increase in the low frequency side in ε′ vs. f or σ′′ vs. f at elevated temperatures. Its characteristic deviates from the single step signature in ε′ vs. f as described by Serghei et al.⁵⁶ for low molecular weight ILs which reflects the complex nature of PILs. This dependency is further documented by a reduction of the step in ε′ vs. f by almost one order of magnitude for sample P[BDMAEMA-NTf₂] at 300 K (Fig. 1). In fact the authors expect that the increased inertia and sterical constraints of the polymerized ions prevent the formation of a classical double-layer structure. Charge transport (ii) is characterized by the DC-conductivity σ₀ that shows up in ε′′ vs. f representation as a steep increase with a slope of −1 or as a (distinct) plateau in σ′ vs. f. The critical frequency ω_c in the latter representation marks the onset of a power law dependence σ′ ∼ ω^χ and is – according to the Dyre-model – the attempt frequency to overcome the largest barrier determining the DC-conductivity σ₀.^57,58 Both quantities (σ₀ and ω_c) are fitted with the corresponding Dyre-formula. Molecular dynamics (iii) is reflected by dielectrically active relaxation processes with mean structural relaxation rates ω_max = τ_max⁻¹ that are to the best obtained in ε′′ vs. f as peaks reflecting the dissipation of energy and are analysed using the empirical Havriliak–Negami formula,⁵⁹ which extends the Debye-formula⁶⁰ by two shape parameters, β and γ.

Fig. 1 Real and imaginary parts of the complex dielectric function (ε* = ε′ − iε′′) as well as the complex conductivity (σ* = σ′ + iσ′′) versus frequency of the sample P[BDMAEMA-NTf₂]. Dielectrically active relaxation processes reflecting molecular dynamics are best observable in ε′′ vs. f and analysed using Havriliak–Negami-function with mean relaxation times τ_α (solid line), τ_β1 (dashed line) and τ_β2 (dotted line). Charge transport is characterized by the DC-conductivity σ₀ and the critical frequency ω_c = 2πf_c. The former appears as a (distinct) plateau in σ′ vs. f, whereas the latter is the attempt frequency to overcome the largest barrier determining DC-conductivity and marks the onset of a power law dependence σ′ ∼ ω^χ, respectively. σ₀ and ω_c are analysed by the Dyre-function (dashed-dotted lines) in σ′ vs. f. The logarithm is to base 10; the error-bars are smaller than the symbols-size, unless explicitly specified otherwise.

For all samples under study three different molecular relaxation processes are obtained, whereas one of them is thermally in accordance with the glassy systems well established Vogel–Fulcher–Tammann (VFT)-equation

while the others tentatively follow the Arrhenius law (Fig. 2). Regarding eqn 1, τ_∞ denotes the high temperature limit of the relaxation time, D is a shape constant interpreted as fragility index and T₀ is the Vogel-temperature.

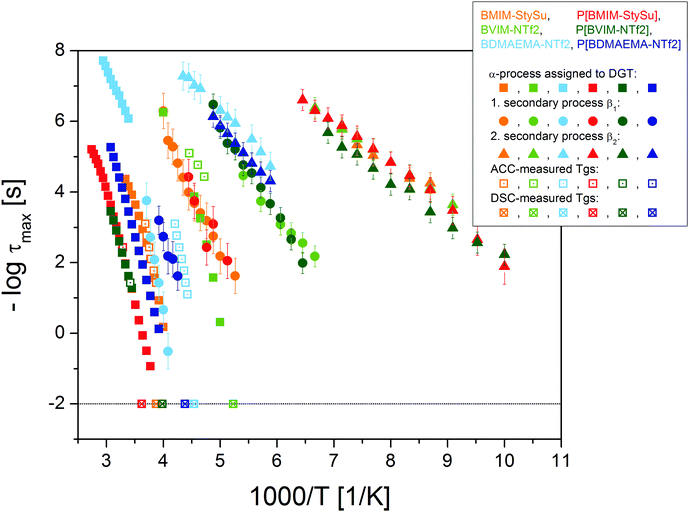Fig. 2 Activation plot of all six (low molecular weight and polymeric) ionic liquids under study. The different colours represent the particular sample molecule (see Scheme 1). The dielectrically observed relaxation processes are depicted with closed symbols, (squares: α-process, circles and triangles: secondary processes). The DSC-measured glass transition temperatures at the conventional relaxation time of 100 s are included as crossed squares and the AC-chip calorimetry measured evolution of the dynamic glass transition as dotted squares. The polymeric ionic liquids are depicted in strong colours (red, dark green and dark blue) and the low molecular weight counterparts in brighter ones (orange, light green and light blue). The logarithm is to base 10 and the error-bars are smaller than the symbol-size, unless explicitly specified otherwise.

The mean structural relaxation time τ_α of the dynamic glass transition as measured using BDS and AC calorimetry scales well with the calorimetric glass transition temperature T_g determined using conventional DSC. The sample P[BVIM-NTf₂] differs in T_g by almost 80 K from the reported value for P[PVIM-NTf₂].²⁴ This is attributed to (i) the different chemical structure of P[PVIM-NTf₂] having an additional CH₂-unit in the flexible linker, (ii) the different residual water contents (P[BVIM-NTf₂]: 32 ppm, PVIM-NTf₂ from which P[BVIM-NTf₂] is polymerised: 830 ppm) and (iii) possibly different molecular weights.

Furthermore, by exchanging the anionic or cationic moiety one is able to assign the secondary processes to librational fluctuations of the individual ions. The fastest τ_β2 is similar for BMIM-StySu and BVIM-NTf₂, as well as their polymeric counterparts. This process is ascribed to a libration of the imidazolium ion with a mean activation energy E_A = 0.24 eV K⁻¹. The τ_β1 process of BVIM-NTf₂ is similar to the τ_β2 process of BDMAEMA-NTf₂, likewise for the respective PILs. Thus, this process is assigned to the libration of the NTf₂ ion (E_A = 0.48 eV K⁻¹). Third and fourth, the τ_β1 process of BMIM-StySu and P[BMIM-StySu] and the τ_β1 process of BDMAEMA-NTf₂ and P[BDMAEMA-NTf₂] represent librational fluctuations of the styrene-sulfonate ion (E_A = 0.69 eV K⁻¹) and the BDMAEMA-ion (E_A = 0.73 eV K⁻¹), respectively. In addition to the structural relaxation processes charge transport obeys the Barton–Namikawa–Nakajima (BNN) relation between the DC-conductivity σ₀ and the charge carrier hopping rate ω_c. This correlation is well fulfilled for all ILs as well as PILs under study by over 9 orders of magnitude (Fig. 3), as widely observed for many low molecular weight ionic liquids.^33,61–72 In addition to the BNN-relation one observes a strong correlation (over 7 orders of magnitude) between τ_α and ω_c (lower right inset in Fig. 3). The interrelation between the structural relaxation time τ_α which is assigned to fluctuations determining the glassy nature of the systems and the DC-conductivity σ₀ by means of the charge carrier hopping rate ω_c reveals the primary charge transport mechanism as a dynamic glass transition assisted hopping conduction.^31,33,71,73 Due to the fact that ions are the dominating type of charge carriers it is reversely conclusive to assign the α-process molecularly to fluctuations of transient anion–cation-pairs.

Fig. 3 Barton–Namikawa–Nakajima (BNN)-relation between the DC-conductivity σ₀ and the charge carrier hopping rate ω_c for all samples under study. The T_σ0 corresponding values are indicated as framed diamonds. The upper left inset presents the temperature dependence of σ₀ and the lower right one the correlation between ω_c and the mean structural relaxation time τ_α which is assigned to the dynamic glass transition. The colour code is identical to Fig. 2, the dotted lines indicate the slope 1; the logarithms are to base 10. The error-bars are smaller than the symbol-size, unless explicitly specified otherwise.

Concerning the BNN-relation which is directly derived from the Einstein–Smoluchowski equation describing the diffusion dependence of Brownian motion it has been previously demonstrated that dielectric data agree well with diffusion coefficients of neat ILs deduced by PFG-NMR under the assumption to treat the molecules as spheres.^65,68,74 Thus, it is remarkable in the authors view that the interrelation τ_α ∼ ω_c ∼ σ₀ holds true for PILs, even though one of the ionic species is covalently bound to the polymeric backbone. Nevertheless, one has to raise the question whether (and how) the charge transport is affected by polymerization. In contrast to many low molecular weight ILs the data in our studies (see Fig. 3) do not collapse into each other. The physical understanding of this finding is ambitious; it might be interpreted as a measure of efficiency regarding the mechanism of glassy dynamics assisted hopping in the different PILs under study. However, it cannot be excluded that in the polymeric systems conduction paths are formed along the contour of the chain influencing the efficiency of charge transport as well. To unravel this, continuative studies with special focus on systematic and broad variations (especially the molecular weight) of the PILs are essential in the authors view. On the one hand, the thermal activation of all PILs is generally lower compared to their monomeric counterparts at absolute temperatures which is macroscopically reflected by the higher values of T_g. This results in a decrease of σ₀ at lower temperatures, typically in the order of 3 to 6 decades.

On the other hand, by polymerizing the monomers one observes a change in the thermal activation of σ₀ from a VFT-like dependence to an Arrhenius-law at certain sample-dependent temperatures T_σ0 (upper left inset Fig. 3). In contrast to (several) previous studies where this transition has been discussed to be exactly at T_g,^{24–26,33,34,38} this is the first time one obtained T_σ0 consequently above T_g with considerable deviations in the range of 40–80 K (see Table 1). Disregarding this novel temperature peculiarity the idiosyncrasy of a change in the thermal activation of σ₀, which seems to be characteristic for many PILs,^24,33 has been studied by J. R. Sangoro and coworkers in a comparative framework of BDS and NMR. They demonstrated that the dynamics of the polymeric moieties decreases significantly in the range of this critical transition while the low molecular weight counterions are still highly activated and contribute almost unhindered to the DC-conductivity. Concerning this aspect a decoupling of charge transport from glassy dynamics is widely discussed without delivering an appropriate molecular picture that describes the detailed changes that polymeric ionic liquids undergo in this range.^{24–26,33,35,36,38,39} Moreover, this interpretation has to be carefully scrutinized, especially with regard to (a) the aforementioned relaxation τ_α that is assigned to structural fluctuations of transient ion-pairs which determines both the glassy nature of the overall system as well as charge transport and (b) the novel result that T_g and T_σ0 can differ tremendously with respect to each other. However, this deviation opens the possibility to answer the question whether the polymeric or the IL-like moieties dominate the two-component systems PILs are based of.

Table 1 Comparison of the glass transition temperatures T_g as measured by DSC and extrapolated by BDS as well as the transition temperatures T_σ0 of all PILs under study; where T_σ0 marks the intersection between an VFT-fit above T_σ0 and an Arrhenius-fit below, T_σ0 is derived from the 3-point first order derivative of log σ₀(1000/T) (see S19, ESI)

Chemical structure	T g-DSC (K)	T g-BDS (K)	T σ 0 (K)	T σ 0 (K)
P[BMIM-StySu]	276(±1)	274(±5)	315(±10)	317(±15)
P[BVIM-NTf2]	251(±1)	255(±5)	308(±10)	323(±15)
P[BDMAEMA-NTf2]	228(±1)	235(±5)	311(±10)	317(±15)

---

3.2 FTIR spectroscopy

In order to bridge the gap between intermolecular properties as macroscopically deduced by BDS and the intramolecular dynamics temperature-dependent Fourier transform infrared (FTIR)-spectroscopy has been employed (Fig. 4). Especially this technique enables examination of molecular vibrations in a moiety-specific fashion and hence assign these vibrations and their temperature-dependent alternations to particular molecular groups. In the course of this we specifically selected molecular vibrations allocated to each polar moiety as well as neutral subunits including the polymeric backbone of the PILs under study. An overview of the analysed vibrations in terms of the spectral position as well as the relative absorbance is presented in Table 2. The first reflects the transition energy between the ground and the first excited state, and the latter reflects the number density and oscillator strength of the corresponding vibration. The most relevant ones in view of a molecular picture of the charge transport mechanism are:

Fig. 4 FTIR absorbance spectra of all samples under study at 6 different temperatures as indicated. The arrangement is analogous to the arrangement of samples in Scheme 1. Each column represents the comparison between a low molecular weight IL (top) and its polymeric counterpart (bottom), while the influence of an ion exchange is present in each row. The vibrational band assignment is indicated (Table 2).

Table 2 Vibrational assignment of all 6 samples under study. The upper values in each cell denote the spectral positions in [cm⁻¹] at 400 K the lower ones correspond to absorbances. The following abbreviations and superscript numbers are used to specify the individual vibrational modes: str – stretching, def – deformation, twist – twisting, bend – bending, rock – rocking, wagg – wagging, sciss – scissoring, ip – in-plane, oop – out of plane, sym – symmetric, asym – asymmetric, 1 – BMIM, 2 – BVIM, 3 – BDMAEMA, 4 – StySu and 5 – NTf₂

Vibrational assignment	BMIM-StySu	P[BMIM-StySu]	BVIM-NTf2	P[BVIM-NTf2]	BDMAEMA-NTf2	P[BDMAEMA-NTf2]	Ref. 43	Ref. 44	Ref. 45	Ref. 75	ORCA
C–C str, CH2 wagg	947.0	946.5	951.8	951.0	946.8	953.4	960				949,^1,2 954^3
	0.13	0.13	0.029	0.012	0.045	0.042
CH benzene oop def, vinyl CH oop def	1008.8	1008.6							1011		1008,^4 1015^1
	7.2	7.14
SO3 sym str	1032.5	1032.7							1042	1030–1070	1037^4
	7.94	7.4
Ring sym str, N–CH3 str, N–CH2 str, SO str, ring ip def + vinyl ip def^2			1037.7	1045.6			1038	1040			1045^2
			0.05	0.14
Ring ip asym str, CC str, N–CH3 twist, SNS asym str, ring ip def + CH2 wagg^1,2			1057.3	1059.0	1057.3	1056.6	1051	1055			1058,^2 1062^1
			0.29	0.2	0.43	0.5
6-Ring ip def, vinyl ip def	1113.3	1113.0								1110–1130	1120^4
	3.9	3.4
6-Ring ip str, 6-ring ip def^4	1121.1	1121.7							1130	1130–1190	1134^4
	6.3	5.0
SO2 sym str			1132.7	1129.1	1136.1	1136.3	1132	1135
			0.39	0.53	0.28	0.37
Ring ip asym str, N–CH2 str, N–CH3CN str, CC str, ring ip def + C–C str^2			1139.5	1139.0	1154.9	1157.8	1169	1170			1155^2
			0.22	0.32	0.38	0.28
SO3 asym str	1171.8	1169.3							1184	1140–1250
	14.26	9.5
	1195.4	1193.4	1192.1	1187.5	1183.0	1184.1
	23.8	16.1	0.63	0.7	0.43	0.67
			1181.1 (−)
Ring sym str, N–CH3 str, N–CH2CN str, ring ip def + CH2 sciss^1,2			1196.5 (−)				1182	1185			1182,^1 1185^2
			1209.3 (−)	1203.2	1199.2	1203.4
				0.74	0.79	0.58
			1215.6 (−)
CF3 asym str			1230.0	1231.8	1222.0	1225.1	1227
			0.13	0.31	0.071	0.054
Vinyl CH ip def					1293.8					1240–1330
					0.11
SO2 asym str, ring ip sym str, CC str, N–CH2 str, N–CH3CN str			1329.7	1323.7	1331.1	1328.8	1331	1332
			0.15	0.39	0.077	0.3
SO2 asym str			1351.7	1351.3	1351.7	1351.3	1348	1349		1310–1360
			0.31	0.36	0.5	0.55
C=O str					1726.6	1731.7				1700–1740
					0.25	0.21

---

(i) the asymmetric SO₂ stretching vibration ν_as(SO₂) localized within the NTf₂ counterion which absorbs light at [small nu, Greek, macron] ≈ 1350 cm⁻¹ and the asymmetric SO₃ stretching vibration ν_as(SO₃) of the styrene-sulfonated samples visible at [small nu, Greek, macron] ≈ 1170 cm⁻¹,

(ii) the combination of N–CH and/or N–CH₂ and/or N–CH₃ stretching vibrations ν(N–CH) at [small nu, Greek, macron] ≈ 1200 cm⁻¹ originating from the imidazolium ring or quaternary ammonium, and

(iii) the C–C stretching vibration ν(C–C) within the alkyl chains (and polymeric backbones) at [small nu, Greek, macron] ≈ 950 cm⁻¹ (Fig. 4).

In the spectral region between [small nu, Greek, macron] = 1400 and 1275 cm⁻¹ absorption bands are present which arise from the NTf₂ ion. Among them we concentrate on ν_as(SO₂) around [small nu, Greek, macron] ≈ 1350 cm⁻¹ (molecular vibration (i)). Furthermore, only sample BDMAEMA-NTf₂ exhibits an additional peak at [small nu, Greek, macron] = 1293 cm⁻¹ which is not present in the spectrum of the corresponding PIL. Nagai et al.⁷⁶ assigned this band to a combination of ν(C=C) and ν(C–C–O) vibrations; Sokrates⁷⁵ to a peak arising from the CH in-plane deformation at the outermost carbon atom of the vinyl bond. However, even though the exact vibrational origin is certainly discussed, the general assignment of this band to the vinyl end group is beyond question. Because of a different chemical environment the polymerisable end groups in the other two monomeric structures, the analogous signals appear at different frequencies. On the other hand, only samples containing StySu exhibit two pronounced peaks at [small nu, Greek, macron] ≈ 1010 and 1030 cm⁻¹ arising from the ring in-plane bending, vinyl in-plane rocking; and SO₃ symmetric stretching ν_s(SO₃), respectively. The SO₃ antisymmetric stretching vibration (ν_as(SO₃), [small nu, Greek, macron] ≈ 1170 cm⁻¹) is employed as StySu-based represent for molecular vibration (i).

Around [small nu, Greek, macron] = 1200 cm⁻¹ the combinational vibration of N–CH/N–CH₂/N–CH₃ stretching (molecular vibration 2) appears in the spectra of all samples (Fig. 4). Thus, this band provides information related to the positively charged imidazolium moiety or quarternary ammonium and can be compared between all samples.

At around [small nu, Greek, macron] = 950 cm⁻¹ peaks arising from ν(C–C) (molecular vibration 3) can be found in all spectra. These vibrations are located within the aliphatic chains of low molecular weight ILs and in addition within the polymeric backbone of the PILs. In contrast to the aforementioned molecular vibrations 1 and 2, these vibrations are located in uncharged and hydrophobic parts of the sample molecules.

Interestingly, all samples except BVIM-NTf₂ are fully amorphous over the whole temperature range, whereas the latter crystallizes during the heating run between 241 and 294 K. Crystallization results in narrower and hence higher IR absorption bands (Fig. 4). However, the reason for this phenomenon is not in the scope of the current work.

3.3 Charge transport characteristics

In order to deduce detailed information about the charge transport mechanism and the submolecular moieties involved in this process, we compare the temperature-dependency of the intermolecular interactions with that of intramolecular interactions. In this case the former characteristics τ_α and σ₀ determined by means of BDS are compared with properties of molecular vibrations, which are quantified in terms of the spectral position [small nu, Greek, macron] and the oscillator strength A. The latter is determined on the basis of the integrated absorbance (area under the curve) which is directly proportional to the oscillator strength. Thus, the relative change of the normalized integrated absorbance is identical to the relative change of the oscillator strength (Fig. 5 and 6). The following characteristic temperatures specific for each sample are determined from the dielectric measurements: the glass transition temperatures T_g, as the parameter at which the fitted VFT curve shows a relaxation time of τ_α = 10⁻² s (dotted lines in Fig. 5 and 6), and the transition temperature T_σ0, which indicates the transition from a VFT-dependence to an Arrhenius-like thermal activation of σ₀ (dashed-dotted lines).

Fig. 5 Comparison of the temperature dependencies of the intermolecular mean structural relaxation time τ_α that determines the glassy dynamics as well as the DC-conductivity σ₀ of the investigated samples under study with the FTIR-obtained intramolecular modes assigned to the SO₂ or SO₃ (red arrows) and N–CH_x (blue arrows) stretching vibrations at their frequency position as well as their relative absorbances. The colour code is identical to Fig. 2 and the sample arrangement to Fig. 4. The dielectric data are fitted using Vogel–Fulcher–Tammann (VFT) functions (straight lines), the dotted lines display the calorimetrically measured glass transition temperatures T_g. For DC-conductivity of all PILs one observes a transition in its thermal activation from VFT-like dependence to an Arrhenius-law with decreasing temperature. This transition temperature T_σ0 is depicted with dashed-dotted lines, the double-arrows represent the temperature range of this transition. The logarithms are to base 10, representative error-bars are indicated.

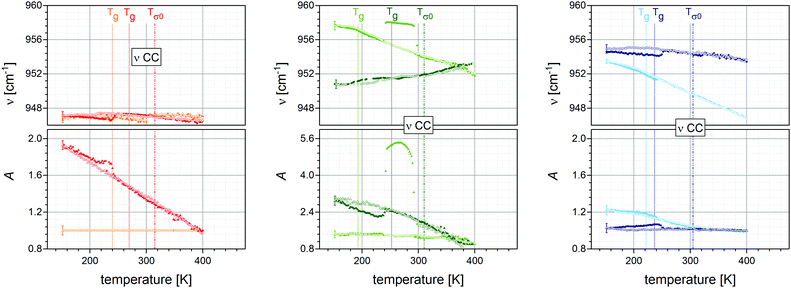Fig. 6 Temperature dependencies of the IR bands assigned to the CC stretching vibration (gray arrows in Fig. 5) at their frequency position as well as their relative absorbance. The colour code is identical to Fig. 2 and the sample arrangement to Fig. 4, likewise the depicted dotted (T_g's) and dashed-dotted (T_σ0) lines. The logarithms are to base 10, representative error-bars are indicated.

Comparing these temperatures with the temperature-dependencies of the selected molecular vibrations (i–iii) one unravels the following three characteristics:

(I) For all low molecular weight ILs one observes kinks either in Δ[small nu, Greek, macron] and/or in A at T_g.

(II) For the molecular vibrations allocated to the ionic moieties in the PILs [vibration (i) and (ii)] one observes no temperature peculiarity at T_g, but kinks either in Δ[small nu, Greek, macron] and/or in A at T_σ0.

(III) For the molecular vibrations of the PILs of the neutral moieties represented by C–C stretching [vibration (iii)] temperature peculiarities are neither observed at T_g, nor at T_σ0.

The detailed analysis of these results is provided and discussed below.

Starting with molecular vibration in (i) (ν_as(SO₂) and ν_as(SO₃)) one observes for all samples a spectral blue shift of the peak positions as a consequence of decreasing temperature, in particular of about 3.0 cm⁻¹, 1.5 cm⁻¹ and 1.0 cm⁻¹ in the case of the monomeric samples BMIM-StySu, BVIM-NTf₂ and BDMAEMA-NTf₂, or of about 2.0 cm⁻¹, 3.0 cm⁻¹ and 2.5 cm⁻¹ in the case of the polymeric samples P[BMIM-StySu], P[BVIM-NTf₂] and P[BDMAEMA-NTf₂], respectively. Furthermore, the frequency shift is strictly monotonic, while it bends off at a sample-specific temperature near the T_g (except for samples BVIM-NTf₂ and BDMAEMA-NTf₂). Although the frequency shifts in the case of the PILs seem to be comparable to the shifts of the ILs, the temperature range of the PILs neither coincides with the T_g's of the monomers nor with the T_g's of the PILs; it rather coincides with the transition temperature T_σ0. This effect is most pronounced for sample P[BVIM-NTf₂], but also observable for P[BMIM-StySu] and P[BDMAEMA-NTf₂]. In a simple approach the frequency position [small nu, Greek, macron] depends on the energy difference between the ground state and the first excited state of the quantized vibrational mode. With decreasing temperature the Morse potential becomes narrower leading to a spectral blue shift. A kink in the temperature dependence of the frequency position directly reflects a change in the temperature dependence of the Morse potential.

Concerning the oscillator strength when cooling from 400 K to 150 K one examines an increase of 33%, 80% and 45% for the monomeric samples BMIM-StySu, BVIM-NTf₂ and BDMAEMA-NTf₂, or of 8%, 57% and 32% for the polymeric systems P[BMIM-StySu], P[BVIM-NTf₂] and P[BDMAEMA-NTf₂], respectively. The oscillator strength is given by the excitation process from the vibrational ground state to the first excited state. Because the states' occupation obeys the Boltzmann distribution, the greatest change in the oscillator strength will occur for the vibration with the lowest frequency (and hence lowest energy difference). Thus, a change of more than 3% cannot be explained on the basis of occupation of states and indicates towards intermolecular interactions. Moreover a slight hysteresis appears, which is tentatively caused by a weak H-bonding network. Analogous to the frequency position the oscillator strength exhibits clear kinks for the low molecular weight ILs which are allocated near the particular glass transition temperatures. This verifies a direct interrelation between the intramolecular potential landscape, which is responsible for the specific infrared absorption, and the intermolecular interactions, which are dominating the dynamics of the glassy systems. In the case of PILs the oscillator strength shows a clear kink for sample P[BMIM-StySu] at T_σ0 and a slight kink for sample P[BDMAEMA-NTf₂] at the corresponding positions, while this dependency is not observed for P[BVIM-NTf₂].

In order to verify the dependence of macroscopic DC-conductivity on microscopic intramolecular interactions we raise the question, whether this dependencies holds true also for molecular vibration (ii). Thus, the frequency position and its shift as well as the relative oscillator strength of the N–CH/N–CH₂/N–CH₃ stretching vibrations allocated at the imidazolium rings or the quaternary ammonium are analysed. As for molecular vibration (i) the frequency position is generally blue shifted while the oscillator strength is enhanced due to the temperature decrease. In the case of samples BMIM-StySu and P[BMIM-StySu] one observes generally weak thermal response without clear kinks neither at one of the T_g's nor at T_σ0. In contrast to these samples for BVIM-NTf₂ a spectral shift of more than 8 cm⁻¹ with a pronounced kink at T_g is evident. The oscillator strength increases by 10% without any temperature-specific peculiarly. For BDMAEMA-NTf₂ the opposite effect can be observed. While the frequency position is monotonously shifted over 6 cm⁻¹, the relative oscillator strength bends off adjoining T_g. In the case of the polymeric counterparts P[BVIM-NTf₂] and P[BDMAEMA-NTf₂], a kink in the spectral shift is evident at T_σ0 likewise for molecular vibration (i), whereas the stretching vibration is fully unaffected at T_g. The absolute values of the shifts (2.5 and 3.0 cm⁻¹) compared to the monomers are rather weak; the values of the oscillator strengths does not show any temperature-specific peculiarity.

In order to obtain a consistent molecular picture not only the charged (ionic) moieties have to be considered in this study but also the neutral units, which are hypothesized to be not involved in the charge transport mechanism. Therefore, the C–C stretching vibration (molecular vibration in iii) assigned to the band at ν(C–C) ≈ 950 cm⁻¹ has been selected. In the case of monomeric structures this mode is almost exclusively located at the butyl chains, whereas for PILs the polymeric backbone contributes significantly. First, for BVIM-NTf₂ and P[BVIM-NTf₂] no significant temperature dependence is deduced (Δν ≤ ±1 cm⁻¹). Second, for BVIM-NTf₂ and BDMAEMA-NTf₂ a blue shift of nearly 6 and 7 cm⁻¹ occur, while their polymeric equivalents P[BVIM-NTf₂] and P[BDMAEMA-NTf₂] are red shifted by about 3 and blue shifted by about 1 cm⁻¹, respectively. The ILs show a kink in the frequency shift around their T_g. Third, the oscillator strength appears constant in the case of sample BMIM-StySu, while in the case of the polymer P[BMIM-StySu] it is strictly monotonically increasing. For BVIM-NTf₂ the oscillator strength appears constant, whereas for P[BVIM-NTf₂] it increases and bends off at T_g. For BDMAEMA-NTf₂ and P[BDMAEMA-NTf₂] the opposite behaviour is detected, for the IL the oscillator strength increases and bends off at T_g, for the PIL it is constant. Although these dependencies appear similar to the analogies of molecular vibrations (i) and (ii), for all samples there is no evidence that molecular vibration in (iii) responds to T_σ0.

Combining the results of the thermal response obtained by investigating IR-active vibrations structurally allocated at both ionic moieties as well as on neutral units one observes a strong correlation between the particular glass transition temperatures T_g and distinct kinks within the spectral position and respective oscillator strength, for all low molecular weight ionic liquids under study. This confirms the so far achieved understanding that the dynamics of neat ILs is dominated by the glassy nature of the samples originating from fluctuations between transient ion pairs, in accord with the relation τ_α ∼ ω_c ∼ σ₀. In contrast to low molecular weight ILs the intramolecular dynamics of polymeric ionic liquids is not affected by the glass transition; neither at the T_g of the PIL, nor at that of a segmental repeat unit. In fact one observes for both molecular vibrations adjoined to the ionic units (i and ii) distinct alterations of the thermal response of the spectral position as well as of the oscillator strength at T_σ0. This leads for the first time to the conclusion that the change in the local, intramolecular potentials of these moieties at T_σ0 is correlated to the change of the macroscopic DC-conductivity, whereas other molecular parts are not involved. Thus, we identify the ionic units as charge transport responsive (CTR) moieties. Correspondingly, the C–C stretching vibration (molecular vibration iii) is fully unaffected by any of the characteristic temperatures and determines the alkylchains as well as the polymeric backbones to be charge transport irresponsive (CTI) moieties. Furthermore, this absence of any response at T_g and T_σ0 proves that the glassy dynamics as well as the charge transport in PILs is dominated by the ionic moieties and not by the polymeric backbone.

4 Conclusion

In the current study three polymeric ionic liquids (PILs) as well as their monomeric correspondents with systematically varied anion–cation composition are investigated by means of broadband dielectric spectroscopy (BDS), Fourier transform infrared spectroscopy (FTIR), and AC-chip and differential scanning calorimetry. First, three dielectric active relaxation processes are found; two of them are assigned to secondary fluctuations (τ_β1,2) of the individual ionic species, whereas the third (τ_α) originates from the relaxations of transient ion pairs and reflects the dynamic glass transition. This relaxation process shows a Vogel–Fulcher–Tammann (VFT) temperature-dependence and scales with the calorimetric glass transition temperature T_g.

Second, the complex conductivity of both, low molecular weight and polymeric ILs, is determined by hopping conduction in a spatially and temporally varying random energy landscape. The mean hopping rate ω_c is found to be proportional to the relaxation rate of the dynamic glass transition τ_α and the DC-conductivity σ₀, thus proving the validity of the Barton–Namikawa–Nakajima (BNN)-relation for all systems under study. In contrast to the low molecular weight ILs, the thermal activation of the DC-conductivity in the polymeric systems changes from a VFT- to an Arrhenius-dependence at a (sample specific) temperature T_σ0. While in many studies T_σ0 was found to be close to the calorimetric glass transition temperature T_g, in the present study PILs are examined for which T_σ0 distinctly differs from the calorimetric glass transition temperatures T_g by as far as 80 K. The fact that the mean structural relaxation rate time τ_α, the charge carrier hopping rate ω_c, and the DC-conductivity σ₀ are proportional to each other well below and above the transition temperature T_σ0 explicitly proves that the mechanism of charge transport is deduced as a glassy dynamics assisted hopping conduction and does not change at T_σ0.

Third, by analysing the temperature dependence of selected moiety-specific IR-active vibrations one observes for all low molecular weight ILs distinct changes in all intra-molecular vibrational potentials at T_g. In the case of the polymeric ILs instead, only the thermal activations of vibrational modes adjoining the ionic moieties are changed at T_σ0. Potentials of neutral moieties as those of the free alkyl-chains or the polymeric backbone are neither affected at T_σ0 nor at T_g. This leads to the identification of charge transport responsive (CTR) and charge transport irresponsive (CTI) moieties (see Fig. 7).

Fig. 7 Scheme of the interplay between glassy dynamics and charge transport as reflected by its inter- and intramolecular interactions for the BMIM-StySu repeat unit. The charge transport mechanism is activated by the dynamic glass transition which is determined by the structural relaxation of transient dipoles between ion pairs (μ_α). When the temperature is decreased below a sample-specific value T_σ0, the thermal activation of the DC-conductivity undergoes a transition from a Vogel–Fulcher–Tammann to an Arrhenius dependence. The alteration of the three-dimensional intermolecular potential landscape is reflected by the response of particular intramolecular vibrations of charged moieties, whereas other vibrations located at the same molecule are not affected. Thus, one is able to identify charge transport responsive (CTR) and charge transport irresponsive (CTI) moieties. The CTR subunits are illustrated by the highest occupied molecular orbitals.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

FF and FK as well as BP and SV acknowledge the financial support from the Deutsche Forschungsgesellschaft under the DFG-project New polymer materials on the basis of functionalized ionic liquids for application in membranes “Knowledge Transfer Project” (KR 1138/24-1, resp. STR 437/7-1); FK and AMA within the SFB/TRR 102, Project B8: “Polymers under multiple constraints: restricted and controlled molecular order and mobility”, too.

References

1. J. Tang, H. Tang, W. Sun, M. Radosz and Y. Shen, J. Polym. Sci., Part A: Polym. Chem., 2005, 43, 5477–5489.
2. S. Craig, Angew. Chem., Int. Ed., 2009, 48, 2645–2647.
3. D. Mecerreyes, Prog. Polym. Sci., 2011, 36, 1629–1648.
4. T. Y. Kim, H. W. Lee, M. Stoller, D. R. Dreyer, C. W. Bielawski, R. S. Ruoff and K. S. Suh, ACS Nano, 2011, 5, 436–442.
5. F. Schüler, B. Kerscher, F. Beckert, R. Thomann and R. Mülhaupt, Angew. Chem., Int. Ed., 2012, 52, 455–458.
6. B. Qiu, B. Lin and F. Yan, Polym. Int., 2013, 62, 335–337.
7. S. J. Yoo, L. Li, C. Zeng and R. D. Little, Angew. Chem., Int. Ed., 2015, 54, 3744–3747.
8. I. Osada, H. de Vries, B. Scrosati and S. Passerini, Angew. Chem., Int. Ed., 2015, 55, 500–513.
9. K. Täuber, A. Zimathies and J. Yuan, Macromol. Rapid Commun., 2015, 36, 2176–2180.
10. H. Cheng, P. Wang, J. Luo, J. Fransaer, D. E. De Vos and Z.-H. Luo, Ind. Eng. Chem. Res., 2015, 54, 3107–3115.
11. K. Grygiel, J.-S. Lee, K. Sakaushi, M. Antonietti and J. Yuan, ACS Macro Lett., 2015, 4, 1312–1316.
12. M. Fernández, L. A. Carreno, F. Bernard, R. Ligabue and S. Einloft, Macromol. Symp., 2016, 368, 98–106.
13. J. L. Freyer, S. D. Brucks, G. S. Gobieski, S. T. Russell, C. E. Yozwiak, M. Sun, Z. Chen, Y. Jiang, J. S. Bandar, B. R. Stockwell, T. H. Lambert and L. M. Campos, Angew. Chem., Int. Ed., 2016, 55, 12382–12386.
14. R. Guterman, M. Ambrogi and J. Yuan, Macromol. Rapid Commun., 2016, 37, 1106–1115.
15. F. N. Ajjan, M. Ambrogi, G. A. Tiruye, D. Cordella, A. M. Fernandes, K. Grygiel, M. Isik, N. Patil, L. Porcarelli, G. Rocasalbas, G. Vendramientto, E. Zeglio, M. Antonietti, C. Detrembleur, O. Inganäs, C. Jérôme, R. Marcilla, D. Mecerreyes, M. Moreno, D. Taton, N. Solin and J. Yuan, Polym. Int., 2017, 66, 1119–1128.
16. S. M. Morozova, A. S. Shaplov, E. I. Lozinskaya, D. Mecerreyes, H. Sardon, S. Zulfiqar, F. Suáez-García and Y. S. Vygodskii, Macromolecules, 2017, 50, 2814–2824.
17. Q. Xu, Z. Zheng, B. Wang, H. Mao and F. Yan, ACS Appl. Mater. Interfaces, 2017, 9, 14656–14664.
18. H. Ohno and K. Ito, Chem. Lett., 1998, 751–752.
19. H. Ohno, Electrochim. Acta, 2001, 46, 1407–1411.
20. H. Ohno, M. Yoshizawa and W. Ogihara, Electrochim. Acta, 2004, 50, 255–261.
21. S. Washiro, M. Yoshizawa, H. Nakajima and H. Ohno, Polymer, 2004, 45, 1577–1582.
22. H. Ohno, Macromol. Symp., 2007, 249–250, 551–556.
23. N. Nishimura and H. Ohno, Polymer, 2014, 55, 3289–3297.
24. J. R. Sangoro, C. Iacob, A. L. Agapov, Y. Wang, S. Berdzinski, H. Rexhausen, V. Strehmel, C. Friedrich, A. P. Sokolov and F. Kremer, Soft Matter, 2014, 10, 3536–3540.
25. F. Fan, W. Wang, A. P. Holt, H. Feng, D. Uhrig, X. Lu, T. Hong, Y. Wang, N.-G. Kang, J. Mays and A. P. Sokolov, Macromolecules, 2016, 49, 4557–4570.
26. C. Gainaru, E. W. Stacy, V. Bocharova, M. Gobet, A. P. Holt, T. Saito, S. Greenbaum and A. P. Sokolov, J. Phys. Chem. B, 2016, 120, 11074–11083.
27. M. Yoshizawa and H. Ohno, Electrochim. Acta, 2001, 46, 1723–1728.
28. M. Yoshizawa, W. Ogihara and H. Ohno, Polym. Adv. Technol., 2002, 13, 589–594.
29. U. H. Choi, M. Lee, S. Wang, W. Liu, K. I. Winey, H. W. Gibson and R. H. Colby, Macromolecules, 2012, 45, 3974–3985.
30. M. Lee, U. H. Choi, R. H. Colby and H. W. Gibson, Chem. Mater., 2010, 22, 5814–5822.
31. F. Frenzel, R. Guterman, A. M. Anton, J. Yuan and F. Kremer, Macromolecules, 2017, 50, 4022–4029.
32. U. H. Choi, Y. Ye, D. S. de la Cruz, W. Liu, K. I. Winey, Y. A. Elabd, J. Runt and R. H. Colby, Macromolecules, 2014, 47, 777–790.
33. F. Frenzel, W. H. Binder, J. R. Sangoro and F. Kremer, in Glassy Dynamics and Charge Transport in Polymeric Ionic Liquids, ed. M. Paluch, Springer International Publishing, 2016, pp. 115–129.
34. C. Iacob, A. Matsumoto, M. Brennan, H. Liu, S. J. Paddison, O. Urakawa, T. Inoue, J. Sangoro and J. Runt, ACS Macro Lett., 2017, 6, 941–946.
35. Z. Wojnarowska, J. Knapik, M. Diaz, A. Ortiz, I. Ortiz and M. Paluch, Macromolecules, 2014, 47, 4056–4065.
36. Z. Wojnarowska, J. Knapik, J. Jacquemin, S. Berdzinski, V. Strehmel, J. R. Sangoro and M. Paluch, Macromolecules, 2015, 48, 8660–8666.
37. M. Zhao, PhD thesis, Rochester Institue of Technology, 2014.
38. F. Fan, Y. Wang, T. Hong, M. F. Heres, T. Saito and A. P. Sokolov, Macromolecules, 2015, 48, 4461–4470.
39. P. Griffin, A. L. Agapov, A. Kisliuk, X.-G. Sun, S. Dai, V. N. Novikov and A. P. Sokolov, J. Chem. Phys., 2011, 135, 114509.
40. J. C. Salamone, C.-C. Tsai and A. C. Watterson, J. Macromol. Sci., Part A: Pure Appl. Chem., 1979, 13, 665–672.
41. S. Berdzinski, B. Strehmel and V. Strehmel, Photochem. Photobiol. Sci., 2015, 14, 714–725.
42. V. Strehmel and V. Senkowski, J. Polym. Sci., Part A: Polym. Chem., 2015, 53, 2849–2859.
43. J. Kiefer, J. Fries and A. Leipertz, Appl. Spectrosc., 2007, 61, 1306–1311.
44. K. Noack, P. S. Schulz, N. Paape, J. Kiefer, P. Wasserscheid and A. Leipertz, Phys. Chem. Chem. Phys., 2010, 12, 14153–14161.
45. J. C. Yang, M. J. Jablonsky and J. W. Mays, Polymer, 2002, 43, 5125–5132.
46. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327.
47. F. Neese, Angew. Chem., Int. Ed., 2017, 56, 11003–11010.
48. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
49. J. D. Dill and J. A. Pople, J. Chem. Phys., 1975, 62, 2921.
50. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
51. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
52. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
53. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
54. C. Timothy, C. Jayaraman, V. R. Schleyer and S. P. V. Rague, J. Comput. Chem., 1983, 4, 294–301.
55. H. Huth, A. A. Minakov, A. Serghei, F. Kremer and C. Schick, Eur. Phys. J.-Spec. Top., 2007, 141, 153–160.
56. A. Serghei, M. Tress, J. R. Sangoro and F. Kremer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 184301.
57. J. C. Dyre and T. B. Schroder, Rev. Modern Phys., 2000, 72, 873–892.
58. Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer, Berlin, 2003.
59. S. Havriliak and S. Negami, Polymer, 1967, 8, 161–210.
60. P. Debye, Polare Molekeln, Verlag von S. Hirzel in Leipzig, 1929.
61. J. L. Barton, Verres Réfr., 1966.
62. H. Namikawa, J. Non-Cryst. Solids, 1975, 18, 173–195.
63. T. Nakajima, Annual Report, Conference on Electric Insulation and Dielectric Phenomena, 1971, p. 168.
64. C. Iacob, J. R. Sangoro, W. K. Kipnusu, R. Valiullin, J. Kärger and F. Kremer, Soft Matter, 2012, 8, 289–293.
65. C. Iacob, J. R. Sangoro, A. Serghei, S. Naumov, Y. Korth, J. Kärger, C. Friedrich and F. Kremer, J. Chem. Phys., 2008, 129, 234511.
66. C. Krause, J. R. Sangoro, C. Iacob and F. Kremer, J. Phys. Chem. B, 2010, 114, 382–386.
67. J. R. Sangoro, T. Cosby and F. Kremer, in Dielectric Properties of Ionic Liquids, ed. M. Paluch, Springer International Publishing Switzerland 2016, 2016.
68. J. R. Sangoro and F. Kremer, Acc. Chem. Res., 2012, 45, 525–532.
69. J. R. Sangoro, M. Mierzwa, C. Iacob, M. Paluch and F. Kremer, RSC Adv., 2012, 2, 5047–5050.
70. J. R. Sangoro, A. Serghei, S. Naumov, P. Galvosas, J. Kärger, C. Wespe, F. Bordusa and F. Kremer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 051202.
71. F. Frenzel, M. Y. Folikumah, M. Schulz, A. M. Anton, W. H. Binder and F. Kremer, Macromolecules, 2016, 49, 2868–2875.
72. D. A. Turton, T. Sonnleitner, A. Ortner, M. Walther, G. Hefter, K. R. Seddon, S. Stana, N. V. Plechkova, R. Buchner and K. Wynne, Faraday Discuss., 2012, 154, 145–153.
73. J. R. Sangoro, C. Iacob, A. Serghei, C. Friedrich and F. Kremer, Phys. Chem. Chem. Phys., 2009, 11, 913–916.
74. J. R. Sangoro, C. Iacob, S. Naumov, R. Valiullin, H. Rexhausen, J. Hunger, R. Buchner, V. Strehmel, J. Karger and F. Kremer, Soft Matter, 2011, 7, 1678–1681.
75. G. Sokrates, Infrared and Raman characteristic group frequencies: Tables and charts, John Wiley & Sons, Ltd, 2004, vol. 35, 905–905.
76. H. Nagai, J. Appl. Polym. Sci., 1963, 7, 1697–1714.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm02135j

---