Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Marangoni-driven spreading of miscible liquids in the binary pendant drop geometry†
Robin B. J.
Koldeweij‡
 ab,
Bram F.
van Capelleveen‡
ab,
Bram F.
van Capelleveen‡
 a,
Detlef
Lohse
a,
Detlef
Lohse
 ac and
Claas Willem
Visser
ac and
Claas Willem
Visser
 *ad
*ad
aPhysics of Fluids Group & Max Planck Center Twente for Complex Fluid Dynamics, Department of Science and Technology, J. M. Burgers Center for Fluid Dynamics, University of Twente, 7500 AE Enschede, The Netherlands. E-mail: c.visser@utwente.nl
bEquipment for Additive Manufacturing, TNO, 5612 AP Eindhoven, The Netherlands
cMax Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany
dEngineering Fluid Dynamics group, Department of Thermal and Fluid Engineering, Faculty of Engineering Technology, University of Twente, 7500 AE Enschede, The Netherlands
First published on 8th October 2019
Abstract
When two liquids with different surface tensions come into contact, the liquid with lower surface tension spreads over the other liquid. This Marangoni-driven spreading has been studied for various geometries and surfactants, but the dynamics of miscible liquids in the binary geometry (drop–drop) has hardly been investigated. Here we use stroboscopic illumination by nanosecond laser pulses to temporally resolve the distance L(t) over which a low-surface-tension drop spreads over a miscible high-surface-tension drop. L(t) is measured as a function of time, t, for various surface tension differences between the liquids and for various viscosities, revealing a power-law L(t) ∼ tα with a spreading exponent α ≈ 0.75. This value is consistent with previous results for viscosity-limited spreading over a deep bath. The universal power law ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) ∝
∝ ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 3/4 that describes the dimensionless distance
3/4 that describes the dimensionless distance ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) as a function of the dimensionless time
as a function of the dimensionless time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) reasonably captures our experiments, as well as previous experiments for different geometries, miscibilities, and surface tension modifiers (solvents and surfactants). The range of this power law remarkably covers ten orders of magnitude in dimensionless time. This result enables engineering of drop encapsulation for various liquid–liquid systems.
reasonably captures our experiments, as well as previous experiments for different geometries, miscibilities, and surface tension modifiers (solvents and surfactants). The range of this power law remarkably covers ten orders of magnitude in dimensionless time. This result enables engineering of drop encapsulation for various liquid–liquid systems.
1 Introduction
Liquids of low surface tension spread over liquid with high surface tension, which is known as Marangoni spreading. This phenomenon has been studied in various contexts, such as oil spills on the sea,1–5 pulmonary surfactant replacement therapy,6,7 foam destruction,8 and fabrication of soft polymer actuators.9 Recently, Marangoni spreading has been used for encapsulation of a high-surface tension drop by a lower surface tension liquid, as shown in Fig. 1a. This mechanism is used in pharmacy,10,11 for manufacturing of biomaterials,12 electronics,13 food and vitamins,14 microparticles with multiple compartments,15,16 and rapid 3D-bioprinting with in-air microfluidics.17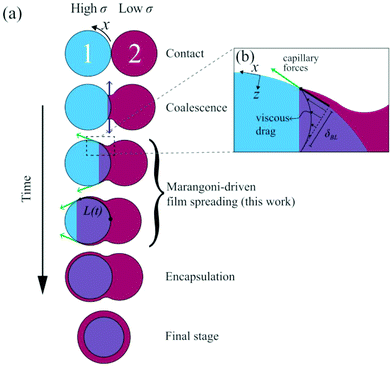 | ||
| Fig. 1 Overview of binary drop spreading; (a) at t = 0 the drops touch. Initially, coalescence radially expands the neck due to local curvature as indicated by the blue arrows.31 This regime is followed by Marangoni-driven spreading of the drop with lower surface tension over the other one (green arrows). Ultimately, this mechanism results in encapsulation of drop 1. (b) Indicative flows of Marangoni-driven spreading, where the Marangoni stress is balanced by a viscous boundary layer. | ||
The morphological outcome of two colliding drops in air, such as encapsulation or breakup, has been assessed for miscible10,17 and immiscible18–22 liquid pairs with different surface tensions. Encapsulation can also be achieved by impacting drops with different sizes23 or different viscosities.24 However, to our best knowledge, their surface-tension-driven encapsulation dynamics have hardly been visualized. Drops can also be encapsulated by gentle deposition onto a bath with a lower surface tension, but here the film dynamics were only assessed during coalescence (an earlier regime that precedes encapsulation)25 or for surface tension induced necking,26,27 rather than encapsulation. Encapsulation in the binary drop geometry was studied for submerged drop pairs, revealing a constant velocity of the spreading film both experimentally28,29 and numerically.23,30 However, it is unclear whether this result also applies to drop pairs in air, since the viscosity of the surrounding liquid plays an important role.
Knowledge of Marangoni spreading over a flat liquid surface with a higher surface tension could also provide clues to describe spreading over drops. This topic has been studied in many configurations, of which most can be classified according to four criteria: (i) liquid-driven versus surfactant-driven spreading, (ii) miscible versus immiscible liquid pairs, (iii) shallow versus deep liquid “carrier” layers, and (iv) spreading from a finite reservoir versus a source. Here, we focus on spreading of ethanol/water mixtures over water drops, corresponding to surfactant-free and miscible liquid pairs. For a drop pair, the transition between deep and shallow carrier layers may depend on the thickness of the flow-induced viscous boundary layer as sketched in Fig. 1b. Deep-layer behavior is expected if the boundary layer thickness δBL < D1/4, with D1 ≈ 2 mm the inner drop's diameter.32 Using typical values for the density ρ = 1000 kg m−3, viscosity η = 1 mPa s, and time t = 10 ms, we obtain δBL = (η1t/ρ1)1/2 ≈ 0.1 mm. Therefore, the comparison to the spreading of a drop over a deep layer is considered. Finally, the outer drop is assumed to be an infinite source, as its volume suffices to form a thick film around the inner drop. The configuration of a spreading drop over a deep layer was first studied by Suciu et al.33–36 for a quasi-steady regime. However, the preceding initial expansion of the film is the relevant regime for drop encapsulation.
The spreading distance L(t) of a low-surface tension liquid over a liquid with a higher surface tension can be described by a power law:3
| L(t) = βtα. | (1) |
The spreading exponent α and the dimensional prefactor β, are usually reported as a function of the geometric and material parameters,37 and are the scope of this study. The canonical result for spreading on a deep bath is α = 3/4 and β = kS1/2(ρη)−1/4, in which k is a dimensionless constant. S ≈ Δσ represents the spreading parameter for liquid pairs in air, and Δσ = σ1 − σ2 is the surface tension difference between the liquids. These values follow from balancing the surface tension gradient with dissipation in the viscous boundary layer that develops while spreading on a deep layer.4,5,38–40 Experiments performed for immiscible, non-evaporative liquids,41,42 immiscible surfactant solutions,43 liquid spreading over a liquid covered with insoluble surfactants,44 and for immiscible micro-drops spreading over free-flowing thin films32 validated this scaling argument. For miscible surfactant solutions, the spreading exponent is maintained around α = 0.75 for low solubility,45,46 but it can decrease to α = 0.4 for highly soluble surfactants.47 An indicative value for the constant k ≈ 0.88 applies to spreading of immiscible liquids in the radial geometry, but values in the range of k = 0.665 to k = 1.52 have been reported.41
For spreading of a low −σ drop over a deep bath of a miscible liquid as considered here, a spreading exponent in the range α = 0.53 ± 0.03 was measured for nitroethane, ethyl acetate,48 and isopropanol drops49 deposited on water. Molecular dynamics simulations of ethanol solutions spreading over water revealed a similar exponent of α = 0.55 ± 0.05.50 These reduced values, as well as a decrease of the prefactor to k ≈ 0.3, were attributed to dissolution of the spreading liquid into the bath by convective rolls that form at the film's edge.48,51 A similar reduction in the spreading exponent is observed for evaporation-driven formation of convective rolls.41 An even lower exponent (α ≈ 0.25) was measured for ethanol drops on a water bath,52 and explained by balancing Δσ with viscous dissipation within the spreading film.53
As the existing literature indicates that spreading exponents 1/4 ≲ α ≲ 1 could apply to the binary drop geometry, here we observe and quantify the Marangoni-driven spreading dynamics of miscible drop pairs. By encapsulating a fluorescent inner drop by an optically absorbing low-σ liquid, we obtain the spreading distance as a function of time, the surface tension difference, and the viscosity. Subsequently, we determine the spreading exponents and compare these to systems with different geometries, surfactants and miscibilities. The paper is organized as follows: In Section 2, the experimental setup and liquids are described. The results and discussion are described in Section 3, followed by the conclusions in Section 4.
2 Experimental set-up and materials
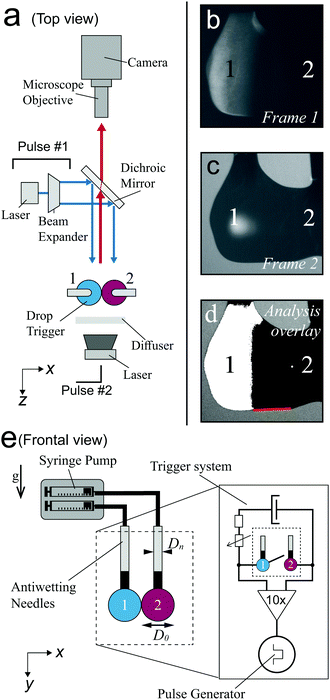
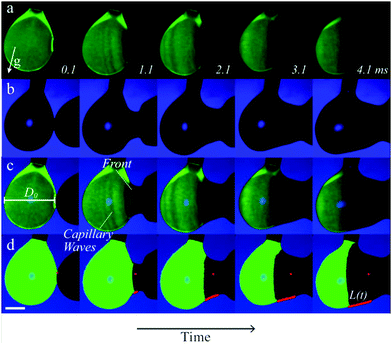
To create the binary drop geometry, two pendant drops were dispensed from Teflon needles (Hamilton Company). The needles were fed by identical syringes mounted on a syringe pump (Harvard PHD 2000), pumping with a typical rate of 0.25 mL min−1 that resulted in the formation of approximately 25 drops per minute. The needles were placed at a 2.5 mm center-to-center distance, resulting in drops with a diameter D0 = 2.5 ± 0.5 mm, just before the first contact. For each drop pair, the ratio was 0.95 < D1/D2 < 1.05. The high-σ drop consisted of Milli-Q water as a base, to which fluorescein (emission at 525 nm) was added for fluorescent visualization. The low-σ drop consists of a 15 vol% inkjet printer ink solution (Brother LC-800), to provide an optically absorbing film that blocks the fluorescent light of the high-σ drop during spreading. The surface tension gradient was modified by adding ethanol to the low-σ drop, and measured by the hanging drop method as shown in (ESI†) Fig. S1 and S2. The measured values were constant in time (ESI,† Fig. S3), confirming that evaporation does not affect the surface tension over the duration of the drop formation in the experiments. The viscosity of the liquids was controlled by adding glycerol, as shown in ESI,† Fig. S4 and S5. The viscosity of glycerol-free mixtures of ethanol, water, and ink was measured to be 1.5 ± 0.5 mPa s.The visualization setup is depicted in Fig. 2a. Stroboscopic imaging was used to generate two images of the drop pair at a controlled time after contact. The first image was illuminated with a pulsed laser (Litron Nano S PIV 400 mJ, wavelength 532 nm, pulse duration 8 ns), of which the optical path is shown by the blue arrows in Fig. 2a. Only the fluorescent light is observed, as shown in Fig. 2b. The second frame was exposed by diffuse illumination from behind both drops, resulting in images of the drop contours as shown in Fig. 2c. Here, the pulse was provided by a second pulsed laser (evergreen 600 mJ, wavelength 532 nm) that was diffused with a fluorescent diffuser (LaVision) to prevent fringes. The delay time between both laser pulses was set to 500 ns, and the corresponding images were captured in separate frames of a dedicated dual-frame camera (PCO Sensicam qe). As this delay time is approximately 4 orders of magnitude shorter than the capillary time scale (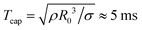 ), no significant motion occurs between frames 1 and 2. The frames were overlaid with excellent spatial collapse, as shown in Fig. 2d, revealing the spreading extent of the film and the outer contour of the drops. Time series were generated by repeating the above procedure for different delays between the moment of drop-drop contact (t = 0) and image capture. The moment of contact was obtained by closing an electrical circuit with the drops, as shown in Fig. 2e (inset). The drops were made conductive by dissolving 1 vol% NaCl into both liquids, which hardly affects the surface tension.54 Experimental differences between two drop pairs sometimes result in 'flickering' of the video and additional noise on the measurements, as for example observed in Fig. 4 for the 20 mPa s and 50 mPa s drops. Still we use this stroboscopic method, as it enables visualizing both liquids at frame rates >104 s−1.
), no significant motion occurs between frames 1 and 2. The frames were overlaid with excellent spatial collapse, as shown in Fig. 2d, revealing the spreading extent of the film and the outer contour of the drops. Time series were generated by repeating the above procedure for different delays between the moment of drop-drop contact (t = 0) and image capture. The moment of contact was obtained by closing an electrical circuit with the drops, as shown in Fig. 2e (inset). The drops were made conductive by dissolving 1 vol% NaCl into both liquids, which hardly affects the surface tension.54 Experimental differences between two drop pairs sometimes result in 'flickering' of the video and additional noise on the measurements, as for example observed in Fig. 4 for the 20 mPa s and 50 mPa s drops. Still we use this stroboscopic method, as it enables visualizing both liquids at frame rates >104 s−1.
Fig. 3a and b show an example time series of the fluorescent drop and both drops' contours, respectively. The overlay in Fig. 3c reveals the spreading extent of the film. The relative light transmission of I/I0 = 5% as compared to the uncovered (green) drop was chosen to determine the covered part with automated image analysis, corresponding to a film thickness of 63 μm. The exact value of this threshold had a minor influence on the spreading distance (see ESI,† Fig. S6 and S7). Still, we would like to stress that we measure the spreading of relatively thick films that are relevant to encapsulation, rather than micrometer- or nanometer-thin films as reported previously.36,55 The location of contact was determined in the first image after contact was measured. We traced the spreading along the bottom of the drop pair to prevent errors due to out-of-plane motion, as indicated by the red lines in Fig. 2d and 3d. To reduce the risk of errors, we averaged three measurements of the spreading distance for each configuration and each time step, and performed scans of the control parameters Δσ and η over the largest feasible range for which spreading still occurs. Still, differences between individual drop pairs sometimes resulted in scatter of the data, as for example observed in Fig. 4a for η = 10 mPa s. To obtain the spreading rate for each measurement series, we used a nonlinear least squares power law fit on the measured spreading curves.
3 Results and discussion
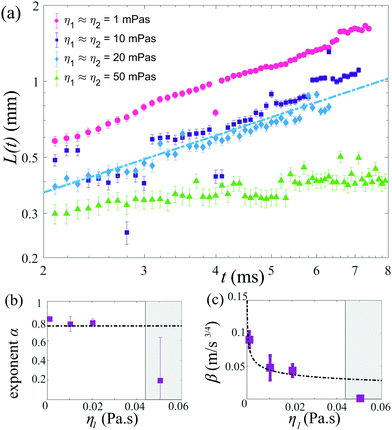
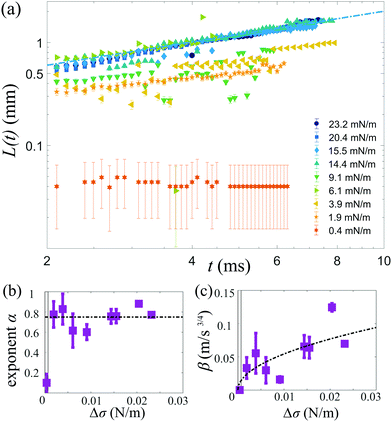
The position of the spreading front L(t) was measured as a function of time and viscosity, as shown in Fig. 4, revealing power-law behavior with an approximate scaling exponent α = 3/4 for low viscosities (η1 ≈ η2 ≤ 20 mPa s). The prefactor is reasonably described by k ≈ 0.6, i.e. L(t) = 0.6Δσ1/2(ρη)−1/4t3/4. Increasing the viscosity to η1 ≈ η2 = 50 mPa s leads to a significant decrease in the spreading rate. The Ohnesorge number for this case is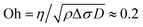 , i.e. spreading seems to be significantly slower than predicted by eqn (1) when global viscous forces become comparable to surface tension forces.
, i.e. spreading seems to be significantly slower than predicted by eqn (1) when global viscous forces become comparable to surface tension forces.
Fig. 5a shows the spreading distance as a function of the surface tension difference, which was varied from Δσ = 0.4 mN m−1 to Δσ = 23.2 mN m−1. The spreading exponents are still consistent with α = 3/4, as shown in Fig. 5b. The prefactors exhibit substantial statistical errors and data scattering, but a value of 0.6Δσ1/2(ρη)1/4 still reasonably well captures the measured data as shown in Fig. 5c. Spreading is inhibited for Δσ = 0.4 mN m−1, for which Oh ≈ 0.15.
 | ||
| Fig. 5 (a) Time evolution of L(t) as a function of Δσ, with η2 = 1.5 mPa s and 1 < η1/η2 < 1.9. (b) The exponent α as a function of Δσ. (c) Prefactor β as a function of Δσ. In (b and c), the shaded areas close to the origin indicate Oh > 0.2 and the dash–dotted lines correspond to those in Fig. 4. The error bars indicate a confidence interval of 95%. | ||
The effect of changing the viscosity ratio η1/η2 between the drops is shown in Fig. 6a. The fastest spreading is observed for a ratio of unity (η1 = η2 ≈ 1.5 mPa s), as the viscosity of both liquids is set to their lowest values for this case. Increasing the viscosity of liquid 1 results in a decrease in spreading over the entire temporal domain. The spreading exponent α (Fig. 6b) does not depend on the viscosity ratio η1/η2 and is around α ≈ 3/4 for all cases. The reduction in spreading is captured by the prefactor, which is consistent with theory for viscosity ratios η1/η2 ≥ 1 (Fig. 6c). Measurements for which the viscosity of drop 2 is increased (that is, η1/η2 < 1), also exhibit reduced spreading. To assess whether this reduction reflects a transition to film-limited dissipation, we compare the dissipation in the spreading film and the boundary layer of drop 1. The dissipation in the spreading film is described by Ωfη2(![[L with combining dot above]](https://www.rsc.org/images/entities/i_char_004c_0307.gif) /L)2, with Ωf ∼ Lhf the film volume (assuming a 2-dimensional system) and hf the film thickness.53 The dissipation in the boundary layer developing in drop 1 is described by ΩBLη1(
/L)2, with Ωf ∼ Lhf the film volume (assuming a 2-dimensional system) and hf the film thickness.53 The dissipation in the boundary layer developing in drop 1 is described by ΩBLη1(![[L with combining dot above]](https://www.rsc.org/images/entities/i_char_004c_0307.gif) /δBL)2 with boundary layer volume ΩBL ∼ LδBL. Hence, the boundary layer dissipation is expected to be dominant over the internal dissipation in the film as long as:
/δBL)2 with boundary layer volume ΩBL ∼ LδBL. Hence, the boundary layer dissipation is expected to be dominant over the internal dissipation in the film as long as:
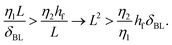 | (2) |
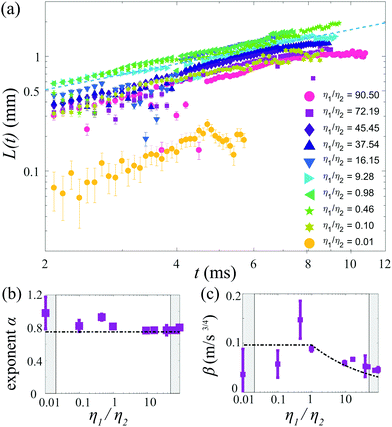 | ||
| Fig. 6 (a) Time evolution of the spreading edge L(t) for various viscosity ratios η1/η2, with 19.8 ≤ Δσ ≤ 28.3 mN m−1. For η1/η2 < 1, η1 = 1.5 mPa s and for η1/η2 > 1, η2 = 1.5 mPa s. (b) Spreading exponent α and (c) prefactor β as a function of η1/η2. In (b and c), the shaded areas indicate Oh > 0.2 (based on the highest viscosity) and the dash–dotted lines correspond to those in Fig. 4. The error bars indicate a confidence interval of 95%. | ||
Assuming L(t) = βt3/4 with β ≈ 0.05 ms−4/3 (as observed in Fig. 5), δBL = (η1t/ρ1)1/2, a film thickness hf = 100 μm (comparable to the measurement threshold), and the most viscous film (η1/η2 = 0.01), the transition to film-limited spreading would be expected after approximately 4 ms. Indeed, a strong reduction of the spreading is observed for t ≈ 5 ms. At earlier times, the measured spreading exponent α ≈ 3/4 suggests that spreading is limited by the boundary layer, but the strongly reduced prefactor shows that the film viscosity still has a strong influence. This behavior may reflect a transition between two different regimes, which deserves further attention as it has not yet been addressed.
As a final step, we rescale our results and compare these to Marangoni-driven spreading in other geometries, with different surfactants, and with immiscible liquids. The dimensionless spreading time and distance were formulated as proposed by:56
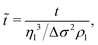 | (3) |
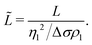 | (4) |
Our measurements are generally described by
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = 0.6 = 0.6![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 3/4, 3/4, | (5) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) and 7.5 orders of magnitude in dimensionless spreading distance
and 7.5 orders of magnitude in dimensionless spreading distance ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) .
.
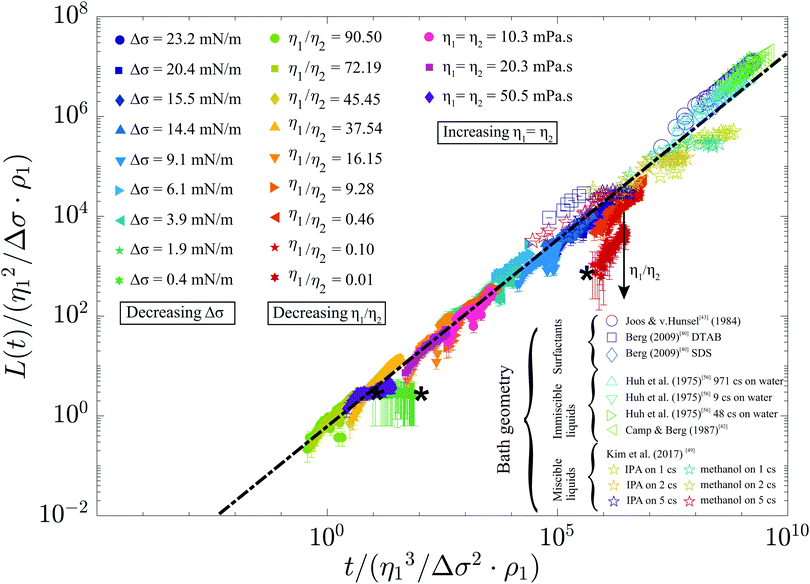 | ||
Fig. 7 Rescaled spreading distance as a function of rescaled time, for our measurements and literature data for different geometries, miscibility, and surfactants.40,42,43,49,56 The dash–dotted line indicates ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = 0.6 = 0.6![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 3/4, and the stars (*) indicate measurements for which Oh > 0.2. 3/4, and the stars (*) indicate measurements for which Oh > 0.2. | ||
Our measurements with reduced exponents are still partly congruent to eqn (5). Similarly, the measurements by Kim et al.49 collapse onto this master curve for a bath with η = 5 mPa s, whereas spreading over a bath with lower viscosity only initially follows eqn (5) and then stops at later times. This transition to a spreading coefficient α = 0 was attributed to Marangoni-induced mixing,49 and may thus indicate a transition to miscibility-dominated effects. Our case may be essentially immiscible as (1) the diffusion length scale over the experimental duration of 10 ms (δD = (Dmt)1/2 ≈ 3 μm with Dm the mass diffusivity) is much smaller than the thickness of the measured film and (2) a spreading exponent α ≈ 3/4 is typically observed. However, a prefactor k ≈ 0.88 was reported41 for immiscible liquids whereas we observe k ≈ 0.6. This reduced value may indicate that miscibility has a minor but observable influence, as k ≈ 0.3 was reported for miscible48,51 liquid pairs in which vortex formation slows down spreading. As these vortices were observed both in larger48 and smaller50 systems, vortices are likely to develop in our system as well. As the influence of miscibility cannot yet be determined from the literature, even for the flat geometry, future work will be required to investigate the details of this parameter.
Our measurements with η1/η2 < 1 do not collapse on eqn (5), since the film viscosity was not included in the dimensionless variables. As discussed, the exact influence of the viscosity in the low-σ film is still unclear. Measurements with a spreading exponent α = 1/4 were recently reported for larger ethanol–water systems, but could only be modeled by assuming a no-slip condition for the film.52 This is a strong assumption, since the film was only in contact with a deep bath on the bottom and free-flowing air on the top. Therefore, the transition between film-limited and substrate-limited spreading as well as the spreading of ethanol over water also deserve future research.
We expected that the geometry would play an important role, as a toroidal convection pattern will develop within drop 147 as shown in Fig. S8 of the ESI.† When this flow is fully developed, the shear profile may resemble spreading over a thin film on a solid substrate, for which α = 1/2.57–59 This transition to film-limited spreading may occur at the end of our temporal domain, as discussed in the ESI,† Section S5. However, the observed temporally sustained spreading exponent α = 3/4 suggests that drop encapsulation can be modeled as a deep bath for most of our control parameters. Finally, our measurements confirm that the surrounding fluid plays an important role, as a constant spreading velocity (α = 1) was reported for binary drops that were submerged in a liquid.28,29
4 Conclusions
The dynamics of Marangoni spreading were experimentally studied for miscible pendant drop pairs in the millimeter size range. Stroboscopic image sequences revealed the spreading distance as a function of time in a new temporal domain. The spreading distance is consistent with L(t) ≈ 0.6Δσ1/2(ρη)−1/4t3/4 for sufficiently low Ohnesorge numbers (Oh ≲ 0.2), and moderate viscosity ratios (0.1 ≲ η1/η2 ≲ 10). Marangoni-driven encapsulation is suppressed for Oh ≳ 0.2, when viscous forces become comparable to capillary effects. Non-dimensionalizing our results and literature experiments for different surfactants, and miscibilities revealed that a universal power law![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = 0.6
= 0.6![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) 3/4 reasonably captures all data over 10 orders of magnitude in dimensionless time, as shown in Fig. 7. This power law can therefore exploited to estimate the encapsulation time scale in a wide range of encapsulation applications.
3/4 reasonably captures all data over 10 orders of magnitude in dimensionless time, as shown in Fig. 7. This power law can therefore exploited to estimate the encapsulation time scale in a wide range of encapsulation applications.
Comparing our results to the literature revealed that Marangoni spreading of miscible liquids is not yet adequately understood, since the transition from essentially immiscible liquids (as observed here) to miscible liquids is unclear. Furthermore, the transition from boundary layer-dominated dissipation in the bath to film-dominated dissipation during elongation deserves attention. As the dynamics of the spreading film are challenging to visualize, especially at the early time scales, we expect that theory, numerics, and experiments will all be required to substantially advance the understanding of Marangoni spreading over the full temporal domain.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge insightful discussions with S. Wildeman, S. Karpitschka, J. H. Snoeijer and T. Kamperman, and we thank E. Zijlma for his contributions to the dedicated electronics.Notes and references
- B. Franklin, W. Brownrigg and M. Farish, Philos. Trans. R. Soc. London, 1774, 64, 445–460 CrossRef.
- L. Rayleigh, Proc. R. Soc. London, 1889, 47, 364–367 Search PubMed.
- J. A. Fay and D. P. Hoult, Physical processes in the spread of oil on a water surface, 1971 Search PubMed.
- D. P. Hoult, Annu. Rev. Fluid Mech., 1972, 4, 341–368 CrossRef CAS.
- M. Foda and R. G. Cox, J. Fluid Mech., 1980, 101, 33–51 CrossRef CAS.
- D. P. Gaver and J. B. Grotberg, J. Fluid Mech., 1990, 213, 127–148 CrossRef CAS.
- R. V. Craster and O. K. Matar, Rev. Mod. Phys., 2009, 81, 1131–1198 CrossRef CAS.
- N. D. Denkov, Langmuir, 2004, 20, 9463–9505 CrossRef CAS PubMed.
- Y. Tian, X. Wei, Z. J. Wang, P. Pan, F. Li, D. Ling, Z. L. Wu and Q. Zheng, ACS Appl. Mater. Interfaces, 2017, 9, 34349–34355 CrossRef CAS PubMed.
- Y. Yeo, O. A. Basaran and K. Park, J. Controlled Release, 2003, 93, 161–173 CrossRef CAS PubMed.
- Y. Yeo, A. U. Chen, O. A. Basaran and K. Park, Pharm. Res., 2004, 21, 1419–1427 CrossRef CAS PubMed.
- B. Duan, L. A. Hockaday, K. H. Kang and J. T. Butcher, J. Biomed. Mater. Res., Part A, 2013, 101, 1255–1264 CrossRef PubMed.
- A. T. Ten Cate, C. H. Gaspar, H. L. K. Virtanen, R. S. A. Stevens, R. B. J. Koldeweij, J. T. Olkkonen, C. H. A. Rentrop and M. H. Smolander, J. Mater. Sci., 2014, 49, 5831–5837 CrossRef CAS.
- N. Blanco-Pascual, R. B. J. Koldeweij, R. S. A. Stevens, M. P. Montero, M. C. Gómez-Guillén and A. T. Cate, Food Bioprocess Technol., 2014, 7, 2472–2483 CrossRef CAS.
- M. Hayakawa, H. Onoe, K. H. Nagai and M. Takinoue, Sci. Rep., 2016, 6, 20793 CrossRef CAS PubMed.
- T. Kamperman, V. D. Trikalitis, M. Karperien, C. W. Visser and J. Leijten, ACS Appl. Mater. Interfaces, 2018, 10, 23433–23438 CrossRef CAS PubMed.
- C. W. Visser, T. Kamperman, L. P. Karbaat, D. Lohse and M. Karperien, Sci. Adv., 2018, 4, eaao1175 CrossRef PubMed.
- R. H. Chen and C. T. Chen, Exp. Fluids, 2006, 41, 453–461 CrossRef CAS.
- R. H. Chen, Appl. Therm. Eng., 2007, 27, 604–610 CrossRef CAS.
- C. Planchette, E. Lorenceau and G. Brenn, Fluid Dyn. Mater. Process., 2011, 7, 279–302 Search PubMed.
- C. Focke and D. Bothe, Phys. Fluids, 2012, 24, 73105 CrossRef.
- C. Planchette, S. Petit, H. Hinterbichler and G. Brenn, Phys. Rev. Fluids, 2018, 3, 93603 CrossRef.
- D. Liu, P. Zhang, C. K. Law and Y. Guo, Int. J. Heat Mass Transfer, 2013, 57, 421–428 CrossRef.
- C. Focke, M. Kuschel, M. Sommerfeld and D. Bothe, Int. J. Multiphase Flow, 2013, 56, 81–92 CrossRef CAS.
- S. T. Thoroddsen, B. Qian, T. G. Etoh and K. Takehara, Phys. Fluids, 2007, 19, 72110 CrossRef.
- F. Blanchette, L. Messio and J. W. M. Bush, Phys. Fluids, 2009, 21, 72107 CrossRef.
- K. Sun, P. Zhang, Z. Che and T. Wang, Phys. Rev. Fluids, 2018, 3, 23602 CrossRef.
- E. Nowak, N. M. Kovalchuk, Z. Che and M. J. H. Simmons, Colloids Surf., A, 2016, 505, 124–131 CrossRef CAS.
- E. Nowak, Z. Xie, N. M. Kovalchuk, O. K. Matar and M. J. H. Simmons, Soft Matter, 2017, 13, 4616–4628 RSC.
- F. Blanchette, Phys. Rev. Lett., 2010, 105, 13–16 Search PubMed.
- J. D. Paulsen, J. C. Burton and S. R. Nagel, Phys. Rev. Lett., 2011, 106, 114501 CrossRef PubMed.
- C. Vernay, L. Ramos and C. Ligoure, Phys. Rev. Lett., 2015, 115, 198302 CrossRef PubMed.
- D. G. Suciu, O. Smigelschi and E. Ruckenstein, AIChE J., 1967, 13, 1120–1124 CrossRef CAS.
- D. G. Suciu, O. Smigelschi and E. Ruckenstein, AIChE J., 1969, 15, 686–689 CrossRef CAS.
- D. G. Suciu, O. Smigelschi and E. Ruckenstein, J. Colloid Interface Sci., 1970, 33, 520–528 CrossRef CAS.
- E. Ruckenstein, O. Smigelschi and D. G. Suciu, Chem. Eng. Sci., 1970, 25, 1249–1254 CrossRef CAS.
- O. E. Jensen, J. Fluid Mech., 1995, 293, 349–378 CrossRef.
- J. A. Fay, Oil Sea, Springer, US, Boston, MA, 1969, pp. 53–63 Search PubMed.
- P. Joos and J. Pintens, J. Colloid Interface Sci., 1977, 60, 507–513 CrossRef CAS.
- S. Berg, Phys. Fluids, 2009, 21, 32105 CrossRef.
- A. D. Dussaud and S. M. Troian, Phys. Fluids, 1998, 10, 23–38 CrossRef CAS.
- D. W. Camp and J. C. Berg, J. Fluid Mech., 1987, 184, 445–462 CrossRef CAS.
- P. Joos and J. V. Hunsel, J. Colloid Interface Sci., 1985, 106, 161–167 CrossRef CAS.
- V. Bergeron and D. Langevin, Phys. Rev. Lett., 1996, 76, 3152–3155 CrossRef CAS PubMed.
- M. Roché, Z. Li, I. M. Griffiths, S. Le Roux, I. Cantat, A. Saint-Jalmes and H. A. Stone, Phys. Rev. Lett., 2014, 112, 208302 CrossRef.
- B. Wang and S. A. Socolofsky, Phys. Fluids, 2015, 27, 103301 CrossRef.
- V. V. Tarasov, N. F. Kovalenko, G. S. Shcherbakova and D. Zhang, Theor. Found. Chem. Eng., 2006, 40, 111–115 CrossRef CAS.
- M. Santiago-Rosanne, M. Vignes-Adler and M. G. Velarde, J. Colloid Interface Sci., 2001, 234, 375–383 CrossRef CAS PubMed.
- H. Kim, K. Muller, O. Shardt, S. Afkhami and H. A. Stone, Nat. Phys., 2017, 13, 1105–1110 Search PubMed.
- F. Taherian, V. Marcon, E. Bonaccurso and N. F. A. van der Vegt, J. Colloid Interface Sci., 2016, 479, 189–198 CrossRef CAS PubMed.
- H. Kim, J. Lee, T. H. Kim and H. Y. Kim, Langmuir, 2015, 31, 8726–8731 CrossRef CAS PubMed.
- R. Dandekar, A. Pant and B. A. Puthenveettil, J. Fluid Mech., 2017, 829, 304–327 CrossRef CAS.
- L. Bacri and G. Debrégeas, Langmuir, 1996, 12, 6708–6711 CrossRef CAS.
- G. M. Schmid, R. M. Hurd and E. S. Snavely, J. Electrochem. Soc., 1962, 109, 852 CrossRef CAS.
- E. K. Mann and D. Langevin, Langmuir, 1991, 7, 1112–1117 CrossRef CAS.
- C. Huh, M. Inoue and S. G. Mason, Can. J. Chem. Eng., 1975, 53, 367–371 CrossRef CAS.
- J. Ahmad and R. S. Hansen, J. Colloid Interface Sci., 1972, 38, 601–604 CrossRef CAS.
- J. F. Hernández-Sánchez, A. Eddi and J. H. Snoeijer, Phys. Fluids, 2015, 27, 32003 CrossRef.
- M. Jehannin, S. Charton, S. Karpitschka, T. Zemb, H. Möhwald and H. Riegler, Langmuir, 2015, 31, 11484–11490 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm02074d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |