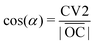Open Access Article
Open Access ArticleCholesterol in phospholipid bilayers: positions and orientations inside membranes with different unsaturation degrees†
Inna
Ermilova
* and
Alexander P.
Lyubartsev

Department of Materials and Environmental Chemistry, Stockholm Universtity, Stockholm, Sweden. E-mail: ina.ermilova@gmail.com; alexander.lyubartsev@mmk.su.se; Tel: +46 728487773 Tel: +46 8161193
First published on 23rd November 2018
Abstract
Cholesterol is an essential component of all animal cell membranes and plays an important role in maintaining the membrane structure and physical–chemical properties necessary for correct cell functioning. The presence of cholesterol is believed to be responsible for domain formation (lipid rafts) due to different interactions of cholesterol with saturated and unsaturated lipids. In order to get detailed atomistic insight into the behaviour of cholesterol in bilayers composed of lipids with varying degrees of unsaturation, we have carried out a series of molecular dynamics simulations of saturated and polyunsaturated lipid bilayers with different contents of cholesterol, as well as well-tempered metadynamics simulations with a single cholesterol molecule in these bilayers. From these simulations we have determined distributions of cholesterol across the bilayer, its orientational properties, free energy profiles, and specific interactions of molecular groups able to form hydrogen bonds. Both molecular dynamics and metadynamics simulations showed that the most unsaturated bilayer with 22:6 fatty acid chains shows behaviour which is most different from other lipids. In this bilayer, cholesterol is relatively often found in a “flipped” configuration with the hydroxyl group oriented towards the membrane middle plane. This bilayer has also the highest (least negative) binding free energy among liquid phase bilayers, and the lowest reorientation barrier. Furthermore, cholesterol molecules in this bilayer are often found to form head-to-tail contacts which may lead to specific clustering behaviour. Overall, our simulations support ideas that there can be a subtle interconnection between the contents of highly unsaturated fatty acids and cholesterol, deficiency or excess of each of them is related to many human afflictions and diseases.
1 Introduction
Nowadays cholesterol is a matter of discussions in many areas, from fitness to drug design. People became concerned over the levels of fat in their bodies without thinking about the importance of having some necessary amounts of this compound in different tissues.1 Cholesterol is present in biomembranes of all animal cells, but its content varies in different parts of organisms. In particular a high content of cholesterol can be found in the brain, which contains about 25% of the whole cholesterol of a human body.2 Furthermore, the ratio between the amounts of cholesterol and lipids is important in the diagnosis of diseases such as Alzheimer's disease,3–11 cancer,3,12,13 HIV,14 atherosclerosis,15 depression16,17 and many others. At the same time many of these diseases are related to the amount of polyunsaturated fatty acids (PUFA) in cells. For instance low ratios of PUFA in frontal gray matter are related to Alzheimer's disease.18 Cholesterol also plays a big role in the development of this disease and is seen as a regulating factor for the accumulation of β-amyloid proteins in specific brain regions.19 Another point of high interest is the role of cholesterol in cancer. Many studies starting from the beginning of the twentieth century have shown that cholesterol molecules do accumulate in solid tumors20 and, for example, in the case of prostatic cancer high levels of this fat in tissues determine it's unhealthiness.12 Understanding the interplay between these principle compounds of biomembranes on the molecular level could help to develop effective drugs for different diseases and even explain why some medicines of a certain class do work for some problems while others from the same “family” do not. For example, statins are known drugs which are used for lowering cholesterol but only a few of these compounds help in decreasing the probability of getting Alzheimer's disease.21,22From the physical–chemical point of view, the complex molecular interactions between saturated lipids, unsaturated lipids and cholesterol give rise to a rich phase behaviour of biomembranes composed of these molecules. Of particular importance are lipid raft structures23–27 which are highly ordered domains with high content of saturated lipids and cholesterol. It is believed that lipid rafts have an important role in cell signalling, which, through the lipid rafts can be affected by changes in lipids and cholesterol composition and thus be related to certain afflictions. In modern soft matter lipid raft domains are well-studied experimentally and by simulations.28–36 The actual ability of cholesterol to build clusters as well as the most common locations of cholesterol in the membrane were investigated by fluorescence spectroscopy,37,38 X-ray diffraction,39 neutron scattering,40–43 and nuclear magnetic resonance (NMR) spectroscopy.44–46 A number of simulation studies reproduced experimental results on clustering of cholesterol, its preferable orientations and the effects on deuterium order parameters of acyl chains in different bilayers.43,47–50 It was also found that in polyunsaturated bilayers cholesterol may adopt alternative orientations with the hydroxyl group located in the center of membrane.43,50 Bennett et al.51 have calculated, by atomistic and coarse-grained simulations, free energies for cholesterol inside 16:0–16:0 PC and 20:4–20:4 PC and found that cholesterol prefers the saturated bilayer with symmetric lipid tails over the polyunsaturated one with symmetric tails as well. Still regardless of the large number of studies, systematic investigation on the role of lipid unsaturation in the behavior of cholesterol in lipid membranes seems to be lacking.
From the computational point of view there are different ways to study the behaviour of a certain molecule in a particular system. One can perform longer molecular dynamics simulations in order to observe the evolution of the system in time and determine various ensemble averages such as the most probable positions and distributions of different molecules, electron and mass density profiles, radial distribution functions, angular distributions, etc. Computations of such properties are meaningful if proper equilibration can be reached on the time scale relevant for molecular dynamics (MD) simulations, which is on the order of microseconds for the current state of hardware development. Understanding of the driving forces leading to a certain behaviour on a longer time scale requires computations of free energy related properties, such as potentials of mean force and binding free energies. These properties determine partitioning (distribution) of a solvent across a bilayer, equilibrium between contents in the solvent and in the bilayer, and are also related to the transfer rate of the molecules through the membrane. For heterogeneous membranes showing domain-like behaviour particular interest is in binding free energy of a molecule to bilayers composed of different lipids since difference in such binding energies shows preference of the molecule to domains with specific lipid composition. In the case of lipid bilayers with cholesterol these free energies characterize to which lipids cholesterol prefers to bind to and which lipid it tries to avoid, and knowledge of such free energies as a function of concentrations would allow explaining the phase diagrams of bilayers composed of different lipids and cholesterol and eventual domain formation.
Computation of free energy related properties usually cannot be done in standard MD simulations due to too long time needed to observe the relevant phenomena. Accelerated sampling methods, such as metadynamics (MetaD), are now well established tools to provide efficient sampling along one or several collective variables (CVs, also called reaction coordinates) and compute changes in free energy for all accessible values of the CVs. The choice of relevant CVs to address specific problems is not a trivial one, and the usefulness of MetaD can depend strongly on the appropriate choice of CVs. To address the problem of distribution of cholesterol in a membrane, a natural choice for CV is the distance between the cholesterol center of mass and the membrane mid-plane. However, with this choice of CV eventual flip-flop moves of cholesterol (which may be responsible for its transport across membrane) are not sampled efficiently. We therefore suggest, alongside CV characterizing the distance between cholesterol and membranes’ centre of mass, to use a second CV which characterizes the orientation of the cholesterol long axis relative to the membrane normal.
In this work we study the behaviour of cholesterol in lipid membranes composed of lipids with varying degrees of unsaturation and length using both standard MD at different cholesterol/lipid fractions and two-dimensional MetaD with a single cholesterol molecule in a bilayer. We have considered ten different bilayers, from fully saturated with fatty acid chains having between 12 and 22 carbons, to strongly unsaturated with fatty acid chains having 22 carbons and six double bonds (22:6-cis chains). Some of the considered lipids form bilayers in a gel phase while being in a pure state, still these lipids are present in certain amounts in biomembranes of living organisms. The choice of lipids studied in this paper covers typical variations of fatty acid chains in living systems and allowed us to investigate systematically the effect of lipid unsaturation and the chain length on how cholesterol affects the corresponding bilayers.
2 Methods and computational details
2.1 Classical molecular dynamics simulations
In order to investigate the behaviour of cholesterol in lipid bilayers with different degrees of unsaturation, and its effect on bilayer properties, a series of microsecond-long MD simulations have been carried out. The lipid/cholesterol ratio was chosen as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, bearing in mind that such a ratio is relevant to human brain tissues.18 Furthermore, for two bilayers, fully saturated (14:0–14:0 PC, or DMPC) and strongly unsaturated (22:6–22:6 PC, or DDPC), we have carried out simulations at several different concentrations of cholesterol. As a reference, we simulated also pure bilayers consisting of the considered lipids, or took data from our previous work.50 The full account of systems studied by MD simulations is given in Table 1.
1, bearing in mind that such a ratio is relevant to human brain tissues.18 Furthermore, for two bilayers, fully saturated (14:0–14:0 PC, or DMPC) and strongly unsaturated (22:6–22:6 PC, or DDPC), we have carried out simulations at several different concentrations of cholesterol. As a reference, we simulated also pure bilayers consisting of the considered lipids, or took data from our previous work.50 The full account of systems studied by MD simulations is given in Table 1.
| Lipid, PC | Number of PC | Number of chol. | Number of water mol. |
|---|---|---|---|
| 14:0–14:0 | 128 | 32 | 6400 |
| 14:0–14:0 | 128 | 64 | 6400 |
| 14:0–14:0 | 128 | 85 | 6400 |
| 14:0–14:0 | 128 | 128 | 6400 |
| 22:6–22:6 | 128 | 32 | 6400 |
| 22:6–22:6 | 128 | 64 | 6400 |
| 22:6–22:6 | 128 | 85 | 6400 |
| 22:6–22:6 | 128 | 128 | 6400 |
| 18:0–22:6 | 128 | 128 | 6400 |
| 22:0–22:0 | 128 | 128 | 6400 |
| 18:0–20:4 | 128 | 128 | 6400 |
| 20:4–20:4 | 128 | 128 | 6400 |
| 20:0–20:0 | 128 | 128 | 6400 |
| 18:0–18:0 | 128 | 128 | 6400 |
| 18:0–18:2 | 128 | 128 | 6400 |
| 18:2–18:2 | 128 | 128 | 6400 |
| 14:0–14:0 | 128 | 0 | 3840 |
| 22:6–22:6 | 128 | 0 | 5120 |
| 22:0–22:0 | 128 | 0 | 3840 |
| 20:4–20:4 | 128 | 0 | 5120 |
| 20:0–20:0 | 128 | 0 | 3840 |
| 18:0–18:0 | 128 | 0 | 3840 |
| 18:0–18:2 | 128 | 0 | 3840 |
| 18:2–18:2 | 128 | 0 | 3840 |
Each system was simulated under a pressure of 1 atm and a temperature of 303 K in the NPT ensemble. This temperature is typical for many experimental studies. The leap-frog integrator was chosen with a time-step of 2 fs. Electrostatics was taken care of by the Fast Smooth Particle Mesh Ewald algorithm with a Fourier spacing of 0.12 nm.52 The cut-off distance for the real space Coulomb and Lennard-Jones interactions was set to 0.9 nm. The temperature coupling was performed using velocity rescaling53 with a stochastic term while the pressure coupling was carried out using a Berendsen barostat54 with a semi-isotropic coupling type (with separate fluctuations in the XY-plane and along the Z-axis). The time constants were equal to 0.5 ps and 10 ps for the temperature and pressure couplings respectively. The compressibility was set to 4.5 × 10−5 bar−1. The LINCS algorithm has been used in order to put constraints on all bonds with the number of iterations equal to 12.55 The output for trajectories was done every 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. Averages were collected over the last 500 ns of the simulated trajectories.
000 steps. Averages were collected over the last 500 ns of the simulated trajectories.
All simulations were performed using all-atomistic SLipids force field50,56–58 and Gromacs (v.4.6.7) software.59
2.2 Well-tempered MetaD simulations with two collective variables
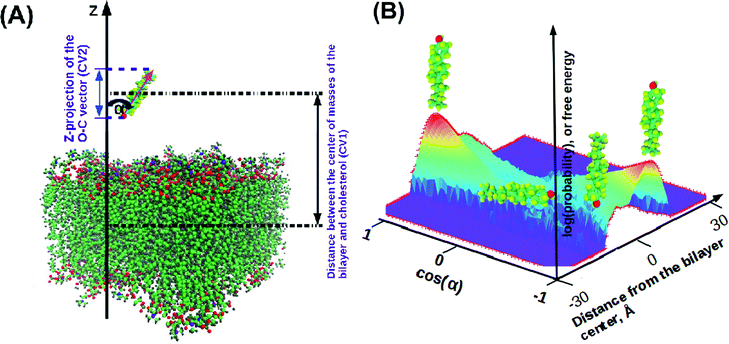
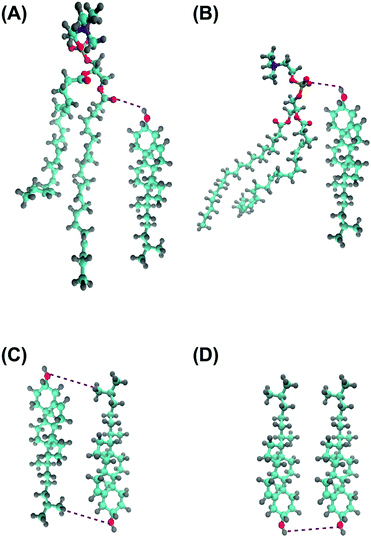
In order to characterize the behaviour of cholesterol in lipid bilayers in the thermodynamic long-term limit and to compute the potentials of mean force and binding free energies, we carried out metadynamics simulation of a single cholesterol molecule in bilayers of different compositions, listed in Table 2. In this work we employed a well-tempered MetaD algorithm60–62 with two collective variables (see Fig. 1(A)): the z-distance between the center of mass of the cholesterol molecule and the center of mass of the bilayer (denoted as CV1), and the Z-projection of the O–C vector in the cholesterol molecule, going from the oxygen of the hydroxyl group to the last junction carbon in the cholesterol tail (denoted as CV2). The length of the O–C vector in cholesterol is about 15 Å with relatively small fluctuations (typically within 1 Å), thus the second collective variable, being divided by the length of the O–C vector, becomes equal to the cosine of the angle between the cholesterol long axis and membrane normal (denoted as α, see Fig. 1A). The resulting free energy landscape presented as a function of CV1 and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α thus shows the most probable locations of the cholesterol molecule in the bilayer and its orientation.
α thus shows the most probable locations of the cholesterol molecule in the bilayer and its orientation.
| Lipid, PC | Num. of lipids | Num. of water | Time, μs |
|---|---|---|---|
| 12:0–12:0 | 98 | 4900 | 6 |
| 14:0–14:0 | 98 | 4900 | 6 |
| 18:0–18:0 | 98 | 4900 | 6 |
| 18:0–18:2 | 98 | 4900 | 6 |
| 18:2–18:2 | 98 | 4900 | 6 |
| 20:0–20:0 | 98 | 4900 | 8 |
| 20:4–20:4 | 98 | 4900 | 6 |
| 22:0–22:0 | 98 | 4900 | 6 |
| 22:6–22:6 | 98 | 4900 | 6 |
For MetaD simulations we used Plumed plugin (v 2.2.3) to Gromacs.63 All MetaD simulations were performed in the NVT ensemble, using 2 fs time-step. Most of the settings were the same as for NPT MD simulations except that we did not use any pressure coupling in the canonical ensemble. In each case the simulation box was preliminary equilibrated using classical MD in the NPT ensemble with parameters T = 303 K and p = 1 atm before the MetaD runs with included bias have started. The CV limits were determined as [−4;4] nm for CV1 and [−1.5;1.5] nm for CV2, with Gaussian widths of 0.05 nm and 0.02 nm respectively. The initial height of Gaussians was set to 1.2 kJ mol−1 and the bias factor was chosen to be equal to 25. The simulations were running for 6 μs, except one which was prolonged to 8 μs. Evaluation of the convergence of MetaD simulations is given in the ESI,† Fig. S18–S24. We evaluate the uncertainty of the free energy calculations as being within 3 kJ mol−1 except the case of the gel-phase 22:0–22:0 PC bilayer which we evaluate as not fully converged.
3 Results
3.1 Areas per lipid
The area per lipid is an important characteristic of a bilayer. This value is often used as a reference of membrane organization, other properties often show correlations with the average area per lipid. Analysis of lipid areas for mixtures of DPPC (16:0/16:0 PC) with cholesterol was carried out in previous works.64,65 In a multicomponent bilayer, the average lipid area can be determined either with respect to all kinds of molecules including cholesterol, or as partial area with respect to a certain lipid type.65 Accurate calculations of partial lipid area require the determination of derivatives of the total area with respect to concentrations,65 which pose certain numerical problems. We therefore provide, in Table 3, the results for the total area divided by the total number of molecules (lipids and cholesterols, atot), and the total area divided by the number of PC lipids only (alip). While the first type of area decreases with the added cholesterol (which is natural since a cholesterol molecule takes less space than a PC lipid), the area determined in the second way is typically increasing (since cholesterol still takes some space). However, the behaviour of areas in the mixed systems is certainly not additive (or non-ideal). Thus, addition of 20% of cholesterol to the DMPC bilayer does not change the lipid area, and addition of 33% of cholesterol results only in a small increase of the area (from 62.7 to 65.8 Å2 per lipid), which is consistent with the observation of paper65 for liquid phase 16:0–16:0 PC bilayers. In the 22:6–22:6 PC bilayer, addition of 20% of cholesterol results in a decrease of the area from 70 to 59.3 Å2 per lipid. This effect is related to the “condensing effect” of cholesterol66,67 which makes lipids more ordered, while cholesterol occupies space released by the lipids. Data of Table 3 show that this effect is noticeably stronger in unsaturated bilayers. Our results on changes in areas upon addition of cholesterol are also qualitatively consistent with earlier Langmuir film balance measurements in monolayers by Smaby et al.,68 where reduction of the area per molecule upon addition of 50% of cholesterol was from 75 to 50 Å2 in the case of 22:6–22:6 PC and from 58 to 40 Å2 for 14:0–14:0 PC. Analysis of other data of work68 also shows stronger reduction of area per molecule in polyunsaturated monolayers compared to monounsaturated or fully saturated. On the other hand, the results of paper68 suggest also that a change in elasticity of monolayers is minimal for polyunsaturated lipids. While there exists data that cholesterol has little effect on certain properties of highly unsaturated bilayers such as 20:4–20:4 and 22:6–22:6 PC,69,70 other properties can be strongly affected.| Lipid (PC) + chol. | a tot | a (0)lip | a lip | a chol |
|---|---|---|---|---|
| 14:0–14:0 + 20% | 50.1 | 62.7 | 62.7 | 0 |
| 14:0–14:0 + 33% | 44.1 | 65.8 | 6.2 | |
| 14:0–14:0 + 40% | 42.5 | 70.6 | 11.9 | |
| 14:0–14:0 + 50% | 40.3 | 80.5 | 17.8 | |
| 22:6–22:6 + 20% | 48.6 | 70.0 | 59.3 | −42.8 |
| 22:6–22:6 + 33% | 52.2 | 74.9 | 9.8 | |
| 22:6–22:6 + 40% | 48.6 | 76.3 | 9.5 | |
| 22:6–22:6 + 50% | 40.5 | 81.0 | 11.0 | |
| 18:0–22:6 + 50% | 40.0 | 68.850 | 79.9 | 11.1 |
| 22:0–22:0 + 50% | 38.3 | 50.4 | 76.6 | 26.2 |
| 18:0–20:4 + 50% | 42.3 | 69.650 | 84.6 | 15.0 |
| 20:4–20:4 + 50% | 43.6 | 73.8 | 87.0 | 14.0 |
| 20:0–20:0 + 50% | 38.9 | 49.0 | 78.0 | 29.0 |
| 18:0–18:0 + 50% | 39.3 | 49.0 | 78.5 | 29.5 |
| 18:0–18:2 + 50% | 43.5 | 67.0 | 86.9 | 19.9 |
| 18:2–18:2 + 50% | 45.4 | 70.4 | 90.7 | 20.3 |
The condensing effect of cholesterol is related to the ordering effect.67 It is well documented that addition of cholesterol to liquid phase bilayers increases the order of acyl chains which is manifested by an increase of the NMR order parameters.67,71 The effect of cholesterol on gel phase lipid bilayers is however opposite, addition of a large amount of cholesterol changes their state to a more disordered liquid ordered phase.72 This ordering effect can be seen in our simulations and is illustrated in Fig. S1 of the ESI:† while simulated order parameters increase upon addition of cholesterol in 14:0–14:0 and 22:6–22:6 PC bilayers, they generally decrease (particularly in the lower parts of the lipid tails) in the case of gel phase 20:0–20:0 PC bilayers.
To characterize the effect of cholesterol on areas for different lipid mixtures, we define the contribution of cholesterol to the total bilayer area (we call it the excess cholesterol area) according to:
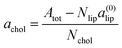 | (1) |
3.2 Electron and mass density profiles
Information about cholesterol distribution inside bilayers can be gained from the analysis of the electron and mass density profiles, which can be experimentally obtained by X-ray and neutron scattering respectively. Electron density profiles are calculated from the total number of electrons on each type of atom (which is equal to the atom number in the periodic table), corrected by the partial atom charge, while mass density profiles are calculated from the masses of atoms. For these calculations we have used a trajectory analysis suite from the MDynaMix74 package. In Fig. 2 the electron density profiles for bilayers formed by 14:0–14:0 PC and 22:6–22:6 PC with different concentrations of cholesterol and difference profiles are displayed. The mass density profiles for the same bilayers can be found in the ESI† in Fig. S2, and their shape is similar to that of the electron density profiles. For other bilayers, electron and mass density profiles are shown in Fig. S3–S5 of the ESI.†For 14:0–14:0 PC bilayers the electron and mass density profiles behave similarly with the change in cholesterol content: the more we add cholesterol, the deeper minima we have in the center of the bilayer on all curves, and the more separated are the maxima showing the locations of the lipid head groups. Bulky and rigid cholesterol molecules inserted among acyl chains create an extra space in the bilayer centre. The width of such a created low density region depends on the relative lengths of the phospholipid and cholesterol molecules and on the amount of cholesterol (see difference profiles in Fig. 2(B) and Fig. S2(B), ESI†). For polyunsaturated bilayer 22:6–22:6 PC (Fig. 2(C and D)) we see somewhat different behavior when we add more cholesterol. The minimum in the bilayer center goes deeper with an increasing concentration of cholesterol and, furthermore, we can see two local maxima on each side of the curves for 50%. A similar behavior with minor variations is seen for other unsaturated bilayers. The results on electron and mass density profiles for saturated lipid bilayers with longer chains (18:0–18:0, 20:0–20:0, 22:0–22:0), which adopt a gel phase, are collected in the ESI† (Fig. S3(A, B) and S5(A–D)). In these bilayers the maxima of electron and mass density from the lipid head groups are shifted towards the bilayer center, which is different from the liquid crystalline phase bilayers, and is consistent with the discussed above “disordering” effect of cholesterol on gel phase bilayers.
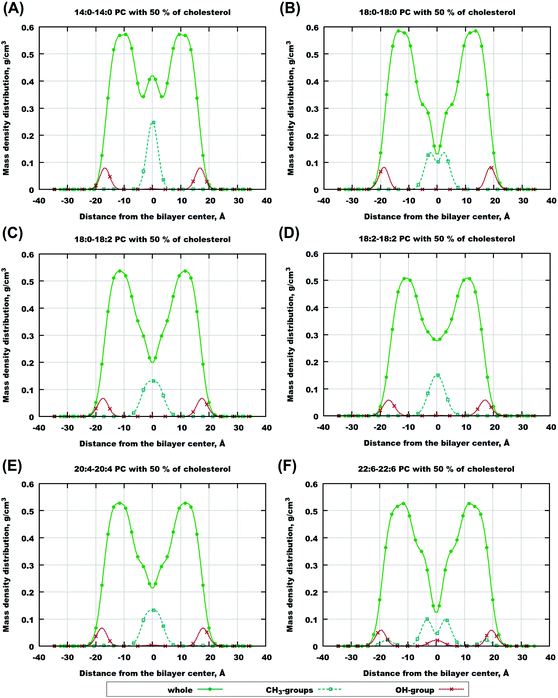
More insight into what affects various features of the electron and mass density profiles and which atoms are responsible for them can be gained from contributions of different atoms to the profiles. In Fig. 3, a comparison of such contributions obtained from simulations at 50% of cholesterol for six selected bilayers is shown. The contributions were calculated from the whole cholesterol molecules, and from two groups: the OH-group in the cholesterol head and two methyl groups in the end of the cholesterol tail (denoted here and below as “CH3-groups”), and are displayed in Fig. 3 and in Fig. S6–S8 of the ESI.† For 14:0–14:0 PC (Fig. 3(A)) one can see a sharp peak in the middle of the bilayer from methyl groups, and two sharp peaks from OH-groups on both sides from the bilayer center. These features correspond to the traditional “upright” position of cholesterol, with OH-groups orienting themselves towards the head groups of lipids, and ends of cholesterol tails from both monolayers meeting at the bilayer center. For bilayers with longer chains (18:0–18:0, Fig. 3(B)), we have two separated maxima in the methyl group density near the center of the bilayer, which means that cholesterol molecules belonging to different layers become separated. Also we can suggest more restricted relocation of cholesterol across the bilayer due to a sharper local minimum of the cholesterol density in the center of the bilayer. If we compare bilayers consisting of lipids with 18 carbons in lipid tails we can see that for both unsaturated 18:0–18:2 PC and 18:2–18:2 PC separation of CH3 group density maxima disappears, and the profiles are similar to each other. Then if we go further to highly unsaturated bilayers we can notice that the total contribution from cholesterol molecules decreases in the center of the bilayer with increasing unsaturation and chain length (see Fig. 3(D–F)).
Furthermore, in the most unsaturated bilayers, 22:6/22:6 PC and 22:6–18:0 PC, we see a new feature (actually, it is also seen very weakly for 20:4–20:4 PC bilayers): additional maxima of the hydroxyl group in the bilayer center and maxima of methyl groups closer to the location of the lipid headgroups. This is related to the alternative orientations of cholesterol: the one in which cholesterol is oriented parallel to the bilayer normal with the headgroup in the bilayer center and the tail directed to the membrane surface (“flipped” orientation), and the one in which the whole cholesterol is located in the bilayer center parallel to the membrane plane. These alternative configurations were discussed previously in experimental studies40,42,75 and observed in simulations.50 Noticeably, water molecules, eventually interacting with the cholesterol hydroxyl group while cholesterol is in the “upright” position, do not follow the hydroxyl group when it moves to the membrane center: density profiles of water remain zero in the bilayer central region even in polyunsaturated bilayers.
Comparing cholesterol density profiles for the same bilayers but with different concentrations of cholesterol (see Fig. S6, ESI†) one can conclude that they have a similar shape. For example, in the case of 20% of cholesterol in 14:0–14:0 PC bilayers (Fig. S6(A) in the ESI†) the total density has 3 local maxima as in the case of 50% cholesterol concentration, while for 22:6–22:6 PC (Fig. S6(B) in the ESI†) we can only see two maxima corresponding to two leaflets, which corresponds also to the case of 50% cholesterol concentration in 22:6–22:6 PC bilayers. The same picture is observed for 33% and 40% cholesterol concentration, as well as for distributions of hydroxyl and methyl groups of cholesterol.
3.3 Radial distribution functions (RDFs)
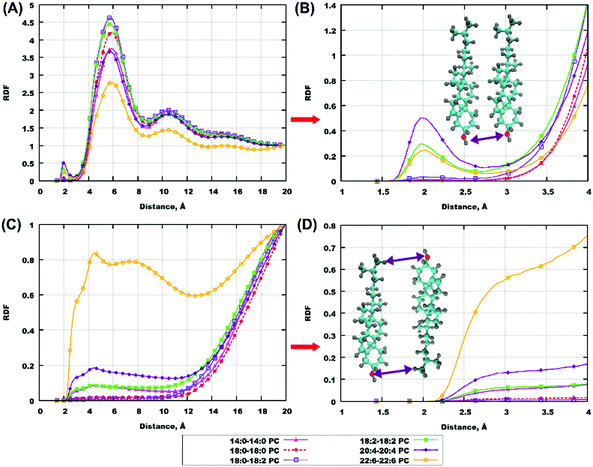
Radial distribution functions (RDFs) provide important information on the associative behaviour of different atoms and molecular groups, and thus on specific interactions, leading to a certain type of behaviour. Interactions between molecules in biological systems can quite often be explained by hydrogen bonding,76–82 which, in MD simulations, comes as a result of a combination of an electrostatic attraction and short-range repulsion between a positively charged hydrogen atom on one molecule (donor) and a negatively charged atom on another molecule (acceptor). In order to investigate the role of hydrogen bonding in the behaviour of cholesterol-containing bilayers, we calculated RDFs for some atoms which can be potential donors and acceptors of hydrogen bonds. Furthermore, we calculated some other RDFs relevant for understanding eventual clustering of cholesterol in lipid bilayers which was discussed in previous works.50,75 All results of this subsection refer to bilayers with 50% ratio of cholesterol.Fig. 4(A and B) shows RDFs between hydroxyl groups on cholesterol molecules and in Fig. 4(C and D) one can see RDFs between the ending methyl-group and hydroxyl group of cholesterol, with panels (A and C) showing RDFs in the whole range of distances and panels (B and D) showing RDFs at close distances. For some bilayers the same information is shown in Fig. S8 and S9 of the ESI.† One can see a small maximum of the hydroxyl-hydroxyl RDF at 2 Å distance in the case of polyunsaturated lipids (18:2–18:2, 20:4–20:4 and 22:6–22:6 PC) indicating the possibility of hydrogen bond formation between cholesterol molecules in these bilayers. A major maximum at about 6 Å is present in all hydroxyl-hydroxyl RDFs; it corresponds to some close association of cholesterol molecules but without the formation of hydrogen bonds between hydroxyl groups. In the case of RDFs between cholesterol hydroxyl and methyl groups, the highly unsaturated 22:6–22:6 PC shows clearly different behavior from others: the RDF is relatively high already at small (from 3 Å) distances. This indicates the presence of conformations with close head-to-tail contacts of cholesterol. It is likely that such configurations are responsible for the presence of cholesterol headgroups in the central bilayer region, which was noted in the previous section.
Cholesterol molecules are also involved in hydrogen bonding with lipids, which was discussed in a number of previous studies.31,47,67 In our simulations, for all bilayers there is a high RDF maximum for interactions between hydrogen of the cholesterol hydroxyl group and oxygens on ester groups of lipid tails (Fig. 5(A, B) and Fig. S9(A, B), S10(A, B) in the ESI†). These maxima appear at approximately the same distance for all bilayers, which is about 1.8 Å indicating the presence of hydrogen bonds. Another interesting point is RDF between hydrogens of CH3-groups of lipid tails and oxygen in the hydroxyl group of cholesterol molecules. While for most of the lipids this RDF is low at short distances, we can observe a relatively high RDF maximum at 3–4 Å for the most polyunsaturated 22:6–22:6 PC bilayer (Fig. 5(C and D)), and a similar but weaker maximum for 18:0–22:6 PC (Fig. S10(C and D) in the ESI†). This is again confirmation that in bilayers containing 22:6 chains there is a not negligible content of “flipped” cholesterol molecules with the head in the membrane center.
Some other RDFs, between hydrogen of the hydroxyl group of cholesterol and oxygen of the phosphate group of lipids, and oxygen of the hydroxyl group of cholesterol and hydrogen of the CH-group (which is a joint point of the two tails), are shown in the ESI,† Fig. S11–S14. These RDFs show that hydrogen bonding of cholesterol to phosphate groups of lipids is essential but generally weaker than to lipid ester groups.
3.4 Angular distributions
Analysis of the mass density profiles and RDFs indicates the presence of different orientations of cholesterol in bilayers with a high degree of unsaturation. In order to get more clear information about cholesterol orientational behavior, angular distributions of cholesterol molecules have been calculated depending on the positions of these molecules in the simulated bilayers. The Z-position of cholesterol was determined by half of the O–C vector connecting oxygen in the hydroxyl group and carbon in the end of the cholesterol tail, and angle α was taken between the O–C vector and the direction of the Z-axis, see Fig. 1. A similar analysis for cholesterol in DMPC bilayers, but with a molecular vector bound to the cholesterol ring system, was used previously by Khelashvili et al.83Density maps (in terms of logarithm of probability) of the distribution of the position and orientation of cholesterol in different bilayers (all in 50% mixtures with cholesterol) are shown in Fig. 6 and Fig. S15 and S16 of the ESI.† The distributions are not symmetrized, while in principle they should be symmetrical relative to inversion around the central point. All distributions show maxima at cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = ±1 and at about 10 Å from the bilayer center, with opposite signs of cos
α = ±1 and at about 10 Å from the bilayer center, with opposite signs of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α and the Z-coordinate of cholesterol, which corresponds to the “upright” position of cholesterol aligned along the bilayers normal with the head group directed to the membrane surface.
α and the Z-coordinate of cholesterol, which corresponds to the “upright” position of cholesterol aligned along the bilayers normal with the head group directed to the membrane surface.
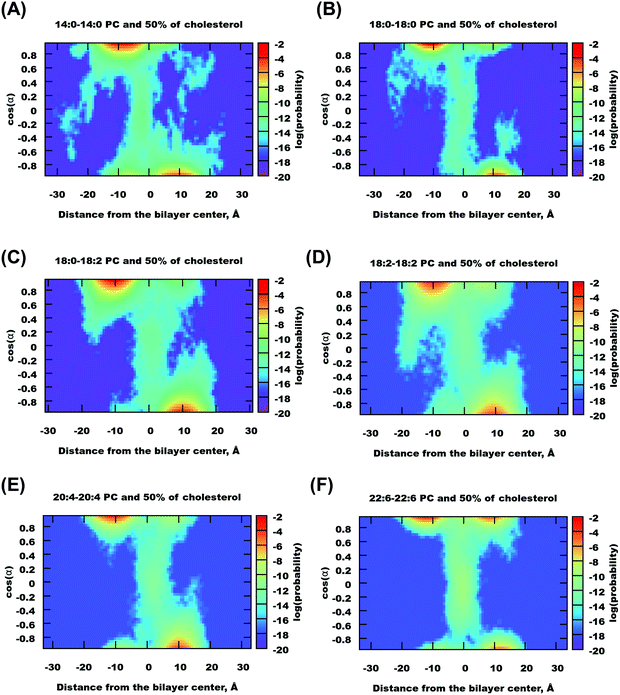 | ||
| Fig. 6 Density maps showing distribution of cholesterol as a function of its distance to the membrane middle plane and orientation, for selected bilayers containing 50% mol of cholesterol. | ||
A distinguishing feature appears for unsaturated 22:6–22:6 PC bilayers (which is also seen in the case of 18:0–22:6 bilayers, as well as in some others in a weaker fashion): a density maximum with a positive coordinate of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α and a Z-coordinate of cholesterol. This corresponds to the flipped orientation of cholesterol with the hydroxyl group near the membrane center and tail directed to the membrane surface. Note that such configurations appeared in our simulation mostly in one of the monolayers. We can note that for all bilayers which adopt a liquid disordered phase in a pure state (without cholesterol), we observed relatively frequent, on the time scale of the order of 10 ns, translocations of cholesterol from one monolayer to the other (while no flip-flop motions of lipids were observed). It might be because the preference for the “flipped” orientation of cholesterol in 22:6–22:6 PC bilayers is related to the presence of “head-to-tail” contacts of cholesterol molecules discussed in the previous section. However processes of association and cluster formation between cholesterol molecules may take longer time so that even 1 μs simulation may not be enough to reach a full convergence. Note also that in experiments, asymmetric distribution of cholesterol was observed experimentally in unilamellar vesicles of monounsaturated phospholipids84 and was ascribed to different curvatures of the two layers.
α and a Z-coordinate of cholesterol. This corresponds to the flipped orientation of cholesterol with the hydroxyl group near the membrane center and tail directed to the membrane surface. Note that such configurations appeared in our simulation mostly in one of the monolayers. We can note that for all bilayers which adopt a liquid disordered phase in a pure state (without cholesterol), we observed relatively frequent, on the time scale of the order of 10 ns, translocations of cholesterol from one monolayer to the other (while no flip-flop motions of lipids were observed). It might be because the preference for the “flipped” orientation of cholesterol in 22:6–22:6 PC bilayers is related to the presence of “head-to-tail” contacts of cholesterol molecules discussed in the previous section. However processes of association and cluster formation between cholesterol molecules may take longer time so that even 1 μs simulation may not be enough to reach a full convergence. Note also that in experiments, asymmetric distribution of cholesterol was observed experimentally in unilamellar vesicles of monounsaturated phospholipids84 and was ascribed to different curvatures of the two layers.
Besides strong maxima, one can see, for all bilayers, a “transition path” connecting both monolayers. It is more populated for unsaturated bilayers (22:6–22:6, 18:2–18:2, 20:4–20:4, and 18:0–22:6) with a local maximum at zero cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α and Z-coordinate, which correspond to cholesterol lying plain in the middle of the bilayer. Translocations of cholesterol between the monolayer go typically through this “transition state”. We estimated typical time which cholesterol molecules spent in the center of the bilayer with orientation parallel to the bilayer surface (defined by conditions that the cholesterol center of mass is within 3 Å from the bilayer center, and the angle between the cholesterol long axis and the membrane plane is within 30°), and found that this time is short and typically below 100 ps, while the fraction of such molecules is within 2% in the case of 22:6–22:6 PC bilayers or lower. For bilayers with 22:6 chains, one can also observe translocations when a cholesterol molecule goes from one monolayer to the other without a change in orientation, thus adopting a “flipped” orientation in the new location.
α and Z-coordinate, which correspond to cholesterol lying plain in the middle of the bilayer. Translocations of cholesterol between the monolayer go typically through this “transition state”. We estimated typical time which cholesterol molecules spent in the center of the bilayer with orientation parallel to the bilayer surface (defined by conditions that the cholesterol center of mass is within 3 Å from the bilayer center, and the angle between the cholesterol long axis and the membrane plane is within 30°), and found that this time is short and typically below 100 ps, while the fraction of such molecules is within 2% in the case of 22:6–22:6 PC bilayers or lower. For bilayers with 22:6 chains, one can also observe translocations when a cholesterol molecule goes from one monolayer to the other without a change in orientation, thus adopting a “flipped” orientation in the new location.
Fig. S15 of the ESI† shows density maps for cholesterol in 14:0–14:0 and 22:6–22:6 PC bilayers at different cholesterol concentrations. The maps for the same bilayer are similar. One can note that “flipped” configurations almost disappear with lower cholesterol concentration, thus the presence of such configurations is most likely related to high cholesterol concentration at which cluster formation with “head-to-tail” cholesterol orientations becomes favourable.
3.5 Metadynamics simulations
We have also carried out metadynamics simulation of a single cholesterol molecule in a number of bilayers, using collective variables equivalent to the coordinates of density maps analysed in the previous section. The aim is to compare free energy profiles of cholesterol in bilayers composed of different lipids, in order to determine free energy barriers characterising which bilayers cholesterol molecules go easier through and how the saturation of lipid tails affects this process. Metadynamics simulation yields two-dimensional maps of free energy as a function of position and orientation of cholesterol W(z,x) (with x = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α), which also define the logarithm of probability for cholesterol to have specific values of z and x. These maps are similar to the two-dimensional distributions of cholesterol molecules discussed in the previous section, with two important differences: (i) they are computed for a single cholesterol molecule in pure bilayers (that is, in the limit of low cholesterol concentration) and (ii) due to advanced sampling used in metadynamics, the free energy maps can be evaluated in the whole space of collective variables and not only in configurations visited during canonical MD simulations.
α), which also define the logarithm of probability for cholesterol to have specific values of z and x. These maps are similar to the two-dimensional distributions of cholesterol molecules discussed in the previous section, with two important differences: (i) they are computed for a single cholesterol molecule in pure bilayers (that is, in the limit of low cholesterol concentration) and (ii) due to advanced sampling used in metadynamics, the free energy maps can be evaluated in the whole space of collective variables and not only in configurations visited during canonical MD simulations.
Two-dimensional free energy maps can be further integrated into one-dimensional profiles (potential of mean force, or PMF):
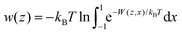 | (2) |
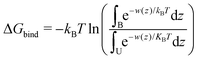 | (3) |
Two-dimensional maps for cholesterol in a number of bilayers are shown in Fig. 7 and for some other bilayers in Fig. S17 of the ESI.† One can see that for most of the bilayers, there are free energy minima corresponding to traditional “upright” positions, i.e. when cholesterol “likes” to be oriented with the hydroxyl group towards lipid head-groups and it is less common to find it in the center of the bilayer. With an increase of lipid unsaturation (18:2–18:2, 20:4–20:4, and especially 22:6–22:6 PC) the minima become wider, and the path connecting them becomes lower. These features correlate well with the observation from the cholesterol probability maps in the previous section, confirming that in highly unsaturated membranes cholesterol more easily adopts a position in the center of the membrane and transfers from one monolayer to another. Generally we can observe that in polyunsaturated bilayers cholesterol has more freedom to move visiting a wider area of (z, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α) parameters.
α) parameters.
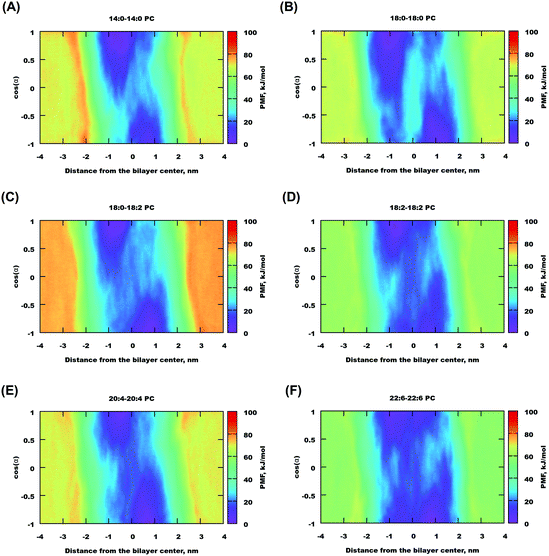 | ||
| Fig. 7 Free energy maps for selected lipid bilayers (the free energy minimum is set to zero) as a function of cholesterol distance to the membrane middle plane and orientation. | ||
The free energy profiles for gel-phase bilayers 20:0–20:0 PC and 22:0–22:0 PC (shown in Fig. S15(B and C) of the ESI†) are not symmetric, which we prescribe that metadynamics did not fully converge even in several μs simulations. It is certainly difficult to push a cholesterol molecule through a gel-phase bilayer even in metadynamics simulations using bias potential.
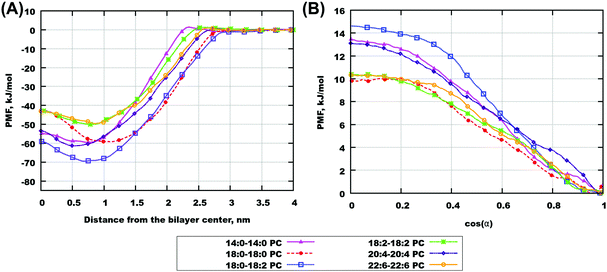
Fig. 8(A) and Fig. S18 of the ESI† show one-dimensional PMF for different bilayers. The zero of these PMFs was chosen in the water phase, so that differences between the PMFs show preference of cholesterol to one or another type of lipid. All PMFs have a minimum between −50 and −70 kJ mol−1 located at distances of 5–10 Å from the bilayer center and a local maximum in the bilayer center. A similar result was obtained previously by Bennett et al. for simulations of 16:0–16:0 and 20:4–20:4 PC using GROMOS-Berger force field.51 The minimum of PMF in that work was located at somewhat larger distance from the membrane center than in our work, which is explained by that in the work by Bennett et al.51 the PMF was computed relative to the hydroxyl group of cholesterol.
Binding free energies computed by integration of the PMFs according to eqn (3) are given in Table 4. All calculations except 22:0–22:0 PC have reached the desired criteria of convergence within 3 kJ mol−1. The strongest binding free energies of cholesterol were obtained for 18:0–18:2 PC and then for 12:0–12:0 PC bilayers, while the lowest (except the not well converged gel phase 22:0–22:0 PC bilayer) was observed for 22:6–22:6 PC and 18:2–18:2 PC bilayers. It is difficult to see a clear dependence of the binding free energy on lipid unsaturation, likely because they differ also by the length of hydrocarbon chains, and that some of the bilayers appears in a gel phase. Still, some trend of stronger binding with less unsaturation and with shorter chains can be noted.
| Lipid, PC | ΔGbind, kJ mol−1 | ΔGorient, kJ mol−1 |
|---|---|---|
| 12:0–12:0 | −65.1 | 14.9 |
| 14:0–14:0 | −57.0 | 15.6 |
| 18:0–18:0 | −57.4 | 13.3 |
| 18:0–18:2 | −68.9 | 14.6 |
| 18:2–18:2 | −47.8 | 11.4 |
| 20:0–20:0 | −58.3 | 21.6 |
| 20:4–20:4 | −58.9 | 12.7 |
| 22:0–22:0 | −32.8 | 33.2 |
| 22:6–22:6 | −47.0 | 10.4 |
Integration of the two-dimensional energy surface over the first collective variable, z, produces a free energy profile as a function of orientational angle α. Since positive values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α in the upper bilayer are equivalent to negative values of cos
α in the upper bilayer are equivalent to negative values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α (of the same magnitude) in the lower bilayer, we symmetrized the profile and show it only for positive cos
α (of the same magnitude) in the lower bilayer, we symmetrized the profile and show it only for positive cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α in Fig. 8(B). The height of the profile in the point of maxima (for most of the bilayers at cos
α in Fig. 8(B). The height of the profile in the point of maxima (for most of the bilayers at cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = 0, corresponding to cholesterol orientation parallel to the bilayer surface) is given in Table 4. This quantity, having sense of the free energy barrier of flip-flop motion of cholesterol, is found in the range of 10–16 kJ mol−1 for a liquid-crystalline phase bilayer, with lower values for the most unsaturated bilayers. One can see a trend of lower orientational free energy barrier for bilayers composed of polyunsaturated lipids. Note that this barrier corresponds to the reorientation of cholesterol relative to the z-axis, and not necessary to the motion of cholesterol between bilayer leaflets which can go without reorientation. For saturated bilayers with long chains, which are in the gel phase, the barrier is higher (see also Fig. S16(B) of the ESI†). Moreover minima of the free energy profiles are found at some angles other than 0°. The reason is that these bilayers are present in a gel phase where lipids are tilted, and cholesterol may have a preference to be tilted alongside lipids.
α = 0, corresponding to cholesterol orientation parallel to the bilayer surface) is given in Table 4. This quantity, having sense of the free energy barrier of flip-flop motion of cholesterol, is found in the range of 10–16 kJ mol−1 for a liquid-crystalline phase bilayer, with lower values for the most unsaturated bilayers. One can see a trend of lower orientational free energy barrier for bilayers composed of polyunsaturated lipids. Note that this barrier corresponds to the reorientation of cholesterol relative to the z-axis, and not necessary to the motion of cholesterol between bilayer leaflets which can go without reorientation. For saturated bilayers with long chains, which are in the gel phase, the barrier is higher (see also Fig. S16(B) of the ESI†). Moreover minima of the free energy profiles are found at some angles other than 0°. The reason is that these bilayers are present in a gel phase where lipids are tilted, and cholesterol may have a preference to be tilted alongside lipids.
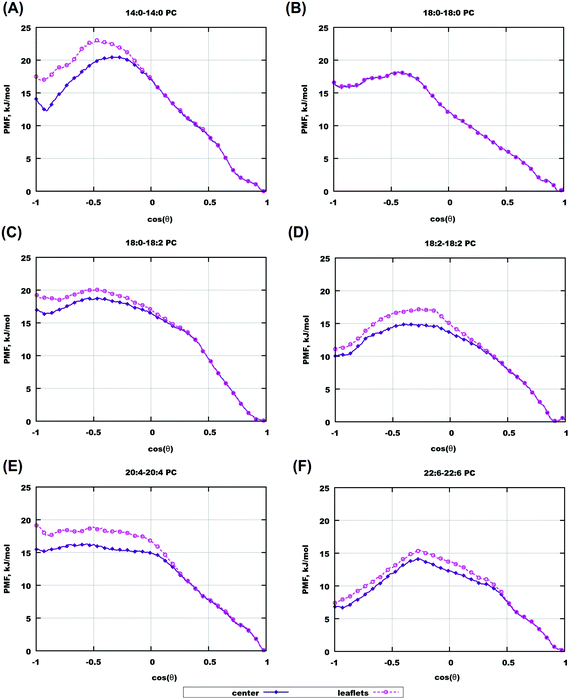
Orientational free energies displayed in Fig. 8(B) are functions of angle α between the O–C cholesterol vector and the Z-axis of the system, and e.g. α = 0° corresponds to the upright cholesterol orientation in the lower bilayer while to the “flipped” configuration for cholesterol in the upper layer. It might be of interest to determine orientational free energies relative to the bilayer normal directed always from the bilayer surface to the midplane. That is, we define angle θ which is equal to α for z < 0 (cholesterol in the lower leaflet) and θ = 180° − α for z > 0 (cholesterol in the upper monolayer). Furthermore, we define such orientational free energy relative to different depths in the bilayer. Such “relative” orientational free energies, which distinguish directions “in” and “out” of bilayers, are shown in Fig. 9 and in Fig. S19 of the ESI.† In all cases, these free energy profiles were calculated over two z-ranges, one when cholesterol is clearly located in one of the monolayers (between 3 and 15 Å from the center), and another with cholesterol located within 3 Å from the center. One can see that for all bilayers (except the gel-phase saturated bilayers with long chains), the free energy minimum appears at cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 1 which corresponds to the “upright” orientation of cholesterol in the bilayer. For some bilayers there exists another metastable free energy minimum at cos
θ = 1 which corresponds to the “upright” orientation of cholesterol in the bilayer. For some bilayers there exists another metastable free energy minimum at cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = −1 corresponding to the “flipped” orientation of cholesterol, which is most strongly seen for 22:6–22:6 PC bilayers. There is however no local minima at cos
θ = −1 corresponding to the “flipped” orientation of cholesterol, which is most strongly seen for 22:6–22:6 PC bilayers. There is however no local minima at cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 0 which corresponds to cholesterol orientation parallel to the bilayer surface, for all considered bilayers. Thus positioning of cholesterol lying in the center of the bilayer, while possible and becoming noticeably populated for polyunsaturated bilayers at high cholesterol content, is thermodynamically unstable for a single cholesterol molecule in pure bilayers, including the case of 22:6–22:6 PC bilayers. One can also note that there is no straightforward relationship between lipid unsaturation and the free energy difference between upright and flipped orientations, for example the free energy of the flipped conformation becomes large for 20:4–20:4 bilayers, but then again becomes smaller for 18:2–18:2 bilayers.
θ = 0 which corresponds to cholesterol orientation parallel to the bilayer surface, for all considered bilayers. Thus positioning of cholesterol lying in the center of the bilayer, while possible and becoming noticeably populated for polyunsaturated bilayers at high cholesterol content, is thermodynamically unstable for a single cholesterol molecule in pure bilayers, including the case of 22:6–22:6 PC bilayers. One can also note that there is no straightforward relationship between lipid unsaturation and the free energy difference between upright and flipped orientations, for example the free energy of the flipped conformation becomes large for 20:4–20:4 bilayers, but then again becomes smaller for 18:2–18:2 bilayers.
4 Discussion
Behaviour of cholesterol in saturated and unsaturated bilayers has been studied in many experimental and theoretical works.40,43,47–50,68,69,85–88 A common conclusion is that polyunsaturated lipid bilayers show generally lower affinity to cholesterol compared to saturated ones, and that this effect can be responsible for phase separation and domain formation in mixed bilayers containing saturated and unsaturated lipids and cholesterol. Our metadynamics simulations confirm this picture demonstrating differences of 10–20 kJ mol−1 of insertion of cholesterol in the considered bilayers, with the highest (less negative) value obtained for the most unsaturated 22:6–22:6 PC bilayer. Furthermore, the absolute values of our binding free energies, which are found to be in the range of −47 to 69 kJ mol−1, agree well with the atomic force microscopy experiments by Stetter et al.,89 who have measured the extraction force of cholesterol from domains formed on supported mixed lipid bilayers consisting of DOPC, POPC, SM and some other lipids, and found extraction free energies in the range of −45 to 52 kJ mol−1. Our metadynamics simulations, though carried out for different lipids, shows similar free energies, as well as differences between different bilayers.The free energy maps obtained in the metadynamics simulations showed that the most preferable positions and orientations of cholesterol in lipid bilayers are those in which cholesterol, located in the membrane interior, is oriented with the hydroxyl group toward the membrane surface (dark blue regions in Fig. 7). The probability distributions of cholesterol obtained in MD simulations of 1:1 cholesterol–lipid mixed bilayers show maxima in the same regions (red areas in Fig. 6). There is however clear difference in these maxima: while in the metadynamics simulations (single cholesterol molecule in a pure bilayer) low free energy minimum areas are widely spread over angles, in MD simulations of cholesterol-rich bilayers fluctuations of orientations are much more restricted. This can be related with the ordering effect of cholesterol: fluctuations of orientations are more restricted in cholesterol rich bilayer compared to bilayers without cholesterol.
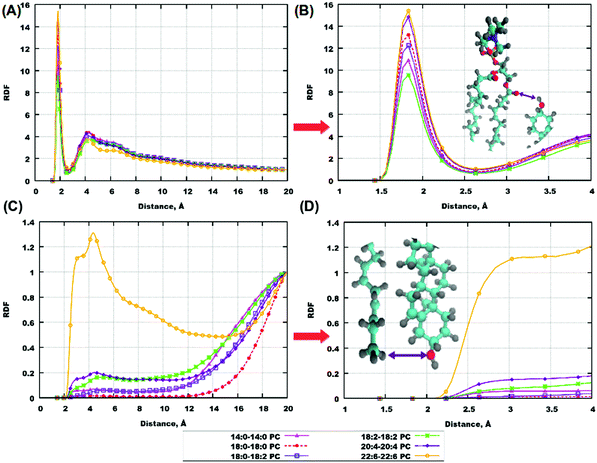
Analysis of RDFs carried out for conventional MD simulations of lipid–cholesterol mixed bilayers (Section 3.3) identified several typical coordinations of cholesterol with lipids and with other cholesterol molecules. They are shown in Fig. 10. Thus, hydroxyl group of cholesterol often forms hydrogen bonds with oxygens of lipids phosphate and ester groups, and the corresponding RDFs show highest peaks among those calculated. Importance of hydrogen bonding of cholesterol to lipids ester groups was discussed already in earlier simulation works85,90 addressing behaviour of cholesterol in lipid membranes. These interactions are arguably responsible for “upright” orientation of cholesterol which is its preferential orientation in all considered bilayers. However, phosphate and ester groups are identical in all considered bilayers, that is why they can not be origin of different behavior of cholesterol in different bilayers. Essential direct cholesterol–cholesterol interactions were noted only for cholesterol in 22:6–22:6 PC bilayer, where, besides rather expected hydrogen bonding between cholesterol hydroxyl groups, coordination of the hydroxyl group to the methyl group of the cholesterol tail is possible. The later leads to appearance of head-to-tail association of cholesterol molecules, which is likely related with a higher fraction of “flipped” cholesterol orientations in 22:6 chain containing PC bilayer.
5 Conclusions
We have carried out microsecond-long classical MD simulations of several cholesterol-containing bilayers composed of lipids differing by the degree of unsaturation, and multi-microsecond two-dimensional metadynamics simulation of cholesterol in pure bilayers composed of the same lipids. The focus of interest was to investigate how lipid unsaturation affects the behaviour of cholesterol in the bilayers, as well as how cholesterol affects the properties of the bilayers. Analysis of the MD simulations included calculated average areas per lipid and per molecule, electron and mass density distributions, radial distribution functions, distribution maps of position and orientation of cholesterol in the bilayer. MetaD simulations give us a complementary view on the behavior of cholesterol in lipid bilayers. These simulations were carried out for a single cholesterol molecule in the bilayers composed of different kinds of lipids, and provided free energy maps as functions of the position and orientation of the cholesterol in these bilayers. Comparison of binding free energies obtained in these simulations provides information on the preferences of cholesterol for different lipids. Our simulations showed generally stronger binding free energies of cholesterol to bilayers composed of saturated lipids, which can explain the preference of cholesterol to be surrounded by such lipids, and which can be the “driving force” behind domain formation in mixed lipid bilayers.While our analysis did not show an unambiguous relationship between the degree of unsaturation of lipids and properties of cholesterol in bilayers composed of these lipids, the most unsaturated 22:6–22:6 PC bilayer evidently behaved differently from the others. This is seen in the relatively high presence of the cholesterol hydroxyl groups in the middle of bilayer, higher fraction of “flipped” cholesterol molecules, presence of “head-to-tail” cholesterol contacts, higher (less negative) binding free energy and lower reorientational barrier. Also, the average area per lipid shows strongly non-linear behaviour upon addition of cholesterol. It does not seem that special properties of 22:6–22:6 PC are related to the presence of some specific atoms or atomic groups because the same atomic groups are present in other bilayers. It is more likely that for this lipid, almost the whole hydrocarbon chain consists of repeated –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CH2– fragments, which has different conformational properties than fully saturated hydrocarbon chains, and this results in differences in cholesterol behaviour in such bilayers. One can further hypothesise that the high presence of cholesterol and 22:6 fatty acids in neuronal membranes of brain tissues is related to the special physical–chemical relationships between them which might be of importance for their biological functioning. Possible relationships between the properties of 22:6 chains and their physiological function, including the role in neuronal diseases have been a matter of discussion during the last few decades.70,91–93 Our simulations support the ideas that there can be a subtle interconnection on the molecular level between the content of highly unsaturated fatty acids and cholesterol, a deficiency or excess of each of them is related to many human afflictions and diseases related to the functioning of the central nervous system.
CH–CH2– fragments, which has different conformational properties than fully saturated hydrocarbon chains, and this results in differences in cholesterol behaviour in such bilayers. One can further hypothesise that the high presence of cholesterol and 22:6 fatty acids in neuronal membranes of brain tissues is related to the special physical–chemical relationships between them which might be of importance for their biological functioning. Possible relationships between the properties of 22:6 chains and their physiological function, including the role in neuronal diseases have been a matter of discussion during the last few decades.70,91–93 Our simulations support the ideas that there can be a subtle interconnection on the molecular level between the content of highly unsaturated fatty acids and cholesterol, a deficiency or excess of each of them is related to many human afflictions and diseases related to the functioning of the central nervous system.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Swedish Research Council (Vetenskapsrådet). The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) through Center for Parallel Computing (PDC), National Supercomputer Center (NSC), and High Performance Computing Center North (HPC2N).Notes and references
- A. A. Spector and M. A. Yorek, J. Lipid Res., 1985, 26, 1015–1035 CAS.
- I. Björkhem and S. Meaney, Arterioscler., Thromb., Vasc. Biol., 2004, 124, 806–815 CrossRef PubMed.
- P. D. Schley, D. N. Brindley and C. J. Field, J. Nutr., 2007, 137, 548–553 CrossRef CAS.
- S. A. Shobab, G.-Y. Hsiung and H. H. Feldman, Lancet Neurol., 2005, 4, 841–852 CrossRef.
- P. C. Reid, Y. Urano, T. Kodama and T. Hmakubo, J. Cell. Mol. Med., 2007, 11, 383–392 CrossRef CAS.
- G. D. Paolo and T.-W. Kim, Nat. Rev. Neurosci., 2011, 12, 284–296 CrossRef PubMed.
- R. Mason, W. J. Shoemaker, L. Shajenko, T. E. Chambers and L. G. Herbette, Neurobiol. Aging, 1992, 13, 413–419 CrossRef CAS.
- C. R. Hooijmans, F. Rutters, P. J. Dederen, G. Gambarota, A. Veltien, T. Groen, L. M. Broersen, D. Lütjohann, A. Heerschap, H. Tanila and A. J. Kiliaan, Neurobiol. Dis., 2007, 28, 16–29 CrossRef CAS.
- S. Florent-Bechard, C. Malaplate-Armand, V. Koziel, B. Kriem, J.-L. Olivier, T. Pillot and T. Oster, J. Neurol. Sci., 2007, 262, 27–36 CrossRef CAS.
- W. Wood, G. P. Eckert, U. Igbavboa and W. E. Müller, Biochim. Biophys. Acta, 2003, 1610, 281–290 CrossRef.
- G. Vitiello, S. Marino, A. M. D'Ursi and G. D'Errico, Langmuir, 2013, 29, 14239–14245 CrossRef CAS.
- M. R. Freeman and K. R. Solomon, J. Cell. Biochem., 2004, 91, 54–69 CrossRef CAS.
- C. R. Santos and A. Schulze, FEBS J., 2012, 279, 2610–2623 CrossRef CAS PubMed.
- Z. Liao, L. M. Cimakasky, R. Hampton, D. H. Nguyen and J. K. Hildreth, AIDS Res. Hum. Retroviruses, 2001, 17, 1009–1019 CrossRef CAS PubMed.
- D. Papahadjopoulos, J. Theor. Biol., 1974, 43, 329–337 CrossRef CAS.
- J. R. Hibbeln and N. Salem, Am. J. Clin. Nutr., 1995, 62, 1–9 CrossRef CAS.
- F. R. Maxfield and I. Tabas, Nature, 2005, 438, 612–621 CrossRef CAS.
- M. Söderberg, C. Edlund, K. Kristenssin and G. Dallner, Lipids, 1991, 26, 421–425 CrossRef.
- L. Puglielli, R. E. Tanzi and D. M. Kovacs, Nat. Neurosci., 2003, 6, 345–351 CrossRef CAS.
- C. P. White, J. Pathol., 1909, 13, 11–13 CrossRef.
- M. D. Haag, A. Hofman, P. J. Koudstaal, B. H. Stricker and M. M. Breteler, J. Neurol., Neurosurg. Psychiatry, 2009, 80, 13–17 CrossRef CAS.
- H. L. Daneschvar, M. D. Aronson and G. W. Smetana, Eur. J. Intern. Med., 2015, 26, 666–669 CrossRef CAS PubMed.
- K. Simons and E. Ikonen, Nature, 1997, 387, 569–572 CrossRef CAS PubMed.
- K. Simons and R. Ehehalt, J. Clin. Invest., 2002, 110, 597–603 CrossRef CAS.
- P. S. Niemelä, S. Ollila, M. T. Hyvönen, M. Karttunen and I. Vattulainen, PLoS Comput. Biol., 2007, 3, 304–312 CrossRef PubMed.
- Z. Korade and A. K. Kenworthy, Neuropharmacology, 2008, 55, 1265–1273 CrossRef CAS PubMed.
- D. Lingwood and K. Simons, Science, 2010, 327, 46–50 CrossRef CAS PubMed.
- J. R. Silvius, Biochim. Biophys. Acta, 2003, 1610, 174–183 CrossRef CAS.
- M. L. Berkowitz, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 86–96 CrossRef CAS.
- H. Martinez-Seara, T. Róg, M. Karttunen, I. Vattulainen and R. Reigada, PLoS One, 2010, 5, e11162 CrossRef PubMed.
- C. T. Boughter, V. Monje-Galvan, W. Im and J. B. Klauda, J. Phys. Chem. B, 2016, 120, 11761–11772 CrossRef CAS PubMed.
- C. M. MacDermaid, H. K. Kashyap, R. H. DeVane, W. Shinoda, J. B. Klauda, M. L. Klein and G. Fiorin, J. Chem. Phys., 2015, 143, 12B625 CrossRef PubMed.
- B. D. Madej, I. R. Gould and R. C. Walker, J. Phys. Chem. B, 2015, 119, 12424–12435 CrossRef CAS PubMed.
- Z. Zhang, L. Lu and M. L. Berkowitz, J. Phys. Chem. B, 2008, 112, 3807–3811 CrossRef CAS.
- S. Vainio, M. Jansen, M. Koivusalo, T. Róg, M. Karttunen, I. Vattulainen and E. Ikonen, J. Biol. Chem., 2006, 281, 348–355 CrossRef CAS PubMed.
- A. J. Sodt, M. L. Sandar, K. Gawrisch, R. W. Pastor and E. Lyman, J. Am. Chem. Soc., 2014, 136, 725–732 CrossRef CAS PubMed.
- J. M. Crane and L. K. Tamm, Biophys. J., 2004, 86, 2965–2979 CrossRef CAS PubMed.
- T. M. Konyakhina and G. W. Feigenson, Biochim. Biophys. Acta, 2016, 1858, 153–161 CrossRef CAS.
- J. Pan, S. Tristram-Nagle and J. F. Nagle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021931 CrossRef PubMed.
- T. A. Harroun and J. K. S. R. Wassal, Biochemistry, 2006, 45, 1227–1233 CrossRef CAS PubMed.
- N. Kučerka, J. D. Perimutter, J. Pan, S. Tristram-Nagle and J. Katsaras, Biophys. J., 2008, 95, 2792–2805 CrossRef PubMed.
- N. Kučerka, D. Marquardt, T. A. Harroun, M.-P. Nieh, S. R. Wassal, D. de Jong, L. V. Schäfer, S. J. Marrink and J. Katsaras, Biochemistry, 2010, 49, 7485–7493 CrossRef PubMed.
- D. Marquardt, F. A. Heberle, D. V. Greathouse, R. E. Koeppe, R. E. Standaert, B. J. V. Oosten, T. A. Harroun, J. J. Kinnun, J. A. Williams, S. R. Wassall and J. Katsaras, Soft Matter, 2016, 12, 9417–9428 RSC.
- M. R. Brzustovicz, W. Stillwell and S. R. Wassall, FEBS Lett., 1999, 451, 197–202 CrossRef.
- A. Filippov, G. Oradd and G. Lindblom, Biophys. J., 2007, 93, 3182–3190 CrossRef CAS PubMed.
- R. E. Minto, P. R. Adhikari and G. A. Lorigan, Chem. Phys. Lipids, 2004, 132, 55–64 CrossRef CAS.
- A. M. Smondyrev and M. L. Berkowitz, Biophys. J., 1999, 77, 2075–2089 CrossRef CAS.
- S. A. Pandit, V. S. W. Chiu, R. J. Mashl, E. Jakobsson and H. L. Scott, Biophys. J., 2004, 87, 1092–1100 CrossRef CAS PubMed.
- S. A. Pandit, S.-W. Chiu, E. Jakobsson, A. Grama and H. Scott, Langmuir, 2008, 24, 6858–6865 CrossRef CAS PubMed.
- I. Ermilova and A. P. Lyubartsev, J. Phys. Chem. B, 2016, 120, 12826–12842 CrossRef CAS PubMed.
- W. D. Bennett, J. L. MacCallum, M. J. Hinner, S. J. Marrink and D. P. Tieleman, J. Am. Chem. Soc., 2009, 131, 12714–12720 CrossRef CAS PubMed.
- M. J. Abraham and J. E. Gready, J. Comput. Chem., 2011, 32, 2031–2040 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Brendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- J. P. M. Jämbeck and A. P. Lyubartsev, J. Chem. Theory Comput., 2012, 8, 2938–2948 CrossRef PubMed.
- J. P. M. Jämbeck and A. P. Lyubartsev, J. Phys. Chem. B, 2012, 116, 3164–3179 CrossRef PubMed.
- J. P. M. Jämbeck and A. P. Lyubartsev, J. Chem. Theory Comput., 2013, 9, 774–784 CrossRef.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- M. Bonomi and M. Parinello, Phys. Rev. Lett., 2010, 104, 190601 CrossRef CAS PubMed.
- D. Branduardi, F. L. Gervasio and M. Parinello, J. Chem. Phys., 2007, 126, 054103 CrossRef PubMed.
- D. Branduardi, G. Bussi and M. Parinello, J. Chem. Theory Comput., 2012, 8, 2247–2254 CrossRef CAS PubMed.
- M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parinello, Comput. Phys. Commun., 2009, 180, 1961–1972 CrossRef CAS.
- S. W. Chiu, E. Jakobsson, R. J. Mashl and H. Scott, Biophys. J., 2002, 83, 1842–1853 CrossRef CAS.
- O. Edholm and J. F. Nagle, Biophys. J., 2005, 89, 1827–1832 CrossRef CAS.
- W.-C. Hung, M.-T. Lee, F.-Y. Chen and H. W. Huang, Biophys. J., 2007, 92, 3960–3967 CrossRef CAS PubMed.
- T. Róg, M. Pasenkiewicz-Gierula, I. Vattulainen and M. Karttunen, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 97–121 CrossRef PubMed.
- J. M. Smaby, M. M. Momsen, H. L. Brockman and R. E. Brown, Biophys. J., 1997, 73, 1492–1505 CrossRef CAS.
- M. R. Brzustowicz, V. Cherezov, M. Caffrey, W. Stillwell and S. R. Wassall, Biophys. J., 2002, 82, 285–298 CrossRef CAS.
- W. Stillwell and S. R. Wassall, Chem. Phys. Lipids, 2003, 126, 1–27 CrossRef CAS.
- M. C. Pitman, F. Suits, A. D. MacKerell and S. E. Feller, Biochemistry, 2004, 43, 15318–15328 CrossRef CAS PubMed.
- D. Marsh, Biochim. Biophys. Acta, 2005, 1798, 688–699 CrossRef PubMed.
- F.-M. de Meyer, A. Benjamini, J. M. Rodgers, Y. Misteli and B. Smit, J. Phys. Chem. B, 2010, 114, 10451–10461 CrossRef CAS PubMed.
- A. P. Lyubartsev and A. Laaksonen, Comput. Phys. Commun., 2000, 128, 565–589 CrossRef CAS.
- D. Marquardt, N. Kučerka, S. R. Wassall, T. A. Harroun and J. Katsaras, Chem. Phys. Lipids, 2016, 199, 17–25 CrossRef CAS PubMed.
- A. Sjödin, L. Hagmar, E. Klasson-Wehler, K. Kronholm-Diab, E. Jakobson and Å. Bergman, Environ. Health Perspect., 1999, 107, 643–648 Search PubMed.
- F. Hibbert and J. Emsley, Adv. Phys. Org. Chem., 1990, 26, 255–378 CrossRef CAS.
- G. A. Jeffrey, Food Chem., 1996, 56, 241–246 CrossRef CAS.
- K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340 CrossRef CAS.
- S. Horowitz and R. C. Trievel, J. Biol. Chem., 2012, 287, 41576–41582 CrossRef CAS.
- W. M. Latimer and W. H. Rodebush, Contribution from the Chemical Laboratory of the University of California, 1920, pp. 1419–1433 Search PubMed.
- R. E. Koehler, Hist. Stud. Phys. Sci., 1976, 3, 343–376 Search PubMed.
- G. Khelashvili, G. Pabst and D. Harries, J. Phys. Chem. B, 2010, 114, 7524–7534 CrossRef CAS PubMed.
- N. Kučerka, M.-P. Nieh and J. Katsaras, Langmuir, 2009, 25, 13522–13527 CrossRef PubMed.
- M. Pasenkiewicz-Gierula, T. Rog, K. Kitamura and A. Kusumi, Biophys. J., 2000, 78, 1376–1389 CrossRef CAS PubMed.
- S. R. Wassall, M. R. Brzustovicz, S. R. Shaikh, V. Cherezov, M. Caffrey and W. Stillwell, Chem. Phys. Lipids, 2004, 132, 79–88 CAS.
- S. R. Shaikh, V. Cherezov, M. Caffrey, S. P. Soni, D. LoCascio, W. Stillwell and S. R. Wassall, J. Am. Chem. Soc., 2006, 128, 5375–5383 CrossRef CAS PubMed.
- A. L. Rabinovich, V. V. Kornilov, N. K. Balabaev, F. A. M. Leermakers and A. V. Filippov, Membr. Cell Biol., 2007, 1, 343–357 Search PubMed.
- F. W. Stetter, L. Cwiklik, P. Jungwirth and T. Hugel, Biophys. J., 2014, 107, 1167–1175 CrossRef CAS PubMed.
- A. M. Smondyrev and M. L. Berkowitz, Biophys. J., 2001, 80, 1649–1658 CrossRef CAS.
- S. E. Feller and K. Gawrisch, Curr. Opin. Struct. Biol., 2005, 15, 416–422 CrossRef CAS PubMed.
- S. R. Wassall and W. Stillwell, Biochim. Biophys. Acta, 2009, 1788, 24–32 CrossRef CAS PubMed.
- J. A. Williams, S. E. Batten, M. Harris, B. D. Rockett, S. R. Shaikh, W. Stillwell and S. R. Wassal, Biophys. J., 2012, 103, 228–237 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm01937a |
| This journal is © The Royal Society of Chemistry 2019 |