Irradiance and temperature considerations in the design and deployment of high annual energy yield perovskite/CIGS tandems

Abstract

The annual energy yields for metal halide perovskite/copper indium gallium diselenide (CIGS) tandem photovoltaics have been calculated for 16 different bandgap combinations, using both 2 terminal and 4 terminal device designs, with fixed-tilt mounting as well as 1- and 2-axis tracking. Measured complex index of refraction data were used for the materials comprising the devices, and hourly irradiance data were extracted from Version 3 of the National Solar Radiation Database. Simulations were performed for Toledo OH, Golden CO, Phoenix AZ, and New Orleans LA, and the effect of local temperature variation was also considered. The combination of irradiance and temperature variations throughout the year cause different devices to be optimal at different times of the year. Interestingly, devices constructed to maximize AM1.5 photoconversion efficiency do not necessarily maximize the annual energy yield. A detailed analysis of the monthly energy yields at the different locations reveals the interplay between the changing light and temperature conditions. Over the course of the year these effects average to some degree so that annual energy yields that are close to the maximum possible value can be achieved by several different tandem device designs. The conclusions are valid for devices made with relatively thin perovskite layers, such as those used in champion efficiency devices. When the perovskite layers are thicker, however, the device is less tolerant to variation. Our results show that close matching of bandgap pairs is not essential for the fabrication of high-performance tandems. These findings should allow manufacturing efforts to proceed without the need for precise compositional control during formation of the absorber layers.

---

Introduction

In recent years, the photoconversion efficiencies (PCEs) of polycrystalline, thin-film photovoltaic (PV) devices based on CdTe, Cu_y(In_1−xGa_x)Se₂ (CIGS), and metal halide perovskite have all exceeded 22% under standard test conditions (AM1.5G irradiance, 25 °C).¹ As these devices begin to approach their internal Shockley–Queisser limit, researchers are investigating tandem device structures to access even higher PCEs.² Multi-junction architectures are already well known for devices based on a-Si:H and its alloys,³ and also for devices based on epitaxially grown III–V materials.^4,5 In the first case, multijunction devices are in fact necessary to achieve PCEs greater than even 14% ⁵⁹ due to limitations associated with the Staebler–Wronski effect.⁶ In contrast, III–V multijunctions have achieved PCEs of 38% under AM1.5G conditions⁴ and PCEs greater than 45% with concentrated sunlight,⁵ but large-scale terrestrial deployment has been limited by the high cost of the material growth processes. Concepts based on new high efficiency polycrystalline, thin-film options promise both high efficiency and low-cost manufacturing. Recent analyses show that production costs for thin-film tandems should be comparable to single junction devices, suggesting the possibility of a jump to a new, lower cost curve as well as short energy payback times.^7–10

Early work on polycrystalline thin-film tandems was hindered by low subcell efficiencies and integration issues associated with subcell incompatibilities.¹¹ Recently, the development of solution processable perovskite solar cells, with band-gap tunability from 1.1 to 2.2 eV,¹² has opened up many new avenues for exploration. Several high efficiency tandem devices have been demonstrated recently by combining a wide bandgap perovskite top cell with a narrow bandgap bottom cell. These include all-thin-film tandems which have a narrow bandgap perovskite^13–15 or Cu_y(In_1−xGa_x)Se₂ (CIGS)^16–22 thin-film bottom cell device as well tandems that have been constructed on a crystalline Si bottom cell.^23–26 Though much of the initial excitement in this area has been generated by early success found with crystalline Si, the all-thin-film versions hold the potential for roll-to-roll processing. So far, there have been only a few reports of perovskite on CIGS¹⁸ and perovskite on Si^26,27 where the PCE of the tandem is greater than the record efficiency of either one of the single junction cells involved in the structure. However, the extensive level of effort in this area suggests that tandems with PCEs near 30% will soon be possible. In addition to tremendous progress in experimental work, several studies have analyzed the optical limitations,^28,29 the best bandgap combinations,^30,31 the environmental impacts³² and the production costs of tandem PV cells.^7–10,33

Nearly all studies on tandems have used the standard AM1.5G irradiance spectrum³⁴ at normal incidence for optimizing the structure and efficiency of devices. This spectrum, used to benchmark the performance of devices and modules under both laboratory and manufacturing conditions, has been adopted by international committees as a standard which is intended to be representative of a typical midday power density distribution across wavelength (W m⁻² nm⁻¹) under clear sky conditions. Under real world conditions, however, solar cells rarely, if ever, experience normally incident illumination that closely corresponds to the AM1.5G spectrum with its integrated power density of 1000 W m⁻². More typically, the total incident power density at any given time may be higher or lower than this value, the light is incident non-normally, and the shape (i.e. the spectral distribution of the power) is likely to be different, as well. The actual irradiance experienced by a PV installation depends on the location of the deployment, whether tracking is employed, the time of day, the humidity, the cloud cover, and other environmental effects such as aerosol scattering due to, e.g., local pollution. Such effects cause the performance in the field to differ substantially from the performance in the laboratory. The change in irradiance throughout the hours of the day and the days of the year at each specific deployment location impacts the annual energy yield (AEY), which is a key quantity of economic interest.

The first paper to estimate the AEY for all thin-film tandems was focused on CdTe-related devices and simulated the performance for fixed bandgap combinations and fixed material thicknesses under a clear sky model.³⁵ A few studies have appeared since then which have considered the AEY of tandems fabricated with perovskites. Studies on perovskite/Si devices^36,37 used more realistic irradiance data but were, of course, limited to a fixed bandgap for the bottom cell. Work has also been done on perovskite/CIGS tandems,³⁸ but this study also used a fixed bottom cell bandgap (1.2 eV). A recent study on perovskite/perovskite tandems has appeared in which both the top and bottom subcell bandgaps were allowed to be varied.³⁹

Here we present a comprehensive examination of the AEY of perovskite/CIGS tandems where both the top and bottom cells bandgaps were varied, and the performance was simulated under real world conditions. We compared the performance of two- and four-terminal (2T and 4T) devices at four different locations (Golden CO, New Orleans LA, Phoenix AZ, and Toledo OH) which are representative of high (New Orleans and Toledo) and low (Golden and Phoenix) humidity climates and relatively high (Golden and Toledo) and low (New Orleans and Phoenix) latitudes within the US. We used the measured optical properties of each layer in the device stack and the optical transfer matrix method to optimize the efficiency by varying both the bandgap and thickness of the top perovskite cell as well as the bandgap of the bottom CIGS cell. We used the most advanced hourly solar irradiance data that is available and determined the hourly module temperature and the power coupled to the device throughout the hours of the year. This allowed a determination of how the energy yields depend on the bandgap pair selections for the different deployment scenarios. A detailed analysis of the monthly energy yields at the different locations revealed the interplay between the changing irradiance and temperature conditions.

Results and discussion

AM1.5 PCE

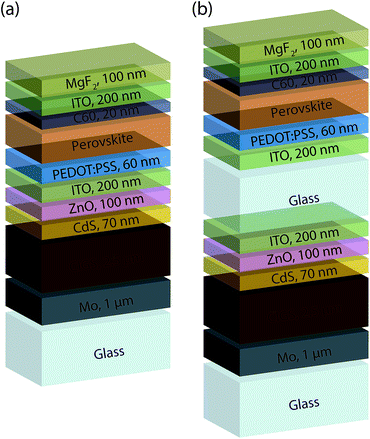
We modeled 2T and 4T perovskite/CIGS tandem devices using materials and device structures that have been shown to yield high performance results in experiments^13,16,21,40 (Fig. 1(a) and (b)). The external quantum efficiencies (EQEs) were determined by using the complex index of refraction data for the device materials layers within a transfer matrix formalism^31,41 while taking the internal quantum efficiencies to be unity and zero for light absorbed in the photoactive and photoinactive portions of the devices, respectively. Complex index of refraction data were collected from the literature³⁰ for mixed-cation, mixed-anion perovskites of the general formula FA_xCs_1−xPbI_yBr_3−y where FA is formamidinium. Data for chemical compositions of FA_0.85Cs_0.15PbI_2.72Br_0.28, FA_0.85Cs_0.15PbI_2.15Br_0.85, FA_0.9Cs_0.1PbI_2.3Br_0.7 and FA_0.83Cs_0.17PbI₂Br allowed perovskite materials with bandgaps of 1.62, 1.65, 1.69 and 1.80 eV, respectively, to be modeled. Unfortunately, devices with top cell bandgaps between 1.69 and 1.80 eV could not be included in the study due to the absence of the needed data. Data for bottom cell CIGS absorbers with compositions of CuInSe₂, Cu(In_0.903Ga_0.097)Se₂, Cu(In_0.767Ga_0.233)Se₂ and Cu(In_0.613Ga_0.383)Se₂ were taken from previous work,^42,43 allowing modeling of bottom cells with bandgaps of 1.00, 1.08, 1.16, and 1.24 eV, respectively. The complex index of refraction data for remaining material were collected from literature.^42,44,45 Data for CdS, Mo, ZnO layers were taken from ref. 43 and those for ITO and MgF₂ were taken from ref. 44 and 45 respectively. Refractive index data for C60 and poly(3,4-ethylenedioxythiophene)–poly(styrenesulfonate) (PEDOT:PSS) were measured by spectroscopic ellipsometry.⁴⁶

Fig. 1 (a) Two- and (b) four-terminal tandem device structures used for modelling.

Fig. 2 shows the calculated AM1.5 PCEs for tandems formed with top cell perovskite thicknesses of 300 nm to 2 μm in 50 nm steps for the sixteen combinations of perovskite and CIGS bandgaps that were examined in both 2T and 4T configurations. The results were generated by first integrating the product of the subcell EQE and the AM1.5G spectrum to determine the photogenerated short circuit current density (J_SC), and then determining the reverse saturation current density (J₀) by integrating the product of the EQE and the blackbody spectral irradiance at a device temperature of 25 °C. The PCEs were then determined using the diode equation⁴⁷ with an assumed diode quality factor of 1. Shunt and series resistance values were taken as 5 Ω and 50 kΩ, respectively, for the perovskite device, and 2 Ω and 1.3 kΩ, respectively, for the CIGS cell, in accordance with findings for high efficiency cells in the literature.^13,48 The J/V characteristics of the subcells were then combined to determine the performance of the 2T and 4T tandems.⁴⁹ In the 2T arrangement the two cells share an electrode and the current through the two cells is in series. Thus, there is a single maximum power operating point for the coupled subcells. In contrast, the subcells in the 4T arrangement are only optically coupled, so the two cells can be operated independently. For more details on the calculations see the ESI.†

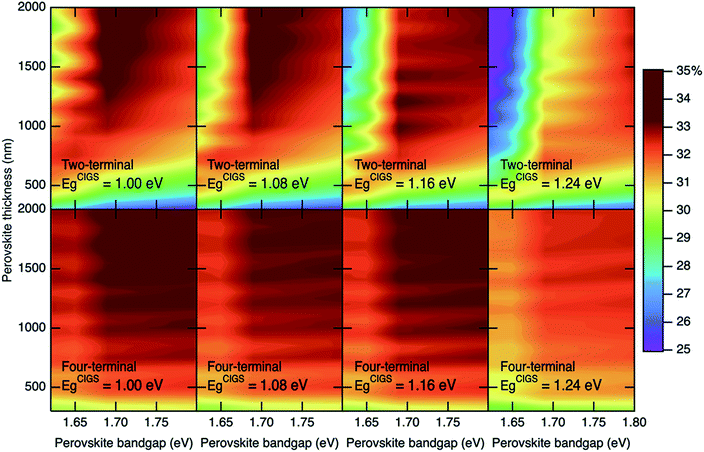Fig. 2 Device efficiency of (top) two- and (bottom) four-terminal tandems as a function of perovskite top layer bandgap and thickness for multiple CIGS bottom layer bandgaps.

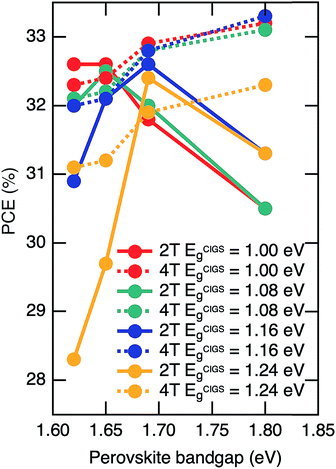
The PCEs (Fig. 2) were found to be slowly varying with thickness across a fairly large area of the bandgap/thickness space for both 2T and 4T configurations. To proceed with the AEY analysis, we chose to fix the top cell thickness at values corresponding to champion cells.^50–52Fig. 3 shows the AM1.5 PCE as a function of CIGS and perovskite bandgaps for 2T devices with a top cell thickness of 650 nm and 4T devices with a top cell thickness of 500 nm. For the 2T devices, there are 8 different bandgap combinations yielding AM1.5 PCEs greater than 32%, while the relaxation of the current matching requirement for the 4T tandems leads to 16 bandgap combinations with PCEs greater than 32%. The AM1.5 PCEs for the 2T devices vary somewhat more across the range of parameters than the AM1.5 PCEs for the 4T devices, but the maximum performance is similar in each case at 32.6 and 33.3%, respectively. There are actually three “champion” 2T devices with the same AM1.5 PCE of 32.6% (with bottom/top subcell bandgaps of 1.00/1.62, 1.00/1.65, and 1.16/1.69 eV), while there is only one champion 4T device at 33.3% (1.16/1.8 eV). Clearly, there are many ways to achieve very high efficiency perovskite/CIGS devices. There is slight preference for smaller bandgap perovskite top cells in 2T devices and for a larger bandgap perovskite layer in 4T devices but, overall, it is surprising that the devices are not more sensitive to the choice of bandgap combinations. Other studies that have explored the optimization of tandem devices with perovskite top cells conclude that the PCE maximized at thicknesses above 1 micron,³⁶ but this choice of thickness leads to a greater dependence on band gap matching (vide infra). Our results indicate that the AM1.5 PCE optimization is not as sensitive to the subcell bandgaps when the perovskite layer is relatively thin. This has important implications for manufacturing and large-scale deployment due to the expanded range of acceptable material properties.

Fig. 3 Device efficiency for two-terminal tandems with a 650 nm perovskite top cell (solid lines) and four-terminal tandems with 500 nm thick perovskite top cell (dashed lines) for varying CIGS bandgaps.

To understand why the perovskite/CIGS tandem devices are so forgiving and able to yield very high PCEs in a variety of different configurations we examined the EQE response in greater detail. Fig. 4 shows example EQEs for two specific device structures. The EQE plots show parasitic absorption losses in the electrodes and charge selective layers, as well as significant reflection losses even with MgF₂ as an antireflection layer. Interference fringes can also be seen in the EQE, particularly in the 4T case in the wavelength range from 900 to 1100 nm. This is due to the coherent optical treatment that was used for all of the interfaces in the structure. A more thorough treatment that would introduce incoherence through surface roughness would be expected to average-out the interference fringes but not change the area integrated under the curve.⁵³ Interestingly, if the optical losses could be reduced by 50%, the PCEs would increase by 8 percent. This latter observation points to an important area for future research.

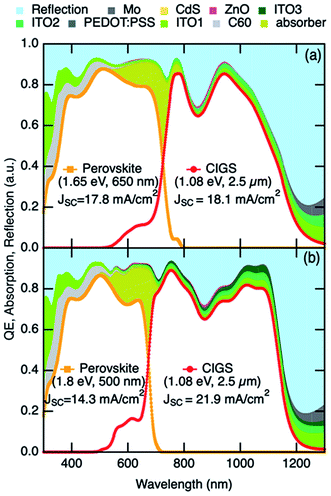Fig. 4 EQE for (a) two- and (b) four-terminal devices with a top cell bandgap of 1.65 eV and bottom cell bandgap of 1.08 eV. The parasitic losses and reflections are added as function of wavelength.

It is interesting to note that the subcell EQE curves overlap significantly in the wavelength range from 550 to 800 nm, where both subcells are contributing to the overall device performance. This contrasts with a recent analysis of perovskite/Si tandems where the perovskite layer was much thicker (1.2 μm) and light with energy above the top cell bandgap was more effectively blocked from entering the bottom cell.³⁶ In this case the EQE curves for the two cells overlapped by only ∼50 nm. Without a sharp cutoff in optical absorption in the top cell, the design criteria for the two subcells is relaxed when the top cell is relatively thin. Consequently, both cells generate significant current in this region of the spectrum, and multiple top/bottom bandgaps pairs can be found with high performance. Our calculations with a 1.2 μm perovskite layer confirm that the performance of the tandem becomes much more sensitive to the bandgap pair combinations when the perovskite layer is relatively thick (see ESI†).

Energy yield

While the AM1.5 efficiency provides information on how the devices function in the laboratory, energy yield is the important parameter for deployment in the field. With specific values for the thicknesses of all of the layers, the annual energy yields can be determined for the bandgap combinations at the locations of interest under real world conditions. To begin, one must consider that the total energy output is the integration over time of the power output, which will depend on the EQE of the device, the incident light, and the device temperature. As the sun traverses across the sky each day over the course of the year, the angle between the light from the sun and the normal to the plane of the mounted PV device, i.e. the angle of incidence, θ_i(t), will change. θ_i(t) will also depend on whether fixed-tilt (zero axis, 0A), 1-axis (1A), or 2-axis (2A) tracking mounting is used. Only in the case of 2A tracking will θ_i be constant at 0°. To account for a changing θ_i(t), we utilized the optical transfer matrix to determine the angular dependence of the absorption, transmission, and reflection for each layer and interface in the device stack to determine an angle dependent external quantum efficiency, EQE(θ_i).

The irradiance at the plane of the device, which is the sum of direct and diffuse components, will also vary with time of day for each day of the year at each of the locations. The direct component received by a plane normally oriented toward the sun is termed the direct normal irradiance (DNI(t)), and the amount of direct light that strikes a non-normally oriented device is then DNI(t) × cos(θ_i). Direct light is randomly polarized but can be decomposed into orthogonal transverse-magnetic and transverse-electric components. These components couple to the device stack differently based on θ_i and EQE(θ_i). The diffuse component of the irradiance is produced by scattering by molecules and particles in the atmosphere. To account for the directionality of the diffuse irradiance we assumed an anisotropic distribution model.⁵⁴ The hourly power distribution spectrum of overhead diffuse light incoming to the device from the sky was determined using a grid generated by 2° steps in both polar and azimuthal angles. Based on the location of each grid point in the sky, the current generated by each component of the diffuse light was determined using the angle of incidence and the same EQE(θ_i) model used for the DNI light. Integration over the polar and azimuthal angles yielded the photocurrent due to the diffuse light. The scattered light was also considered to be randomly polarized and was decomposed into polarization components. A more complete treatment would account for the polarization induced by scattering in the atmosphere, but this is beyond the scope of the current effort.

The changes in the spectral distribution of the irradiance throughout the year must also be considered, and this will be affected by the atmospheric conditions at the locations of interest. Irradiance spectra were generated using the TMYSPEC model,⁵⁵ which takes broadband irradiance data and meteorological parameters such as temperature, wind speed, aerosol optical depth and precipitable water vapor to generate hourly direct and diffuse light spectra. Accurate inputs are essential to achieve high quality spectral irradiance data from the model, so we used broadband irradiance Typical Meteorological Year (TMY) data from Version 3 of the National Solar Radiation Database (NSRDB).⁵⁶ The TMY hourly spectral data produced with NSRDB Version 3 data and associated meteorological data sets are much improved over those produced by Version 2. Version 3 incorporates meteorological data from the Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). MERRA-2 uses a more advanced data integration method and better simulates the amount of aerosols, precipitable water vapor, and other variables.⁵⁷ These parameters are inputs to the radiative transfer model that is used to generate the broadband irradiance and meteorological input parameters that are needed by the TMYSPEC model. NSRDB Version 3 also adapts the comparatively lower-resolution MERRA-2 output to the higher-resolution NSRDB (4 km by 4 km grid) data and uses more accurate meteorological parameters such as hourly aerosol optical depth instead of the climatic averages used in Version 2.

To account for temperature departures from 25 °C that occur in the field, we used a model developed by Sandia National Laboratories⁵⁸ which predicts the module temperature (T_M) on an hourly basis as a function of environmental parameters:

T_M = P_OA exp(a + b × WS) + T_A (1)

Here P_OA, WS and T_A are the power incident on the array, wind speed, and ambient temperature, respectively, each of which can vary on an hourly basis. The constants a and b relate to the module construction and racking. For the present case we chose open rack mounting and glass covers, leading to values of −3.47 and −0.0594, for a and b, respectively.⁵⁸ The incident power density was calculated by integrating the hourly solar irradiance spectra, while the hourly wind speed and ambient temperature data were taken from NREL's Physical Solar Model (PSM) data source.⁵⁶ To have a representative dataset, the wind speed and ambient temperature for each hour of the year were averaged over the 1998–2016 dataset. The predicted module temperatures were used in the calculation of the reverse saturation current without further modification. Fig. S4† shows that temperature variation can have a significant effect on the PCE and energy yield performance of 2T and 4T devices.

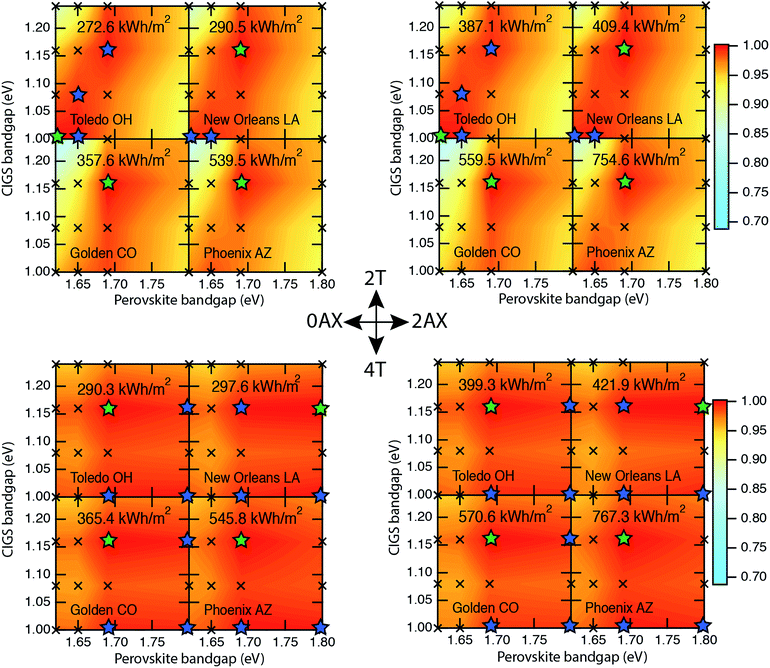
Table 1 shows the maximum energy production values in both 2T and 4T configurations for the locations that were examined, with 0A, 1A, and 2A tracking. In general, we see energy production increasing in the order of Toledo, New Orleans, Golden, and Phoenix, as may be expected from qualitative considerations of the latitude and the prevailing weather and humidity. For a given city, we see increasing energy yield as the degree of tracking is increased. The fraction of the maximum available (2A) energy that may be captured with fixed-tilt mounting (0A) is approximately constant at ∼70% for both 2T and 4T configurations. Addition of one axis of tracking increases the fraction of captured energy to ∼90% of the maximum available. Clearly, decisions associated with tracking investments should consider the cost/benefit ratio for tracking and include the energy production as well as levelized costs associated with racking and tracking hardware and software.

Table 1 Maximum AEYs expected from two- and four-terminal tandems (2T, 4T) with different modes of tracking for the four locations. Note that different bandgap pairs may be responsible for different maxima at different locations and for 2T versus 4T operation (see Fig. 5). The degree of tracking does not affect the choice of the bandgap pairs for the 2T (650 nm) and 4T (500 nm) perovskite thicknesses considered here. The ratio of 4T to 2T AEY for fixed tilt (0A) and 1- and 2-axis tracking are also shown

	Max 2T annual energy yield (kW h m^−2)			Max 4T annual energy yield (kW h m^−2)			4T/2T energy production ratio
	OA	1A	2A	OA	1A	2A	OA	1A	2A
Toledo	272.6	356.9	387.1	290.3	367.9	399.3	106.49%	103.08%	103.15%
% of max	70%	92%	100%	73%	92%	100%
N.O.	290.5	363.3	409.4	297.6	373.2	421.9	102.44%	102.73%	103.05%
% of max	71%	89%	100%	71%	88%	100%
Golden	357.6	491.5	559.5	365.4	501.3	570.6	102.18%	101.99%	101.98%
% of max	64%	88%	100%	64%	88%	100%
Phoenix	539.5	674.6	754.6	545.8	684.3	767.3	101.17%	101.44%	101.68%
% of max	71%	89%	100%	71%	89%	100%

---

Interestingly, the 4T energy production is only 1–2% higher than the 2T energy production in the locations with the most abundant sunshine (Golden and Phoenix) and only 3–6% higher in Toledo and New Orleans. With comparable energy production but lower balance of systems costs (e.g. less wiring, fewer inverters), potentially lower materials costs, and the absence of additional labor and/or manufacturing associated with subcell integration, we expect that 2T devices will have more success in the marketplace. Clearly, 4T devices would only be pursued when the costs per kW per h of energy production were lower. This is unlikely to occur, especially for the device structures considered here. On the other hand, 2T device designs place tremendous pressures on the materials and processing compatibilities. Overcoming such challenges, ideally within a roll-to-roll process, would lead to a new paradigm in low cost and high efficiency PV.

The entries in Table 1 are the maximum energy yields in each case and do not specify which bandgap pairs are responsible for the maximum production. Fig. 5 shows the annual energy yield as a function of the 16 bandgap combinations and reveals that many different devices are top energy yield performers. Data are shown for fixed-tilt (0A) and 2-axis tracking (2A) in the 4 cities for both 2T and 4T devices. A first observation to note is that the 0A and 2A data are qualitatively similar. The 1A data is also similar, as shown in the ESI.†

Fig. 5 (top) Two-terminal (with 650 nm thick perovskite) and (bottom) four-terminal (with 500 nm thick perovskite) tandem AEYs are shown as functions of top and bottom cell bandgap for (right) no-tracking and (left) two-axis tracking for the four different locations. The results are normalized to the maximum AEY of each panel. The 16 bandgap combinations studied are shown with cross symbols while the bandgap pair with maximum AEY in each panel is given with green star. Bandgap pairs with AEYs within 1% of the maximum point are shown with blue stars.

Looking more closely at the 2T/2A data for Phoenix, we see a single maximum in annual energy yield for the 1.16/1.69 eV pair. This is one of the three 2T champion devices that displayed a PCE of 32.6% under AM1.5 irradiance (Fig. 3). The other two 2T AM1.5 PCE champion devices, comprised of 1.00/1.65 and 1.00/1.62 eV bandgap pairs have the 2^nd and 5^th highest energy yields, which are 1.3% and 2.4% lower than the maximum value, respectively. The 2T/2A data for Golden also shows a single maximum at the 1.16/1.69 eV AM1.5 champion as well, but the other two 2T AM1.5 champions have significantly lower energy yields, −5.7% and −3.3%, respectively, and have the 9^th and 4^th highest energy yields. In Golden, two other devices, comprised of 1.08/1.69 and 1.00/1.69 eV pairs, take 2^nd and 3^rd place with AEYs of −1.6% and −1.8%, respectively. Similar conclusions can be reached from the 0A and 1A data. Clearly, a maximum in AM1.5G PCE does not necessarily translate into a maximum AEY under real world conditions.

Turning to the 2T/2A plots for Toledo and New Orleans, we see color patterns that differ from those of Phoenix and Golden. In these cases, rather than a single clear maximum for the 1.16/1.69 pair, there are several other maxima that are nearly as intense. Here, the three champion devices exhibit AEYs that are very close to one another within 0.39% in the case of New Orleans, and within 0.53% for Toledo, while many other devices operate at close to the peak value. Specifically, 8 and 7 of the 16 devices are within 2% of the energy production peak in New Orleans and Toledo, respectively. In general, devices in humid climates yield annual energy values that are close to the maximum value for more bandgap pairs in the 2T configuration.

Turning to the 4T data, the color plots are nearly identical to one another in each of the four cities. The maximum energy yields vary as expected for qualitative considerations of the sunniness of the locations, and the top performing devices and those within 1% in AEY remain the same independent of the location. Here we also see that the top performing devices are not necessarily the ones with the greatest AM1.5 PCE (Fig. 3), but relaxation of the current matching conditions evidently allows for closer correspondence between AM1.5 performance and AEY. It's clear that both 2T and 4T constructions with relatively thin perovskite layers allow for a fairly wide tolerance in compositional variation and operational space. This factor may provide built-in flexibility in future manufacturing operations.

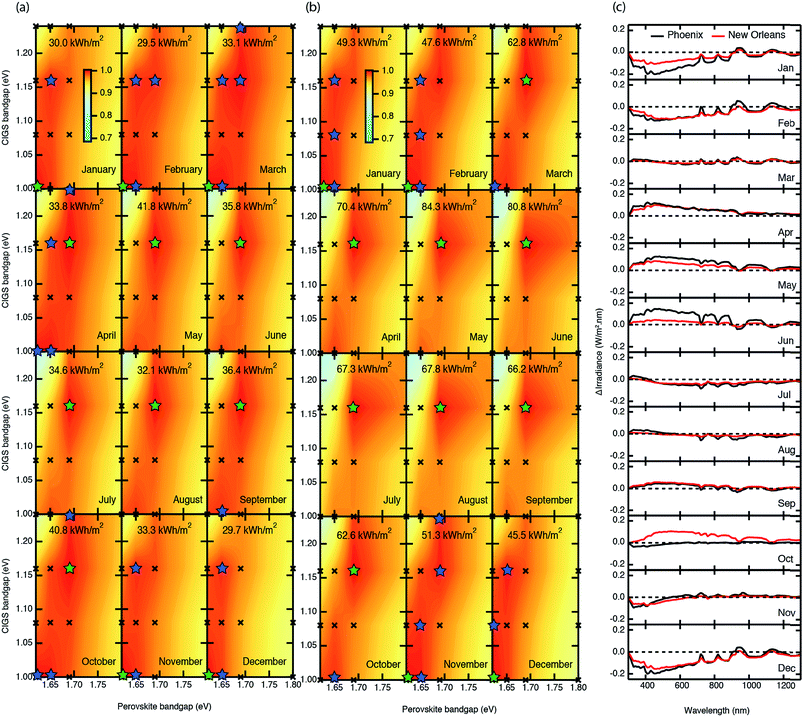
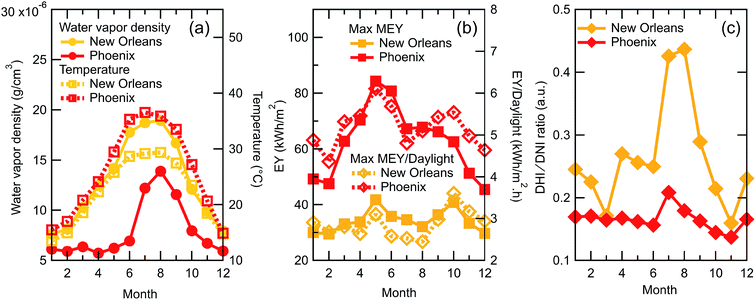
Because 2T operation and 4T operation produce very similar EYs, and 2T operation is expected be significantly less costly from a balance of materials and systems point of view (vide supra), it is interesting to consider 2T operation in more detail, and to understand why 2T devices in Phoenix and Golden show greater sensitivity to the bandgap pair selection than do the 2T devices deployed in Toledo or New Orleans. This is a general conclusion, independent of whether the tracking is 0A, 1A, or 2A. The reasons for the differences in the ordering and spacing of the AM1.5 PCE and AEY performances of the bandgap pairs can be traced to differences in the irradiance and prevailing weather conditions at the deployment locations. More can be learned by analyzing the monthly averages. Fig. 6(a) and (b) show the 2T/2A monthly energy yields as a function of the bandgap pairs in Phoenix and New Orleans, respectively, while Fig. 6(c) displays the average monthly irradiance expressed as a deviation from the average annual irradiance spectrum at each location. Note that the latter are very similar in shape to the AM1.5G spectrum but are reduced by a factor of 0.77 and 0.59 for Phoenix and New Orleans, respectively (Fig. S5†).

Fig. 6 MEY results shown for 2-terminal tandems with 650 nm thick perovskite layer for (a) New Orleans LA and (b) Phoenix AZ as a function of top and bottom cell bandgap. The maximum monthly energy yield (MEY) is given in each panel and the color scale is normalized to this value. Green symbols in each panel identify the bandgap pair with the maximum MEY while the blue symbols show the bandgap pairs with MEYs within 1% of the maximum value. All of the 16 bandgap pairs studied are shown with cross symbols. (c) The deviation of the average monthly irradiance from the average annual irradiance for Phoenix AZ and New Orleans LA.

Comparing the data in Fig. 6(a) and (b) for the first quarter of the year (January, February, and March) we see a tendency for better performance from lower bandgap top cells. This is consistent with the spectra in Fig. 6(c), which show a lower integrated power density and a relative reduction in the blue portion of the irradiance, leading to a red-rich spectrum. Under these conditions it is preferential that the top cell has a narrower band gap to absorb light at longer wavelengths to better balance the current in the bottom cell. However, the average spectrum for March is very close to the annual average spectrum (i.e. close to zero deviation), so it is somewhat surprising that the March EY plots do not more closely correspond to the respective yearly average color plots in Fig. 5. This discrepancy can be explained by considering that the average ambient temperature in March at both locations is low in comparison to the average annual temperature (Fig. 7(a)). This factor also leads to improved performance for the lower bandgap cells, which also leads to a preference for a smaller bandgap top cell.

Fig. 7 (a) Water vapor density (left axis) and temperature (right axis) in Phoenix AZ and New Orleans LA for each month of the year. (b) Maximum MEY (left axis) and MEY per daylight hours (right axis) for each month of the year in Phoenix AZ and New Orleans LA. (c) The ratio of total DHI to total DNI light in Phoenix AZ and New Orleans LA for each month.

In April, May, and June the irradiance spectra become blue-rich, the integrated power density becomes higher than the average annual spectrum, and the ambient temperature increases, as do the module temperatures (according to eqn (1)). Collectively, these factors shift the EY maximum to the larger 1.16/1.69 bandgap pair. Since the daylight hours also increase, maximizing at the summer solstice, the monthly EYs peak in these months and, thus, make a relatively large contribution to the AEY (Fig. 7(b)). It interesting to note that the maximum monthly energy yield (MEY) for the year occurs in May rather than in June, despite the larger number of daylights in June, due to the increased temperature and humidity (Fig. 7(a)) in June. The 1.16/1.69 bandgap pair remains the dominant device in the third quarter in both Phoenix and New Orleans as the spectra remain blue rich due to increased humidity and the temperature remains higher than average. Though Phoenix is typically thought of as a low humidity climate, it is interesting that the concentration of water molecules in the air in August is 75% of the concentration found at the same time in New Orleans. In the final quarter, the humidity begins to wane as the temperatures fall, and the irradiance becomes, once again, red-rich in comparison to the yearly average. This combination of factors moves the EY maxima to the smaller bandgap cells. October in New Orleans is an unusual case for the Fall where the lower temperatures and humidity lead to a blue-rich spectrum with a higher-than-average integrated power density. In this case the MEY is very close the maximum value in May, despite the fact that the number of daylight hours is less.

With information of the monthly EY patterns, it is straightforward to see how the yearly averages are built-up from the monthly contributions. The clear single maximum in AEY for Phoenix at the 1.16/1.69 bandgap pair is due to the large MEY contributions from the months of the second and third quarters (April, May, June, July, August, and September). These 6 months contribute 58% of the total AEY, while the second quarter alone contributes 31%. Interestingly, the July and August MEY contributions per daylight hour (Fig. 7(b)) are actually close to the minimum values for both New Orleans and Phoenix. This is due to an increase in the ratio of the DHI to DNI light (Fig. 7(c)) and gives rise to the two local maxima in the MEY data.

Conclusions

Using measured optical properties of perovskite and CIGS device stacks, we calculated realistic EQE curves for 16 different device configurations. The modeled EQE data were paired with modeled module temperature and hourly irradiance data to determine AEY under a variety of conditions, including zero-, one-, and two-axis tracking. The AEY values were compared to the PCEs and we found that the bandgap pair that resulted in the highest AEY does not necessarily correspond to the bandgap pair that results in the highest PCE. We showed that increasing the top cell perovskite thickness leads to a small increase in the PCE and AEY values but gives rise to a greater sensitivity to the values of the subcell bandgaps. However, when the perovskite thickness was between 500 to 700 nm thick, a large portion of the bandgap parameter space gives AEY values within 5% of the maximum value. This flexibility in bandgap is due to cooperative absorption of photons in both the top and bottom cells in the 500 to 800 nm wavelength range as well as the interplay between the irradiance and temperature variations. These results suggest that manufacturing conditions for high performance tandem devices need not be strict.

Author contributions

R. H. A. developed the simulation code and performed the calculations. K. G. and N. J. P. performed spectral ellipsometry measurements on C60 and PEDOT:PSS, while P. K., H. M. B. and R. W. C. performed measurement on CIGS and assisted in QE interpretation. A. H. and M. S. provided the needed solar irradiance data. R. H. A., A. B. P., Z. S., Y. Y., R. J. E., M. J. H. developed the models and interpreted the results. R. H. A., A. B. P., and M. J. H. wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported in part by the National Science Foundation (ECCS-1665172) and in part by the Office of Naval Research (N00014-17-1-2223).

References

1. https://www.nrel.gov/pv/cell-efficiency.html .
2. A. De Vos, J. Phys. D: Appl. Phys., 1980, 13, 839–846.
3. J. Yang, B. Yan and S. Guha, Thin Solid Films, 2005, 487, 162–169.
4. P. T. Chiu, D. C. Law, R. L. Woo, S. B. Singer, D. Bhusari, W. D. Hong, A. Zakaria, J. Boisvert, S. Mesropian, R. R. King and N. H. Karam, in 2014 IEEE 40th Photovoltaic Specialist Conference, PVSC 2014, 2014.
5. F. Dimroth, M. Grave, P. Beutel, U. Fiedeler, C. Karcher, T. N. D. Tibbits, E. Oliva, G. Siefer, M. Schachtner, A. Wekkeli, A. Bett, R. Krause, M. Piccin, N. Blanc, C. Drazek, E. Guiot, B. Ghyselen, T. Salvetat, A. Tauzin, T. Signamarcheix, A. Dobrich, T. Hannappel and K. Schwarzburg, Prog. Photovoltaics Res. Appl., 2014, 22, 277–282.
6. D. L. Staebler and C. R. Wronski, Appl. Phys. Lett., 1977, 31, 292–294.
7. S. E. Sofia, J. P. Mailoa, D. N. Weiss, B. J. Stanbery, T. Buonassisi and I. M. Peters, Nat. Energy, 2018, 3, 387–394.
8. Z. Li, Y. Zhao, X. Wang, Y. Sun, Z. Zhao, Y. Li, H. Zhou and Q. Chen, Joule, 2018, 2, 1559–1572.
9. I. Celik, A. B. Philips, Z. Song, Y. Yan, R. J. Ellingson, M. J. Heben and D. Apul, IEEE Journal of Photovoltaics, 2018, 8, 305–309.
10. Z. Song, A. B. Phillips, I. Celik, G. K. Liyanage, D. Zhao, Y. Yan and M. J. Heben, in 2018 IEEE 45th Photovoltaic Specialist Conference, PVSC 2018, 2018.
11. T. J. Coutts, J. S. Ward, D. L. Young, K. A. Emery, T. A. Gessert and R. Noufi, Prog. Photovoltaics Res. Appl., 2003, 11, 359–375.
12. J. P. Correa-Baena, M. Saliba, T. Buonassisi, M. Grätzel, A. Abate, W. Tress and A. Hagfeldt, Science, 2017, 358, 739–744.
13. D. Zhao, C. Chen, C. Wang, M. M. Junda, Z. Song, C. R. Grice, Y. Yu, C. Li, B. Subedi, N. J. Podraza, X. Zhao, G. Fang, R.-G. Xiong, K. Zhu and Y. Yan, Nat. Energy, 2018, 3, 1093–1100.
14. D. Zhao, Y. Yu, C. Wang, W. Liao, N. Shrestha, C. R. Grice, A. J. Cimaroli, L. Guan, R. J. Ellingson, K. Zhu, X. Zhao, R. Xiong and Y. Yan, Nat. Energy, 2017, 2, 17018.
15. G. E. Eperon, T. Leijtens, K. A. Bush, R. Prasanna, T. Green, J. T. W. Wang, D. P. McMeekin, G. Volonakis, R. L. Milot, R. May, A. Palmstrom, D. J. Slotcavage, R. A. Belisle, J. B. Patel, E. S. Parrott, R. J. Sutton, W. Ma, F. Moghadam, B. Conings, A. Babayigit, H. G. Boyen, S. Bent, F. Giustino, L. M. Herz, M. B. Johnston, M. D. Mcgehee, H. J. Snaith, G. E. Eperon, T. Leijtens, K. A. Bush, R. Prasanna, T. Green, J. T. W. Wang, D. P. McMeekin, G. Volonakis, R. L. Milot, R. May, A. Palmstrom, J. Daniel, R. A. Belisle, J. B. Patel, E. S. Parrott, R. J. Sutton, W. Ma, B. Conings, A. Babayigit, H. G. Boyen, S. Bent, F. Giustino, M. Herz, M. B. Johnston, M. D. Mcgehee and H. J. Snaith, Science, 2016, 354, 861–865.
16. F. Fu, T. Feurer, T. P. Weiss, S. Pisoni, E. Avancini, C. Andres, S. Buecheler and A. N. Tiwari, Nat. Energy, 2016, 2, 16190.
17. A. R. Uhl, A. Rajagopal, J. A. Clark, A. Murray, T. Feurer, S. Buecheler, A. K.-Y. Jen and H. W. Hillhouse, Adv. Energy Mater., 2018, 8, 1801254.
18. H. Shen, T. Duong, J. Peng, D. Jacobs, N. Wu, J. Gong, Y. Wu, S. K. Karuturi, X. Fu, K. Weber, X. Xiao, T. P. White and K. Catchpole, Energy Environ. Sci., 2018, 11, 394–406.
19. Y. H. Jang, J. M. Lee, J. W. Seo, I. Kim and D.-K. Lee, J. Mater. Chem. A, 2017, 5, 19439–19446.
20. F. Fu, S. Pisoni, T. P. Weiss, T. Feurer, A. Wäckerlin, P. Fuchs, S. Nishiwaki, L. Zortea, A. N. Tiwari and S. Buecheler, Adv. Sci., 2018, 5, 1700675.
21. Q. Han, Y.-T. Hsieh, L. Meng, J.-L. Wu, P. Sun, E.-P. Yao, S.-Y. Chang, S.-H. Bae, T. Kato, V. Bermudez and Y. Yang, Science, 2018, 361, 904–908.
22. M. Jost, T. Bertram, D. Koushik, J. Marquez, M. Verheijen, M. D. Heinemann, E. Köhnen, A. Al-Ashouri, S. Braunger, F. Lang, B. Rech, T. Unold, M. Creatore, I. Lauermann, C. A. Kaufmann, R. Schlatmann and S. Albrecht, ACS Energy Lett., 2019, 4, 583–590.
23. F. Sahli, J. Werner, B. A. Kamino, M. Bräuninger, R. Monnard, B. Paviet-salomon, L. Barraud, L. Ding, J. J. D. Leon, D. Sacchetto, G. Cattaneo, M. Boccard, M. Despeisse, S. Nicolay, Q. Jeangros, B. Niesen and C. Ballif, Nat. Mater., 2018, 17, 820–826.
24. J. Zheng, C. F. J. Lau, H. Mehrvarz, F.-J. Ma, Y. Jiang, X. Deng, A. Soeriyadi, J. Kim, M. Zhang, L. Hu, X. Cui, D. S. Lee, J. Bing, Y. Cho, C. Chen, M. A. Green, S. Huang and A. W. Y. Ho-Baillie, Energy Environ. Sci., 2018, 11, 2432–2443.
25. K. A. Bush, A. F. Palmstrom, Z. J. Yu, M. Boccard, R. Cheacharoen, J. P. Mailoa, D. P. McMeekin, R. L. Z. Hoye, C. D. Bailie, T. Leijtens, I. M. Peters, M. C. Minichetti, N. Rolston, R. Prasanna, S. Sofia, D. Harwood, W. Ma, F. Moghadam, H. J. Snaith, T. Buonassisi, Z. C. Holman, S. F. Bent and M. D. McGehee, Nat. Energy, 2017, 2, 17009.
26. M. Jaysankar, B. A. L. Raul, J. J. P. Bastos, C. H. Burgess, C. Weijtens, T. Aernouts, Y. Kuang, R. Gehlhaar, A. Hadipour and J. Poortmans, ACS Energy Lett., 2019, 4, 259–264.
27. M. A. Green, Y. Hishikawa, E. D. Dunlop, D. H. Levi, J. Hohl-Ebinger, M. Yoshita and A. W. Y. Ho-Baillie, Prog. Photovoltaics Res. Appl., 2019, 27, 3–12.
28. K. Jager, L. Korte, B. Rech and S. Albrecht, Opt. Express, 2017, 25, 473–482.
29. M. Filipič, P. Löper, B. Niesen, S. De Wolf, J. Krč, C. Ballif and M. Topič, Opt. Express, 2015, 23, A263–A278.
30. J. Werner, G. Nogay, F. Sahli, C. T. Yang, G. Christmann, A. Walter, B. Kamino, P. Fiala, S. Nicolay, Q. Jeangros, B. Niesen and C. Ballif, ACS Energy Lett., 2018, 3, 742–747.
31. R. H. Ahangharnejhad, Z. Song, A. B. Phillips, S. C. Watthage, Z. S. Almutawah, D. R. Sapkota, P. Koirala, R. W. Collins, Y. Yan and M. J. Heben, MRS Adv., 2018, 3, 3111–3119.
32. I. Celik, A. B. Phillips, Z. Song, Y. Yan, R. J. Ellingson, M. J. Heben and D. Apul, Energy Environ. Sci., 2017, 10, 1874–1884.
33. I. M. Peters, S. Sofia, J. Mailoa and T. Buonassisi, RSC Adv., 2016, 6, 66911–66923.
34. https://rredc.nrel.gov/solar//spectra/am1.5/ .
35. J. P. Mailoa, M. Lee, I. M. Peters, T. Buonassisi, A. Panchula and D. N. Weiss, Energy Environ. Sci., 2016, 9, 2644–2653.
36. M. T. Hörantner and H. Snaith, Energy Environ. Sci., 2017, 10, 1983–1993.
37. J. Lehr, M. Langenhorst, R. Schmager, S. Kirner, U. Lemmer, B. S. Richards, C. Case, U. W. Paetzold, J. Lehr, M. Langenhorstb, R. Schmagerb, S. Kirnerc, U. Lemmera, B. S. Richards, C. Case and U. W. Paetzold, Sustainable Energy Fuels, 2018, 2, 2754–2761.
38. M. Langenhorst, B. Sautter, R. Schmager, J. Lehr, E. Ahlswede, M. Powalla, U. Lemmer, B. S. Richards and U. W. Paetzold, Prog. Photovoltaics Res. Appl., 2019, 27(4), 290–298.
39. M. T. Hörantner, T. Leijtens, M. E. Ziffer, G. E. Eperon, M. G. Christoforo, M. D. McGehee and H. J. Snaith, ACS Energy Lett., 2017, 2, 2506–2513.
40. A. Chirilă, P. Reinhard, F. Pianezzi, P. Bloesch, A. R. Uhl, C. Fella, L. Kranz, D. Keller, C. Gretener, H. Hagendorfer, D. Jaeger, R. Erni, S. Nishiwaki, S. Buecheler and A. N. Tiwari, Nat. Mater., 2013, 12, 1107–1111.
41. L. A. A. Pettersson, L. S. Roman and O. Inganäs, J. Appl. Phys., 1999, 86, 487–496.
42. A. R. A. Ibdah, P. Koirala, P. Aryal, P. Pradhan, M. J. Heben, N. J. Podraza, S. Marsillac and R. W. Collins, J. Energy Chem., 2017, 27, 1151–1169.
43. S. Minoura, T. Maekawa, K. Kodera, A. Nakane, S. Niki and H. Fujiwara, J. Appl. Phys., 2015, 117, 195703.
44. T. A. F. Konig, P. A. Ledin, J. Kerszulis, M. A. Mahmoud, M. A. El-sayed, J. R. Reynolds and V. V. Tsukruk, ACS Nano, 2014, 8, 6182–6192.
45. L. V. Rodríguez-de Marcos, J. I. Larruquert, J. A. Méndez and J. A. Aznárez, Opt. Mater. Express, 2017, 7, 989–1006.
46. K. Ghimire, D. Zhao, C. Wang, Y. Yan and N. J. Podraza, in 2017 IEEE 44th Photovoltaic Specialist Conference, PVSC 2017, 2017.
47. A. Jain and A. Kapoor, Sol. Energy Mater. Sol. Cells, 2004, 81, 269–277.
48. R. Kamada, T. Yagioka, S. Adachi, A. Handa, K. F. Tai, T. Kato and H. Sugimoto, in 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), 2016, pp. 1287–1291.
49. A. Hadipour, B. de Boer and P. W. M. Blom, Org. Electron., 2008, 9, 617–624.
50. W. S. Yang, B. W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. Il Seok, Science, 2017, 356, 1376–1379.
51. Q. Jiang, Z. Chu, P. Wang, X. Yang, H. Liu, Y. Wang, Z. Yin, J. Wu, X. Zhang and J. You, Adv. Mater., 2017, 29, 1703852.
52. Q. Jiang, L. Zhang, H. Wang, X. Yang, J. Meng, H. Liu, Z. Yin, J. Wu, X. Zhang and J. You, Nat. Energy, 2016, 2, 16177.
53. R. Santbergen, A. H. M. Smets and M. Zeman, Opt. Express, 2013, 21, A262–A267.
54. A. P. Brunger and F. C. Hooper, J. Sol. Energy, 1993, 51, 53–64.
55. D. R. Myers, J. Sol. Energy, 2012, 86, 2771–2782.
56. M. Sengupta, Y. Xie, A. Lopez, A. Habte, G. Maclaurin and J. Shelby, Renew. Sustain. Energy Rev., 2018, 89, 51–60.
57. R. Gelaro, W. McCarty, M. J. Suárez, R. Todling, A. Molod, L. Takacs, C. A. Randles, A. Darmenov, M. G. Bosilovich, R. Reichle, K. Wargan, L. Coy, R. Cullather, C. Draper, S. Akella, V. Buchard, A. Conaty, A. M. da Silva, W. Gu, G. K. Kim, R. Koster, R. Lucchesi, D. Merkova, J. E. Nielsen, G. Partyka, S. Pawson, W. Putman, M. Rienecker, S. D. Schubert, M. Sienkiewicz and B. Zhao, J. Clim., 2017, 30, 5419–5454.
58. M. K. Fuentes, A Simplified Thermal Model of Photovoltaic Modules, 1985, vol. SAND85-033.
59. J. Yang, A. Banerjee and S. Guha, Appl. Phys. Lett., 1997, 70, 2975.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9se00237e

---