Energetic effects of hybrid organic/inorganic interfacial architecture on nanoporous black silicon photoelectrodes†
Abstract
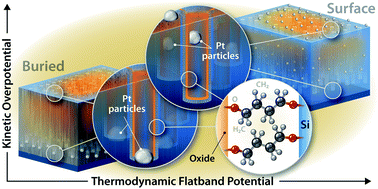
Photoelectrochemical cells have been the subject of great interest in the research community as a route for fuel formation directly from sunlight. Interfacial layers are frequently employed on the surface of light-absorbing semiconductor photoelectrodes to enhance the activity and stability of the semiconductor. Here we consider the energetic effects of such layers on a nanoporous ‘black’ silicon photocathode. We construct hybrid organic/inorganic films by growing an oxide-nucleating molecular monolayer on the nanostructured Si surface and burying this molecular monolayer under TiO2 deposited by atomic layer deposition. We examine the energetic effects of this hybrid interfacial architecture via our recently developed intensity-modulated high-frequency resistivity (IMHFR) impedance spectroscopy technique and quantify the change in thermodynamic flatband potential as the oxide thickness is increased from 0–15 nm. By comparing the IMHFR data with traditional voltammetry, we are able to deconvolute the thermodynamic and kinetic contributions that determine the observed proton reduction onset potential. We also study these photoelectrodes with Pt nanoparticles either (i) deposited on top of the molecular/TiO2 interfacial layer or (ii) etched into the Si surface. In the first architecture, a beneficial positive shift in the thermodynamic flatband potential is achieved from the Si|molecular|TiO2 p–n junction, but the lack of a direct Si|Pt contact results in large kinetic charge transfer losses. In contrast, the second architecture allows for facile charge transfer due to the direct Si|Pt contact but negates any beneficial thermodynamic effect of the molecular/TiO2 bilayer. Despite the lack of thermodynamic effect of the hybrid molecular/TiO2 interfacial layer, we find that there is still a significant kinetic benefit from this layer. This work demonstrates the sensitive nature of the thermodynamics and kinetics on the interfacial architecture and yields critical insights into the design of photoelectrochemical interfaces.
- This article is part of the themed collection: 2019 Sustainable Energy and Fuels HOT Articles


 Please wait while we load your content...
Please wait while we load your content...
