 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Desorption reaction in MgH2 studied with in situ μ+SR
Jun
Sugiyama
 *a,
Izumi
Umegaki
a,
Mitsuru
Matsumoto
a,
Kazutoshi
Miwa
a,
Hiroshi
Nozaki
a,
Yuki
Higuchi
a,
Tatsuo
Noritake
a,
Ola K.
Forslund
b,
Martin
Månsson
b,
Stephen P.
Cottrell
c,
Akihiro
Koda
d,
Eduardo J.
Ansaldo
e and
Jess H.
Brewer
*a,
Izumi
Umegaki
a,
Mitsuru
Matsumoto
a,
Kazutoshi
Miwa
a,
Hiroshi
Nozaki
a,
Yuki
Higuchi
a,
Tatsuo
Noritake
a,
Ola K.
Forslund
b,
Martin
Månsson
b,
Stephen P.
Cottrell
c,
Akihiro
Koda
d,
Eduardo J.
Ansaldo
e and
Jess H.
Brewer
 fg
fg
aToyota Central Research & Development Laboratories, Inc., 41-1 Yokomichi, Nagakute, Aichi 480-1192, Japan. E-mail: e0589@mosk.tytlabs.co.jp; juns@triumf.ca; Fax: +81-561-63-6920; Tel: +81-561-71-8029
bDepartment of Applied Physics, KTH Royal Institute of Technology, Electrum 229, SE-16440 Kista, Stockholm, Sweden
cISIS Muon Facility, Rutherford Appleton Laboratory, Didcot, Oxfordshire, OX11 0QX UK
dMuon Laboratory, J-PARC, KEK, Tokai, Ibaraki 319-1106, Japan
eDepartment of Physics & Engineering Physics, University of Saskatchewan, Saskatoon, SK, S7N 5E2 Canada
fDepartment of Physics & Astronomy, University of British Columbia, Vancouver, BC, V6T 1Z1 Canada
gTRIUMF, 4004 Wesbrook Mall, Vancouver, BC, V6T 2A3 Canada
First published on 29th January 2019
Abstract
In order to study the mechanism determining the desorption temperature (Td) of hydrogen storage materials, we have measured positive muon spin rotation and relaxation (μ+SR) in MgH2 over a wide temperature range including its Td. The pressure in the sample cell due to desorbed H2 was measured in parallel with the μ+SR measurements under static conditions. Such in situ μ+SR measurements revealed that hydrogen starts to diffuse in MgH2 well below Td. This indicates the important role of hydrogen diffusion in accelerating the desorption reaction by removing the reaction product, i.e. H2, from the reaction system.
1 Introduction
Positive muon spin rotation and relaxation (μ+SR) techniques are widely used for studying local magnetic environments in solids1,2 for both static and dynamic behaviors of the internal magnetic field(s) Hint at the muon site(s). However, due to limited counting rates for recording μ+SR spectra, past μ+SR measurements were usually performed under fixed conditions, i.e. at a constant temperature, pressure and magnetic field. Consequently, it was hitherto impractical to use μ+SR to study changes in Hint during chemical reactions of materials.Recent developments in pulsed muon beams at ISIS in the UK3 and at J-PARC in Japan,4 together with the installation of multi-detector counting systems,5–7 have increased the counting rate to above 100 M events per h. This means that one μ+SR spectrum with acceptable statistics is recorded within 5–30 minutes. Therefore, if we select a suitable material, μ+SR can provide information on the change in Hint during a fairly rapid reaction, in an in situ manner. Here we report our first in situ μ+SR study of magnesium hydride, MgH2 (see Fig. 1), in order to reveal the change in Hint during its hydrogen desorption reaction at high temperatures.
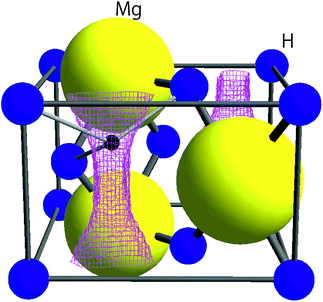 | ||
| Fig. 1 The crystal structure of MgH2 in tetragonal symmetry with the space group P42/mnm together with the μ+ sites predicted by DFT calculations (see Section 3.1). The lattice parameters determined from synchrotron radiation powder diffraction data8 are a = 4.5198(7) Å, c = 3.0250(6) Å, and V = 61.80 Å3. The pink lines represent the iso-surface of potential energy ϕE = 600 meV. A small black sphere represents the muon site, at which ϕE shows a local minimum. | ||
An ideal hydrogen storage material is expected to absorb and desorb hydrogen gas reversibly without capacity fading, preferably at room temperature.9 Magnesium hydride (MgH2) is known to be one of the promising hydrogen storage materials, because of its relatively low cost and high gravimetric and volumetric hydrogen densities.10–13 However, its high enthalpy of decomposition leads to a high hydrogen desorption temperature (Td) and slow reaction rate. Such disadvantages for applications are alleviated significantly by milling14–16 and by adding catalytic agents, such as Nb2O5.17–20 In fact, the measurements under dynamic conditions, i.e. with a temperature programmed desorption (TPD) and/or thermogravimetry (TG) technique, revealed that Td = 710 K for bulk MgH2,21,22 while milling decreases Td by about 100 K (ref. 21 and 22) and about another 100 K decrease can be achieved by milling together with 5 wt% of Nb2O5.23–25 Such a large decrease in Td, i.e. 200 K in total, and a simple crystal structure make MgH2 a very attractive model material11–13 to understand the way to control Td in storage materials.
Based on macroscopic measurements and numerical calculations, the desorption reaction in MgH2 is thought to consist of the following five steps under the assumption that a MgH2 core is surrounded by a Mg shell in each particle:12,26
(1) decomposition of MgH2 at the interface between MgH2 and Mg;
(2) diffusion of H across the Mg shell;
(3) penetration of H at the surface of the Mg shell;
(4) recombination of chemisorbed H and physisorption;
(5) desorption to the gas phase.
A past quasi-elastic neutron scattering experiment27 revealed that the diffusion coefficient of hydrogen (DH) in MgH2 ranges below 2.5 × 10−9 cm2 s−1 even at 650 K, which is lower by at least three orders of magnitude than DH in Mg (10−9 cm2 s−1 at 300 K).12 Considering the rates of the above five reaction steps, the third and/or fourth steps are thought to be a rate-determining process for the overall desorption reaction,12,19,26,28 although the nucleation of Mg and formation of the channels by Mg metal nuclei are proposed to be crucial for bulk MgH2.29 The hydrogen diffusion in MgH2 is thus believed to be unessential for the desorption reaction in MgH2. Nevertheless, a 1H-NMR study on MgH2,30 which provides microscopic information of hydrogen dynamics, suggests a faster H motion even at 333 K in milled MgH2 with Nb2O5 than in bulk MgH2. Indeed, there are still large discrepancies between experimental results and calculated predictions for hydrogen diffusion in MgH2.31–36
We have therefore used μ+SR to study Hint in MgH2 (where it arises mainly from the nuclear magnetic moment of 1H), since the diffusion coefficients of Li+ and Na+ are estimated for many battery materials using the fluctuation rate of Hint detected with μ+SR.37–46 Due to the fact that the natural abundance of 25Mg with I = 5/2 is 10%, the μ+SR spectrum caused by the μ+s stopped in a Mg phase should be time independent, particularly above room temperature. Taking into account a very small concentration of diffusing H in Mg, H diffusion in Mg is invisible with μ+SR, but such behavior in MgH2 should be visible. This is because H diffusion enhances the fluctuation rate of Hint in MgH2 formed by 1H. In fact, our previous μ+SR measurements on MgH2 (ref. 47 and 48) showed a clear difference in Hint among the three MgH2 samples: as-prepared MgH2, milled MgH2, and MgH2 milled together with 5 wt% of Nb2O5. That is, although Hint is static up to Td in the as-prepared sample, Hint of the two milled samples becomes dynamic below Td.
Remembering that μ+ behaves as a light isotope of H+ in solids,1,2 μ+ is expected to be mobile in any system where H is diffusing, regardless of the charge state of H. However, the differences between the diffusive behaviors observed by μ+SR in the three MgH2 samples imply that μ+ diffusion is not equivalent to H diffusion in MgH2. This naturally motivated us to study the hydrogen desorption reaction in MgH2 with a more sophisticated μ+SR experiment, using a combination of an intense muon beam and simultaneous pressure monitoring—namely an in situ μ+SR technique. Here, we report the result of our first attempt to observe the diffusive behavior in MgH2 with in situ μ+SR.
2 Experimental
2.1 Sample preparation
A powder sample of MgH2 was purchased from Wako Pure Chemical Industries, Ltd., which will be referred to as ap-MgH2 in the text. Then 3 g of ap-MgH2 powder was milled with 300 g stainless steel balls in a stainless steel pot by using a planetary ball mill (Fritsch Japan Co., Ltd, P-5/4) for 24 hours; this sample will be referred to as m-MgH2 in the text. Then a mixture of 2.85 g of ap-MgH2 powder and 0.15 g (5 wt%) of Nb2O5 powder (Aldrich) was also milled for 24 hours in the same way as the above; this sample will be referred to as mwn-MgH2 in the text.2.2 μ+SR
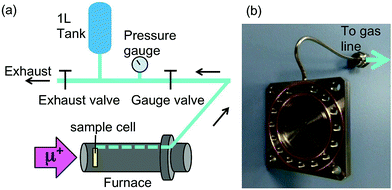
In order to observe hydrogen dynamics, the μ+SR spectra were measured in a zero field (ZF), longitudinal field (LF), and transverse field (TF) on the EMU5 surface muon beam line at the ISIS facility of the Rutherford Appleton Laboratory in the U.K. Here TF (LF) means the magnetic field perpendicular (parallel) to the initial muon spin polarization. The statistics of each spectrum were 40 M events for ZF, 30 M events for LF, and 10 M events for TF with a counting rate of about 80 M events per h. Since the LF-spectra were measured at LF = 5 and 10 Oe, it took about 1.4 hours to obtain the data at one temperature point. Then, the sample was heated to the next temperature at a rate of 1–2 K min−1. The temperature range for the measurements was maintained between 300 and 800 K using a furnace [Fig. 2(a)].Each sample was sealed in a stainless steel cell (grade 316) with two gold O-rings [Fig. 2(b)] in a He-filled glove box. The window of the cell was also made of stainless steel foil with 50 μm thickness. Then the cell was mounted onto the furnace so that the direction of the muon beam is perpendicular to the window. As a result, the muons were implanted into the sample through the window. The released gas was collected through the aforementioned 1/16′′ capillary tube, also made from stainless steel, connecting the cell to a one liter tank [Fig. 2(a)]. Before the measurements, the cell, gas line, and tank were evacuated at room temperature, then, the exhaust valve was closed, and then, the sample was heated by the furnace. The total amount of the gas released was determined by measuring the pressure (p) in the gas tank with a Baratron pressure gauge. Prior to the in situ experiment at ISIS as explained above, μ+SR spectra were also measured at both TRIUMF and J-PARC.47,48 The details of μ+SR techniques are explained elsewhere.1,2 The obtained μ+SR data were analyzed with musrfit.49
3 Results
3.1 Predicted muon sites
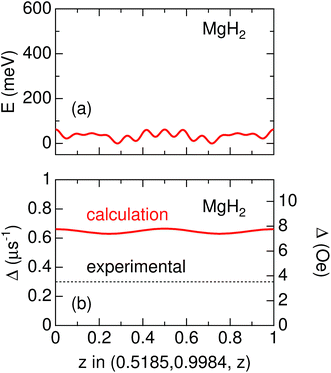
Knowledge of the site(s) for the implanted μ+s in the lattice is essential to understanding the μ+SR data. According to electrostatic potential (E) calculations using a first principles DFT+GGA method, there is likely one shallow E minimum for the implanted μ+ in the MgH2 lattice (Fig. 1). However, the distribution of E in the lattice describes a “chimney-shaped” one-dimensional (1D) channel along the c-axis, connecting many local E minima between two neighboring hydrogens, as described in Section 4.1.The zero-point energy (Ezero) of an H atom in solids is typically about 200 meV.50 Since Ezero is approximately scaled by a factor of the inverse of the square root of the mass, Ezero for μ+ is expected to be about 600 meV. The “extended minimum” for E < 600 meV, within which the implanted μ+ will be located, is illustrated by the region within pink shaded cylinders in Fig. 1. This indicates that the μ+s will be in a delocalized state within the 1D channel, particularly at high temperatures. It should be noted that we ignored the local lattice distortion due to the implanted μ+ in the above calculations. Therefore, the observed μ+SR spectrum is probably either a superposition of multiple spectra from muons at different sites or the signature of a μ+ in a delocalized quantum state.
3.2 μ+SR spectra
The ZF-μ+SR spectrum exhibits a characteristic oscillation for the all three samples below 350 K [Fig. 3(a)], as already reported. This indicates the formation of a collinear three-spin-½ system (H-μ-H) and a two spin-½ system (H-μ), as is the case for many hydrogen storage materials.51,52 The muon spin depolarization function in ZF caused by collinear H-μ-H [PZFHμH(t)] is given by53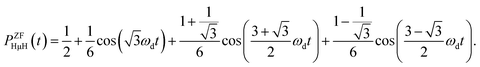 | (1) |
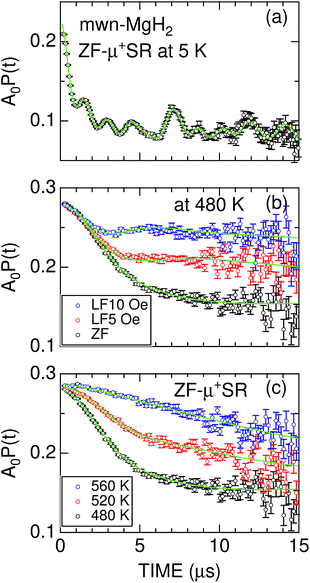 | ||
| Fig. 3 (a) The ZF-μ+SR spectrum of mwn-MgH2 at 5 K; (b) the ZF- and LF-μ+SR spectra of mwn-MgH2 at 480 K; and (c) the ZF-μ+SR spectra of mwn-MgH2 at 480, 520, and 560 K. In (a), a solid line represents the best fit using a combination of one H-μ-H and eight H-μ signals. In (b) and (c), solid lines represent the best fit obtained using eqn (3). The fitted initial asymmetry is A0 = 0.24 for (a) and 0.28 for (b) and (c); based on the measurement of a silver reference sample, this means that only a small fraction of the implanted μ+ form a hydrogen-like muonium (μ+e−) state in MgH2 at 5 K. | ||
On the other hand, PZFHμ(t) is given by54
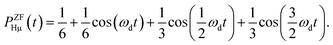 | (2) |
In fact, the ZF-μ+SR spectrum was well fitted by a combination of one PZFHμH(t) and eight PZFHμ(t) signals, indicating the presence of multiple muon sites in the lattice. Since the fit shows that about 10% of the implanted μ+s form a H-μ-H state with r = 1.16 Å at 5 K, such muons sit at the middle of the two neighboring H−s. However, the distance between the two nearest neighbor H−s in the MgH2 lattice is 3.27 Å.8 This means that μ+ attracts the two neighboring H−s, as in the case for alkali halides.53 Considering the presence of the other eight muon sites evidenced by the formation of H-μ systems, the obtained μ+SR result is very consistent with the predictions from the first principles calculations.
At temperatures above 300 K, the ZF-μ+SR spectrum clearly shows a Kubo–Toyabe (KT) type relaxation [Fig. 3(b)] due to random nuclear magnetic fields. This means that both H-μ-H and H-μ are no longer stable at high temperatures, because of the thermal vibration of H, being consistent with the findings of 1H-NMR.55 Since the applied LF = 10 Oe significantly suppresses the relaxation by decoupling Hint,56 the magnitude of the random nuclear magnetic fields at the muon sites is comparable to the applied LF. This is a typical value for nuclear magnetic fields in solids.1,2,42
For both m-MgH2 and mwn-MgH2, as temperature increases from 300 K, the KT behavior changes from static to dynamic above around 450 K and finally the relaxation rate becomes very small compared with that at lower temperatures [Fig. 3(c)]. This indicates that the field fluctuation rate (ν) is very rapid compared with the static width (Δ) due to Hint, as in the case for Li- and Na-diffusion in battery materials.37–46
In order to extract Δ and ν from the μ+SR data for the three samples, the ZF- and LF-μ+SR spectra were fitted by a combination of two dynamic Gaussian KT signals (GDGKT)57 and a time-independent background signal coming from the muons stopping in the sample cell:
| A0P(t) = AKT1GDGKT(Δ1, v1, t, HLF) + AKT2GDGKT(Δ2, v2, t, HLF) + ABG, | (3) |
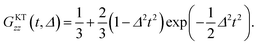
At first, we fitted all the ZF- and LF-spectra using a common ABG over the whole temperature range and common, i.e. HLF-independent, Δi and ν (v1 = v2) at each temperature using eqn (3). Then, since both AKT1 and AKT2 were found to be approximately temperature-independent, we finally used common AKT1 and AKT2 for fitting the ZF- and LF-spectra. Here, Δ corresponds to a spin–spin relaxation rate (1/T2), while ν corresponds to a combination of the muon hop rate and the nuclear spin-lattice relaxation rate (1/T1).
3.3 Nature of diffusion in the three samples
 | ||
| Fig. 4 The temperature dependences of the gas pressure and μ+SR parameters for ap-, m-, and mwn-MgH2 samples: (a), (e), and (i) gas pressure in the cell; (b), (f), and (j) the field distribution static widths (Δ1 and Δ2); (c), (g), and (k) the field fluctuation rates (v1 and v2); and (d), (h), and (l) the asymmetries (AKT1, AKT2, and ABG). Except for pressure, the values shown were obtained by fitting the set of ZF- and LF-μ+SR spectra with eqn (3). Dotted lines show Tmidd determined from the p(T) curve. | ||
Concerning the μ+SR parameters, both Δ1 and Δ2 decrease slightly with increasing temperature, but are roughly temperature independent up to Td, below which Δ1 of the dominant AKT1 signal ranges between 0.33 and 0.31 μs−1 (equivalent to 3.8–3.6 Oe) and Δ2 of the smaller AKT2 signal varies between 0.13 and 0.12 μs−1 (equivalent to 1.5–1.3 Oe) [Fig. 4(b)]. Above Td, Δ abruptly drops down to ∼0.07 μs−1 (equivalent to 0.8 Oe), as the AKT2 signal merges into the AKT1 signal [Fig. 4(d)]. The presence of the two AKT signals below Tmidd suggests that about 30% of the implanted muons are located outside of the one-dimensional channel along the c-axis (Fig. 1), but still in the sample.
In addition, ν is very small and almost temperature independent up to around 670 K, but leaps up to ∼0.26 μs−1 at 700 K and increases with further increasing temperature [Fig. 4(c)]. Based on the p(T) curve, MgH2 fully decomposes into Mg and H2 at 700 K. This indicates that the sudden decrease in Δ at Td is most likely not caused by a motional narrowing behavior due to H and/or μ+ diffusion, but by a change in the phase from MgH2 to Mg due to the hydrogen desorption reaction, as proposed by macroscopic measurements.12,26
It should be noted that v/Δ1 ∼ 1/9 at temperatures below Td. Furthermore, the magnitude of Δ1 is about 1/2 of that determined by dipole field calculations with Dipelec,58i.e. Δcalc = 0.63–0.66 μs−1 (7.4–7.8 Oe) for an entirely static state. This suggests that μ+ in MgH2 is in a delocalized state even at room temperature, as predicted from the first principles calculations (see Fig. 1). However, since both Δ and ν are almost independent of temperature, H is most likely not mobile but rather vibrating at its equilibrium position. We will discuss this later in Section 4.1.
The most significant difference between m-MgH2 and ap-MgH2 is found in the temperature dependence of Δ. That is, as seen in Fig. 4(f), although the magnitude of Δ1 at 400 K is very close to that of Δ1 for ap-MgH2, Δ2 is much larger than Δ2 in ap-MgH2. Since Δ2 at 450 K is larger than Δcalc, about 19% (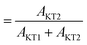 ) of the implanted muons are thought to sit at fresh surfaces produced by milling, probably trapped by a dangling H− bond. Furthermore, as temperature increases from 400 K, both Δ1 and Δ2 decrease monotonically up to around Tmidd, and then decrease faster (larger |dΔ/dT|), and are likely to level off to a constant value at around Tmidd.
) of the implanted muons are thought to sit at fresh surfaces produced by milling, probably trapped by a dangling H− bond. Furthermore, as temperature increases from 400 K, both Δ1 and Δ2 decrease monotonically up to around Tmidd, and then decrease faster (larger |dΔ/dT|), and are likely to level off to a constant value at around Tmidd.
By contrast, as temperature increases from 400 K, ν decreases slightly with temperature up to Tmidd, and then increases rapidly with temperature [Fig. 4(g)]. The steady decrease of Δ1 and Δ2 below 500 K, at which p = 0, suggests a motional narrowing behavior due to H diffusion in m-MgH2. This is because μ+ diffusion is temperature independent up to 700 K, based on the v(T) curve in ap-MgH2. The decrease in ν also indicates that both species are diffusing below Tmidd. However, above Tmidd the phase change from MgH2 to Mg is the predominant reaction, resulting in a decrease in Δ and a rapid increase in ν.
The temperature dependences of Δ1, Δ2, and ν are similar to those for m-MgH2, particularly below 450 K, at which p = 0. Above 450 K, both Δ1 and Δ2 decrease with temperature more rapidly, but ν increases slowly compared with ν in m-MgH2. Overall results reveal that the changes in Δ and ν below 450 K are caused by H diffusion in MgH2, while those above 450 K are induced by a gradual phase change from MgH2 to Mg due to a hydrogen desorption reaction.
The ratio between AKT2 and (AKT1 + AKT2) is about 20%, which is comparable to that of m-MgH2 (19%). Thus, the surface structure of mwn-MgH2 is most likely the same to that of m-MgH2.
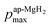 ), defining the normalized pmax as
), defining the normalized pmax as 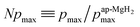 .
.
For samples exhibiting multiple asymmetries, each asymmetry is roughly proportional to the volume fraction of each phase. Since we used the same measurement setup for the three samples, the volume fraction (VF) of the sample is given by
Therefore the normalized VF, which is given by 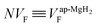 , also provides a rough estimate for the amount of each sample. In fact, as seen in Fig. 5, a linear relationship between Npmax and NVF demonstrates the reliability of the above explanation.
, also provides a rough estimate for the amount of each sample. In fact, as seen in Fig. 5, a linear relationship between Npmax and NVF demonstrates the reliability of the above explanation.
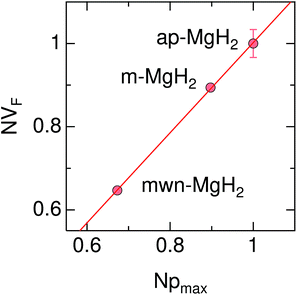 | ||
| Fig. 5 The relationship between the normalized volume fraction of the sample (NVF) and the normalized maximum pressure (Npmax) for the three MgH2 samples. Here, the volume fraction of the sample is defined as VF = (AKT1 +AKT2)/(AKT1 + AKT1 + ABG). For NVF, each VF is divided by VF for ap-MgH2. pmax is the pressure at the highest temperature measured [see Fig. 4(a), (e), and (i)], and, for Npmax, each pmax is divided by pmax for ap-MgH2. | ||
4 Discussion
4.1 Implanted muons in MgH2
As predicted by first principles calculations, μ+ is most likely in a delocalized state in a 1D channel of MgH2 even at room temperature [see Fig. 6(a)]. This has been confirmed by a very recent negative muon (μ−) spin rotation and relaxation experiment on ap-MgH2.59 That is, from the fixed position of μ− captured on Mg, μ−SR shows that Δ = 0.520(7) μs−1 [equivalent to 6.11(8) Oe], which is very close to the calculated value (Δcalc = 0.5807 μs−1) at the Mg site in MgH2. By contrast, the present μ+SR shows that Δ ∼ 0.3 μs−1 [equivalent to 2.55 Oe] for MgH2 below 400 K, while the calculated Δ in the 1D channel ranges between 0.629 and 0.664 μs−1 [equivalent to 7.39 and 7.80 Oe] [see Fig. 6(b)]. This clearly indicates that μ+ is not immobile, but delocalized along the 1D channel.Since ν for ap-MgH2 is independent of temperature up to around 670 K, the delocalized state of μ+ is not altered with temperature in the temperature range between 300 and 760 K, probably due to a very small energy barrier in the 1D channel [see Fig. 6(a)]. Nevertheless, the Δ(T) curves show a motional narrowing behavior below 550 K for m- and 500 K for mwn-MgH2 samples. This means that the delocalized μ+ feels a fluctuating Hint caused by H diffusion, which occurs even at temperatures for which p = 0. We wish to emphasize again that μ+feels a static and/or dynamic nuclear field formed by 1H in MgH2, but does not sense it in Mg due to dilute concentration of H. Consequently, μ+SR clearly detects H diffusion in MgH2, where a desorption reaction does not occur, although it would be difficult to reliably estimate the diffusion coefficient of H under this circumstance, i.e. the observation of mobile H from a delocalized viewpoint.
4.2 Activation energy
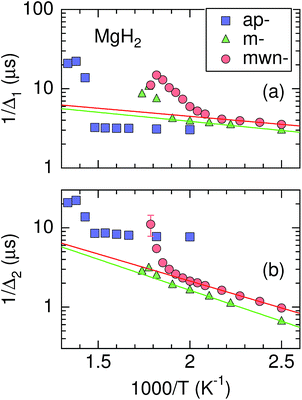
When ν is due only to ion diffusion, the v(T) curve is well explained by a thermal activation process. However, the ν values in the three MgH2 samples are not simply determined by a single diffusion process, as mentioned above. Hence, Fig. 7 shows instead the relationship between 1/Δ and inverse temperature. The activation energy (Ea) for 1/Δ1 in m-MgH2 and mwn-MgH2 is estimated to be 0.045(2) and 0.040(2) eV, respectively, while Ea for 1/Δ2 in m-MgH2 and mwn-MgH2 is 0.155(3) and 0.134(3) eV, respectively. This means that Ea values for m-MgH2 are similar to those for mwn-MgH2. These values are comparable to the diffusion activation energy for MgH2 predicted by first principles calculations.33,34 In contrast, past 1H-NMR measurements on 1/T1 in ap-MgH2 revealed that Ea = 1.72 eV in the temperature range between 500 and 666 K,30 but no data for m- and mwn-MgH2 were reported.Therefore, the milling is found to enhance H diffusion in MgH2 through the formation of fresh surfaces. Such an enhancement leads to a decrease in Td. However, since there are no clear differences in the μ+SR parameters below 500 K between m-MgH2 and mwn-MgH2, the role of Nb2O5 in reducing Td is still not clarified. In order to further understand the dynamic behavior in MgH2, we definitely need to separate the contribution of μ+ diffusion from the μ+SR data. For this purpose, we have initiated a negative muon spin rotation and relaxation experiment on MgH2,59 because μ− is captured by Mg nuclei and thus μ−SR provides information on Hint from a fixed viewpoint.
5 Conclusions
We have carried out an “in situ” μ+SR experiment on MgH2 to measure the pressure in the sample cell in parallel to the μ+SR spectrum under static conditions. The motivation behind this experiment is to clarify the role of H diffusion in solid MgH2 in determining the hydrogen desorption temperature (Td). This is, to our knowledge, the first in situ experiment to observe such a reaction in solids with μ+SR.We have found that, as Td is decreased by milling or milling with Nb2O5, the diffusive behavior of H in MgH2 is observed well below Td, where the Mg phase does not exist. This suggests that rapid H diffusion in MgH2 is one of the key factors to reduce Td, since the liberated H from the MgH2 phase should be removed through the surface with H diffusion.
Finally, we wish to emphasize that in situ μ+SR experiments will provide clear insights into many reaction mechanisms through measurements of ion diffusion in solids and its thermal activation energy. This is because many reactions are often accompanied by mass transport in solids.
Author contribution statement
J.S. conceived the experiments. I.U. prepared and performed the experiments at ISIS together with J.S., H.N., Y.H., O.K.F., M. Månsson and the local ISIS support from S.P.C. J.S., H.N., and I.U. joined the μ+SR experiments at J-PARC and A.K. assisted them. J.S., H.N., T.N., E.J.A., and J.H.B. performed the μ+SR experiments at TRIUMF. M. Matsumoto and I.U. prepared the m- and mwn-MgH2 samples. K.M. performed the first principles calculations. J.S. analyzed the data and created the first draft with I.U. J.H.B. and M. Månsson edited the draft, and all authors reviewed the manuscript in several steps.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the staff of TRIUMF, J-PARC, and ISIS for help with the μ+SR experiments with the following proposal numbers: M1175, 2012A0089, 2013A0019, RB1510262, and RB1520259. We are particularly grateful to Chris Goodway, Paul McIntyre, Adam Sears, and Mark Kibble of the pressure and furnace group at ISIS, for their support that was essential for a successful experiment. J.S. specially thanks Dr Shinichi Towata of the Aichi Synchrotron Radiation Center for his encouragement to this work. M. Månsson and O.F.K. are partly supported by a Marie Skłdowska Curie Action, International Career Grant through the European Commission and Swedish Research Council (VR), Grant No. INCA-2014-6426 as well as a VR neutron project grant (BIFROST, Dnr. 2016-06955). Further support was also granted by the Carl Tryggers Foundation for Scientific Research (CTS-16:324 and CTS-17:325). This work was supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan, KAKENHI Grant no. JP23108003 and JP26108722 and Japan Society for the Promotion Science (JSPS) KAKENHI Grant no. JP26286084 and JP18H01863.References
- G. M. Kalvius, D. R. Noakes and O. Hartmann, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner, J. L. Eyring and G. H. Lander, North-Holland, Amsterdam, 2001, vol. 32, ch. 206, pp. 55–451 Search PubMed.
- A. Yaouanc and P. D. de Réotier, in Muon Spin Rotation, Relaxation, and Resonance, Application to Condensed Matter, Oxford, New York, 2011 Search PubMed.
- P. J. C. King, R. de Renzi, S. P. Cottrell, A. D. Hillier and S. F. J. Cox, Phys. Scr., 2013, 88, 068502 CrossRef.
- Y. Miyake, K. Shimomura, N. Kawamura, A. Koda, P. Strasser, K. M. Kojima, H. Fujimori, S. Makimura, Y. Ikedo, Y. Kobayashi, J. Nakamura, Y. Oishi, S. Takeshita, T. Adachi, A. D. Pant, H. Okabe, S. Matoba, M. Tampo, M. Hiraishi, K. Hamada, S. Doiuchi, W. Higemoto, T. U. Ito and R. Kadono, JPS Conf. Proc., 2018, 21, 011054 Search PubMed.
- S. Giblin, S. Cottrell, P. King, S. Tomlinson, S. Jago, L. Randall, M. Roberts, J. Norris, S. Howarth, Q. Mutamba, N. Rhodes and F. Akeroyd, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 751, 70 CrossRef CAS.
- A. D. Hillier, M. Aramini, P. J. Baker, A. Berlie, P. K. Biswas, S. P. Cottrell, K. Ishida, T. Loe, J. S. Lord, D. E. Pooley, F. L. Pratt, N. J. Rhodes, R. J. da Silva Afonso, M. T. F. Telling and K. Yokoyama, JPS Conf. Proc., 2018, 21, 011055 Search PubMed.
- K. M. Kojima, T. Murakami, Y. Takahashi, H. Lee, S. Y. Suzuki, A. Koda, I. Yamauchi, M. Miyazaki, M. Hiraishi, H. Okabe, S. Takeshita, R. Kadono, T. Ito, W. Higemoto, S. Kanda, Y. Fukao, N. Saito, M. Saito, M. Ikeno, T. Uchida and M. M. Tanaka, J. Phys.: Conf. Ser., 2014, 551, 012063 CrossRef.
- T. Noritake, M. Aoki, S. Towata, Y. Seno, Y. Hirose, E. Nishibori, M. Takata and M. Sakata, Appl. Phys. Lett., 2002, 81, 2008–2010 CrossRef CAS.
- L. Schlapbach and A. Züttel, Nature, 2001, 414, 353 CrossRef CAS PubMed.
- J. F. Stampfer, C. E. Holley and J. F. Suttle, J. Am. Chem. Soc., 1960, 82, 3504–3508 CrossRef CAS.
- B. Sakintuna, F. Lamari-Darkrim and M. Hirscher, Int. J. Hydrogen Energy, 2007, 32, 1121–1140 CrossRef CAS.
- J.-C. Crivello, B. Dam, R. V. Denys, M. Dornheim, D. M. Grant, J. Huot, T. R. Jensen, P. de Jongh, M. Latroche, C. Milanese, D. Milčius, G. S. Walker, C. J. Webb, C. Zlotea and V. A. Yartys, Appl. Phys. A: Mater. Sci. Process., 2016, 122, 97 CrossRef.
- Y. Wang and Y. Wang, Prog. Nat. Sci.: Mater. Int., 2017, 27, 41–49 CrossRef CAS.
- P. Tessier and E. Akiba, J. Alloys Compd., 1999, 293–295, 400–402 CrossRef CAS.
- G. Liang, J. Huot, S. Boily, A. V. Neste and R. Schulz, J. Alloys Compd., 1999, 292, 247–252 CrossRef CAS.
- J.-L. Bobet, B. Chevalier, M. Song, B. Darriet and J. Etourneau, J. Alloys Compd., 2002, 336, 292–296 CrossRef CAS.
- G. Barkhordarian, T. Klassen and R. Bormann, Scr. Mater., 2003, 49, 213–217 CrossRef CAS.
- G. Barkhordarian, T. Klassen and R. Bormann, J. Alloys Compd., 2004, 364, 242–246 CrossRef CAS.
- G. Barkhordarian, T. Klassen and R. Bormann, J. Alloys Compd., 2006, 407, 249–255 CrossRef CAS.
- N. Hanada, T. Ichikawa and H. Fujii, J. Alloys Compd., 2007, 446–447, 67–71 CrossRef CAS.
- H. Reule, M. Hirscher, A. Weißhardt and H. Kronmüller, J. Alloys Compd., 2000, 305, 246–252 CrossRef CAS.
- N. Hanada, T. Ichikawa, S.-I. Orimo and H. Fujii, J. Alloys Compd., 2004, 366, 269–273 CrossRef CAS.
- N. Hanada, T. Ichikawa and H. Fujii, J. Alloys Compd., 2005, 404–406, 716–719 CrossRef CAS.
- N. Hanada, T. Ichikawa, S. Hino and H. Fujii, J. Alloys Compd., 2006, 420, 46–49 CrossRef CAS.
- K. Alsabawi, E. Gray and C. Webb, Int. J. Hydrogen Energy, 2019, 44, 2976–2980 CrossRef CAS.
- M. Martin, C. Gommel, C. Borkhart and E. Fromm, J. Alloys Compd., 1996, 238, 193–201 CrossRef CAS.
- J. Töpler, H. Buchner, H. Säufferer, K. Knorr and W. Prandl, J. Less-Common Met., 1982, 88, 397–404 CrossRef.
- V. P. Zhdanov, A. Krozer and B. Kasemo, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 11044–11048 CrossRef CAS.
- E. Evard, I. Gabis and V. Yartys, Int. J. Hydrogen Energy, 2010, 35, 9060–9069 CrossRef CAS.
- R. L. Corey, T. M. Ivancic, D. T. Shane, E. A. Carl, R. C. Bowman, J. M. Bellosta von Colbe, M. Dornheim, R. Bormann, J. Huot, R. Zidan, A. C. Stowe and M. S. Conradi, J. Phys. Chem. C, 2008, 112, 19784–19790 CrossRef CAS.
- A. J. Du, S. C. Smith and G. Q. Lu, J. Phys. Chem. C, 2007, 111, 8360–8365 CrossRef CAS.
- X. Yao, Z. Zhu, H. Cheng and G. Lu, J. Mater. Res., 2008, 23, 336–340 CrossRef CAS.
- S. Hao and D. S. Sholl, Appl. Phys. Lett., 2008, 93, 251901 CrossRef.
- M. S. Park, A. Janotti and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 064102 CrossRef.
- S. Hao and D. S. Sholl, J. Phys. Chem. Lett., 2010, 1, 2968–2973 CrossRef CAS.
- E. German and R. Gebauer, J. Phys. Chem. C, 2016, 120, 4806–4812 CrossRef CAS.
- J. Sugiyama, K. Mukai, Y. Ikedo, H. Nozaki, M. Månsson and I. Watanabe, Phys. Rev. Lett., 2009, 103, 147601 CrossRef PubMed.
- A. S. Powell, J. S. Lord, D. H. Gregory and J. J. Titman, J. Phys. Chem. C, 2009, 113, 20758–20763 CrossRef CAS.
- J. Sugiyama, H. Nozaki, M. Harada, K. Kamazawa, O. Ofer, M. Månsson, J. H. Brewer, E. J. Ansaldo, K. H. Chow, Y. Ikedo, Y. Miyake, K. Ohishi, I. Watanabe, G. Kobayashi and R. Kanno, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 054430 CrossRef.
- P. J. Baker, I. Franke, F. L. Pratt, T. Lancaster, D. Prabhakaran, W. Hayes and S. J. Blundell, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 174403 CrossRef.
- J. Sugiyama, H. Nozaki, M. Harada, K. Kamazawa, Y. Ikedo, Y. Miyake, O. Ofer, M. Månsson, E. J. Ansaldo, K. H. Chow, G. Kobayashi and R. Kanno, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054111 CrossRef.
- M. Månsson and J. Sugiyama, Phys. Scr., 2013, 88, 068509 CrossRef.
- A. S. Powell, Z. Stoeva, J. S. Lord, R. I. Smith, D. H. Gregory and J. J. Titman, Phys. Chem. Chem. Phys., 2013, 15, 816–823 RSC.
- J. Sugiyama, H. Nozaki, I. Umegaki, K. Mukai, K. Miwa, S. Shiraki, T. Hitosugi, A. Suter, T. Prokscha, Z. Salman, J. S. Lord and M. Månsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 014417 CrossRef.
- I. Umegaki, S. Kawauchi, H. Sawada, H. Nozaki, Y. Higuchi, K. Miwa, Y. Kondo, M. Månsson, M. Telling, F. C. Coomer, S. P. Cottrell, T. Sasaki, T. Kobayashi and J. Sugiyama, Phys. Chem. Chem. Phys., 2017, 19, 19058–19066 RSC.
- J. Sugiyama, I. Umegaki, T. Uyama, R. M. L. McFadden, S. Shiraki, T. Hitosugi, Z. Salman, H. Saadaoui, G. D. Morris, W. A. MacFarlane and R. F. Kiefl, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 094402 CrossRef.
- I. Umegaki, H. Nozaki, M. Harada, Y. Higuchi, T. Noritake, M. Matsumoto, S. i. Towata, E. J. Ansaldo, J. H. Brewer, A. Koda, Y. Miyake and J. Sugiyama, J. Phys.: Conf. Ser., 2014, 551, 012036 CrossRef.
- J. Sugiyama, J. Phys. Soc. Jpn., 2016, 85, 091012 CrossRef.
- A. Suter and B. Wojek, Phys. Procedia, 2012, 30, 69–73 CrossRef CAS.
- K. Miwa and A. Fukumoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155114 CrossRef.
- R. Kadono, K. Shimomura, K. H. Satoh, S. Takeshita, A. Koda, K. Nishiyama, E. Akiba, R. M. Ayabe, M. Kuba and C. M. Jensen, Phys. Rev. Lett., 2008, 100, 026401 CrossRef CAS PubMed.
- J. Sugiyama, Y. Ikedo, T. Noritake, O. Ofer, T. Goko, M. Månsson, K. Miwa, E. J. Ansaldo, J. H. Brewer, K. H. Chow and S.-I. Towata, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 092103 CrossRef.
- J. H. Brewer, S. R. Kreitzman, D. R. Noakes, E. J. Ansaldo, D. R. Harshman and R. Keitel, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7813–7816 CrossRef CAS.
- K. Nishiyama, S. Nishiyama and W. Higemoto, Phys. B, 2003, 326, 41–45 CrossRef CAS.
- Y. Itoh and R. Kado, J. Phys. Soc. Jpn. Conf. Proc., 2014, 1, 012013 Search PubMed.
- R. S. Hayano, Y. J. Uemura, J. Imazato, N. Nishida, T. Yamazaki and R. Kubo, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 850–859 CrossRef CAS.
- R. Kubo and T. Toyabe, in Magnetic Resonance and Relaxation, ed. R. Bline, North-Holland, Amsterdam, 1996 Search PubMed.
- K. M. Kojima, J. Yamanobe, H. Eisaki, S. Uchida, Y. Fudamoto, I. M. Gat, M. I. Larkin, A. Savici, Y. J. Uemura, P. P. Kyriakou, M. T. Rovers and G. M. Luke, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 094402 CrossRef.
- J. Sugiyama, I. Umegaki, H. Nozaki, W. Higemoto, K. Hamada, S. Takeshita, A. Koda, K. Shimomura, K. Ninomiya and M. K. Kubo, Phys. Rev. Lett., 2018, 121, 087202 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2019 |

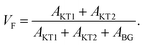
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−
exp(−