Open Access Article
Open Access ArticleSurface phonons of lithium ion battery active materials†
Peter
Benedek
 a,
Nuri
Yazdani
a,
Nuri
Yazdani
 a,
Hungru
Chen
a,
Hungru
Chen
 b,
Nils
Wenzler
b,
Nils
Wenzler
 a,
Fanni
Juranyi
a,
Fanni
Juranyi
 c,
Martin
Månsson
c,
Martin
Månsson
 d,
M. Saiful
Islam
d,
M. Saiful
Islam
 b and
Vanessa C.
Wood
b and
Vanessa C.
Wood
 *a
*a
aDepartment of Information Technology and Electrical Engineering, ETH Zurich, CH-8092 Zurich, Switzerland. E-mail: vwood.ethz.ch
bDepartment of Chemistry, University of Bath, Bath BA2 7AY, UK
cLaboratory for Neutron Scattering and Imaging, Paul Scherrer Institute, CH-5232 Villigen PSI, Switzerland
dDepartment of Applied Physics, KTH Royal Institute of Technology, SE-164 40 Stockholm, Kista, Sweden
First published on 7th January 2019
Abstract
Surfaces of active materials are understood to play an important role in the performance and lifetime of lithium-ion batteries, but they remain poorly characterized and therefore cannot yet be systematically designed. Here, we combine inelastic neutron scattering and ab initio simulations to demonstrate that the structure of the surface of active materials differs from the interior of the particle. We use LiFePO4 (LFP) as a model system, and we find that carbon coating influences the Li–O bonding on the (010) LFP surface relative to the bulk. Our results highlight how coatings can be used to systematically engineer the vibrations of atoms at the surface of battery active materials, and thereby impact lithium ion transport, charge transfer, and surface reactivity.
Introduction
Interface reactions of lithium ion battery active materials in their electrode environment are key to further improvements in performance, safety, and lifetime. Such active material interface reactions include ion exchange to or from the electrolyte, electron charge transfer1–3 to or from the conducting additives (e.g., carbon-black and binder composite), or electrolyte reactions which can create solid electrolyte interfaces4,5 and enable catalytic phase changes.5,6 Local distortions of the crystal lattice of the active material and their vibrational energy can influence the rates at which these physical and chemical processes occur.1,7,8 Here, we experimentally and computationally investigate how surface vibrational modes at the surface of active materials can differ from those in the interior of an active material particle and how surface coatings can be used to control the vibrational structure of the surface.In this study, we select LiFePO4 (LFP) as a model material (Fig. 1a–c). First, due to its olivine structure, LFP features one-dimensional bulk transport of lithium ions in the [010] direction9 and therefore exhibits one surface (the (010) surface) that is particularly important to consider when studying interface effects. Second, because the lithium channels along the [010] direction can be easily blocked by antisite defects,10–14 commercial LFP is found as nanoparticles with short channel lengths (i.e. short L[010]) and large surface to volume ratios. Both these aspects make LFP a useful system to systematically study how vibrational modes at the surface of a battery active material differ from those in the interior of the particle.
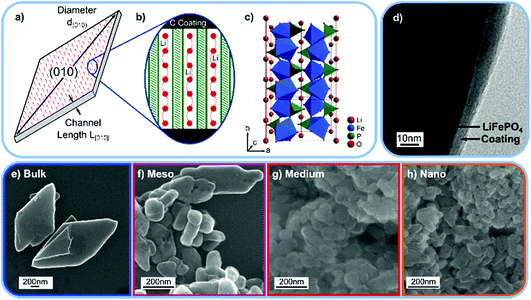 | ||
| Fig. 1 (a) Schematic drawing of the LiFePO4 (LFP) platelet particles. (b) Schematic view of the Li ion transport channels along the [010] direction and the carbon coating at the particle surface. (c) Crystal structure of LFP. (d) Transmission electron microscopy (TEM) image of the “Bulk” LFP sample with the carbon coating. TEM images of the “Medium” and “Nano” sample are shown in Fig. S8.† (e–h) Scanning electron microscopy (SEM) images of the “Bulk”, “Meso”, “Medium”, and “Nano” LFP samples used for the INS experiment. | ||
To experimentally observe differences between surface and interior vibrational modes, we produce platelet-shaped, carbon coated (Fig. 1d) LFP particles of four different sizes, “Bulk”, “Meso”, “Medium”, and “Nano”, and measure their phonon density of states using inelastic neutron scattering (INS). The ratio of atoms at the (010) surface to atoms in the particle interior ranges over from 0.4% for large particles to 11% for small particles. Hence, we can link changes in measured the phonon density of states of the differently (?) sized particles to differences between vibration modes at the (010) surface and those in the bulk.
We prepare platelet-shaped LFP particles with four different sizes (and thus different ratios of (010) surface atoms to bulk atoms) via hydrothermal synthesis.16 To reduce 6Li neutron absorption,15 we prepare enriched 7LFP samples. Platelet size can be systematically decreased by increasing the reaction temperature and the percentage of ethylene glycol (EG) as a co-solvent, which increases supersaturation and decreases nucleation rate.17–22 We make “Bulk” platelets in 0.4 v% EG at a reaction temperature of 115 °C,16 “Meso” platelets in 0.4 v% EG at 180 °C, “Medium” platelets in 50 v% EG at 180 °C, and “Nano” platelets in 100 v% EG at 180 °C. All particles are coated with 3 wt% carbon and annealed at 600 °C in Ar/H2. This annealing temperature was chosen such that the carbon layer has a high percentage of sp2 type graphitic bonds (see Raman spectrum in Fig. S4†) without reducing the LFP surface.35 A transmission electron microscopy (TEM) image of the “Bulk” LFP sample with the carbon coating is shown in Fig. 1d, TEM images of the “Medium” and “Nano” samples and a selected area electron diffraction (SAED) pattern of the “Bulk” sample are shown in Fig. S5.†
Results and discussion
Fig. 1e–h shows scanning electron microscopy (SEM) images of the platelet samples, and Table 1 summarizes the size and shape parameters of the particles. We measure platelet thickness, which is equivalent to the [010] channel length L[010] and the diameter d(010) of the platelet (010) surface (Fig. 1a). Assuming a circular platelet shape, we then estimate (details in the ESI) characteristic parameters such as a length to thickness aspect ratio and the percentage of atoms located at the (010) surface. Due to the platelet-morphology, for all samples, the majority of the surface is a (010) facet. In the case of the “Nano” sample, almost 11% of the atoms thus populate the (010) surface, while in the “Bulk” sample only 0.4% of atoms occupy this surface. This means that the vibrational density of states of the “Nano” LFP sample will exhibit a significant contribution from the (010) surface, while the contribution from the (010) surface will be negligible for the “Bulk” LFP.| Article | Length L[010] (nm) | Diameter d(010) (nm) | Aspect ratio | Atoms on (010) surface | (010) to entire surface ratio | Atoms on other surfaces |
|---|---|---|---|---|---|---|
| Nano | 11(2) | 55(13) | 5.0(24) | 10.9(20)% | 71(8)% | 5.7(13)% |
| Medium | 48(13) | 117(29) | 2.4(13) | 2.5(7)% | 55(12)% | 2.7(7)% |
| Meso | 66(23) | 270(120) | 4.1(32) | 1.8(6)% | 67(17)% | 1.2(5)% |
| Bulk | 300(90) | 1600(500) | 5.3(33) | 0.40(12)% | 73(12)% | 0.20(6)% |
In order to identify the contribution of lithium atoms in the vibrational states observed, we electrochemically delithiated these LFP particles to FePO4 (ESI). Due to the limited charge capacity of the “Bulk” FePO4 sample, we delithiated the “Nano” and “Meso” LFP particles (see electrochemical data of samples in Fig. S8 and S9†). We therefore study three LFP particle sizes (“Nano”, “Medium”, and “Bulk”) and two delithiated LFP sizes (“Nano” and “Meso”).
Using the samples above, we perform inelastic neutron scattering (INS) measurements to measure the phonon density of states (PDOS). The data from the low- (below 15 meV) and high- energy (above 100 meV) range of the INS spectra partly lack accuracy due to paramagnetic scattering of Fe3+ and neutron time-of-flight acquisition frame overlap, respectively. To minimize the influence of the paramagnetic scattering, we discard the scattering vectors with values less than 3 Å−1.23,24 More details are found in the Experimental methods in the ESI.†
The measured PDOS of the “Nano”, “Medium”, and “Bulk” LFP platelets are shown in Fig. 2a and that of “Nano” and “Meso” delithiated LFP (i.e. FePO4) are shown in Fig. 2b. The PDOS of the “Bulk” LFP are consistent with previous INS measurements.24 PDOS calculations based on density functional theory (DFT) methods25–29 show good agreement with the experimental “Bulk” LFP and “Meso” FePO4 measurements.
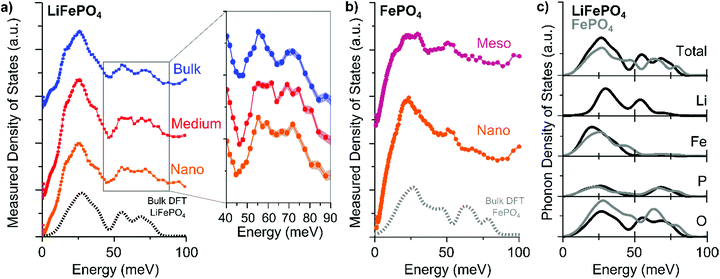 | ||
| Fig. 2 The experimentally-measured phonon density of states for (a) LiFePO4 (LFP) and (b) delithiated LFP (i.e., FePO4) samples of different sizes. The shading around the points indicates the error of the measurement. The dashed lines show the calculated phonon density of states. (c) Calculated total and elemental partial phonon density of states of LFP (black) and FePO4 (gray) from bulk density functional theory simulations. Full spectra are shown in the ESI.† | ||
In the energy range between 50 and 80 meV (Fig. 2a inset), we observe a difference in the phonon density of states as a function of particle size. With decreasing particle size, the two distinct peaks seen in the “Bulk” LFP sample merge into a plateau feature in the “Nano” sample. The phonon density of states spectra of the delithiated FePO4 (Fig. 2b), however, show no difference between the “Meso” and “Nano” sample, indicating that the change in the phonon density of states in LFP as a function of particle size is potentially related to different vibrations involving Li ions. Indeed, the element specific partialphonon density of states (Fig. 2c) indicate that in the vibration modes around 50–80 meV primarily P–O and Li–O bonds are involved. We perform Fourier transform infrared spectroscopy (FTIR) and XRD in order to confirm that the changes in the phonon density of states as a function of size stem from the percentage of (010) surface atoms relative to atoms in the interior of the LFP bulk and not from impurities or structural defects. The most common structural defects in LiFePO4 are Li/Fe antisite defects,10,14 which have been shown to influence the stretching P–O vibration mode at ∼120 meV (980 cm−1).16,17 However, FTIR analyses of the “Bulk”, “Medium”, and “Nano” particles show no substantial changes of that mode (Fig. S15†). From XRD, we find traceable amounts (<10 wt%) of Li3PO4 in the XRD spectra of the “Nano”-sized sample (Fig. S16†). However, the P–O phonon mode in the range of 50 to 80 meV in Li3PO4 is broad,30 which suggests that the influence of Li3PO4 is unlikely to be the sole cause of the merging of the peaks into a plateau (Fig. S17†).
Having confirmed that the changes in the phonon density of states as a function of particle size most likely come from the differences between vibrational modes at the (010) surface and those in the bulk of LFP, we look into the possible atomistic origins of these surface modes. Fig. 2a shows that as the sample size decreases (i.e., the percentage of (010) surface atoms increases), a feature appears between the P–O and Li–O modes suggesting a redshift (reduction of phonon energy) of the P–O or a blue-shift (increase of phonon energy) of the Li–O vibrations with additional broadening.
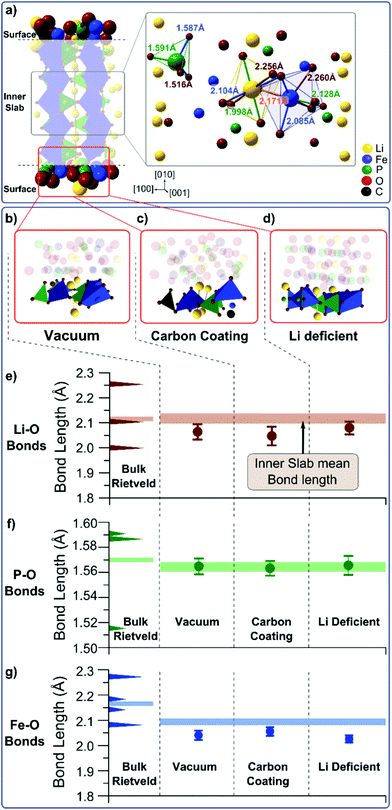
Shifts in vibrational energies can occur under tensile or compressive stress31 or due to surface reconstruction.32 Since Rietveld refinements (performed with the Maud software33) on our samples do not show any tendency of a change in the lattice parameter when moving from bulk to nano-sized particles (Fig. S18†), we therefore conclude that the shift in the vibrational energies comes from how the LFP (010) surface interacts with the carbon coating or from Li deficiencies and surface defects at the particle surface.34
The exact nature of the coated carbon is not known35 and different surface reconstructions are possible: loosely bound carbon coating atoms could leave the LFP surface unaffected as if it were surrounded by vacuum. Alternatively, the affinity of carbon and oxygen could lead to a weak C–O bond between coated carbon atoms and the phosphate groups in LFP. Residual oxygen atoms in the coating are not likely due to the reductive Ar/H2 environment used during the coating process. Finally, Li vacancies could result in a lithium-deficient LFP surface with local Fe3+ centers.
To determine whether any of these scenarios explain the observed change in the phonon density of states, we perform DFT calculations on slabs with dimensions of 1 unit cell length in [100], 3.5 unit cell lengths in [010], and 2 unit cell lengths in [001] (Fig. 3a).30,36–40 The (010) surface has one of three different terminations: vacuum (Fig. 3b), a carbon atom in the vicinity of a surface oxygen (Fig. 3c), or missing Li ion (Fig. 3d). Each structure is relaxed, and we extract the distributions of Li–O, P–O, and Fe–O bond lengths for the surface and the interior of the slab (Fig. S20 and S21†). The mean Li–O, P–O, and Fe–O bond lengths from the interior of the slab and the slab surface are plotted in Fig. 3e–g and compared to the experimental bond lengths. Despite the average Fe–O bond lengths being underestimated by about 0.08 Å, the average bond lengths in the slab interior match well with the values found experimentally, indicating that our simulations are representative of observed trends.
While the calculated Li–O, P–O, and Fe–O bond lengths in the interior of the slab are independent of surface termination, the Li–O and Fe–O bond lengths change as a function of the slab surface; these results indicate that surface reconstruction and the vibrations at the (010) surface of LFP will be different than in the interior of the particle. Only the P–O bond (Fig. 3f) is unaffected by the three different surface terminations. The mean Fe–O bond length decreases at the particle surface for all three surface terminations (Fig. 3g), particularly in the case of a Li deficient surface (Fig. 3d). This can be explained by the fact that the absence of one lithium atom (Li vacancy) changes the oxidation state of an Fe from Fe2+ to Fe3+, thereby increasing the strength of the ionic bond. The weakest effect on the Fe–O bond length is found in the case of a carbon environment, where a C–O bond in the vicinity of the Fe atom may counteract the bond length reduction of an undercoordinated Fe atom at the surface. The mean Li–O bond length is also shorter at the vacuum terminated surface and the carbon terminated surface, compared to the particle interior (Fig. 3e). Both a vacuum termination and a carbon termination result in an undercoordinated Li ion. This ion will try to compensate its electronic charge by moving towards the oxygen atoms thus reducing the Li–O bond length. This is reduced in the Li deficient case due to the smaller number of surface Li atoms.
The reduction of the Li–O bond length with a vacuum or a carbon termination at the (010) surface of LFP helps to rationalize the dependence of the phonon density of states on the particle size. A shorter Li–O bond suggests a larger bond strength and higher energy vibrations, in agreement with the observed blue-shift in the phonon density of states in the region of Li–O vibrations (Fig. 2). This effect is strongest when the surface is terminated by vacuum or carbon atoms. Li deficiency at the surface, however, only weakly reduces the Li–O bond lengths, but changes the Fe–O bonds in a strong manner that should manifest itself in the Fe–O vibrations. A small blue shift in the Fe–O vibrational energy predicted from the DFT calculations should also be present when comparing vacuum and carbon terminated (010) surfaces. However, these small shifts may not be observed because these vibrations are in an energy range dominated by paramagnetic scattering (Fig. 2c).
Conclusions
In conclusion, using an effective combination of INS and ab initio simulation techniques we found that the Li–O bonding character at the (010) surface and the interior of the LFP particle are different. This surface reconstruction is related to the carbon surface termination of the LFP.These findings have implications for lithium ion transport in battery active materials. Lattice vibrations assist the quasi one-dimensional lithium ion transport and the (de)intercalation of the lithium into and out of the material.1,7 Indeed, the important role of phonons in enabling lithium ion conduction7,41 is seen by the fact that lithium ion vacancy hopping is reported at a temperature of 250 K (corresponding to a thermal energy of ∼20 meV);42,43 while Li ion diffusion along the [010] channels occurs with an estimated migration barrier energy of 200–400 meV.44–47 Changing the vibrational densities and energies at the surface will influence, for example, the relative activation energies of lithium ion transport on the surface and in the bulk of the particle and therefore the rate-dependent lithiation behavior.48 Furthermore, the predicted shift in the Fe–O bonding in the case of a lithium deficient region (i.e., during delithiation) suggests that the activation energy associated with lithium transport may vary as a function of state-of-charge.
This work highlights the fundamental importance of active particle coatings of battery electrodes. We showed that changing the coordination and bonding of surface atoms can be used to selectively tune the vibrational energies at the surface. These insights are of significant importance for further improvements in the electrochemical performance of lithium ion battery materials and devices, particularly in relation to reducing surface reactivity and degradation.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge funding from the European Research Council (Project number 680700), the EPSRC Supergen Energy Storage Hub (EP/L019469/1) and the Swedish Research Council (VR) through a neutron project grant (Dnr. 2016-06955). We thank Nukem Isotopes for providing us with 7-LiOH. This work is partially based on experiments performed at the Swiss spallation neutron source SINQ, Paul Scherrer Institut, Villigen, Switzerland.Notes and references
- H. Ma, X. Xiong, P. Gao, X. Li, Y. Yan, A. A. Volinsky and Y. Su, Sci. Rep., 2016, 6, 26897 CrossRef CAS PubMed.
- N. M. Marković, B. N. Grgur and P. N. Ross, J. Phys. Chem. B, 1997, 101, 5405 CrossRef.
- X. H. Liu, H. Zheng, L. Zhong, S. Huang, K. Karki, L. Q. Zhang, Y. Liu, A. Kushima, W. T. Liang, J. W. Wang, J.-H. Cho, E. Epstein, S. A. Dayeh, S. T. Picraux, T. Zhu, J. Li, J. P. Sullivan, J. Cumings, C. Wang, S. X. Mao, Z. Z. Ye, S. Zhang and J. Y. Huang, Nano Lett., 2011, 11, 3312 CrossRef CAS PubMed.
- P. Verma, P. Maire and P. Novák, Electrochim. Acta, 2010, 55, 6332 CrossRef CAS.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243 RSC.
- J. W. Fergus, J. Power Sources, 2010, 195, 939 CrossRef CAS.
- P. M. Richards, Phys. Rev. B: Solid State, 1977, 16, 1393 CrossRef CAS.
- A. Van der Ven, J. Bhattacharya and A. A. Belak, Acc. Chem. Res., 2013, 46, 1216 CrossRef CAS PubMed.
- S. Nishimura, G. Kobayashi, K. Ohoyama, R. Kanno, M. Yashima and A. Yamada, Nat. Mater., 2008, 7, 707 CrossRef CAS PubMed.
- S. Chung, Y. Kim and S. Choi, Adv. Funct. Mater., 2010, 20, 4219 CrossRef CAS.
- R. Malik, D. Burch, M. Bazant and G. Ceder, Nano Lett., 2010, 10, 4123 CrossRef CAS PubMed.
- C. Masquelier and L. Croguennec, Chem. Rev., 2013, 113, 6552 CrossRef CAS PubMed.
- C. M. Julien, A. Mauger and K. Zaghib, J. Mater. Chem., 2011, 21, 9955 RSC.
- M. S. Islam and C. A. J. Fisher, Chem. Soc. Rev., 2014, 43, 185 RSC.
- V. F. Sears, J. Neutron Res., 1992, 3, 26 CrossRef.
- P. Benedek, N. Wenzler, M. Yarema and V. C. Wood, RSC Adv., 2017, 7, 17763 RSC.
- X. Qin, J. Wang, J. Xie, F. Li, L. Wen and X. Wang, Phys. Chem. Chem. Phys., 2012, 14, 2669 RSC.
- K. Dokko, S. Koizumi, H. Nakano and K. Kanamura, J. Mater. Chem., 2007, 17, 4803 RSC.
- B. Ellis, W. H. Kan, W. R. M. Makahnouk and L. F. Nazar, J. Mater. Chem., 2007, 17, 3248 RSC.
- Y. Wang, D. Zhang, C. Chang, L. Deng and K. Huang, Mater. Chem. Phys., 2014, 148, 933 CrossRef CAS.
- O. Xiuqin, P. Lin, G. Haichen, W. Yichen and L. Jianwei, J. Mater. Chem., 2012, 22, 9064 RSC.
- C. A. J. Fisher and M. S. Islam, J. Mater. Chem., 2008, 18, 1209 RSC.
- R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341 CrossRef CAS PubMed.
- P. Goel, M. K. Gupta, R. Mittal, S. Rols, S. J. Patwe, S. N. Achary, A. K. Tyagi and S. L. Chaplot, J. Mater. Chem. A, 2014, 2, 14729 RSC.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223 CrossRef.
- M. Sumita, Y. Tanaka, M. Ikeda and T. Ohno, J. Phys. Chem. C, 2015, 119, 14 CrossRef CAS.
- D. Şopu, J. Kotakoski and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245416 CrossRef.
- W. Goldammer, W. Ludwig, W. Zierau and C. Falter, Surf. Sci., 1984, 141, 139 CrossRef CAS.
- L. Lutterotti, D. Chateigner, S. Ferrari and J. Ricote, Thin Solid Films, 2004, 450, 34 CrossRef CAS.
- P. Axmann, C. Stinner, M. Wohlfahrt-Mehrens, A. Mauger, F. Gendron and C. M. Julien, Chem. Mater., 2009, 21, 1636 CrossRef CAS.
- J. Wang and X. Sun, Energy Environ. Sci., 2012, 5, 5163 RSC.
- J. Vandevondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103 CrossRef CAS.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477 CrossRef CAS.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641 CrossRef CAS.
- L. Wang, F. Zhou, Y. S. Meng and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165435 CrossRef.
- K. Toyoura, Y. Koyama, A. Kuwabara, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 214303 CrossRef.
- J. Sugiyama, H. Nozaki, M. Harada, K. Kamazawa, O. Ofer, M. Månsson, J. H. Brewer, E. J. Ansaldo, K. H. Chow, Y. Ikedo, Y. Miyake, K. Ohishi, I. Watanabe, G. Kobayashi and R. Kanno, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 054430 CrossRef.
- T. E. Ashton, J. V. Laveda, D. A. MacLaren, P. J. Baker, A. Porch, M. O. Jones and S. A. Corr, J. Mater. Chem. A, 2014, 2, 6238 RSC.
- G. K. P. Dathar, D. Sheppard, K. J. Stevenson and G. Henkelman, Chem. Mater., 2011, 23, 4032 CrossRef CAS.
- D. Morgan, A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2004, 7, A30 CrossRef CAS.
- C. Ouyang, S. Shi, Z. Wang, X. Huang and L. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 104303 CrossRef.
- M. S. Islam, D. J. Driscoll, C. A. J. Fisher and P. R. Slater, Chem. Mater., 2005, 17, 5085 CrossRef CAS.
- Y. Li, H. Chen, K. Lim, H. D. Deng, J. Lim, D. Fraggedakis, P. M. Attia, S. C. Lee, N. Jin, J. Moskon, Z. Guan, J. Hong, Y. S. Yu, M. Gaberscek, M. S. Islam, M. Z. Bazant and W. C. Chueh, Nat. Mater., 2018, 17, 915 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental section, electrochemical delithiation of LiFePO4, particle size calculations, electrochemical analyses, frame overlap discussion, impurity and defect analysis, LFP nanoparticle slabs for the DFT calculations, histograms of bond lengths. See DOI: 10.1039/c8se00389k |
| This journal is © The Royal Society of Chemistry 2019 |