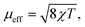Temperature induced valence phase transition in intermediate-valent YbPd₂Al₃

Abstract

A temperature induced valence phase transition from Yb³⁺ at higher temperatures to Yb²⁺ at lower temperatures was observed at T = 110(1) K for intermetallic YbPd₂Al₃. The title compound has been prepared from the elements in sealed tantalum ampoules. The structure was refined from single-crystal data and the title compound was found to crystallize in the hexagonal YNi₂Al₃ type structure with space group P6/mmm and lattice parameters of a = 929.56(7) and c = 420.16(3) pm (300 K data). Full ordering of the Pd and Al atoms within the [Pd₂Al₃]^δ− polyanion was observed. Magnetic measurements revealed an anomaly in the dc susceptibility data and intermediate valent Yb at higher temperature, as observed from the effective magnetic moment. The proposed valence phase transition was also observed as a λ-type anomaly in heat capacity measurements (T = 108.4(1) K), however, no systematic shift of the λ-peak was observed in field dependent heat capacity measurements. An antiferromagnetic ordering at this temperature, however, could be excluded, based on field-dependent susceptibility measurements and magnetization isotherms. No dynamic phenomenon was observed in ac susceptibility measurements, excluding e.g. spin-glass behavior. Subsequent temperature dependent single-crystal and powder X-ray diffraction experiments indicated a steep increase in the length of the c axis around T = 110 K upon cooling. However, no structural phase transition was found via single-crystal diffraction experiments conducted at 90 K. The anomaly was also observed in other physical measurements of e.g. the electrical resistivity, indicating a clear change in the electronic structure of the material. X-ray photoelectron spectroscopy conducted at room temperature shows the presence of both, Yb²⁺ and Yb³⁺, underlining the mixed-valent state. Members of the solid solution Yb_1−xCa_xPd₂Al₃ (x = 0.33, 0.67, 1) were finally used to further study the charge ordering and the present temperature induced valence phase transition.

---

1 Introduction

In the field of rare-earth element chemistry, the predominant oxidation state of the lanthanoides is the trivalent one. Cerium, praseodymium or terbium exhibit an additional tetravalent oxidation state while for samarium, europium and ytterbium an additional divalent oxidation state exists.^1–3 The resulting physical phenomena are numerous, e.g. mixed/intermediate valences in compounds with inequivalent crystallographic cationic sites (Eu₃O₄,^4–6 HP-Tb₃O₅,⁷ EuSr₂Bi₂S₄F₄ and Eu₂SrBi₂S₄F₄,⁸ Ce₂Rh₃Sn₅ (ref. 9)), inhomogeneous mixed valence states (Sm₃S₄,^10,17 Eu₃S₄,¹⁰ or EuPtP¹¹) as well as intermetallic valence fluctuating materials (CeAl₃,^12,13 Yb₄Pt₉Ga₂₄,¹⁴ CeMo₂Si₂C,¹⁵ CeRu_1−xNi_xAl¹⁶).¹⁸ Kondo states or heavy fermion behavior are other prominent physical features, attributed to valence instabilities. Temperature or pressure dependent valence phase transitions in contrast are rather rare. Transitions of this type are found e.g. in metallic Ce,¹⁹ in the double perovskites Ba₂PrRu_1−xIr_xO₆ (ref. 20) or in the samarium monochalcogenides SmCh (Ch = S, Se, Te).^21,22 In EuPtP two new pressure induced valence ordered structures were observed,²³ while EuCo₂As₂ (ref. 24) and YbAl₃ (ref. 25) exhibit pressure dependent shifts of their valence. Finally, intermetallic EuPd₂Si₂ (T_trans ∼ 200 K)²⁶ and Eu₂Pt₆Al₁₅ (T_trans ∼ 45 K)²⁷ as well as the solid solutions CeNi_1−xCo_xSn (x = 0.4; T_trans ∼ 95 K)²⁸ and Yb_xIn_1−xCu₂ (x = 0.4; T_trans ∼ 50 K)^29–31 exhibit temperature dependent valence phase transitions.

Herein, we report on the temperature induced valence phase transition in intermetallic YbPd₂Al₃ (YNi₂Al₃ type,³²P6/mmm, Z = 3) from intermediate valent Yb at high temperatures to divalent Yb at low temperatures. Upon localization of an electron, a paramagnetic to Pauli-paramagnetic transition occurs at T_anomaly = 110(1) K, which can be observed as a drastic drop in the magnetic susceptibility. The Yb³⁺ → Yb²⁺ valence phase transition is furthermore visible in an expansion of the c lattice parameter during cooling, observed in temperature dependent single-crystal and powder X-ray diffraction experiments of YbPd₂Al₃ and the solid solution Yb_1−xCa_xPd₂Al₃ (x = 0.33, 0.67, 1). The (field dependent) specific heat capacity and the electrical resistivity were investigated to underline the proposed valence phase transition, XPS measurements underline the mixed-valent Yb state at room temperature.

2 Experimental section

2.1 Synthesis

Starting materials for the syntheses of YbPd₂Al₃ and the members of the Yb_1−xCa_xPd₂Al₃ series (x = 0.33, 0.67) as well as CaPd₂Al₃ were ingots of ytterbium (Smart Elements, 99.99%), calcium pieces (Alfa Aesar, 99.5%), palladium sheets (Agosi, 99.99%), and aluminum turnings (Koch chemicals, 99.99%). The calcium ingots were stored under argon; surface impurities were removed mechanically prior to the synthesis. The elements were weighed in the respective atomic ratios and arc-welded³³ in tantalum tubes under a dried argon atmosphere of about 800 mbar. The argon gas was purified over titanium sponge (873 K), molecular sieves and silica gel prior to use. The metal tubes were placed in the water-cooled sample chamber of a high-frequency furnace (Hüttinger Elektronik, Freiburg, type TIG 1.5/300 and TIG 5.0/300) in flowing argon.³⁴ The samples were rapidly heated to 1473 K, kept at that temperature for 10 min, annealed for another 5 h at 1023 K and finally rapidly quenched by switching off the high-frequency generator. The temperature was controlled using a radiation pyrometer (Metis MS09, Sensortherm, accuracy: ±50 K). In all cases, the compounds could easily be separated from the ampoules and no reactions with the container material were observed.

2.2 X-ray diffraction

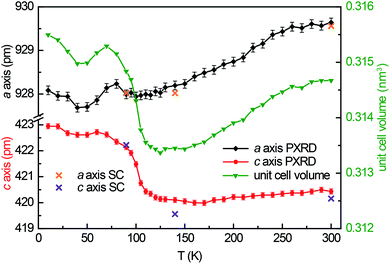
The polycrystalline Yb_1−xCa_xPd₂Al₃ (x = 0, 0.33, 0.67, 1) samples were characterized by Guinier patterns (imaging plate detector, Fujifilm BAS-1800) with Cu Kα1 radiation and α-quartz (a = 491.30 and c = 540.46 pm) as an internal standard. The lattice parameters were deduced from least-squares fits of the Guinier data³⁵ using the structural models determined by single-crystal X-ray diffraction experiments. For the solid solution Yb_1−xCa_xPd₂Al₃ (x = 0, 0.33, 0.67, 1) Vegard's law-like behavior was observed for the unit cell volume along with a linear trend of the hexagonal lattice parameters (Table 1). Temperature dependent powder X-ray diffraction experiments between 10 and 300 K were conducted on a Huber G670 Guinier Imaging Plate diffractometer (Co Kα1 radiation, Ge-111 monochromator, silicon as external standard) with Low Temperature Device 670.4 and closed cycle He cryostat (Lakeshore temperature controller, model 331). The lattice parameters of the temperature dependent measurements are listed in Table S1.†

Table 1 Lattice parameters of the Yb_1−xCa_xPd₂Al₃ series (x = 0, 0.33, 0.67, 1), space group P6/mmm, Z = 3, determined by temperature dependent single-crystal X-ray diffraction and by room temperature Guinier powder X-ray diffraction

Compound	T (K)	a (pm)	c (pm)	V (nm^3)
a Single-crystal data. b Guinier powder X-ray data.
YbPd2Al3^a	90(2)	928.02(6)	422.22(3)	0.3149
YbPd2Al3^a	140(2)	928.02(6)	419.56(3)	0.3129
YbPd2Al3^a	300(2)	929.56(7)	420.16(3)	0.3144
YbPd2Al3^b	RT	928.9(2)	420.25(9)	0.3140
Yb0.68(1)Ca0.32(1)Pd2Al3^a	RT	930.98(7)	421.40(3)	0.3163
Yb0.67Ca0.33Pd2Al3^b	RT	932.3(1)	421.73(4)	0.3174
Yb0.34(1)Ca0.66(1)Pd2Al3^a	RT	933.53(7)	422.66(3)	0.3190
Yb0.33Ca0.67Pd2Al3^b	RT	934.1(2)	423.0(1)	0.3197
CaPd2Al3^a	RT	936.28(6)	423.96(3)	0.3219
CaPd2Al3^b	RT	936.3(1)	423.86(5)	0.3218

---

Small single-crystals of the Yb_1−xCa_xPd₂Al₃ (x = 0, 0.33, 0.67, 1) series were selected from the obtained samples. The crystals were glued to thin quartz fibers using beeswax and investigated by Laue photographs taken on a Buerger camera (white molybdenum radiation; imaging plate technique, Fujifilm, BAS-1800) in order to check their quality. Temperature dependent intensity data sets of YbPd₂Al₃ were collected with a Stoe StadiVari four-circle diffractometer (Mo Kα radiation; λ = 71.073 pm; μ-source; oscillation mode; hybrid-pixel-sensor, Dectris Pilatus 100 K (ref. 36)) with an open Eulerian cradle setup. Additional measurements at room temperature were conducted on a Stoe IPDS-II image plate system (graphite monochromatized Mo Kα radiation; λ = 71.073 pm; oscillation mode). Numerical absorption corrections along with scaling (for the StadiVari data sets) were applied. To obtain further information about possible site preferences (Yb:Ca) within the solid solution, four independent single-crystals of the samples with the nominal compositions Yb_0.33Ca_0.67Pd₂Al₃ and Yb_0.33Ca_0.67Pd₂Al₃ were collected each (Table S2†). Details about the data collection and the crystallographic parameters are summarized in Tables S3–S6.†

CCDCs 1868211, 1868849, 1875396, 1880784–1880786, 1892594, 1892597–1892598, 1895369–1895370 and 1910744 contain the supplementary crystallographic data for this paper.†

2.3 Physical property investigations

Susceptibility measurements. Magnetic susceptibility measurements were conducted on a Quantum Design Physical Property Measurement System (PPMS). For the dc-susceptibility measurements, powdered samples of the Yb_1−xCa_xPd₂Al₃ (x = 0, 0.33, 0.67, 1) series were loaded in polyethylene (PE) capsules and attached to the sample holder rod of a Vibrating Sample Magnetometer (VSM) unit for measuring the magnetization M(T,H). The samples were investigated in the temperature range of 3–395 K with external magnetic fields up to 90 kOe. YbPd₂Al₃ was further investigated by ac-magnetic susceptibility measurements. Therefore, the powdered sample was enclosed in a thin-walled gelatin capsule attached to a drinking straw (Quantum Design). In-phase χ′(ω,T) and out-of-phase susceptibilities χ′′(ω,T) were recorded in the temperature range of 97 to 117 K with external dc magnetic fields up to 20 kOe and one data point every 0.5 K.

Heat capacity. For the heat capacity measurements of YbPd₂Al₃, one piece of the sample was fixed to a pre-calibrated heat capacity puck using Apiezon N grease and investigated in the temperature range of 2–300 K. Additionally field dependent heat capacity measurement with external fields of 10, 50 and 90 kOe were conducted.

Electrical resistivity. For the resistivity measurements, a polycrystalline sample of YbPd₂Al₃ was cold-pressed into a pellet with ø = 4.5 mm, d = 1.2 mm and sintered at 823 K for 14 d in an evacuated silica ampoules in order to reduce grain boundaries. The resistivity measurement was carried out in the AC transport mode³⁷ of the PPMS. The ACT puck was modified by a van-der-Pauw³⁷ press contact assembly purchased from Wimbush Science & Technology. The probes are spring contacts, gold plated over nickel; the distance between the pins was set to 2 mm. The resistivity was measured between 2–300 K with a data point every 1 K up to 95 K, every 0.1 K between 95.1 and 119.9 K and a data point every 2 K up to 300 K. A maximum current of 10 mA was used; the AC frequency was set to 29 Hz with a measurement time of 1 s. The recorded data of channel 1 & 2 was converted according to the van-der-Pauw equation given in the Quantum Design Application Note 1076-304.

2.4. X-ray photoelectron spectroscopy (XPS)

X-ray photoelectron spectra were measured using an Axis-Ultra spectrometer (Kratos, Manchester, UK) in ultrahigh vacuum (pressure < 10⁻⁷ Pa). Monochromatic Al Kα radiation (hν = 1486.6 eV) was used with a 12 kV accelerating voltage and 10 mA emission current. The charge neutralizer was run with a filament current of 1.82 A, a charge balance of 2.25 V and a filament bias of 1.0 V. A pass energy filter of 40 eV was applied to the hemispherical analyzer (electrostatic lens mode), enabling high-energy resolution for narrow scans with a step size of 0.1 eV at a dwell time of 4 s. Cold-pressed pellets (ø = 4.5 mm, d = 1.0–1.5 mm) of polycrystalline YbPd₂Al₃, Yb_0.67Ca_0.33Pd₂Al₃, Yb_0.33Ca_0.67Pd₂Al₃, and CaPd₂Al₃ along with a piece of elemental palladium were attached to the XPS sample holder using conductive carbon tape. An area of about 1 × 2 mm² on the samples surfaces were irradiated at an X-ray incidence angle of 30° relative to the sample normal. Due to different static charge phenomena of the samples, the C 1s signal, caused by organic surface contaminations, was used as an internal reference and its binding energy was set to 285.0 eV (referenced to the Fermi level) for all samples. The peak positions were determined by Gaussian fits of the spectra and are listed in Table 2.

Table 2 Binding energies determined by XPS for YbPd₂Al₃, Yb_0.67Ca_0.33Pd₂Al₃, Yb_0.33Ca_0.67Pd₂Al₃ and CaPd₂Al₃ along with data from the literature. Standard deviations are within ±0.2 eV

	Yb^0 4d	Yb^2+ 4d	Yb^3+ 4d	Pd 3d	Ca 2p
a This work.
YbPd2Al3^a	—	182.5	185.6	335.1	—
Yb0.67Ca0.33Pd2Al3^a	—	182.4	185.7	335.3	347.3
Yb0.33Ca0.67Pd2Al3^a	—	182.8	185.9	335.3	347.3
CaPd2Al3^a	—	—	—	335.4	347.3
Yb^71	181.2	—	—	—	—
Yb2O3 (ref. 71)	—	—	185.4	—	—
Pd^a	—	—	—	335.5	—
Pd^72	—	—	—	335.2	—
Pd^73	—	—	—	335.3	—
PdAl3 (ref. 72)	—	—	—	337.7	—
CaO^65	—	—	—	—	347.1
CaCO3 (ref. 66)	—	—	—	—	347.1
CaMoO4 (ref. 67)	—	—	—	—	347.4

---

3 Results and discussion

3.1 Structure refinement

A selected single-crystal of YbPd₂Al₃ was first measured at 300 K and a careful analysis of the obtained data set indicated a hexagonal primitive lattice. During the refinement, space group P6/mmm was found to be correct; isotypism with the YNi₂Al₃ type structure³² was already evident from the Guinier powder pattern and from a systematic check of the Pearson database.³⁸ The structure solution was conducted using the SuperFlip algorithm.³⁹ All structures were refined on F² with anisotropic displacement parameters for all atoms using Jana2006.^40,41 As a check for the correct composition, the occupancy parameters were refined in a separate series of least-squares cycles. All sites were fully occupied within three standard deviations with exception of the solid solution (vide infra). No significant residual peaks were evident in the final difference Fourier syntheses. The final positional parameters and interatomic distances are listed in Tables S5 and S6.† The Yb:Ca site occupancies of the single-crystals obtained for members of the solid solutions are additionally listed in Table S2.† Due to the unusual anomaly visible in the susceptibility measurement (vide infra) additional data sets of YbPd₂Al₃ were recorded at 140 and 90 K. Data sets of the single-crystals obtained from the samples with nominal compositions Yb_0.67Ca_0.33Pd₂Al₃ and Yb_0.33Ca_0.67Pd₂Al₃ as well as CaPd₂Al₃ were recorded at room temperature. The obtained data sets of all measurements were handled as described above; the results will be discussed in the crystal chemistry section below.

3.2 Temperature dependent powder X-ray diffraction

Guinier powder patterns were recorded of all prepared samples to check for phase purity and refine the lattice parameters (Table 1). Additionally, temperature dependent powder X-ray diffraction patterns of YbPd₂Al₃ were recorded between 10–300 K upon cooling with intervals of 10 K from 10–90 and 120–300 K, between 90 and 120 K intervals of 5 K were used. In order to obtain the powder lattice parameters, the unit cell dimensions of the 90 K single-crystal measurement were used as starting point and refined using WinPLOTR⁴² of the FullProf Suite.⁴³ The lattice parameters and the unit cell volumes obtained from these measurements are listed in Table S2† and depicted in Fig. 1, along with the unit cell parameters obtained from the single-crystal X-ray diffraction experiments. With decreasing temperature, both a and c axis initially contract until ∼120 K. At lower temperatures, however, a quite drastic expansion of ∼3 pm for the c axis is visible, starting around 105 K. The a axis in contrast does not show this effect.

Fig. 1 Temperature dependent lattice parameters of YbPd₂Al₃ obtained from temperature dependent powder X-ray diffraction experiments upon cooling from 300 to 10 K and from single-crystal X-ray diffraction experiments.

3.3 Crystal chemistry

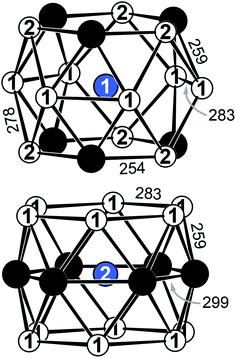
YbPd₂Al₃ and the other representatives of the solid solution Yb_1−xCa_xPd₂Al₃ (x = 0.33, 0.67, 1) all crystallize in the hexagonal crystal system with space group P6/mmm in the YNi₂Al₃ type structure. No superstructure reflections as in ErPd₂Al₃ (ref. 44) were observed. The structure description and discussion in the following paragraphs is based on the 300 K measurement of YbPd₂Al₃. The crystal structure can be described by a polyanionic [Pd₂Al₃]^δ− framework with two crystallographically independent Yb atoms residing in the cavities of the polyanion (Fig. 2). Within the polyanionic network short heteroatomic Pd–Al distances of 254 (Pd–Al2) and 259 pm (Pd–Al1) are found along with longer homoatomic Al–Al (278 and 283 pm) and Pd–Pd distances (299 pm). The observed interatomic Pd–Al distances are in line with those found in binary PdAl⁴⁵ (264 pm, CsCl type), PdAl₂ (ref. 46) (255 pm, Co₂Si type), Pd₅Al₃ (ref. 46) (250–287 pm, Rh₅Ge₃ type) or ternary YbPdAl^47,48 (256–267 pm, TiNiSi type) and Yb₈Pd₂₄Al⁴⁹ (253 pm, Ce₈Pd₂₄Sb type). The homoatomic distances are in line with those reported e.g. for elemental Al⁵⁰ (286 pm), binary Pd₅Al₃ (ref. 46) (Pd–Pd = 271–306 pm) or ternary Yb₈Pd₂₄Al⁴⁹ (Pd–Pd = 266–307 pm). The two independent Yb atoms both reside in a sixfold capped hexagonal prism, depicted in Fig. 3. The interatomic Yb–Pd distances range from 300–317 pm, the Yb–Al contacts from 324–352 pm. Both are in the same range as those in e.g. YbPdAl^47,48 (Yb–Pd = 286–303 pm, Yb–Al = 306–326 pm).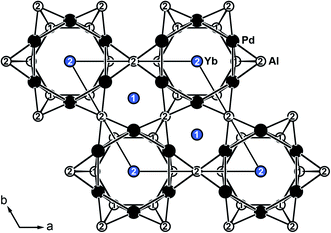

Fig. 2 Extended unit cell of hexagonal YbPd₂Al₃ (YNi₂Al₃ type) depicted along [001]. Yb atoms are shown in blue, Pd atoms in black and Al atoms in white.

Fig. 3 Sixfold capped hexagonal prisms surrounding the two crystallographically independent Yb atoms in YbPd₂Al₃. Interatomic distances are given in pm. Yb atoms are shown in blue, Pd atoms in black and Al atoms in white.

Upon cooling, the unit cell contracts (vide supra), therefore the respective interatomic distances contract accordingly when cooling from 300 to 140 K. When decreasing the temperature further to 90 K, the Yb1–Al1, Yb1–Al2, Yb2–Al1 (Fig. S1,† top) and Yb1–Pd (Fig. S1,† bottom) distances increase, also in line with the observed unit cell changes. The interatomic Yb2–Pd and Pd–Pd distances in contrast slightly decrease (Fig. S1,† bottom). This, however, is not surprising since they form the caps of the hexagonal prism. Upon expansion of the prism along [001] the caps move towards the center of the prisms, shortening the respective Yb2–Pd and Pd–Pd distances. It is important to note again, that no structural transition was observed, the hexagonal space group symmetry remains at 90 K.

For the members of the solid solutions Yb_1−xCa_xPd₂Al₃ with x = 0.33 and 0.67, mixing of Yb and Ca on the two crystallographic Yb sites (1a and 2d) was observed. For both compositions, four single-crystals each were selected and investigated, showing the same Yb/Ca distribution. For nominal Yb_0.67Ca_0.33Pd₂Al₃ a distribution of 80(1)% Yb and 20(1)% Ca on the 2d site and 46(1)% Yb and 54(1)% Ca on the 1a site was observed resulting to a refined composition of Yb_0.68(1)Ca_0.32(1)Pd₂Al₃ for all compounds. For nominal Yb_0.33Ca_0.67Pd₂Al₃ a distribution of 44(1)% Yb and 56(1)% Ca on the 2d site and 15(1)% Yb and 85(1)% Ca on the 1a site was found leading to Yb_0.34(1)Ca_0.66(1)Pd₂Al₃ (Table S2†). This narrow distribution is very intriguing and points towards a potential charge ordering.

3.4 Physical properties

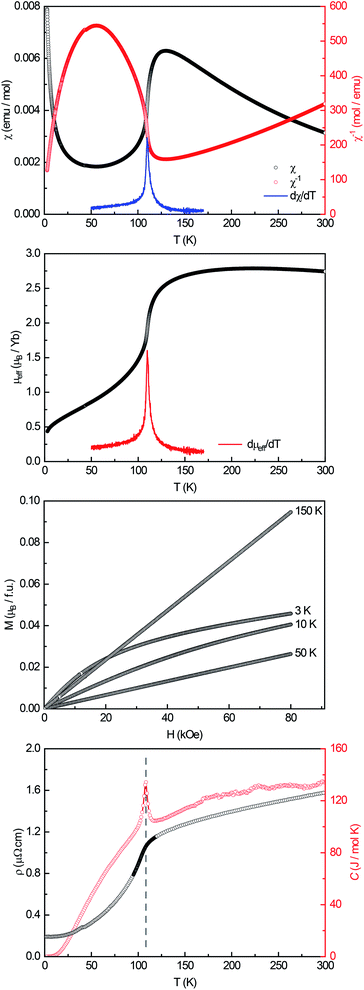
A powdered sample of YbPd₂Al₃ was first investigated by dc-magnetic susceptibility measurements between 3–300 K in zero-field-cooled mode (ZFC) at 10 kOe. The susceptibility χ and its inverse χ⁻¹ are depicted in Fig. 4 (top). With decreasing temperature the susceptibility starts to rise, followed by a sharp decrease at T_anomaly = 110(1) K. The temperature of the anomaly was determined from the maximum of dχ/dT, plotted in blue. Below 25 K the susceptibility rises again reaching χ = 0.0079(1) emu mol⁻¹ at 3 K. This feature is likely to be caused by traces of paramagnetic impurities such as Yb₂O₃ that orders antiferromagnetically at 2.3 K.⁵¹ In order to determine the effective magnetic moment, a fit of the inverse magnetic susceptibility between 175 and 300 K using the modified Curie–Weiss law with χ₀ = −1.28(1) × 10⁻⁴ emu mol⁻¹ (obtained from CaPd₂Al₃ at 300 K) was conducted. The effective magnetic moment is μ_eff = 2.75(1) μ_B, in line with the observations of the temperature dependence of the effective magnetic moment (vide infra). The Weiss constant is θ_P = 0.9(2) K, suggesting no dominant magnetic interaction in the paramagnetic temperature regime. In order to understand the behavior around T = 110 K, the temperature dependent effective magnetic moment per Yb atom was calculated according to
and is plotted in Fig. 4 (middle, top). The effective magnetic moment initially increases almost linear with increasing temperature starting at μ_eff = 0.43(1) μ_B at 3 K before again a rapid increase around T_anomaly = 110(1) K is observed. Above 150 K the moment saturates with μ_eff = 2.72(1) K at 300 K measured at 10 kOe (μ_eff = 2.59(5) K at 300 K measured at 50 Oe, see Fig. S6†). The magnetization isotherms recorded at 3 and 10 K are slightly curved, the isotherm at 50 K is linear, typical for a paramagnetic material, while the isotherm recorded at 150 K finally exhibits a much stronger increase, in line with a higher contribution of paramagnetic Yb³⁺ at this temperature (Fig. 4, middle, bottom). The saturation magnetization at 3 K and 80 kOe is μ_sat = 0.05(2) μ_B, which is drastically lower compared to the expected saturation magnetization of 4 μ_B according to g_J × J for Yb³⁺. The reported magnetic behavior (reduced effective magnetic moment and low saturation magnetization), along with the structural investigations, can only be explained if YbPd₂Al₃ contains partially paramagnetic Yb³⁺ cations (4f¹³) at higher temperatures, which are reduced to diamagnetic Yb²⁺ cations (4f¹⁴) below T_anomaly = 110(1) K by a spontaneous electron localization from the conduction band.

Fig. 4 Magnetic properties of YbPd₂Al₃. Top: temperature dependence of the magnetic susceptibility (χ and χ⁻¹ data) measured in ZFC mode at 10 kOe; dχ/dT is shown in blue. Middle, top: temperature dependence of the effective magnetic moment; dμ_eff/dT is plotted in red. Middle, bottom: magnetization isotherms recorded at 3, 10, 50 and 150 K. Bottom: temperature dependence of the electrical resistivity (black) and heat capacity (red).

A similar behavior, also featuring a sharp rise of the magnetic susceptibility, was observed in the solid solution Yb_xIn_1−xCu₂ with the strongest effect for x = 0.4.^29–31 The sharp rise was attributed to a spontaneous valence change from Yb²⁺ at low temperatures to Yb³⁺ at high temperatures with T_anomaly ∼ 50 K. The observed magnetic behavior is furthermore significantly different compared to intermediate valence or valence fluctuating ytterbium compounds like YbCu₂Si₂,⁵² Yb_1−xSc_xAl₂,⁵³ Yb₂PdGe₆,⁵⁴ or Yb₄Pt₉Ga₂₄,¹⁴ which can be described by the interconfiguration fluctuation (ICF) model introduced by Sales and Wohlleben.⁵² The explanation of the susceptibility data via a valence phase transition is also in line with the observed structural effects (vide supra), since Yb²⁺ is significantly larger than Yb³⁺ (113 vs. 86 pm²). An only partial Yb³⁺ character above T_anomaly can be derived from the calculated magnetic moment of μ_eff = 2.72(1) μ_B at 300 K measured at 10 kOe, which is significantly lower compared to the calculated moment of μ_calc = 4.536 μ_B of a free Yb³⁺ ion. When looking back at the crystal structure, the two Yb sites have different site multiplicities (Yb1 on 2d, Yb2 on 1a). Therefore, a charge separation into Yb²⁺ and Yb³⁺ is possible. When calculating the net magnetic moment with the paramagnetic Yb³⁺ solely on the 2d site an effective moment of μ_eff,calc = 3.70 μ_B is obtained, while Yb³⁺ solely on the 1a site results in μ_eff,calc = 2.62 μ_B. The latter matches the observed effective moment quite well. This assumption is additionally underlined by the fact that the Yb1–Pd and Yb1–Al distances enlarge upon the valence change from Yb³⁺ → Yb²⁺ as seen from the temperature dependent single crystal X-ray diffraction experiments. In order to check for a structural segregation of Yb²⁺ and Yb³⁺, members of the solid solution Yb_1−xCa_xPd₂Al₃ with x = 0.33 and 0.67 have been synthesized. The results of these investigations will be discussed below.

In addition to the dc-magnetization experiments, heat capacity and electrical resistivity measurements have been performed. The heat capacity (Fig. 4, bottom, red) clearly shows a sharp and intense λ-shaped anomaly at T_anomaly = 108.4(1) K, in line with the other observed temperatures. Moreover, field dependent heat capacity measurements were conducted with applied magnetic fields of H = 0, 10, 50 and 90 kOe (Fig. S2†) within a temperature range of ±20 K around the anomaly. The observed temperature shifts are negligible, since all peak temperature are the same within three standard deviations. The change in the integrated areas can be explained by the stronger magnetic fields. Field dependent susceptibility measurements also indicate no temperature dependence of the anomaly (Fig. S3†). As both, the heat capacity and the susceptibility measurements show no significant temperature dependent shifts, no magnetic ordering takes place at the anomaly, in line with the M(H) investigations. Additional ac-magnetic susceptibility measurements conducted on YbPd₂Al₃ revealed no frequency dependency of the zero-field as well as field dependent in-phase χ′(ω,T) and out-of-phase χ′′(ω,T) susceptibilities, therefore excluding dynamic processes or spin-glass behavior⁵⁵ (Fig. S4†). In the resistivity measurements (Fig. 4, bottom, black) a nearly linear decrease is visible from 300 to 150 K before again an abrupt decrease is observed, coinciding with the anomaly visible in the heat capacity. This decrease can be explained by the localization of an electron into the open-shell 4f¹³ configuration of Yb³⁺ to form the close-shell Yb²⁺ (4f¹⁴) ion. The present behavior is comparable to the Kondo/impurity scattering observed for trivalent intermetallic cerium compounds (4f¹), e.g. Ce₃Al⁵⁶ or Ce₃Al₁₁,⁵⁷ in which the resistivity drops significantly below the Kondo temperature. Trivalent Yb compounds act as ‘hole’ equivalents to the cerium compounds.

As mentioned before, the calculated magnetic moment of YbPd₂Al₃ is nearly in line with one Yb³⁺ and two Yb²⁺ ions per unit cell. Therefore, the divalent Yb²⁺ ions were replaced by the also diamagnetic Ca²⁺ ions, which are similar in size (Ca²⁺: 106 pm; Yb²⁺: 113 pm²) leading to an ideal formula of Yb_0.33Ca_0.67Pd₂Al₃. Additionally, also Yb_0.67Ca_0.33Pd₂Al₃ and the diamagnetic CaPd₂Al₃ were synthesized. All compounds were structurally as well as magnetically characterized. They exhibit a linear trend in the unit cell volume, known as Vegard behavior as well as a linear trend in the hexagonal lattice parameters (Table 1). The magnetic behavior is plotted in Fig. S5.† In comparison with YbPd₂Al₃, the Ca-containing members of the solid solutions Yb_0.33Ca_0.67Pd₂Al₃ and Yb_0.67Ca_0.33Pd₂Al₃ also exhibit a paramagnetic behavior, in line with Yb³⁺ contributions. From the magnitude of the magnetic susceptibility and the effective magnetic moment, it is evident that the amount of trivalent Yb atoms is decreasing (Fig. S6†). As expected, CaPd₂Al₃ finally exhibits a temperature independent diamagnetic behavior (χ_dia = −1.28(1) × 10⁻⁴ emu mol⁻¹ at 300 K). When looking at the data of Yb_0.33Ca_0.67Pd₂Al₃ and Yb_0.67Ca_0.33Pd₂Al₃, the “bump-like” feature is smeared and stretched over a larger temperature region; hence measurements up to 395 K were conducted. This behavior can be explained by the disorder in the solid solutions and the distribution of Ca and Yb on the two available crystallographic sites (1a and 2d), which has been proven by single-crystal structure investigations (Table S2†). However, due to the mixing of Yb and Ca, no strict charge separation is present.

3.5 X-ray photoelectron spectroscopy (XPS)

When looking at intermetallic compounds with the general composition RE_xT_yX_z (RE: rare-earth element, T: transition metal/group 6–12, X: element of group 13–15) the transition metal, especially when being a 5d element, is the most electronegative element involved. We have shown for a number of gold (e.g. Na₂Au₃Al,⁵⁸ AEAuX (AE = Ca–Ba, X = Al–In),⁵⁹ AEAu₂Al₂ (AE = Ca, Sr)⁶⁰ or Ba₃Au₅Al₆ (ref. 60)) or platinum intermetallics (e.g. Ba₃Pt₄Al₄ (ref. 61) and REPt₂Al₃ (RE = Y, Dy–Tm) series⁶²) that a significant electron transfer onto the 5d metal takes places. For the presented compounds, electronegativities of 1.00 (Ca), 2.20 (Pd) and 1.61 (Al), according to the Pauling scale, are found.² For Yb no value is listed on this scale, however, for the neighboring elements values of 1.25 (Tm) and 1.27 (Lu) are reported, making Pd again the most electronegative element.² Since the most electronegative elements acquire additional electron density, a shift towards lower binding energies can be observed in the respective XPS measurements.^58–61

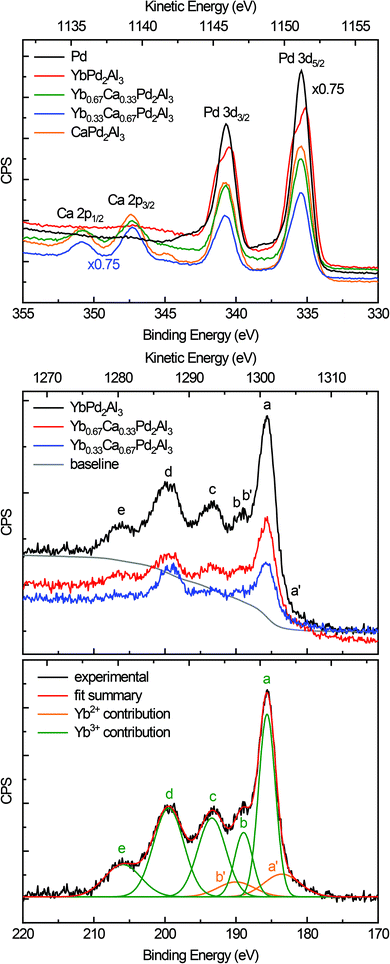
Fig. 5 (top) depicts the XPS spectra of the Pd 3d and Ca 2p lines of elemental Pd (black), YbPd₂Al₃ (red), Yb_0.67Ca_0.33Pd₂Al₃ (green), Yb_0.33Ca_0.67Pd₂Al₃ (blue), and CaPd₂Al₃ (orange). As can be seen from the plot and the data in Table 2, only minor shift of the 3d_5/2 and 3d_3/2 lines of the Pd reference and the investigated compounds can be observed. This is at the first glimpse slightly surprising, but can be explained in a straightforward manner. First, the electronegativity difference between Pd and Al is smaller compared to e.g. Pt/Al or Au/Al. Also all investigated compounds exhibit more Al than Pd atoms (atomic ratio 3 : 2). Hence, electrons are needed for additional bonds in the [Pd₂Al₃]^δ− polyanion, reducing the electron density at the Pd atoms. In total, the electron density is close to metallic palladium with a small shift to lower binding energies, indicating a slightly negative charge on the Pd atoms. Additionally, a rather pronounced ‘two-peak’ structure is observed for YbPd₂Al₃. For the other investigated compounds, a tailing of the peaks towards higher binding energies is visible. This can be explained by so-called shake-up related effects.^63,64 After photoionization, ions can be left in an excited energy state, which lies a few eV above the ground state. In these cases, the kinetic energy of the emitted photoelectron is reduced and can be seen as an additional peak at a higher binding energy compared to the main line. For metals, conduction electrons also can undergo shake-up events that follow the basic core electron photoemission. In these cases, instead of a discrete structure also only a tail on the higher binding energy side of the main can be evident. Similar effects, also causing satellite transitions are shake-down and shake-off events. For Yb_0.67Ca_0.33Pd₂Al₃, Yb_0.33Ca_0.67Pd₂Al₃ and CaPd₂Al₃, additionally the Ca 2p lines are observed in this region. These are in line with typical inorganic calcium compounds, e.g. CaO,⁶⁵ CaCO₃,⁶⁶ or CaMoO₄,⁶⁷ proving the electron transfer from the alkaline-earth atoms and the formal divalent oxidation state for calcium.

Fig. 5 (Top) X-ray photoemission spectra of the Pd 3d and Ca 2p lines of elemental Pd (black), YbPd₂Al₃ (red), Yb_0.67Ca_0.33Pd₂Al₃ (green), Yb_0.33Ca_0.67Pd₂Al₃ (blue), and CaPd₂Al₃ (orange). (Middle) X-ray photoemission spectra of the Yb 4d lines of YbPd₂Al₃ (black), Yb_0.67Ca_0.33Pd₂Al₃ (red), and Yb_0.33Ca_0.67Pd₂Al₃ (blue). The background of YbPd₂Al₃ is depicted as solid grey line. (bottom) Fit of the X-ray photoemission spectra of the Yb 4d lines of YbPd₂Al₃. The sum is depicted in red. (CPS = counts per second, linear scale).

Fig. 5 (middle) depicts the XPS spectra of the Yb 4d lines of YbPd₂Al₃ (black), Yb_0.67Ca_0.33Pd₂Al₃ (red) and Yb_0.33Ca_0.67Pd₂Al₃ (blue). The spectrum consists of five peaks that are easy visible (labeled a to e), which are caused by Coulomb and exchange interactions of the Yb³⁺ (4f¹³) open shell ions. According to the literature,^68,69 the peak a is attributed to ³H₆ and ¹G₄ terms, the small peak c corresponds to the ³G₆ and ¹F₃ terms, while finally the broad peaks d and e can be assigned to the ³G₄, ³D₃ and ³P₂ as well as the ¹H₅ terms, respectively. Peak b originates from the ¹D₂ and ³H₅ terms, which overlaps the 4d_3/2 peak (b′) of the divalent Yb atoms. These Yb²⁺ ions show a rather simple spectrum due to the completely filled 4f states. Hence, the exchange interaction between a core hole and the 4f electrons is negligible. The spectrum consists of a doublet of the 4d_5/2 (a′) and 4d_3/2 (b′) peaks with a relative intensity ratio of 3 : 2, which has been fixed during fitting. The observed fit of the spectrum of YbPd₂Al₃ is depicted in Fig. 5 (bottom), the fits of the spectra of Yb_0.67Ca_0.33Pd₂Al₃ and Yb_0.33Ca_0.67Pd₂Al₃ are shown in the ESI† in Fig. S7 and S8.† Since no cleaving or Ar⁺ sputtering of the specimen was possible, surface oxidation due to sample handling in air or oxidation under X-ray radiation occurred. Similar X-ray induced oxidation processes have been observed for e.g. EuCl₂,⁷⁰ where besides Eu²⁺ also significant amounts of Eu³⁺ are visible in the XPS investigations. Subsequently, the relative Yb³⁺/Yb²⁺ ratio is significantly biased and cannot be used for the determination of the amount of Yb²⁺ present in the sample. However, the presence of both lines still proves the presence of both, di- and trivalent Yb atoms. A better quantification might be achievable using Hard X-ray Photoelectron Spectroscopy (HAXPES) investigations which can monitor the Yb 3d_3/2 and 3d_5/2 or XANES measurements.

4. Conclusion

YbPd₂Al₃ and its solid solution Yb_1−xCa_xPd₂Al₃ (x = 0.33, 0.67, 1) have been synthesized from the elements using sealed tantalum ampoules. The compounds crystallize in the hexagonal YNi₂Al₃ type structure (P6/mmm) with lattice parameters of a = 930–936 and c = 420–424 pm. During dc magnetic susceptibility measurements, an anomaly at T_anomaly ∼ 110 K was observed. Antiferromagnetic ordering was discarded due to the recorded magnetization isotherms, the observed expansion of the unit cell below T_anomaly and the absence of a significant shift in field dependent heat capacity and dc susceptibility measurements. The observed feature is also visible in measurements of the electrical resistivity and the heat capacity, in contrast, no dynamic features were observed in ac magnetization experiments. Therefore, this feature can only be attributed to a temperature induced ytterbium valence change. While above 110 K a mixed-valent Yb state (as seen from the effective magnetic moment) is present, an intrinsic one electron reduction upon formation of a nearly diamagnetic compound at low temperatures takes place. The temperature induced valence change is not only characterized by the drastically expansion of the c axis, observed in temperature dependent powder and single-crystal X-ray measurements, but also by a significant distortion of the Yb1 polyhedra. XPS investigation proved the presence of Yb²⁺ and Yb³⁺, however, overestimating the amounts of trivalent Yb due to surface oxidation of the specimen. A possible explanation for this valence change is the lower overall energy of the purely divalent system at low temperatures, since the open shell 4f¹³ system of Yb³⁺ transitions into a fully closed shell Yb²⁺ (4f¹⁴) system.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dipl.-Chem. Simon Gausebeck for the help with the sample preparation, Dr R.-D. Hoffmann, Dipl.-Ing. U. Ch. Rodelwald and Dipl.-Ing. J. Kösters for the collection of the single-crystal diffractometer data.

References

1. A. Szytuła and J. Leciejewicz, Handbook of Crystal Structures and Magnetic Properties of Rare Earth Intermetallics, CRC Press, Boca Raton, 1994.
2. J. Emsley, The Elements, Clarendon Press, Oxford University Press, Oxford, New York, 1998.
3. S. Cotton, Lanthanides & Actinides, Macmillan Education LTD, Houndsmillo, Basingstoke, Hampsire, London, 1991.
4. H. Bärnighausen and G. Brauer, Acta Crystallogr., 1962, 15, 1059.
5. R. Rau, Acta Crystallogr., 1966, 20, 716–723.
6. F. F. Y. Wang, Phys. Status Solidi B, 1966, 14, 189–192.
7. M. Glätzle, O. Janka, V. Svitlyk, D. Chernyshov, M. Bartsch, H. Zacharias, R. Pöttgen and H. Huppertz, Chem.–Eur. J., 2018, 24, 15236–15245.
8. Z. Haque, G. S. Thakur, R. Parthasarathy, B. Gerke, T. Block, L. Heletta, R. Pöttgen, A. G. Joshi, G. K. Selvan, S. Arumugam, L. C. Gupta and A. K. Ganguli, Inorg. Chem., 2017, 56, 3182–3189.
9. M. B. Gamża, R. Gumeniuk, U. Burkhardt, W. Schnelle, H. Rosner, A. Leithe-Jasper and A. Ślebarski, Phys. Rev. B, 2017, 95, 165142.
10. F. L. Carter, J. Solid State Chem., 1972, 5, 300–313.
11. N. Lossau, H. Kierspel, J. Langen, W. Schlabitz, D. Wohlleben, A. Mewis and C. Sauer, Z. Phys. B: Condens. Matter, 1989, 74, 227–232.
12. K. H. J. Buschow and H. J. Vandall, Solid State Commun., 1970, 8, 363–365.
13. K. H. Mader and W. M. Swift, J. Phys. Chem. Solids, 1968, 29, 1759–1764.
14. O. Sichevych, Y. Prots, Y. Utsumi, L. Akselrud, M. Schmidt, U. Burkhardt, M. Coduri, W. Schnelle, M. Bobnar, Y.-T. Wang, Y.-H. Wu, K.-D. Tsuei, L. H. Tjeng and Y. Grin, Inorg. Chem., 2017, 56, 9343–9352.
15. U. B. Paramanik, U. Anupam, U. Burkhardt, R. Prasad, C. Geibel and Z. Hossain, J. Alloys Compd., 2013, 580, 435–441.
16. O. Niehaus, U. C. Rodewald, P. M. Abdala, R. S. Touzani, B. P. T. Fokwa and O. Janka, Inorg. Chem., 2014, 53, 2471–2480.
17. B. Batlogg, E. Kaldis, A. Schlegel, G. von Schulthess and P. Wachter, Solid State Commun., 1976, 19, 673–676.
18. B. Batlogg, E. Kaldis and P. Wachter, J. Magn. Magn. Mater., 1976, 3, 96–98.
19. D. C. Koskenmaki and K. A. Gschneidner Jr, Handbook on the Physics and Chemistry of Rare Earths, 1978, vol. 1, p. 337.
20. M. Wakeshima, Y. Izumiyama, Y. Doi and Y. Hinatsu, Solid State Commun., 2001, 120, 273–278.
21. A. Jayaraman, V. Narayanamurti, E. Bucher and R. G. Maines, Phys. Rev. Lett., 1970, 25, 1430–1433.
22. E. Kaldis and P. Wachter, Solid State Commun., 1972, 11, 907–912.
23. M. Akihiro, M. Shigeki, U. Masafumi, W. Hirofumi, M. Kazuyuki, U. Yoshiya, M. Masaichiro, K. Naomi, N. Kiyofumi, H. Naohisa, O. Yasuo and I. Naoki, J. Phys.: Condens. Matter, 2018, 30, 105603.
24. A. P. Menushenkov, A. A. Yaroslavtsev, A. Y. Geondzhian, R. V. Chernikov, L. Nataf, X. Tan and M. Shatruk, J. Supercond. Novel Magn., 2017, 30, 75–78.
25. R. S. Kumar, A. Svane, G. Vaitheeswaran, V. Kanchana, E. D. Bauer, M. Hu, M. F. Nicol and A. L. Cornelius, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075117.
26. E. V. Sampathkumaran, L. C. Gupta, R. Vijayaraghavan, K. V. Gopalakrishnan, R. G. Pillay and H. G. Devare, J. Phys. C: Solid State Phys., 1981, 14, L237.
27. M. Radzieowski, F. Stegemann, T. Block, J. Stahl, D. Johrendt and O. Janka, J. Am. Chem. Soc., 2018, 140, 8950–8957.
28. D. T. Adroja, B. D. Rainford, J. M. de Teresa, A. del Moral, M. R. Ibarra and K. S. Knight, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 12790–12797.
29. I. Felner and I. Nowik, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 617–619.
30. I. Felner, I. Nowik, D. Vaknin, U. Potzel, J. Moser, G. M. Kalvius, G. Wortmann, G. Schmiester, G. Hilscher, E. Gratz, C. Schmitzer, N. Pillmayr, K. G. Prasad, H. de Waard and H. Pinto, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 6956–6963.
31. H. Müller, E. Bauer, E. Gratz, K. Yoshimura, T. Nitta and M. Mekata, J. Magn. Magn. Mater., 1988, 76, 159–160.
32. O. S. Zarechnyuk and R. M. Rykhal', Visnyk Lvivskoho Derzhavnoho Universytetu Serija Khimichna, 1981, 23, 45–47.
33. R. Pöttgen, T. Gulden and A. Simon, GIT Labor-Fachz., 1999, 43, 133–136.
34. D. Kußmann, R.-D. Hoffmann and R. Pöttgen, Z. Anorg. Allg. Chem., 1998, 624, 1727–1735.
35. K. Yvon, W. Jeitschko and E. Parthé, J. Appl. Crystallogr., 1977, 10, 73–74.
36. Dectris, Pilatus 100K-S Detector System, Technical Specification and Operating Procedure (version 1.7), Baden, 2011.
37. L. J. van der Pauw, Philips research reports, 1958, 13, 1–9.
38. P. Villars and K. Cenzual, Pearson's Crystal Data: Crystal Structure Database for Inorganic Compounds (on DVD), ASM International®, Materials Park, Ohio (USA), release 2018/2019.
39. L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786–790.
40. V. Petříček, M. Dušek and L. Palatinus, Jana2006, The crystallographic computing system, Institute of Physics, Praha, Czech Republic, 2006.
41. V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr., 2014, 229, 345–352.
42. T. Roisnel and R. Rodríguez-Carvajal, Materials Science Forum, Proceedings of the Seventh European Powder Diffraction Conference (EPDIC 7), 2000, pp. 118–123.
43. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69.
44. F. Eustermann, R.-D. Hoffmann and O. Janka, Z. Kristallogr., 2017, 232, 573–581.
45. H. Pfisterer and K. Schubert, Naturwissenschaften, 1950, 37, 112–113.
46. K. Schubert, H. Breimer, W. Burkhardt, E. Günzel, R. Haufler, H. L. Lukas, H. Vetter, J. Wegst and M. Wilkens, Naturwissenschaften, 1957, 44, 229–230.
47. G. Cordier, T. Friedrich, R. Henseleit, A. Grauel, U. Tegel, C. Schank and C. Geibel, J. Alloys Compd., 1993, 201, 197–201.
48. G. Cordier and R. Henseleit, Z. Kristallogr., 1993, 203, 144–145.
49. S. Surjeet and S. K. Dhar, J. Phys.: Condens. Matter, 2002, 14, 11795.
50. A. W. Hull, Phys. Rev., 1917, 10, 661–696.
51. R. M. Moon, W. C. Koehler, H. R. Child and L. J. Raubenheimer, Phys. Rev., 1968, 176, 722–731.
52. B. C. Sales and D. K. Wohlleben, Phys. Rev. Lett., 1975, 35, 1240–1244.
53. G. J. Lehr, D. T. Morelli, H. Jin and J. P. Heremans, J. Appl. Phys., 2013, 114, 223712.
54. D. Kaczorowski, A. V. Gribanov, P. Rogl and S. F. Dunaev, J. Alloys Compd., 2016, 685, 957–961.
55. J. A. Mydosh, J. Magn. Magn. Mater., 1996, 157–158, 606–610.
56. M. Sera, T. Satoh and T. Kasuya, J. Magn. Magn. Mater., 1987, 63–64, 82–84.
57. H. J. Van Daal and K. H. J. Buschow, Phys. Lett. A, 1970, 31, 103–104.
58. F. Stegemann, C. Benndorf, Y. Zhang, M. Bartsch, H. Zacharias, B. P. T. Fokwa, H. Eckert and O. Janka, Inorg. Chem., 2017, 56, 1919–1931.
59. C. Benndorf, F. Stegemann, S. Seidel, L. Schubert, M. Bartsch, H. Zacharias, B. Mausolf, F. Haarmann, H. Eckert, R. Pöttgen and O. Janka, Chem.–Eur. J., 2017, 23, 4187–4196.
60. F. Stegemann, C. Benndorf, Y. Zhang, M. Bartsch, H. Zacharias, B. P. T. Fokwa, H. Eckert and O. Janka, Z. Anorg. Allg. Chem., 2017, 643, 1379–1390.
61. F. Stegemann, C. Benndorf, T. Bartsch, R. S. Touzani, M. Bartsch, H. Zacharias, B. P. T. Fokwa, H. Eckert and O. Janka, Inorg. Chem., 2015, 54, 10785–10793.
62. F. Eustermann, S. Gausebeck, C. Dosche, M. Haensch, G. Wittstock and O. Janka, Crystals, 2018, 8, 169.
63. D. Briggs, Surface analysis by Auger and X-ray photoelectron spectroscopy SurfaceSpectra, Manchester, 2003.
64. S. Hüfner, Photoelectron spectroscopySpringer, Berlin, 2010.
65. H. Van Doveren and J. A. T. H. Verhoeven, J. Electron Spectrosc. Relat. Phenom., 1980, 21, 265–273.
66. Q. Liu, J. S. Laskowski, Y. Li and D. Wang, Int. J. Miner. Process., 1994, 42, 251–266.
67. V. I. Nefedov, M. N. Firsov and I. S. Shaplygin, J. Electron Spectrosc. Relat. Phenom., 1982, 26, 65–78.
68. Y. Ohno, J. Electron Spectrosc. Relat. Phenom., 2008, 165, 1–4.
69. I. Chorkendorff, J. Onsgaard, J. Schmidt-May and R. Nyholm, Surf. Sci., 1985, 160, 587–598.
70. D. Kim, Y.-H. Jin, K.-W. Jeon, S. Kim, S.-J. Kim, O. H. Han, D.-K. Seo and J.-C. Park, RSC Adv., 2015, 5, 74790–74801.
71. S. B. M. Hagström, P. O. Hedén and H. Löfgren, Solid State Commun., 1970, 8, 1245–1248.
72. F. U. Hillebrecht, J. C. Fuggle, P. A. Bennett, Z. Zołnierek and C. Freiburg, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 2179–2193.
73. K. Kishi, Y. Motoyoshi and S. Ikeda, Surf. Sci., 1981, 105, 313–324.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1868211, 1868849, 1875396, 1880784–1880786, 1892594, 1892597–1892598, 1895369–1895370 and 1910744. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc04437j

---