Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Two-dimensional UV spectroscopy: a new insight into the structure and dynamics of biomolecules
R.
Borrego-Varillas†
a,
A.
Nenov†
 b,
L.
Ganzer
a,
A.
Oriana
a,
C.
Manzoni
a,
A.
Tolomelli
b,
L.
Ganzer
a,
A.
Oriana
a,
C.
Manzoni
a,
A.
Tolomelli
 c,
I.
Rivalta
c,
I.
Rivalta
 b,
S.
Mukamel
b,
S.
Mukamel
 d,
M.
Garavelli
d,
M.
Garavelli
 *b and
G.
Cerullo
*b and
G.
Cerullo
 *a
*a
aIFN-CNR, Dipartimento di Fisica, Politecnico di Milano, Piazza Leonardo da Vinci 32, I-20133 Milano, Italy. E-mail: giulio.cerullo@polimi.it
bDipartimento di Chimica Industriale, Universitá degli Studi di Bologna, Viale del Risorgimento 4, I-40136 Bologna, Italy. E-mail: marco.garavelli@unibo.it
cDipartimento di Chimica, Universitá degli Studi di Bologna, Via Selmi 2, I-40126 Bologna, Italy
dDepartment of Chemistry, Department of Physics and Astronomy, University of California, Irvine, California 92697-2025, USA
First published on 15th October 2019
Abstract
Two-dimensional (2D) spectroscopy, originally developed for nuclear magnetic resonance, has been recently extended to the infrared and visible regimes. In this technique sequences of femtosecond light pulses are used to interrogate molecular systems and show, by a double Fourier transform, the correlation between excitation and detection frequencies. Extension to the ultraviolet (UV) regime is of great interest and promises to deliver rich structural and dynamical information on biomolecules such as DNA and proteins; however, it must overcome significant technical challenges. This review summarizes the current development status of 2DUV spectroscopy. After discussing the scientific case for the technique, we introduce its basic principles and review its experimental implementations, as well as the computational tools that have been developed to model the experiments. We conclude by giving a few application examples, which highlight the potential of 2DUV spectroscopy and motivate its further development.
1. Introduction
Nuclear Magnetic Resonance (NMR) has revolutionized structural biology, allowing the determination of molecular structures with high spatial resolution.1 In two-dimensional (2D) NMR the molecular system under study is excited by a sequence of properly timed, phase-coherent radio-frequency (RF) pulses. The signal is recorded as a function of two time delay variables and the data are Fourier transformed twice to generate a spectrum which is a function of two frequency variables. 2D-NMR provides detailed information on the structure of complex molecules; it can also study dynamics, although directly only on a millisecond timescale, limited by the duration of the RF driving pulses (nanosecond timescales can be probed indirectly through frequency dependent relaxation).A wealth of novel information can be obtained by extending 2D techniques to the optical frequency domain, using sequences of ultrashort light pulses with a femtosecond duration to interrogate a molecular system.2–6 Initially, 2D optical spectroscopy was mainly applied in the infrared (IR) spectral range, resonant with vibrational transitions of molecules. 2DIR spectroscopy has allowed measuring couplings between vibrational modes of a molecule7 and capturing transient molecular structures on the picosecond timescale.8,9 Recently, 2D optical techniques have been extended to the visible range,10,11 targeting electronic transitions. Two-dimensional electronic spectroscopy (2DES) has provided new insights into the structure and dynamics of complex multi-chromophore aggregates,12,13 by measuring how the units within a molecular architecture interact and transfer electronic excitation energy.
By spreading the information content of the nonlinear signal along two frequency axes, 2DES offers several advantages as compared to conventional 1D femtosecond transient absorption (TA) spectroscopy: (i) it allows measuring the homogeneous linewidth of optical transitions, enabling to single out the individual levels in strongly broadened and congested spectra, and to follow loss of excitation memory through spectral diffusion; (ii) it enables to separate, and thus distinguish, contributions to the nonlinear signal which spectrally overlap in the TA experiments; (ii) it allows direct observation and quantification of couplings between different chromophores, which appear as cross peaks in the 2DES maps; (iv) it can monitor in real time energy relaxation and energy transfer processes between coupled electronic states and chromophores.
2DES is currently well established in the near-IR and visible spectral regimes and has proven its power in the study of a wide variety of systems, from photosynthetic complexes12,14 to semiconductors.15,16 However, many molecules of biochemical interest, such as DNA and proteins, possess strong absorption bands in the ultraviolet (UV) range. While the backbone of proteins strongly absorbs at wavelengths shorter than 250 nm (corresponding to photon energies higher than 5 eV), some amino acids (tryptophan, tyrosine, and phenylalanine) and nucleobases (adenine, guanine, cytosine, thymine and uracil) and the corresponding nucleosides/nucleotides show intense absorption bands at longer deep UV (DUV) wavelengths, between 250 and 300 nm (photon energies between 4 and 5 eV). These bands correspond to the ππ* transitions of the aromatic rings within these molecules, which are clearly separated from their backbone absorption. Other important molecular cofactors, such as flavins, plastoquinones, thiobases and nicotinamide adenine dinucleotide, display absorption bands at even longer near UV (NUV) wavelengths (300–400 nm, corresponding to 3.2–4 eV photon energies). In addition, UV absorbing molecules are typically small enough to enable highly accurate computations of their energy level structure and dynamics, allowing the effective benchmarking of computational approaches with experiments.17,18 This multitude of spectroscopic targets makes 2DES spectroscopy in the UV region (2DUV) a powerful investigation tool for the photophysics and photochemistry of biomolecular processes.
Despite the clear scientific interest,19,20 the extension of 2D spectroscopy to the UV range has to face a number of technical challenges, which have been addressed over the past few years. The generation, characterization and manipulation of ultrashort light pulses in the UV region are difficult, due to the lack of suitable broadband optical gain media and the strong material dispersion.21 Moreover, 2D spectroscopy requires interferometric stability between pulse pairs, which amounts to controlling their path-length difference to be within a small fraction of the wavelength. This requirement is harder to satisfy in the UV region due to the short wavelengths. Finally, in condensed-phase UV experiments one needs to minimize the strong nonlinear non-resonant background of the solvent, which may mask the resonant response of interest,22,23 and avoid multiphoton absorption in the solvent, which may generate unwanted species such as solvated electrons24 that yield transient signals overlapping with those of the system under study.
This paper surveys the current status of the development of experimental and computational tools for 2DUV spectroscopy and gives a few examples of applications, which highlight the potential of the technique and motivate its further development. The paper is organized as follows: Section 2 discusses the scientific case for the development of 2DUV spectroscopy, focusing on studies of DNA and peptides; Section 3 summarizes the principles of 2D spectroscopy and its experimental implementations, and describes the different technical solutions so far adopted for 2DUV spectroscopy; Section 4 presents the theoretical framework for modelling 2DUV spectroscopy and introduces the computational tools that have been developed for this purpose; Section 5 presents selected examples, both experimental and computational, of the application of 2DUV spectroscopy; finally, Section 6 draws conclusions and presents the open challenges.
2. The scientific case for 2DUV spectroscopy
In this section we describe two applications of 2DUV spectroscopy to fundamental biochemical problems, which call for the technical efforts which have been made towards its development.2.1 DNA photophysics: towards an understanding of photoprotection mechanisms
Due to the aromatic rings present in nucleotides, DNA has strong absorption bands in the DUV region. The excess of electronic energy in the excited state could initiate a variety of photoreactions, such as pyrimidine dimerization,25,26 which involve structural rearrangements and corrupt the information encoded in the base sequence. The quantum yield of such photoproducts is remarkably low, because DNA manages to efficiently protect itself by dissipating the absorbed energy through harmless non-radiative decay channels.27–29 This property is not merely an interesting feature of DNA photophysics, but it is thought to be an essential requirement for the very existence and the replication of life.Experimental and computational studies of DNA have revealed a rather complex photophysical scenario, in which energy dissipation occurs by a cascade of non-radiative pathways. In single isolated nucleotides the bright photoexcited ππ* state relaxes very rapidly (sub-ps to ps timescale) to the ground state S0 through a direct (ππ* → S0) internal conversion (IC) process.24,30,31 For pyrimidine bases an additional, slower indirect decay route has been identified, involving an intermediate nπ* (dark) state (ππ* → nπ* → S0).32 Theoretical investigations have shown that these ultrafast IC processes are mediated by conical intersections (CIs), i.e. low-energy real crossings between different electronic states.33 CIs serve as doorways for highly efficient non-reactive decay routes whereby electronic energy is rapidly converted into vibrational energy.
Moving to oligomers, and eventually to the double-stranded DNA helix, the photoexcitation scenario changes dramatically and the excited state lifetimes increase by several orders of magnitude. The mechanisms by which DNA strands engineer their photoprotection are still heavily debated.34,35 Intra-strand dipolar interactions between bases that are stacked one above another within a DNA strand (base stacking), and inter-strand interactions mediated by the hydrogen bonds between the bases of the two complementary single strands in the double-helix (Watson-Crick base pairing) play key roles. For single stranded (i.e. stacked) multimers the excited state is predicted to be a Frenkel exciton,36 whose characteristics and degree of delocalization are largely unknown. Then, whether the excitation localizes on a single nucleobase, leading to intra-base IC mechanisms, or/and it evolves into an excimer/exciplex state with partial charge-transfer character and longer lifetime, is a matter of active debate.37,38 Additionally, inter-strand photo-induced mechanisms, involving electron transfer from one to the other of two paired nucleobases, followed by an aborted proton transfer, have been suggested in double helixes.39 2DUV spectroscopy is the technique of choice to disentangle spectral signatures of competitive decay channels, otherwise leading to spectrally congested signals in TA spectra, thus offering a decisive insight into the nature and fate of photoexcitation in DNA. This insight will help to understand the way nature has designed the energy landscape of such molecules to achieve photoprotection by efficiently dissipating, over an ultrafast timescale, the absorbed UV energy.
2.2 2DUV study of the secondary structure and dynamics of peptides and proteins
Predicting the secondary structures of proteins requires the understanding of the interactions causing them to fold from a disordered, random-coil state into their unique native structures.40 This is particularly important because protein misfolding and the formation of insoluble aggregates (also known as amyloid fibrils) can give rise to highly debilitating diseases, such as Alzheimer's and Parkinson's.41 Mechanistic information is vital to the understanding of the way proteins misfold and to the design of suitable drugs that inhibit amyloid formation. Protein point mutations leading to misfolding and diseases have been discovered in clinical studies. A fast experimental technique able to provide structural information would allow the rapid screening of different mutations and monitoring fibril formation in real time.X-ray crystallography determines static protein structures with atomic resolution, but many interesting systems, such as protein aggregates, are non-crystalline. NMR provides 3D structural information with atomic resolution, but it is a time consuming procedure involving several steps, such as data collection, resonance assignment, restraint generation and final structure calculation and refinement. NMR is thus unsuitable for rapidly screening different point mutations or solution conditions for a particular protein. Optical techniques (UV and IR absorption, electronic and vibrational circular dichroism and UV resonance Raman scattering) have been widely used to study the secondary structure of proteins. These techniques are faster, but provide only partial spectroscopic information and cannot address subtle differences in the secondary structure. 2DIR spectroscopy has recently emerged as a powerful technique in structural biology.7–9 In combination with isotope labelling to resolve spectral congestion and address specific residues in the chain, 2DIR has been used to probe the structural rearrangements during the misfolding and aggregation processes.42,43 However, specific isotope labelling is experimentally very challenging and labour intensive even in small proteins.
2DUV spectroscopy has the potential to provide valuable information on the secondary structure of proteins.44–47 It can be considered an extension of UV absorption and circular dichroism spectroscopies, in which the spectra are spread along a second frequency axis, greatly enhancing the information content and structural sensitivity. An advantage of 2DUV is that it does not require isotope labelling, but rather uses three relatively rare aromatic residues (tryptophan, tyrosine, and phenylalanine) as local probes (see Section 5.3 for an example). 2DUV spectroscopy thus holds promise as a diagnostic tool for structural studies of polypeptides and proteins. This method could combine the simplicity and speed of operation of optical techniques with a much greater information content, bridging the experimental gap between crude estimates of protein unfolding and full structure determination.
3. 2DUV spectroscopy: principles and techniques
3.1 Principle of 2D spectroscopy
An optical 2D experiment is schematically sketched in Fig. 1. The system under study is excited by three consecutive ultrashort pulses, with controllable relative delays. Interaction with pulse 1 builds up a macroscopic polarization in the sample (i.e. a coherent superposition of oscillating dipoles); interaction with pulse 2, delayed by a time t1 known as coherence time, leads to a change in the population of the sample; finally, interaction with pulse 3, delayed by a time t2 (the population or waiting time), creates a macroscopic third-order nonlinear polarization P(3)(t1,t2,t3), which follows pulse 3 with a delay t3 and emits a nonlinear field E(3)(t1,t2,t3) ∝ iP(3)(t1,t2,t3).48 This field is collinearly superimposed with pulse 4, also known as the local oscillator (LO), and sent to a spectrometer, which performs a Fourier transform (FT) with respect to t3, obtaining the “detection frequency” ω3. Spectral interferometry49 between the nonlinear field and the LO allows full retrieval of the amplitude and phase of the nonlinear field Ẽ(3)(t1,t2,ω3), and thus of the nonlinear polarization![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (3)(t1,t2,ω3). Finally, by performing another FT with respect to t1 for a fixed value of the waiting time t2, one obtains the 2D map
(3)(t1,t2,ω3). Finally, by performing another FT with respect to t1 for a fixed value of the waiting time t2, one obtains the 2D map ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (3)(ω1,t2,ω3), where ω1 is the “excitation frequency”.
(3)(ω1,t2,ω3), where ω1 is the “excitation frequency”.
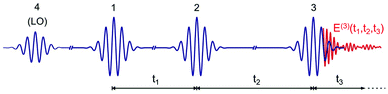 | ||
| Fig. 1 Scheme of the ultrashort pulse sequence used for 2D spectroscopy. LO: local oscillator. E(3)(t1,t2,t3) is the nonlinear emitted field. | ||
Fig. 2 shows an example of a 2D map, where the excitation (detection) axis is horizontal (vertical). Each vertical line in the map can be interpreted as a TA spectrum obtained for a specific value of the excitation frequency, corresponding to excitation with a narrowband pulse. However, while a narrowband excitation pulse would have necessarily a long duration, thus compromising the temporal resolution of the measurement, in 2D spectroscopy it is possible to use a short and broadband excitation pulse, obtaining resolution in the excitation frequency range through the FT approach. 2D spectroscopy thus overcomes the Fourier limit and provides simultaneously high temporal and spectral resolution. The map in Fig. 2 presents positive differential transmission (ΔT/T) peaks along the diagonal, which correspond to the ground state bleaching (GSB) and stimulated emission (SE) of the transitions resonant with the excitation pulse. It also contains positive peaks outside the diagonal (cross peaks), which identify coupling between different transitions, which may belong to the same or to different chromophores. Finally, a 2D map may also contain negative peaks due to photoinduced absorption (PA), which correspond to transitions from bright or dark excited states or from the hot ground state (see discussion in Sections 4 and 5).
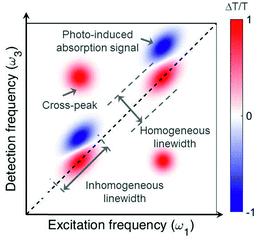 | ||
| Fig. 2 Typical 2D map, showing diagonal peaks and cross peaks with both positive (GSB and SE) and negative (PA) signals. | ||
3.2 Experimental configurations of 2D spectroscopy
Compared to TA, 2D spectroscopy has an additional technical difficulty: in the time intervals t1 and t3 the signal oscillates at the frequencies of the resonantly excited optical transitions, so that, in order to record these oscillations with fidelity, one needs to control the delays with a precision much higher than the optical period (i.e. ≈2 fs for visible light and ≈1 fs for UV light). This requires interferometric stability between the corresponding pulse pairs (pulses 1–2 and pulses 3–4), i.e. stabilization of their path-length difference within a small fraction (of the order of 1/100 or better) of the wavelength. The two experimental configurations used so far in 2D spectroscopy are schematically shown in Fig. 3: the non-collinear, heterodyne detected three-pulse photon echo (3PPE)10,11 and the partially collinear pump–probe (PP)50–52 geometry.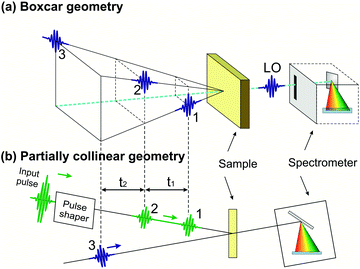 | ||
| Fig. 3 The experimental configurations used for 2D spectroscopy: the non-collinear 3PPE (a) and the partially collinear PP geometry (b). | ||
In 3PPE the three driving pulses are arranged in a non-collinear geometry with their propagation directions located at three vertexes of a square (boxcar geometry, see Fig. 3(a)); in this way the third-order nonlinear signal (also known as the “echo”) is emitted in a background-free direction, dictated by phase matching, at the fourth vertex of the square. The LO pulse is then aligned collinearly with the echo signal and both are sent to a spectrometer for spectral interferometry. This scheme requires interferometric stability of two pulse pairs (pulses 1–2 and 3–4), which is typically obtained by splitting the beams using diffraction gratings,10,11,53 to generate pulse pairs that impinge on the same optics and are thus intrinsically phase-locked; their relative delays are precisely changed by the insertion of glass with controlled thicknesses. Alternatively, one can use active path-length stabilization54 or a configuration with delay lines that handle the four pulses always in pairs, so that the two pulses from any pair induce opposite phase shifts in the interference signal.55
The partially collinear PP geometry (Fig. 3(b)) employs two interferometrically stable collinear pump pulses and a non-collinear probe pulse, which is dispersed on a spectrometer. The probe pulse has the dual purpose of generating nonlinear polarization and acting as a LO (in the so-called self-heterodyning configuration). The main technical challenge of this scheme is the generation of a pair of collinear interferometrically stable pump pulses. Michelson/Mach–Zehnder interferometers with active path-length stabilization or inline measurement of the path-length difference are commonly used in the mid-IR region,56 but are challenging to extend to shorter wavelengths. Alternatively, a pulse pair can be generated by a pulse shaper providing the required sinusoidal spectral amplitude and phase modulation. Pulse shapers inherently produce phase-locked pulses due to the common path experienced by the generated replicas. Several solutions, including a liquid crystal spatial light modulator,52 an acousto-optic modulator (AOM)57 and an acousto-optic programmable dispersive filter (AOPDF),58 have been implemented. Recently, a common-path interferometer based on birefringent wedges, the Translating-Wedge-based Identical pulse eNcoding System (TWINS),59 has been introduced as a simple method for generating the pair of collinear phase-locked pulses and demonstrated for 2DES in the visible region.60
3.3 2DUV spectroscopy: experimental configurations
In the following we review the different schemes for 2DUV spectroscopy that have been proposed and experimentally demonstrated so far. Pioneering non-heterodyne detected 3PPE experiments in the UV region were performed by the Chergui group on dye molecules61,62 and tryptophan.63 Moran and coworkers64,65 employed the 3PPE geometry, using diffraction gratings for the generation of non-collinear phase-locked UV pulse pairs in a boxcar geometry and fused silica wedges for delay control. UV pulses with an ≈900 cm−1 bandwidth were generated by four-wave-mixing, in an argon-filled hollow-core fiber, of the fundamental wavelength and the second harmonic of a Ti:sapphire laser; the pulses were compressed to ≈25 fs by a fused silica prism pair. The setup was used to study relaxation dynamics in adenine and thymine, as well as photoinduced ring opening dynamics in cyclohexadiene and its derivatives.A similar configuration was developed by Selig and coworkers,66 who built a fully non-collinear miniaturized all-reflective setup driven by 50 fs pulses produced by second-harmonic generation (SHG) of a non-collinear optical parametric amplifier (NOPA). The 3PPE 2DUV configuration with the greatest spectral coverage was developed by Prokhorenko and coworkers,24,67 who also employed a reflective diffractive optics beam splitter. Ultra-broadband UV pulses, covering the 250–300 nm wavelength range (≈6000 cm−1 bandwidth), were generated by SHG of a visible NOPA using achromatic phase matching (APM); the pulses were compressed to a 6–7 fs duration using a deformable mirror. The setup was applied to the study of the ππ* transitions in DNA nucleobases, both pyrimidines and purines.23
The first 2DUV setup in the partially collinear PP geometry was developed by Weinacht and coworkers,68 who used a pulse shaper based on an AOM for the generation of phase-locked pump pulses. Phase cycling between the pump pulses, enabled by the AOM, was employed to suppress background noise. Using 50 fs, 260 nm pulses obtained as the third harmonic of a Ti:sapphire laser system, they studied ultrafast relaxation processes in adenine and uracyl nucleobases.69 A similar system was implemented by Riedle and coworkers,70 where tunable pump pulses were generated either by SHG of a NOPA or by sum-frequency-generation (SFG) of the NOPA with the fundamental wavelength of the Ti:sapphire laser. The pump pulses, with an energy of ≈3 μJ, were then spectrally broadened by self-phase modulation in a CaF2 plate, and finally compressed to ≈16 fs with the combination of a prism compressor and an AOPDF. The AOPDF was also used as a pulse shaper to generate the phase-locked pump pulse pair with a variable delay and controlled phase. The probe pulse was a white light continuum (WLC) generated in a CaF2 plate, which covers the spectral range of 290–720 nm. The setup, which thanks to the WLC has a very broad spectral coverage on the detection axis, was applied to pyrene and 2,2-diphenyl-5,6-benzo(2H)chromene and allowed the study of the excitation energy dependence of the relaxation processes in these molecules.
The birefringent TWINS interferometer has proven to be very convenient for the generation of phase-locked visible pulses;59 however, its direct application in the UV range is challenging, because its refractive optical components introduce a large amount of dispersion which would be difficult to compensate for. To overcome this limitation and generate phase-locked UV pulses, Borrego-Varillas and coworkers71 combined pulse shaping by TWINS in the visible region with frequency up-conversion and nonlinear phase transfer. They generated ultrashort UV pulse pairs by SFG between a pair of phase-locked visible pulses and a quasi-monochromatic infrared pulse, obtained by spectral filtering of the output of a Ti:sapphire laser. This approach allowed avoiding the very high dispersion introduced by direct pulse shaping in the UV region, while fulfilling the phase stability requirements. They demonstrated 16 fs UV pulse pairs with a 2000 cm−1 spectrum extending from 320 to 360 nm and relative delay controlled to an accuracy better than λ/450, which were combined with a WLC probe and applied to 2DUV spectroscopy of pyrene.
An alternative setup for 2DUV spectroscopy in the PP geometry was introduced by Chergui and coworkers72,73 combining a narrowband and frequency tunable pump pulse with a broadband probe pulse. A fraction of the output of a broadband NOPA was frequency doubled in a thick (2 mm) β-barium borate crystal mounted on a motorized rotation stage, obtaining narrowband (≈1.5 nm bandwidth) pump pulses with ≈150 fs duration, up to 75 nJ energy and wavelength tunability from 250 to 380 nm, thus covering an ultrabroad bandwidth of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1. The remaining fraction of the NOPA output was sent to a SHG stage using APM to generate broadband probe pulses with the spectrum spanning the 280–370 nm range. Pump and probe pulses were combined non-collinearly in a standard broadband TA spectroscopy setup. 2DUV maps can then be acquired serially by stacking TA spectra measured for different pump pulse wavelengths. This setup has the merits of simplicity and exceptionally broad spectral coverage, but the drawback of a limited temporal resolution (≈150 fs) which prevents the observation of the fastest dynamical processes.
500 cm−1. The remaining fraction of the NOPA output was sent to a SHG stage using APM to generate broadband probe pulses with the spectrum spanning the 280–370 nm range. Pump and probe pulses were combined non-collinearly in a standard broadband TA spectroscopy setup. 2DUV maps can then be acquired serially by stacking TA spectra measured for different pump pulse wavelengths. This setup has the merits of simplicity and exceptionally broad spectral coverage, but the drawback of a limited temporal resolution (≈150 fs) which prevents the observation of the fastest dynamical processes.
4. Modelling of 2DUV signals
4.1 Theoretical framework of 2DUV spectroscopy
The nonlinear optical response generated by the interaction of matter with the sequence of ultrashort light pulses used in 2D spectroscopy, i.e. the third-order polarization P(3)(t1,t2,t3), can be computed by following the evolution of the system's density matrix![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t) in the Liouville space,48 as described by the Liouville–von Neumann equation:
(t) in the Liouville space,48 as described by the Liouville–von Neumann equation: | (1) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (t) and integrating the resulting equations. Formulating the evolving density matrix as a function of the time interval ti between the light pulses, the system-specific third-order nonlinear response R(3)(t1,t2,t3) can be written as
(t) and integrating the resulting equations. Formulating the evolving density matrix as a function of the time interval ti between the light pulses, the system-specific third-order nonlinear response R(3)(t1,t2,t3) can be written as | (2) |
Eqn (2) describes the field-free evolution of the system, which is in a coherence state during delay times t1 and t3 and in a population state during delay time t2, coupling the various electronic states of the system through the dipole operator ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) . Here, the free evolution of the (unperturbed) density matrix is described by Green's operator Ĝ(t) as
. Here, the free evolution of the (unperturbed) density matrix is described by Green's operator Ĝ(t) as
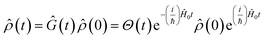 | (3) |
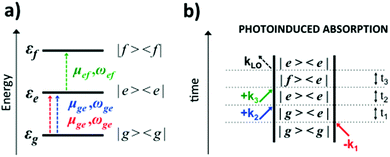
Eqn (2) can be solved in a straightforward way if the target chromophore (or chromophore aggregate) is treated as a closed quantum system, i.e. decoupled from the bath of vibrational degrees of freedom which represent the environment. In this approximation, the electronic states of the system are eigenstates of the system's Hamiltonian possessing infinite lifetimes and dynamics reduced to the phase factor e−iεft. Thus, considering for instance the manifold of ground (g) and excited (e,f) states (see Fig. 4(a)) the expression for the PA detected in a 3PPE experiment reads:
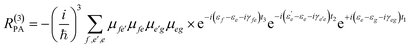 | (4) |
In eqn (4), all dephasing processes, the source of the broadening of each i → j electronic transition, are condensed into the (phenomenological) dephasing constants γij. Among these sources we distinguish: (a) the lifetime broadening due to the finite lifetime of the excited state; (b) homogeneous broadening (also known as dynamic disorder) which originates from the interaction of the chromophore with its environment; (c) inhomogeneous broadening (also known as static disorder) which accounts for the different instantaneous local environment felt by each chromophore in the sample or for the different conformations explored by an aggregate of chromophores at a given instant in time. Moreover, the coupling between the electronic structure and the intramolecular nuclear degrees of freedom induces fluctuations of the transition energies εi of a few thousand cm−1. These fluctuations introduce a vibrational fine structure and intensity beats into the spectral signatures. Finally, non-adiabatic population transfer between electronic states translates into intensity dynamics of their spectral signatures. The field of theoretical spectroscopy deals with developing generalized models for incorporating the above phenomena into the simulations beyond the phenomenological treatment of eqn (4) which would enable comparison with the experiment, as well as with the development of methods for extracting physical quantities associated with the phenomena responsible for the lineshapes from the raw experimental data.75–77 Much less attention has been devoted to the accurate computation of the transition energies εi and the transition dipole moments μij, the key ingredients required for simulating the third-order nonlinear response recorded in 2DUV maps. This aspect is addressed in the next section.
4.2 Calculating spectroscopic parameters
Computations77–88 and ultrafast spectroscopy experiments17,18,89 have demonstrated that, in single chromophores and small aggregates, PA peaks probing high-lying excited states can provide characteristic spectral signatures in 2DUV maps, besides GSB and SE signals. Since the PA peaks are ubiquitous and very often overlap with GSB and SE signals, their presence complicates the interpretation of the spectral dynamics,89,90 making theoretical modeling essential for the analysis of experimental 2DUV maps. On the positive side, the abundance of PA signals allows designing experiments with tailored probe pulses (i.e. “two-color” experiments) aimed at probing the intense PA peaks predicted by simulations. PA peaks exhibit intensity oscillations at short t2 waiting times, due to coherent vibrational dynamics along the photoactive state17 and, at longer waiting times, they feature energy shifts associated with internal energy redistribution and dissipation in the environment.18,89 Furthermore, PA peaks are system-dependent and state-specific and allow studying non-adiabatic population dynamics.18 In certain cases, PAs represent the only signature of an electronic state, e.g. due to relaxation in a non-emitting excited state.17,18,89,91Accurate prediction of εi and μij for the high-lying states involved in PA signals is a serious computational challenge. The excited state manifolds of UV-active chromophores comprise various types of electronic states with a multiconfigurational wavefunction character, generally involving single and double electron excitations with a varying level of covalent and ionic character, the latter caused by intra- and inter-molecular charge transfer/redistribution. Wavefunction-based approaches which combine multiconfigurational wavefunction theory92 and perturbative energy correction,93 such as complete active space self-consistent field theory corrected with second order perturbation theory (i.e. CASSCF//CASPT2), are the most widely used methodologies to handle such a variety of excited states on an equal footing94 generally providing good quantitative predictions of transition energies, with expected errors below 0.2 eV.
The CASSCF//CASPT2 methodology has undergone considerable progress during the last three decades, including the introduction of the restricted active space (RASSCF//RASPT2)95 and the generalized active space (GASSCF//GASPT2) methodologies,96 efficient approximations for two-electron integral estimates,97 and parallelization.98 In general, the accuracy of CASSCF//CASPT2 predictions strongly depends on the choice of two parameters that encompass a critical increase of the computational costs, i.e. the active spaces (AS) and the basis set sizes. In the UV regime, the high density of electronic states requires the use of state-averaging procedures in the multiconfigurational treatment in order to achieve a complete characterization of the electronic structure. Recently, we presented a RASSCF//RASPT2 based protocol for computing reliable transition energies and dipole moments of isolated bio-chromophores and their homo- and hetero-dimers from first principles, capable of computing up to 100 electronic states, thereby encompassing the entire IR to NUV regime.77–88 In these studies, we observed that full valence π-orbital active spaces are often insufficient to achieve the desired accuracy in conjugated systems. Thus, we have adopted the RASSCF//RASPT2 methodology since it allows increasing the AS size beyond the full valence π-orbital space, treating a significant part of the dynamic correlation already (variationally) at the RASSCF level. We have applied this strategy to describe the electronic structure of aromatic amino acids and nucleobases, as well as their homo- and hetero-dimers. Furthermore, we have started benchmarking low-cost approaches (reduced AS80 and density functional theory based methods99) that can then be applied to larger chromophoric systems. The results are a step forward towards making simulations independent of the experiment, enhancing their predictive power and thus not only assisting the interpretation of experimental spectra but also allowing the design of problem-driven experimental setups.
4.3 Towards realistic simulations of 2DUV correlation maps
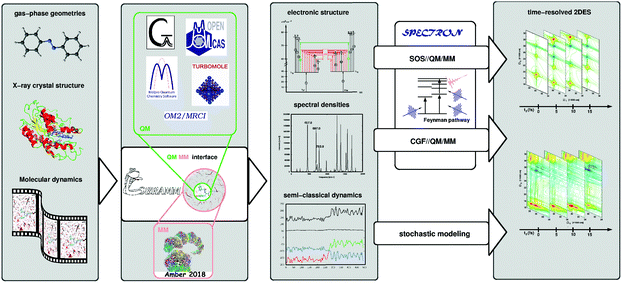
Accurate characterization of molecular electronic structures requires a quantum mechanical (QM) treatment. However, as elucidated in Section 4.1, a realistic simulation requires to consider coupling to intra- and inter-molecular degrees of freedom, non-adiabatic effects and static disorder. Our COBRAMM package100 is interfaced with widely known commercial and academic software for ground and excited state electronic structure computations at a pure QM or at hybrid QM/molecular mechanical (QM/MM) level, thus allowing environmental effects on molecular electronic structures to be accounted for.101 We have recently interfaced the COBRAMM package with SPECTRON software,102 a code for simulating multi-pulse optical spectroscopies utilizing non-linear response theory (see Fig. 5). This approach currently allows using a plethora of electronic structure methods, ranging from multiconfigurational wavefunction theory (CAS- and RAS-SCF//CASPT2) to time-dependent density functional theory (TD-DFT) and semi-empirical methods (OM2-MRCI), for simulations of the linear and nonlinear optical properties of molecular systems, involving conformational dynamics in the ground state and non-adiabatic dynamics in the excited state, all accounting for environmental effects by the QM/MM methodology. In particular, the interface allows in semi-automatized fashion optimizing critical points on the potential energy surfaces of the electronic states and calculating the associated PA peaks at the SOS level.This SOS//QM/MM77 protocol was applied to simulate 2DUV maps of folding/unfolding in small peptides,80,103 π-stacking in a dinucleoside homo-dimer88 and non-adiabatic dynamics in a dinucleoside hetero-dimer.87 This approach is particularly appealing due to its simplicity and affordable computational cost and it is suitable for obtaining spectral fingerprints of photo-intermediates, in systems where the underlying conformational dynamics is slow, i.e. the system is trapped in a local minimum on a picosecond time scale. In order to resolve spectral features in the sub-ps range subject to ultra-fast population transfer and vibrational dynamics, the SOS protocol can be augmented by incorporating a linear coupling to a bath within the formalism of lineshape functions, i.e. assuming a classical bath following Gaussian statistics and using the cumulant expansion of Gaussian fluctuations (CGF) method.74 The required parameters can be obtained through projection techniques integrated in the COBRAMM package and relying on quantum-mechanical gradients or normal mode analysis. Recently, we applied the CGF//QM/MM approach to compute TA and 2DUV spectra of azobenzene, pyrene and 4-thiouracil,17,18,89 thereby resolving characteristic intensity beats of the PA signals, which allowed us to decipher the underlying decay mechanism.
The COBRAMM/SPECTRON interface allows taking into account realistic pulse envelopes, whereas the tuning of pulse parameters such as the central frequency, bandwidth and polarization provides access to more elaborate cross-polarized79 and chiral techniques.74 Beyond the approximation of Gaussian statistics, the COBRAMM/SPECTRON interface allows the stochastic modelling of bath fluctuations in a mixed quantum-classical fashion by means of trajectory-based algorithms. Therefore, the evolution of the electronic wavefunction is treated quantum-mechanically by solving the time-dependent Schrödinger equation, while the nuclei follow Newton's equations of motion. Non-adiabatic effects are considered via Tully's fewest switches surface-hopping algorithm.104 The spectroscopy simulations, modeled with TA approximation (i.e. assuming a narrowband, tuneable pump pulse), require computing the electronic structure of the system along each trajectory. The 2DES map at each waiting time is then obtained by stacking TA spectra for the different trajectories. The stochastic approach can be extended to the coherent regime in order to obtain maps with femtosecond temporal resolution, as proposed by Richter and coworkers.105 While this is a rather resource- and time-consuming approach, the stochastic modelling is an intrinsically parallel problem (each trajectory can be treated independently) which makes it affordable in nowadays available multi-core high performance computing architectures.
5. Applications of 2DUV spectroscopy
In this section we present a few examples of experimental and computational results obtained with 2DUV spectroscopy, which demonstrate the capabilities and the current potential of the methodology and motivate its further development.5.1 Pyrene: a testbed for benchmarking 2DUV experiments with theory
Pyrene (see the inset of Fig. 6(a) for the molecular structure) is a polycyclic aromatic hydrocarbon with intriguing features which make it an excellent candidate for assessing novel spectroscopic techniques:21,71,89,106,111 (i) well-resolved vibronic progressions in the UV region (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–33
000–33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and 36
000 cm−1 and 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–40
000–40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) associated with two bright states (labelled S2 and S4, see the inset in Fig. 6(b)); (ii) ultrafast (i.e., in the sub-100 fs regime) photophysics involving non-adiabatic population decay mediated through CIs (mechanisms shown in the inset of Fig. 6(b)); (iii) few symmetry-allowed bright transitions associated with each one of the electronic states involved in the non-adiabatic decay giving rise to fingerprint PA signals.
000 cm−1) associated with two bright states (labelled S2 and S4, see the inset in Fig. 6(b)); (ii) ultrafast (i.e., in the sub-100 fs regime) photophysics involving non-adiabatic population decay mediated through CIs (mechanisms shown in the inset of Fig. 6(b)); (iii) few symmetry-allowed bright transitions associated with each one of the electronic states involved in the non-adiabatic decay giving rise to fingerprint PA signals.
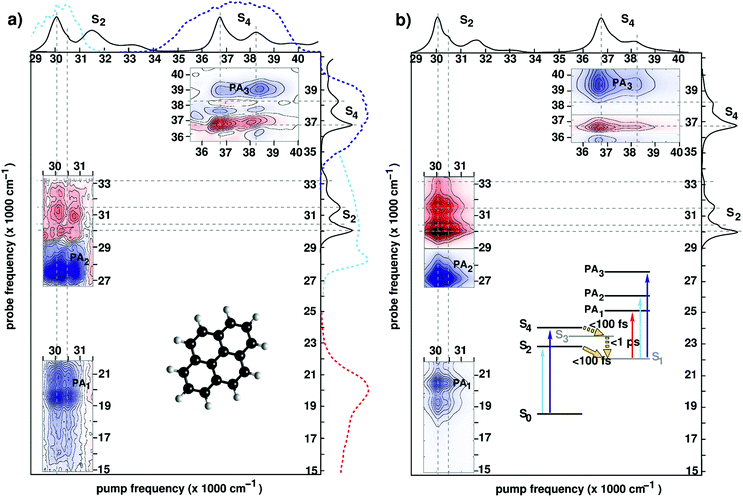 | ||
| Fig. 6 (a) Experimental 2DUV maps for pyrene in methanol pumped in the NUV71 and in the DUV89 range for a waiting time t2 = 1 ps. Solid lines on the sides of the plot represent the absorption spectrum of pyrene, while dashed lines represent the excitation and detection spectra used in the different experiments. Inset shows the molecular structure. (b) Computed 2DUV maps for pyrene in methanol for a waiting time t2 = 1 ps. Inset shows the energy level scheme of pyrene. Reproduced from ref. 71 with permission from the Optical Society, copyright 2016 and from ref. 89 with permission from the American Chemical Society, copyright 2019. | ||
Upon photoexcitation, the bright states S2 and S4 are depopulated on a sub-100 fs time scale, as inferred from the disappearance of their state-specific PA signals.21,71 Eventually, the population relaxes to the lowest (dark) electronic state (labelled S1) where it remains trapped on a ns-timescale exhibiting long-lived fluorescence. The S1 state is characterized by PA signals in the visible (PA1 band peaking at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) and the UV region (PA2 band peaking at 27
500 cm−1) and the UV region (PA2 band peaking at 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 and PA3 band peaking at 39
500 cm−1 and PA3 band peaking at 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). Fig. 6 compares experimental (panel (a)) and simulated (panel (b)) 2DUV maps for a waiting time t2 = 1 ps, at which the population has relaxed to the dark S1 state.
000 cm−1). Fig. 6 compares experimental (panel (a)) and simulated (panel (b)) 2DUV maps for a waiting time t2 = 1 ps, at which the population has relaxed to the dark S1 state.
Let us first discuss the experimental results with excitation of the S2 transition, performed in the partially collinear pump–probe geometry with a 16 fs, 2000 cm−1 bandwidth pump pulse centred at 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 combined with a broadband WLC probe covering the visible and UV ranges.71 The pump pulse excites the 400 cm−1 progression in the S2 absorption spectrum associated with a totally symmetric breathing mode of the carbon scaffold. Correspondingly, positive (red, GSB) and negative (blue, PA) contributions are recorded along two stripes at pump frequencies 30
000 cm−1 combined with a broadband WLC probe covering the visible and UV ranges.71 The pump pulse excites the 400 cm−1 progression in the S2 absorption spectrum associated with a totally symmetric breathing mode of the carbon scaffold. Correspondingly, positive (red, GSB) and negative (blue, PA) contributions are recorded along two stripes at pump frequencies 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and 30
000 cm−1 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 associated with the fundamental and the first overtone of the 400 cm−1 vibronic progression (Fig. 6(a)). Notably, a checkerboard pattern in the GSB signal (29
400 cm−1 associated with the fundamental and the first overtone of the 400 cm−1 vibronic progression (Fig. 6(a)). Notably, a checkerboard pattern in the GSB signal (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–33
000–33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) arises as the probe pulse excites the entire S2 band, the fundamental peak at 30
000 cm−1) arises as the probe pulse excites the entire S2 band, the fundamental peak at 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 being largely suppressed due to interference with the intense PA2 band. 2DUV maps in the upper right corner of Fig. 6(a) are recorded using an all-reflective 3PPE setup featuring broadband (FWHM ≈ 6000 cm−1) pump and probe pulses centred at 37
000 cm−1 being largely suppressed due to interference with the intense PA2 band. 2DUV maps in the upper right corner of Fig. 6(a) are recorded using an all-reflective 3PPE setup featuring broadband (FWHM ≈ 6000 cm−1) pump and probe pulses centred at 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and exhibiting a 6 fs temporal resolution.89 In this case the excitation is resonant with the fundamental (36
000 cm−1 and exhibiting a 6 fs temporal resolution.89 In this case the excitation is resonant with the fundamental (36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1) and first overtone (38
700 cm−1) and first overtone (38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1) of the S4 absorption band dominated by a totally symmetric carbon–carbon stretch mode. Positive (GSB) and negative (PA) contributions are observed. Also in this case, the checkerboard GSB pattern (36
200 cm−1) of the S4 absorption band dominated by a totally symmetric carbon–carbon stretch mode. Positive (GSB) and negative (PA) contributions are observed. Also in this case, the checkerboard GSB pattern (36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–40
000–40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) is largely suppressed due to overlap with the intense PA band (labelled PA3) leaving only the signals due to the fundamental frequency at 36
000 cm−1) is largely suppressed due to overlap with the intense PA band (labelled PA3) leaving only the signals due to the fundamental frequency at 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1.
700 cm−1.
Previous studies have demonstrated that the RASSCF//RASPT2 protocol reproduces with a remarkable accuracy the state-specific PA features of all electronic states involved in the photoinduced dynamics in pyrene.89,106,111 Moreover, line shape modelling from first principles showed that the spectral dynamics of the PA are dominated by the coupling of the electronic degrees of freedom to carbon–carbon stretching modes giving rise to coherent quantum beats which are clearly visible in the spectra recorded with 6 fs resolution.89Fig. 6(b) shows the theoretical counterparts of the aforementioned experimental spectra at a waiting time of 1 ps. Theory manages to describe quite accurately the experimental results; in particular, the positions and the shapes of the peaks in the visible (PA1) and the UV (PA2 and PA3) region are reproduced by the simulations. The GSB/PA overlap makes the analysis of one-color (i.e. pump and probe having the same frequency) experiments cumbersome. WLC facilitates probing in a GSB-free spectral region which is preferable from a practical standpoint. In this context electronic structure theory is particularly valuable as it can help design experiments aimed at selective detection of spectroscopic fingerprints in 2DUV spectra.
5.2 Observation of ultrafast electron transfer from tryptophan to heme in myoglobins by 2DUV
One of the first studies demonstrating the spectroscopic power of 2DUV was performed by Consani and coworkers73 on ferric myoglobin proteins (MbCN and metMb) using their ultra-broadband system72 covering the 270–320 nm excitation wavelength range. Fig. 7(d) shows the details of the molecular structure of horse myoglobin, highlighting the heme moiety as well as two tryptophan (Trp) residues, Trp7 and Trp14, located in the α helix A. Previous studies have shown that the fluorescence of Trp7 (Trp14) is quenched on a timescale of 110–140 (20–30) ps, and attributed this process to fluorescence resonance energy transfer (FRET) to the heme.107,108 2DUV over the 325–280 nm excitation range reveals a different scenario. In this range the heme absorbs at all wavelengths, while the Trps absorb only at wavelengths shorter than 305 nm.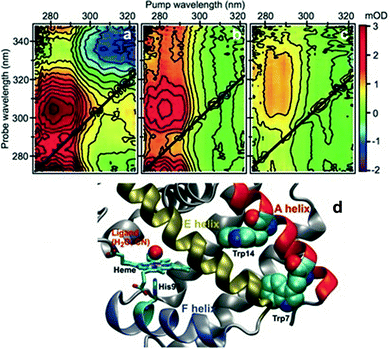 | ||
| Fig. 7 (a–c) 2DUV spectra of MbCN at t2 = 2.5 ps (a), 17 ps (b) and 200 ps (c); (d) molecular structure of horse MbCN, highlighting the heme and the two Trp residues. Reproduced from ref. 73 with permission from the American Association for the Advancement of Science, copyright 2013. | ||
Fig. 7(a)–(c) show a set of 2DUV maps of MbCN for different waiting times t2, ranging from 2.5 to 200 ps. At pump wavelengths longer than 305 nm, only the heme is excited, which features in the UV range a GSB signal recovering within 10 ps, in agreement with the previously measured heme photocycle in MbCN.109 At shorter pump wavelengths, both heme and Trps are excited and PA peaks appear, which display a complex evolution. In particular, one can observe a PA peak centered at the 315 nm probe wavelength, which is assigned to Trp due to its long lifetime. Global analysis of the 2DUV maps reveals several time constants; the shorter ones (<300 fs, 1.1 ps and 4.4 ps) are in good agreement with the previously measured heme recovery dynamics, while the longer ones (19 ps and 140 ps) match the known fluorescence lifetimes for Trp14 and Trp7, respectively. However, a long-lived (>2.5 ns) component arises, which is not compatible with a scenario in which both Trps undergo FRET to the heme, since in this case they would not display a long-living signal. Analysis of the decay associated spectra shows that the 19 ps one has a component that matches the mirror image of the long-lived decay associated spectrum, indicating that the long-lived species is generated by decay of Trp14. Taken together, these data allow assigning the 19 ps time constant to electron transfer from Trp14 to the heme, resulting in the formation of ferrous MbCN, and provide one of the first examples of long-range electron transfer in proteins.
5.3 2DUV tracking of the structure and dynamics of polypeptides
As discussed in Section 2.2, a number of studies have proposed the use of the aromatic side-chains in amino acids (tryptophan, tyrosine, and phenylalanine) as endogenous highly specific markers to determine the secondary structure of proteins and follow in real time their structural rearrangements through 2DUV spectroscopy. Here we summarize the results of computational studies demonstrating this capability on a simple model system, a tetrapeptide with two aromatic side chains. Fig. 8(a and b) report the schematic representations of two different configurations of a small prototype tetrapeptide cysteine–phenylalanine–tyrosine–cysteine (CFYC): an unfolded (open) configuration with unstacked aromatic side chains and a folded configuration closed through a disulphide bridge.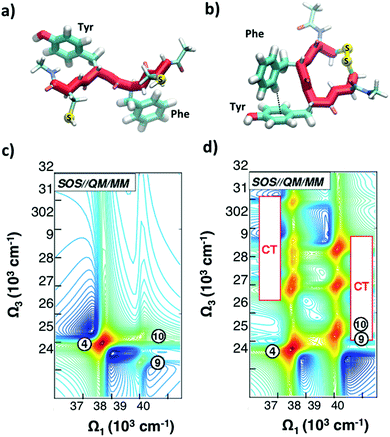 | ||
| Fig. 8 (a and b) Selected conformations of the unstacked (a) and T-stacked (b) CFYC tetrapeptide. (c and d) Simulated 2DUV spectra obtained with the SOS//QM/MM protocol with a two-color setup and parallel polarizations for: (c) open CFYC; (d) closed CFYC. Reproduced from ref. 110 with permission from the American Chemical Society, copyright 2014. | ||
Fig. 8(c and d) report 2DUV maps obtained by Nenov and coworkers,110 using the SOS//QM/MM approach, for the open and closed CFYC polypeptides at t2 = 0. The excitation bandwidth is tuned in resonance with the ππ* transitions (11A1g → 11B2u) of tyrosine and phenylalanine (at 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 and 39
500 cm−1 and 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 respectively), while the detection bandwidth is red-shifted to cover the 24
000 cm−1 respectively), while the detection bandwidth is red-shifted to cover the 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–32
000–32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range (two-colour 2DUV), to emphasize the differences between the two configurations. In the unstacked tetrapeptide one observes only the PA signals originating from the 11B2u → 11E2g transition (peak 4 for Tyr and peaks 9 and 10 for Phe; Fig. 8(c)). In the folded configuration, on the other hand, the spatial proximity of the aromatic side chains results in their interaction which gives rise to new signals in the 2DUV maps. In particular, a number of charge transfer (CT) states exhibit a red shift by around 15
000 cm−1 range (two-colour 2DUV), to emphasize the differences between the two configurations. In the unstacked tetrapeptide one observes only the PA signals originating from the 11B2u → 11E2g transition (peak 4 for Tyr and peaks 9 and 10 for Phe; Fig. 8(c)). In the folded configuration, on the other hand, the spatial proximity of the aromatic side chains results in their interaction which gives rise to new signals in the 2DUV maps. In particular, a number of charge transfer (CT) states exhibit a red shift by around 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 upon stacking (peaks labelled “CT” in Fig. 8(d)). The oscillator strength of these states increases by several orders of magnitude with respect to the unstacked configuration.
000 cm−1 upon stacking (peaks labelled “CT” in Fig. 8(d)). The oscillator strength of these states increases by several orders of magnitude with respect to the unstacked configuration.
The dramatic difference in the 2DUV maps between the unfolded and folded configurations should allow easy differentiation between them and even tracking the unfolding dynamics. In a subsequent computational study, Nenov and coworkers showed that 2DUV spectroscopy can follow in real time the unstacking dynamics of the cyclic CYFC tetrapeptide, triggered by the ultrafast photocleavage of the disulphide bond which keeps the peptide folded.80 The unfolding process occurs in three steps, proceeding from a T-shaped to a twisted offset stacked to an unstacked configuration. 2DUV spectroscopy offers the highest sensitivity to the unfolding process, by allowing us to distinguish between the PA signals belonging to different aromatic chromophores and to correlate them with the conformational dynamics. 2DUV spectroscopy displays structural sensitivity also in the amide absorption bands of the protein backbone, at wavelengths shorter than 250 nm, as shown in globular and fibrillar proteins,47,112 amyloid fibrils44 and Trp-cage.113 2DUV maps carry rich information of both local (secondary) and global (tertiary) structures; however, simulations indicate that only chiral configurations provide the necessary sensitivity, thus significantly reducing the available signal. In summary, 2DUV has the potential to become a powerful method to detect the folding state and the folding/unfolding dynamics in unlabelled peptides, complementary to the established NMR and 2DIR techniques as well as to the recently developed ultrafast UV circular dichroism,114 which has also shown the ability to monitor conformational changes in a peptide in real time.115
6. Conclusions and outlook
2D spectroscopy techniques, based on the application of a sequence of time delayed pulses followed by Fourier transform with respect to the delays, allow correlation of excitation and detection frequencies for a molecular system and tracking the evolution of these correlations in time. Well established in NMR, they have been successfully translated to optical frequencies over the last two decades. Nowadays they are widely used in the infrared and visible spectral ranges, to the point that they have become standard tools to solve problems in biochemistry and materials science. There is a very strong scientific motivation to extend these techniques to the UV range, where several spectroscopic targets of great interest, such as DNA and proteins, are available. However, this has been slowed down by several technical challenges, such as the difficulty in generating broadband UV pulses, the challenge of maintaining phase locking at very short wavelengths and the strong nonlinear response of the solvent in the UV range, which overlaps with the spectroscopic signal of interest.A variety of experimental techniques for 2DUV spectroscopy have been proposed, each with its advantages and drawbacks. There is not yet a method of choice which should depend on the characteristics of the specific system to be studied. On the theoretical side powerful simulation tools, which combine perturbation theory with accurate ab initio calculations of energy levels and transition dipole moments, have reached a very high level of sophistication and are able not only to accurately reproduce experiments on benchmark molecular systems, but also to predict spectroscopic signals and to guide the design of new experiments.
While the first results of 2DUV spectroscopy, both experimental and computational, are promising, it is clear that much work still remains to be done in order to make it a mainstream technique. It is likely that in the coming decade further advances, both in the spectroscopic methods and in the computational capabilities, will broaden its applicability to a wide range of problems in physical chemistry and life sciences. In particular, it will be very important to reach the experimentally very challenging but spectroscopically rich region below 250 nm, corresponding to the amide ππ* and nπ* excitations of proteins and where different secondary structures display clear signals. Beyond UV, 2D X-ray techniques116,117 are now made possible by the development of X-ray free electron lasers (XFELs), which allow accessing core excitations. The recent demonstration of nonlinear optical techniques, such as four-wave-mixing, at both extreme UV118,119 and hard X-ray120 frequencies, is a critical step towards the extension of 2D techniques to this important spectral window.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. Borrego Varillas and A. Nenov contributed equally to this work. G. C. and M. G. acknowledge support by the European Research Council Advanced Grant STRATUS (ERC-2011-AdG No. 291198), the Marie Curie actions (FP7-PEOPLE-IEF-2012), and the H2020 Grant Agreement number 765266 (LightDyNAmics). S. M. gratefully acknowledges the support of NSF (grant CHE-1663822). S. M. and M. G. were supported by the Chemical Sciences, Geosciences, and Biosciences division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy through awards No. DESC0019484.References
- R. R. Ernst, G. Bodenhausen and A. Wokaunh, Principles of Nuclear Magnetic Resonances in One and Two Dimensions, Clarendon, Oxford, 1987 Search PubMed.
- S. Mukamel, Annu. Rev. Phys. Chem., 2000, 51, 691–729 CrossRef CAS PubMed.
- J. D. Hybl, A. A. Ferro and D. M. Jonas, J. Chem. Phys., 2001, 115, 6606–6622 CrossRef CAS.
- D. M. Jonas, Annu. Rev. Phys. Chem., 2003, 54, 425–463 CrossRef CAS PubMed.
- R. M. Hochstrasser, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 14190–14196 CrossRef CAS PubMed.
- M. Cho, Chem. Rev., 2008, 108, 1331–1418 CrossRef CAS PubMed.
- P. Hamm, M. Lim and R. M. Hochstrasser, J. Phys. Chem. B, 1998, 102, 6123–6138 CrossRef CAS.
- C. Kolano, J. Helbing, M. Kozinski, W. Sander and P. Hamm, Nature, 2006, 444, 469–472 CrossRef CAS PubMed.
- A. Ghosh, J. S. Ostrander and M. T. Zanni, Chem. Rev., 2017, 117, 10726–10759 CrossRef CAS PubMed.
- M. L. Cowan, J. P. Ogilvie and R. J. D. Miller, Chem. Phys. Lett., 2004, 386, 184–189 CrossRef CAS.
- T. Brixner, I. V. Stiopkin and G. R. Fleming, Opt. Lett., 2004, 29, 884–886 CrossRef CAS PubMed.
- T. Brixner, J. Stenger, H. M. Vaswani, M. Cho, R. E. Blankenship and G. R. Fleming, Nature, 2005, 434, 625–628 CrossRef CAS PubMed.
- F. Milota, J. Sperling, A. Nemeth, T. Mančal and H. F. Kauffmann, Acc. Chem. Res., 2009, 42, 1364–1374 CrossRef CAS PubMed.
- E. Thyrhaug, R. Tempelaar, M. J. P. Alcocer, K. Žídek, D. Bína, J. Knoester, T. L. C. Jansen and D. Zigmantas, Nat. Chem., 2018, 10, 780–786 CrossRef CAS PubMed.
- K. W. Stone, K. Gundogdu, D. B. Turner, X. Li, S. T. Cundiff and K. A. Nelson, Science, 2009, 324, 1169–1173 CrossRef CAS PubMed.
- D. B. Turner and K. A. Nelson, Nature, 2010, 466, 1089–1092 CrossRef CAS PubMed.
- A. Nenov, R. Borrego-Varillas, A. Oriana, L. Ganzer, F. Segatta, I. Conti, J. Segarra-Marti, J. Omachi, M. Dapor, S. Taioli, C. Manzoni, S. Mukamel, G. Cerullo and M. Garavelli, J. Phys. Chem. Lett., 2018, 9, 1534–1541 CrossRef CAS PubMed.
- R. Borrego-Varillas, D. C. Teles-Ferreira, A. Nenov, I. Conti, L. Ganzer, C. Manzoni, M. Garavelli, A. M. de Paula and G. Cerullo, J. Am. Chem. Soc., 2018, 140, 16087–16093 CrossRef CAS PubMed.
- M. Chergui, J. Chem. Phys., 2019, 150, 070901 CrossRef PubMed.
- A. Cannizzo, Phys. Chem. Chem. Phys., 2012, 14, 11205–11223 RSC.
- R. Borrego-Varillas, L. Ganzer, G. Cerullo and C. Manzoni, Appl. Sci., 2018, 8, 989 CrossRef.
- B. A. West and A. M. Moran, J. Phys. Chem. Lett., 2012, 3, 2575–2581 CrossRef CAS PubMed.
- V. I. Prokhorenko, A. Picchiotti, M. Pola, A. G. Dijkstra and R. J. Dwayne Miller, J. Phys. Chem. Lett., 2016, 7, 4445–4450 CrossRef CAS PubMed.
- J.-M. L. Pecourt, J. Peon and B. Kohler, J. Am. Chem. Soc., 2001, 123, 10370–10378 CrossRef CAS PubMed.
- W. J. Schreier, P. Gilch and W. Zinth, Annu. Rev. Phys. Chem., 2015, 66, 497–519 CrossRef CAS PubMed.
- D. Markovitsi, Photochem. Photobiol., 2016, 92, 45–51 CrossRef CAS PubMed.
- C. E. Crespo-Hernandez, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2019 CrossRef CAS PubMed.
- C. T. Middleton, K. de La Harpe, C. Su, Y. K. Law, C. E. Crespo-Hernandez and B. Kohler, Annu. Rev. Phys. Chem., 2009, 60, 217–239 CrossRef CAS PubMed.
- B. Kohler, J. Phys. Chem. Lett., 2010, 1, 2047–2053 CrossRef CAS.
- J. M. L. Pecourt, J. Peon and B. Kohler, J. Am. Chem. Soc., 2000, 122, 9348–9349 CrossRef CAS.
- D. Onidas, D. Markovitsi, S. Marguet, A. Sharonov and T. Gustavsson, J. Phys. Chem. B, 2002, 106, 11367–11374 CrossRef CAS.
- P. M. Hare, C. E. Crespo-Hernandez and B. Kohler, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 435–440 CrossRef CAS PubMed.
- R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540–3593 CrossRef CAS PubMed.
- C. E. Crespo-Hernández, B. Cohen and B. Kohler, Nature, 2005, 436, 1141–1144 CrossRef PubMed.
- D. Markovitsi, D. Onidas, T. Gustavsson, F. Talbot and E. Lazzarotto, J. Am. Chem. Soc., 2005, 127, 17130–17131 CrossRef CAS PubMed.
- I. Buchvarov, Q. Wang, M. Raytchev, A. Trifonov and T. Fiebig, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 4794–4797 CrossRef CAS PubMed.
- T. Takaya, C. Su, K. de La Harpe, C. E. Crespo-Hernández and B. Kohler, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 10285–10290 CrossRef CAS PubMed.
- R. Borrego-Varillas, G. Cerullo and D. Markovitsi, J. Phys. Chem. Lett., 2019, 10, 1639–1643 CrossRef CAS PubMed.
- A. L. Sobolewski, W. Domcke and C. Hattig, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17903–17906 CrossRef CAS PubMed.
- C. M. Dobson, Nature, 2003, 426, 884–890 CrossRef CAS PubMed.
- F. Chiti and C. M. Dobson, Annu. Rev. Biochem., 2006, 75, 333–366 CrossRef CAS PubMed.
- Y. S. Kim, L. Liu, P. H. Axelsen and R. M. Hochstrasser, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 7720–7725 CrossRef CAS.
- D. B. Strasfeld, Y. L. Ling, S. H. Shim and M. T. Zanni, J. Am. Chem. Soc., 2008, 130, 6698–6699 CrossRef CAS.
- J. Jiang, D. Abramavicius, C. Falvo, B. M. Bulheller, J. D. Hirst and S. Mukamel, J. Phys. Chem. B, 2010, 114, 12150–12156 CrossRef CAS PubMed.
- J. Jiang and S. Mukamel, J. Phys. Chem. B, 2011, 115, 6321–6328 CrossRef CAS PubMed.
- J. Jiang and S. Mukamel, Phys. Chem. Chem. Phys., 2011, 13, 2394–2400 RSC.
- J. Jiang and S. Mukamel, Angew. Chem., 2010, 49, 9666–9669 CrossRef CAS PubMed.
- S. Mukamel, Principles of Nonlinear Optical Spectroscopy, Oxford University Press, Oxford, 1995 Search PubMed.
- L. Lepetit, G. Chériaux and M. Joffre, J. Opt. Soc. Am. B, 1995, 12, 2467–2474 CrossRef CAS.
- L. P. DeFlores, R. A. Nicodemus and A. Tokmakoff, Opt. Lett., 2007, 32, 2966–2968 CrossRef CAS PubMed.
- S.-H. Shim, D. B. Strasfeld, Y. L. Ling and M. T. Zanni, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 14197–14202 CrossRef CAS PubMed.
- E. M. Grumstrup, S.-H. Shim, M. A. Montgomery, N. H. Damrauer and M. T. Zanni, Opt. Express, 2007, 15, 16681–16689 CrossRef PubMed.
- A. Nemeth, J. Sperling, J. Hauer, H. F. Kauffmann and F. Milota, Opt. Lett., 2009, 34, 3301–3303 CrossRef CAS PubMed.
- T. Zhang, C. N. Borca, X. Li and S. T. Cundiff, Opt. Express, 2005, 13, 7432–7441 CrossRef CAS PubMed.
- U. Selig, F. Langhojer, F. Dimler, T. Löhrig, C. Schwarz, B. Gieseking and T. Brixner, Opt. Lett., 2008, 33, 2851–2853 CrossRef.
- J. Helbing and P. Hamm, J. Opt. Soc. Am. B, 2011, 28, 171–178 CrossRef CAS.
- S.-H. Shim and M. T. Zanni, Phys. Chem. Chem. Phys., 2009, 11, 748–761 RSC.
- J. A. Myers, K. L. Lewis, P. F. Tekavec and J. P. Ogilvie, Opt. Express, 2008, 16, 17420–17428 CrossRef CAS PubMed.
- D. Brida, C. Manzoni and G. Cerullo, Opt. Lett., 2012, 37, 3027–3029 CrossRef PubMed.
- J. Réhault, M. Maiuri, A. Oriana and G. Cerullo, Rev. Sci. Instrum., 2014, 85, 123107 CrossRef.
- A. Ajdarzadeh Oskouei, O. Bräm, A. Cannizzo, F. van Mourik, A. Tortschanoff and M. Chergui, Chem. Phys., 2008, 350, 104–110 CrossRef.
- A. Ajdarzadeh Oskouei, A. Tortschanoff, O. Bräm, F. van Mourik, A. Cannizzo and M. Chergui, J. Chem. Phys., 2010, 133, 064506 CrossRef PubMed.
- A. Ajdarzadeh, C. Consani, O. Bräm, A. Tortschanoff, A. Cannizzo and M. Chergui, Chem. Phys., 2013, 422, 47–52 CrossRef CAS.
- B. A. West, J. M. Womick and A. M. Moran, J. Phys. Chem. A, 2011, 115, 8630–8637 CrossRef CAS PubMed.
- B. A. West, J. M. Womick and A. M. Moran, J. Chem. Phys., 2011, 135, 114505 CrossRef PubMed.
- U. Selig, C.-F. Schleussner, M. Foerster, F. Langhojer, P. Nuernberger and T. Brixner, Opt. Lett., 2010, 35, 4178–4180 CrossRef PubMed.
- V. I. Prokhorenko, A. Picchiotti, S. Maneshi and R. J. D. Miller, Ultrafast Phenomena XIX, Springer International Publishing, 2015, pp. 432–435 Search PubMed.
- C. Tseng, S. Matsika and T. C. Weinacht, Opt. Express, 2009, 17, 18788–18793 CrossRef CAS.
- C. Tseng, P. Sándor, M. Kotur, T. C. Weinacht and S. Matsika, J. Phys. Chem. A, 2012, 116, 2654–2661 CrossRef CAS PubMed.
- N. Krebs, I. Pugliesi, J. Hauer and E. Riedle, New J. Phys., 2013, 15, 085016 CrossRef.
- R. Borrego-Varillas, A. Oriana, L. Ganzer, A. Trifonov, I. Buchvarov, C. Manzoni and G. Cerullo, Opt. Express, 2016, 24, 28491–28499 CrossRef CAS PubMed.
- G. Auböck, C. Consani, F. van Mourik and M. Chergui, Opt. Lett., 2012, 37, 2337–2339 CrossRef PubMed.
- C. Consani, G. Auböck, F. van Mourik and M. Chergui, Science, 2013, 339, 1586–1589 CrossRef CAS PubMed.
- D. Abramavicius, B. Palmieri, D. V. Voronine, F. Sanda and S. Mukamel, Chem. Rev., 2009, 109, 2350–2408 CrossRef CAS PubMed.
- F. Šanda, V. Perlík, C. N. Lincoln and J. Hauer, J. Phys. Chem. A, 2015, 119, 10893–10909 CrossRef PubMed.
- M. K. Lee, P. Huo and D. F. Coker, Annu. Rev. Phys. Chem., 2016, 67, 639–668 CrossRef CAS PubMed.
- J. Segarra-Martí, F. Segatta, T. A. Mackenzie, A. Nenov, I. Rivalta, M. Bearpark and M. Garavelli, Faraday Discuss., 2019 10.1039/c9fd00072k.
- I. Rivalta, A. Nenov, G. Cerullo, S. Mukamel and M. Garavelli, Int. J. Quantum Chem., 2014, 114, 85–93 CrossRef CAS.
- A. Nenov, I. Rivalta, S. Mukamel and M. Garavelli, Comput. Theor. Chem., 2014, 1040, 295–303 CrossRef.
- A. Nenov, S. A. Beccara, I. Rivalta, G. Cerullo, S. Mukamel and M. Garavelli, ChemPhysChem, 2014, 15, 3282–3290 CrossRef CAS PubMed.
- A. Nenov, J. Segarra-Marti, A. Giussani, A. Conti, I. Rivalta, E. Dumont, V. K. Jaiswal, S. F. Altavilla, S. Mukamel and M. Garavelli, Faraday Discuss., 2015, 177, 345–362 RSC.
- I. Rivalta, A. Nenov, O. Weingart, G. Cerullo, M. Garavelli and S. Mukamel, J. Phys. Chem. B, 2014, 118, 8396–8405 CrossRef CAS PubMed.
- A. Nenov, A. Giussani, J. Segarra-Martí, V. K. Jaiswal, I. Rivalta, G. Cerullo, S. Mukamel and M. Garavelli, J. Chem. Phys., 2015, 142, 212443 CrossRef.
- J. Segarra-Marti, A. J. Pepino, A. Nenov, S. Mukamel, M. Garavelli and I. Rivalta, Theor. Chem. Acc., 2018, 137, 47 Search PubMed.
- A. Nenov, S. Mukamel, M. Garavelli and I. Rivalta, J. Chem. Theory Comput., 2015, 11, 3755–3771 CrossRef CAS PubMed.
- A. Giussani, J. Segarra-Martí, A. Nenov, I. Rivalta, A. Tolomelli, S. Mukamel and M. Garavelli, Theor. Chem. Acc., 2016, 135, 1–18 Search PubMed.
- Q. Li, A. Giussani, J. Segarra-Martí, A. Nenov, I. Rivalta, A. A. Voityuk, S. Mukamel, D. Roca-Sanjuán, M. Garavelli and L. Blancafort, Chem.–Eur. J., 2016, 22, 7497–7507 CrossRef CAS PubMed.
- J. Segarra-Marti, V. K. Jaiswal, A. J. Pepino, A. Giussani, A. Nenov, S. Mukamel, M. Garavelli and I. Rivalta, Faraday Discuss., 2018, 207, 233–250 RSC.
- A. Picchiotti, A. Nenov, A. Giussani, V. I. Prokhorenko, R. J. Dwayne Miller, S. Mukamel and M. Garavelli, J. Phys. Chem. Lett., 2019, 10, 3481–3487 CrossRef CAS PubMed.
- M. H. Farag, T. L. C. Jansen and J. Knoester, Phys. Chem. Chem. Phys., 2018, 20, 12746–12754 RSC.
- I. Breen, R. Tempelaar, L. A. Bizimana, B. Kloss, D. R. Reichman and D. B. Turner, J. Am. Chem. Soc., 2017, 139, 11745–11751 CrossRef CAS PubMed.
- B. O. Roos, The complete active space self-consistent field method and its applications in electronic structure calculations, in Advances in chemical physics, John Wiley & Sons, Inc., 1987, pp. 399–445 Search PubMed.
- K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- D. Roca-Sanjuán, F. Aquilante and R. Lindh, Multiconfiguration second-order perturbation theory approach to strong electron correlation in chemistry and photochemistry, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(4), 585–603 Search PubMed.
- P. A. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477–5482 CrossRef CAS.
- K. D. Vogiatzis, G. Li Manni, S. J. Stoneburner, D. Ma and L. Gagliardi, J. Chem. Theory Comput., 2015, 11, 3010–3021 CrossRef CAS PubMed.
- F. Aquilante, R. Lindh and T. B. Pedersen, J. Chem. Phys., 2007, 127, 114107 CrossRef PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. Bondo Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- J. Segarra-Marti, E. Zvereva, M. Marazzi, J. Brazard, E. Dumont, X. Assfeld, S. Haacke, M. Garavelli, A. Monari, J. Leonard and I. Rivalta, J. Chem. Theory Comput., 2018, 14, 2570–2585 CrossRef CAS PubMed.
- O. Weingart, A. Nenov, P. Altoè, I. Rivalta, J. Segarra-Martí, I. Dokukina and M. Garavelli, J. Mol. Model., 2018, 24, 271 CrossRef PubMed.
- The COBRAMM set of routines can be obtained free of charge upon request to Prof. Marco Garavelli (E-mail: marco.garavelli@unibo.it).
- https://mukamel.ps.uci.edu/software.html .
- A. Giussani, J. Marcheselli, S. Mukamel, M. Garavelli and A. Nenov, Photochem. Photobiol., 2017, 93, 1368–1380 CrossRef CAS PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- M. Richter and B. P. Fingerhut, J. Chem. Theory Comput., 2016, 127, 3284–3294 CrossRef PubMed.
- A. Nenov, A. Giussani, B. P. Fingerhut, I. Rivalta, E. Dumont, S. Mukamel and M. Garavelli, Phys. Chem. Chem. Phys., 2015, 17, 30925–30936 RSC.
- R. M. Hochstrasser and D. K. Negus, Proc. Natl. Acad. Sci. U. S. A., 1984, 81, 4399–4403 CrossRef CAS PubMed.
- K. J. Willis, A. G. Szabo, M. Zuker, J. M. Ridgeway and B. Alpert, Biochemistry, 1990, 29, 5270–5275 CrossRef CAS PubMed.
- J. Helbing, L. Bonacina, R. Pietri, J. Bredenbeck, P. Hamm, F. van Mourik, F. Chaussard, A. Gonzalez-Gonzalez, M. Chergui, C. Ramos-Alvarez, C. Ruiz and J. Lopez-Garriga, Biophys. J., 2004, 87, 1881–1891 CrossRef CAS PubMed.
- A. Nenov, I. Rivalta, G. Cerullo, S. Mukamel and M. Garavelli, J. Phys. Chem. Lett., 2014, 5, 767–771 CrossRef CAS PubMed.
- J. Segarra-Martí, S. Mukamel, M. Garavelli, A. Nenov and I. Rivalta, in Multidimensional Time-Resolved Spectroscopy, Topics in Current Chemistry Collections, ed. T. Buckup and J. Léonard, Springer International Publishing, 2019 Search PubMed.
- D. Abramavicius, J. Jiang, B. M. Bulheller, J. D. Hirst and S. Mukamel, J. Am. Chem. Soc., 2010, 132, 7769–7775 CrossRef CAS PubMed.
- J. Jiang, Z. Lai, J. Wang and S. Mukamel, J. Phys. Chem. Lett., 2014, 5, 1341–1346 CrossRef CAS PubMed.
- M. Oppermann, B. Bauer, T. Rossi, F. Zinna, J. Helbing, J. Lacour and M. Chergui, Optica, 2019, 6, 56–60 CrossRef CAS.
- M. Oppermann, J. Spekowius, B. Bauer, R. Pfister, M. Chergui and J. Helbing, J. Phys. Chem. Lett., 2019, 10, 2700–2705 CrossRef CAS PubMed.
- I. V. Schweigert and S. Mukamel, Phys. Rev. Lett., 2007, 99, 163001 CrossRef PubMed.
- I. V. Schweigert and S. Mukamel, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 052509 CrossRef.
- F. Bencivenga, R. Cucini, F. Capotondi, A. Battistoni, R. Mincigrucci, E. Giangrisostomi, A. Gessini, M. Manfredda, I. P. Nikolov, E. Pedersoli, E. Principi, C. Svetina, P. Parisse, F. Casolari, M. B. Danailov, M. Kiskinova and C. Masciovecchio, Nature, 2015, 520, 205–208 CrossRef CAS PubMed.
- H. J. B. Marroux, A. P. Fidler, D. M. Neumark and S. R. Leone, Sci. Adv., 2018, 4, eaau3783 CrossRef PubMed.
- C. Svetina, R. Mankowsky, G. Knopp, F. Koch, G. Seniutinas, B. Rösner, A. Kubec, M. Lebugle, I. Mochi, M. Beck, C. Cirelli, J. Krempasky, C. Pradervand, J. Rouxel, G. F. Mancini, S. Zerdane, B. Pedrini, V. Esposito, G. Ingold, U. Wagner, U. Flechsig, R. Follath, M. Chergui, C. Milne, H. T. Lemke, C. David and P. Beaud, Opt. Lett., 2019, 44, 574–577 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |