Open Access Article
Open Access ArticleWhy are photosynthetic reaction centres dimeric?
Natasha
Taylor
 a and
Ivan
Kassal
a and
Ivan
Kassal
 *b
*b
aSchool of Chemistry and University of Sydney Nano Institute, University of Queensland, QLD 4072, Australia
bSchool of Chemistry, University of Sydney Nano Institute, University of Sydney, NSW 2006, Australia. E-mail: ivan.kassal@sydney.edu.au
First published on 26th August 2019
Abstract
All photosynthetic organisms convert solar energy into chemical energy through charge separation in dimeric reaction centres. It is unknown why early reaction centres dimerised and completely displaced their monomeric ancestors. Here, we discuss several proposed explanations for reaction-centre dimerism and conclude—with only weak assumptions about the primordial dimerisation event—that the most probable explanation for the dimerism is that it arose because it enhanced light-harvesting efficiency by deepening the excitonic trap, i.e., by enhancing the rate of exciton transfer from an antenna complex and decreasing the rate of back transfer. This effect would have outweighed the negative effect dimerisation would have had on charge transfer within the reaction centre. Our argument implies that dimerisation likely occurred after the evolution of the first antennas, and it explains why the lower-energy state of the special pair is bright.
Photosynthetic energy conversion takes place in reaction centres (RC), where energy from the absorbed light drives charge separation. In all photosynthetic architectures, light is absorbed by an antenna complex to form an exciton, which is transferred to the RC. All extant RCs are dimeric pigment-protein complexes, the arrangement of whose core pigment cofactors is strongly conserved.1,2 The most important feature of RC dimerism is that the monomers interact strongly at the special pair (P), a pair of tightly coupled (bacterio)chlorophylls, which is both the exciton acceptor and the primary charge donor1 (Fig. 1).
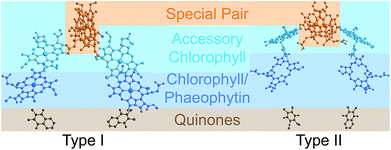 | ||
| Fig. 1 Photosynthetic reaction centres (RCs). All extant RCs are dimeric, comprising special pair chlorophylls, accessory chlorophylls, secondary chlorophylls or phaeophytins, and quinones. Bacteria use bacteriochlorophyll and bacteriophaeophytin instead. Shown are crystallographic structures,9,10 with chlorophyll tails and supporting protein removed for clarity. | ||
The ancestor of modern RCs is thought to be a monomeric pigment–protein complex containing the core RC cofactors,3 which we call the primordial RC. Prior to dimerisation, the primordial RC may have been photosynthetic, or it may have been appropriated from another membrane protein role, such as UV protection4 or energetic metabolism.5 Whatever its original purpose, the primordial RC dimerised, creating a homodimeric RC coded for by a single gene.3 The homodimer gradually diverged into the ancestors of the modern RCs, all of which retain its general structure.6–8
Our aim is to survey possible explanations for the dominance of RC dimerism and, especially, for the strong coupling between the two pigments in the special pair. As with any attempt to reconstruct reasons for long-ago evolutionary change, we cannot offer definite answers. Evolution rarely has an unambiguous explanation, with large differences in phenotype usually being end results of an undirected and disorderly process influenced by many kinds of selection pressures. More generally, evolutionary reasoning is often abductive, trying to find the best explanation (which may be a combination of multiple reasons) for a set of observations. Abductive conclusions are never logically certain and should be qualified as “most likely” or “best available”, and they may change in light of new evidence. So, to be more precise, our goal is to identify the likeliest explanation(s) of the RC dimerism and of the strong coupling in P, given the current evidence.
This goal is hampered by over three billion years of evolutionary distance from the primordial dimerisation event. Because there is little certainty about any detail of the primordial RC, our discussion and models are qualitative. We only seek general trends that hold across a broad range of possibilities about the primordial RC. Even so, we are able to conclude that the most likely explanation of dimerisation (or, at least, of the strong coupling in P) is that it improved exciton transfer from an antenna to the RC, possibly by a large margin, despite having a deleterious influence on charge transfer. On balance, the improvement to exciton transfer was likely more significant, leading to an overall increase in RC performance.
Possible explanations of reaction-centre dimerism
Evolutionary background
We reconstruct the primordial dimerisation event based on features of modern RCs. The generally accepted evolutionary relationships are shown in Fig. 2. A monomeric RC dimerised to a homodimer, which diverged into several variants, some of which underwent gene duplication, allowing them to replace the homodimer with a heterodimer.3,6,8,11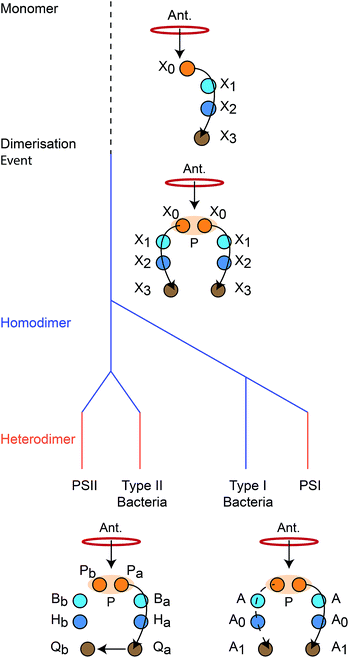 | ||
| Fig. 2 Evolution of reaction centres (RC).1 The primordial RC was monomeric, likely comprising three BChls (X0, X1, X2) and a quinone (X3). An antenna (Ant.) would transfer an exciton to X0, which would also serve as the charge donor. The charge would transfer through X1 and X2 before arriving at X3. The monomeric RC dimerised, producing a homodimer with two identical copies of the monomer, connected at the special pair (P). Excitons from the antenna could delocalise over P before charge separation, with charge transfer occurring along either branch. The homodimer subsequently diverged into type I and type II RCs, some of which experienced gene duplication events that led to heterodimerism. In modern type I RCs, each branch consists of three (B)Chls (P, A, and A0) and a quinone (A1). In heterodimeric PSI, charge transfer occurs exclusively down one branch, while in homodimeric systems (such as heliobacteria) charge can move down either branch with equal probability. In modern type II RCs, each branch consists of two (B)Chls (P and B), a phaeophytin (H) and a quinone (Q). Charge travels down one branch before being transferred to the inactive-branch quinone. | ||
As a result, there is considerable diversity among modern RCs. A basic distinction is based on the final electron acceptor: in type I RCs, it is a ferredoxin, whereas in type II RCs, it is a quinone. Many organisms have only a single type of RC, but cyanobacteria, green algae, and plants have both type I and type II, present in photosystem I (PSI) and photosystem II (PSII), respectively. Type I RCs can be either homodimeric (e.g., in heliobacteria) or heterodimeric (e.g., PSI), unlike type II RCs, all of which are heterodimeric.
Despite differences in the final electron acceptor, the structures mediating initial exciton- and charge-transfer steps are remarkably conserved across all extant RCs. All RCs are dimeric, with two branches that only interact at a strongly coupled special pair (P) of chlorophyll (Chl) or bacteriochlorophyll (BChl) molecules. P is the dominant acceptor of excitons from antenna complexes and the primary charge donor.12–14 From P, the charges are transferred down either branch in homodimeric RCs (such as heliobacteria11,15) or down only one branch in heterodimers. The pigments involved in the initial charge-transfer step always come from a small set of closely related tetrapyrroles (Chl, BChl, or (bacterio)phaeophytin, (B)Phe).
We emphasise that the purpose of discussing modern RCs is only to reconstruct features of the primordial one—we make no claims about the subsequent evolution and diversification, including the rise of heterodimers.
Candidate explanations
We group proposed explanations for RC dimerism into six categories.(1) Explanation 1 is that dimerisation was simply a random, fitness-neutral event that became fixed by genetic drift. We think this is unlikely, because fixation of a particular fitness-neutral mutation is very improbable in large populations,16 such as those of bacteria. In other words, if dimerisation were fitness neutral, it would be difficult to explain the complete extinction of all competing, monomer-carrying organisms.
In contrast to Explanation 1, the remaining explanations assume that the initial dimerisation event conferred a fitness advantage. They differ in the proposed mechanism for this advantage, the central question being what can a dimer do that a monomer cannot.
(2) Explanation 2 is that dimerisation served a structural purpose. For example, by altering the structure of the supporting protein, it could have aided in assembly or in finding a particularly favourable packing of transmembrane helices.2 This explanation, however, does not account for the strong coupling within P; similar large-scale structural changes could presumably have occurred even without the two P pigments coming into extremely close contact. It is possible that protein dimerisation occurred first and the strong coupling within P evolved later. If so, the problem is moved one step down the evolutionary timeline, and the interesting question becomes why the two weakly interacting branches of the dimer eventually evolved to have a strongly coupled P.
(3) Explanation 3, offered in the context of Type II RCs, is that the presence of two quinones allows them to have different potentials and to stabilise the electron by transfer from Qa to Qb (see Fig. 2).17 Transfer between quinones, however, is evolutionarily recent, requiring a heterodimeric RC. In the primordial dimer, the two quinones were symmetric (as in modern heliobacteria15), meaning that the quinones cannot explain the primordial dimerisation event.11
Unlike the explanations above, the remaining explanations all assume that the strong coupling within P served an evolutionary purpose.
(4) Explanation 4 is that the coupling within P shifted its absorption peak to the red (see below), allowing it to harvest longer wavelengths. An organism with this mutation could survive in an environment where all shorter wavelengths were harvested by monomeric organisms. This mechanism would be particularly relevant if the primordial organisms lacked antennas and relied on RCs for light absorption as well. This explanation, however, does not account for the extinction of monomeric RCs; the success of dimeric organisms in the long-wavelength niche is consistent with the continuation of monomers using shorter wavelengths. Similarly, modern organisms with apparent long-wavelength adaptations (such as chlorophyll f18) have not displaced dominant species. Explanation 4 could only account for universal dimerism if the initial spectral-niche dimerism enabled a subsequent evolutionary advantage that allowed the dimers to displace the monomers. Although this sequence of events cannot be ruled out, it requires the conjunction of three circumstances, each of which appears quite uncertain: (a) there were no antennas in the primordial RC, (b) the dimers arose to occupy the long-wavelength niche, and (c) there was some future advantage, which could not have evolved directly.
(5) Explanation 5 proposes that the coupling within P increased its redox potential Em, improving performance of donor-side electron transfer by making it easier for P+ to be re-reduced. In oxygenic organisms, an increased Em might facilitate water oxidation and reduce oxidative stress through the decreased lifetime of P+.17 The primordial RC, however, was not oxygenic, and, like modern anoxygenic RCs, did not need a particularly high redox potential. Most importantly, the coupling within P would have actually hindered the re-reduction of P+. The re-reduction occurs in the ground state, Pg, which is split by the coupling into two states, the higher-lying Pg+ and the lower-lying Pg−. In the P+ state that is to be re-reduced, the hole occupies the higher-energy state Pg+, i.e., the full state P+ has a doubly occupied Pg− and a singly occupied Pg+. Because the coupling increases the energy of Pg+, there is a smaller driving force for electron transfer from the re-reductant to the dimer compared to the monomer, making the processes both kinetically and thermodynamically less favourable in the dimer.
(6) Explanation 6 is that dimerisation directly improved one of the two central functions of the RC. The first of these is RC's role as an exciton acceptor, accepting optically generated excitations from pigments in the antenna. The second is charge separation, separating the electron and the hole onto separate pigment. The overall efficiency of the RC is the probability that an antenna exciton gives rise to charge separation before it is lost to recombination, and an improvement in the efficiency would confer a fitness advantage on the dimeric organism compared to the monomeric competition.
For the reasons given above, we view Explanations 1–5 as unlikely to explain the origin of RC dimerism or, at least, of the strong coupling in P. Therefore, this paper examines the plausibility of Explanation 6, which is considerably more complicated than the others. Readers unconvinced by our arguments against Explanations 1–5 can read the rest of this paper as an examination of how dimerism and the strong coupling in P affected the efficiency of the RC, an effect that would have contributed to RC performance even if one of Explanations 1–5 were the dominant reason for the dimerisation.
Analysing Explanation 6 requires understanding how the dimerisation affected the exciton- and charge-transfer functions in the RC. Intriguingly, the constituent pigments within P are the only ones in the RC close enough to influence each other, meaning that the part of the RC most affected by dimerisation is also both the ultimate acceptor of excitonic energy and the location of charge separation.12–14 Therefore, to understand the role of dimerisation, we must consider how both exciton transfer to P and charge transfer out of it would have been affected by dimerisation.
Model
In the following, we model the primordial monomeric RC and the homodimer formed by the initial dimerisation, before studying how the dimerisation affected exciton transfer, charge transfer, and the overall efficiency. As the exact properties of the primordial RC are unknown, our model is necessarily general and qualitative. We are not looking for precise predictions of efficiencies, but for strong trends that hold across a broad parameter range.Modelling the primordial dimerisation event
As the positions and orientations of the cofactors are well conserved across all RCs, we assume that the primordial homodimer had a similar structure to modern RCs. Therefore, the pigments of each branch are assumed to be too distant to strongly perturb each other, apart from the two composing P.The precise identity of the pigments in the primordial RC are not important to our argument, and we agnostically refer to them as X0 through X3 in Fig. 2. That said, these cofactors were most likely BChls, which is probably the most primitive of the modern RC tetrapyrroles,19–21 although this is not universally accepted.22
We also make no assumptions about which pigment was the primary electron acceptor. In modern RCs, X1 is either an electron acceptor itself or a bridge for transfer to X2.15,23,24 We only assume that one of the pigments is the primary acceptor—which we call XA—and that it is lower in energy than P; whether charge transfer involves intermediate bridging states does not affect our argument.
We also assume an antenna (Ant.) that transfers excitons to P. The great diversity of modern antenna complexes1 means we cannot say anything definitive about the structure of primordial antenna(s), so we treat them quite generally.
Finally, we assume the primordial monomer to be simply one half of the homodimer just described. Its antenna is assumed to be the same as the homodimer's.
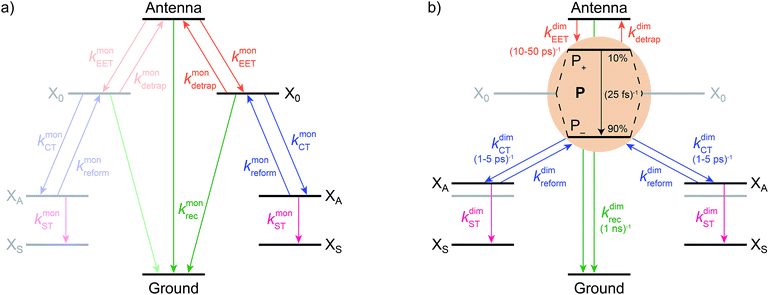
We model the monomeric and dimeric RCs as multi-level systems governed by the rate processes shown in Fig. 3. The rates for the monomer and dimer carry superscripts “mon” and “dim”, respectively, and include the rate kEET of excitation energy transfer (EET) from the antenna to X0/P and the rate kdetrap of the reverse detrapping process. Charge transfer (CT) from P to the charge acceptor XA is at rate kCT, while the reverse process, exciton re-formation, occurs at rate kreform. Subsequent transfer out of XA to subsequent state(s) XS occurs at rate kST and is assumed to be irreversible.
We also include exciton recombination to ground at rate kmonrec; in modern organisms, this rate is small (∼1 ns−1),25 and without knowing the structure of the primordial exciton donor, we take the modern value as representative.
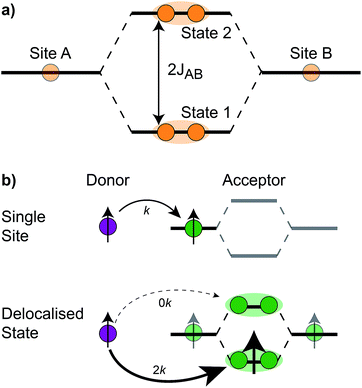
The homodimer model also includes excitonic coupling JP between the two X0 molecules in P, resulting in two excitonic states, P+ and P−, which are respectively JP higher and lower in energy than X0 (Fig. 4a). For modern plants, about 90% of the oscillator strength is in the lower state P−.26 We assume that the relaxation from P+ to P− is faster than any other process, occurring at a rate of (25 fs)−1.13 Therefore, even if P+ is excited, rapid internal conversion to P− ensures that all subsequent EET and CT take place from P−.
Light-harvesting efficiency as figure of merit
The RC converts excitons into charges, and if dimerism increased fitness, it would have done so by increasing the efficiency of this fundamental process. As further CT from the primary charge XA acceptor is identical in both the monomer and the dimer, we define the efficiency as the probability that an antenna exciton yields an electron on XS, as opposed to being lost to recombination.The efficiency is maximised by having forward transfer rates kCT, kEET, and kST that are large relative to krec, kdetrap, and kreform. Slow recombination implies high efficiency because recombination is the only way for the exciton to be lost, while slow detrapping ensures that the exciton, once it reaches P, has a chance to drive CT.
For both the monomer and the dimer, state populations obey a set of rate equations (superscripts “mon” and “dim” omitted from the rates):
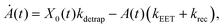 | (1) |
 | (2) |
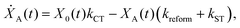 | (3) |
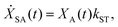 | (4) |
| η = kCTkEETkST(kreformkrec(kdetrap + kEET + krec) + kSTkEETkCT + kSTkrec(kCT + kdetrap + kEET + krec))−1. | (5) |
We will generally calculate the relative efficiency ηdim/ηmon, which indicates whether dimerisation improved or diminished the light harvesting. The following sections survey how dimerisation would have affected the relative efficiency through changes in EET and CT.
Dimerism enhances excitation energy transfer (EET) to the special pair
The effect of EET on the relative efficiency ηdim/ηmon is determined by how the EET rates in eqn (5) are affected by dimerisation. For high efficiency, kEET should be large relative to kdetrap and krec, to allow the exciton to stay in X0/P for as long as possible and increase the chance for CT to occur.Coupling between RCs and their antennas is weak, meaning that both EET and detrapping can be described perturbatively, by Förster resonant energy transfer (FRET).27,28 If either the donor or the acceptor (or both) feature excitonic delocalisation, FRET should be replaced by generalised FRET (gFRET),29 which describes EET in delocalised systems and has been widely used to describe photosynthetic systems.29–32 In particular, it is necessary to use gFRET for modelling the dimeric RC because the excitonic states of P are delocalised. The gFRET transfer rate is
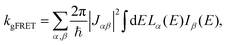 | (6) |
Dimerisation can affect gFRET rates by two mechanisms: supertransfer and the creation of an energetic trap. The former affects the |Jαβ|2 factor in eqn (6), and the latter the spectral overlap integral.
The first effect, supertransfer, is the enhancement of EET due to increases in |Jαβ|2 in eqn (6), arising from the constructive interference between EET pathways. For example, in EET between a single donor D and a single acceptor A, the EET rate ksingle is proportional to |JDA|2. By contrast, multi-site gFRET occurs between the delocalised eigenstates of the donor and the acceptor, rather than as a sum of rates between individual sites (Fig. 4b). With two EET acceptors, supertransfer can accelerate EET up to a factor of two; if the transition dipoles of the donor and the acceptors are parallel, the acceptor state is fully delocalised over the two acceptor molecules, meaning that the donor couples to an effective acceptor transition dipole that is larger by a factor of 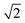 , giving a gFRET rate of
, giving a gFRET rate of
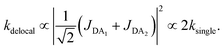 | (7) |
The second way that dimerisation affects EET is the creation of an energetic trap, which enters eqn (6) through the overlap integral. The coupling JP between X0 molecules in P means that P− is energetically stabilised relative to a single X0. This energy shift affects EET in two ways: forward EET is accelerated by dimerisation because of the larger driving force and detrapping is slowed down because of the greater activation energy. Although the precise magnitude of these effects could be calculated using eqn (6) and a microscopic model, we focus only on the dominant effect, which is the change in detailed balance due to the energy shift. To do so, we assume the simplest case, that forward EET and detrapping are affected symmetrically, i.e., that forward EET is accelerated by a factor of exp(JP/2kBT), while detrapping is slowed down by a factor of exp(JP/2kBT). Our results would not be significantly different if, say, only forward EET were accelerated by exp(JP/kBT) or only detrapping slowed down by exp(JP/kBT). Finally, this approach is valid if, as is the case in all RCs, JP is small compared to the widths of absorption and emission peaks; a very large JP could eventually lead to a decrease in the overlap integral in eqn (6), but this is not biologically relevant.
We can combine the effects of supertransfer and energetic trapping to calculate the overall effect of dimerisation on EET rates and the efficiency. Dimerisation enhances the forward EET,
| kdimEET = γexp(JP/2kBT)kmonEET. | (8) |
| kdimdetrap = γexp(−JP/2kBT)kmondetrap, | (9) |
Dimerism diminishes charge transfer (CT) from the special pair
For high efficiency, kCT should be high compared to kdetrap and krec. The smaller kCT is relative to kdetrap, the longer the exciton spends in the antenna, offering more chance of recombination, while if krec is large, recombination can occur in P itself.It is not clear what is the best theoretical model for CT in the primordial RCs. Unlike with EET—which always has weak antenna-RC couplings, making FRET the safe choice—CT couplings between modern special pairs and the primary charge acceptors are not weak, although they could have been in the past. The uncertainty in the strength of the primordial CT couplings translates to an uncertainty about the best theoretical description of primordial CT. The two extremes of CT are diabatic CT (also known as Marcus theory, and applicable for weak CT couplings) and adiabatic CT (applicable for strong CT couplings). Our approach is to carry out the calculations with both approaches; fortunately, it turns out that the final conclusions are not significantly affected by the choice.
First, we consider the diabatic limit. Just as describing EET in delocalised systems requires gFRET, diabatic CT in delocalised systems is described using our recently described generalised Marcus theory (gMT),33 which predicts a CT rate of
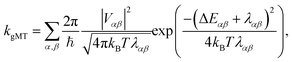 | (10) |
Like gFRET, gMT allows for supertransfer through constructively interfering pathways.33 However, it is more sensitive to geometry than gFRET because CT is mediated by wavefunction overlaps, which decay exponentially with distance.33 In modern systems, the X0 molecule that is more distant from the acceptor is so far away that its CT coupling to XA would be negligible compared with the nearer X0. Consequently, |VP−,XA|2 = |VX0,XA|2/2, leading to a halving of the CT rates.
Also similarly to gFRET, transfer from P to XA is affected by changes in energy levels upon dimerisation, of which there are two kinds. Firstly, the coupling inside the special pair decreases the energy difference between P− and XA by JP. Secondly, delocalisation also affects the electrostatics: since the two charges are closer together in the monomer state X−0X+A than in the corresponding dimer state P+−X−A, the latter has weaker Coulomb binding and, therefore, a higher energy. This electrostatic energy difference also decreases the driving force for charge separation by an amount we call ΔECoul,A. Together, the two contributions imply that ΔEP−,XA = ΔEX0,XA + ΔECoul,A + JP.
It is not immediately clear how energy changes affect the rates, because the Franck-Condon factor in eqn (10) also depends on the reorganisation energy, which is also affected by delocalisation: a donor (or acceptor) aggregate consisting of N molecules, each with reorganisation energy λ, has, in a fully delocalised state, λα = λ/N.33 For the RC, this implies λP−,XA = λX0/2 + λXA. Assuming that λX0 ≈ λXA, we have λP−,XA = 3/4λX0,XA, where λX0,XA is the reorganisation energy for CT between X0 and XA.
Overall, the CT rate for the dimer becomes
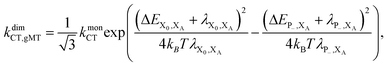 | (11) |
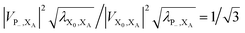 . In most cases, dimerisation decreases the gMT rate; in particular, kdimCT,gMT < kmonCT if, as in modern RCs, JP > 0 and
. In most cases, dimerisation decreases the gMT rate; in particular, kdimCT,gMT < kmonCT if, as in modern RCs, JP > 0 and 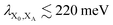 . Since gMT obeys detailed balance, the rate kdimreform,gMT of charge back-transfer is calculated by reversing the signs of ΔEX0,XA and ΔEP−,XA.
. Since gMT obeys detailed balance, the rate kdimreform,gMT of charge back-transfer is calculated by reversing the signs of ΔEX0,XA and ΔEP−,XA.
The second limit we consider is adiabatic charge transfer, which, in its simplest form,34 predicts a CT rate (whether forward or backward) of
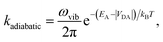 | (12) |
Upon dimerisation, the electronic coupling VDA is reduced by a factor of 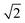 , and there are energetic shifts due to changes in the Coulomb binding. Analogously to our discussion of EET, we assume that forward CT is slowed down by the reduced driving force by a factor of exp(−ΔECoul,A/2kBT), while the backward CT is accelerated by the reduced uphill barrier by a factor of exp(ΔECoul,A/2kBT). Overall, the rate of forward CT in the dimer becomes
, and there are energetic shifts due to changes in the Coulomb binding. Analogously to our discussion of EET, we assume that forward CT is slowed down by the reduced driving force by a factor of exp(−ΔECoul,A/2kBT), while the backward CT is accelerated by the reduced uphill barrier by a factor of exp(ΔECoul,A/2kBT). Overall, the rate of forward CT in the dimer becomes
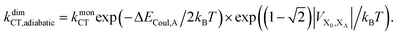 | (13) |
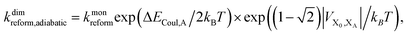 | (14) |
Subsequent charge transfer is also affected by delocalisation due to changes in electrostatics. Because the subsequent transfer occurs farther from P, the energetic destabilisation is smaller than for transfer from P to XA, giving a net increase in the driving force, which we call ΔECoul,ST. In both gMT and adiabatic CT treatments, we include the effect through kdimST = exp(ΔECoul,ST/kBT)kmonST.
Overall, dimerisation is expected to decrease the rate of CT whether it is described using gMT or adiabatic theory.
Parameter space
Our goal is to determine, over a plausible parameter space, whether and how the primordial dimerisation could have affected the RC efficiency. Table 1 lists the free parameters of the model and their ranges within the parameter space. The monomer rates were taken as fundamental, and dimer rates were calculated from monomer rates and the dimerisation parameters (JP, ΔEX0,XA, λX0,XA, VX0,XA, γ, ΔECoul,A, and ΔECoul,ST) using eqn (8), (9), and (11) or (13).| Parameter | Symbol | Minimum | Maximum |
|---|---|---|---|
| Exciton recombination rate in monomer | k monrec | 109 s−1 | 109 s−1 |
| Exciton transfer rate in monomer (antenna to RC) | k monEET | 109 s−1 | 1011 s−1 |
| Exciton detrapping rate in monomer (RC to antenna) | k mondetrap | 109 s−1 | 1011 s−1 |
| Charge transfer rate in monomer | k monCT | 109 s−1 | 1012 s−1 |
| Excitonic coupling in special pair | J P | 10 meV | 50 meV |
| Driving force for charge transfer in monomer | ΔEX0,XA | −λX0,XA | 0 meV |
| Reorganisation energy for charge transfer in monomer | λ X0,XA | 80 meV | 270 meV |
| Electronic coupling for charge transfer in monomer | V X0,XA | 1 meV | 18 meV |
| Supertransfer enhancement factor in dimer | γ | 1.5 | 1.8 |
| Electrostatic energy shift of XA upon dimerisation | ΔECoul,A | 0 meV | 30 meV |
| Electrostatic energy shift of XS upon dimerisation | ΔECoul,ST | 0 meV | 10 meV |
We determined the limits of the parameter space by considering modern RCs. We assume that the monomer was no faster at EET or CT than modern RCs, implying that the monomer EET and CT rates are less than the natural rates: kmonEET ≤ 1011 s−1 and kmonCT ≤ 1012 s−1.1,13,14,35 We also assume that these rates are larger than the recombination rate kmonrec = 109 s−1, which is assumed constant, essentially setting the timescale. We make no assumption about whether detrapping is faster than or comparable to forward EET (as in modern plants36,37) or slower (as in purple bacteria38), instead limiting kmondetrap to at most 1011 s−1, the maximal rate of kmonEET.
In modern RCs, JP ranges between about 20 and 50 meV,15,39–42 setting the upper bound JP ≤ 50 meV. As the coupling in the monomer may have been weaker than in modern RCs, we take 10 meV as the lower bound for JP. Modern RCs have a coupling between the special pair and the charge acceptor of between 0.7 and 13 meV;39,43–45 we compensate for the decrease in coupling through dimerisation by multiplying these values by 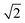 to find the range of VX0,XA. We assume CT takes place in the normal or activationless regime (as opposed to the inverted regime), meaning ΔEX0,XA ≥ −λX0,XA, and that EX0 ≥ EXA, meaning ΔEX0,XA ≤ 0. The reorganisation energy λX0,XA is assumed to be between 80 and 270 meV, typical ranges for CT in biological structures.46–49
to find the range of VX0,XA. We assume CT takes place in the normal or activationless regime (as opposed to the inverted regime), meaning ΔEX0,XA ≥ −λX0,XA, and that EX0 ≥ EXA, meaning ΔEX0,XA ≤ 0. The reorganisation energy λX0,XA is assumed to be between 80 and 270 meV, typical ranges for CT in biological structures.46–49
We estimate γ, the supertransfer enhancement factor for EET, to have been between 1.5 and 1.8. As RC geometry is strongly conserved and EET depends on relative transition-dipole orientations in the special pair, we assume the distribution of oscillator strengths in the primordial dimer was similar to the modern cases. If, as in modern special pairs, P− carried about 90% of the oscillator strength,26γ ≈ 1.8; the lower estimate of 1.5 allows for the primordial dimer to have been somewhat less efficient.
Finally, we consider the electrostatic energy differences ΔECoul,A and ΔECoul,ST. We estimate the former as
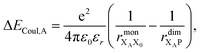 | (15) |
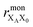 the distance between XA and X0 in the monomer,
the distance between XA and X0 in the monomer, 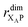 and the distance between XA and the centre of P in the dimer. ΔECoul,ST is defined analogously, using distances between X0/P and the subsequent acceptors. For ΔECoul,A, we assume a range of 0 meV to 30 meV, based on the separations between pigments in several modern RCs, and on an effective εr ranging between 5 and 10. ΔECoul,ST is smaller because of the larger distances, and we take it to be at most 10 meV.
and the distance between XA and the centre of P in the dimer. ΔECoul,ST is defined analogously, using distances between X0/P and the subsequent acceptors. For ΔECoul,A, we assume a range of 0 meV to 30 meV, based on the separations between pigments in several modern RCs, and on an effective εr ranging between 5 and 10. ΔECoul,ST is smaller because of the larger distances, and we take it to be at most 10 meV.
Results
While we have shown above that dimerisation has opposite effects on EET and CT, enhancing the former and diminishing the latter, the total effect on the efficiency depends on which of these two effects is larger. We express the results of our parameter survey (Fig. 5) as the relative efficiency of a dimer relative to a monomer, ηdim/ηmon.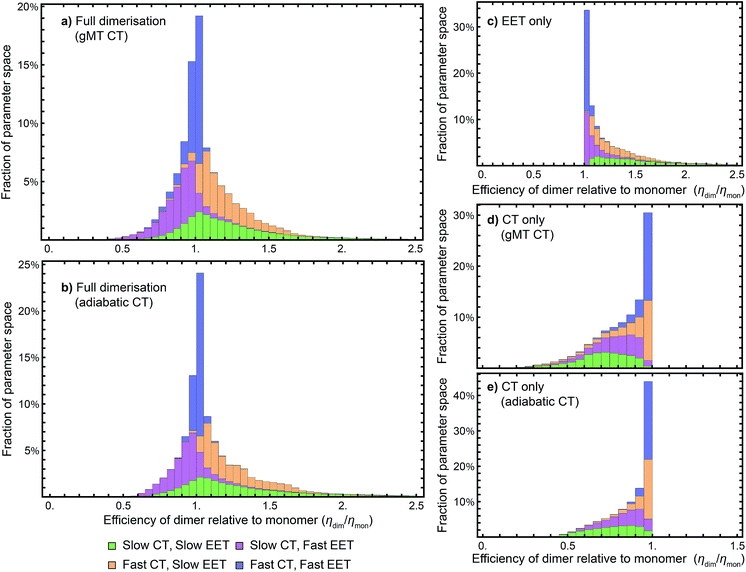 | ||
| Fig. 5 Efficiency of the dimer relative to the monomer across the parameter space of Table 1, if charge transfer (CT) is described using (a) generalised Marcus theory (gMT) or (b) adiabatic rates. (c) Relative efficiency if only exciton transfer (EET) effects are considered (i.e., assuming CT is unaffected by dimerisation), showing that dimerisation enhances EET and the efficiency within the parameter range surveyed. (d) Relative efficiency if only CT effects are considered, modelled using gMT (i.e. assuming EET is unaffected by dimerisation), showing that dimerisation always diminishes CT and the efficiency. (e) As (d), but with CT described using adiabatic rates. In all cases, the recombination rate is 109 s−1; in the legend, ‘slow’ indicates rates comparable to recombination (below 1010 s−1), and ‘fast’ those much faster (above 1010 s−1). In all panels, the histograms are stacked. | ||
Our results show that between about half and three-quarters of the parameter space (depending on whether CT is described using gMT or adiabatic theory) leads to improved relative efficiency (Fig. 5a and b). When divided into individual contributions of EET (Fig. 5c) and CT (Fig. 5d and e) it can be seen that dimerisation enhances EET and is detrimental to CT. The differences in efficiency between the gMT and adiabatic treatments are caused by the fact that adiabatic CT rates are diminished less by dimerisation, meaning that the final efficiency can be increased more by the EET.
The results in Fig. 5 are divided into four regimes, depending on whether EET and CT are fast (above 1010 s−1, i.e., much faster than recombination), or slow (below 1010 s−1, i.e., comparable to recombination). First, when both CT and EET are much faster than recombination, the exciton does not have time to recombine and the efficiency is high. In that case, small changes in rates due to dimerisation do not meaningfully affect the efficiency, making the relative efficiency close to 1. Second, if CT is much faster than recombination but EET is comparable to recombination, the exciton may recombine on the antenna. However, if it is transferred to X0/P, the fast CT removes it before detrapping can occur. Since dimerisation improves EET, this regime consists largely of relative efficiencies greater than 1. Third, if CT is comparable to the recombination rate but EET is much faster, detrapping limits the amount of time CT has to occur and so the exciton spends much of its time transferring between the antenna and X0/P. Because dimerisation makes CT even slower, detrapping is more likely following dimerisation, and so this regime consists largely of relative efficiencies less than 1. Finally, the case where both CT and EET are comparable to the recombination rate has low efficiency, with recombination occurring in both X0/P and the antenna. This regime is the most sensitive to small changes in EET and CT rate, and has the broadest distribution of relative efficiencies.
Discussion
Our results show that Explanation 6 is a plausible account of the rise of RC dimerism. In a large fraction of the parameter space, the strong coupling in P would have caused changes in EET and CT that, overall, would have considerably increased the RC efficiency. In non-negligible regions of the parameter space, the enhancement was larger than 50%, a performance improvement that could have provided a sufficient fitness advantage to displace the monomeric competition.We emphasise that the parameter space we surveyed was deliberately broad, whereas the actual dimerisation event corresponded to only one point in that space. Therefore, the panels of Fig. 5 are not probability distributions for what would happen if evolution were repeated; rather, they reflect ignorance about the primordial RC and the rather arbitrary assumptions about the limits of the parameter space and of the distribution of each parameter (which we took to be uniform). To argue for a likely evolutionary explanation of dimerism, it suffices to establish that there is a large range of primordial parameters for which the argument holds.
While we surveyed a broad parameter space, we do think some areas of that space are more likely than others to represent the primordial RC. In particular, if the primordial RC was like modern RCs, it would fall in the orange panels of Fig. 5, corresponding to fast CT and slow EET. Of the four domains in Fig. 5, that is the one that shows the greatest efficiency enhancement.
If the efficiency enhancement was the actual driver of RC dimerism, it would tell us more about the early stages of the evolution of photosynthesis. First, because the efficiency enhancement is caused by improved EET from the antenna to P, the pre-dimerisation RC, like all modern RCs, would have had an antenna. In other words, antennas likely evolved before RC dimerism (or at least before the strong coupling in P). If the earliest antennas were poor at EET, as one might expect, the enhancement due to dimerism could have been very large. After the dimerisation event, the antennas diversified to the wide range seen today,1 but all RCs retained their dimerism.
Our argument also explains why the lower state of P is bright. Whether P+ or P− is lower in energy depends on the sign of JP, which can change based on the alignment of the transition-dipole moments of the (B)Chls. One might think it would be better for the lower state to be dark, because that would slow down radiative relaxation (fluorescence), giving the exciton more time to dissociate, an idea called dark-state protection.50 Indeed, if the RC were responsible for light absorption, the reversal of bright and dark states would improve the efficiency. However, if the driver of dimerisation was lowering the energy of the bright state of P relative to an antenna, then the bright state must have been the lower one.
Conclusion
We have used modern RCs to construct a model and a plausible parameter space for the primordial dimerisation event, finding that dimerisation could have increased RC efficiency, perhaps by as much as 50%, offering a good evolutionary explanation for the dimeric structure. The coupling between the two halves of P created an exciton trap, enhancing EET into the system and diminishing back transfer. While dimerisation decreased the forward CT rate, in large parts of the explored parameter space the slower CT was more than compensated for by the EET enhancement. In particular, if CT in the monomer was as fast as it is in modern dimers, the benefit to EET would have far exceeded the small decrease in efficiency due to the reduction in CT rates. Our findings could be experimentally tested through the engineering of fully monomeric RCs, which could also narrow the possible parameter regime through a combination of structural and more accurate computational studies.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank James Allen, Noel Hush, Kevin Redding, Jeffrey Reimers, and Thomas Renger for valuable feedback. We were supported by a Westpac Bicentennial Foundation Research Fellowship, by an Australian Government Research Training Program scholarship, and by a University of Sydney Nano Institute Grand Challenge.References
- R. Blankenship, Molecular Mechanisms of Photosynthesis, Wiley Blackwell, 2nd edn, 2014 Search PubMed.
- J. Allen and J. Williams, FEBS Lett., 1998, 438, 5 CrossRef CAS PubMed.
- R. E. Blankenship, Photosynth. Res., 1992, 33, 91 CrossRef CAS PubMed.
- A. Y. Mulkidjanian and W. Junge, Photosynth. Res., 1997, 51, 27 CrossRef CAS.
- T. Meyer, Biosystems, 1994, 33, 167 CrossRef CAS PubMed.
- M. Büttner, D. L. Xie, H. Nelson, W. Pinther, G. Hauska and N. Nelson, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 8135 CrossRef PubMed.
- W. D. Schubert, O. Klukas, W. Saenger, H. T. Witt, P. Fromme and N. Krauß, J. Mol. Biol., 1998, 280, 297 CrossRef CAS PubMed.
- R. E. Blankenship, Plant Physiol., 2010, 154, 434 CrossRef CAS PubMed.
- S. Y. Netzer-El, I. Caspy and N. Nelson, Front. Plant Sci., 2019, 9, 1 Search PubMed.
- A. W. Roszak, V. Moulisová, A. D. P. Reksodipuro, A. T. Gardiner, R. Fujii, H. Hashimoto, N. W. Isaacs and R. J. Cogdell, Biochem. J., 2012, 442, 27 CrossRef CAS PubMed.
- G. S. Orf, C. Gisriel and K. E. Redding, Photosynth. Res., 2018, 138, 11 CrossRef CAS PubMed.
- F. Müh, M. Plöckinger and T. Renger, J. Phys. Chem. Lett., 2017, 8, 850 CrossRef PubMed.
- A. Niedringhaus, V. R. Policht, R. Sechrist, A. Konar, P. D. Laible, D. F. Bocian, D. Holten, C. Kirmaier and J. P. Ogilvie, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 3563 CrossRef CAS PubMed.
- F. Ma, E. Romero, M. R. Jones, V. I. Novoderezhkin and R. van Grondelle, J. Phys. Chem. Lett., 2018, 9, 1827 CrossRef CAS PubMed.
- A. Chauvet, J. Sarrou, S. Lin, S. P. Romberger, J. H. Golbeck, S. Savikhin and K. E. Redding, Photosynth. Res., 2013, 116, 1 CrossRef CAS PubMed.
- D. L. Hartl and A. G. Clark, Principles of Population Genetics, Sinauer Associates, 4th edn, 2006 Search PubMed.
- H. Ishikita, W. Saenger, J. Biesiadka, B. Loll and E. W. Knapp, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9855 CrossRef CAS PubMed.
- M. Chen, M. Schliep, R. D. Willows, Z. L. Cai, B. A. Neilan and H. Scheer, Science, 2010, 329, 1318 CrossRef CAS PubMed.
- D. H. Burke, J. E. Hearst and A. Sidow, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 7134 CrossRef CAS PubMed.
- J. M. Olson and R. E. Blankenship, in Discoveries in Photosynthesis, Springer, 2003, pp. 1073–1086 Search PubMed.
- J. Xiong, Science, 2000, 289, 1724 CrossRef CAS PubMed.
- L. O. Björn and Govindjee, Photobiology: The Science of Light and Life, ed. L. O. Björn, Springer, 3rd edn, 2015, ch. 16, pp. 207–230 Search PubMed.
- C. Gisriel, I. Sarrou, B. Ferlez, J. H. Golbeck, K. E. Redding and R. Fromme, Science, 2017, 357, 1021 CrossRef CAS PubMed.
- T. Arlt, S. Schmidt, W. Kaiser, C. Lauterwasser, M. Meyer, H. Scheer and W. Zinth, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 11757 CrossRef CAS PubMed.
- G. H. Schatz, H. Brock and A. R. Holzwarth, Biophys. J., 1988, 54, 397 CrossRef CAS.
- D. C. Arnett, C. C. Moser, P. L. Dutton and N. F. Scherer, J. Phys. Chem. B, 1999, 103, 2014 CrossRef CAS.
- I. Kassal, J. Yuen-Zhou and S. Rahimi-Keshari, J. Phys. Chem. Lett., 2013, 4, 362 CrossRef CAS PubMed.
- R. D. J. León-Montiel, I. Kassal and J. P. Torres, J. Phys. Chem. B, 2014, 118, 10588 CrossRef PubMed.
- H. Sumi, J. Phys. Chem. B, 1999, 103, 252 CrossRef CAS.
- G. Scholes, X. Jordanides and G. Fleming, J. Phys. Chem. B, 2001, 105, 1640 CrossRef CAS.
- S. Baghbanzadeh and I. Kassal, J. Phys. Chem. Lett., 2016, 7, 3804 CrossRef CAS PubMed.
- S. Baghbanzadeh and I. Kassal, Phys. Chem. Chem. Phys., 2016, 18, 7459 RSC.
- N. B. Taylor and I. Kassal, Chem. Sci., 2018, 9, 2942 RSC.
- V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VCH, 3rd edn, 2011 Search PubMed.
- T. Cardona, A. Sedoud, N. Cox and A. W. Rutherford, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 26 CrossRef CAS PubMed.
- G. Raszewski and T. Renger, J. Am. Chem. Soc., 2008, 130, 4431 CrossRef CAS PubMed.
- D. I. Bennett, K. Amarnath and G. R. Fleming, J. Am. Chem. Soc., 2013, 135, 9164 CrossRef CAS PubMed.
- R. M. Pearlstein, Photochem. Photobiol., 1982, 35, 835 CrossRef CAS.
- J. R. Durrant, D. R. Klug, S. L. Kwa, R. van Grondelle, G. Porter and J. P. Dekker, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 4798 CrossRef CAS PubMed.
- G. S. Beddard, J. Phys. Chem. B, 1998, 102, 10966 CrossRef CAS.
- G. Raszewski, W. Saenger and T. Renger, Biophys. J., 2005, 88, 986 CrossRef CAS PubMed.
- M. E. A. Madjet, F. Müh and T. Renger, J. Phys. Chem. B, 2009, 113, 12603 CrossRef PubMed.
- P. O. J. Scherer and S. F. Fischer, Chem. Phys., 1989, 131, 115 CrossRef CAS.
- D. Kolbasov and A. Scherz, J. Phys. Chem. B, 2000, 104, 1802 CrossRef CAS.
- W. Parson and A. Warshel, in Purple Phototrophic Bacteria, ed. N. Hunter, F. Daldal, M. C. Thurnauer and J. T. Beatty, Springer, Rotterdam, 2008, ch. 19, pp. 355–377 Search PubMed.
- M. Bixon, J. Jortner, M. E. Michel-Beyerle, A. Ogrodnik and W. Lersch, Chem. Phys. Lett., 1987, 140, 626 CrossRef CAS.
- W. W. Parson, Z. T. Chu and A. Warshel, Biophys. J., 1998, 74, 182 CrossRef CAS PubMed.
- M. Volk, G. Aumeier, T. Langenbacher, R. Feick, A. Ogrodnik and M. E. Michel-Beyerle, J. Phys. Chem. B, 2002, 102, 735 CrossRef.
- V. I. Novoderezhkin, E. Romero, J. P. Dekker and R. van Grondelle, ChemPhysChem, 2011, 12, 681 CrossRef CAS PubMed.
- C. Creatore, M. A. Parker, S. Emmott and A. W. Chin, Phys. Rev. Lett., 2013, 111, 1 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2019 |