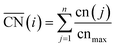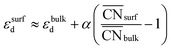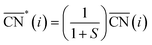Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Revealing the nature of active sites in electrocatalysis
Batyr
Garlyyev
 a,
Johannes
Fichtner
a,
Oriol
Piqué
a,
Johannes
Fichtner
a,
Oriol
Piqué
 b,
Oliver
Schneider
c,
Aliaksandr S.
Bandarenka
b,
Oliver
Schneider
c,
Aliaksandr S.
Bandarenka
 *ad and
Federico
Calle-Vallejo
*ad and
Federico
Calle-Vallejo
 *b
*b
aPhysics of Energy Conversion and Storage, Technical University of Munich, James-Franck-Straße 1, 85748 Garching, Germany. E-mail: bandarenka@ph.tum.de
bDepartament de Ciència de Materials i Química Fisica, Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, Martí i Franquès 1, 08028 Barcelona, Spain. E-mail: f.calle.vallejo@ub.edu
cElectrochemical Research Group, Technische Universität München, Schleißheimerstraße 90a, 85748 Garching, Germany
dCatalysis Research Center, TUM, Ernst-Otto-Fischer-Straße 1, 85748 Garching, Germany
First published on 23rd July 2019
Abstract
Heterogeneous electrocatalysis plays a central role in the development of sustainable, carbon-neutral pathways for energy provision and the production of various chemicals. It determines the overall efficiency of electrochemical devices that involve catalysis at the electrode/electrolyte interface. In this perspective, we discuss key aspects for the identification of active centers at the surface of electrocatalysts and important factors that influence them. The role of the surface structure, nanoparticle shape/size and the electrolyte composition in the resulting catalytic performance is of particular interest in this work. We highlight challenges that from our point of view need to be tackled, and provide guidelines for the design of “real life” electrocatalysts for renewable energy provision systems as well as for the production of industrially important compounds.
Introduction
Many would agree that our lives today would be radically different without the Haber–Bosch process, as this revolutionary work in heterogeneous catalysis on nitrogen fixation enabled the fast growth of the world's population.1 Since then, landmark contributions were made especially by Sabatier,2 Langmuir,3 Taylor,4 Balandin5 and Ertl6 to understand chemical reactions at surfaces. To recognize the importance of catalytic reactions at solid surfaces, Nobel prizes were awarded to P. Sabatier for his work on hydrogenation reactions catalyzed by metals in 1912, to F. Haber for his research on ammonia synthesis in 1918, to I. Langmuir for the study about surface reactions and adsorption in 1932, and G. Ertl for his work on understanding of chemical processes at solid surfaces in 2007. Nowadays, heterogeneous catalysis partakes in the production of nearly 90% of the chemicals used in our daily life; and with the growing concerns about climate change, the development of sustainable, carbon-neutral pathways for the production of energy and industrially essential chemicals is paramount.7–9 Rationally increasing the efficiency of catalysts mainly depends on elucidation of the nature of active sites that control the overall catalytic performance.10–12The idea that only several active sites at the catalyst surface control the overall catalyst performance was introduced by Taylor in 1925.4 Ever since, especially over the past decades, advances were made on the development of model single-crystal surfaces and ultra-high vacuum methodologies. These, in turn, enabled experimental studies of the electronic and structural properties of the catalytic centers on well-defined surfaces. In parallel, great advances in theoretical chemistry in combination with the rapid development of computer technologies led to the establishment of new approaches to understand and predict the reaction rates at different surface sites as a function of their composition and structure. In particular, density functional theory (DFT) has provided deep insight into heterogeneous catalysis as a whole.7In situ experimental and computational studies concur that catalytic activities are dictated by the nature of the active sites, which strongly depends on the materials' composition13–22 and surface structure,23–26 and the electrolyte composition.27–31
In this perspective, we analyze several fundamental issues related to the elucidation of the electrocatalysts' active centers and factors that modify their catalytic efficiency. Firstly, aspects related to the electronic structure of the active sites are briefly discussed; then the role of surface defects is considered, as it is pertinent to ask if surface defects are the only sites able to catalyze electrochemical reactions. Subsequently, we elaborate on how the activity changes with the size and shape of nanoparticles and whether the intrinsic activity can be controlled solely by adjusting the coordination environment of the active sites. Afterwards, the influence of the electrolyte composition, especially the role of the so-called spectator species, is analyzed. Finally, we mention the possibilities for the prediction of the selectivity and stability of catalytic active sites.
Electronic structure of active sites
A suitable strategy to enhance the catalytic activity of pure transition-metal catalysts is to alloy them with other metals.32–34 In the following, we refer to ligand effects as those introduced by a guest (alloying) atom on a host substrate. More specifically, ligand effects refer to the modification of the adsorption energies and catalytic activities induced by the presence of an alloying atom in the proximities of the active sites. The alloying atoms are not in direct contact with the adsorbates, so that ligand effects are due to the modification of the active sites' electronic structure. On the other hand, geometric effects (discussed in the next section) appear when the spatial configuration of the active sites is changed, which can happen if (I) the interatomic distances of the active sites are stretched/contracted, or (II) atoms are added to the active sites or removed from them. In this context, a pure metal may only experience geometric effects, while an alloy can experience both electronic and geometric effects.Different kinds of alloys have been explored in the literature, including bulk alloys (BAs), thin films (TFs), surface alloys (SAs) and near-surface alloys (NSAs). The variation in adsorption energies in BAs with respect to the respective pure metals is attributed to strain and ligand effects, while in TFs we only have strain effects—when thicker than 3 atomic layers—and in NSAs only ligand effects.
In the particular case of oxygen electroreduction (ORR, O2 + 4H+ + 4e− → H2O), which requires large overpotentials and is of interest in proton-exchange membrane fuel cells (PEMFCs), it is well known that the ideal cathode catalyst should bind *OH intermediates more weakly than Pt(111) by approximately 0.1 to 0.15 eV: ΔGXOH − ΔGPt(111)OH = (0.1–0.15) eV.35 Note in passing that this criterion usually applies to ORR electrocatalysts with Pt active sites, for which it is reasonable to assume that the prefactors are comparable.36 Following this energetic design principle, TFs of Pt on top of a Cu bulk were devised that display a 4–6 fold enhancement in ORR activity over pure Pt.37 Those catalysts seize the strain effects on the Pt layers, as Pt and Cu have appreciably different lattice constants. For Pt, compressive lattice strain weakens the binding of the surface to adsorbed intermediates, whereas tensile strain has the opposite effect.
Strasser and coworkers suggested that the high ORR activity of dealloyed PtCux could be attributed to the weakening of the adsorption energy of *OH via strain.37 The same effect causes the high activity of Pt-rare-earth alloys: after exposure to electrolyte, rapid dissolution of the non-noble component takes place due to the very high reactivity of rare earth metals, leaving behind a 5–6 layer thick, compressively strained layer of pure Pt.20,38–40 This layer shows a large ORR activity (a factor of 6 in surface-specific activity compared to pure Pt), and stabilizes the alloy bulk against further dissolution. Moreover, PtCo and PtNi alloys have shown promising results in terms of activity and long term stability.41–43
On the other hand, in NSAs solute atoms are only located in the proximities of the surface in submonolayer amounts and mostly induce ligand effects on the catalyst layer. Ligand effects are more pronounced when the solute atoms are at the subsurface (i.e. the second atomic layer), and are already negligible when they are located in the fourth atomic layer. Chorkendorff and co-workers have shown that subsurface Cu in Pt suitably weakens the binding of ORR intermediates, thereby inducing an 8-fold activity improvement.32 In addition, subsurface Cu atoms in Pt have been successfully tested for the hydrogen evolution reaction33 and CO oxidation,34 in view of the suitable modification of adsorption energies of the respective intermediates with respect to Pt(111).
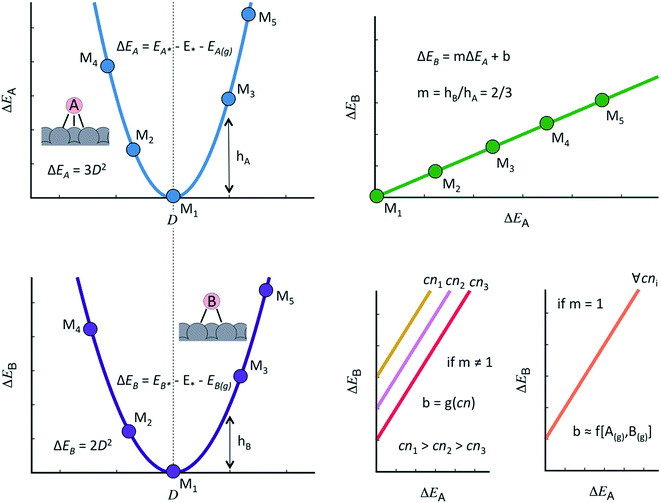
The discovery of linear relations between sets of adsorbates similarly bound to transition metal active sites is one of the milestones of computational surface science and heterogeneous catalysis of the past fifteen years.44 Formally, when the adsorption energies of species B scale linearly with those of species A as: ΔEB = mΔEA + b, m can be estimated as the ratio between the lack of bonds of species A and B to fulfill the octet rule, and b is a constant that depends on the coordination of the surface atoms,45,46 see Fig. 1. Such relations have also been shown to hold on surfaces of oxides, nitrides, sulfides, carbides, porphyrins and single-atom catalysts on graphite layers,47,48 among others. Moreover, scaling relations are not restricted to species occupying the same adsorption sites, and thus scalability may exist between, e.g., adsorbates on top sites and adsorbates on bridge or hollow sites. The general condition for scalability is that the extrema of the curves that correlate adsorption energies with the electronic structure be the same for species A and B.45,46 This is illustrated in Fig. 1 where, for simplicity, we assume a quadratic dependence with a hypothetical electronic-structure descriptor D. Before continuing, we emphasize that the dependence needs not be quadratic, it can have any other functionality. In practice, D may be a simple descriptor such as the number of valence electrons of the metal atoms at the adsorption sites,45,47,48 work functions, electronic charges on the adsorbates, d-band centers, or a more sophisticated descriptor such as the crystal orbital overlap population (coop) or the crystal orbital Hamilton population.49
As shown in Fig. 1, the offset b depends on the value of the slope:46,50 if m ≠ 1, the offset is proportional to the coordination of the adsorption sites. This is the case of *OH vs. *O, the slope of which is 1/2, as *O lacks two electrons to fulfill the octet rule and the oxygen atom in *OH lacks one. If m = 1, the offset is surface independent and depends on the gas-phase energetics of the species involved. This is the case of *OOH vs. *OH, the slope of which is 1.
Note in passing that there are also scaling relations between adsorption energies and other types of energetics, for example bulk energies of formation.51 Besides, scaling relations with negative slopes also exist between certain adsorbates. Conventional scaling relations are formed between electronegative adsorbates such as F, O, N, and C. Conversely, anomalous scaling relations with negative slopes are established between those and less electronegative adsorbates such as B.49
The downside of scaling relations is that they allegedly limit the efficiency of electrocatalysts. For instance, the scaling relation between *OOH vs. *OH is thought to limit the oxygen evolution and reduction reactions (OER, ORR): while the energetic separation of those intermediates should ideally be 2.46 eV, on most catalysts it is ∼3.20 eV.52,53 Another example is the scaling relation between *CO and *CHO, which is supposedly responsible for the high overpotentials of CO2 reduction to CH4.54 However, a word of warning is needed here, as recent works have shown that: (a) breaking the *OOH vs. *OH scaling relation is a necessary yet insufficient condition to achieve ideal OER/ORR electrocatalysts,55,138 and such breaking can actually increase the overpotential. (b) *CHO is not always formed during CO2 reduction.50,56 (c) For some materials, *CHO formation does not influence the overpotential.57 In brief, breaking a given scaling relation is not an infallible recipe for the optimization of all electrocatalysts. Instead, one should focus on the specific reaction steps and intermediates that are problematic.
Thermodynamically, the only general guideline for optimal performance is electrocatalytic symmetry,58,138 which is achieved when all the reaction steps have free energies numerically equal to the equilibrium potential (or its additive inverse). For example, the OER (H2O → O2 + 4H+ + 4e−) has an equilibrium potential E0 = 1.23 V, and the free energies of the four proton–electron transfers are each 1.23 eV on the ideal catalyst. In this context, a metric for symmetry is provided by the electrochemical-step symmetry index (ESSI), the minimization of which effectively corresponds to lower calculated overpotentials.55,138 It is defined as: 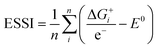 , where
, where 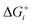 are the reaction free energies for which ΔGi ≥ e−E0 (as only those can control the potential), and n is the number of electrochemical steps for which ΔGi ≥ e−E0.
are the reaction free energies for which ΔGi ≥ e−E0 (as only those can control the potential), and n is the number of electrochemical steps for which ΔGi ≥ e−E0.
Geometric structure of the active sites
The spatial arrangement of the active sites influences their adsorption behavior and catalytic activity. The most common and probably simplest geometric descriptor is the conventional coordination number (cn), which for metals is nothing but the number of atoms located in the proximities of atom i, taking as a reference the interatomic distance observed in the bulk. Usually, there is a (nearly) linear relationship between cn and adsorption energies, in which high coordination corresponds to weak adsorption energies, and low coordination corresponds to strong adsorption energies.46,50,59 The trends are clearer for extended surfaces, as finite-size effects in nanoparticles may induce large deviations, in particular for small particles.60,61 Finite-size effects are illustrated in Fig. 2A, where all of the blue sites on nanoparticles and extended surfaces have cn = 9 but their adsorption energies of *OH differ by more than 0.5 eV. The differences arise not from the number of nearest neighbors but from their respective coordination numbers, which vary appreciably.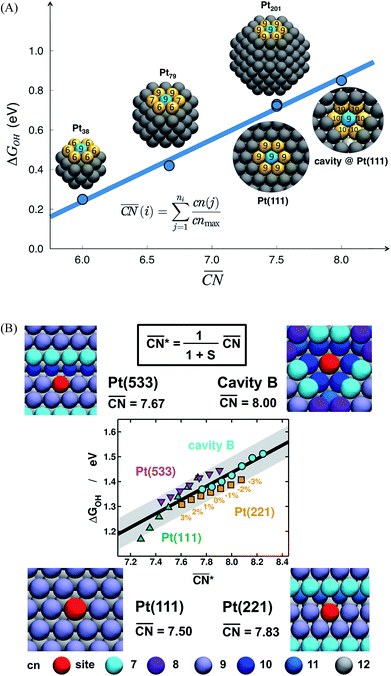 | ||
Fig. 2 Adsorption energies as a function of generalized coordination numbers 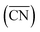 for various surface sites. (A) Trends in *OH adsorption energies for Pt sites (in blue) with 9 nearest neighbors (yellow) but different coordination of such neighbors. Values taken from ref. 67 and 73. (B) Trends in *OH adsorption energies for Pt sites with 9 nearest neighbors but differently coordinated second nearest neighbors and with positive (stretching) and negative (contracting) strain. Adapted from ref. 62 with permission from John Wiley & Sons. for various surface sites. (A) Trends in *OH adsorption energies for Pt sites (in blue) with 9 nearest neighbors (yellow) but different coordination of such neighbors. Values taken from ref. 67 and 73. (B) Trends in *OH adsorption energies for Pt sites with 9 nearest neighbors but differently coordinated second nearest neighbors and with positive (stretching) and negative (contracting) strain. Adapted from ref. 62 with permission from John Wiley & Sons. | ||
Fig. 2A also shows that generalized coordination numbers 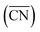 can capture the trends in adsorption energies for extended surfaces and nanoparticles,61 which is achieved by taking into account not only the number of nearest neighbors but also their respective conventional coordination number:
can capture the trends in adsorption energies for extended surfaces and nanoparticles,61 which is achieved by taking into account not only the number of nearest neighbors but also their respective conventional coordination number:
Moreover, the following analytical relationship between 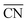 and d-band centers has been shown to exist, which has important implications61 in surface science and catalysis:
and d-band centers has been shown to exist, which has important implications61 in surface science and catalysis:
This equation connects the electronic and geometric structures of a (late) transition metal by means of the d-band center of the surface sites (εsurfd) of the material, the d-band center in the bulk (εbulkd), the generalized coordination number of the surface sites  , and that of the bulk (
, and that of the bulk (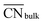 , which is 12 for an fcc crystal). In this formula, α is a material-specific constant that depends on the cohesive energy and the average occupancy of the d-band (α ≈ 1.44 eV for Pt). The link between the electronic and geometric structures of materials suggests that geometric descriptors may as well be used to design enhanced (electro)catalysts, as we will show later in this review.
, which is 12 for an fcc crystal). In this formula, α is a material-specific constant that depends on the cohesive energy and the average occupancy of the d-band (α ≈ 1.44 eV for Pt). The link between the electronic and geometric structures of materials suggests that geometric descriptors may as well be used to design enhanced (electro)catalysts, as we will show later in this review.
Before, we mentioned that strain is one of the most widely used strategies for the enhancement of Pt-based alloys for the ORR.20,37–40 In the context of geometric descriptors, strain (S) can be regarded as a manifestation of generalized coordination in which the number of nearest neighbors is constant but the interatomic distances are different. This consideration leads to a strain-sensitive version of generalized coordination numbers 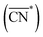 :62
:62
The trends in adsorption energies of *OH for stretched (S > 0) and contracted (S < 0) Pt sites are shown in Fig. 2B as a function of 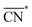 . In agreement with experiments, a contraction of the Pt–Pt bonds leads to a weakening of the *OH adsorption energies on Pt, and the opposite is true when stretching. Note that the S factor is the average degree of strain (in %) of the interatomic distances with respect to the bulk of the material. Recent works on Pt alloys with lanthanide elements have shown that S can be as large as 6%.20 However, at the surface layer the actual strain is lower, so that S is not larger than 3%.63
. In agreement with experiments, a contraction of the Pt–Pt bonds leads to a weakening of the *OH adsorption energies on Pt, and the opposite is true when stretching. Note that the S factor is the average degree of strain (in %) of the interatomic distances with respect to the bulk of the material. Recent works on Pt alloys with lanthanide elements have shown that S can be as large as 6%.20 However, at the surface layer the actual strain is lower, so that S is not larger than 3%.63
Before concluding this section, it is worth noting that generalized coordination numbers can be calculated on metals other than Pt64–67 and have been used to analyze trends for a variety of (electro)catalytic reactions.33,64,66–70
The role of surface defects
Nowadays, the rational design of heterogeneous electrocatalysts is mainly based on the modification of surface properties. In the case of the ORR on Pt, for example, numerous theoretical as well as experimental approaches have been used to modify the surface properties through e.g. alloying, size and shape effects. For instance, nearly spherical, unstrained Pt particles show theoretical maxima in mass activity for diameters around 1, 2 and 3 nm.71,72 These maxima are constrained by a narrow size distribution (±0.2 nm), which is difficult to transfer to real-life applications using conventional methods, although recent experimental results are rather encouraging.72 Therefore, it is desirable to provide further possibilities for tailoring surface properties.A facile way to rationally improve activity by means of surface modifications is based on the generation of structural defects, leading to the introduction of particularly active surface sites. We stress here that not all sorts of defects improve the activity. To discern specifically active surface configurations one can use 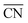 61 and its associated coordination-activity plots.62,67–70
61 and its associated coordination-activity plots.62,67–70
As said before, for the ORR on Pt the activity is typically correlated to the adsorption energy of *OH, which according to the Sabatier principle should not be bound too strong nor too weak in order to enable an efficient electrocatalysis. Instead of the usual correlation between activity and binding properties, within the 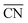 approach the correlations are based on the connection between coordination environment and adsorption energies as described in the previous section. This enables a fast prediction of the ideal geometrical environment of the active sites compared to the time-consuming calculations of electronic-structure descriptors.71
approach the correlations are based on the connection between coordination environment and adsorption energies as described in the previous section. This enables a fast prediction of the ideal geometrical environment of the active sites compared to the time-consuming calculations of electronic-structure descriptors.71
As shown in Fig. 3A, Pt(111) has a 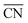 of 7.5, while the optimum is located at ∼8.3. A way to bring the value closer to the optimum is to modify the coordination of the nearest neighbors by increasing the number of second nearest neighbors (see Fig. 2). This can be done, for example, by creating cavities through the removal of surface layer atoms. Experimental investigations at such defect sites validated the theoretical predictions, leading to
of 7.5, while the optimum is located at ∼8.3. A way to bring the value closer to the optimum is to modify the coordination of the nearest neighbors by increasing the number of second nearest neighbors (see Fig. 2). This can be done, for example, by creating cavities through the removal of surface layer atoms. Experimental investigations at such defect sites validated the theoretical predictions, leading to 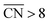 . For example, the dealloying of a Cu/Pt(111) surface alloy showed that the increase in activity of the Pt skin can be traced back to the presence of surface cavities. Moreover, it turns out that, in terms of activity, certain Pt structures are able to outperform Pt(111) by a factor of ∼3.5 and even some of the best Pt-based ORR catalysts known (Fig. 3A).
. For example, the dealloying of a Cu/Pt(111) surface alloy showed that the increase in activity of the Pt skin can be traced back to the presence of surface cavities. Moreover, it turns out that, in terms of activity, certain Pt structures are able to outperform Pt(111) by a factor of ∼3.5 and even some of the best Pt-based ORR catalysts known (Fig. 3A).
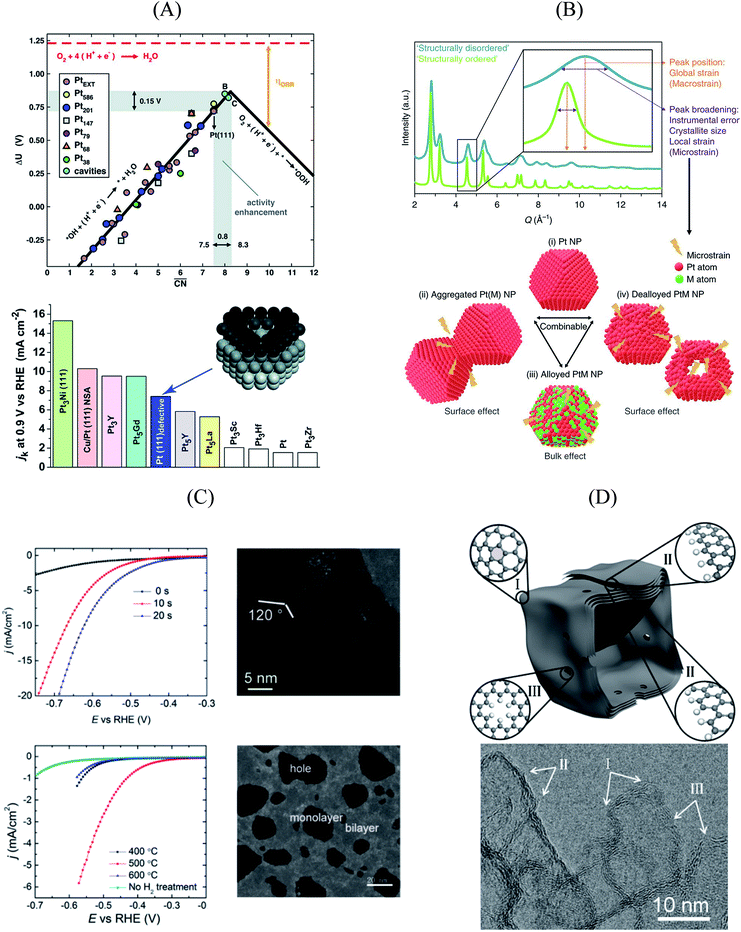 | ||
| Fig. 3 (A) Coordination-activity plot of various Pt surfaces (top), indicating a close-to-optimum coordination environment of surface cavities. A comparison of the defective Pt(111) surface with plain Pt shows a ∼3.5 times increased activity (bottom). Figures reproduced from ref. 67 with permission from American Association for the Advancement of Science. (B) WAXS spectrum peak broadening, induced by microstrain. The presence of microstrain in (i) conventional Pt nanoparticles, (ii) aggregated particles, (iii) alloyed Pt–M nanoparticles and (iv) dealloyed Pt–M nanoparticles is indicated in the Figure. Figures reproduced from ref. 77 with permission from Nature Publishing Group. (C) HER activity of oxygen plasma treated (top left) and H2 annealed (bottom left) MoS2, indicating an increased performance using both methods. The activity increase is caused by the generation of step-like edge sites in the basal plane of the catalyst, as shown in the corresponding TEM image (top and bottom right). Figures reproduced from ref. 78 with permission from American Chemical Society. (D) Schematic description (top) and TEM image (bottom) of possible defective sites on carbon nanocages, improving the ORR activity of the catalyst. Figures reproduced from ref. 81 with permission from American Chemical Society. | ||
Studies on nanoparticles revealed that for typical convex particle shapes a maximum 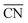 of 7.5 can be reached, due to the sole presence of (111) and (100) surface facets.73 Conversely, concave surface defect sites, as e.g. present at the boundary of coalescent nanoparticles, can be used to increase the generalized coordination number, thereby suitably weakening the *OH binding. Experimental evidence of the enhanced activity of concave sites towards the ORR has been shown by Xia's group74 and Strasser's group,75 among others. However, shape-specific synthesis of such structures is still a challenging task. Similar active sites were also simulated at hollow, frame-like nanoparticles, matching with experimental observations provided by e.g. Dubau et al.76
of 7.5 can be reached, due to the sole presence of (111) and (100) surface facets.73 Conversely, concave surface defect sites, as e.g. present at the boundary of coalescent nanoparticles, can be used to increase the generalized coordination number, thereby suitably weakening the *OH binding. Experimental evidence of the enhanced activity of concave sites towards the ORR has been shown by Xia's group74 and Strasser's group,75 among others. However, shape-specific synthesis of such structures is still a challenging task. Similar active sites were also simulated at hollow, frame-like nanoparticles, matching with experimental observations provided by e.g. Dubau et al.76
An experimental way to assess the impact of defective sites on the ORR performance of bimetallic electrocatalysts (e.g. PtNi-based nanoalloys) was recently proposed by Chattot et al.77 In their work, surface distortion is introduced as a novel descriptor correlating electrochemical activities and properties such as structural surface defects and strain. A combination of different X-ray and microscopic techniques was exploited to prove that, in fact, initial structural disorder of bimetallic electrocatalysts leads to improved efficiency (that is, combination of initial activity and long-term stability) in simulated hydrogen fuel cell operation. This metric can be derived from the so-called “microstrain” introduced into the catalyst as a result of atomic disorder, which was determined by Rietveld refinement of synchrotron wide-angle X-ray scattering (WAXS) patterns (Fig. 3B).
Essentially, they found that while catalysts based on an ordered, surface-science-based approach (“downscaling” of active bulk surfaces) contain a maximum number of certain catalytic active sites, rapid degradation under operating conditions could be observed. However, particles with structural surface defects tend to have various surface sites, including a few particularly active ones, enabling both high initial activity and stability. These results pave the way for the rational design of particularly active and stable catalysts, turning away from well-established design criteria based on the investigation of extended surfaces.
The influence of disordered surfaces can be further extended to other important reactions taking place in energy conversion and storage devices. Investigating MoS2, a promising future catalyst for the hydrogen evolution reaction (HER), Ye et al. improved the activity of a MoS2 monolayer using a facile technique.78 Both oxygen plasma exposure and annealing in hydrogen atmosphere were separately utilized to introduce defects to the basal plane of the catalyst, which is rather inactive towards the HER compared to the defect-rich catalyst edges. Herein, released edge-like structures greatly promote the HER activity of MoS2 in both cases, as indicated in Fig. 3C.
In the emerging field of non-precious metal electrocatalysis, surface defects also play an important role by replacing common dopants (such as e.g. N and S) as active sites. This is of particular interest, as carbon-based ORR materials doped with N and Fe or Co could drastically reduce the catalyst costs compared to currently used Pt nanoparticles.79,80 However, an activity and stability similar to Pt-based materials has to be achieved. For instance, Jiang et al. investigated the impact of different defect types on the activity of pure-carbon nanocages using both experimental and computational techniques.81 They observed that, in fact, pure carbon outperforms certain doped carbon materials in alkaline media, presupposing the presence of defective surface sites. In particular, pentagon structures on the hexagonal surface (Fig. 3D(I)) and “zigzag” edge sites (Fig. 3D(II)) have been found to increase the activity of the nanocages.
In general, surface defects can help increase the electrocatalytic activity of various materials. However, defects on the catalyst support can contribute to its degradation. For instance, high surface area carbon, used in hydrogen fuel-cell catalysts, contains a large number of structural defects, owed to its heterogeneous structure. During typical fuel-cell operation potentials and conditions, defective carbon sites tend to hydrolyze, forming unstable carbon oxides that promote fast degradation of the support material.82
In summary, defect engineering is a simple way to improve the electrocatalytic activity of a material. Computational models combined with experiments can be used to determine whether defects or terraces control the activity. If defects predominate, theory can ascertain whether the active sites are located at concave (high 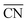 ) or convex (low
) or convex (low 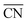 ) defects. On Pt, for the ORR62,67,73 and the HER68 concave defects and strain increase the activity, while convex defects enhance CO oxidation.69 A particular case are Pt(100) terraces, which catalyze a variety of electrocatalytic reactions such as dimethyl ether oxidation and ammonia oxidation,59,83 and their activity is downgraded by defects.
) defects. On Pt, for the ORR62,67,73 and the HER68 concave defects and strain increase the activity, while convex defects enhance CO oxidation.69 A particular case are Pt(100) terraces, which catalyze a variety of electrocatalytic reactions such as dimethyl ether oxidation and ammonia oxidation,59,83 and their activity is downgraded by defects.
It ought to be considered as well that defects could strongly affect durability, which is particularly true for carbon-based catalysts and support materials. Moreover, nanoparticle synthesis with suitable surface defects and good stability is still a challenging task. Thus, future research should find facile ways to specifically implement defects that grant control over the catalytic properties of nanostructures. In addition, simple catalyst design criteria should be available in order to reach maximal efficiency. In this order of ideas, geometric descriptors (such as generalized coordination numbers) are more recommendable than energetic descriptors (such as adsorption energies or band centers), as their connection to experiments is more straightforward. The ORR on Pt(111) illustrates this point: increasing the coordination of the active sites and weakening the *OH adsorption energy both lead to optimality. From an experimental standpoint, the former is probably more informative than the latter, as it contains information about the spatial configuration of the active sites. Energetic descriptors are, nonetheless, more widely used nowadays in computational electrocatalysis.44
Size effects
The catalytic activity of metal nanoparticles has been investigated for nearly 4 decades. With the emergence of synthetic routes for size- and shape-controlled nanostructured particles in the late 20th and early 21st centuries by the groups of El-Sayed84,85 and Somorjai,86 measuring size- and shape-dependent activity studies was made possible. In electrocatalysis, the Strasser11 and Xia74 groups have driven the research focused on the electrocatalytic applications of size- and shape-controlled nanoparticles.The catalytic activity of nanostructured particles is governed by a set of physical parameters including size, shape and geometric structure. In this subsection we will focus on the size-dependent activity87–90 of several nanostructured catalysts and the efforts made to locate the active sites within those.
Platinum and Pt-group metals are known to be the best catalysts for the ORR in acid. The surface-area specific (jk in mA cm−2) and mass-specific activity (jm in A mgPt−1) of Pt nanoparticles of different sizes (between 2–11 nm) towards the ORR is compared in Fig. 4A.91 The area-specific activity increases alongside the nanoparticle size and approaches bulk Pt surface activity near 11 nm. To locate the ORR active sites, temperature programmed CO desorption (CO-TPD) experiments were conducted in vacuum. From CO-TPD measurements the authors estimated the percentage of terraces present in a given nanoparticle. Previously, theoretical studies92 had predicted that the active sites were located at the terraces of the Pt surface and, as shown in Fig. 4A, the surface-specific activity of nanoparticles increases with the percentage of terraces. Briefly, the percentage of terrace atoms increases with the nanoparticle size and consequently the number of active sites. However, the activity per mass has an optimal surface-to-volume ratio and the nanoparticles with 3 nm size have shown the highest mass activity (see Fig. 4A). For alloyed PtxY93 and PtxGd40 nanoparticles the size dependence curve is similar to that of pure Pt nanoparticles; however, the highest activity is observed for the 8–9 nm nanoparticles. This is mainly because only beyond those dimensions a stable strained Pt skin can form, so that smaller particles are unstable and dealloy rather quickly.
 | ||
| Fig. 4 Mass and specific activities of (A) pure Pt nanoparticles and (B) PtxGd and PtxY nanoparticles as a function of the particle size. The activities at 0.9 V vs. RHE are extracted from cyclic voltammograms recorded in O2-saturated 0.1 M perchloric acid, at 1600 rpm, and the scan speed was 50 mV s−1. (A) and (B) reproduced from ref. 91 and 40 with permission from John Wiley & Sons and Elsevier, respectively. (C) Oxygen evolution reaction performance of NiFeOxHy nanoparticles with various sizes. The cyclic voltammograms were recorded in N2-saturated 1 M KOH at 1600 rpm, and the scan speed was 10 mV s−1. Reproduced from ref. 94 with permission from Nature Publishing Group. | ||
In summary, the ORR active centers are located at the terraces of regular Pt nanoparticles and the interplay between surface area to mass determines the quantity of the active sites with nearly optimal binding energy towards the key reaction intermediate *OH, which determines to a large extent the overall performance of the electrocatalyst.
The OER is important for water electrolyzers. NiFeOxHy nanoparticles have shown the highest activity towards the OER in alkaline solution.94 The size-dependent mass activity of NiFeOxHy nanoparticles towards the OER in alkaline electrolyte is depicted in Fig. 4C. Similar to Pt nanoparticles under ORR conditions, the smaller nanoparticles of 3.9 and 5.4 nm sizes showed higher mass activities compared to larger particles with 6.7 and 8.4 nm in diameter, although the activity does not scale linearly with size. Moreover, the surface-area-specific activities were size independent. From isotope labeling and mass spectrometry experiments the authors concluded that the active centers are located at the near-surface region (∼3 atomic layers) of the nanoparticles and that lattice oxygen atoms are not involved in the OER. In brief, when designing the catalysts for the OER it is important to control the atoms at the near-surface region rather than the bulk atoms.
Shape effects
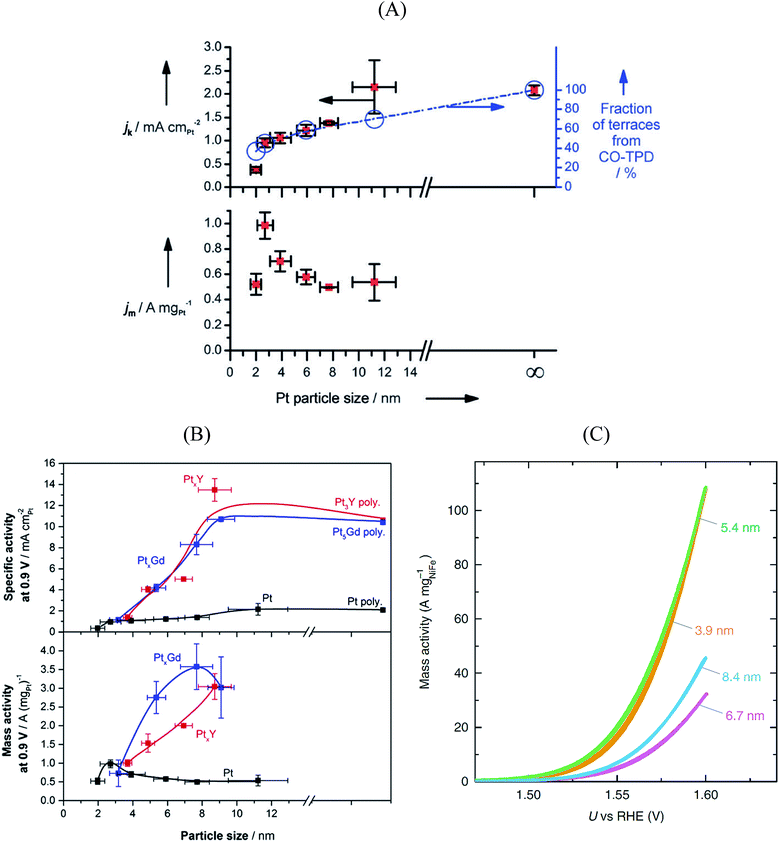
Size and composition are two crucial parameters in determining nanoparticle reactivity. Additionally, the structural sensitivity of certain electrocatalytic reactions makes nanoparticle shapes another important aspect to be considered.95–99 The shape of the particle usually dictates which crystallographic facets are exposed: for instance, octahedra and tetrahedrons expose (111) facets, cubes expose (100) facets, whereas truncated octahedra and cuboctahedra expose a combination of (111) and (100) facets.Pt3Ni{111} single crystalline surfaces are known to be exceptionally active in catalyzing the ORR reaction.100 Over the past decade several studies reported on PtxNi alloyed nanoparticles that resulted in new benchmark mass activities for the ORR. Fig. 5A shows the ORR mass activities of various shapes of PtxNi alloyed nanoparticles. Theoretical studies predict that the octahedral nanoparticles mainly contain {111} facets and show highest mass activity towards the ORR.101 As seen in Fig. 5A, the highest mass activity is observed for octahedral PtxNi nanoparticles.11 The mass activity of commercial Pt/C catalyst is indicated by a dashed line. Because of the instability of Ni in acidic solutions, Ni atoms are leached out during the ORR activity tests; however, the high ORR activity of the nanoparticles is predominantly maintained. From these observations, one can conclude that after Ni atoms are leached out from the initially {111}-oriented PtxNi surfaces, highly active sites with specific arrangement of Pt atoms are formed that determine the overall catalytic performance. The mass activities reported in Fig. 5A are measured in a half-cell three-electrode rotating disk electrode (RDE) setup. The activity of commercially available Pt/C catalysts from RDE is in good agreement with the activities measured in fuel cells, but the situation is quite different for highly active catalysts. The high performance of PtxNi alloyed nanoparticles has not yet been reproduced in real fuel cells.102Fig. 6B shows the mass activities of various nanoparticles measured in liquid half-cell setups and PEM fuel cells. As seen in the graph, translating the high performances observed in liquid half-cell setups into real fuel cells remains a challenge. This is mainly due to the differences in operating environment, structure of the catalyst layers, and operation temperature. Particularly in the case of Pt-based alloyed nanoparticles, the contamination of the membrane due to the de-alloying of the solute metal decreases the performance.103,104 Conversely, in RDE this does not influence the activity, as the solute metal is dispersed in the electrolyte bulk.
 | ||
| Fig. 5 (A) Mass activity of various PtNi nanoparticles measured at 0.9 V vs. RHE plotted against their publication year. Reproduced from ref. 11 with permission from Royal Society of Chemistry. (B) Performance of various Pt-based catalysts. Mass activities measured in half-cell setups (light blue) compared with performance in fuel cell (dark blue). Reproduced from ref. 102 with permission from American Association for the Advancement of Science. | ||
 | ||
| Fig. 6 (A) Kinetic current densities of Pt(221) and Pt(331) electrodes in different alkali metal hydroxide solutions as a function of the corresponding hydration energies. Specific activity of Pt(111) in acidic and basic solutions are shown by dotted lines. The activity of Pt(221) in 0.1 M HClO4 is also shown with a dotted line for comparison. (B) Schematics of the interaction between water-solvated alkali metal cations and the steps and terraces of Pt(221) surfaces. White, red, and black spheres represent H, O, and Pt, respectively. (A) and (B) are reproduced from ref. 109 with permission from American Chemical Society. (C) Energetics of the first electrochemical steps of CO reduction, both in vacuum and with cations, for the C1 and C2 pathways on Cu(100) at 0 V vs. RHE. Reproduced from ref. 31 with permission from American Chemical Society. | ||
The stability of the particle shape over the lifetime of the catalyst is another important aspect.98 For Pt3Ni catalysts, a beneficial effect of doping with other transition elements has been reported, both with respect to activity (cf.Fig. 5A) and shape stability.97 Also, a larger stability of (less active) cuboctahedral Pt3Ni as compared to octahedral NPs was reported.75
Solvent and electrolyte effects
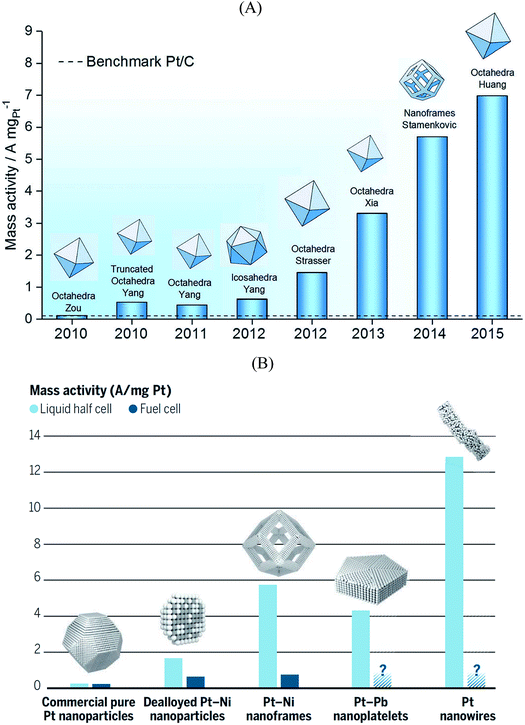
The electrolyte composition is another parameter that can substantially modulate the overall catalyst performance.29,105–108 The ORR activities of various single crystalline Pt electrodes in different alkaline solutions have been investigated by Garlyyev et al.109 Interestingly, the influence of the alkali metal cations is surface structure sensitive. As shown in Fig. 6A, the activity of Pt(111) increases if the electrolyte pH is changed from acidic to basic; however, the trend is reversed for high-index stepped Pt surfaces, such as Pt(221) and Pt(331). This is attributed to the presence of different types of active sites for stepped surfaces compared to pristine (111) surfaces. Fig. 6B illustrates how the alkali metal cations interact with Pt(221) surfaces. As said before, for an optimal ORR activity in acid the sites should have ca. 0.1–0.15 eV weaker *OH adsorption energy than Pt(111) terrace sites,35 which is found at concave defects or strained (111) terraces.20,62,67,73 In alkaline solutions the metal cations somehow modify *OH adsorption so that the optimal binding is found at (111) terraces. Thus, the presence of defects, either concave or convex, results in lower overall ORR performance for Pt electrodes in presence of alkali cations.To derive the aforementioned *OH adsorption energy criterion for ORR materials screening (i.e. ΔGXOH − ΔGPt(111)OH = (0.1–0.15) eV), some approximations need to be made. In particular, the identical solvation of the ORR adsorbates on all Pt-based catalysts is assumed, regardless of the lattice constant and alloying elements present in the structure. Solvation has been, therefore, habitually regarded as an adsorbate-dependent but structure- and composition-independent correction. However, recent works showed that this assumption is only suitable for the analysis of overall trends, and should be cautiously used when predicting the ORR activity of new Pt-based materials, as the differences in adsorbate solvation energies can be significant, particularly for *OH, the archetypal ORR intermediate.110 The same is true for other materials such as metalloporphyrins.111 Here it is worth mentioning that generalized coordination numbers in conjunction with micro-solvation can also be used to calculate average water stabilization values for extended surfaces and nanoparticles.112
Additionally, solvation is a crucial factor in studies aimed at breaking scaling relations in solution. As seen in the recent literature,111 adsorption-energy scaling relations broken under vacuum conditions can, in some cases, be restored in solution by virtue of solvation. As said before, it is not always advisable to include solvation as an external, constant correction, regardless of the nature of the active site.
Another important factor when modelling electrocatalytic systems are cation and anion effects. Numerous works have shown in the literature that the selectivity of CO2 and CO reduction depends on the size and concentration of halides and alkali cations.113–115 Moreover, in the recent literature it has been shown that cation effects are structure- and potential-dependent.31 For instance, DFT calculations show that during CO electroreduction on Cu, the hydrogenation of species containing C–C bonds is substantially enhanced by cations with respect to C1 species, justifying the selectivity towards ethylene at low overpotentials. This is illustrated in Fig. 6C, where the energetics of *CO hydrogenation to *CHO and *OCCOH are compared.
Furthermore, the impregnation of catalyst layers with ionic liquids (ILs) can have a beneficial effect on the catalytic activity, especially for those showing high oxygen solubility.116 This approach was applied to Pt–Ni nanoframes, resulting in an additional enhancement of their activity.86 Oxygen solubility is only one of many aspects, and the modification of the interfacial properties at the triple phase boundary is crucial.117 For example, recent systematic studies for Pt catalysts showed that preventing the formation of non-reactive oxygenated species at the catalyst surface is another important factor, and that the blocking of surface sites by ILs must as well be minimized.118
Predicting the selectivity and stability of catalytic centers
While most current research on electrocatalysis focuses on increasing the activity of catalysts, one has to consider two additional factors for the commercial realization of fuel cells and electrolyzers: the stability and selectivity of catalytic centers, as they strongly influence lifetime and efficiency. For instance, investigating the catalytic processes at the H2/Air fuel-cell interfaces, Pt nanoparticles supported on nanostructured carbon (Pt/C) are typically used as active material on both the anode and cathode catalyst layers. Two key factors limiting the industrial implementation of this technology can be described as: (i) degradation of Pt/C at elevated temperatures, leading to large performance losses over time, as well as (ii) poisoning of the Pt active sites by e.g. CO residues present in the gas phase,119 leading to a continuously reduced performance.Increasing the stability of Pt/C catalysts has been the objective of numerous studies over the past decades. Possible solutions such as improved carbon support stability, improved Pt–C anchoring or thermal treatment have been found through experimental work.120 Monitoring the durability of fuel cells is challenging in view of the long operation time. Typical post-mortem analysis by disassembly and analysis of a degraded fuel-cell stack can take months, making it unsuitable for catalyst screening.41–43,121 Accelerated stress tests, performed in an electrochemical half-cell setup (RDE setup), can drastically reduce screening times, but monitoring the impact of different degradation phenomena requires different supporting techniques.122
Conversely, a protocol for quick catalyst stability evaluation was proposed by Frydendal et al.123 By coupling the conventional RDE technique with an electrochemical quartz microbalance and inductively coupled plasma mass spectrometry,124 they collected corrosion and mass loss data for RuO2 and MnOx within a short period of time that provided preliminary guidelines for stable catalyst design. Although only OER catalysts were examined, the principle can be extended to other electrochemical reactions. Importantly, as the method is not capable of long-time stability prediction, further advances are much-needed.
In this sense, a novel stability descriptor proposed by Geiger et al.125 shows potential improvements over current methods, as it only depends on the dissolution properties of the catalyst material, excluding other typically critical parameters. The so-called stability number (S-number) monitors the ratio of catalytically produced molecules and dissolved catalyst material, giving an indication about the lifetime of the catalyst. The approach was tested and verified for prominent OER catalysts based on Ir, and should be easily extendable to other reactions and materials. The correlation between the S-number, predicted lifetime and the applied current density of different Ir-oxide-based powders is given in Fig. 7A. Remarkably, a long-time prediction of the catalyst stability of up to 10 years was derived from the S-number values, showing its potential for future catalyst design. Moreover, a convenient metric to guide future sustainable OER catalyst design was proposed by Markovic et al.126 The so-called activity–stability factor (ASF) correlates both the O2 generation and the dissolution rate of the catalytically active material.
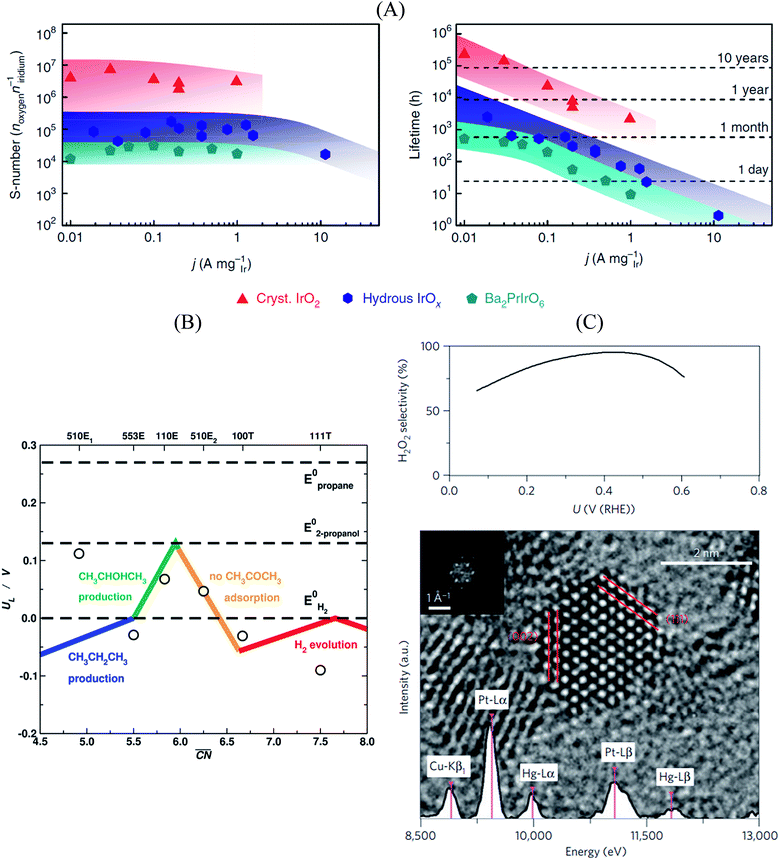 | ||
| Fig. 7 (A) Correlation between S-number (left), lifetime (right) and current density of different Ir-based materials. The stability prediction in a long-time period was calculated using the S-number of the corresponding materials. Figures reproduced from ref. 125 with permission from Nature Publishing Group. (B) Selectivity map of different Pt single-crystal surfaces towards the electrochemical reduction of acetone to isopropanol and propane, as a function of the generalized coordination number of the active centers. Figure reproduced from ref. 70 with permission from Nature Publishing Group. (C) H2O2 selectivity (top) and TEM image (bottom) of Pt–Hg/C, indicating a selectivity optimum of almost 100% at a potential of ∼0.4 V vs. RHE. Figures reproduced from ref. 129 with permission from Nature Publishing Group. | ||
Regarding the selective oxidation of CO on Pt, Cao et al.127 recently deposited iron hydroxide clusters on Pt nanoparticles using atomic layer deposition. The system achieves a 100% oxidation of CO over a broad range of temperatures, showing its huge potential as integrated gas purifier during hydrogen fuel-cell operation. Importantly, DFT was used to identify particularly active interfacial structures and captured Pt sites, giving the opportunity to design and tailor catalysts that enable full CO oxidation, thus circumventing CO poisoning during fuel cell operation.
There is another emerging field that requires catalysts with both high activity and selectivity: the electrochemical synthesis of high added-value and commodity chemicals. This area is becoming increasingly important, mainly because it can use excess renewable energy (e.g. from wind power) to enable cheap production. On top of that, electrosynthesis can help valorize biomass. The procedure can be applied to various valuable chemicals, as exemplarily highlighted by the work of Xue et al.128 In their work, they showed that n-butylamine, when added into the aqueous electrolyte of a water electrolysis cell, can be selectively oxidized to n-butyronitrile. This is remarkable, as typical Ni-, Co- and Fe-based OER catalysts can be used in the cell. In addition, no poisoning was observed at the cathode, where Pt active centers catalyze the hydrogen evolution reaction (HER).
Furthermore, Bondue et al.70 recently inspected the intriguing electroreduction of acetone on Pt single-crystal electrodes. While the experiments show that Pt(111) and Pt(100) are catalytically inert, Pt(110) and Pt(553) reduce acetone to isopropanol, and Pt(510) does it to propane. Generalized coordination numbers and DFT calculations were used to build the structure-sensitive selectivity map in Fig. 7B. Basically, not only does the activity depend on the geometry of the active sites but also their selectivity. In this case, high coordination sites are not able to adsorb molecular acetone, which renders them inactive, whereas sites with moderate coordination produce isopropanol and those with low coordination are selective towards propane.
Siahrostami et al.129 used DFT calculations to screen over promising catalysts for the electrochemical H2O2 production in acidic media. This process is particularly interesting, as it permits an efficient synthesis of H2O2 from its elements, compared to the conventional energy-intensive, environmentally harmful industrial processes. The catalyst is highly active and selective towards the reaction, while simultaneously being stable during the rough synthesis conditions.130 In their work, Siahrostami et al. focused on noble metal-based materials, in view of their high stability under reaction conditions. Catalyst screening based on adsorption thermodynamics of the reaction intermediates concluded that PtHg4 meets all the requirements for an efficient H2O2 synthesis, as the surface spatial configuration of Pt and Hg guarantees suitable *OOH binding and avoids *O formation, which implies that O2 reduction to H2O is hindered. Experimental studies on nanostructured Pt–Hg/C catalysts validated the prediction, with selectivities to H2O2 close to 100% at certain conditions together with high cycling stability (Fig. 7C).
In summary, considerable progress has been made in the design of more stable and selective electrocatalysts, although trial-and-error attempts often form the basis of these results. Quick prediction of both phenomena, however, significantly accelerates the development of promising catalysts and allows for a favorable compromise of activity, stability and selectivity. As the current computational power increases and new approaches based on e.g. machine learning are routinely used,131 DFT-based screening will hopefully predict not only more accurate activities but also the selectivity and stability of electrocatalysts. Novel metrics, in line with the experimental “stability number”, would facilitate the prediction of stable catalysts. For instance, there exist descriptors to evaluate the reactivity of lattice oxygen132 and activity–stability plots have also been proposed.51,133 Both approaches may help prevent the undesirable decomposition of oxide catalysts during the OER.
Concluding remarks
The past two decades witnessed blooming progress in the development of electrocatalysts for clean energy conversion, capitalizing on the advances in experimental and theoretical methodologies7,67,134,135 for the study of electrified interfaces. Advancements in the preparation of atomically precise single crystalline surfaces and in operando characterization methodologies of surfaces enabled in several cases the identification of catalytically active centers. The emerging field of nanoparticle electrocatalysis with controlled shape and defined surface atom arrangements has benefited from those advancements. Importantly, tuning the size and shape of nanostructured catalysts is shown to provide control over their catalytic activity and selectivity. Taking actual advantage of this enhancement requires that both size and shape are stable over the required lifetime of the catalyst. Another vital parameter to consider in electrocatalysis is the electrolyte composition, as recent studies show its influence on the activity, selectivity, and stability of the catalyst.All these advances have opened up new, knowledge-based ways to enhance the intrinsic activity of a catalyst instead of using just trial-and-error-based experiments and computational models. Nevertheless, having a highly active and stable electrode is only the first – but very important – step towards commercially viable electrocatalysts: for applications in (electro)chemical syntheses, large turnover rates are required. The same is true for fuel cells: the performance of an MEA at low currents can be to a certain extent predicted by the characterization of catalyst layers in liquid environments using rotating disc electrodes and, at even higher currents, by the floating electrode technique.136 For the actual operation in a PEM fuel cell, large areal current and power densities (>1.5 W cm−2) are required. Under these conditions, mass transport is crucial. The mass transport behavior depends on the catalyst, its distribution on the support, and the thickness and porosity of the catalyst layer. It has been shown that with respect to mass transport behavior, large nanoparticles (for the same loading) might show considerably poorer performance than 2–3 nm nanoparticles, even if they have excellent activity at low overpotentials.136 The role of the mesoscale structure, in particular for the reactant diffusion and re-adsorption of intermediates, was demonstrated in the literature for CO2 electroreduction.137
In brief, the identification of active surface sites, preparation of stable catalysts with a large number of such sites, and the optimization of the catalyst layer structure are paramount endeavors in contemporary electrocatalyst research. We hope to have shown here that the collaborative interplay of theory and experiments can help in the rational prediction and elaboration of enhanced electrocatalysts.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We kindly acknowledge the financial support from German Research Foundation (DFG) under Grant No. 355784621, under Germany's Excellence Strategy–EXC 2089/1–390776260, under Germany's Excellence cluster “e-conversion” and DFG projects BA 5795/4-1 and BA 5795/3-1. F. C. V. thanks the Spanish MICIU for a Ramón y Cajal research contract (RYC-2015-18996) and financial support through the program “Units of Excellence María de Maeztu” (grant MDM-2017-0767). O. S. would like to acknowledge funding from the INSPIRE project: this project has received funding from the Fuel Cells and Hydrogen 2 Joint Undertaking under grant agreement No 700127. This Joint Undertaking receives support from the European Union's Horizon 2020 Research and Innovation Program and Hydrogen Europe and Hydrogen Europe Research.References
- F. Haber, Resonance, 2002, 7, 86–94 CrossRef.
- P. Sabatier, Eur. J. Inorg. Chem., 1911, 44, 1984–2001 CAS.
- I. Langmuir, Trans. Faraday Soc., 1922, 17, 607–620 RSC.
- H. S. Taylor, Proc. R. Soc. London, Ser. A, 1925, 108, 105–111 CrossRef CAS.
- A. A. Balandin, Adv. Catal., 1969, 19, 1 CAS.
- G. Ertl, Angew. Chem., Int. Ed., 2008, 47, 3524–3535 CrossRef CAS PubMed.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- J. Zhan, Z. Zhao, Z. Xia and L. Dai, Nat. Nanotechnol., 2015, 10, 444–452 CrossRef PubMed.
- M. K. Debe, Nature, 2012, 486, 43–51 CrossRef CAS PubMed.
- J. Kibsgaard, Z. Chen, B. N. Reinecke and T. F. Jaramillo, Nat. Mater., 2012, 11, 963–969 CrossRef CAS PubMed.
- P. Strasser, M. Gliech, S. Kuehl and T. Moeller, Chem. Soc. Rev., 2018, 47, 715–735 RSC.
- B. Garlyyev, Y. Liang, S. Xue, S. Watzele, J. Fichtner, W. J. Li, X. Ding and A. S. Bandarenka, Curr. Opin. Electrochem., 2019, 14, 206–213 CrossRef CAS.
- P. Strasser, S. Koh, T. Anniyev, J. Greeley, K. More, C. Yu, Z. Liu, S. Kaya, D. Nordlund, H. Ogasawara, M. F. Toney and A. Nilsson, Nat. Chem., 2010, 2, 454–460 CrossRef CAS PubMed.
- T. Bligaard and J. K. Nørskov, Electrochim. Acta, 2007, 52, 5512–5516 CrossRef CAS.
- M. Mavrikakis, B. Hammer and J. K. Nørskov, Phys. Rev. Lett., 1998, 81, 2819–2822 CrossRef.
- H. E. Hoster, O. B. Alves and M. T. M. Koper, ChemPhysChem, 2010, 11, 1518–1524 CrossRef CAS PubMed.
- V. R. Stamenkovic, B. S. Mun, K. J. J. Mayrhofer, P. N. Ross, N. M. Markovic, J. Rossmeisl, J. Greeley and J. K. Nørskov, Angew. Chem., Int. Ed., 2006, 45, 2897–2901 CrossRef CAS PubMed.
- E. A. Heider, T. Jacob and L. A. Kibler, J. Electroanal. Chem., 2018, 819, 289–295 CrossRef CAS.
- R. Lin, X. Cai, H. Zeng and Z. Yu, Adv. Mater., 2018, 30, 1705332 CrossRef PubMed.
- M. Escudero-Escribano, P. Malacrida, M. H. Hansen, U. G. Vej-Hansen, A. Velázquez-Palenzuela, V. Tripkovic, J. Schiøtz, J. Rossmeisl, I. E. L. Stephens and I. Chorkendorff, Science, 2016, 352, 73–76 CrossRef CAS PubMed.
- V. Čolić and A. S. Bandarenka, ACS Catal., 2016, 6, 5378–5385 CrossRef.
- V. R. Stamenkovic, B. S. Mun, M. Arenz, K. J. J. Mayrhofer, C. A. Lucas, G. Wang, P. N. Ross and N. M. Markovic, Nat. Mater., 2007, 6, 241–247 CrossRef CAS PubMed.
- J. E. Mueller, P. Krtil, L. A. Kibler and T. Jacob, Phys. Chem. Chem. Phys., 2014, 16, 15029–15042 RSC.
- N. Takehiro, P. Liu, A. Bergbreiter, J. K. Nørskov and R. J. Behm, Phys. Chem. Chem. Phys., 2014, 16, 23930–23943 RSC.
- N. Erini, V. Beermann, M. Gocyla, M. Gliech, M. Heggen, R. E. Dunin-Borkowski and P. Strasser, Angew. Chem., Int. Ed., 2017, 56, 6533–6538 CrossRef CAS PubMed.
- I. Katsounaros, M. C. Figueiredo, X. Chen, F. Calle-Vallejo and M. T. M. Koper, ACS Catal., 2017, 7, 4660–4667 CrossRef CAS.
- T. Kumeda, H. Tajiri, O. Sakata, N. Hoshi and M. Nakamura, Nat. Commun., 2018, 9, 4378 CrossRef PubMed.
- I. Ledezma-Yanez, W. D. Z. Wallace, P. Sebastián-Pascual, V. Climent, J. M. Feliu and M. T. M. Koper, Nat. Energy, 2017, 2, 17031 CrossRef CAS.
- D. Strmcnik, K. Kodama, D. van der Vliet, J. Greeley, V. R. Stamenkovic and N. M. Markovic, Nat. Chem., 2009, 1, 466 CrossRef CAS PubMed.
- B. Garlyyev, S. Xue, S. Watzele, D. Scieszka and A. S. Bandarenka, J. Phys. Chem. Lett., 2018, 9, 1927–1930 CrossRef CAS PubMed.
- E. Pérez-Gallent, G. Marcandalli, M. C. Figueiredo, F. Calle-Vallejo and M. T. M. Koper, J. Am. Chem. Soc., 2017, 139, 16412–16419 CrossRef PubMed.
- I. E. L. Stephens, A. S. Bondarenko, F. J. Perez-Alonso, F. Calle-Vallejo, L. Bech, T. P. Johansson, A. K. Jepsen, R. Frydendal, B. P. Knudsen, J. Rossmeisl and I. Chorkendorff, J. Am. Chem. Soc., 2011, 133, 5485–5491 CrossRef CAS PubMed.
- J. Tymoczko, F. Calle-Vallejo, W. Schuhmann and A. S. Bandarenka, Nat. Commun., 2016, 7, 10990 CrossRef CAS PubMed.
- A. S. Bandarenka, A. S. Varela, M. Karamad, F. Calle-Vallejo, L. Bech, F. J. Perez-Alonso, J. Rossmeisl, I. E. L. Stephens and I. Chorkendorff, Angew. Chem., Int. Ed., 2012, 51, 11845–11848 CrossRef CAS PubMed.
- J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jarmillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556 CrossRef CAS PubMed.
- Z.-D. He, Y.-X. Chen, E. Santos and W. Schmickler, Angew. Chem., Int. Ed., 2018, 57, 7948 CrossRef CAS PubMed.
- R. Yang, J. Leisch, P. Strasser and M. F. Toney, Chem. Mater., 2010, 22, 4712–4720 CrossRef CAS.
- J. Fichtner, B. Garlyyev, S. Watzele, H. A. El-sayed, J. Schwaemmlein, W. Li, F. Maillard, L. Dubau, J. Michalicka, J. Macak, A. W. Holleitner and A. S. Bandarenka, ACS Appl. Mater. Interfaces, 2019, 11, 5129–5135 CrossRef CAS PubMed.
- B. Garlyyev, M. Pohl, V. Čolić, Y. Liang, F. K. Butt, A. Holleitner and A. S. Bandarenka, Electrochem. Commun., 2018, 88, 10–14 CrossRef CAS.
- A. Velázquez-Palenzuela, F. Masini, A. F. Pedersen, M. Escudero-Escribano, D. Deiana, P. Malacrida, T. W. Hansen, D. Friebel, A. Nilsson, I. E. L. Stephens and I. Chorkendorff, J. Catal., 2015, 328, 297–307 CrossRef.
- B. Han, C. E. Carlton, A. Kongkanand, R. S. Kukreja, B. R. Theobald, L. Gan, R. O'Malley, P. Strasser, F. T. Wagner and Y. Shao-Horn, Energy Environ. Sci., 2015, 8, 258–266 RSC.
- L. Dubau, M. Lopez-Haro, L. Castanheira, J. Durst, M. Chatenet, P. Bayle-Guillemaud, L. Guétaz, N. Caqué, E. Rossinot and F. Maillard, Appl. Catal., B, 2013, 142, 801–808 CrossRef.
- L. Dubau, F. Maillard, M. Chatenet, L. Guetaz, J. André and E. Rossinot, J. Electrochem. Soc., 2010, 157, B1887–B1895 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, J. Roosmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, J. Rossmeisl and M. T. M. Koper, Phys. Rev. Lett., 2012, 108, 116103 CrossRef CAS PubMed.
- F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410 CrossRef CAS PubMed.
- F. Calle-Vallejo, N. G. Inoglu, H. Su, J. I. Martínez, I. C. Man, M. T. M. Koper, J. R. Kitchin and J. Rossmeisl, Chem. Sci., 2013, 4, 1245–1249 RSC.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, E. Abad and M. T. M. Koper, Surf. Sci., 2013, 607, 47–53 CrossRef CAS.
- H. Su, K. Sun, W. Wang, Z. Zeng, F. Calle-Vallejo and W. Li, J. Phys. Chem. Lett., 2016, 7, 5302–5306 CrossRef CAS PubMed.
- F. Calle-Vallejo and M. T. M. Koper, ACS Catal., 2017, 7, 7346–7351 CrossRef CAS.
- F. Calle-Vallejo, O. A. Díaz-Morales, M. J. Kolb and M. T. M. Koper, ACS Catal., 2015, 5, 869–873 CrossRef CAS.
- I. C. Man, H. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- M. T. M. Koper, J. Electroanal. Chem., 2011, 660, 254–260 CrossRef CAS.
- Y. Li and Q. Sun, Adv. Energy Mater., 2016, 6, 1600463 CrossRef.
- N. Govindarajan, M. T. M. Koper, E. J. Meijer and F. Calle-Vallejo, ACS Catal., 2019, 9, 4218–4225 CrossRef CAS.
- X. Nie, M. R. Esopi, M. J. Janik and A. Asthagiri, Angew. Chem., Int. Ed., 2013, 52, 2459–2462 CrossRef CAS PubMed.
- Q. H. Low, N. W. X. Loo, F. Calle-Vallejo and B. S. Yeo, Angew. Chem., Int. Ed., 2019, 58, 2256–2260 CrossRef CAS PubMed.
- C. H. Kjaergaard, J. Rossmeisl and J. K. Nørskov, Inorg. Chem., 2010, 49, 3567–3572 CrossRef CAS PubMed.
- H. Li, Y. Li, M. T. M. Koper and F. Calle-Vallejo, J. Am. Chem. Soc., 2014, 136, 15694–15701 CrossRef CAS PubMed.
- F. Viñes, J. R. B. Gomes and F. Illas, Chem. Soc. Rev., 2014, 43, 4922–4939 RSC.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, P. Sautet and D. Loffreda, Angew. Chem., Int. Ed., 2014, 53, 8316–8319 CrossRef CAS PubMed.
- F. Calle-Vallejo and A. S. Bandarenka, ChemSusChem, 2018, 11, 1824–1828 CrossRef CAS PubMed.
- A. F. Pedersen, E. T. Ulrikkeholm, M. Escudero-Escribano, T. P. Johansson, P. Malacrida, C. M. Pedersen, M. H. Hansen, K. D. Jensen, J. Rossmeisl, D. Friebel, A. Nilsson, I. Chorkendorff and I. E. L. Stephens, Nano energy, 2016, 29, 249–260 CrossRef CAS.
- Z. Zhao, Z. Chen, X. Zhang and G. Lu, J. Phys. Chem. C, 2016, 120, 28125–28130 CrossRef CAS.
- M. Núñez, J. L. Lansford and D. G. Vlachos, Nat. Chem., 2019, 11, 449–456 CrossRef PubMed.
- D. Liuzzi, F. J. Pérez-Alonso, F. J. García-García, F. Calle-Vallejo, J. L. G. Fierro and S. Rojas, Catal. Sci. Technol., 2016, 6, 6495–6503 RSC.
- F. Calle-Vallejo, J. Tymoczko, V. Čolić, Q. Huy Vu, M. D. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. S. Bandarenka, Science, 2015, 350, 185–189 CrossRef CAS PubMed.
- M. D. Pohl, S. Watzele, F. Calle-Vallejo and A. S. Bandarenka, ACS Omega, 2017, 2, 8141–8147 CrossRef CAS.
- F. Calle-Vallejo, M. Pohl and A. S. Bandarenka, ACS Catal., 2017, 7, 4355–4359 CrossRef CAS.
- C. J. Bondue, F. Calle-Vallejo, M. C. Figueiredo and M. T. M. Koper, Nat. Catal., 2019, 2, 243–250 CrossRef CAS.
- M. Rück, A. Bandarenka, F. Calle-Vallejo and A. Gagliardi, J. Phys. Chem. Lett., 2018, 9, 4463–4468 CrossRef PubMed.
- B. Garlyyev, K. Kratzl, M. Rück, J. Michalička, J. Fichtner, J. Macak, T. Kratky, S. Günther, M. Cokoja, A. S. Bandarenka, A. Gagliardi and R. Fischer, Angew. Chem., Int. Ed., 2019, 58, 9596–9600 CrossRef CAS PubMed.
- F. Calle-Vallejo, M. D. Pohl, D. Reinisch, P. Sautet and A. S. Bandarenka, Chem. Sci., 2017, 8, 2283–2289 RSC.
- T. Yu, D. Y. Kim, H. Zhang and Y. Xia, Angew. Chem., Int. Ed., 2011, 50, 2773–2777 CrossRef CAS PubMed.
- S. Kühl, M. Gocyla, H. Heyen, S. Selve, M. Heggen, R. E. Dunin-Borkowski and P. Strasser, J. Mater. Chem. A, 2019, 7, 1149–1159 RSC.
- L. Dubau, J. Durst, F. Maillard, L. Guétaz, M. Chatenet, J. André and E. Rossinot, Electrochim. Acta, 2011, 56, 10658–10667 CrossRef CAS.
- R. Chattot, O. Le Bacq, V. Beermann, S. Kühl, J. Herranz, S. Henning, L. Kühn, T. Asset, L. Guétaz, G. Renou, J. Drnec, P. Bordet, A. Pasturel, A. Eychmüller, T. J. Schmidt, P. Strasser, L. Dubau and F. Maillard, Nat. Mater., 2018, 17, 827–833 CrossRef CAS PubMed.
- G. Ye, Y. Gong, J. Lin, B. Li, Y. He, S. T. Pantelides, W. Zhou, R. Vajtai and P. M. Ajayan, Nano Lett., 2016, 16, 1097–1103 CrossRef CAS PubMed.
- M. Lefèvre, E. Proietti, F. Jaouen and J. P. Dodelet, Science, 2009, 324, 71–74 CrossRef PubMed.
- U. Martinez, S. Komini Babu, E. F. Holby, H. T. Chung, X. Yin and P. Zelenay, Adv. Mater., 2019 DOI:10.1002/adma.201806545.
- Y. Jiang, L. Yang, T. Sun, J. Zhao, Z. Lyu, O. Zhuo, X. Wang, Q. Wu, J. Ma and Z. Hu, ACS Catal., 2015, 5, 6707–6712 CrossRef CAS.
- K. Kinoshita, Carbon: Electrochemical and physicochemical properties, John Wiley & Sons, New York, 1988 Search PubMed.
- H. Li, F. Calle-Vallejo, M. J. Kolb, Y. Kwon, Y. Li and M. T. M. Koper, J. Am. Chem. Soc., 2013, 135, 14329–14338 CrossRef CAS PubMed.
- R. Narayanan and M. A. El-Sayed, Nano Lett., 2004, 4, 1343–1348 CrossRef CAS.
- M. A. Mahmoud, B. Garlyyev and M. A. El-Sayed, J. Phys. Chem. C, 2013, 117, 21886–21893 CrossRef CAS.
- C. Chen, Y. Kang, Z. Huo, Z. Zhu, W. Huang, H. L. Xin, J. D. Snyder, D. Li, J. A. Herron, M. Mavrikakis, M. Chi, K. L. More, Y. Li, N. M. Markovic, G. A. Somorjai, P. Yang and V. R. Stamenkovic, Science, 2014, 343, 1339–1343 CrossRef CAS PubMed.
- K. Kinoshita, J. Electrochem. Soc., 1990, 137, 845–848 CrossRef CAS.
- A. Kabbabi, F. Gloaguen, F. Andolfatto and R. Durand, J. Electroanal. Chem., 1994, 373, 251–254 CrossRef CAS.
- L. Genies, R. Faure and R. Durand, Electrochim. Acta, 1998, 44, 1317–1327 CrossRef CAS.
- C. Wang, D. van der Vliet, K. C. Chang, H. You, D. Strmcnik, J. A. Schlueter, N. M. Markovic and V. R. Stamenkovic, J. Phys. Chem. C, 2009, 113, 19365–19368 CrossRef CAS.
- F. J. Perez-Alonso, D. N. McCarthy, A. Nierhoff, P. Hernandez-Fernandez, C. Strebel, I. E. L. Stephens, J. H. Nielsen and I. Chorkendorff, Angew. Chem., Int. Ed., 2012, 51, 4641–4643 CrossRef CAS PubMed.
- G. A. Tritsaris, J. Greeley, J. Rossmeisl and J. K. Nørskov, Catal. Lett., 2011, 141, 909–913 CrossRef CAS.
- P. Hernandez-Fernandez, F. Masini, D. N. McCarthy, C. E. Strebel, D. Friebel, D. Deiana, P. Malacrida, A. Nierhoff, A. Bodin, A. M. Wise, J. H. Nielsen, T. W. Hansen, A. Nilsson, I. E. L. Stephens and I. Chorkendorff, Nat. Chem., 2014, 6, 732–738 CrossRef CAS PubMed.
- C. Roy, B. Sebok, S. B. Scott, E. M. Fiordaliso, J. E. Sørensen, A. Bodin, D. B. Trimarco, C. D. Damsgaard, P. C. K. Vesborg, O. Hansen, I. E. L. Stephens, J. Kibsgaard and I. Chorkendorff, Nat. Catal., 2018, 1, 820–829 CrossRef CAS.
- N. S. Porter, H. Wu, Z. Quan and J. Fang, Acc. Chem. Res., 2013, 46, 1867–1877 CrossRef CAS PubMed.
- V. Beermann, M. Gocyla, E. Willinger, S. Rudi, M. Heggen, R. E. Dunin-Borkowski, M.-G. Willinger and P. Strasser, Nano Lett., 2016, 16, 1719–1725 CrossRef CAS PubMed.
- X. Huang, Z. Zhao, L. Cao, Y. Chen, E. Zhu, Z. Lin, M. Li, A. Yan, A. Zettl, Y. M. Wang, X. Duan, T. Mueller and Y. Huang, Science, 2015, 348, 1230–1234 CrossRef CAS PubMed.
- M. Gocyla, S. Kuehl, M. Shviro, H. Heyen, S. Selve, R. E. Dunin-Borkowski, M. Heggen and P. Strasser, ACS Nano, 2018, 12, 5306–5311 CrossRef CAS PubMed.
- L. Huang, X. Zhang, Q. Wang, Y. Han, Y. Fang and S. Dong, J. Am. Chem. Soc., 2018, 140, 1142–1147 CrossRef CAS PubMed.
- V. R. Stamenkovic, B. Fowler, B. S. Mun, G. Wang, P. N. Ross, C. A. Lucas and N. M. Markovic, Science, 2007, 315, 493–497 CrossRef CAS PubMed.
- V. Tripković, I. Cerri, T. Bligaard and J. Rossmeisl, Catal. Lett., 2014, 144, 380–388 CrossRef.
- I. E. L. Stephens, J. Rossmeisl and I. Chorkendorff, Science, 2016, 354, 1378–1379 CrossRef CAS PubMed.
- W. Vielstich, A. Lamm and H. A. Gasteiger, Handbook of fuel cells: fundamentals technology and applications, Wiley, New York, 2003 Search PubMed.
- B. Kienitz, B. Pivovar, T. Zawodzinski and F. H. Garzon, J. Electrochem. Soc., 2011, 158, B1175–B1183 CrossRef CAS.
- F. Lu, Y. Zhang, S. Liu, D. Lu, D. Su, M. Liu, Y. Zhang, P. Liu, J. X. Wang, R. R. Adzic and O. Gang, J. Am. Chem. Soc., 2017, 139, 7310–7317 CrossRef CAS PubMed.
- A. Izgorodin, E. Izgorodina and D. R. MacFarlane, Energy Environ. Sci., 2012, 5, 9496–9501 RSC.
- K. D. Jensen, J. Tymoczko, J. Rossmeisl, A. S. Bandarenka, I. Chorkendorff, M. Escudero-Escribano and I. E. L. Stephens, Angew. Chem., Int. Ed., 2018, 57, 2800–2805 CrossRef CAS PubMed.
- S. Xue, B. Garlyyev, S. Watzele, Y. Liang, J. Fichtner, M. D. Pohl and A. S. Bandarenka, ChemElectroChem, 2018, 5, 2326–2329 CrossRef CAS.
- B. Garlyyev, S. Xue, M. D. Pohl, D. Reinisch and A. S. Bandarenka, ACS Omega, 2018, 3, 15325–15331 CrossRef CAS.
- Z. He, S. Hanselman, Y. Chen, M. T. M. Koper and F. Calle-Vallejo, J. Phys. Chem. Lett., 2017, 8, 2243–2246 CrossRef CAS PubMed.
- F. Calle-Vallejo, A. Krabbe and J. M. García-Lastra, Chem. Sci., 2017, 8, 124–130 RSC.
- F. Calle-Vallejo, R. F. de Morais, F. Illas, D. Loffreda and P. Sautet, J. Phys. Chem. C, 2019, 123, 5578–5582 CrossRef CAS.
- A. Murata and Y. Hori, Bull. Chem. Soc. Jpn., 1991, 64, 123–127 CrossRef CAS.
- A. S. Varela, W. Ju, T. Reier and P. Strasser, ACS Catal., 2016, 6, 2136–2144 CrossRef CAS.
- S. Lee, D. Kim and J. Lee, Angew. Chem., 2015, 127, 14914–14918 CrossRef.
- J. Snyder, T. Fujita, M. W. Chen and J. Erlebacher, Nat. Mater., 2010, 9, 904–907 CrossRef CAS PubMed.
- M. Qiao and M.-M. Titirici, Chem.–Eur. J., 2018, 24, 18374–18384 CrossRef CAS PubMed.
- G. Zhang, T. Wolker, D. J. S. Sandbeck, M. Munoz, K. J. J. Mayrhofer, S. Cherevko and B. J. M. Etzold, ACS Catal., 2018, 8, 8244–8254 CrossRef CAS PubMed.
- J. J. Baschuk and X. Li, Int. J. Energy Res., 2001, 25, 695–713 CrossRef CAS.
- X. Yu and S. Ye, J. Power Sources, 2007, 172, 145–154 CrossRef CAS.
- N.-I. Kim, Y. Seo, K. B. Kim, N. Lee, J.-H. Lee, I. Song, H. Choi and J.-Y. Park, J. Power Sources, 2014, 253, 90–97 CrossRef CAS.
- Y. Zhang, S. Chen, Y. Wang, W. Ding, R. Wu, L. Li, X. Qi and Z. Wie, J. Power Sources, 2015, 273, 62–69 CrossRef CAS.
- R. Frydendal, E. A. Paoli, B. P. Knudsen, B. Wickman, P. Malacrida, I. E. L. Stephens and I. Chorkendorff, ChemElectroChem, 2014, 1, 2075–2081 CrossRef CAS.
- A. A. Topalov, I. Katsounaros, M. Auinger, S. Cherevko, J. C. Meier, S. O. Klemm and K. J. Mayrhofer, Angew. Chem., Int. Ed., 2012, 51, 12613–12615 CrossRef CAS PubMed.
- S. Geiger, O. Kasian, M. Ledendecker, E. Pizzutilo, A. M. Mingers, W. T. Fu, O. Diaz-Morales, Z. Li, T. Oellers, L. Fruchter, A. Ludwig, K. J. J. Mayrhofer, M. T. M. Koper and S. Cherevko, Nat. Catal., 2018, 1, 508–515 CrossRef CAS.
- Y.-T. Kim, P. P. Lopes, S.-A. Park, A.-Y. Lee, J. Lim, H. Lee, S. Back, Y. Jung, N. Danilovic, V. Stamenkovic, J. Erlebacher, J. Snyder and N. M. Markovic, Nat. Commun., 2017, 8, 1449 CrossRef PubMed.
- L. Cao, W. Liu, Q. Luo, R. Yin, B. Wang, J. Weissenrieder, M. Soldemo, H. Yan, Y. Lin, Z. Sun, C. Ma, W. Zhang, S. Chen, H. Wang, Q. Guan, T. Yao, S. Wei, J. Yang and J. Lu, Nature, 2019, 565, 631–635 CrossRef CAS PubMed.
- S. Xue, S. Watzele, V. Čolić, K. Brandl, B. Garlyyev and A. S. Bandarenka, ChemSusChem, 2017, 10, 4812–4816 CrossRef CAS PubMed.
- S. Siahrostami, A. Verdaguer-Casadevall, M. Karamad, D. Deiana, P. Malacrida, B. Wickman, M. Escudero-Escribano, E. A. Paoli, R. Frydendal, T. W. Hansen, I. Chorkendorff, I. E. L. Stephens and J. Rossmeisl, Nat. Mater., 2013, 12, 1137–1143 CrossRef CAS PubMed.
- J. M. Campos-Martin, G. Blanco-Brieva and J. L. Fierro, Angew. Chem., 2006, 45, 6962–6984 CrossRef CAS PubMed.
- A. A. Peterson, R. Christensen and A. Khorshidi, Phys. Chem. Chem. Phys., 2017, 19, 10978–10985 RSC.
- V. Fung, F. F. Tao and D. Jiang, J. Phys. Chem. Lett., 2017, 8, 2206–2211 CrossRef CAS PubMed.
- K. S. Exner, ChemElectroChem, 2018, 5, 3243 CrossRef CAS.
- J. H. K. Pfisterer, Y. Liang, O. Schneider and A. S. Bandarenka, Nature, 2017, 549, 74–77 CrossRef CAS PubMed.
- O. M. Magnussen and A. Groß, J. Am. Chem. Soc., 2019, 141, 4777–4790 CrossRef CAS PubMed.
- S. Martens, L. Asen, G. Ercolano, F. Dionigi, C. Zalitis, A. Hawkins, A. M. Bonastre, L. Seidl, A. C. Knoll, J. Sharman, P. Strasser, D. Jones and O. Schneider, J. Power Sources, 2018, 392, 274–284 CrossRef CAS.
- H. Mistry, F. Behafarid, R. Reske, A. S. Varela, P. Strasser and B. R. Cuenya, ACS Catal., 2016, 6, 1075–1080 CrossRef CAS.
- N. Govindarajan, J. M. García-Lastra, E. J. Meijer and F. Calle-Vallejo, Curr. Opin. Electrochem., 2018, 8, 110–117 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |