DOI:
10.1039/C9SC01690B
(Edge Article)
Chem. Sci., 2019,
10, 6957-6965
Glycerol transport through the aquaglyceroporin GlpF: bridging dynamics and kinetics with atomic simulation†
Received
6th April 2019
, Accepted 17th June 2019
First published on 18th June 2019
Abstract
The aquaglyceroporin GlpF is a member of the aquaporin family. It selectively conducts small molecules, such as glycerol, across the cell membrane under a concentration gradient of the substrate. Atomistic molecular dynamics (MD) simulation would provide great insight into the substrate transport mechanism of GlpF and membrane channels alike. Ideally, non-equilibrium simulations under various concentration gradients of glycerol are desired to emulate the transportation in cells, but this kind of simulation is difficult due to a complicated system setup and high computational cost. Here, we present a new strategy to extract non-equilibrium kinetic information from equilibrium MD simulation. We first performed long-time (totally 22.5 μs) multi-copy equilibrium MD simulations of glycerol conduction through GlpF. Tens of times the spontaneous permeation of glycerol through GlpF was observed, allowing us to elucidate the detailed mechanism of the stereoselectivity for glycerol. Then we employed Markov state model (MSM) analysis of the MD trajectories to identify the intermediate states during glycerol transport and calculate the inter-state transition rate constants. Based on the results of MSM analysis, we built the kinetic models of glycerol transport and calculated the glycerol fluxes under various concentration gradients by solving the master equations. The results agree well with the experimental measurement at a certain glycerol concentration, and provide holistic information on the glycerol conduction capacity of GlpF. Our work demonstrates that long-time atomistic MD simulations can now bridge the microscopic dynamics and the kinetic description of substance transport through membrane channels, hopefully facilitating the engineering of new selective channels for various molecules.
1. Introduction
Facilitated translocation of molecules through channels and pores is important for transmembrane transport in biological systems. Molecular dynamics (MD) simulation is a powerful tool for the detailed mechanistic study of channel transport.1,2 However, realistic simulation of non-equilibrium substrate translocation through channels under a concentration gradient across the membrane is not straightforward. Due to the periodic conditions of the simulation system, explicitly maintaining a substrate concentration difference requires a large simulation system and/or special setups.3,4 On the other hand, simulating sustained steady states under various concentration differences is computationally expensive. Alternatively, substrate translocation could be simulated under equilibrium conditions, and kinetic information, such as transport flux and rate constant, is estimated based on the potential of mean force (PMF) of substrate permeation and transition state theory. Although the pore axis is a natural reaction coordinate for substrate transport, generally PMF does not govern dynamics, especially in the case of wide pores. Furthermore, as the interaction between the substrate and the channel entails multiple energy barriers and substrate binding sites inside the channel, the transport process could not be approximated by an elementary reaction model. Alternatively, the transport kinetics is better described by a discrete-state Markovian model. However, using PMF profiles to discretize the state space along the translocation pathway is highly arbitrary. Recently, a more rigorous method, the Markov state model (MSM) method,5–12 has been widely applied to MD simulations of biomolecules. Combined with large scale multi-copy MD simulations, the MSM method has been successfully applied to kinetic analysis of problems like protein folding, and various conformational changes of proteins.5,13–18 By using MSM analysis, we could obtain more reasonable discretization of the state space and rate constants, based on which the non-equilibrium steady-state kinetics could be calculated through constructing a discrete-state kinetic model and solving master equations under various boundary conditions.
GlpF, the glycerol facilitator in Escherichia coli, is responsible for uptake of water, glycerol and other small alditols (or linear polyalcohols) into the cell.19–21 It belongs to the aquaglyceroporin subfamily in the large aquaporin (AQP) protein family.22 Once they are translocated into the cytoplasm, glycerol molecules are phosphorylated and participate in the glycolytic pathway to generate energy.23 GlpF embedded in the membrane forms a homotetramer (Fig. 1a). Each monomer contains a right-handed bundle of six transmembrane α-helices and two half-membrane-spanning α-helices, which enclose an hourglass-shaped pore in each monomer (Fig. 1b).20,24 The cytoplasmic and periplasmic ends of the pore entail two conically shaped vestibules, while the middle part is narrowed by two constrictive regions. The NPA region features two Asn-Pro-Ala (NPA) motifs conserved among most AQPs, which form an electrostatic area excluding protons (Fig. 1b).25 The selectivity filter region (SF region, also named the ar/R region) forms the narrowest constriction of the pore with a radius of only ∼1.7 Å (Fig. 1b). It is strongly amphipathic, lined by an arginine (Arg206) and two aromatic amino acids (Trp48 and Phe200), which are important for substrate selectivity.20,26–28
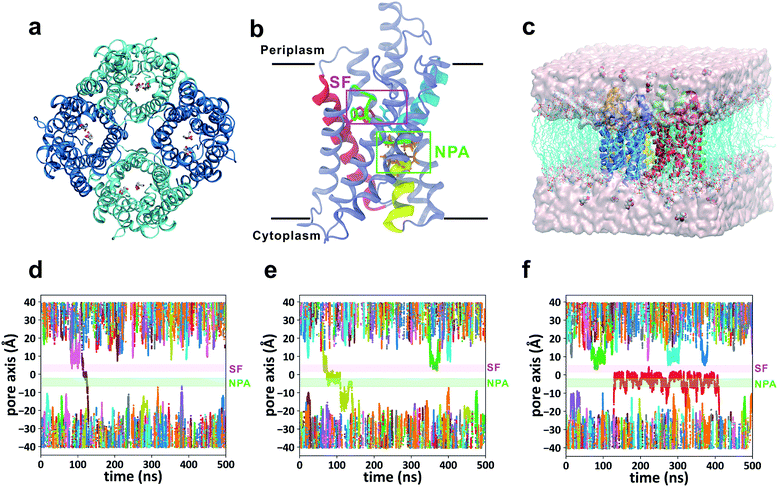 |
| | Fig. 1 Simulation of glycerol conduction through GlpF. (a) Top view of the crystal structure of the GlpF tetramer from the periplasmic side. (b) Atomic structure of one monomer of GlpF represented by cartoon mode. The three crucial residues (Trp48, Phe200, and Arg206) in the SF region are rendered by licorice mode and colored red, green, and cyan, respectively. The secondary structures they belong to are colored similarly. The two half helices (M3 and M7) are colored yellow and cyan, and the NPA motifs on them are rendered by licorice mode and colored orange. The NPA and SF regions are framed out by green and purple squares, respectively. Other parts of the protein are colored ice blue. (c) Simulation system of the GlpF tetramer embedded in a POPC lipid bilayer in the presence of 0.036 M glycerol. (d–f) Three representative trajectories of the equilibrium MD simulations. All the trajectories of 12 glycerols in the simulation system are shown with different colors. The NPA and SF regions are highlighted by green and purple bars, respectively. | |
Previous MD simulation studies of glycerol translocation through GlpF have employed various enhanced sampling methods to calculate the PMF profile, including steered MD,29 umbrella sampling,30 and adaptive biasing force (ABF) methods.31 All these simulations found the highest energy barrier in the SF region but with different heights (4.0, 3.2, and 8.7 kcal mol−1 in ref. 29, 30, and 31, respectively). Besides the barrier in the SF region, the overall profiles of PMF from the three studies exhibit different features. The PMF calculated by the steered MD simulation demonstrates a rugged profile with a deep minimum at the periplasmic side,29 and this ‘attractive vestibule’ was suggested to be functionally important.29,32,33 On the other hand, the PMFs obtained by umbrella sampling and ABF calculations are smoother, and do not have the periplasmic ‘attractive vestibule’.30,31 The kinetics of glycerol permeation have been estimated based on PMFs calculated by steered MD29,32 and ABF,31 giving quite different results.31,32 The discrepancies in both PMF estimation and kinetic analysis indicate the two challenging aspects of membrane transport simulation: sufficient sampling and proper construction of the kinetic model.
Here, we performed extensive unbiased MD simulations of a GlpF system to achieve an adequate sampling of glycerol permeation. In addition to calculating the permeation PMF, we constructed a Markov state model (MSM) of glycerol transport and obtained all the rate constants of state transitions. Based on the MSM analysis, we built two stepwise kinetic models of glycerol translocation and solved the master equations under various boundary conditions, i.e. various glycerol concentrations at the two sides of the membrane. The calculated glycerol transport flux is in reasonable agreement with the experimental measurement at a certain extracellular glycerol concentration. More importantly, we achieved a holistic view of the glycerol transport capacity of GlpF under various conditions.
2. Methods
2.1 System setup
The crystal structure of GlpF was obtained from the Protein Data Bank (PDB ID: 1FX8). Missing atoms of residue Arg257 were added using the PDB2PQR server.34 pKa values were estimated by using PROPKA 3.0,35 and it turns out that all titratable residues are in their default protonation states at pH 7.0. The GlpF tetramer was inserted into a pre-equilibrated palmitoyloleoyl-phosphocholine (POPC) lipid bilayer containing 256 lipids by using the “shrinking” method.36 Twelve glycerol molecules were added to the system, initially placed >10 Å away from the protein. Water, Na+, and Cl− were added to solvate and neutralize the system, and to maintain a physiological salinity of 150 mM. The final system contains 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 173 atoms including 240 lipids and 18
173 atoms including 240 lipids and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 763 water molecules (Fig. 1c).
763 water molecules (Fig. 1c).
2.2 Simulation parameters and data analysis
We used the GROMACS 5.0 software package37 to conduct MD simulations with the all-atom CHARMM36 force field38 and the TIP3P water model. A steepest descent algorithm was used for energy minimization for 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps and the system equilibration lasted 20 ns with position restraints on the heavy atoms of protein in the NPT ensemble. We used semi-isotropic coupling to keep the pressure at 1 bar using the Berendsen algorithm39 with a time constant of 1 ps, and used the V-rescale algorithm40 with a time constant of 0.1 ps to maintain a constant temperature of 310 K. 45 trajectories were produced without any restraints, and each lasted 500 ns, leading to an aggregation time of 22.5 μs. All bonds were constrained by the LINCS algorithm,41 and a time step of 2 fs was used. The cutoffs of electrostatic interactions and van der Waals interactions were both set to 1.2 nm. Long-range electrostatic interactions were computed by using the particle mesh Ewald (PME) method.42 The trajectories were analyzed using MDAnalysis.43 The pore radius was evaluated with the HOLE program.44 VMD45 was used for structure visualization.
000 steps and the system equilibration lasted 20 ns with position restraints on the heavy atoms of protein in the NPT ensemble. We used semi-isotropic coupling to keep the pressure at 1 bar using the Berendsen algorithm39 with a time constant of 1 ps, and used the V-rescale algorithm40 with a time constant of 0.1 ps to maintain a constant temperature of 310 K. 45 trajectories were produced without any restraints, and each lasted 500 ns, leading to an aggregation time of 22.5 μs. All bonds were constrained by the LINCS algorithm,41 and a time step of 2 fs was used. The cutoffs of electrostatic interactions and van der Waals interactions were both set to 1.2 nm. Long-range electrostatic interactions were computed by using the particle mesh Ewald (PME) method.42 The trajectories were analyzed using MDAnalysis.43 The pore radius was evaluated with the HOLE program.44 VMD45 was used for structure visualization.
2.3 Potential of mean force (PMF) calculation
PMF G(z) of glycerol translocation along the pore axis of GlpF was calculated according to the formula| | G(z) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈n(z)〉 + C ln〈n(z)〉 + C | (1) |
where z is the displacement of the center of mass (COM) of glycerol relative to the COM of GlpF along the pore axis, kB is the Boltzmann constant, T is the temperature, and C is a constant to shift the value of PMF to zero when z falls in the bulk phase. The pore of each GlpF monomer was defined as a cylinder with a radius of 17 Å and the cylinder is extended into the bulk solvent as well. To merge the glycerol number statistics of the four monomers, we set one of the monomers in the crystal structure as the reference and superimposed the monomers in trajectories one by one to the reference. Glycerol molecules within the cylinder of each monomer were moved together with the protein during superimposition. Then we counted the number of glycerols in the cylinder by dividing them into bins with a length of 0.25 Å. n(z) is the average number of glycerol molecules in a bin beginning at z. The error bars of PMF were estimated by using the bootstrapping method.46
The state-dependent PMF of the conformational and prochiral state i of glycerol, Gi(z), was defined as
| | Gi(z) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈ni(z)〉 + C ln〈ni(z)〉 + C | (2) |
where
ni(
z) is the average number of state
i glycerols in the bin at
z per snapshot, and
C has the same value as in
eqn (1). Because
| | 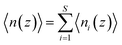 | (3) |
where
S = 18 (the total number of different conformational and prochiral states of glycerol that we defined), the relationship between the integral PMF
G(
z) and the state-dependent PMFs
Gi(
z) can be explicitly expressed as
| | 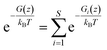 | (4) |
2.4 Markov state model analysis
PyEMMA software47 was used to construct the Markov state model (MSM) of glycerol translocation. First, we split all trajectories into individual glycerol trajectories, i.e. each original trajectory was split into 12 one-glycerol trajectories. To ensure that the glycerol molecule moves continuously inside the cylinder of each monomer, we made further modifications. Once the glycerol moves across the periodic boundary of the system or out of the cylinder, we assumed that this trajectory is terminated and the remaining part was considered as a new trajectory. In this way, each one-glycerol trajectory was further divided into short and continuous trajectory fragments. Trajectory fragments that lasted for more than 1 ns were selected for further analysis. We define the system states with the COM of glycerol at the cytoplasmic side (z < −25.5) and periplasmic side (z > 24.5) as state 0 and state N, respectively. Other states with the COM of glycerol between z = −25.5 and z = 24.5 were named state 1 to N − 1, with each spanning a length of 0.25 Å. By this definition, we got 202 microstates. Next, by projecting all the trajectories onto the 202 states, we constructed the count matrix Cij(τ), whose elements correspond to the number of observed transitions of glycerol from state i to state j after a lag time τ. From the count matrix, we used the Bayesian estimator48,49 to obtain the transition probability matrix T. If the model is Markovian, the dynamics can be propagated to long time scale dynamics:
The relaxation times, or implied timescales, τk, are computed from the eigenvalues:
| | 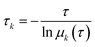 | (6) |
where
μk is the
kth eigenvalue (sorted from the largest to the smallest, and the eigenvalue that equals to 1 is not considered) of the transition matrix with the lag time
τ. In general, if the model is Markovian, the implied timescales plateau and become constant with the increase of lag time. We then applied the PCCA + algorithm
50 to lump all the microstates into 8 macrostates.
2.5 Transition path theory analysis
To estimate the rates of glycerol transport through the pore, we used transition path theory (TPT).51–53 In TPT, two sets of states, source states A and sink states B, are defined to specify the transition from A to B. All remaining states are considered to be intermediate states. Then, the forward-committor probability qi+, defined as the probability that the system, when being in state i, will reach state B next rather than state A, can be computed from the transition matrix. Similarly, the backward-committor probability qi− is calculated as the probability that the system, being in state i, was previously in state A rather than in state B. The total flux F from A to B per unit time τ is calculated using the relationship| | 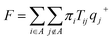 | (7) |
where πi is the stationary population of state i and Tij is the element of the transition matrix specifying the transition probability from state i to state j. The rate constant of the transition from A to B can be calculated as| | 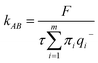 | (8) |
where the summation runs over all states in the model. Here, we calculated the transition rate constants between the eight macrostates based on the 202-microstate MSM. It is worth noting that the step of glycerol entering the channel from the bulk solvent (either the periplasm or cytoplasm) is a second order reaction, in which glycerol binds to the protein. However, if the glycerol concentration remains constant at both sides of the membrane, this step could be viewed as a pseudo-first order reaction. The rate constants derived from the MSM correspond to pseudo-first order rate constants at a glycerol concentration of 0.036 M. Therefore, we give the second-order rate constants (k01 and k76) in Fig. 4 and Table S2† by dividing them by 0.036 M.
3. Results and discussion
3.1 Equilibrium MD simulations of spontaneous glycerol permeation
Forty-five 500 ns unbiased all-atom MD simulations (total simulation time of 22.5 μs) were performed for the membrane-embedded GlpF tetramer with a glycerol concentration of 0.036 M at both sides of the lipid bilayer (Fig. 1c). We have observed 24 times the spontaneous permeation of glycerol through the entire pore of GlpF, among which 15 involved translocations from the periplasmic side to the cytoplasmic side (P → C) and the other 9 times the translocations were in the opposite direction (C → P). In addition, another 15 times glycerol passage through the narrowest SF region was observed, but in these cases, glycerol diffused back and did not permeate to the other side of the membrane. Inspection of the trajectories reveals several interesting points. First, in the 24 spontaneous permeations of glycerol, the average time a conducting glycerol molecule spends inside the channel is short (40 ± 25 ns, Table S1†) relative to the total simulation time. For a majority of the simulation time, glycerols were in the bulk solution or bound somewhere inside the channel, while the successful permeations were fleeting (Fig. 1d–f). In this scenario, glycerol translocations are barrier-crossing rare events. Second, there exist several sites inside the channel where glycerol has relatively long residence time (Fig. 1f), indicating that there are several stable states during the translocation process. Third, at the glycerol concentration used in our simulation, it is more probable that there is only one glycerol molecule inside the channel during translocation. The probability of finding one glycerol inside the channel is 24.1% with respect to the total simulation time, while the probability of finding two or more glycerol molecules simultaneously inside the same channel is 3.7%. This implies that we may ignore the interaction between glycerol molecules during translocation.
3.2 Potential of mean force (PMF) for glycerol translocation
To obtain a quantitative thermodynamic description of glycerol transport, we calculated the 1-dimensional PMF of glycerol translocation along the pore axis (z axis) from the MD trajectories (Fig. 2a and b, see the Methods section). As expected, the highest energy barrier (3.1 ± 0.1 kcal mol−1) in the PMF profile is located in the SF region (Fig. 2b, z = 2.0 Å). This is generally in agreement with the previous PMF calculations.29–31 The PMF estimation using umbrella sampling gave an SF barrier of 3.2 kcal mol−1, which is very close to our result.30 However, differences are evident when our result is compared with those derived from the steered MD29 and ABF methods,31 which gave higher barriers (4.0 and 8.7 kcal mol−1) and different shapes at several places. For example, the PMF from the steered MD simulation gave a deep energy well at the periplasmic vestibule,29 but our simulation and the other two studies30,31 did not find this feature (Fig. 2b). In the crystal structure of GlpF, three glycerol molecules were trapped inside the channel,20 the positions of which all correspond to local minima in our PMF profile (Fig. 2a and b). The second glycerol sits near the SF region with relatively high free energy (Fig. 2). This ‘unfavorable’ location of glycerol is most likely due to the high glycerol concentration in the crystallographic experiment (∼1.6 M). In general, our PMF profile is more similar to the PMF calculated by umbrella sampling.30 It is worth noting that our simulation time is much longer and there is no bias in our simulation. The convergence of our PMF calculation was also verified (Fig. S1†). Another notable difference between our simulation and the previous studies is that our simulation system contains twelve glycerol molecules and there is a probability for multiple glycerols appearing inside the channel, while single glycerol translocation was forced in the other simulations.
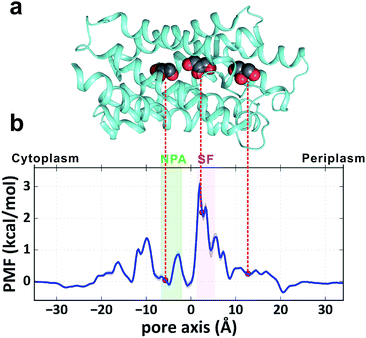 |
| | Fig. 2 PMF of glycerol transport through the GlpF channel. (a) Crystal structure of one monomer of GlpF. The three cocrystallized glycerol molecules are shown in a sphere model. (b) 1D PMF of glycerol transport along the pore axis. The zero point of the pore axis is at the center of mass of GlpF and the zero point of free energy is set when glycerol is in the bulk solvent. The positions corresponding to the bound glycerols in the crystal structure are indicated by red circles. | |
3.3 Stereoselectivity of the SF region of GlpF for glycerol permeation
Both the crystal structure and the PMF profile suggest that the motion of glycerol is highly restrained as it passes through the SF region. To analyze the stereoselectivity of the SF region, we used three Euler angles (φ, θ, and ψ) to characterize the orientation of glycerol with respect to the protein (Fig. 3a). The reference state with all three angles being zero is defined as the most probable orientation of glycerol in the SF region. In bulk solution, the three angles (θ, φ, and ψ) exhibit even or cosine distributions (Fig. 3b, black curves), indicating random orientation. In the SF region, the three Euler angles are highly restricted around 0° or ±180° (Fig. 3b, red curves). Accordingly, two orientational or prochiral states of glycerol can be defined as C1 (φ ≈ θ ≈ ψ ≈ 0°) and C3 (φ ≈ 180°, θ ≈ ψ ≈ 0°), with the C1 or C3 atom of glycerol (see Fig. 3a for atom numbering) entering the SF constriction first from the periplasmic side, respectively. On the other hand, glycerol has intramolecular conformational flexibility. To characterize the conformational selectivity, we examined the two backbone torsion angles α12 (O1–C1–C2–O2) and α23 (O3–C3–C2–O2), and the three hydroxyl-involving torsion angles ω1, ω2, and ω3 of glycerol (Fig. 3a). The distributions of the five torsion angles in the SF region are different from those in the bulk phase (Fig. 3b, red curves vs. black curves). Torsion angles ω1, ω2, and ω3 display broad and even distributions in solution and in the pore (Fig. 3b). The SF region slightly restricts the rotation of the C–O bonds, leading to narrowed distributions (Fig. 3b). The backbone torsion angles α12 and α23 distribute mainly around 75° and −75°, corresponding to the so-called gauche+ or g+ (0–120°) and gauche− or g− (−120–0°) conformations, respectively (Fig. 3b). The anti or a (−180 to −120° or 120–180°) conformation, however, is much less probable (Fig. 3b). For simplicity, we only use the backbone torsion angles α12 and α23 to categorize the conformational states of glycerol, and the combinations of the three states (g+, g− and a) of the two torsion angles give nine conformational states (g+–g+, g−–g+, g+–g−…). By combining the two prochiral (C1 and C3) and nine conformational states, we define eighteen overall states of a glycerol molecule, named C1–g−–g+, C3–g−–g+, etc.
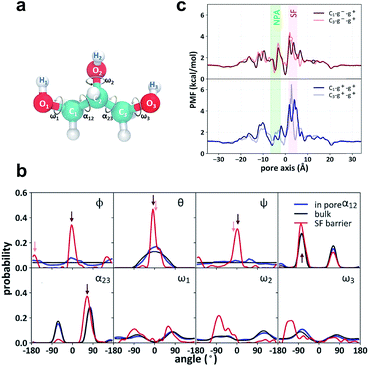 |
| | Fig. 3 Stereoselectivity of the SF region for glycerol. (a) Structure of glycerol and the definition of the torsion angles α12, α23, ω1, ω2, and ω3. (b) Distributions of the Euler angles ϕ, θ, and ψ, backbone torsion angles α12 and α23 and the side chain torsion angles ω1, ω2, and ω3. The Euler angles denote sequential rotations of glycerol around the x-, y′-, and z′′-axis to overlap with one representative structure of the C1–g−–g+ state. The angles corresponding to C1–g−–g+ and C3–g−–g+ states are indicated by dark red and light red arrows, respectively. (c) State-dependent PMFs of the C1–g−–g+, the C3–g−–g+, the C1–g+–g+ and the C3–g+–g+ states along the pore axis. The zero points of the state-dependent PMFs were set according to that of the integral PMF to explicitly account for the confinement penalty from isolating the selected conformational and prochiral state from the state mixture in the bulk phase. The three glycerol molecules co-crystallized with GlpF are in the C1–g−–g+, C3–g−–g+ and C3–g+–g+ states, respectively. Their positions are indicated by circles in the respective PMF curves. | |
The definition of the prochiral-conformational state of glycerol enables us to decompose the PMF of glycerol translocation (Fig. 2b) into 18 state-dependent PMFs (Fig. 3c and S2,† see the Methods section for details). These state-dependent PMFs provide a comprehensive picture of the selectivity of the SF for glycerol permeation. The PMF of C1–g−–g+ has the lowest energy barrier in the SF region (Fig. 3c), where this state occupies 52.8% of the total population of the permeable glycerols. The C3–g−–g+ state is less permeable with a population of 13.7% in the SF region and a slightly higher energy barrier (Fig. 3c). The g+–g+ conformation is less permeable and forms fewer hydrogen bonds with the SF region than the g−–g+ one. Therefore, the PMFs of C1–g+–g+ and C3–g+–g+ have higher energy barriers in the SF region (Fig. 3c). The other states, such as C1–g−–g−, C3–g−–g−, C1–g+–g−, and C3–g+–g−, are totally impermeable during the simulation (Fig. S2†). This result generally agrees with the crystal structure and the previous simulation studies.29,31 In the crystal structure, the glycerol near the SF region adopts the C3–g−–g+ state.
In line with the stereoselectivity of the SF region shown in the state-dependent PMFs, the probability of transitions among different prochiral-conformational states of glycerol is extremely low in the SF region (Fig. S3†). We examined all 39 passages through the SF region by tracing the prochiral-conformational state evolution of glycerol (Fig. S4†). It was found that 14 times glycerol passed through the SF region in the C1–g−–g+ state without transitions (Fig. S4a†), and for another 4 passages the C1–g−–g+ state was predominant with only one or two transitions (Fig. S4a†). The C3–g−–g+ state is similarly favorable by being exclusive in 8 of the passages and being predominant in another 8 (Fig. S4b†). The g+–g+ conformer, however, always experienced transitions during the passages (Fig. S4c†). Overall, the state-dependent PMFs and the state transition analysis all indicate that the SF region has high stereoselectivity for glycerol. Nevertheless, it is notable that the non-polarizable force field employed in this study may limit the accuracy of a detailed description of the conformational motion of glycerol in a highly complicated environment.
3.4 Markov state model analysis of the glycerol transport process
The 1-D PMF of glycerol permeation reveals several local energy minima along the pore axis (Fig. 2b), entailing translocation intermediate states. To obtain kinetic information on glycerol transport, we performed Markov state model (MSM) analysis of the MD simulation trajectories. First, we divided the channel along the pore axis (running from z = −25.5 Å to 24.5 Å) into 200 bins, each of which spans 0.25 Å. The microstates of the system are defined by the locations of the glycerol molecule in these bins. Therefore, snapshots with the COM of glycerol at the same bin belong to the same microstate. For the snapshots with no glycerol inside the channel, two microstates are defined with glycerol in the periplasmic and cytoplasmic side bulk solutions, respectively. The 202 microstates are further lumped into eight macrostates (see the Methods section for more details). The implied timescales for both 202-microstate and 8-macrostate MSMs reach the plateau when the lag time is more than 80 ps, indicating that the model is Markovian (Fig. S5a and c†), and we further validated the MSM using the Chapman–Kolmogorov test54 (Fig. S5b and d†). The 1-D PMF of glycerol translocation calculated based on the MSM agrees well with that calculated using raw MD trajectories (Fig. 4). Macrostates were numbered 0 to 7 from the periplasm side to the cytoplasm side dictating the positions of glycerol. States 1 to 6 represent glycerol locations inside the channel (Fig. 4). State 0 and state 7, the states with glycerol in the periplasm and cytoplasm respectively, have a total equilibrium population of ∼55% (Fig. 4). Among the six states with glycerol inside the pore, state 1 has a relatively large probability of 11.04%. This corresponds to the periplasmic vestibule. A previous simulation study found that this area is the global minimum in the PMF profile,55 and a glycerol molecule is trapped here in the crystal structure.20 State 6, the state near the cytoplasmic entrance, has a comparable population (12.5%) to state 1. Therefore, the asymmetry of GlpF in our calculation is not as significant as shown in the previous simulation.55 The rate constants of all transitions between two adjacent states were calculated using the TPT51–53 from the 202-microstate MSM (Fig. 4 and Table S2,† see the Methods section for more details). In line with the PMF profile, the slowest step during permeation is crossing the SF barrier. It is worth noting that the detailed balance conditions are satisfied in the rate constant estimations,47,56 ensuring the reliability of the following kinetic analysis using these rate constants.
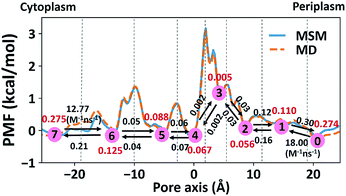 |
| | Fig. 4 Markov state model analysis of glycerol transport through GlpF. Eight macrostates (state 0 to 7) were constructed from the MSM and are labeled in red circles and the corresponding populations are in red. Dashed lines represent the boundaries between different states, lying at −19, −10, −3, 2.25, 5, 11.5, and 19 Å, respectively. The values near the black arrows are rate constants of the state transitions with units of ns−1 if not specified. | |
3.5 Glycerol permeation flux under various concentration gradients
The above MD simulations were performed under equilibrium conditions, which assume equal glycerol concentration (0.036 M) in the periplasm and the cytoplasm. This is quite different from the in vivo situation in E. coli, where there is a glycerol concentration difference across the inner membrane. Glycerol molecules are phosphorylated by glycerol kinase once they are translocated into the cytoplasm; therefore, the cytoplasmic glycerol concentration is supposed to remain at a low level. To calculate the glycerol transport flux under various concentration gradients, we employed two kinetic models, under the assumption that the rate constants derived from the equilibrium MD simulation are still valid at non-equilibrium conditions. In the first model, only one glycerol molecule is allowed to appear in the channel during translocation, and a 7-state kinetic model based on the MSM was constructed (Fig. 5a). Here, different from the MSM, states 0 and 7 merge into one state (state 0), which represents the state with no glycerol inside the channel. The master equations of this kinetic model are as follows:| | 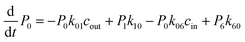 | (9) |
| | 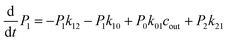 | (10) |
| | 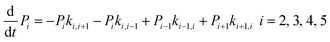 | (11) |
| | 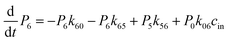 | (12) |
| | 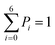 | (13) |
where P1–P6 are probabilities of the six states with one glycerol in the channel, P0 is the probability of state 0, kij is the rate constant for the transition from state i to state j, and cout and cin are constant concentrations of glycerol in the periplasm and cytoplasm, respectively. The values of the rate constant (kij) are obtained from the above MSM analysis (Fig. 4 and Table S2†). Note that k06 and k60 correspond to k76 and k67 in the MSM, respectively. The master equations were solved numerically as time evolved till all the state probabilities remained unchanged, indicating the achievement of a steady state. The net flux of glycerol from the periplasm to the cytoplasm JP→C can be calculated as| | | JP→C = P6k60 − P0k06cin | (14) |
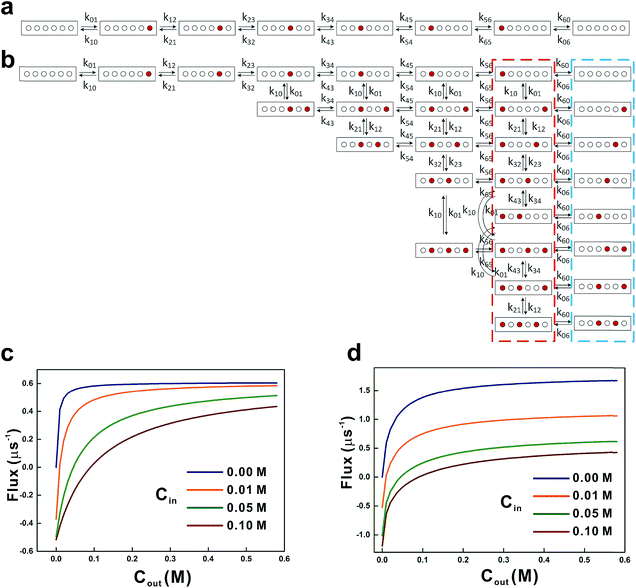 |
| | Fig. 5 Kinetic models for glycerol transport. The 7-state kinetic model (a) and the 21-state kinetic model (b) were used to calculate the glycerol influx rates. Red and open circles represent the glycerol occupied and the vacant sites, respectively. Transition rate constants between various states are indicated near the arrow. All the states encircled by the red and blue dashed lines (with probabilities Pr and Pb, respectively) contribute to the net influx J![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0050_20d1.gif) C in eqn (16). Net influxes of glycerol at various periplasmic (Cout) and cytoplasmic (Cin) glycerol concentrations were calculated using the 7-state kinetic model (c) and the 21-state kinetic model (d). C in eqn (16). Net influxes of glycerol at various periplasmic (Cout) and cytoplasmic (Cin) glycerol concentrations were calculated using the 7-state kinetic model (c) and the 21-state kinetic model (d). | |
In the second model, the channel is allowed to accommodate more than one glycerol molecule. Considering the size of glycerol (∼5 Å), we assume that the adjacent sites inside the pore cannot accommodate glycerols at the same time. Consequently, there are totally 21 possible states with at most three glycerols inside the channel (Fig. 5b). If we further assume that only one glycerol moves in all the state transitions (referred to as the ‘one-glycerol-hopping’ model), a 21-state kinetic model is thus established (Fig. 5b). The corresponding master equation reads as follows:
| | 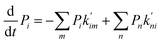 | (15) |
where
Pi is the probability of state
i,
m denotes all the states into which state
i could transform through one-glycerol-hopping,
n denotes all the states that could transform into state
i through one-glycerol-hopping, and
i = 1, 2, …, 21.

and
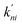
are the rate constants for transition among the different states. Note that these rate constants can also be derived from the MSM since we assume the one-glycerol-hopping model (see
Fig. 5b for more details). The steady-state net flux
JP→C in this kinetic model can be calculated as
| | 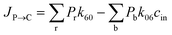 | (16) |
where
Pr and
Pb refer to the probabilities of the states in the red and blue dotted boxes (
Fig. 5b), respectively.
By solving the master equations of the two above-mentioned kinetic models at cin and cout, we obtained glycerol transport flux rates under various non-equilibrium conditions (Fig. 5c and d). Although glycerol is phosphorylated in the cytoplasm, the cytoplasmic glycerol concentration is unnecessarily zero. Here, we chose four values of cin (0 M, 0.01 M, 0.05 M, and 0.1 M) to calculate the steady-state influx rate of glycerol while varying the cout in the range of 0–0.6 M. In the first model, with the increase of cout the net flux J![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0050_20d1.gif) C saturates very quickly at low cytoplasmic concentrations (cin = 0 M and 0.01 M, Fig. 5c). The saturated flux rate is ∼0.6 μs−1. In the second model where the channel may accommodate multiple glycerol molecules, the net fluxes are generally larger and saturate slowly (Fig. 5d). At zero cytoplasmic glycerol concentration, the saturated flux rate is ∼1.6 μs−1 (Fig. 5d). Experimentally, the glycerol flux rate was estimated to be 0.2 μs−1 based on measurement at a cout of 0.5 M,57 while cin is unknown. In our two models, when cout = 0.5 M, the influx rates range from 0.4 to 0.6 μs−1 (model 1) and 0.4 to 1.6 μs−1 (model 2), respectively (Fig. 5c and d). It is worth noting that the experimental estimation has a large uncertainty. For example, it was assumed that the copy number of GlpF in E. coli equals to that of glycerol kinase, and the copy number of glycerol kinase (6 × 103 molecules per cell) is estimated based on enzyme activity. A recent proteomic study using a mass spectrometer, however, gave a quite different estimation (1.1 × 103 molecules per cell), which implies a higher glycerol flux rate. Although the second model seemingly overestimates the influx rate of glycerol, it is probably the more reasonable model. The glycerol concentration in our equilibrium simulation is quite low (0.036 M); therefore, under the non-equilibrium conditions close to the experimental situation, GlpF is very likely to accommodate more glycerols than observed in the above MD simulation. To test this hypothesis, we performed additional simulations at several higher glycerol concentrations of 0.1 M, 0.15 M, 0.2 M, and 0.25 M, respectively. Five 50 ns long simulations were conducted at each concentration. It turns out that with the increase of glycerol concentration, it is possible that more binding sites in the channel are occupied simultaneously (Fig. S6†). At higher concentrations, there is a small probability of accommodating more than three glycerols in the channel (∼3% under 0.25 M) (Fig. S6†). It should be noted that the simulation is conducted under equilibrium conditions, and there should be fewer glycerols in the channel under non-equilibrium conditions with concentration gradients. Therefore, the 21-state model that allows at most three glycerols in the channel is a good approximation.
C saturates very quickly at low cytoplasmic concentrations (cin = 0 M and 0.01 M, Fig. 5c). The saturated flux rate is ∼0.6 μs−1. In the second model where the channel may accommodate multiple glycerol molecules, the net fluxes are generally larger and saturate slowly (Fig. 5d). At zero cytoplasmic glycerol concentration, the saturated flux rate is ∼1.6 μs−1 (Fig. 5d). Experimentally, the glycerol flux rate was estimated to be 0.2 μs−1 based on measurement at a cout of 0.5 M,57 while cin is unknown. In our two models, when cout = 0.5 M, the influx rates range from 0.4 to 0.6 μs−1 (model 1) and 0.4 to 1.6 μs−1 (model 2), respectively (Fig. 5c and d). It is worth noting that the experimental estimation has a large uncertainty. For example, it was assumed that the copy number of GlpF in E. coli equals to that of glycerol kinase, and the copy number of glycerol kinase (6 × 103 molecules per cell) is estimated based on enzyme activity. A recent proteomic study using a mass spectrometer, however, gave a quite different estimation (1.1 × 103 molecules per cell), which implies a higher glycerol flux rate. Although the second model seemingly overestimates the influx rate of glycerol, it is probably the more reasonable model. The glycerol concentration in our equilibrium simulation is quite low (0.036 M); therefore, under the non-equilibrium conditions close to the experimental situation, GlpF is very likely to accommodate more glycerols than observed in the above MD simulation. To test this hypothesis, we performed additional simulations at several higher glycerol concentrations of 0.1 M, 0.15 M, 0.2 M, and 0.25 M, respectively. Five 50 ns long simulations were conducted at each concentration. It turns out that with the increase of glycerol concentration, it is possible that more binding sites in the channel are occupied simultaneously (Fig. S6†). At higher concentrations, there is a small probability of accommodating more than three glycerols in the channel (∼3% under 0.25 M) (Fig. S6†). It should be noted that the simulation is conducted under equilibrium conditions, and there should be fewer glycerols in the channel under non-equilibrium conditions with concentration gradients. Therefore, the 21-state model that allows at most three glycerols in the channel is a good approximation.
4. Conclusion
In this work, we conducted large scale equilibrium MD simulations of glycerol translocation through GlpF. Tens of times spontaneous glycerol permeation was observed. The PMF profile of glycerol transport confirms the functional importance of the SF region, and the stereoselectivity analysis shows that the C3–g−–g+ state of glycerol has the highest permeability. By performing MSM analysis, we obtained the rate constants of state transitions during glycerol transport, based on which we were able to build kinetic models for glycerol influx under non-equilibrium conditions. The calculated net fluxes under various glycerol concentration gradients using the two kinetic models provide a holistic view of the glycerol transport capacity of GlpF. Our work demonstrates that long-timescale equilibrium simulation combined with MSM analysis could achieve the ‘ab initio’ calculation of kinetics and complement the structural and physiological experiments, providing a detailed understanding of channel transport.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Ministry of Science and Technology of the People's Republic of China (No. 2016YFA0501702), National Natural Science Foundation of China (21473034, 21773038, 21877017). This research made use of the resources of the computer clusters at the computer center at Fudan University.
Notes and references
- C. Maffeo, S. Bhattacharya, J. Yoo, D. Wells and A. Aksimentiev, Chem. Rev., 2012, 112, 6250–6284 CrossRef CAS PubMed.
- J. Weng and W. Wang, Adv. Exp. Med. Biol., 2014, 805, 305–329 CrossRef CAS PubMed.
- C. Kutzner, H. Grubmuller, B. L. de Groot and U. Zachariae, Biophys. J., 2011, 101, 809–817 CrossRef CAS PubMed.
- C. Kutzner, D. A. Kopfer, J. P. Machtens, B. L. de Groot, C. Song and U. Zachariae, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 1741–1752 CrossRef CAS PubMed.
- F. Noe, I. Horenko, C. Schutte and J. C. Smith, J. Chem. Phys., 2007, 126, 155102 CrossRef PubMed.
- C. Schütte, A. Fischer, W. Huisinga and P. Deuflhard, J. Comput. Phys., 1999, 151, 146–168 CrossRef.
- W. C. Swope, J. W. Pitera and F. Suits, J. Phys. Chem. B, 2004, 108, 6571–6581 CrossRef CAS.
- J. H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schutte and F. Noe, J. Chem. Phys., 2011, 134 Search PubMed.
- R. Zwanzig, J. Stat. Phys., 1983, 30, 255–262 CrossRef.
- A. C. Pan and B. Roux, J. Chem. Phys., 2008, 129, 064107 CrossRef PubMed.
- V. Schultheis, T. Hirschberger, H. Carstens and P. Tavan, J. Chem. Theory Comput., 2005, 1, 515–526 CrossRef CAS PubMed.
- N. Singhal, C. D. Snow and V. S. Pande, J. Chem. Phys., 2004, 121, 415–425 CrossRef CAS PubMed.
- N. V. Buchete and G. Hummer, J. Phys. Chem. B, 2008, 112, 6057–6069 CrossRef CAS PubMed.
- W. Zheng, M. Andrec, E. Gallicchio and R. M. Levy, J. Phys. Chem. B, 2009, 113, 11702–11709 CrossRef CAS PubMed.
- V. A. Voelz, G. R. Bowman, K. Beauchamp and V. S. Pande, J. Am. Chem. Soc., 2010, 132, 1526–1528 CrossRef CAS PubMed.
- Y. Feng, L. Zhang, S. Wu, Z. Liu, X. Gao, X. Zhang, M. Liu, J. Liu, X. Huang and W. Wang, Angew. Chem., Int. Ed. Engl., 2016, 55, 13990–13994 CrossRef CAS PubMed.
- D. Wang, J. Weng and W. Wang, J. Comput. Chem., 2019, 40, 1440–1448 CrossRef CAS PubMed.
- J. Weng and W. Wang, J. Chem. Inf. Model., 2019, 59, 2359–2366 CrossRef CAS PubMed.
- H. Tsukaguchi, C. Shayakul, U. V. Berger, B. Mackenzie, S. Devidas, W. B. Guggino, A. N. Van Hoek and M. A. Hediger, J. Biol. Chem., 1998, 273, 24737–24743 CrossRef CAS PubMed.
- D. Fu, A. Libson, L. J. Miercke, C. Weitzman, P. Nollert, J. Krucinski and R. M. Stroud, Science, 2000, 290, 481–486 CrossRef CAS PubMed.
- C. Maurel, J. Reizer, J. I. Schroeder, M. J. Chrispeels and M. H. Saier, J. Biol. Chem., 1994, 269, 11869–11872 CAS.
- G. M. Preston, T. P. Carroll, W. B. Guggino and P. Agre, Science, 1992, 256, 385–387 CrossRef CAS PubMed.
-
E. C. Lin, Escherichia coli and Salmonella: cellular and molecular biology, ASM Press, Washington, DC, 2nd edn, 1996, pp. 307–342 Search PubMed.
- E. Tajkhorshid, P. Nollert, M. O. Jensen, L. J. Miercke, J. O'Connell, R. M. Stroud and K. Schulten, Science, 2002, 296, 525–530 CrossRef CAS PubMed.
- B. L. de Groot and H. Grubmuller, Science, 2001, 294, 2353–2357 CrossRef CAS PubMed.
- M. J. Borgnia, D. Kozono, G. Calamita, P. C. Maloney and P. Agre, J. Mol. Biol., 1999, 291, 1169–1179 CrossRef CAS PubMed.
- E. Beitz, B. Wu, L. M. Holm, J. E. Schultz and T. Zeuthen, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 269–274 CrossRef CAS PubMed.
- D. F. Savage, P. F. Egea, Y. Robles-Colmenares, J. D. O'Connell III and R. M. Stroud, PLoS Biol., 2003, 1, e72 CrossRef PubMed.
- M. O. Jensen, S. Park, E. Tajkhorshid and K. Schulten, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 6731–6736 CrossRef CAS PubMed.
- J. S. Hub and B. L. de Groot, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 1198–1203 CrossRef CAS PubMed.
- J. Henin, E. Tajkhorshid, K. Schulten and C. Chipot, Biophys. J., 2008, 94, 832–839 CrossRef CAS PubMed.
- D. Lu, P. Grayson and K. Schulten, Biophys. J., 2003, 85, 2977–2987 CrossRef CAS PubMed.
- I. Kosztin and K. Schulten, Phys. Rev. Lett., 2004, 93, 238102 CrossRef PubMed.
- T. J. Dolinsky, J. E. Nielsen, J. A. McCammon and N. A. Baker, Nucleic Acids Res., 2004, 32, W665–W667 CrossRef CAS PubMed.
- M. H. Olsson, C. R. Sondergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537 CrossRef CAS PubMed.
- C. Kandt, W. L. Ash and D. P. Tieleman, Methods, 2007, 41, 475–488 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- R. B. Best, X. Zhu, J. Shim, P. E. Lopes, J. Mittal, M. Feig and A. D. Mackerell Jr, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef CAS PubMed.
- H. J. Berendsen, J. v. Postma, W. F. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- O. S. Smart, J. G. Neduvelil, X. Wang, B. Wallace and M. S. Sansom, J. Mol. Graphics, 1996, 14, 354–360 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- B. Efron and R. Tibshirani, Stat. Sci., 1986, 1, 54–75 CrossRef.
- M. K. Scherer, B. Trendelkampschroer, F. Paul, G. Pérezhernández, M. Hoffmann, N. Plattner, C. Wehmeyer, J. H. Prinz and F. Noé, J. Chem. Theory Comput., 2015, 330, 341–445 Search PubMed.
- B. Trendelkamp-Schroer, H. Wu, F. Paul and F. Noe, J. Chem. Phys., 2015, 143, 174101 CrossRef PubMed.
-
F. Noé, Preprint, 2015.
- S. Röblitz, Advances in Data Analysis and Classification, 2013, 7, 147–179 CrossRef.
- E. Weinan and E. Vanden-Eijnden, J. Stat. Phys., 2006, 123, 503–523 CrossRef.
- P. Metzner, C. Schutte and E. Vanden-Eijnden, Multiscale Model. Simul., 2009, 7, 1192–1219 CrossRef CAS.
- F. Noe, C. Schutte, E. Vanden-Eijnden, L. Reich and T. R. Weikl, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19011–19016 CrossRef CAS PubMed.
- J. H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schutte and F. Noe, J. Chem. Phys., 2011, 134, 174105 CrossRef PubMed.
- D. Lu, P. Grayson and K. Schulten, Biophys. J., 2003, 85, 2977–2987 CrossRef CAS PubMed.
- M. Senne, B. Trendelkamp-Schroer, A. S. J. S. Mey, C. Schutte and F. Noe, J. Chem. Theory Comput., 2012, 8, 2223–2238 CrossRef CAS PubMed.
- K. B. Heller, E. C. Lin and T. H. Wilson, J. Bacteriol., 1980, 144, 274–278 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Convergence of the MD simulation, state-dependent PMFs of different conformational and prochiral states of glycerol, inter-state transition probability after a time span of 10 ps versus the position of glycerol along the pore, projections of 39 successful passages through the major barrier region, MSM validation, statistics of simultaneously occupied sites inside the channel at various glycerol concentrations, summary of the dwell time of spontaneous glycerol conduction events, and the rate constants of the transitions between the eight macrostates obtained from the 202-state Markov model. See DOI: 10.1039/c9sc01690b |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Wenning
Wang
* and
Wenning
Wang
 *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 173 atoms including 240 lipids and 18
173 atoms including 240 lipids and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 763 water molecules (Fig. 1c).
763 water molecules (Fig. 1c).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps and the system equilibration lasted 20 ns with position restraints on the heavy atoms of protein in the NPT ensemble. We used semi-isotropic coupling to keep the pressure at 1 bar using the Berendsen algorithm39 with a time constant of 1 ps, and used the V-rescale algorithm40 with a time constant of 0.1 ps to maintain a constant temperature of 310 K. 45 trajectories were produced without any restraints, and each lasted 500 ns, leading to an aggregation time of 22.5 μs. All bonds were constrained by the LINCS algorithm,41 and a time step of 2 fs was used. The cutoffs of electrostatic interactions and van der Waals interactions were both set to 1.2 nm. Long-range electrostatic interactions were computed by using the particle mesh Ewald (PME) method.42 The trajectories were analyzed using MDAnalysis.43 The pore radius was evaluated with the HOLE program.44 VMD45 was used for structure visualization.
000 steps and the system equilibration lasted 20 ns with position restraints on the heavy atoms of protein in the NPT ensemble. We used semi-isotropic coupling to keep the pressure at 1 bar using the Berendsen algorithm39 with a time constant of 1 ps, and used the V-rescale algorithm40 with a time constant of 0.1 ps to maintain a constant temperature of 310 K. 45 trajectories were produced without any restraints, and each lasted 500 ns, leading to an aggregation time of 22.5 μs. All bonds were constrained by the LINCS algorithm,41 and a time step of 2 fs was used. The cutoffs of electrostatic interactions and van der Waals interactions were both set to 1.2 nm. Long-range electrostatic interactions were computed by using the particle mesh Ewald (PME) method.42 The trajectories were analyzed using MDAnalysis.43 The pore radius was evaluated with the HOLE program.44 VMD45 was used for structure visualization.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈n(z)〉 + C
ln〈n(z)〉 + C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈ni(z)〉 + C
ln〈ni(z)〉 + C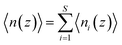
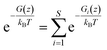
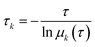
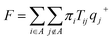
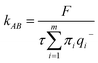
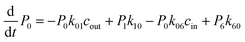
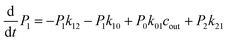
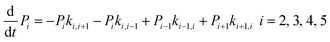
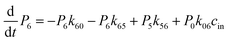
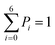

![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0050_20d1.gif) C in eqn (16). Net influxes of glycerol at various periplasmic (Cout) and cytoplasmic (Cin) glycerol concentrations were calculated using the 7-state kinetic model (c) and the 21-state kinetic model (d).
C in eqn (16). Net influxes of glycerol at various periplasmic (Cout) and cytoplasmic (Cin) glycerol concentrations were calculated using the 7-state kinetic model (c) and the 21-state kinetic model (d).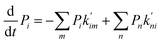
 and
and 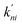 are the rate constants for transition among the different states. Note that these rate constants can also be derived from the MSM since we assume the one-glycerol-hopping model (see Fig. 5b for more details). The steady-state net flux JP→C in this kinetic model can be calculated as
are the rate constants for transition among the different states. Note that these rate constants can also be derived from the MSM since we assume the one-glycerol-hopping model (see Fig. 5b for more details). The steady-state net flux JP→C in this kinetic model can be calculated as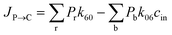
![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0050_20d1.gif) C saturates very quickly at low cytoplasmic concentrations (cin = 0 M and 0.01 M, Fig. 5c). The saturated flux rate is ∼0.6 μs−1. In the second model where the channel may accommodate multiple glycerol molecules, the net fluxes are generally larger and saturate slowly (Fig. 5d). At zero cytoplasmic glycerol concentration, the saturated flux rate is ∼1.6 μs−1 (Fig. 5d). Experimentally, the glycerol flux rate was estimated to be 0.2 μs−1 based on measurement at a cout of 0.5 M,57 while cin is unknown. In our two models, when cout = 0.5 M, the influx rates range from 0.4 to 0.6 μs−1 (model 1) and 0.4 to 1.6 μs−1 (model 2), respectively (Fig. 5c and d). It is worth noting that the experimental estimation has a large uncertainty. For example, it was assumed that the copy number of GlpF in E. coli equals to that of glycerol kinase, and the copy number of glycerol kinase (6 × 103 molecules per cell) is estimated based on enzyme activity. A recent proteomic study using a mass spectrometer, however, gave a quite different estimation (1.1 × 103 molecules per cell), which implies a higher glycerol flux rate. Although the second model seemingly overestimates the influx rate of glycerol, it is probably the more reasonable model. The glycerol concentration in our equilibrium simulation is quite low (0.036 M); therefore, under the non-equilibrium conditions close to the experimental situation, GlpF is very likely to accommodate more glycerols than observed in the above MD simulation. To test this hypothesis, we performed additional simulations at several higher glycerol concentrations of 0.1 M, 0.15 M, 0.2 M, and 0.25 M, respectively. Five 50 ns long simulations were conducted at each concentration. It turns out that with the increase of glycerol concentration, it is possible that more binding sites in the channel are occupied simultaneously (Fig. S6†). At higher concentrations, there is a small probability of accommodating more than three glycerols in the channel (∼3% under 0.25 M) (Fig. S6†). It should be noted that the simulation is conducted under equilibrium conditions, and there should be fewer glycerols in the channel under non-equilibrium conditions with concentration gradients. Therefore, the 21-state model that allows at most three glycerols in the channel is a good approximation.
C saturates very quickly at low cytoplasmic concentrations (cin = 0 M and 0.01 M, Fig. 5c). The saturated flux rate is ∼0.6 μs−1. In the second model where the channel may accommodate multiple glycerol molecules, the net fluxes are generally larger and saturate slowly (Fig. 5d). At zero cytoplasmic glycerol concentration, the saturated flux rate is ∼1.6 μs−1 (Fig. 5d). Experimentally, the glycerol flux rate was estimated to be 0.2 μs−1 based on measurement at a cout of 0.5 M,57 while cin is unknown. In our two models, when cout = 0.5 M, the influx rates range from 0.4 to 0.6 μs−1 (model 1) and 0.4 to 1.6 μs−1 (model 2), respectively (Fig. 5c and d). It is worth noting that the experimental estimation has a large uncertainty. For example, it was assumed that the copy number of GlpF in E. coli equals to that of glycerol kinase, and the copy number of glycerol kinase (6 × 103 molecules per cell) is estimated based on enzyme activity. A recent proteomic study using a mass spectrometer, however, gave a quite different estimation (1.1 × 103 molecules per cell), which implies a higher glycerol flux rate. Although the second model seemingly overestimates the influx rate of glycerol, it is probably the more reasonable model. The glycerol concentration in our equilibrium simulation is quite low (0.036 M); therefore, under the non-equilibrium conditions close to the experimental situation, GlpF is very likely to accommodate more glycerols than observed in the above MD simulation. To test this hypothesis, we performed additional simulations at several higher glycerol concentrations of 0.1 M, 0.15 M, 0.2 M, and 0.25 M, respectively. Five 50 ns long simulations were conducted at each concentration. It turns out that with the increase of glycerol concentration, it is possible that more binding sites in the channel are occupied simultaneously (Fig. S6†). At higher concentrations, there is a small probability of accommodating more than three glycerols in the channel (∼3% under 0.25 M) (Fig. S6†). It should be noted that the simulation is conducted under equilibrium conditions, and there should be fewer glycerols in the channel under non-equilibrium conditions with concentration gradients. Therefore, the 21-state model that allows at most three glycerols in the channel is a good approximation.



