Influence of ligand encapsulation on cobalt-59 chemical-shift thermometry

Abstract

Thermometry via magnetic resonance imaging (MRI) would provide a powerful noninvasive window into physiological temperature management. Cobalt-59 nuclear spins demonstrate exceptional temperature dependence of their NMR chemical shifts, yet the insight to control this dependence via molecular design is lacking. We present the first systematic evidence that encapsulation of this spin system amplifies the temperature sensitivity. We tested the temperature dependence of the ⁵⁹Co chemical shift (Δδ/ΔT) in a series of five low-spin cobalt(III) complexes as a function of increasing encapsulation within the 1st coordination sphere. This study spans from [Co(NH₃)₆]Cl₃, with no interligand connectivity, to a fully encapsulated dinitrosarcophagine (diNOsar) complex, [Co(diNOsar)]Cl₃. We discovered Δδ/ΔT values that span from 1.44(2) ppm °C⁻¹ in [Co(NH₃)₆]Cl₃ to 2.04(2) ppm °C⁻¹ in [Co(diNOsar)]Cl₃, the latter among the highest for a molecular complex. The data herein suggest that designing ⁵⁹Co NMR thermometers toward high chemical stability can be coincident with high Δδ/ΔT. To better understand this phenomenon, variable-temperature UV-Vis, ⁵⁹Co NMR relaxation, Raman spectroscopic, and variable-solvent investigations were performed. Data from these measurements highlight an unexpected impact of encapsulation – an increasingly dynamic and flexible inner coordination sphere. These results comprise the first systematic studies to reveal insight into the molecular factors that govern Δδ/ΔT and provide the first evidence of ⁵⁹Co nuclear-spin control via vibrational means.

---

Introduction

The structural flexibilities of metal complexes are key design principles for applications in the areas of reactivity,^1,2 medicine,³ photophysical properties,⁴ and magnetic information storage.⁵ Flexibility engenders stimuli-dependent changes in the coordination geometry of a metal, hence impacting d-orbital energies and any properties stemming from electronic structure.⁶ Thus, the control of flexibility is potentially a powerful way for targeting applications for metal complexes. One such application is biomedical thermometry by magnetic resonance imaging (MRI),^7,8 where the temperature-dependent structure of a flexible complex induces highly temperature-dependent spin-Hamiltonian parameters or relaxation times. If this variation could be harnessed to develop an imaging technique, such an application would circumvent many of the challenges associated with invasive thermometry, e.g. the point-like nature of the measurement.

One promising system for such thermometry by magnetic resonance is the cobalt-59 nucleus in low-spin cobalt(III) complexes. This NMR-active nucleus is 100% naturally abundant, I = 7/2, and has a receptivity of ca. 30% that of ¹H. Furthermore, the nucleus displays a wide reported chemical shift (δ) window (20 000 ppm) as a result of a paramagnetic contribution to δ that is directly tied to the ligand field splitting, Δ_o.^9–11 For complexes that contain cobalt-59 nuclei, changes in solution structure, such as lengthening Co–ligand bonds, can impact Δ_o, imparting changes in δ, and providing a mechanism for thermometry. In principle, then, the ⁵⁹Co chemical shift could be used to spatially map temperature through a technique known as chemical shift imaging.^12–14 Initial studies reveal sensitivities (Δδ/ΔT) on the order of 1–3 ppm °C⁻¹,^15–20 order-of-magnitude upgrades to the possibilities for conventional ¹H NMR thermometry.^21,22 Hence, these species may be useful to develop as new probes for chemical-shift imaging of temperature.¹² However, fundamental insight about the factors to govern that sensitivity is lacking (this manuscript explores one factor – encapsulation – as depicted in Fig. 1). As a result, design principles for enhancing Δδ/ΔT values are absent, and the true potential of cobalt-59 NMR thermometers for MRI remains unrealized.

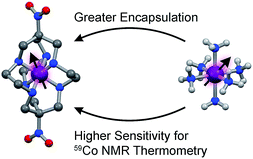Fig. 1 Tested design parameter in this manuscript. Molecular structures of (left) [Co(diNOsar)]³⁺ (diNOsar = dinitrosarcophagine) and (right) [Co(NH₃)₆]³⁺ are taken from crystal structures in ref. 23 and 24. Anions and hydrogens omitted for clarity where necessary. Purple, blue, red, grey, and light grey spheres correspond to cobalt, nitrogen, oxygen, carbon, and hydrogen atoms, respectively.

This manuscript details the first systematic exploration of the molecular factors that govern Δδ/ΔT in a family of cobalt-59 NMR thermometers (Fig. 1 and 2). As a first step, we sought to explore the role of ligand encapsulation on the temperature sensitivity of the ligand field and cobalt-59 NMR properties. Encapsulation is known to afford enhanced stability for metal complexes via the chelate and related macrocyclic effects.²⁵ Such stability is an important property for any imaging agent, as release of the metal can both induce toxicity and deactivate the magnetic species being used as a sensor. At the same time, a rigid, encapsulated ion can be readily envisioned to lack the flexibility needed for thermometry via structural change. Hence, encapsulation, while affording significant chemical stability, might simultaneously subdue the ability to sense temperature via cobalt-59 NMR.

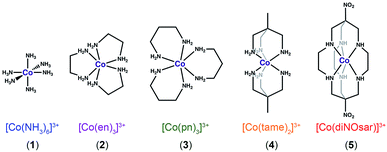Fig. 2 Bond-line representations of complexes 1–5, the systems studied in this manuscript. Anions and hydrogens bound to carbons are omitted for clarity.

To test this hypothesis, we investigated Δδ/ΔT for the ⁵⁹Co nuclei of the low-spin Co(III) complexes (Fig. 2) [Co(NH₃)₆]Cl₃ (1),²⁶ [Co(en)₃]Cl₃ (2, en = ethylenediamine),²⁷ [Co(pn)₃]Cl₃ (3, pn = 1,3-diaminopropane),²⁸ [Co(tame)₂]Cl₃ (4, tame = triaminomethylethane),²⁹ [Co(diNOsar)]Cl₃ (5, = dinitrosarcophagine),²³ and K₃[Co(CN)₆], the ⁵⁹Co NMR standard. This series of complexes was selected to enable an investigation of both molecular and electronic structure on Δδ/ΔT. First, we hypothesized that the increasing connectivity between the nitrogen donor atoms in 1–5 would engender an increasingly rigid coordination environment and, hence, suppress Δδ/ΔT. Thus, we expected that sensitivity to temperature would be compromised in favor of chemical stability. Indeed, the fully-encapsulating sarcophagine scaffold^23,25,30 will only surrender its NMR-active Co(III) ion under harsh conditions – heating in concentrated cyanide solution or acidic media.^31,32 The second investigation enabled by this set of complexes is the test of whether Δδ/ΔT directly correlates with Δ_o. The ⁵⁹Co chemical shift is proportional to 1/Δ_o,¹⁰ hence, δ should be more sensitive to tiny fluctuations in Δ_o at lower Δ_o.¹⁰ These studies are the first to reveal three key facts about Δδ/ΔT. Firstly, in contrast to our expectations, encapsulation enhances Δδ/ΔT. That is – the “rigid” ligand frameworks in 5 and 4 induce a stronger temperature-dependence in Δ_o (and δ) than the less-encapsulated species 1–3. Indeed, variable-temperature UV-Vis and ⁵⁹Co spin-lattice relaxation studies indicate that encapsulation counterintuitively supports higher temperature dependence in the coordination geometry. Second, our studies show that Δ_o alone does not correlate to the magnitude of Δδ/ΔT. Finally, third, Raman spectroscopy studies suggest molecular vibrational lifetimes – prolonged by high interconnectivity among donor atoms – are important factors governing Δδ/ΔT. Together, the data highlight a new implication for rigidity in molecular magnetism.

Results and discussion

Understanding the temperature sensitivity of the chemical shift requires first establishing the electronic structures of the cobalt(III) ions in 1–5. UV-Vis electronic absorption spectra of compounds 1–5 and K₃[Co(CN)₆] in H₂O reproduce reported results for the individual complexes (Fig. 3), wherein the lowest energy peak indicates the ¹A_1g → ¹T_1g transition and the higher energy peak indicates the ¹A_1g → ¹T_2g transition.^10,23 The energies of these two peaks and a Tanabe-Sugano diagram permit quantitation of Δ_o, which increases from 3 (22 376 cm⁻¹) to 5 (22 754 cm⁻¹) and 1 (23 018 cm⁻¹) to 4 (23 276 cm⁻¹) to 2 (23 321 cm⁻¹) (Table S1†). These values are consistent with literature values for 1–5 and stand in contrast to the strong ligand field of K₃[Co(CN)₆] that engenders a Δ_o of 38 000 cm⁻¹.³³⁵⁹Co resonant frequencies were observed for 1–5 over the range of 6800 to 8400 ppm (referenced to K₃[Co(CN)₆]). According to the ⁵⁹Co chemical shifts, the magnitude of Δ_o increases in the order 3 < 1 < 4 < 2 < 5 < K₃[Co(CN)₆]. This order is at odds with the trend obtained from electronic absorption spectroscopy measurements (see Fig. S1†). However, reported correlations between UV-Vis peak position and δ are only approximate, not quantitative.^9,10 Nevertheless, these measurements provide (i) two points of reference to test for a correlation between Δδ/ΔT and Δ_o, and (ii) the location of the ⁵⁹Co NMR resonances for variable-temperature analyses.

Fig. 3 Characterization of Co(III) electronic structure in 1–5. Top: electronic absorption (UV-Vis) spectra for 1–5 and K₃[Co(CN)₆] in H₂O at room temperature. The lower-energy peak is the ¹A_1g to ¹T_1g transition while the higher-wavenumber peak is ¹A_1g to ¹T_2g. Bottom: 500 MHz ⁵⁹Co NMR spectra for 1–5 in H₂O at room temperature.

Variable-temperature ⁵⁹Co NMR spectra were collected for 1–5 and K₃[Co(CN)₆] in H₂O from 10–60 °C (see Fig. 4, 5 and S2–S7†) to explore the temperature dependence of δ. With increasing temperature, peaks for 1–5 and K₃[Co(CN)₆] shift downfield to higher δ. This temperature-dependent shift of peaks is consistent with varying coordination geometry in solution.^18,34 As temperature is increased, energy is introduced into the vibrational modes of the cobalt complex, expanding M–L bond distances and engendering generally weaker Δ_o.^18,35

Fig. 4 Variable-temperature ⁵⁹Co NMR for 4 at 500 MHz in H₂O, collected in increments of 5 °C. The system was allowed to equilibrate for at least 5 minutes between each temperature point prior to measurement.

Fig. 5 Chemical shift values for 1–5 and K₃[Co(CN)₆] as a function of temperature. Solid lines are the result of linear regression – see main text for further details.

Precise determination of the sensitivity of the ⁵⁹Co NMR peak to temperature (Δδ/ΔT) was achieved via linear regression of the temperature-dependent data (see Fig. 5, S8, and Table S2†). These analyses revealed Δδ/ΔT values for K₃[Co(CN)₆] and 1–5, respectively, of 1.44(1), 1.44(2), 1.38(1), 1.30(2), 1.71(1), and 2.04(2) ppm °C⁻¹. These values are within the ranges of sensitivity reported for the few ⁵⁹Co NMR thermometers,^15–18,20 but it's worth noting that, to the best of our knowledge, the Δδ/ΔT of 5 is eclipsed only by Co(acac)₃, a molecule that is completely unsuitable for aqueous (e.g. physiological) applications.^16,20 Most importantly (and surprisingly), these data indicate that the highest sensitivity to changes in temperature is held by the completely encaged complex 5.

The values of Δδ/ΔT follow an opposing trend to the initial hypothesis, in that 5, with the highest degree of encapsulation, displays the strongest Δδ/ΔT. Complex 4, with the second highest degree of encapsulation, displays the second highest sensitivity of our studied complexes. Yet, a comprehensive trend for all complexes on the basis of encapsulation is not indicated by these data. For example, in 1 and K₃[Co(CN)₆], the ligand donor atoms are not connected in any manner. Yet, these species demonstrate higher Δδ/ΔT than both 2 and 3, which contain bidentate chelates. Furthermore, the collected data show that electronic structure considerations alone (specifically, Δ_o) do not govern sensitivity. Here, neither the trend in Δ_o extracted from UV-Vis (3 < 5 < 1 < 4 < 2 < K₃[Co(CN)₆]) nor that from the 25 °C ⁵⁹Co NMR (3 < 1 < 4 < 2 < 5 < K₃[Co(CN)₆]) reproduce the trend in Δδ/ΔT (see Fig. S9 and Table S3†).

The foregoing results highlight the need for deeper studies to derive fundamental insight. An important implication of the foregoing results is the concept that the encaged complex counterintuitively demonstrates the highest fluxionality in the inner-coordination structure. Four key experiments were applied to further test this rationale.

If the molecular structure of [Co(diNOsar)]Cl₃ is truly more temperature-dependent than 1–4, then Δ_o for 5 should show the greatest temperature dependence. Variable-temperature UV-Vis spectra for 1–5 show slight shifts to lower energy with increasing temperature (Fig. 6 and S10–S12†). Analyses of these data reveal a change in Δ_o as a function of temperature, ΔΔ_o/ΔT. Over 1–5, ΔΔ_o/ΔT assumes values of −2.78(4), −1.36(17), −2.91(5), −3.70(17), and −5.65(32) cm⁻¹ °C⁻¹ for 1–5 respectively. These spectral changes are consistent with studies probing temperature-dependent UV-Vis spectra for metal complexes wherein spin-state changes are absent^36,37 (versus systems displaying spin-crossover³⁸ or valence tautomerization³⁹). These data trend in a manner (particularly for 2–5) that seems opposed to an association between encapsulation and increased rigidity of the coordination environment. Indeed, 5 exhibits the largest change in temperature, followed by 4, then 3 and 1, and finally 2. Hence, these data point to a more dynamic inner coordination sphere.

Fig. 6 Variable temperature UV-Vis analysis. Top: normalized variable-temperature spectra for 5 in H₂O at 4.5 mM concentration. Bottom: temperature dependence of Δ_o for 1–5. Linear regression yielded the grey lines and ΔΔ_o/ΔT – see main text for more detail.

If the inner coordination sphere is less rigid upon encapsulation, then cobalt-59 spin lattice relaxation times should reflect that point. Indeed, the I = 7/2 cobalt-59 nucleus is quadrupolar, and, hence, its spin-lattice relaxation rate (1/T₁) is dominated by fluctuations in the local electric field gradient.⁴⁰ Hence, the anticipated higher fluxionality in the CoN₆ environment of 4 and 5versus1–3 should correspondingly engender shorter T₁. Analysis of the inversion recovery traces for 1–5 (Fig. 7) reveal T₁ parameters for 1–5 that follow a trend with encapsulation, wherein [Co(NH₃)₆]Cl₃ (1) displays the longest T₁ (48.47(5) ms), followed by 2 (9.09(2) ms) and 3 (2.73(1) ms). In contrast, the species of highest encapsulation, 4 and 5, have the shortest T₁ values (346(1) and 323(1) μs, respectively). For 1 and 2, these values match previously reported results.^40–42 Quadrupolar relaxation is also enhanced in systems with a higher ⁵⁹Co quadrupole coupling constant, and this constant is smaller for high-symmetry complexes.⁹ Compound 1 is clearly higher symmetry (O_h) than 2–5 (D₃). This symmetry difference is likely an important contributor to the T₁ of 1versus2–5, but quadrupolar couplings in this latter set of compounds are similar (when known).^42,43 Moreover, solution-phase rotational rates for the series extrema, 1 and 5, are similar,⁴² suggesting rotational correlation is also not driving the difference in T₁ across the series. Together, these points suggest that considerations beyond symmetry/rotation define T₁ for these compounds. In light of the other data in this paper, we propose that the T₁ trend evidences a more dynamic coordination environment upon encapsulation, though deeper investigations are needed to test this hypothesis.

Fig. 7 Spin-lattice relaxation data for 1–5. (a) ⁵⁹Co NMR spectrum as a function of delay time for 3 following the 22.5 μs inversion pulse. (b) Specific inversion recovery sequence used, and intensity of the peaks as a function of the delay time. Grey lines are exponential fits to the data, yielding T₁. See main text for more information on the fits. All data were collected at 25 °C and 33 mM concentration.

Vibrational spectra in the 100–650 cm⁻¹ window, wherein metal–ligand vibrations typically occur, ought to vary with rigidity as well.⁴⁴ To test this concept, microcrystalline powders of 1–5 were analyzed via Raman spectroscopy. As the probed molecules increase in structural complexity, so do the Raman spectra, with compound 1 exhibiting 8, 2 displaying 12, and 5 producing 21 bands below 650 cm⁻¹ (Fig. 8). Previous reports identify symmetric Co–N bond stretches at 500 and 486 cm⁻¹ for 1, and 526, 444, and 476 cm⁻¹ for 2.^45,46 For 3–5, in contrast, no Raman spectra are reported to the best of our knowledge. Closer inspection of the Raman spectra reveals a general sharpening of transitions with increasing encapsulation. This sharpening is most noticeable when comparing the spectra of lesser encapsulated compounds 1–3 with the completely encapsulated species 5. Linewidth analyses of the observed vibrations for 1–5 permitted relative quantitation of the general degree of sharpness of these spectra (Fig. S13–S17 and Table S4†). The averages of the peak linewidths for the spectra are ordered from 5 < 2 < 4 < 1 < 3, where the fully encapsulated species, 5, exhibits the smallest average peak width.

Fig. 8 Room-temperature Raman spectra collected on pure powder samples of 1–5. All spectra are baseline corrected.

On the basis of the variable-temperature NMR and UV-Vis data, the highest flexibility is observed for 5. However, the lifetime of the NMR experiment is much longer than that of vibrational spectroscopy.⁴⁷ Hence, one may therefore expect the greater structural variability from the NMR/UV-Vis analyses to result in greater inhomogeneous broadening of the vibrational peaks for 5. The observations from the Raman spectra are in contrast to this expectation, as 5 demonstrates the sharpest peaks. One alternative mechanism that governs peak linewidths is homogeneous broadening, which causes sharper peaks for excitations that have longer lifetimes.⁴⁸ This mechanism is acknowledged as dominant in studies of M(CO)_n at room temperature in solution.^49,50 If operative and dominant in powders of 1–5, this admittedly simplistic model of broadening would suggest that the lifetimes of the vibrations of the coordination sphere are enhanced by encapsulation. Translation of the average linewidths of 1–5 into average vibrational, spectroscopic lifetimes (via the relationship FWHM = 1/πτ) yields lifetimes of 0.4(2), 0.6(3), 0.4(2), 0.8(4), and 1.3(4) ps for 1–5, respectively.

The foregoing linewidth interpretation should be treated with caution owing to three specific factors. First, differences in microcrystalline environment can have an important impact on Raman linewidths (e.g.ref. 51 and 52). We note, however, that a preliminary powder diffraction analysis of the same samples measured by Raman spectroscopy did not reveal a noticeable trend of crystallinity correlating to the observed lifetimes (Fig. S18†). Second, modes of differing symmetries can yield different linewidths,⁴⁹ as is likely evidenced here in the spread of linewidths in the deconvoluted peaks. Third, true elucidation of the vibration lifetimes requires time-resolved methods, which would also help differentiate inhomogeneous versus homogeneous broadening mechanisms.⁵⁰ These data clearly motivate further solution-phase, time-resolved vibrational studies, a critical component of planned follow up work. Nevertheless, the obtained lifetimes are in the general picosecond range expected for metal complexes.^49,50

If encapsulation affects Δδ/ΔT via modulating vibration lifetimes, that insight would provide a new design principle for vibrational control of molecular spin. Variable-solvent studies of 2 were performed as one final test of this concept. In particular, as the polar N–H bonds of the coordinated nitrogen atoms in 1–5 likely interact with the aqueous environment, this interaction should mediate the vibrations and structure of the [Co(en)₃]³⁺ moiety, potentially imparting large differences to Δδ/ΔT. Indeed, such hydrogen bonding interactions are demonstrated to enable modulation of M–N and M–O bonds in other molecular systems.^53,54 Here, this concept is being tested for temperature-dependent magnetic effects.

Initial studies focused on one member of the series, [Co(en)₃]Cl₃ (2), dissolved in four additional solvents: dimethylformamide (DMF), hexamethylphosphoramide (HMPA),§ dimethylsulfoxide (DMSO) and d₆-dimethylsulfoxide (d₆-DMSO). The solvents DMF, HMPA, and DMSO were selected to test polarity, and d₆-DMSO chosen to test the impact of environmental deuteration. While solvent/deuteration impacts on ⁵⁹Co δ are reported,⁵⁵ their role on thermometry is not yet understood. ⁵⁹Co NMR spectra collected at 25 °C reveal a peak position that shifts over a range of 200 ppm as a function of solvent identity (see Fig. 9). This solvent-dependent effect is known for the ClO₄⁻ salt of the [Co(en)₃]³⁺ cation, stemming from modulation of the N-atom ligand field via hydrogen bonding between the solvent and N–H protons.⁵⁶ Furthermore, only a tiny shift in δ is observed between DMSO and d₆-DMSO, also in line with expected results.⁵⁵

Fig. 9 Variable-solvent ⁵⁹Co NMR studies of [Co(en)₃]Cl₃ (2). Top: ⁵⁹Co NMR spectra of 2 in solvents of differing polarity. All data are reported at 25 °C from a 500 MHz NMR. Middle: temperature dependence of peak position as a function of solvent for 2. Solid lines are the result of linear regression to yield Δδ/ΔT (see main text). Bottom: sensitivity of ⁵⁹Co δ to changes in temperature as a function of solvent π* polarity index. Error bars are less than the symbol size, except for DMF. The solid line is the result of linear regression with R² = 0.9.

Variable-temperature analyses tested the impact of these differing solvent cages on Δδ/ΔT (Fig. S19–S22 and Table S5†). Here, analysis of the variable-temperature ⁵⁹Co NMR peak positions as a function of solvent demonstrate a noticeable impact of solvent identity on Δδ/ΔT (Fig. 9). As in H₂O, all ⁵⁹Co NMR chemical shifts move downfield with increasing temperature. Linear regression of these temperature-dependent data reveal Δδ/ΔT values of 1.19(2), 1.23(1), 1.27(1), and 1.28(1) ppm °C⁻¹, respectively, for DMF, HMPA, DMSO, and d₆-DMSO. These values are all lower than in H₂O (Δδ/ΔT = 1.38(1) ppm °C⁻¹) and indicate nearly no role for solvent deuteration on Δδ/ΔT in the present compound.

Comparison of the solvent-dependent Δδ/ΔT results for 2 against measures of solvent–solute interaction potentially provide deeper insight into the role of the solvent cage (Fig. 9, S23 and Table S5†). In particular, the trend in Δδ/ΔT was contrasted against (1) the solvent acceptor and donor numbers,^57,58 (2) the π* solvent polarity scale,^59,60 and (3) the β and α hydrogen-bonding donor/acceptor scales.^60–62 There may be an approximate correlation between Δδ/ΔT and acceptor number, whereas there is clearly none for donor number and little, if any with β (see Fig. S23†). Analysis with α values is complicated as α is 0 for all solvents here except H₂O.⁶⁰ However, the π* scale clearly reveals a correlation (R² = 0.9, Fig. 9, bottom).

The foregoing data point toward a coordination environment that is counterintuitively more flexible and dynamic with increasing encapsulation. Electron transfer studies of sarcophagine-like ligands provided the first assertions of rigidity in encapsulated Co(III) complexes based on a conformationally inflexible environment.^63–67 We propose that this conformation-based description of rigidity is insufficient for understanding the trend of Δδ/ΔT. Instead, we tentatively posit an alternative, spin-relevant interpretation in this context. Here, the enhanced connectivity in 4 and 5 ensures a higher rigidity in the coordination environment, except in this case the rigidity permits vibrations of the encapsulated coordination environment to persist longer. Such longer lifetimes ultimately sustain a change in the coordination sphere by lengthening the equilibrium Co–N bond distances. Hence, there is a temperature dependence of Δ_o and δ in 4 and 5 that is larger than 1–3. This tentative interpretation of the data is also consistent with the solvent dependence of Δδ/ΔT in 2, as the solvent cage is known for impacting vibration lifetimes in coordination complexes.^49,68,69 The fundamental argument we propose here is an analogue to the justification of long phonon lifetimes in materials like diamond,^70,71 except here related to the molecular vibrations of a complex in solution. These studies clearly motivate future investigations to evaluate the validity of this picture of vibration-controlled spin properties.

Furthermore, the solvent-dependent data hint at a rich area of inquiry into the role of the second coordination sphere and counterions. When considering the [Co(en)₃]³⁺ unit, interactions with the solvent are most easily intuited via the N–H protons accepting electron density from solvent molecule lone pairs. The association of a higher Δδ/ΔT with a higher π* index of solvent polarity⁵⁹ would mesh with this intuited picture. This model would also be consistent with the match between a lower β value and a higher Δδ/ΔT, as a low β occurs when a solute will only weakly accept a proton.⁶² Thus, these data suggest that the N–H interactions are key to understanding Δδ/ΔT. However, the interpretation isn't without some uncertainty. To the extent that there is any correlation of Δδ/ΔT with solvent properties, it is with their acceptor number, not donor number, meaning that [Co(en)₃]³⁺ acts as a donor. This argument only makes sense if one also considers the lone pairs of a bound Cl⁻ counterion, not the N–H bonds. Indeed, earlier studies of [Co(en)₃]³⁺ and [Co(diNOsar)]³⁺ demonstrate a close association between these species and their Cl⁻ counterions that persists in solution.^43,67,72 Noted reservations about generalizing the acceptor/donor number scale lend caution to the second explanation of the solvent-dependent data.⁷³ Nevertheless, the conflict between these two interpretations underlines the necessity of further investigations into the role of the counterion and solvent cage on Δδ/ΔT.

Conclusions and outlook

The foregoing results are the first evidence of synergy between ligand encapsulation and enhanced temperature-dependent magnetic changes in metal-ion nuclear spins. Such knowledge is of broad impact, as exploiting molecular rigidity to control magnetism is an emerging trend in designing molecules for other spin-based technologies, e.g. molecular quantum bit development.^74–76 Importantly, the presented arguments potentially tie vibration lifetimes to nuclear magnetism – necessitating future time-resolved measurements to test the validity of this analysis. Finally, our studies reveal that in addition to the ligand, manipulations of the counterion and solvent cage are the next stage for understanding the mechanisms that control Δδ/ΔT. Beyond the targeted applications in thermometry, the concepts herein could be extended to understanding the impacts of molecular rigidity on other spin-based applications, for example, designing electron paramagnetic resonance imaging probes,⁷⁷ rigid systems for dynamic nuclear polarization^78–80 (particularly with metal ions),^81,82 or molecular quantum sensors.^83,84

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge Mr B. Gerold, Ms L. Beck, Dr C. Rithner and E. Ellison, and Profs. M. Nippe and E. Johnston-Halperin for useful discussions and experimental assistance. We are further grateful to some exceptionally helpful reviewers. This research was performed with the support of Colorado State University (CSU) and the NIH (R21-EB027293). NMR experiments were performed at the CSU Central Instrument Facility, which is supported by an NIH-SIG award (1S10OD021814-01) and the CSU-CORES Program. A portion of this work was performed at the Raman Microspectroscopy Laboratory in the Department of Geological Science at the University of Colorado-Boulder.

Notes and references

1. S. Bestgen, N. H. Rees and J. M. Goicoechea, Organometallics, 2018, 37, 4147–4155.
2. G. W. Coates and R. M. Waymouth, Science, 1995, 267, 217–219.
3. L. Riccardi, V. Genna and M. De Vivo, Nat. Rev. Chem., 2018, 2, 100–112.
4. M. W. Mara, K. A. Fransted and L. X. Chen, Coord. Chem. Rev., 2015, 282–283, 2–18.
5. M. Mannini, F. Pineider, C. Danieli, F. Totti, L. Sorace, P. Sainctavit, M. A. Arrio, E. Otero, L. Joly, J. C. Cezar, A. Cornia and R. Sessoli, Nature, 2010, 468, 417–421.
6. B. Figgis and M. Hitchman, Ligand field theory and its applications, Wiley-VCH, New York, 2000.
7. V. Rieke and K. B. Pauly, J. Magn. Reson. Imaging, 2008, 27, 376–390.
8. D. Townsend, Z. Cheng, D. Georg, W. Drexler and E. Moser, Frontiers in Physics, 2013, 1, 1–6.
9. J. C. C. Chan and S. C. F. Au-Yeung, Annu. Rep. NMR Spectrosc., 2000, 41, 1–54.
10. R. Bramley, M. Brorson, A. M. Sargeson and C. E. Schaeffer, J. Am. Chem. Soc., 1985, 107, 2780–2787.
11. A. Yamasaki, J. Coord. Chem., 1991, 24, 211–260.
12. L. Brateman, Am. J. Roentgenol., 1986, 146, 971–980.
13. A. Haase, J. Frahm, W. Hanicke and D. Matthae, Phys. Med. Biol., 1985, 30, 341–344.
14. T. R. Brown, B. M. Kincaid and K. Ugurbil, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 3523–3526.
15. A. G. Webb, M. Wong, M. Niesman, K. J. Kolbeck, L. J. Wilmess, R. L. Magin and K. S. Suslick, Int. J. Hyperthermia, 1995, 11, 821–827.
16. G. C. Levy, T. J. Bailey and D. A. Wright, J. Magn. Reson., 1980, 37, 353–356.
17. D. G. Gillies, L. H. Sutcliffe and A. J. Williams, Magn. Reson. Chem., 2002, 40, 57–64.
18. G. B. Benedek, R. Englman and J. A. Armstrong, J. Chem. Phys., 1963, 39, 3349–3363.
19. M. Kanakubo, H. Ikeuchi and G. P. Satô, J. Magn. Reson., Ser. A, 1995, 112, 13–16.
20. M. Kanakubo, T. Uda, H. Ikeuchi and G. P. Satô, J. Solution Chem., 1998, 27, 645–653.
21. J. De Poorter, C. De Wagter, Y. De Deene, C. Thomsen, F. Ståhlberg and E. Achten, Magn. Reson. Med., 1995, 33, 74–81.
22. D. L. Carter, J. R. MacFall, S. T. Clegg, X. Wan, D. M. Prescott, H. C. Charles and T. V Samulski, Int. J. Radiat. Oncol., Biol., Phys., 1998, 40, 815–822.
23. R. J. Geue, T. W. Hambley, J. M. Harrowfield, A. M. Sargeson and M. R. Snow, J. Am. Chem. Soc., 1984, 106, 5478–5488.
24. X. Wang, R. Justice and S. C. Sevov, Inorg. Chem., 2007, 46, 4626–4631.
25. Y. Voloshin, I. Belaya and R. Krämer, The Encapsulation Phenomenon: Synthesis, Reactivity and Applications of Caged Ions and Molecules, Springer International Publishing, Switzerland, 2016.
26. J. Bjerrum and J. P. McReynolds, Inorg. Synth., 1946, II, 216–221.
27. J. B. Work, Inorg. Synth., 1946, II, 221–222.
28. J. C. Bailar and J. B. Work, J. Am. Chem. Soc., 1946, 68, 232–235.
29. R. J. Geue and M. R. Snow, Inorg. Chem., 1977, 16, 231–241.
30. L. R. Gahan and J. M. Harrowfield, Polyhedron, 2015, 94, 1–51.
31. H. Cai, J. Fissekis and P. S. Conti, Dalton Trans., 2009, 5395.
32. G. A. Bottomley, I. J. Clark, I. I. Creaser, L. M. Engelhardt, R. J. Geue, K. S. Hagen, J. M. Harrowfield, G. A. Lawrance, P. A. Lay, A. M. Sargeson, A. J. See, B. W. Skelton, A. H. White and F. R. Wilner, Aust. J. Chem., 1994, 47, 143–179.
33. J. J. Alexander and H. B. Gray, J. Am. Chem. Soc., 1968, 90, 4260–4271.
34. C. J. Jameson, D. Rehder and M. Hoch, J. Am. Chem. Soc., 1987, 109, 2589–2594.
35. R. Englman, Mol. Phys., 1960, 3, 23–34.
36. L. V. Koplitz, K. Kim and D. S. McClure, Inorg. Chem., 1994, 33, 702–704.
37. O. G. Holmes and D. S. McClure, J. Chem. Phys., 1957, 26, 1686–1694.
38. P. Gütlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419–427.
39. T. Tezgerevska, K. G. Alley and C. Boskovic, Coord. Chem. Rev., 2014, 268, 23–40.
40. R. Ader and A. Loewenstein, J. Magn. Reson., 1971, 5, 248–261.
41. S. C. F. F. Au-Yeung, R. J. Buist and D. R. Eaton, J. Magn. Reson., 1983, 55, 24–38.
42. C. W. Kirby, C. M. Puranda and W. P. Power, J. Phys. Chem., 1996, 100, 14618–14624.
43. Y. Masuda and H. Yamatera, J. Phys. Chem., 1988, 92, 2067–2071.
44. K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, John Wiley & Sons, Hoboken, NJ, 2009.
45. Y. Chen, D. H. Christensen, G. O. Sørensen, O. F. Nielsen and E. Pedersen, J. Mol. Struct., 1993, 299, 61–72.
46. P. Stein, V. Miskowski, W. H. Woodruff, J. P. Griffin, K. G. Werner, B. P. Gaber and T. G. Spiro, J. Chem. Phys., 1976, 64, 2159–2167.
47. R. S. Drago, Physical Methods for Chemists, Surfside Scientific Publishers, Gainesville, 2nd edn, 1992.
48. J. L. McHale, Molecular Spectroscopy, CRC Press, 2nd edn, 2017.
49. J. J. Turner, Coord. Chem. Rev., 2002, 230, 213–224.
50. A. Tokmakoff and M. D. Fayer, Acc. Chem. Res., 1995, 28, 437–445.
51. H. Inada, K. Ohnishi, S. Nomura, A. Higuchi, H. Nakano and Y. Shirota, J. Mater. Chem., 1994, 4, 171.
52. J. Petzelt, S. Kamba and I. Gregora, Phase Transitions, 1997, 63, 107–145.
53. A. S. Borovik, Acc. Chem. Res., 2005, 38, 54–61.
54. R. L. Lucas, D. R. Powell and A. S. Borovik, J. Am. Chem. Soc., 2005, 127, 11596–11597.
55. H. Grahn, U. Edlund and T. A. Holak, Magn. Reson. Chem., 1987, 25, 497–502.
56. G. Gonzalez, U. Mayer and V. Gutmann, Inorg. Nucl. Chem. Lett., 1979, 15, 155–159.
57. W. R. Fawcett, J. Phys. Chem., 1993, 97, 9540–9546.
58. U. Mayer, V. Gutmann and W. Gerger, Monatsh. Chem., 1975, 106, 1235–1257.
59. M. J. Kamlet, J. L. M. Abboud and R. W. Taft, J. Am. Chem. Soc., 1977, 99, 6027–6038.
60. M. J. Kamlet, J. L. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887.
61. M. H. Abraham, Chem. Soc. Rev., 1993, 22, 73.
62. R. W. Taft, W. J. Shuely, R. M. Doherty and M. J. Kamlet, J. Org. Chem., 1988, 53, 1737–1741.
63. R. J. Geue, M. G. McCarthy and A. M. Sargeson, J. Am. Chem. Soc., 1984, 106, 8282–8291.
64. P. V. Bernhardt, A. M. T. Bygott, R. J. Geue, A. J. Hendry, B. R. Korybut-Daszkiewicz, P. A. Lay, J. R. Pladziewicz, A. M. Sargeson and A. C. Willis, Inorg. Chem., 1994, 33, 4553–4561.
65. A. M. Sargeson and P. A. Lay, Aust. J. Chem., 2009, 62, 1280–1290.
66. A. G. Algarra, Eur. J. Inorg. Chem., 2015, 2015, 503–511.
67. I. Ling, A. N. Sobolev, R. Hashim and J. M. Harrowfield, CrystEngComm, 2014, 16, 11058–11063.
68. G. M. Sando, Q. Zhong and J. C. Owrutsky, J. Chem. Phys., 2004, 121, 2158–2168.
69. J. T. King, M. R. Ross and K. J. Kubarych, J. Phys. Chem. B, 2012, 116, 3754–3759.
70. L. Bergman and R. J. Nemanich, Annu. Rev. Mater. Sci., 1996, 26, 551–579.
71. K. C. Lee, B. J. Sussman, J. Nunn, V. O. Lorenz, K. Reim, D. Jaksch, I. A. Walmsley, P. Spizzirri and S. Prawer, Diamond Relat. Mater., 2010, 19, 1289–1295.
72. M. Iida, T. Nakamori, Y. Mizuno and Y. Masuda, J. Mol. Liq., 1995, 65–66, 269–272.
73. C. Laurence and J.-F. Gal, Lewis Basicity and Affinity Scales, John Wiley & Sons, Ltd, Chichester, UK, 2009.
74. M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731–740.
75. M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338–4341.
76. L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Chem. Sci., 2018, 9, 3265–3275.
77. In Vivo EPR (ESR), ed. L. J. Berliner, Springer US, Boston, MA, 2003, vol. 18.
78. M. K. Kiesewetter, B. Corzilius, A. A. Smith, R. G. Griffin and T. M. Swager, J. Am. Chem. Soc., 2012, 134, 4537–4540.
79. A. Zagdoun, G. Casano, O. Ouari, G. Lapadula, A. J. Rossini, M. Lelli, M. Baffert, D. Gajan, L. Veyre, W. E. Maas, M. Rosay, R. T. Weber, C. Thieuleux, C. Coperet, A. Lesage, P. Tordo and L. Emsley, J. Am. Chem. Soc., 2012, 134, 2284–2291.
80. E. L. Dane, B. Corzilius, E. Rizzato, P. Stocker, T. Maly, A. A. Smith, R. G. Griffin, O. Ouari, P. Tordo and T. M. Swager, J. Org. Chem., 2012, 77, 1789–1797.
81. B. Corzilius, V. K. Michaelis, S. A. Penzel, E. Ravera, A. A. Smith, C. Luchinat and R. G. Griffin, J. Am. Chem. Soc., 2014, 136, 11716–11727.
82. B. Corzilius, A. A. Smith, A. B. Barnes, C. Luchinat, I. Bertini and R. G. Griffin, J. Am. Chem. Soc., 2011, 133, 5648–5651.
83. G. Balasubramanian, A. Lazariev, S. R. Arumugam and D. Duan, Curr. Opin. Chem. Biol., 2014, 20, 69–77.
84. R. Schirhagl, K. Chang, M. Loretz and C. L. Degen, Annu. Rev. Phys. Chem., 2014, 65, 83–105.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc01689a

‡ Denotes equal contribution to manuscript.

§ HMPA is a Class 1B carcinogen and mutagen and should be handled with extreme care.

---