Open Access Article
Open Access ArticleIRMOF-74(n)–Mg: a novel catalyst series for hydrogen activation and hydrogenolysis of C–O bonds†
Vitalie
Stavila
 *a,
Michael E.
Foster
a,
Jonathan W.
Brown
a,
Ryan W.
Davis
a,
Jane
Edgington
a,
Annabelle I.
Benin
a,
Ryan A.
Zarkesh
a,
Ramakrishnan
Parthasarathi
a,
David W.
Hoyt
*a,
Michael E.
Foster
a,
Jonathan W.
Brown
a,
Ryan W.
Davis
a,
Jane
Edgington
a,
Annabelle I.
Benin
a,
Ryan A.
Zarkesh
a,
Ramakrishnan
Parthasarathi
a,
David W.
Hoyt
 b,
Eric D.
Walter
b,
Amity
Andersen
b,
Nancy M.
Washton
b,
Andrew S.
Lipton
b,
Eric D.
Walter
b,
Amity
Andersen
b,
Nancy M.
Washton
b,
Andrew S.
Lipton
 b and
Mark D.
Allendorf
b and
Mark D.
Allendorf
 *a
*a
aChemistry, Combustion, and Materials Center, Sandia National Laboratories, Livermore, California 94551, USA. E-mail: mdallen@sandia.gov; vnstavi@sandia.gov
bEnvironmental Molecular Sciences Laboratory, Pacific Northwest National Laboratory, Richland, Washington 99354, USA
First published on 3rd September 2019
Abstract
Metal–Organic Frameworks (MOFs) that catalyze hydrogenolysis reactions are rare and there is little understanding of how the MOF, hydrogen, and substrate molecules interact. In this regard, the isoreticular IRMOF-74 series, two of which are known catalysts for hydrogenolysis of aromatic C–O bonds, provides an unusual opportunity for systematic probing of these reactions. The diameter of the 1D open channels can be varied within a common topology owing to the common secondary building unit (SBU) and controllable length of the hydroxy-carboxylate struts. We show that the first four members of the IRMOF-74(Mg) series are inherently catalytic for aromatic C–O bond hydrogenolysis and that the conversion varies non-monotonically with pore size. These catalysts are recyclable and reusable, retaining their crystallinity and framework structure after the hydrogenolysis reaction. The hydrogenolysis conversion of phenylethylphenyl ether (PPE), benzylphenyl ether (BPE), and diphenyl ether (DPE) varies as PPE > BPE > DPE, consistent with the strength of the C–O bond. Counterintuitively, however, the conversion also follows the trend IRMOF-74(III) > IRMOF-74(IV) > IRMOF-74(II) > IRMOF-74(I), with little variation in the corresponding selectivity. DFT calculations suggest the unexpected behavior is due to much stronger ether and phenol binding to the Mg(II) open metal sites (OMS) of IRMOF-74(III), resulting from a structural distortion that moves the Mg2+ ions toward the interior of the pore. Solid-state 25Mg NMR data indicate that both H2 and ether molecules interact with the Mg(II) OMS and hydrogen–deuterium exchange reactions show that these MOFs activate dihydrogen bonds. The results suggest that both confinement and the presence of reactive metals are essential for achieving the high catalytic activity, but that subtle variations in pore structure can significantly affect the catalysis. Moreover, they challenge the notion that simply increasing MOF pore size within a constant topology will lead to higher conversions.
Introduction
Dihydrogen is important in a variety of reactions used to synthesize hydrocarbon fuels, platform chemicals,1 and to desulfurize hydrocarbons.2 Hydrogen is also envisioned as a foundational component of a renewable energy economy,3,4 serving as both a fuel and a reactant to convert lignocellulosic biomass, brown coal, and biomass-derived pyrolysis oil to fuels and value-added chemicals such as phenols, benzene, toluene, xylene, and gasoline-range aromatics. Catalysts are necessary to activate the strong H–H bond (436 kJ mol−1 at 25 °C) and avoid high-temperature pyrolysis that leads to complex product mixtures,5–7 and a variety can be used to achieve milder reaction conditions that improve selectivity and increase hydrogen utilization efficiency. These include noble metals, base metals, metal sulfides, and metal phosphides and carbides.6–8 Typical hydrogenation catalysts combine an oxide support with a transition metal,7 whereas hydrogenolysis catalysts are often noble metals such as palladium.8,9 However, selective hydrogenolysis under mild conditions of the aryl–ether bonds typically found in biomass and coal remains a challenge, in most cases requiring high temperatures and H2 pressures (>250 °C, 30 bar) that lead to poor selectivity and inefficient hydrogen use. Hartwig and coworkers achieved a breakthrough when they reported homogeneous and heterogeneous versions of nickel–carbene complexes that efficiently convert aryl ethers to phenol and the corresponding hydrocarbon,10,11 and there are now numerous recent examples of nickel-based catalysts to promote hydrogenolysis of aryl–ether bonds.12–22 A disadvantage of some of these is that a sacrificial base10,11,17,23 or Lewis acid13 is required. Aryl ether cleavage in water has been achieved using a nickel catalyst supported on SiO2 and HZSM-5;24,25 however, in some cases, selectivity is reduced by ring hydrogenation.24Development of earth-abundant hydrogenolysis catalysts could improve the economics of hydrogen utilization, particularly if they can replace noble metals and more costly transition metals; a heterogeneous iron catalyst reported very recently is a promising example.15 However, catalysts relying on low-cost main-group elements to activate hydrogen are not common. Although they lack the d orbitals known to polarize H2, light main group elements form metal hydrides, suggesting that thermodynamically favorable hydrogen activation pathways involving these elements could exist. Moreover, alumina and magnesium oxide, which are common supports for hydrogenolysis catalysts, are known to perform an active role in the hydrocracking.7 In nature, mild reaction conditions are achieved by hydrogenase enzymes.26 Their active sites are typically complex Fe–S or Fe–Ni–S clusters that allow electron shuttling and stabilization of protons or hydride ions formed during the reaction.27 Although highly efficient, these catalysts are too thermally sensitive for industrial use, lack synthetic tunability needed to adapt them to specific processes, and often require a base or costly cofactor.
Metal–Organic Frameworks (MOFs) are a recent entry into the catalogue of hydrogenolysis catalysts. These crystalline, nanoporous materials possess a large number of synthetic handles that allow their pore dimensions and reactive site properties to be tailored to catalyze a particular reaction. A particularly significant advantage is the ability to independently control the concentrations of Lewis and Brønsted acid sites, as well as the pore size. The possibilities are clearly evidenced by the rapidly expanding repertoire of reactions catalyzed by MOFs,28 which now includes:29–31 addition reactions such as silylation, sulfurization, and cycloaddition; oxidation; epoxidation; decarbonylation; and condensation. Reports of MOFs catalyzing processes using hydrogen as a reactant are rare, however.32 This is surprising, given the extensive efforts to develop MOFs for hydrogen storage, their well-known high-temperature stability, and reports showing that a number of MOFs are stable in the presence of reducing agents such as metal hydrides.33,34 There are now a few reports in which MOFs serving as supports for transition metal nanoparticles to catalyze hydrodeoxygenation, hydrogenation, and hydrogenolysis,32,35–40 but the MOF itself does not appear to be the agent directly responsible for the hydrogenolysis. In one case, the reaction was conducted in liquid water36 and tandem catalytic behavior has been observed using the metal-loaded MOF.37–40 MOFs were also shown to be effective as precursors for metal alloy catalysts.41,42
Recently, we demonstrated that two frameworks in the IRMOF-74 series,43 IRMOF-74(I)–Mg (Mg2(dobdc); dobdc = 2,5-dioxido-1,4-benzenedicarboxylate) and IRMOF-74(II)–Mg (Mg(dobpdc); dobpdc = dobpdc = 4,4′-dihydroxy-[1,1′-biphenyl]-3,3′-dicarboxylate), are intrinsically catalytic for the hydrogenolysis of C–O aryl ether bonds. These MOFs have, respectively, 11.6 Å and 17.7 Å hexagonal channels lined with Mg2+ ions that have unoccupied coordination positions (open metal sites; OMS).44 Very high selectivities were obtained, with ≤1% ring opening and ring hydrogenation observed. Although the conversions were modest (up to 40%) for these MOFs, we found that they can be more than doubled by infiltrating with transition metals known to activate H2. For example, infiltrating IRMOF-74(I)–Mg with TiCl4 increased the conversion of phenylethyl phenyl ether (PPE) to ethylbenzene and phenol from 12% to 51%. Similarly, infiltrating with Ni(0) (in the form of an organometallic) increased the conversion even further (to 68%) with no loss of selectivity in either case. This is consistent with our prior report that doping NaAlH4-infiltrated IRMOF-74(I) with a titanium halide activates H2, enabling the material to reversibly release H2 for hydrogen storage purposes.34 We also found that conversions for three different aromatic ethers, phenylethyl phenyl ether (PPE), benzylphenyl ether (BPE), and diphenyl ether (DPE), were higher using IRMOF-74(II)–Mg, regardless of whether the material was doped with TiClx or Ni(0), supporting the hypothesis that the reaction occurs within the pores, rather than on the surface of the MOF crystals, as has been observed with some other MOF catalysts.29,45 It is logical to expect that hydrogenolysis of these ether molecules will increase with increasing MOF pore diameter if mass transport is rate limiting; however, selectivities should be largely unaffected, unless the pore walls interact with both sides of these relatively flat molecules.
The results of our earlier investigations provided a basis for speculation concerning the precise role of the MOF in catalyzing the hydrogenolysis. Density functional theory (DFT) calculations we performed suggest that the unsaturated coordination sphere of the Mg(II) ions in the activated framework plays an important role in orienting ether molecules within the pore prior to bond cleavage. However, the reason for the higher conversions produced by the catalyst with the larger pores was not determined. Moreover, neither experiments nor modeling clarified whether and how these Mg-based MOFs alone, which lack Pt-group or other transition metals, can activate H2.
Here, we present data from kinetic experiments, H–D exchange reactions, solid-state 25Mg NMR, and density functional theory (DFT) that provide direct insight into the interactions between the catalyst and reaction molecules. In particular, our results indicate that the pores of these MOFs perform several functions during the hydrogenolysis reaction. First, they provide a high density of OMS, in the form of five-coordinate Mg(II) ions (IRMOF-74(I) is the highest known for a MOF). Our data indicate that these bind and orient substrate molecules. Second, these OMS bind to and activate adsorbed H2, as evidenced by H–D exchange reactions. Third, assisting in this process, the MOF pores increase the local concentration of H2 by providing a high surface area to physisorb this weakly interacting gas. Notably, a number of MOFs possess high surface areas and OMS with the ability to adsorb large quantities of H2.46 Our results also shed new light on the role of TiClx and Ni(0) dopants, which increase aryl–ether conversion and accelerate rehydrogenation of metal hydride nanoparticles hosted within the pores of IRMOF-74(1)–Mg.47 Together, these data suggest design rules for MOF hydrogenolysis catalysts. Importantly, however, a non-monotonic change in conversion with pore diameter shows that subtle changes in pore geometry, even within an isoreticular series, can have significant implications for MOF-based catalysis.
Results
Effect of pore size on hydrogenolysis
We systematically probed the effects of pore-size on the hydrogenolysis reaction using three aryl ether compounds: phenylethylphenyl ether (PPE), benzylphenyl ether (BPE), and diphenyl ether (DPE). These were selected because they provide a broad range of C–O bond strengths (Scheme 1) and are thus a useful reactant suite for probing the effectiveness of these MOFs to catalyze hydrogenolysis. In addition, they are the simplest model compounds exhibiting the β-O-4, α-O-4, and 4-O-5 (or 4,4′) linkages commonly found in lignin. The three reactions considered are shown in Scheme 1, with the DFT-computed gas-phase Gibbs free energies of hydrogenolysis, all of which are found to be exoergic at the temperature of the reaction.47 The decreasing magnitude of the thermodynamic driving force (PPE > BPE > DPE) is primarily a reflection of the increasing strength of the C–OC5H6 bond, as the products are similar for the three reactions (Scheme 1).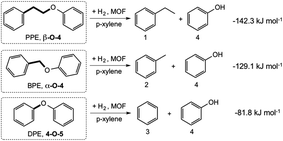 | ||
| Scheme 1 Reactions catalyzed by IRMOF-74(I–IV)Mg, with computed gas-phase Gibbs free energies at 393 K (ref. 47). | ||
Hydrogenolysis experiments conducted using these substrates show that the activated forms of all four IRMOF-74(n)Mg variants catalyze the Scheme 1 reactions under the mild conditions we used (120 °C, 10 bar H2; Table 1 and Fig. 1). As the catalyst pore size increases from IRMOF-74(I) to IRMOF-74(III) (Fig. 1), increasing conversion is seen for all three substrates, extending the trend demonstrated previously using only IRMOF-74(I–II)Mg.47 No reaction was observed in the absence of catalyst. As expected, the conversions are also consistent with the strength of the R–OCH5 bond, i.e. DPE < BPE < PPE.
| Entry | Catalyst | Substrate | T, °C | Time, hours | Conv. % | Selectivity | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||||
| 1 | IRMOF-74(I) | PPE | 120 | 16 | 12 | 87 | 91 | ||
| 2 | IRMOF-74(II) | PPE | 120 | 16 | 39 | 83 | 87 | ||
| 3 | IRMOF-74(III) | PPE | 120 | 16 | 44 | 84 | 88 | ||
| 4 | IRMOF-74(IV) | PPE | 120 | 16 | 35 | 88 | 90 | ||
| 5 | Ti@IRMOF-74(I) | PPE | 120 | 16 | 51 | 89 | 90 | ||
| 6 | Ti@IRMOF-74(II) | PPE | 120 | 16 | 60 | 79 | 83 | ||
| 7 | Ti@IRMOF-74(III) | PPE | 120 | 16 | 62 | 85 | 87 | ||
| 8 | Ti@IRMOF-74(IV) | PPE | 120 | 16 | 56 | 84 | 85 | ||
| 9 | Ni@IRMOF-74(I) | PPE | 120 | 16 | 68 | 91 | 94 | ||
| 10 | Ni@IRMOF-74(II) | PPE | 120 | 16 | 82 | 96 | 98 | ||
| 11 | Ni@IRMOF-74(III) | PPE | 120 | 16 | 84 | 94 | 97 | ||
| 12 | Ni@IRMOF-74(IV) | PPE | 120 | 16 | 70 | 93 | 96 | ||
| 13 | IRMOF-74(I) | BPE | 120 | 16 | 10 | 78 | 84 | ||
| 14 | IRMOF-74(II) | BPE | 120 | 16 | 17 | 73 | 78 | ||
| 15 | IRMOF-74(III) | BPE | 120 | 16 | 28 | 76 | 81 | ||
| 16 | IRMOF-74(IV) | BPE | 120 | 16 | 18 | 77 | 83 | ||
| 17 | Ti@IRMOF-74(I) | BPE | 120 | 16 | 33 | 75 | 79 | ||
| 18 | Ti@IRMOF-74(II) | BPE | 120 | 16 | 42 | 84 | 89 | ||
| 19 | Ti@IRMOF-74(III) | BPE | 120 | 16 | 47 | 82 | 85 | ||
| 20 | Ti@IRMOF-74(IV) | BPE | 120 | 16 | 32 | 83 | 85 | ||
| 21 | Ni@IRMOF-74(I) | BPE | 120 | 16 | 57 | 82 | 85 | ||
| 22 | Ni@IRMOF-74(II) | BPE | 120 | 16 | 76 | 91 | 95 | ||
| 23 | Ni@IRMOF-74(III) | BPE | 120 | 16 | 79 | 89 | 92 | ||
| 24 | Ni@IRMOF-74(IV) | BPE | 120 | 16 | 50 | 89 | 90 | ||
| 25 | IRMOF-74(I) | DPE | 120 | 16 | 4 | 79 | 82 | ||
| 26 | IRMOF-74(II) | DPE | 120 | 16 | 9 | 75 | 78 | ||
| 27 | IRMOF-74(III) | DPE | 120 | 16 | 27 | 80 | 83 | ||
| 28 | IRMOF-74(IV) | DPE | 120 | 16 | 12 | 77 | 79 | ||
| 29 | Ti@IRMOF-74(I) | DPE | 120 | 16 | 19 | 81 | 85 | ||
| 30 | Ti@IRMOF-74(II) | DPE | 120 | 16 | 20 | 77 | 80 | ||
| 31 | Ti@IRMOF-74(III) | DPE | 120 | 16 | 27 | 84 | 84 | ||
| 32 | Ti@IRMOF-74(IV) | DPE | 120 | 16 | 22 | 80 | 84 | ||
| 33 | Ni@IRMOF-74(I) | DPE | 120 | 16 | 29 | 80 | 87 | ||
| 34 | Ni@IRMOF-74(II) | DPE | 120 | 16 | 34 | 85 | 87 | ||
| 35 | Ni@IRMOF-74(III) | DPE | 120 | 16 | 51 | 86 | 90 | ||
| 36 | Ni@IRMOF-74(IV) | DPE | 120 | 16 | 31 | 85 | 88 | ||
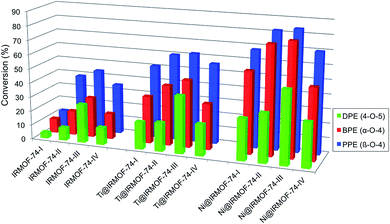 | ||
| Fig. 1 Conversion of aryl ethers by IRMOF-74 catalysts. Left: activated MOFs. Center: TiClx-infiltrated MOFs. Right: Ni-infiltrated MOFs. | ||
Strikingly, however, when IRMOF-74(IV)Mg is the catalyst the conversion for all three ethers decreases from that obtained for IRMOF-74(III)Mg. The decrease is particularly large for DPE, from 27% conversion for IRMOF-74(III)Mg to only 12% for IRMOF-74(IV)Mg. Assuming that the Mg(II) OMS are the active site for the reaction, one might expect the III → IV conversion to decrease to ∼18% due to the lower volumetric density of OMS as the pore dimensions increase (Table 1). However, this is inconsistent with the non-monotonic trend in the conversion. Moreover, the magnitude of the IRMOF-74(III)Mg → IRMOF-74(IV)Mg decrease is not the same for all three substrates. The IRMOF-74(III)Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IRMOF-74(IV)Mg conversion ratios are 0.444, 0.643, and 0.795 for DPE, BPE, and PPE, respectively, whereas the IRMOF-74(III)Mg
IRMOF-74(IV)Mg conversion ratios are 0.444, 0.643, and 0.795 for DPE, BPE, and PPE, respectively, whereas the IRMOF-74(III)Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IRMOF-74(IV)Mg ratio of OMS volumetric density is 0.657 (determined from the crystal structures).43 These results are consistent with the reaction occurring with the pores, but more significantly, they suggest that the geometry of the pore is more important than the density of OMS or mass transport in determining the conversion.
IRMOF-74(IV)Mg ratio of OMS volumetric density is 0.657 (determined from the crystal structures).43 These results are consistent with the reaction occurring with the pores, but more significantly, they suggest that the geometry of the pore is more important than the density of OMS or mass transport in determining the conversion.
The observed selectivities (Table 1) are high in all cases; the small difference in selectivity for the two products of a given reaction (e.g., ethylbenzene and phenol produced by the reaction of PPE) is due to some loss of the more volatile product to the head space of the reaction cell when the hydrogen pressure is released. There is also little variation in the selectivity across the four MOF catalysts. In no case was ring opening observed, as determined by RGA analysis of the head space gases after reaction (Fig. S2†) and the percentage of ring-hydrogenated product (primarily cyclohexanol) is in the low single digits. The uniformity of the selectivities for four different catalysts and three different substrates supports the notion that, once the substrate molecule is adsorbed within the pore, the hydrogenolysis reaction proceeds through a common reaction pathway that is not influenced by the pore size. We note that it is likely that some products and reactant remained in the MOF pores after the supernatant was removed, which will have a small effect on the measured conversions.
H–D exchange reactions
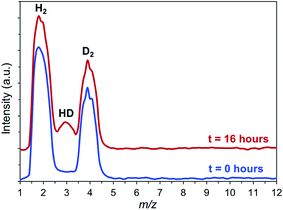
A key unknown regarding the catalytic reaction is the nature of the interaction between the MOF and hydrogen. Physisorption of H2 by MOFs is very weak, with limited charge transfer to the MOF, as indicated by typical isosteric heats of adsorption (Qst) of less than 10 kJ mol−1 at 77 K and ≤7 kJ mol−1 at room temperature.46 Therefore, physisorption is unlikely to activate H2 in any significant way. Adsorption is stronger when OMS are present, as in the IRMOF-74 topology. Long and coworkers obtained a Qst for IRMOF-74(I)Mg of 10.3 kJ mol−1 at 77 K.48 They reported a slightly higher value (10.7 kJ mol−1) for Mg2(dobpdc) (dobpdc = 4,4′-dioxidobiphenyl-3,3′-dicarboxylate)49 (note: this structure is not identical to IRMOF-74(II)Mg, in which the oxido moieties are in the 3,3′ positions), indicating that increased pore size has little effect on H2 binding at low pressures. Neutron diffraction measurements and diffuse reflectance infrared spectroscopy for both IRMOF-74(I)Mg and IRMOF-74(II)Mg confirm that the OMS are the preferred sites for H2 binding.48,50–52 These results suggest direct involvement of the Mg(II) OMS in our catalysts is possible.Consequently, we sought more direct evidence of H2 activation by using hydrogen–deuterium exchange reactions. We reasoned that free hydrogen radicals are unlikely to exist during the hydrogenolysis reaction, but that the high concentration of H2 in the pores, coupled with the relatively strong interaction with the OMS, should lead to some H–D exchange. To confirm this hypothesis, H2/D2 isotope exchange experiments were performed with IRMOF-74(I)Mg in the presence of p-xylene and PPE at 120 °C. As seen in Fig. 2, formation of HD at m/z 3 is clearly observed from an equimolar H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2 mixture after a 16 hours reaction in a quartz reactor. A control experiment carried out in p-xylene with PPE but without the MOF showed no HD formation during comparable amounts of time. This indicates that the MOF presence is required for efficient hydrogen–hydrogen bond activation.
D2 mixture after a 16 hours reaction in a quartz reactor. A control experiment carried out in p-xylene with PPE but without the MOF showed no HD formation during comparable amounts of time. This indicates that the MOF presence is required for efficient hydrogen–hydrogen bond activation.
25Mg solid-state NMR spectroscopy
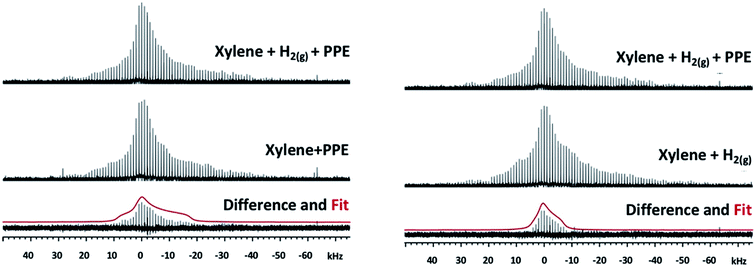
More direct evidence of an interaction between reactant molecules and the Mg(II) OMS can be obtained from static 25Mg solid-state NMR. This potentially powerful diagnostic in this regard can be challenging, however, due to low sensitivity resulting from the quadrupole moment (spin 5/2) and the low natural abundance (10%). As a result, the signal width increases with asymmetry of the environment around Mg-centers, with typical chemical shifts between −50 to 20 ppm. To counteract these factors, double frequency sweep was coupled with Quadrupole Carr-Purcell-Meiboom-Gill (QCPMG) detection to enhance the signal; the resulting spectra of IRMOF-74(I) samples (natural abundance Mg) are shown in Fig. S5–S9.† These data show the overall lineshape divided into sharp lines (“spikelets”). This methodology was recently employed by one of us to successfully monitor the changes in the local environment of the MOF Mg2(dobpdc) upon adsorption of various guest molecules.53 In the present work, we compared the static QCPMG spectrum of the as-synthesized IRMOF-74(I) (spectrum labelled as “Activated” in Fig. S10†) with the spectrum of IRMOF-74(I) in the presence of various combinations of hydrogen, p-xylene and PPE. The results indicate subtle but noticeable differences in certain regions; to guide the eye, some of these are highlighted in Fig. S10 as A–D.†Close examination of the 25Mg spectra suggests that the addition of PPE in xylene under 1.5 MPa H2(g) produces changes to the spectrum indicative of new species (in the vicinity of the marker “B” in Fig. S10†). To more clearly identify the spectroscopic signature of individual species within these complex spectra, we calculated 25Mg difference spectra for samples that differ by only one of the reaction components (Fig. 3). The first of these (Fig. 3, left) should reveal features associated with 25Mg interacting with the H2(g) and comprises the difference between the spectra of IRMOF-74(I) with (p-xylene + PPE + H2(g)) and IRMOF-74(I) with only (p-xylene + PPE). Here, the scale was adjusted so that there are no negative-going signals in the difference spectrum. We fit this lineshape to obtain the electric field gradient parameter Cq and asymmetry parameter ηq. The value of Cq obtained (4.79 MHz) is close to that obtained by directly fitting the spectrum in Fig. S8† (4.4 MHz). Similarly, the difference spectrum obtained by subtracting the spectrum of IRMOF-74(I) with (p-xylene + H2(g)) from that of IRMOF-74(I) with (p-xylene + PPE + H2(g)) reveals features associated with 25Mg interacting with PPE (Fig. 3, right). In this case, a smaller value of Cq (3.14) was obtained by fitting the difference spectrum.
These changes to the NMR spectra are distinct, but the nature of the interaction is difficult to determine a priori. Consequently, we employed DFT to compute 25Mg quadrupole couplings and assess whether the spectral assignments derived from the fits to experimental data are consistent with our hypothesized geometries (obtained from DFT-optimized structures of guest-free IRMOF-74(I), H2-loaded IRMOF-74(I), and PPE-loaded IRMOF-74(I); see below). The DFT-predicted values are compared with those obtained from experiment in Table 3. We expect DFT to reproduce Cq trends, but these methods are known to overestimate the magnitude of Cq (note that first principles-predicted values of Cq can be positive or negative, but NMR can only measure the absolute value, which we used for our comparisons).54 Consequently, quantitative comparison with experiment is not justified. Nevertheless, the trends in Cq exhibited by experiment and theory in Table 3 are consistent and the values of ηq are similar, suggesting that the MOF geometries obtained from DFT are reasonable. As an additional check, if we assume a systematic overestimation of Cq by our DFT method (not unreasonable54), multiplying the ratio of Cq(exp.)/Cq(DFT) for the H2 species (4.79/10.69) by the absolute value of the DFT prediction for the PPE species (6.75 MHz) yields a Cq value close to 3.0 MHz, in good agreement with that extracted from experiment (3.1 MHz). Based on the consistency of the combined experimental NMR data, the values of Cq and ηq obtained by fitting these data, and the DFT predictions, we conclude that the NMR data strongly support the hypothesis that both H2 and PPE (and by inference, the other ethers as well) interact directly with the Mg OMS in the MOF structure.
Effect of TiClx and Ni nanoparticle functionalization
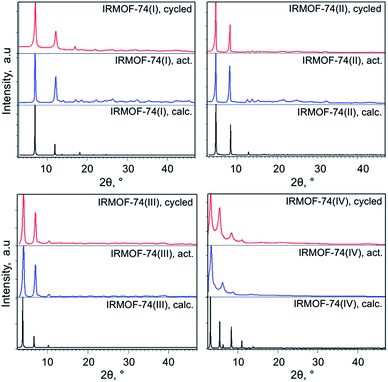
The IRMOF-74(I–IV)Mg samples infiltrated with TiClx and Ni(0) show higher conversions compared to undoped MOF catalysts (Fig. 1 and Table 1). As we observed previously for IRMOF-74(I)Mg and IRMOF-74(II)Mg,47 the highest conversions are achieved using the Ni-functionalized MOFs. The selectivity, however, is largely unchanged by the addition of the two dopants. In all cases, it is clear that the MOF catalysts are responsible for the reaction, as no reaction occurred in the absence of the doped MOF catalyst. PXRD data (see Experimental methods section, Fig. 5) indicate that the crystallinity of the native MOFs is not affected by use in the catalysis reaction. We tested their stability following infiltration and reaction by performing elemental analysis with inductively coupled plasma optical emission spectrometry of the supernatant. No evidence of soluble Mg, Ti, or Ni species that could act as homogeneous catalysts was detected, indicating that the infiltrated metals remain within the MOF pores during the reaction. The bar graphs in Fig. 1 also indicate that the trend with pore size exhibited by the undoped MOFs is maintained in the presence of both dopants, suggesting that the fundamental reaction mechanism is not altered by the acceleration induced by TiClx and Ni(0). Strictly speaking, these data do not rule out the possibility of pore collapse. However, post-reaction PXRD data for the doped versions of IRMOF-74(I)Mg and IRMOF-74(II)Mg indicate no loss of crystallinity.44 Moreover, no new peaks appeared in the PXRD, showing that new crystalline phases are not formed. On this basis, we are confident that it is the doped crystalline MOF that is performing the catalysis.DFT modeling of the MOF–ether interaction
A potential explanation for the non-monotonic conversions as a function of pore size could be unexpected differences in the binding energies of the substrates. To test this hypothesis, we computed the binding energies and preferred orientation of the three substrates (PPE, BPE, and DPE) within the pore cavity of all four MOFs using DFT. The results indicate that the preferred substrate orientation in all cases is parallel to the c axis of the pore (Fig. S4†), with the ether O atom binding to the Mg(II) OMS. As shown by the binding energies given in Table 2 which correspond to the axially oriented geometry, ether binding to IRMOF-74(III)Mg is considerably stronger than to the other three MOFs. For example, the PPE binding energy to IRMOF-74(III)Mg is nearly 40 kJ mol−1 higher than to IRMOF-74(IV)Mg. This is surprising, given the similar binding mode of these molecules in all four MOFs (Fig. S4†). However, it can be rationalized by examining the optimized MOF structures, such as those shown in Fig. 4. Unique among the four MOFs, the Mg(II) ions in the IRMOF-74(III)Mg framework in the absence of substrate are displaced toward the interior of the MOF pore, resulting in a decreased c-lattice parameter: IRMOF-74(I)Mg: 6.7588 Å; IRMOF-74(II)Mg: 6.8483 Å; IRMOF-74(III)Mg: 6.4739 Å; IRMOF-74(IV)Mg: 6.6940 Å. Consequently, a closer approach of the ether molecule to the Mg(II) is enabled by the distortion of the IRMOF-74(III) structure, which facilitates substrate binding. These structural features and energies therefore suggest that IRMOF-74(III)Mg should have the highest catalytic rate, by virtue of a stronger Mg–O bond (i.e., greater O → Mg charge transfer) that both weakens the substrate ether bond and increases the lifetime at the OMS.| IRMOF-74(I)Mg | IRMOF-74(II)Mg | IRMOF-74(III)Mg | IRMOF-74(IV)Mg | |
|---|---|---|---|---|
| DPE | 59.7 | 59.1 | 94.7 | 55.8 |
| BPE | 63.4 | 69.1 | 99.8 | 65.6 |
| PPE | 64.2 | 73.6 | 98.1 | 71.0 |
| Phenol | 63.7 | 75.4 | 117.3 | 69.1 |
| C q (DFT) | η q (DFT) | C q (exp.) | η q (exp.) | |
|---|---|---|---|---|
| IRMOF-74(I)Mg | 11.98 | 0.59 | 7.7 | 0.70 |
| IRMOF-74(I)Mg + H2 | 10.69 | 0.64 | 4.8 | 1.00 |
| IRMOF-74(I)Mg + PPE | −6.75 | 0.85 | 3.1 | 1.00 |
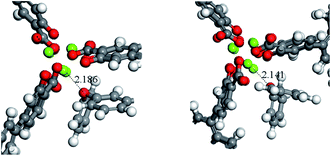 | ||
| Fig. 4 A close up of the preferred binding orientation of DPE in IRMOF-74(II), left, and IRMOF-74(III), right. The distance shown correspond to the Mg–O bond length. | ||
Discussion
The results above demonstrate that the IRMOF-74-n(Mg) (n = I–IV) MOF series catalyzes the hydrogenolysis of aryl ether bonds. The hypothesis that the reaction occurs at the OMS is consistent with the known ability of these sites to bind small molecules43,55,56 and with data we previously described for the first two members of the series.47 However, it is also clear that, in spite of the nominally uniform topology of these MOFs and steady increase in pore size from IRMOF-74(I) to IRMOF-74(IV), several complex and interacting phenomena, including pore dimensions, ether binding energy, and H2 activation rate, combine to yield the non-intuitive behavior exhibited by the four frameworks. In this section, we assemble the conclusions from the experimental and theoretical elements of this investigation to provide insight concerning the multifunctional behavior of these catalysts.First, all four MOFs are intrinsically catalytically active, independent of infiltration with TiCl4 or Ni, and are structurally stable under the reaction conditions. Moreover, pore size influences the conversion of the three ether reactant molecules, all of which are small enough to fit within the pores of these MOFs. The measured selectivities for formation of phenol and C6H5R (R = H, CH3, or C2H5) indicate that the reactions in Scheme 1 occur without ring opening or hydrogenation, consistent with a single reaction channel. A key realization from the DFT modeling is that, although the pores of these MOFs are nominally the same from a topological viewpoint, they are not identical. In particular, the linkers for IRMOF-74(III) and IRMOF-74-(IV) are functionalized with methyl groups to improve solubility. The DFT modeling further suggests that, at least in the case of IRMOF-74(III), these groups affect the catalytic activity. It is important to note that, in contrast to a number of other MOFs, defects in the form of missing linkers or cation vacancies have not been reported for MOF-74.57 In fact, from a structural rigidity and bonding point of view, this is one of the most stable MOFs. Consequently, the catalytic activity should be associated with their expected crystallographic structure.
The 25Mg NMR results indicate that significant changes occur in the coordination environment of Mg(II) upon addition of H2 in the presence of p-xylene and PPE (Fig. 3 and S5–S10†). For as-activated IRMOF-74(I)Mg, the 25Mg NMR spectrum is typical of a second-order quadrupole pattern (Fig. S5†) with electric field gradient parameter Cq of 7.7 and 2.8 MHz, respectively for the ordered and disordered Mg(II) states. Addition of hydrogen gas to IRMOF-74(I) results in the appearance of another species distinct from MOF alone with a Cq value of 5.5 MHz for dry (Fig. S6†) and 4.8 MHz for p-xylene solvated (Fig. 3 and S8†). Since the residence time of H2(g) on the Mg(II) site is fairly short at the experimental temperature (25 °C), it is reasonable to assume that this spectrum is the result of some dynamic or exchange process that is not accounted for in our simulations and might be influenced by the presence of solvent. This new species is due to direct interactions of H2 molecules with the Mg(II) OMS on the MOF, which likely plays a role in activating H2 during the hydrogenolysis process. Similarly, when the solvated MOF is exposed to PPE there is evidence for a direct interaction with the Mg(II) (Fig. 3 and S7†).
The hydrogenolysis reactions in the presence of uninfiltrated MOFs do not go to completion (maximum conversion is ∼45% for PPE/IRMOF-74(III)Mg, Table 1). In general, this could be due to a mass transport limitation, a thermodynamic equilibrium effect, or a kinetic difference resulting from the differing pore structures. In addition, since the reaction occurs in a heterogeneous system with three different phases present (gas, liquid and solid), there are likely multiple processes occurring at simultaneously at different interfaces that may affect the conversion efficiency. We rule out mass transport because the continuous increase in pore size does not lead to corresponding continuous increases in conversion. The pore cross-sectional area increases by factor of ∼9 for IRMOF-74(I)Mg → IRMOF-74(IV)Mg, which should lead to an increase in conversion, or at a minimum, saturation. Since this is counter to observation, we conclude that chemical factors, such as confinement effects, substrate binding energies, and the reaction potential energy surface, are responsible for the non-monotonic conversion trend.
Competition for active sites between the ether substrate and product molecules is an alternative explanation for the incomplete conversions we observe. Confinement of molecules within the pores increases the local concentration and thus reaction inhibition could occur regardless of whether the reaction is near equilibrium or kinetically controlled. The predicted binding energies of phenol (Table 2), a product in each of the reactions (Scheme 1), are either the same (within the uncertainty of the calculations) or larger (for IRMOF-74(III)) than the ether binding energies. This indicates that phenol likely competes with incoming ether molecules for the OMS. To test this hypothesis, we performed hydrogenolysis experiments with PPE and IRMOF-74(I–IV) in the presence of one equivalent of phenol added at the beginning of the reaction. We observe that the PPE conversion efficiency is unchanged for IRMOF-74(I), possibly due to steric constraints imposed by the small pore diameter (1.1 nm). The conversion decreases for the other three MOFs with larger pores (Table S4, ESI†). Notably, the largest decrease in conversion was observed for IRMOF-74(III), which is consistent with the higher phenol binding energy to IRMOF-74(III)Mg compared with the other MOFs (117 kJ mol−1vs. 64–75 kJ mol−1). It is thus apparent that, although product inhibition occurs, this affect cannot alone explain the observed trend in conversion efficiency.
Consequently, we conclude that the observed conversion trends, both with and without additional reaction-inhibiting phenol, are consistent with the computed binding energies (Table 2). In fact, close examination of the data in Table 1 shows that the conversions for IRMOF-74(II) and IRMOF-74(IV) are nearly the same, in agreement with their nearly identical substrate and phenol binding energies. This is in spite of the fact that the pore size of IRMOF-74(IV) is nearly double that of IRMOF-74(II) (Table S1†). As discussed above, the Mg(II)–(ether O) bond distance in IRMOF-74(III) is shorter than in the other three MOFs due to the contracted unit cell. XRD data for the DPE-loaded IRMOF-74(I) and IRMOF(II) catalysts suggest that the unit cell is essentially unchanged upon the infiltration of the MOF with guest ether molecules (Fig. S3†), indicating that a structural distortion upon substrate binding does not occur. Moreover, the predicted ether and phenol binding energies display the same qualitative trend (up–up–down) regardless of substrate, mirroring the conversion trends (Tables 1 and S4†). This leads us to the important conclusion that a common topology within an isoreticular MOF series does not guarantee that differences in chemical behavior will be due only to variations in pore size.
It is also clear that H2 activation must occur for these hydrogenolysis reactions to proceed. The formation of HD under experimental conditions in p-xylene confirms this, a result that is consistent with a large body of data, including neutron diffraction and high-pressure diffuse reflectance IR measurements, showing that H2 binds to the OMS in both IRMOF-74-(I) and IRMOF-74(II).58 The hydrogen isosteric heat of adsorption (Qst) of IRMOF-74-(I) at 298 K is relatively high at 9.4 kJ mol−1.59 Magnesium also forms stable bonds with hydrogen (e.g., MgH2), which provides an additional thermodynamic driving force for H–H bond activation. Infiltration with TiCl4 and Ni nanoparticles provides an additional probe of the H2 activation mechanism. Reduction in H2 prior to reaction with the ethers creates TiCl3 and Ni nanoparticles as seen by XPS, both of which are known to activate H2.47 As a result, conversion increases substantially, as seen in Fig. 1. However, the trend among the four IRMOF-74 catalysts and in the series of the three ethers for a fixed catalyst is similar to that exhibited by the activated MOFs. This indicates that, although TiCl3 and Ni nanoparticles supply additional sites for H2 activation, the factors controlling the conversion are unchanged. It also implies that the OMS binds the ether molecule, possibly with a specific orientation, thereby activating the C6H5O–R bond.
An important remaining issue is the nature of the H2 activation by this MOF. We considered three possible reaction pathways: (1) homolytic H–H bond cleavage, followed by H atom migration via spillover; (2) H2 and ether binding to neighboring OMS, followed by H2 attack on the ether; this could occur either by a concerted process involving an ether–H2 transition state, or via heterolytic H–H bond cleavage followed by reaction of the resulting hydride and proton with the ether molecule; and (3) ether binding to an OMS, followed by H2 binding/attack at the same OMS. Pathway (1) is unlikely, given that the Mg(II) OMS lacks the d orbitals normally involved in homolytic cleavage. However, if homolytic cleavage were to occur, a recent investigation by Karim et al. of hydrogen spillover on nano-patterned oxide substrates demonstrates that H atoms can diffuse long distances across metal oxides.60 They also showed that H atoms formed on Pt can diffuse on an aluminum oxide support as far as 15 nm, albeit inefficiently, which should easily be far enough to encounter an ether molecule.
Regarding pathway (2), in our previous investigation of NaAlH4-infiltrated IRMOF-74-(I)(Mg),34 we estimated that, on average, there was one TiClx molecule for every 50 Mg(II) OMS, giving a distance between Ti atoms of about 3 unit cells in the axial direction (3 × 6.5 Å = ∼20 Å). This light doping was sufficient to make H2 desorption reversible from nanoscale NaAlH4 in the pores. In the present investigation, dopant loadings are significantly higher (>1.5 wt% vs. 0.6 wt% in the earlier study), presumably reducing the diffusion distance required for an activated H2. We estimate that the average separation between TiClx or Ni nanoparticle dopants is at most 8 Å, or about one per unit cell. The shortest distance between Mg(II) OMS in the IRMOF-74(I) structure is ∼5 Å, corresponding to the Mg–O–Mg chain in the continuous helical structure forming the MOF; this is well within the range of hydrogen spillover on Al2O3.60 This suggests that H2 bound to an OMS can react with an ether molecule on a neighboring OMS, either by diffusion from one site to another, or potentially via a concerted mechanism involving a (H2)Mg–O–Mg(ether) transition state. These observations suggest a direction for reaction modeling, in which transition state theory could be applied to evaluate the energetics of the possible ether–H2 binding geometries.
Pathway (3) is the most likely in our estimation. The higher binding energy predicted for the ethers (Table 2) favors this. Moreover, it does not require a more complex, dual-OMS transition state or diffusion of an H atom from one site to another. A recent study of H2 binding to a Mn–S analogue of IRMOF-74-(I) shows that binding of multiple H2 to an OMS is possible.61 The ether substrates used here are obviously much bulkier, raising the question whether there is sufficient space for both the ether and H2 to bind to the same site. This could possibly be resolved by additional DFT calculations, but at a very high level to ensure accurate H2 binding energies, as discussed elsewhere.62
Conclusions
The results presented here show that four members of the isoreticular IRMOF-74 series catalyze hydrogenolysis of aromatic ether bonds with high selectivity, considerably extending and confirming our earlier report concerning only the first two MOFs in the series44 and suggesting that similar catalytic behavior should be exhibited by the rest of the series. Compared with other hydrogenolysis catalysts, these MOFs contain no platinum group elements and do not require a sacrificial base, but yet can activate H–H and C–O bonds. Substrate conversion is enhanced by confinement of Ti and Ni transition metal dopants within the MOF pores. However, this is not required; significant conversions are observed without any Ti or Ni present, indicating that the MOF itself actively participates in the reaction, most likely through the interaction of the ether molecules with the OMS. Although we do not yet have structural data revealing the specific geometry of the ether–MOF complex, the combined evidence from 25Mg NMR spectra and the DFT calculations create a plausible picture of a transition state involving an ether molecule strongly bound to the Mg(II) OMS through the oxygen atom. The ability of the MOF to activate H2 is confirmed by H–D exchange experiments and 25Mg NMR spectroscopy, providing convincing new evidence for a valuable, but unexpected, property of MOFs with OMS. This conclusion is also consistent with prior literature showing that H2 binds to the Mg(II) OMS.48,49 Finally, the unexpected increase in the ether and phenol binding energy predicted for IRMOF-74(III) relative to the other three MOFs, induced by a subtle change in the linker, suggests that careful consideration of correlated steric and energetic effects must be made when attempting to design new MOF catalysts. This result has significant consequences for MOF catalyst design, as it challenges the notion that isoreticular MOFs enable systematic variation in pores size without fundamental changes in reactivity. Overall, the new insight created by this investigation should prompt new reflection upon the factors governing the chemical reactivity of all MOFs, particularly those having OMS.Experimental and theoretical methods
Synthesis
Air-sensitive operations were performed using standard glove-box and Schlenk line techniques under argon. All chemicals and solvents were obtained from commercial sources.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v/v) mixture of DMF (80 mL), ethanol (4 mL), and water (4 mL). The homogeneous solution was then transferred to a 150 mL Teflon-lined stainless-steel autoclave. The autoclave was capped tightly and heated to 125 °C in an oven. After 24 hours the autoclave was removed from the oven and a yellow microcrystalline material was recovered and washed with 10 mL DMF. The product was then soaked in 20 mL DMF and heated to 80 °C for 4 hours. The solvent was carefully decanted from the product and replaced with 20 mL anhydrous methanol and stirred for 2 hours. Fresh methanol was used for solvent exchange for four more times. The yellow precipitate was isolated by filtration and washed thoroughly with methanol. The MOF was activated under a dynamic vacuum at 195 °C for 16 hours, yielding a yellow crystalline material.
1 (v/v/v) mixture of DMF (80 mL), ethanol (4 mL), and water (4 mL). The homogeneous solution was then transferred to a 150 mL Teflon-lined stainless-steel autoclave. The autoclave was capped tightly and heated to 125 °C in an oven. After 24 hours the autoclave was removed from the oven and a yellow microcrystalline material was recovered and washed with 10 mL DMF. The product was then soaked in 20 mL DMF and heated to 80 °C for 4 hours. The solvent was carefully decanted from the product and replaced with 20 mL anhydrous methanol and stirred for 2 hours. Fresh methanol was used for solvent exchange for four more times. The yellow precipitate was isolated by filtration and washed thoroughly with methanol. The MOF was activated under a dynamic vacuum at 195 °C for 16 hours, yielding a yellow crystalline material.
Infiltration methods
Doping of IRMOF-74(n)-Mg with TiClx or Ni(0) was accomplished by vapor-infiltrating the pores with TiCl4 and Cp2Ni using methods we employed previously.34,47 First, the activated MOF was exposed to TiCl4 or Cp2Ni vapors at 90 °C overnight (16 hours). This caused the MOF powder to change color from yellow to dark tan/brown color. Heating these materials to 95 °C in H2 (1.0 MPa) for two hours reduces the TiCl4 to TiCl3 and Ni(II) is converted to Ni(0) species, as indicated by XPS.47 The Ti and Ni metals are homogeneously distributed within the MOF materials, as determined by EDX (Fig. S1B†). Elemental analysis indicates that the Ti loading is in the 1.52 to 1.96 wt% range, whereas the Ni loading is in the 2.91 to 3.43 wt% range (Table S2†).Hydrogenolysis experiments and GC-MS
Catalytic hydrogenolysis reactions were performed in a stainless-steel reactor equipped with a hydrogen feed. In a typical procedure, 45 mg of catalyst powder were placed the reactor, then a solution of the corresponding substrate (PPE, BPE or DPE, 0.5 to 1.0 mmol) in p-xylene (2.5 to 5.0 mL) was added. The reactor was pressurized with gaseous hydrogen, sealed, and heated using a heating mantle equipped with thermocouples. Following the reaction, the reactor was cooled to rt and the catalyst separated by filtration. The composition of the liquid fraction was analyzed by GCMS using an Agilent Varian CP-3800 Gas Chromatograph equipped with a DB-WaxETR column (30 m × 0.25 mm × 0.5 μm) with output split between a Saturn 2000R mass-spectrometer and an FID detector (H2/air). Helium was used as a carrier gas, with a constant column flow of 1.2 mL min−1. The control reactions with all three substrates, but no MOF catalyst present were also performed and consistently showed 0% conversion.Other characterization methods
Liquid-phase 1H and 13C NMR experiments were performed on a Varian 500 MHz spectrometer using d10-xylene solvent. MOF catalyst powders were also characterized using scanning electron microscopy (SEM), X-ray diffraction (XRD), and energy dispersive X-ray spectroscopy (EDX). Powder morphology and composition was analyzed using a JEOL 7600 microscope (JEOL Ltd., Tokyo, Japan). Powder XRD experiments were carried out using a PANalytical Empyrean™ diffractometer equipped with a PIXcel-3D detector and a Cu XRD tube operated at 44 kV and 40 mA (Cu K-alpha radiation, λα = 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418
418![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 704 Å). Experiments were conducted in continuous scanning mode with the goniometer in the theta-2theta orientation. Incident beam optics included a 1/16° divergence slit and a 1/8° anti-scatter slit, as well as a 10 mm fixed incident beam mask and a Soller slit (0.04 rad). Divergent beam optics included a P7.5 anti-scatter slit, a Soller slit (0.04 rad), and a Ni K-beta filter. Inductively coupled plasma optical emission spectrometry (ICP-OES) analysis was performed by ALS Environmental, Inc. Surface area measurements (Brunauer, Emmett and Teller (BET) method) were determined using a Micromeritics ASAP 2020 porosimeter.
704 Å). Experiments were conducted in continuous scanning mode with the goniometer in the theta-2theta orientation. Incident beam optics included a 1/16° divergence slit and a 1/8° anti-scatter slit, as well as a 10 mm fixed incident beam mask and a Soller slit (0.04 rad). Divergent beam optics included a P7.5 anti-scatter slit, a Soller slit (0.04 rad), and a Ni K-beta filter. Inductively coupled plasma optical emission spectrometry (ICP-OES) analysis was performed by ALS Environmental, Inc. Surface area measurements (Brunauer, Emmett and Teller (BET) method) were determined using a Micromeritics ASAP 2020 porosimeter.
H/D exchange reactions
An in-house apparatus that provided calibrated mixtures of H2 and D2 and a residual gas analyzer (RGA) to detect changes in the partial pressures of H2, HD, and D2 as a function of time. The experimental setup consists of a stainless steel manifold interconnecting gas bottles filled with H2 and D2, a turbo-pumped SRS200 RGA, and a 13 cm3 sample cell separated from the manifold by two valves. The sample cell was a commercial 1 cm OD Pyrex glass tube with a glass-to-metal transition to a VCR fitting with a metal seal. MOF samples were loaded into holders in an nitrogen-filled glove box and connected to the manifold.Solid-state NMR spectroscopy
Static 25Mg NMR experiments were performed on a 20.0 T (850 MHz for 1H and 51.99 MHz for 25Mg) Agilent VNMRS spectrometer at the Environmental Molecular Sciences Laboratory (EMSL), Pacific Northwest National Laboratory (PNNL), using a homebuilt 5 mm MAS probe double tuned to 1H/25Mg. Quadrupole Carr-Purcell-Meiboom-Gill (QCPMG)63 experiments were performed on stationary samples of approximately 30 mg of MOF. The spike separation in the QCPMG experiments was 1 kHz. A 25Mg 90° pulse of 7.5 μs was measured for a sample of 1 M MgCl2(aq), corresponding to a selective 90° pulse of 2.5 μs for solid samples. This sample also served as a chemical shift reference at 0.0 ppm. A Double Frequency Sweep (DFS) sequence was utilized in front of the QCPMG sequence to enhance the signal sensitivity.64 The DFS parameters were optimized using a 25Mg(HCOO)2·2H2O sample. The recycle delays were 5 s. To prevent lineshape distortion due to radiofrequency (RF) effects,65 the excitation power was reduced to 25 kHz (selective for the ±1/2 transition) for the QCPMG train and the overall lineshape was reconstructed from several shifted transmitter offsets (10 kHz) with a skyline projection.66 The number of transients for each transmitter offset was 2048. The 1H decoupling scheme used for the static 25Mg SSNMR experiments was SPINAL-16 (ref. 67) with a field strength of approximately 24 kHz.The principal observable in a solid-state NMR experiment on a quadrupolar nuclide is the quadrupole coupling constant, Cq.68 The experimental NMR spectrum is dominated by the quadrupolar Hamiltonian and the lineshape of the observed central transition (±1/2) is broadened by the quadrupolar interaction to second-order. This quadrupolar lineshape is proportional to:
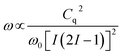 | (1) |
In other words, the width of the lineshape is proportional to the square of Cq and inversely proportional to the Larmor frequency, ω0, of the nucleus in question. This field dependence is an essential tool in the disentanglement of quadrupolar lineshapes. The coupling constant is directly proportional to the electric field gradient at the nuclide of interest and is given by:
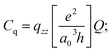 | (2) |
| = qzz × 46.852 MHz (for 25Mg) | (3) |
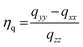 | (4) |
The units for qzz as expressed in eqn (2) are atomic units and the factor of 46.852 MHz can be computed if the atomic constants (e, a0, and h have their usual meanings) are expressed in cgs units and the value of Q is given as 0.1994 × 10−24 cm2.70 The experimentally derived quadrupole coupling constant can therefore be compared to that predicted by an ab initio molecular orbital calculation.
First-principles modeling
All density functional theory (DFT) calculations were performed using the Vienna Ab initio Simulation Package (VASP)72,73 using a single k-point, energy cut of 350 eV, and the non-empirical strongly constrained and appropriately normed (SCAN)74,75 meta-GGA exchange-correlation functional. The SCAN functional was used because it has been shown to predict accurate geometries and energies for non-covalently bonded (e.g. van der Waals) complexes,76 which is important for modeling substrates/molecules adsorbed onto the sidewall of a MOF. The binding energies (BE) were predicted in the usual fashion (BE = substrate@MOF − substrate − MOF). To help identify the preferred binding mode, each substrate molecule was manually placed within the pore cavity of each MOF in several starting orientations and optimized until all forces were less than 0.01 eV Å−1; the cell parameters were fixed to the experimental values.43 In addition, 1 × 1 × 3 supercells were created to extend the length of the pore channel to allow the substrates to adopt orientations parallel to the pore axis. The isolated substrates were placed in 25 Å3 boxes and optimized; all the same computational parameters were used.DFT electric field gradient (EFG) calculations were performed to calculate the 25Mg quadrupolar coupling constant (Cq) and asymmetry parameter (ηq) using the Quantum Espresso electronic structure software.77 The rVV10 functional,78 which accounts for van der Waals effects, and projector-augmented-wave (PAW) pseudopotentials were employed.79,80 A 60 Ry plane-wave energy cutoff and a 400 Ry density cutoff were used in all calculations. The gauge-including projector-augmented-wave (GIPAW)81 software in Quantum Espresso was used to calculate the EFG of the magnesium nuclei.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Sarah D. Burton (PNNL) and Jeff M. Chames (SNL) for their help with the NMR and SEM/EDX experiments. This work was supported by the Sandia Laboratory Directed Research and Development (LDRD) Program and the U.S. Department of Energy (DOE), Office of Energy Efficiency and Renewable Energy (EERE), Bioenergy Technologies Office (BETO), and in collaboration with the Chemical Catalysis for Bioenergy Consortium (ChemCatBio), a member of the Energy Materials Network (EMN). The authors also gratefully acknowledge support from the Hydrogen Materials—Advanced Research Consortium (HyMARC), established as part of the Energy Materials Network under the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Fuel Cell Technologies Office, under Contract Number AC04-94AL85000. Sandia National Laboratories is a multi-mission laboratory managed by National Technology and Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the DOE National Nuclear Security Administration under contract DE-NA0003525. Static 25Mg solid-state NMR experiments and 25Mg DFT spectra calculations were performed at EMSL (grid 436923.9), a DOE Office of Science User Facility sponsored by the Office of Biological and Environmental Research.Notes and references
- R. W. Thring and J. Breau, Fuel, 1996, 75, 795–800 CrossRef CAS.
- C. Higman and S. Tam, Chem. Rev., 2014, 114, 1673–1708 CrossRef CAS.
- J. Andrews and B. Shabani, Wiley Interdiscip. Rev.: Energy Environ., 2014, 3, 474–489 Search PubMed.
- A. Züttel, A. Remhof, A. Borgschulte and O. Friedrichs, Philos. Trans. R. Soc., A, 2010, 368, 3329–3342 CrossRef PubMed.
- A. M. Ruppert, K. Weinberg and R. Palkovits, Angew. Chem., Int. Ed., 2012, 51, 2564–2601 CrossRef CAS PubMed.
- H. Wang, J. Male and Y. Wang, ACS Catal., 2013, 3, 1047–1070 CrossRef CAS.
- J. Zakzeski, P. C. A. Bruijnincx, A. L. Jongerius and B. M. Weckhuysen, Chem. Rev., 2010, 110, 3552–3599 CrossRef CAS PubMed.
- P. N. Rylander, Hydrogenation Methods, Academic Press, London, 1985 Search PubMed.
- M. Wang, H. Shi, D. M. Camaioni and J. A. Lercher, Angew. Chem., Int. Ed., 2017, 56, 2110–2114 CrossRef CAS.
- A. G. Sergeev, J. D. Webb and J. F. Hartwig, J. Am. Chem. Soc., 2012, 134, 20226–20229 CrossRef CAS.
- A. G. Sergeev and J. F. Hartwig, Science, 2011, 332, 439–443 CrossRef CAS PubMed.
- S. Bulut, S. Siankevich, A. P. van Muyden, D. T. L. Alexander, G. Savoglidis, J. G. Zhang, V. Hatzimanikatis, N. Yan and P. J. Dyson, Chem. Sci., 2018, 9, 5530–5535 RSC.
- X. J. Cui, H. K. Yuan, K. Junge, C. Topf, M. Beller and F. Shi, Green Chem., 2017, 19, 305–310 RSC.
- Y. H. Hu, G. Jiang, G. Q. Xu and X. D. Mu, Mol. Catal., 2018, 445, 316–326 CrossRef CAS.
- J. Li, H. Sun, J. X. Liu, J. J. Zhang, Z. X. Li and Y. Fu, Mol. Catal., 2018, 452, 36–45 CrossRef CAS.
- F. Mauriello, E. Paone, R. Pietropaolo, A. M. Balu and R. Luque, ACS Sustainable Chem. Eng., 2018, 6, 9269–9276 CrossRef CAS.
- N. I. Saper and J. F. Hartwig, J. Am. Chem. Soc., 2017, 139, 17667–17676 CrossRef CAS PubMed.
- K. K. Sun, G. P. Lu, J. W. Zhang and C. Cai, Dalton Trans., 2017, 46, 11884–11889 RSC.
- Y. Y. Wang, J. Shen, Q. Chen, L. Wang and M. Y. He, Chin. Chem. Lett., 2019, 30, 409–412 CrossRef CAS.
- Z. Yang, X. Y. Wei, M. Zhang and Z. M. Zong, Fuel Process. Technol., 2018, 177, 345–352 CrossRef CAS.
- C. Zhu, J. P. Cao, X. Y. Zhao, T. Xie, J. Ren and X. Y. Wei, J. Energy Inst., 2019, 92, 74–81 CrossRef CAS.
- F. Gao, J. D. Webb and J. F. Hartwig, Angew. Chem., Int. Ed., 2016, 55, 1474–1478 CrossRef CAS PubMed.
- J. Li and Z. X. Wang, Chem. Commun., 2018, 54, 2138–2141 RSC.
- J. He, L. Lu, C. Zhao, D. Mei and J. A. Lercher, J. Catal., 2014, 311, 41–51 CrossRef CAS.
- J. He, C. Zhao and J. A. Lercher, J. Am. Chem. Soc., 2012, 134, 20768–20775 CrossRef CAS PubMed.
- W. Lubitz, H. Ogata, O. Rudiger and E. Reijerse, Chem. Rev., 2014, 114, 4081–4148 CrossRef CAS PubMed.
- C. Tard and C. J. Pickett, Chem. Rev., 2009, 109, 2245–2274 CrossRef CAS.
- S. M. J. Rogge, A. Bavykina, J. Hajek, H. Garcia, A. I. Olivos-Suarez, A. Sepulveda-Escribano, A. Vimont, G. Clet, P. Bazin, F. Kapteijn, M. Daturi, E. V. Ramos-Fernandez, F. X. Llabres i Xamena, V. Van Speybroeck and J. Gascon, Chem. Soc. Rev., 2017, 46, 3134–3184 RSC.
- Y. B. Huang, J. Liang, X. S. Wang and R. Cao, Chem. Soc. Rev., 2017, 46, 126–157 RSC.
- B. Y. Li, M. Chrzanowski, Y. M. Zhang and S. Q. Ma, Coord. Chem. Rev., 2016, 307, 106–129 CrossRef CAS.
- J. H. Qiu, M. He, M. M. Jia and J. F. Yao, Prog. Chem., 2016, 28, 1016–1028 Search PubMed.
- Z. Chen, J. Chen and Y. Li, Chin. J. Catal., 2017, 38, 1108–1126 CrossRef CAS.
- A. Rossin, G. Tuci, L. Luconi and G. Giambastiani, ACS Catal., 2017, 7, 5035–5045 CrossRef CAS.
- V. Stavila, R. K. Bhakta, T. M. Alam, E. H. Majzoub and M. D. Allendorf, ACS Nano, 2012, 6, 9807–9817 CrossRef CAS PubMed.
- A. E. Anderson, C. J. Baddeley and P. A. Wright, Catal. Lett., 2018, 148, 154–163 CrossRef CAS PubMed.
- I. E. Ertas, M. Gulcan, A. Bulut, M. Yurderi and M. Zahmakiran, Microporous Mesoporous Mater., 2016, 226, 94–103 CrossRef CAS.
- A. A. Ibrahim, A. Lin, F. M. Zhang, K. M. AbouZeid and M. S. El-Shall, ChemCatChem, 2017, 9, 469–480 CrossRef CAS.
- R. Insyani, D. Verma, H. S. Cahyadi, S. M. Kim, S. K. Kim, N. Karanwal and J. Kim, Appl. Catal., B, 2019, 243, 337–354 CrossRef CAS.
- R. Insyani, D. Verma, S. M. Kim and J. Kim, Green Chem., 2017, 19, 2482–2490 RSC.
- F. M. Zhang, S. Zheng, Q. Xiao, Y. J. Zhong, W. D. Zhu, A. Lin and M. S. El-Shall, Green Chem., 2016, 18, 2900–2908 RSC.
- H. J. Wang, X. D. Li, X. C. Lan and T. F. Wang, ACS Catal., 2018, 8, 2121–2128 CrossRef CAS.
- L. P. Zheng, X. W. Li, W. C. Du, D. W. Shi, W. S. Ning, X. Y. Lu and Z. Y. Hou, Appl. Catal., B, 2017, 203, 146–153 CrossRef CAS.
- H. Deng, S. Grunder, K. E. Cordova, C. Valente, H. Furukawa, M. Hmadeh, F. Gándara, A. C. Whalley, Z. Liu, S. Asahina, H. Kazumori, M. O'Keeffe, O. Terasaki, J. F. Stoddart and O. M. Yaghi, Science, 2012, 336, 1018–1023 CrossRef CAS PubMed.
- V. Stavila, R. Parthasarathi, R. W. Davi, F. El Gabaly, K. L. Sale, B. A. Simmons, S. Singh and M. D. Allendorf, ACS Catal., 2016, 6, 55–59 CrossRef CAS.
- A. Herbst and C. Janiak, CrystEngComm, 2017, 19, 4092–4117 RSC.
- M. P. Suh, H. J. Park, T. K. Prasad and D.-W. Lim, Chem. Rev., 2012, 112, 782–835 CrossRef CAS.
- V. Stavila, R. Parthasarathi, R. W. Davis, F. El Gabaly, K. L. Sale, B. A. Simmons, S. Singh and M. D. Allendorf, ACS Catal., 2016, 6, 55–59 CrossRef CAS.
- K. Sumida, C. M. Brown, Z. R. Herm, S. Chavan, S. Bordiga and J. R. Long, Chem. Commun., 2011, 47, 1157–1159 RSC.
- D. Gygi, E. D. Bloch, J. A. Mason, M. R. Hudson, M. I. Gonzalez, R. L. Siegelman, T. A. Darwish, W. L. Queen, C. M. Brown and J. R. Long, Chem. Mater., 2016, 28, 1128–1138 CrossRef CAS.
- S. A. FitzGerald, B. Burkholder, M. Friedman, J. B. Hopkins, C. J. Pierce, J. M. Schloss, B. Thompson and J. L. C. Rowsell, J. Am. Chem. Soc., 2011, 133, 20310–20318 CrossRef CAS PubMed.
- M. T. Kapelewski, S. J. Geier, M. R. Hudson, D. Stuck, J. A. Mason, J. N. Nelson, D. J. Xiao, Z. Hulvey, E. Gilmour, S. A. FitzGerald, M. Head-Gordon, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2014, 136, 12119–12129 CrossRef CAS PubMed.
- T. Pham, K. A. Forrest, R. Banerjee, G. Orcajo, J. Eckert and B. Space, J. Phys. Chem. C, 2015, 119, 1078–1090 CrossRef CAS.
- J. Xu, E. S. M. Blaakrneer, A. S. Lipton, T. M. McDonald, Y. M. Liu, B. Smit, J. R. Long, A. P. M. Kentgens and J. A. Reimert, J. Phys. Chem. C, 2017, 121, 19938–19945 CrossRef CAS.
- L. S. Cahill, J. V. Hanna, A. Wong, J. C. C. Freitas, J. R. Yates, R. K. Harris and M. E. Smith, Chem.–Eur. J., 2009, 15, 9785–9798 CrossRef CAS PubMed.
- S. Jawahery, C. M. Simon, E. Braun, M. Witman, D. Tiana, B. Vlaisavljevich and B. Smit, Nat. Commun., 2017, 8, 13945 CrossRef CAS PubMed.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341 Search PubMed.
- Z. L. Fang, B. Bueken, D. E. De Vos and R. A. Fischer, Angew. Chem., Int. Ed., 2015, 54, 7234–7254 CrossRef CAS PubMed.
- M. Latroche, S. Surblé, C. Serre, C. Mellot-Draznieks, P. L. Llewellyn, J.-H. Lee, J.-S. Chang, S. H. Jhung and G. Férey, Angew. Chem., Int. Ed., 2006, 45, 8227–8231 CrossRef CAS PubMed.
- C. O. Areán, S. Chavan, C. P. Cabello, E. Garrone and G. T. Palomino, ChemPhysChem, 2010, 11, 3237–3242 CrossRef PubMed.
- W. Karim, C. Spreafico, A. Kleibert, J. Gobrecht, J. VandeVondele, Y. Ekinci and J. A. van Bokhoven, Nature, 2017, 541, 68 CrossRef CAS PubMed.
- T. Runcevski, M. T. Kapelewski, R. M. Torres-Gavosto, J. D. Tarver, C. M. Brown and J. R. Long, Chem. Commun., 2016, 52, 8251–8254 RSC.
- M. D. Allendorf, Z. Hulvey, T. Gennett, A. Ahmed, T. Autrey, J. Camp, E. S. Cho, H. Furukawa, M. Haranczyk, M. Head-Gordon, S. Jeong, A. Karkamkar, D. J. Liu, J. R. Long, K. R. Meihaus, I. H. Nayyar, R. Nazarov, D. J. Siegel, V. Stavila, J. J. Urban, S. P. Veccham and B. C. Wood, Energy Environ. Sci., 2018, 11, 2784–2812 RSC.
- F. H. Larsen, H. J. Jakobsen, P. D. Ellis and N. C. Nielsen, J. Phys. Chem. A, 1997, 101, 8597–8606 CrossRef CAS.
- D. Iuga, H. Schäfer, R. Verhagen and A. P. M. Kentgens, J. Magn. Reson., 2000, 147, 192–209 CrossRef CAS.
- A. S. Lipton, R. W. Heck, J. A. Sears and P. D. Ellis, J. Magn. Reson., 2004, 168, 66–74 CrossRef CAS PubMed.
- A. S. Lipton, T. A. Wright, M. K. Bowman, D. L. Reger and P. D. Ellis, J. Am. Chem. Soc., 2002, 124, 5850–5860 CrossRef CAS.
- N. Sinha, C. V. Grant, C. H. Wu, A. A. De Angelis, S. C. Howell and S. J. Opella, J. Magn. Reson., 2005, 177, 197–202 CrossRef CAS PubMed.
- M. H. Cohen and F. Reif, Quadrupole Effects in Nuclear Magnetic Resonance Studies of Solids, Academic Press, New York, 1957 Search PubMed.
- P. Pyykko, Z. Naturforschung A, 1992, 47, 189–196 CAS.
- P. Pyykko, Mol. Phys., 2001, 99, 1617–1629 CrossRef CAS.
- M. H. Cohen and F. Reif, Solid State Phys., 1957, 5, 321–438 CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. W. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115 CAS.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- J. W. Sun, R. C. Remsing, Y. B. Zhang, Z. R. Sun, A. Ruzsinszky, H. W. Peng, Z. H. Yang, A. Paul, U. Waghmare, X. F. Wu, M. L. Klein and J. P. Perdew, Nat. Chem., 2016, 8, 831–836 CrossRef CAS.
- G. Paolo, B. Stefano, B. Nicola, C. Matteo, C. Roberto, C. Carlo, C. Davide, L. C. Guido, C. Matteo, D. Ismaila, C. Andrea Dal, G. Stefano de, F. Stefano, F. Guido, G. Ralph, G. Uwe, G. Christos, K. Anton, L. Michele, M.-S. Layla, M. Nicola, M. Francesco, M. Riccardo, P. Stefano, P. Alfredo, P. Lorenzo, S. Carlo, S. Sandro, S. Gabriele, P. S. Ari, S. Alexander, U. Paolo and M. W. Renata, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Grånäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iuşan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küçükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G.-M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G.-X. Zhang and S. Cottenier, Science, 2016, 351 Search PubMed.
- S. Lebègue, B. Arnaud, M. Alouani and P. E. Bloechl, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155208 CrossRef.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc01018a |
| This journal is © The Royal Society of Chemistry 2019 |