Open Access Article
Open Access ArticleDependence of the fluorination intercalation of graphene toward high-quality fluorinated graphene formation†
Kun
Fan
,
Jiemin
Fu
,
Xikui
Liu
 ,
Yang
Liu
,
Yang
Liu
 ,
Wenchuan
Lai
,
Wenchuan
Lai
 ,
Xiangyang
Liu
,
Xiangyang
Liu
 * and
Xu
Wang
*
* and
Xu
Wang
*
College of Polymer Science and Engineering, State Key Laboratory of Polymer Material and Engineering, Sichuan University, Chengdu 610065, People's Republic of China. E-mail: lxy6912@sina.com; wangxu@scu.edu.cn; Fax: +86 28 85405138; Tel: +86 28 85403948
First published on 30th April 2019
Abstract
A direct gas–solid reaction between fluorine gas (F2) and graphene is expected to become an inexpensive, continuous and scalable production method to prepare fluorinated graphene. However, the dependence of the fluorination intercalation of graphene is still poorly understood, which prevents the formation of high-quality fluorinated graphene. Herein, we demonstrate that chemical defects (oxygen group defects) on graphene sheets play a leading role in promoting fluorination intercalation, whereas physical defects (point defects), widely considered to be an advantage due to more diffusion channels for F2, were not influential. Tracing the origins, compared with the point defects, the unstable hydroxyl and epoxy groups produced active radicals and the relatively stable carbonyl and carboxyl groups activated the surrounding aromatic regions, thereby both facilitating fluorination intercalation, and the former was a preferential and easier route. Based on the above investigations, we successfully prepared fluorinated graphene with an ultrahigh interlayer distance (9.7 Å), the largest value reported for fluorinated graphene, by customizing graphene with more hydroxyl and epoxy groups. It presented excellent self-lubricating ability, with an ultralow interlayer interaction of 0.056 mJ m−2, thus possessing a far lower friction coefficient compared with graphene, when acting as a lubricant. Moreover, it was also easy to exfoliate by shearing, due to the diminutive interlayer friction and eliminated commensurate stacking. The exfoliated number of layers of less than three exceeded 80% (monolayer rate ≈ 40%), and no surfactant was applied to prevent further stacking.
1. Introduction
Due to its excellent mechanical and chemicophysical properties, graphene has received ever-increasing attention around the word and a series of graphene technologies have been developed.1–3 More importantly, it initiated the research upsurge of two-dimensional (2D) materials, including phosphorene, graphdiyne, transition metal dichalcogenides, covalent organic frameworks, and even organic–inorganic hybrid perovskites and so on. Accordingly, the “experience” of graphene guides its preparations, applications and ramifications. The supramaximal aspect ratio (the ratio of the lateral size to thickness) is the most important and intrinsic characteristic of 2D materials, so the broad (transversal direction) and narrow (longitudinal direction) interlayers spontaneously form in the multilayer structure or through self-assembly via weak van der Waals interactions. Recent advances in 2D materials indicate that taking advantage of the interlayer and the corresponding parameters is crucial to numerous applications, such as lubrication,4,5 separation,6 electrochemistry,7 catalysis8 and even exfoliation.9,10 Therefore, meticulously understanding the structure dependence for interlayer regulation, especially for original graphene,11 would bring about a promising harvest in the research of 2D materials.Fluorinated graphene, as an important graphene derivative, effectively regulates the interlayer of graphene, such as increasing the interlayer distance and reducing the interlayer surface energy.12,13 Meanwhile, the introduction of fluorine would result in new properties and functions of the resulting graphene material, which would enable, for example, a tunable energy gap, high functionalization density and fine chemical reactivity, and excellent thermal stability, allowing electromagnetic as well as medical applications.14–17 Thus, fluorinated graphene has great potential for application in a range of fields. However, graphene structure dependence for fluorination intercalation is always ignored, which severely restricts the further development of fluorinated graphene. That is, it still remains challenging to prepare the same quality of fluorinated graphene. High-quality fluorinated graphene possessing an ultrahigh interlayer distance is also difficult to obtain. There is limited guidance for designing specific graphene to meet the need of preparing directed fluorinated graphene toward different service environments.
It should be also noted that great difficulty exists in the investigation of the dependence of fluorination intercalation. In terms of graphene as a raw material, it is a complex matrix with various structural natures, even in different regions of one graphene sheet, such as different defect species,18–20 which makes it difficult to distinguish the respective contributions for fluorination intercalation from different structural factors. Taking the preparation of fluorinated graphene into account, the raw material of liquid-phase exfoliation is graphite fluoride, where the interlayer is relatively stationary and no fluorination intercalation needs consideration.14,21 Expensive xenon difluoride (XeF2) is always chosen to fluoridize monolayer graphene from chemical vapor deposition in a tiny quantity,14 and its surface peculiarity has been the focus of attention. For other fluorine sources such as sulfur hexafluoride (SF6) and fluoropolymer, the generated fluorine species are unclear and impurity elements may be present. Direct fluorination between graphene and fluorination gas (F2) has been achieved by adjusting the F/C ratio (CFn stoichiometry, n = 0–1),22,23 which is a favorable and convenient means to investigate fluorination intercalation. As a typical gas–solid reaction, the advantage is its scalability in practical applications. Nevertheless, in the face of explaining the mechanism, it has been extensively accepted that physical defects (point defects) are advantageous for fluorination intercalation due to more gas diffusion channels,22,24 although only straightforward computational simulation results have been provided and valid experimental evidence is lacking. Therefore, it is urgent to meticulously investigate the dependence of fluorination intercalation, that is, which types are favorable and their respective contribution abilities.
In this work, we reveal the dependence of fluorination intercalation, by meticulously distinguishing and purposefully adjusting the defect species on graphene sheets. It has been confirmed that point defects provide little help for effective fluorination intercalation, although they possess sufficient diffusion channels for F2, which goes against conventional wisdom. Inversely, oxygen group defects play a leading role in promoting fluorination intercalation. Compared with point defects, unstable hydroxyl and epoxy groups produce active radicals and the relatively stable carbonyl and carboxyl groups activate the surrounding aromatic regions, both supporting effective fluorination intercalation, and the former route was preferential and also has a lower reaction energy barrier, as demonstrated by in situ temperature-dependent electron paramagnetic resonance (ISTD-EPR) measurements and density functional theory (DFT) calculations. Afterwards, we prepared fluorinated graphene (FHGO) with an ultrahigh interlayer distance (9.7 Å) by fluorination intercalation of graphene with more hydroxyl and epoxy groups, and it presented lower friction coefficients as solid/liquid lubricants compared with graphene, due to its excellent self-lubricating ability with an interlayer interaction of 0.056 mJ m−2. Moreover, the diminutive interlayer friction and eliminated commensurate stacking made FHGO easy to exfoliate by shearing using ball-milling, presenting a promising prospect for large-scale preparation, which also means that shearing rather than peeling should also be considered for exfoliating 2D materials to render them with good self-lubricating ability.
2. Results and discussion
2.1. Influence of point defects vs. oxygen groups defects
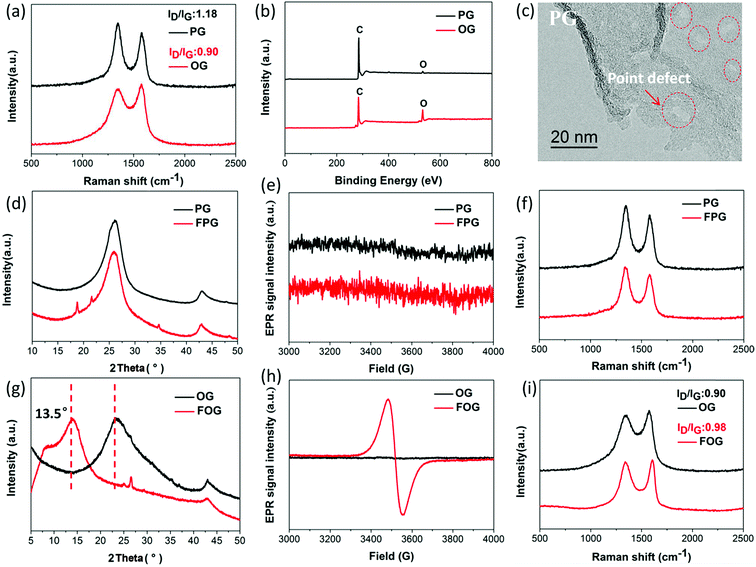
Defects on graphene sheet can be generally divided into two types:18,25 (1) physical defects, namely lattice stacking, cover grain boundaries and point defects, while grain boundaries mainly exist in graphene produced via chemical vapor deposition, where the point defects are predominant;26,27 (2) chemical defects, namely bonding groups, here mainly containing oxygen group defects. In order to expressly investigate the dependence of fluorination intercalation from point defects and oxygen group defects on graphene sheets, two types of graphene namely PG (mainly with point defects) and OG (mainly with oxygen group defects), from the same manufacturer with relatively single defect were chosen as a comparison. As shown in Fig. 1a, a D band is observed in Raman spectra, which indicates that some defects exist on the two types of graphene sheets. The measured D to G band intensity (ID/IG) ratio reflects the total defect density.25,28–30 PG had an ID/IG ratio of 1.18, greater than that of OG (0.90), implying the presence of more defects on the PG sheet. The average defect distance can be further obtained by the amorphization trajectory according to the following formula: LD2 (nm2) = (1.8 ± 0.5) × 10−9 × λL4 × (ID/IG)−1,18 where λL is the excitation laser wavelength (a 532 nm laser was used in the Raman measurements). The calculated LD values of PG and OG are (16.1 ± 0.8) and (18.7 ± 0.7) nm, respectively. From the chemical compositions obtained by X-ray photoelectron spectroscopy (XPS) measurements (Fig. 1b and Table 1), it was found that little oxygen (1.94%) exists in PG while OG possesses over 16% oxygen, and the Fourier-transform infrared spectroscopy (FTIR) spectra (Fig. S2†) are also in good agreement with this observation. These results well demonstrate that PG with more defects mainly contains point defects, and oxygen group defects are dominant in OG. From the high magnification transmission electron microscope (TEM) image in Fig. 1c, it can also be seen that some point defects exist on the PG sheet, while few point defects exist on the OG sheet (Fig. S1†). Meanwhile, the selected area electron diffraction (SAED) image of some regions of the OG sheet does not present typical diffraction spots for the aromatic region, indicating the existence of oxygen group defects,31 as shown in Fig. S1.†| Samples | Chemical compositions of the samples | ||||
|---|---|---|---|---|---|
| C content (atom%) | O content (atom%) | F content (atom%) | O/C ratio | F/C ratio | |
| PG | 98.06 | 1.94 | 0 | 0.02 | 0 |
| OG | 83.55 | 16.45 | 0 | 0.2 | 0 |
| FPG | 87.79 | 5.19 | 7.02 | 0.06 | 0.08 |
| FOG | 69.02 | 14.81 | 16.18 | 0.21 | 0.23 |
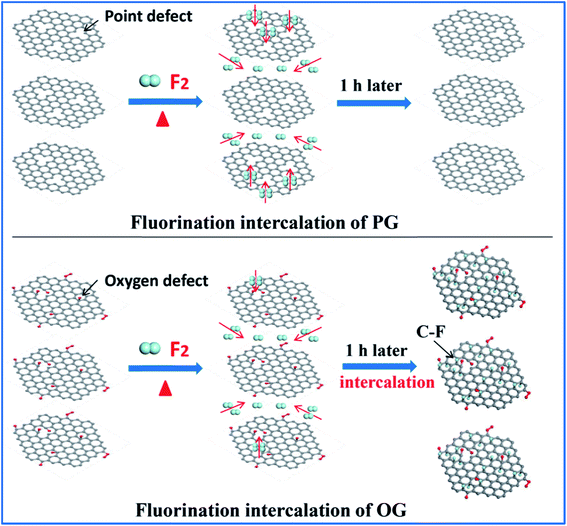
Having defined the defect species of PG and OG, the same fluorination conditions were set for them to perform fluorination intercalation. Beyond expectation, the F/C ratio of fluorinated PG (FPG) was only 0.08, far lower than the 0.23 of the fluorinated OG (FOG), as shown in Table 1. From the wide angle powder X-ray diffraction (PXRD) patterns in Fig. 1d, it can also be found that the peak shape and position of FPG shows little change compared with that of PG. From PG to FPG (Fig. 1e), no obvious signal representing the generation of radicals or paramagnetic structural defects appears in EPR spectra, implying that there is little fluorine atom functionalization or doping in the PG.22,23 The Raman spectra also show little distinction (Fig. 1f). These results indicate that it is difficult for fluorination intercalation to occur in the PG, although the many point defects in PG provide additional channels for F2 entry, as shown in Fig. 2. In other words, point defects do not contribute toward promoting the fluorination intercalation of graphene.
Defects, widely regarded or demonstrated to promote fluorination intercalation, may be mainly attributed to oxygen group defects rather than point defects. As shown in the PXRD patterns (Fig. 1g), from OG to FOG, the peak position shifts to a smaller 2 theta value (13.5°), indicating that the corresponding interlayer distance increases (from 3.91 to 6.55 Å) due to successful fluorination intercalation (the calculated interlayer distance is based on the Bragg equation, 2d × sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = n × λ). A typical EPR signal is observed for FOG (Fig. 1h) and the ID/IG ratio of FOG (0.98) shows an obvious increase compared with that of OG (0.90) (Fig. 1i), indicating fluorine atom functionalization or doping.15,31 These results demonstrate that oxygen group defects indeed promote the fluorination intercalation of graphene, as shown in Fig. 2.
θ = n × λ). A typical EPR signal is observed for FOG (Fig. 1h) and the ID/IG ratio of FOG (0.98) shows an obvious increase compared with that of OG (0.90) (Fig. 1i), indicating fluorine atom functionalization or doping.15,31 These results demonstrate that oxygen group defects indeed promote the fluorination intercalation of graphene, as shown in Fig. 2.
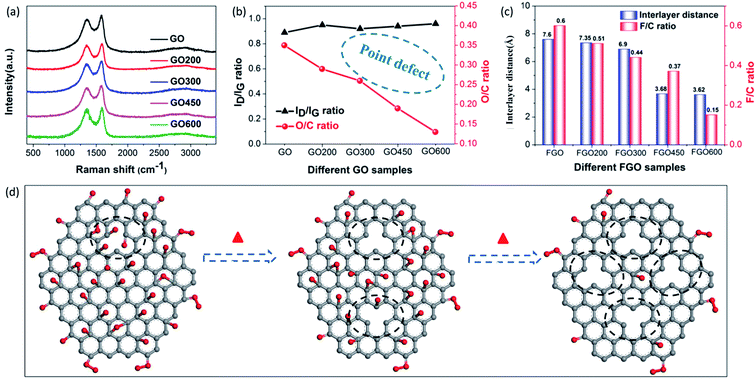
Besides the aforementioned observations, this conclusion still requires further proof to indicate its rationality. Herein, we performed fluorination intercalation for graphene oxide (GO) under the same fluorination conditions as used in the preparation of FOG. GO possesses more oxygen groups (O/C: 0.35) (Fig. 3b) compared with OG (O/C ratio: 0.2, Table 1), so the corresponding fluorinated product (FGO) presents a larger interlayer distance (7.6 Å) (Fig. 3c and S3†) due to more effective fluorination intercalation, further confirming the advantage of oxygen group defects.
In addition, GO was heated to 200, 300, 450 and 600 °C, denoted as GO200, GO300, GO450 and GO600, respectively, then fluorination intercalation was carried out on them. The corresponding fluorinated products (FGO200, FGO300, FGO450 and FGO600) present tapering interlayer distances and the F/C ratios also gradually decreased (Fig. 3c), which indicates that fluorination intercalation gradually becomes more difficult during the process. Coming back to considering the defect species of GO200, GO300, GO450 and GO600, the aromatic region is gradually regained, due to the reduction in the oxygen group defects (or O/C ratio) (Fig. 3b) after heat treatment,25,32 while the values of the ID/IG ratio do not decrease and even show a slight increase (Fig. 3a and b). The Raman spectra imply an increase in the total number of defects due to the heat treatment. It can be explained that the high temperature and removal of the oxygen groups inevitably destroys the graphene sheets, consequently increasing the number of point defects,27,33 as shown in Fig. 3d. From GO200 to GO600, the specific surface area (Brunauer–Emmett–Teller, BET) gradually increases (Fig. S4†), which also demonstrates an increase in the number of point defects. From the TEM image of the GO600 sheet (Fig. S5†), obvious point defects can be also be observed. Therefore, from GO200 to GO600, the oxygen group defects decrease and the point defects increase, but the corresponding fluorination intercalation efficiency gradually decreases. These results further demonstrate the aforementioned conclusion that oxygen group defects play a leading role in promoting fluorination intercalation, while point defects are not influential.
2.2. Advantages of oxygen group defects
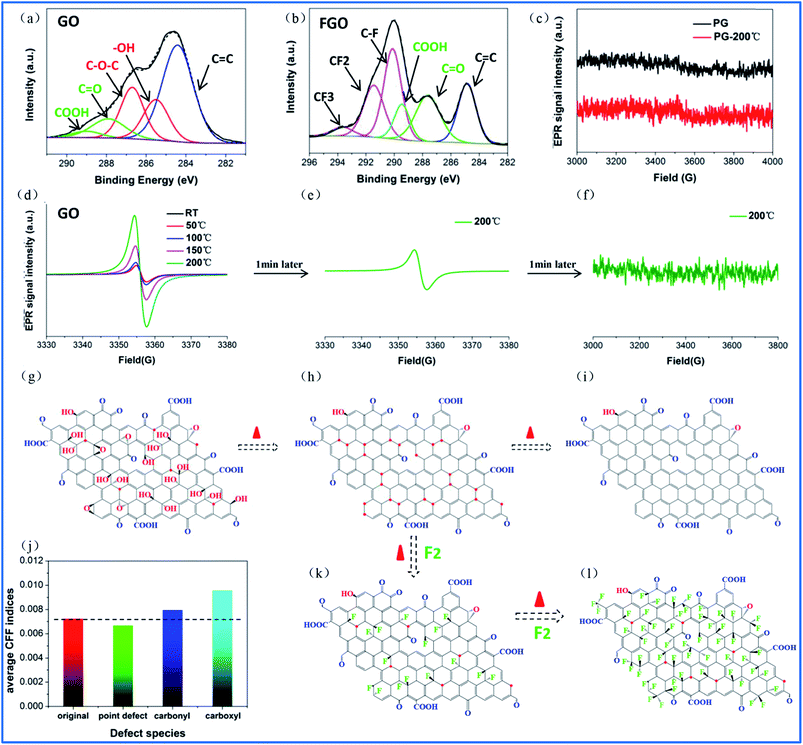
Compared to point defects, why do oxygen group defects effectively promote fluorination intercalation? Here, the effects of oxygen group defects can be divided into two types. As shown in the XPS C1s spectra (Fig. S6† and 4a), the existing oxygen groups on the OG sheet are mainly carbonyl and carboxyl groups, whereas graphene oxide (GO) mainly possesses hydroxyl and epoxy groups rather than carbonyl and carboxyl groups. It has been demonstrated that carbonyl and carboxyl groups on graphene sheets are more stable compared with hydroxyl and epoxy groups, so the latter are difficult to retain on graphene sheets during a reduction preparation process.34–36 The corresponding stability rule of different oxygen groups is also appropriate for fluorination intercalation; that is, after fluorination intercalation for GO, almost all of the hydroxyl and epoxy groups are destroyed, whereas the carbonyl and carboxyl groups are basically preserved (Fig. 4b). These results reveal that hydroxyl and epoxy groups are unstable and carbonyl and carboxyl groups are relatively stable during fluorination intercalation, which may bring about different stimulative effects.Interestingly, unstable hydroxyl and epoxy groups act as “blasting fuses” in promoting fluorination intercalation. As shown in Fig. 4d, in situ temperature-dependent EPR (ISTD-EPR) measurements show that the EPR intensity of GO shows little change before 100 °C, indicating that no new radicals are generated and that all of the oxygen groups are stable. After 100 °C, the EPR intensity begins to increase due to the generation of new radicals, indicating that the unstable hydroxyl and epoxy groups begin to decompose, as shown in Fig. 4g and h. Notably, the EPR spectra in Fig. 4e and f indicate that these new radicals present great activity, and then fade away in a transitory time (within 2 min); that is, these active radicals couple to form new carbon–carbon double bonds (Fig. 4h and i). It should be noted that fluorination of carbon materials (graphene and carbon nanotubes) under a radical mechanism at high temperature has been demonstrated, indicating that the formed radicals are crucial during fluorination intercalation.22,23,37 Herein, generated F˙ from F2 at high temperature rapidly and effectively attacks the active radicals, tremendously decreasing the reaction energy barrier compared with the direct attack of the original aromatic region of graphene, so fluorination intercalation easily occurs, as shown in Fig. 4h–k. However, the ISTD-EPR measurements indicate that PG does not generate active radicals at 200 °C (Fig. 4c), which implies that it is difficult for point defects to promote fluorination intercalation by producing active radicals.
Another type of effect can be attributed to the relatively stable carbonyl and carboxyl groups, which act as “assisting members”. As shown in Fig. S7,† the ISTD-EPR measurements indicate that OG with stable carbonyl and carboxyl groups does not generate active radicals at 200 °C, revealing that they also have limited capacity to achieve the same effect as hydroxyl and epoxy groups. Herein, DFT calculations were applied to quantitatively analyze the chemical environments of the aromatic regions, close to the carbonyl and carboxyl groups and point defects (Fig. S8†). It was found that the carbonyl and carboxyl groups increase the condensed Fukui function (CFF) indices of the surrounding aromatic regions (Fig. 4j), namely an activation effect, which means that there is a greater possibility for corresponding aromatic regions to undergo F˙ attack.22 However, point defects also have limited capacity to achieve the same activation effect, and the corresponding CFF indices show no increase (even showing a little decrease) compared with the original aromatic region (Fig. 4j). Moreover, it should be mentioned that fluorination intercalation of OG with carbonyl and carboxyl groups requires more reaction time compared with that of the rapidly produced active radicals from the hydroxyl and epoxy groups, as demonstrated in Fig. S9.†
Therefore, the fluorination intercalation process can be simply described, as shown in Fig. 4h, k and l; that is, the produced active radicals of the hydroxyl and epoxy groups in a transitory time preferentially react with F˙ (stage 1), then the activated aromatic regions of the carbonyl and carboxyl groups begin to react (stage 2). Interestingly, the different reaction stages also present different fluorination intercalation abilities. As shown in Fig. 1h and S7,† FOG possesses definite radicals, while pristine OG does not have any radicals, regardless of room temperature or high temperature, which reveals that radicals are generated when F˙ attacks the activated aromatic region. Then, the generated radicals play an important role in promoting fluorination intercalation (Scheme S1a†). The unstable hydroxyl and epoxy groups directly produce radicals at high temperature, indicating a lower reaction energy barrier for fluorination intercalation (Scheme S1b†). Therefore, compared with the carbonyl and carboxyl groups, it should be easier for GO with hydroxyl and epoxy groups to react. It is important to distinguish the different stimulative effects for fluorination intercalation from the different oxygen groups. For example, some research groups have recently reported that they have successfully prepared graphene basically with only hydroxyl and epoxy groups or only carbonyl and carboxyl groups.35,36,38 In terms of the former, it is promising to rapidly and easily prepare fluorinated graphene with a high interlayer distance.
2.3. Applications of effective fluorination intercalation
Based on the aforementioned investigations, although we have limited ability to prepare graphene with only hydroxyl and epoxy groups, graphene with more oxygen groups (O/C: 0.58) can be obtained by prolonging the oxidation time during preparation via the Hummers' method, denoted as HGO (Fig. S10†). Moreover, from GO to HGO, the number of hydroxyl and epoxy groups increases compared with the number of carbonyl and carboxyl groups, as shown in Fig. 5a and Table S1,† which provides a foundation for more effective fluorination intercalation. By performing fluorination intercalation for HGO, the fluorinated product (FHGO) (chemical composition in Table S2†) shows an interlayer distance of 9.7 Å (Fig. 5b), which is the biggest value reported for fluorinated graphene up to now.There is no doubt that the interlayer distance is a crucial structural factor to regulate the excellent performances of 2D materials. For example, fluorinated graphene has been supposed to become an advanced lubricant, because effective fluorination intercalation decreases the interlayer surface energy and simultaneously increases the interlayer distance, thus improving its self-lubricating ability.13,39 Its self-lubricating ability, determined by the interlayer van der Waals attraction energy (EvdW), can be calculated by EvdW = −d04γ/h4, where d0 = 0.335 nm, γ is the surface energy and h is the interlayer distance.31,40 As described in the above-mentioned data, the interlayer distances of OG and FHGO are 3.91 and 9.70 Å, their water contact angles are 102° and 138° (Fig. 5c and S11†), and their surface energies are 21.83 and 3.92 mJ m−2, respectively. Therefore, the calculated EvdW values of OG and FHGO are 11.763 and 0.056 mJ m−2, respectively. The excellent self-lubricating ability of FHGO was reflected by the testing of its friction coefficient. As shown in Fig. 5d, FHGO presents a lower friction coefficient of 0.08 compared with that of OG (0.19), when tested as an oil-based lubricating additive. Meanwhile, as a solid lubrication film, FHGO also shows a lower friction coefficient relative to OG (Fig. S12†).
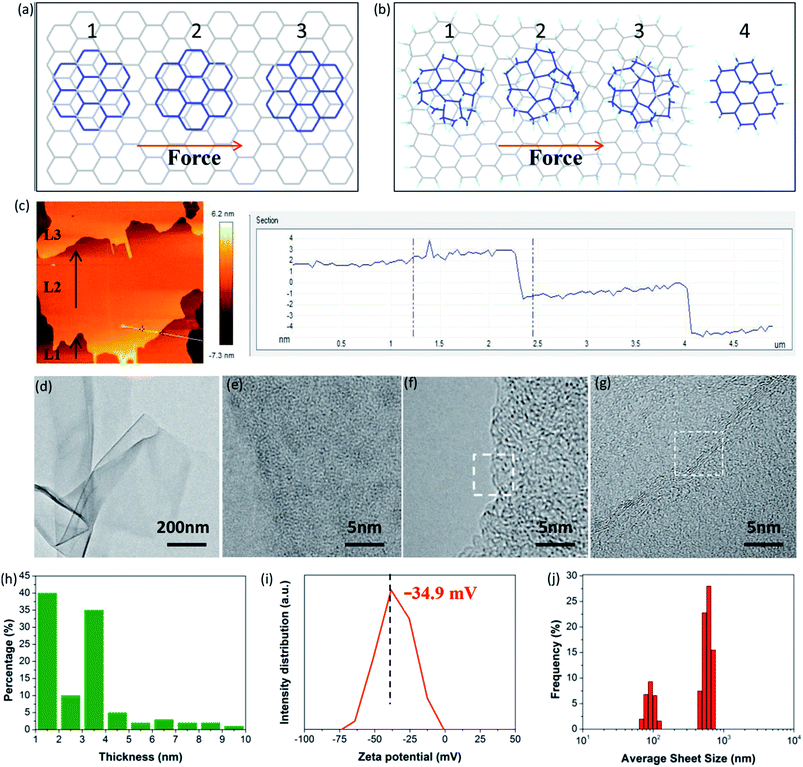
More importantly, FHGO with excellent self-lubricating ability may provide an effective means to guide the exfoliation of graphene-based materials or other 2D materials into few layers or monolayers, which is a crucial precondition for their applications. Taking graphene as an example, Sinclair et al. recently demonstrated that a peeling mechanism should be targeted rather than a shearing mechanism when designing the exfoliation process, including surfactants and intercalation agents for preparing graphene via liquid phase exfoliation.41 They explained that a disadvantageous shearing process was derived from the existing commensurate stacking in graphene (for details see Fig. 6a and S13†). However, here it should be noted that the peeling process needs elaborate operation and that its large-scale application is inevitably restricted. In terms of FHGO, effective fluorination intercalation changes graphene with a disordered lattice due to inevitably possessing multifarious configurations such as boat or chair,13,14 and it also destroys most aromatic regions, thus presenting an amorphous state, as demonstrated by aberration-corrected transmission electron microscopy (AC-TEM) and selected area electron diffraction (SAED) measurements, the results of which can be found in Fig. S14 and S15.† Therefore, commensurate stacking, the most stable state for graphene, was damaged in FHGO. The calculated EvdW value also demonstrates that the interlayer interaction of FHGO is far lower than that of graphene. Once a shear force is applied, the top-FHGO sheet easily moves over the surface of the bottom-FHGO sheet (from 1 to 4 position), due to the lack of the transformation between the commensurate and incommensurate positions, as shown in Fig. 6b. Therefore, a shearing process is favored for easily exfoliating FHGO sheets.
More meaningfully, compared to the peeling process, the shearing process has greater potential of large-scale preparation. For example, ball-milling, a common technology used in practical applications, can provide a strong shear force to exfoliate FHGO. During ball-milling, we extracted the midterm sample to observe its state, as shown in Fig. 6c. It can be clearly seen that the L2 layer of the FHGO sheet has moved a definite distance relative to that of the L1 layer, and that the L3 layer has nearly broken away from the L2 layer, indicating the successful exfoliation of FHGO. Finally, from the TEM image of exfoliated FHGO in Fig. 6d, transparent and ultrathin sheets with a relatively smooth layer structure can be observed. High magnification TEM images (Fig. 6e–g) show the sheet edge with a folded structure, indicating the predominant single-, double- and triple-layered sheets. Moreover, atomic force microscope (AFM) measurements (Fig. S16†) were carried out to statistically measure the sheet thickness for exfoliated FHGO, based on over one hundred sheets. The statistical histogram (Fig. 6h) shows that thicknesses of 1–4 nm (>80%) are dominant in exfoliated FHGO, which also indicates that the layer number of most sheets is lower than three layers. Notably, the exfoliation process does not require any additional intercalation agents; meanwhile, no surfactant was applied to present further stacking, because exfoliated FHGO has a negative zeta potential of −34.9 mV (Fig. 6i), far lower than the −8.2 mV of graphene (Fig. S17†), indicating strong charge repulsion among the sheets. The size distribution of exfoliated FHGO was characterized by dynamic light scattering (DLS) measurements, from 100 nm to 1 μm (Fig. 6j), basically consistent with the results of the AFM measurements (Fig. S16†).
3. Conclusions
In this paper, we demonstrated that oxygen group defects on graphene sheets play a leading role in promoting fluorination intercalation, while point defects are not influential despite the existence of sufficient diffusion pathways for F2. The advantages are that the unstable hydroxyl and epoxy groups produce active radicals and relatively stable carbonyl and carboxyl groups activate the surrounding aromatic regions, thus both facilitating fluorination intercalation, with the former route possessing more advantages. The dependence of fluorination intercalation provides guidance for the specific design of graphene to meet the needs of preparing directed fluorinated graphene toward different service environments. Finally, we successfully in preparing fluorinated graphene with an ultrahigh interlayer distance of 9.7 Å, which presented far lower friction coefficients as solid/liquid lubricants compared with those of graphene, and it was easy to exfoliate using shearing. The high-quality fluorinated graphene, with an ultrahigh interlayer distance after exfoliating, is also expected to be used in more fields, such as batteries, separation and drug delivery.4. Experimental
4.1. Materials
Two types of graphene (PG and OG) were obtained from the Sixth Elementary Materials Technology Co., Ltd (Changzhou). Graphene oxide (GO) was prepared by a modified Hummers' method. A F2/N2 mixture (volume ratio: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9) with a purity of 99.99% was purchased from Kemeite Fluorine Industry Plastic Co., Ltd (Chengdu). Commercial analytical grade liquid paraffin was purchased from Kelong Chemical Reagent Co, Ltd (Chengdu), and was employed without further purification.
9) with a purity of 99.99% was purchased from Kemeite Fluorine Industry Plastic Co., Ltd (Chengdu). Commercial analytical grade liquid paraffin was purchased from Kelong Chemical Reagent Co, Ltd (Chengdu), and was employed without further purification.
4.2. Preparation of fluorinated graphene
Fluorinated graphene was prepared by direct fluorination utilizing fluorine gas, similar to in a previous report.23 100 mg of graphene-based material was placed in an aluminized box, and was then transferred into an airtight stainless steel (SUS316) chamber (20 L). Afterwards, the internal air and moisture were removed by exchanging with N2 up to three times. A measurable F2/N2 amount of 50 kPa was added into the chamber, and it was heated up to 200 °C from room temperature at a heating rate of 5 °C min−1. The fluorination intercalation reaction was maintained for 1 h. After completion, the residual fluorine gas and produced gases such as HF were eliminated by exchanging with N2 three times and were absorbed by an alkali aqueous solution.4.3. Characterization
Raman spectra were recorded at room temperature using a LabRAM HR Raman spectrometer with an excitation wavelength of 532 ± 1 nm. The radical or paramagnetic structural defect signals were captured using electron paramagnetic resonance (EPR) (Bruker Beijing Science and Technology Ltd, USA) recorded using a Bruker EPR EMX Plus, with a frequency of around 9.8 GHz and a standard microwave power of 1 MW. The interlayer distance was obtained by wide angle powder X-ray powder diffraction (PXRD), performed at room temperature using Cu Kα radiation (λ = 0.154 nm, U = 40 kV, I = 40 mA) over an angular range of 3.5–50° (2θ) with a step size of 0.02° using an Ultima IV powder diffractometer (Rigaku Corporation). Chemical compositions were characterized by X-ray photoelectron spectroscopy (XPS) on a Kratos ASAM 800 spectrometer (Kratos Analytical Ltd, UK), equipped with a nonmonochromatic Al Kα (1486.6 eV) X-ray source (a voltage of 15 kV, a wattage of 250 W) of radiation, at a vacuum pressure of 10−6 to 10−7 Pa. FTIR measurements were performed on a Nicolet 560 Fourier-transform spectrometer. Characterization of nitrogen sorption isotherms on a Micromeritics Tristar 3020 analyzer (USA) was applied to measure the specific surface area.TEM (Tecnai G2 F20 S-TWIN) and AFM (Nano-ScopeMultiMole & Explore from Vecco Instruments) measurements were implemented to observe the morphology and obtain a statistical sheet thickness. The water contact angle was obtained by a surface tension meter (Kruss 100, Hamburg, Germany), and the corresponding surface energy was calculated using the Drop Shape Analysis software. The friction coefficients of OG and FHGO as lubricating oil additives were tested by a UTM-2 tribometer (USA) in reciprocating wear mode at room temperature. The applied load, stroke length, speed and test time were 10 N, 8 mm, 5 mm s−1 and 3600 s, respectively. The ball milling experiments were performed in a planetary ball mill Pulverisette (Nan Jing) under ambient conditions with a rotation speed of 600 rpm and a test time of 1 h. Surface charge was characterized from the zeta potential (Zetasizer Nano-ZS, Malvern, UK) with a dispersion concentration of 0.1 mg ml−1 using ethanol as a solvent. Dynamic light scattering (DLS) (Nano-ZS, Malvern, UK) was applied to measure the size distribution of the particles.
DFT calculations for model molecules were carried out taking advantage of the DMol3 module of Materials Studio 8.0, in order to calculate the reactivity of the aromatic regions close to the carbonyl and carboxyl groups and point defects. Geometry optimizations were processed using the generalized gradient approximation (GGA) of the Becke–Lee–Yang–Parr (BLYP) functional, and the basis was set as DND (comparable to Gaussian 6-31G* basis sets) with a basis file 3.5. The self-consistent-field calculations had a convergence criteria of 10−5 hartree.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grant No. 51573105 and Grant No. 51633004) and the State Key Laboratory of Polymer Materials Engineering (Grant No. sklpme2017-2-03). The authors acknowledge the Analytical & Testing Centre of Sichuan University, the College of Polymer Science and Engineering of Sichuan University, the State Key Laboratory of Polymer Materials Engineering (Sichuan University) and the National Demonstration Center for Experimental Materials Science and Engineering Education (Sichuan University) for characterization and computational simulations.Notes and references
- M. Kühne, F. Börrnert, S. Fecher, M. Ghorbani-Asl, J. Biskupek, D. Samuelis, A. V. Krasheninnikov, U. Kaiser and J. H. Smet, Nature, 2018, 564, 234–239 CrossRef PubMed.
- G. Shi, S. Araby, C. T. Gibson, Q. Meng, S. Zhu and J. Ma, Adv. Funct. Mater., 2018, 28, 1706705 CrossRef.
- J. Shim, S. H. Bae, W. Kong, D. Lee, K. Qiao, D. Nezich, Y. J. Park, R. Zhao, S. Sundaram, X. Li, H. Yeon, C. Choi, H. Kum, R. Yue, G. Zhou, Y. Ou, K. Lee, J. Moodera, X. Zhao, J. H. Ahn, C. Hinkle, A. Ougazzaden and J. Kim, Science, 2018, 362, 665–670 CrossRef CAS PubMed.
- O. Hod, E. Meyer, Q. Zheng and M. Urbakh, Nature, 2018, 563, 485–492 CrossRef CAS PubMed.
- S. Zhang, T. Ma, A. Erdemir and Q. Li, Mater. Today, 2018 DOI:10.1016/j.mattod.2018.12.002.
- K. G. Zhou, K. S. Vasu, C. T. Cherian, M. Neek-Amal, J. C. Zhang, H. Ghorbanfekr-Kalashami, K. Huang, O. P. Marshall, V. G. Kravets, J. Abraham, Y. Su, A. N. Grigorenko, A. Pratt, A. K. Geim, F. M. Peeters, K. S. Novoselov and R. R. Nair, Nature, 2018, 559, 236 CrossRef CAS PubMed.
- D. K. Bediako, M. Rezaee, H. Yoo, D. T. Larson, S. Y. F. Zhao, T. Taniguchi, K. Watanabe, T. L. Brower-Thomas, E. Kaxiras and P. Kim, Nature, 2017, 558, 425 CrossRef PubMed.
- Y. Luo, X. Li, X. Cai, X. Zou, F. Kang, H. Cheng and B. Liu, ACS Nano, 2018, 12, 4565–4573 CrossRef CAS PubMed.
- Y. Xiao, T. Zhang, M. Zhou, Z. Weng, X. Chang, K. Yang, J. Liu, J. Li, B. Wei, Z. Wang and L. Fu, Adv. Mater., 2019, 31, 1805976 CrossRef PubMed.
- X. Cai, Y. Luo, B. Liu and H. Cheng, Chem. Soc. Rev., 2018, 47, 6224–6266 RSC.
- S. Seiler, C. E. Halbig, F. Grote, P. Rietsch, F. Börrnert, U. Kaiser, B. Meyer and S. Eigler, Nat. Commun., 2018, 9, 836 CrossRef PubMed.
- R. Ye, X. Han, D. V. Kosynkin, Y. Li, C. Zhang, B. Jiang, A. A. Martí and J. M. Tour, ACS Nano, 2018, 12, 1083–1088 CrossRef CAS PubMed.
- K. Fan, X. Chen, X. Wang, X. Liu, Y. Liu, W. Lai and X. Liu, ACS Appl. Mater. Interfaces, 2018, 10, 28828–28838 CrossRef CAS PubMed.
- W. Feng, P. Long, Y. Feng and Y. Li, Adv. Sci., 2016, 3, 1500413 CrossRef PubMed.
- F. Zhou, H. Huang, C. Xiao, S. Zheng, X. Shi, J. Qin, Q. Fu, X. Bao, X. Feng, K. Müllen and Z. Wu, J. Am. Chem. Soc., 2018, 140, 8198–8205 CrossRef CAS PubMed.
- P. Gong, S. Ji, J. Wang, D. Dai, F. Wang, M. Tian, L. Zhang, F. Guo and Z. Liu, Chem. Eng. J., 2018, 348, 438–446 CrossRef CAS.
- W. Lai, J. Liu, L. Luo, X. Wang, T. He, K. Fan and X. Liu, Chem. Commun., 2018, 54, 10168–10171 RSC.
- Z. Yuan, J. D. Benck, Y. Eatmon, D. Blankschtein and M. S. Strano, Nano Lett., 2018, 18, 5057–5069 CrossRef CAS PubMed.
- Z. Gan, S. Xiong, X. Wu, T. Xu, X. Zhu, X. Gan, J. Guo, J. Shen, L. Sun and P. K. Chu, Adv. Opt. Mater., 2013, 1, 926–932 CrossRef.
- C. Chien, S. Li, W. Lai, Y. Yeh, H. Chen, I. Chen, L. Chen, K. Chen, T. Nemoto, S. Isoda, M. Chen, T. Fujita, G. Eda, H. Yamaguchi, M. Chhowalla and C. Chen, Angew. Chem., Int. Ed., 2012, 51, 6662–6666 CrossRef CAS PubMed.
- W. Wang, Z. Xu, X. Zhang, A. Wimmer, E. Shi, Y. Qin, X. Zhao, B. Zhou and L. Li, Chem. Eng. J., 2018, 343, 61–68 CrossRef CAS.
- W. Lai, X. Wang, Y. Li, Y. Liu, T. He, K. Fan and X. Liu, Carbon, 2018, 132, 271–279 CrossRef CAS.
- W. Lai, D. Xu, X. Wang, Z. Wang, Y. Liu, X. Zhang and X. Liu, Phys. Chem. Chem. Phys., 2017, 19, 19442–19451 RSC.
- Y. Liu, Y. Zhang, C. Zhang, B. Huang, X. Wang, Y. Li, W. Lai and X. Liu, J. Mater. Chem. C, 2018, 6, 9399–9409 RSC.
- Y. Chen, Y. Wang, S. Zhu, K. Fu, X. Han, Y. Wang, B. Zhao, T. Li, B. Liu, Y. Li, J. Dai, H. Xie, T. Li, J. W. Connell, Y. Lin and L. Hu, Mater. Today, 2019, 24, 26–32 CrossRef CAS.
- A. Govind Rajan, K. S. Silmore, J. Swett, A. W. Robertson, J. H. Warner, D. Blankschtein and M. S. Strano, Nat. Mater., 2019, 18, 129–135 CrossRef CAS PubMed.
- W. Zeng, X. Tao, S. Lin, C. Lee, D. Shi, K. Lam, B. Huang, Q. Wang and Y. Zhao, Nano Energy, 2018, 54, 163–174 CrossRef CAS.
- Y. Sun, L. Yang, K. Xia, H. Liu, D. Han, Y. Zhang and J. Zhang, Adv. Mater., 2018, 30, 1803189 CrossRef PubMed.
- D. Voiry, J. Yang, J. Kupferberg, R. Fullon, C. Lee, H. Y. Jeong, H. S. Shin and M. Chhowalla, Science, 2016, 353, 1413–1416 CrossRef CAS PubMed.
- W. Liu, P. Li, W. Wang, D. Zhu, Y. Chen, S. Pen, E. Paek and D. Mitlin, ACS Nano, 2018, 12, 12255–12268 CrossRef CAS PubMed.
- K. Fan, J. Liu, X. Wang, Y. Liu, W. Lai, S. Gao, J. Qin and X. Liu, J. Colloid Interface Sci., 2018, 531, 138–147 CrossRef CAS PubMed.
- H. Cheng, Y. Huang, F. Zhao, C. Yang, P. Zhang, L. Jiang, G. Shi and L. Qu, Energy Environ. Sci., 2018, 11, 2839–2845 RSC.
- H. W. Kim, M. B. Ross, N. Kornienko, L. Zhang, J. Guo, P. Yang and B. D. McCloskey, Nat. Catal., 2018, 1, 282–290 CrossRef.
- Z. Liu, L. Jiang, L. Sheng, Q. Zhou, T. Wei, B. Zhang and Z. Fan, Adv. Funct. Mater., 2018, 28, 1705258 CrossRef.
- M. Yu, S. Zhang, Y. Chen, H. Jin, Y. Zhang, L. Lu, Z. Shu, S. Hou, B. Xie and H. Cui, Carbon, 2018, 133, 101–108 CrossRef CAS.
- H. Chen, W. Du, J. Liu, L. Qu and C. Li, Chem. Sci., 2019, 10, 1244–1253 RSC.
- Y. Liu, X. Wang, W. Wang, B. Li, P. Wu, M. Ren, Z. Cheng, T. Chen and X. Liu, ACS Appl. Mater. Interfaces, 2016, 8, 7991–7999 CrossRef CAS PubMed.
- I. A. Vacchi, J. Raya, A. Bianco and C. Menard-Moyon, 2D Mater., 2018, 5, 035037 CrossRef.
- X. Zeng, Y. Peng, M. Yu, H. Lang, X. A. Cao and K. Zou, ACS Appl. Mater. Interfaces, 2018, 10, 8214–8224 CrossRef CAS PubMed.
- L. Dong, Z. Chen, X. Zhao, J. Ma, S. Lin, M. Li, Y. Bao, L. Chu, K. Leng, H. Lu and K. P. Loh, Nat. Commun., 2018, 9, 76 CrossRef PubMed.
- R. C. Sinclair, J. L. Suter and P. V. Coveney, Adv. Mater., 2018, 30, 1705791 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc00975b |
| This journal is © The Royal Society of Chemistry 2019 |

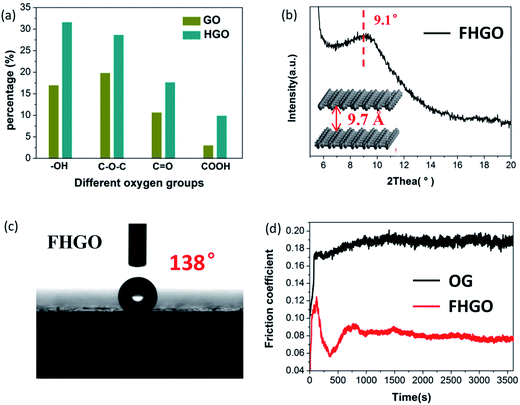
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, COOH) in GO and HGO, (b) the PXRD pattern and the corresponding interlayer distance of FHGO, (c) a photograph of the water contact angle for FHGO, and (d) the friction coefficient lines of OG and FHGO.
O, COOH) in GO and HGO, (b) the PXRD pattern and the corresponding interlayer distance of FHGO, (c) a photograph of the water contact angle for FHGO, and (d) the friction coefficient lines of OG and FHGO.