Open Access Article
Open Access ArticleMechanism of magnetisation relaxation in {MIII2DyIII2} (M = Cr, Mn, Fe, Al) “Butterfly” complexes: how important are the transition metal ions here?†
Yan
Peng
 ab,
Mukesh Kumar
Singh
c,
Valeriu
Mereacre
ab,
Mukesh Kumar
Singh
c,
Valeriu
Mereacre
 a,
Christopher E.
Anson
a,
Christopher E.
Anson
 a,
Gopalan
Rajaraman
a,
Gopalan
Rajaraman
 *c and
Annie K.
Powell
*c and
Annie K.
Powell
 *ab
*ab
aInstitute of Inorganic Chemistry, Karlsruhe Institute of Technology, Engesserstrasse 15, 76131 Karlsruhe, Germany. E-mail: annie.powell@kit.edu
bInstitute of Nanotechnology, Karlsruhe Institute of Technology, Postfach 3640, 76021 Karlsruhe, Germany
cIITB-Monash Research Academy, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India. E-mail: rajaraman@chem.iitb.ac.in
First published on 16th April 2019
Abstract
We describe the synthesis, characterisation and magnetic studies of four tetranuclear, isostructural “butterfly” heterometallic complexes: [MIII2LnIII2(μ3-OH)2(p-Me-PhCO2)6(L)2] (H2L = 2,2′-((pyridin-2-ylmethyl)azanediyl)bis(ethan-1-ol), M = Cr, Ln = Dy (1), Y (2), M = Mn, Ln = Dy (3), Y (4)), which extend our previous study on the analogous 5 {Fe2Dy2}, 6 {Fe2Y2} and 7 {Al2Dy2} compounds. We also present data on the yttrium diluted 7 {Al2Dy2}: 8 {Al2Dy0.18Y1.82}. Compounds dc and ac magnetic susceptibility data reveal single-molecule magnet (SMM) behaviour for complex 3 {Mn2Dy2}, in the absence of an external magnetic field, with an anisotropy barrier Ueff of 19.2 K, while complex 1 {Cr2Dy2}, shows no ac signals even under applied dc field, indicating absence of SMM behaviour. The diluted sample 8 {Al2Dy0.18Y1.82} shows field induced SMM behaviour with an anisotropy barrier Ueff of 69.3 K. Furthermore, the theoretical magnetic properties of [MIII2LnIII2(μ3-OH)2(p-Me-PhCO2)6(L)2] (M = Cr, 1 or Mn, 3) and their isostructural complexes: [MIII2DyIII2(μ3-OH)2(p-Me-PhCO2)6(L)2] (M = Fe, 5 or Al, 7) are discussed and compared. To understand the experimental observations for this family, DFT and ab initio CASSCF + RASSI-SO calculations were performed. The experimental and theoretical calculations suggest that altering the 3dIII ions can affect the single-ion properties and the nature and the magnitude of the 3dIII–3dIII, 3dIII–DyIII and DyIII–DyIII magnetic coupling, thus quenching the quantum tunneling of magnetisation (QTM) significantly, thereby improving the SMM properties within this motif. This is the first systematic study looking at variation and therefore role of trivalent transition metal ions, as well as the diamgnetic AlIII ion, on slow relaxation of magnetisation within a series of isostructural 3d–4f butterfly compounds.
Introduction
Recently, combining 3d and 4f metal ions in a molecule to obtain SMMs has become a hot research topic since 3d ions can give rise to stronger magnetic coupling and/or magnetic anisotropy while 4f ions such as DyIII, TbIII, HoIII, contribute large single-ion magnetic anisotropy.1–3 Through the efforts of several research groups, there is now a rich structural diversity of 3d–4f SMMs.4 However, it is still a challenge to understand the correlation between the structure and the magnetic properties.The single-ion anisotropy of a metal ion depends mainly on its coordination geometry and ligand field,5 while the molecular anisotropy depends on several factors such as ligand field,6 relative orientation of the individual single-ion easy axes,7 magnetic coupling, and the structural topology of the magnetic core.8,9
It is well-known that the magnetic interactions between the 3d–3d, 3d–4f, and 4f–4f ions in heterometallic clusters are rather complicated to figure out, especially for clusters with high nuclearity. Thus, to better understand the magnetic interactions between 3d and 4f metal ions as well as the effect of magnetic interactions on the SMM behaviour,10,11 the construction of simple complexes with a limited number of 3d and 4f ions is required in order to elucidate the magneto-structural correlations. A fruitful test-bed system is provided by the tetranuclear “butterfly” motif. There are two possibilities for 3d/4f butterflies, either the 4f metal ions can be in the body positions and the 3d transition metal M ions are at the wingtips (Type I) or the reverse situation where the 4f metal ions are at the wingtips and the transition metal M ions are in the body positions (Type II). There are relatively few examples of the Type I situation compared with compounds with the Type II motif. The most famous Type I compounds have been reported by the Murray group where the isostructural compounds, {MIII2LnIII2}, (M = Co, Cr and Ln = Dy, Tb, Ho) were studied.12–14 The corresponding {Cr2Ln2} and {Co2Ln2} compounds have similar Ueff values, but open magnetic hysteresis was only observed for the {CrIII2Ln2} compounds where the 3d ion is paramagnetic rather than diamagnetic. It was found using ab initio calculations that this is the direct result of the cooperative 3d–4f coupling between the CrIII and LnIII ions.
A particularly fruitful test-bed system for Type II is the generic [MIII2LnIII2(μ3-OH)2(RCO2)6(L)2] coordination cluster. There are many such examples of 3d–4f butterfly compounds in the literature, including an interesting systematic study by Winpenny, McInnes and their co-workers on a family of {M2Ln2} compounds where M = MgII, MnIII, CoII, NiII, and CuII, Ln = YIII, GdIII, TbIII, DyIII, HoIII, and ErIII. The results revealed that the SMM behaviour observed in the Dy- and Er-based systems are intrinsic to the lanthanide ion and the strength of the 3d–4f exchange interaction plays a key role in the nature of the SMM properties observed.15 For this system, all the metals (M) are bivalent apart from the MnIII analogue. Up to now the equivalent exploration of this type of butterfly system for M = MIII has not been available, probably because of the synthetic challenge to vary the MIII metal ions. On the other hand, it is straightforward to vary the 4f ion, as shown for (Type II) {Fe2Ln2} butterflies.16 We were particularly interested to gauge the effect that changing the electron configuration of the 3d ion has on the magnetic properties, including potential single molecule magnet (SMM) behaviour in a series of compounds incorporating the highly anisotropic DyIII ion. In order to find some clear-cut ground rules, the system should be poised in such a way that the appearance of SMM behaviour allows an easy identification of the “best” choice of 3d configuration to optimise the slow relaxation and therefore SMM properties. With this in mind, and stimulated by our recent work17 on {MIII2DyIII2}, M = Fe and Al, we extended our study on the high spin 3d5 (FeIII) to 3d3 (CrIII) and high spin 3d4 (MnIII), and also the yttrium diluted {Al2Dy2} analogue, {Al2Dy0.18Y1.82}. This allows us to probe the nature of the 3dIII–3dIII, 3dIII–4fIII and 4fIII–4fIII interactions and the effects on SMM behaviour. We have used a combined experimental and theory approach, using detailed ab initio calculations to elucidate the observations from bulk susceptibility and magnetisation data in order to explore the cooperativity and nature of any magnetisation relaxation for the complexes 1 {Cr2Dy2}, 3 {Mn2Dy2}, 5 {Fe2Dy2} and 7 {Al2Dy2}.
Results and discussion
Synthetic description
Reaction of the (3d/AlIII), 4f chloride precursors, HO2CPh-Me-p and H2L in the presence of Et3N in MeOH and MeCN gives a family of isostructural tetrametallic {MIII2LnIII2} clusters. The molecules feature a butterfly core with an {MIII2} body and Ln wingtips, of formula [MIII2LnIII2(μ3-OH)2(L)2(O2CPh-Me-p)6] (M = Cr, Mn, Fe and Al, Ln = Dy and Y), based on the synthetic method for the previously reported Fe and Al analogues.17 In order to figure out the dipolar interaction effect within the {Al2Dy2}, the analogue {Al2Dy0.18Y1.82} was synthesized and magnetic properties were investigated. For the {MnIII2Ln2} analogue, the 3d chloride precursor is MnIICl2, as was the case in the synthesis of {Fe2Dy2}.17 During the crystallisation process, the FeII and MnII were oxidised to FeIII and MnIIIin situ. We found that it was necessary to reduce the amount of base for the synthesis of {Mn2Ln2} compared with the FeIII analogue. MIIICl3 was used to synthesise the Cr and Al compounds with the synthesis for the Cr compound being the same as we reported for the Al compound.17Crystal structures
Compounds 1 {Cr2Dy2}, 2 {Cr2Y2} and 8 {Al2Dy0.18Y1.82} crystallise isomorphously in C2/c with formulae [CrIII2LnIII2(μ3-OH)2(L)2(O2CPh-Me-p)6]·2MeCN (1 and 2) [AlIII2DyIII0.18Y1.82(μ3-OH)2(L)2(O2CPh-Me-p)6]·2MeCN (8) respectively. The structures are also isomorphous with the previously reported {Al2Dy2} compound. Compounds 3 {Mn2Dy2} and 4 {Mn2Y2} are isomorphous, crystallising in P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with formula [MnIII2LnIII2(μ3-OH)2(L)2(O2CPh-Me-p)6]·2MeOH·2MCN. The refinement details are listed in Table S1, ESI.†
with formula [MnIII2LnIII2(μ3-OH)2(L)2(O2CPh-Me-p)6]·2MeOH·2MCN. The refinement details are listed in Table S1, ESI.†
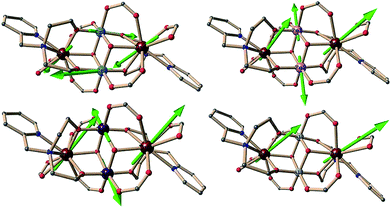
The molecular structures of the complexes are very similar in all cases and always centrosymmetric, which was also the case for the previously reported 5 {Fe2Ln2} (Fig. 1 and S1, ESI†).17 The description of 1 {Cr2Dy2} is given as representative for the description of the features of the molecular structures. The neutral cluster is composed of 2 CrIII, 2 DyIII, 2 μ3-OH, and 6p-Me-PhCOOH. All MIII ions have an octahedral O6 donor set which was established from the crystal data and through a SHAPE 2.1 analysis.18–20 The MIII ions have deviation values of 0.42, 1.37, 0.80 and 0.49 (Table 1) for complexes 1 {Cr2Dy2}, 3 {Mn2Dy2}, 5 {Fe2Dy2} and 7 {Al2Dy2}, respectively.
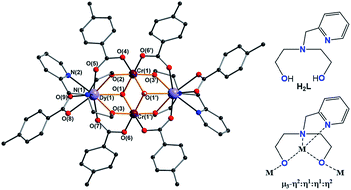 | ||
| Fig. 1 Structure of compound 1 {Cr2Dy2} (left), ligand (right upper) and coordination mode of ligand (right lower) in complexes 1, 3, 5 and 7. | ||
| MIII | 1 {Cr2Dy2} | 3 {Mn2Dy2} | 5 {Fe2Dy2} | 7 {Al2Dy2} |
|---|---|---|---|---|
| Cr | Mn | Fe | Al | |
| a HP (D6h) hexagon, PPY (C5v) pentagonal pyramid, OC (C4v) octahedron, TPR (D3h) trigonal prism, JPPY (C5v) Johnson pentagonal pyramid J2, CSAPR (C4v) spherical capped square antiprism, TCTPR (D3h) spherical tricapped trigonal prism, MFF (Cs) muffin. | ||||
| HP | 30.21 | 32.10 | 31.35 | 30.31 |
| PPY | 25.60 | 25.69 | 24.99 | 25.54 |
| OC | 0.42 | 1.37 | 0.80 | 0.49 |
| TPR | 14.09 | 11.78 | 12.01 | 13.54 |
| JPPY | 29.37 | 28.75 | 29.09 | 29.31 |
| LnIII | 1 {Cr2Dy2} | 3 {Mn2Dy2} | 5 {Fe2Dy2} | 7 {Al2Dy2} |
|---|---|---|---|---|
| Dy | Dy | Dy | Dy | |
| CSAPR | 0.94 | 1.20 | 1.00 | 1.00 |
| TCTPR | 1.43 | 1.25 | 1.22 | 1.90 |
| MFF | 1.51 | 1.67 | 1.47 | 1.44 |
The DyIII ions with an O7N2 donor set were also systematically analysed using SHAPE 2.1 software,18–20 and are best described as having a distorted spherical capped square anti-prism geometry with deviation values of 0.94, 1.20, 1.00 and 1.00 (Table 1) for complexes 1 {Cr2Dy2}, 3 {Mn2Dy2}, 5 {Fe2Dy2} and 7 {Al2Dy2}, respectively. The high spin MnIII ions in {Mn2Dy2} show an axial Jahn–Teller elongation along O4–M–O1′ with an elongated octahedral environment typical for this d4 metal ion (Mn–Oeq range = 1.894(16)–1.972(18) Å, Mn–Oax = 2.161(16)–2.206 (16) Å) (Table 2). The Y analogues were established to be isostructural from the single crystal structure analysis or, in the case of 4, from the unit cell parameters.
| 1 (CrIII) | 3 (MnIII) | 5 (FeIII) | 7 (AlIII) | |
|---|---|---|---|---|
| Dy1–O2 | 2.340 (4) | 2.3183 (18) | 2.3215 (17) | 2.3200 (15) |
| Dy1–O3 | 2.326 (4) | 2.3651 (15) | 2.3416 (16) | 2.3308 (16) |
| Dy1–O7i | 2.430 (4) | 2.4311 (18) | 2.4332 (17) | 2.4046 (16) |
| Dy1–O1 | 2.423 (4) | 2.3742 (17) | 2.3990 (17) | 2.4214 (16) |
| Dy1–O9 | 2.430 (4) | 2.5170 (19) | 2.4388 (17) | 2.4538 (16) |
| Dy1–O5 | 2.402 (5) | 2.3713 (16) | 2.4434 (17) | 2.4212 (16) |
| Dy1–O8 | 2.442 (5) | 2.3943 (18) | 2.4285 (18) | 2.4371 (17) |
| Dy1–N2 | 2.567 (5) | 2.584 (2) | 2.566 (2) | 2.5640 (19) |
| Dy1–N1 | 2.582 (5) | 2.628 (2) | 2.618 (2) | 2.602 (2) |
| M1–M1i | 3.0659 (2) | 3.286 (1) | 3.211 (0) | 3.024 (1) |
| Dy1–M1i | 3.4317 (11) | 3.376 (1) | 3.450 (1) | 3.386 (1) |
| Dy1–M1 | 3.4404 (11) | 3.467 (1) | 3.444 (1) | 3.383 (1) |
| M1–O2 | 1.963 (4) | 1.8963 (16) | 1.9738 (17) | 1.8701 (17) |
| M1–O4i | 1.969 (4) | 2.1610 (16) | 1.9944 (17) | 1.8875 (17) |
| M1–O6 | 1.976 (4) | 1.9496 (18) | 2.0058 (17) | 1.8977 (17) |
| M1–O3 | 1.955 (4) | 1.8944 (16) | 1.9676 (17) | 1.8668 (17) |
| M1–O1 | 2.002 (4) | 1.9727 (18) | 2.0584 (17) | 1.9496 (17) |
| M1–O1i | 1.996 (4) | 2.2036 (16) | 2.0548 (16) | 1.9346 (17) |
| Dy–Dyintra | 6.150 (4) | 6.003 (2) | 6.101 (1) | 6.055 (1) |
| Dy–Dyinter | 7.7708 (5) | 10.1349 (2) | 7.951 (1) | 8.093 (2) |
| M1–O1–M1i | 100.16 (19) | 103.66 (7) | 102.65 (7) | 102.27 (8) |
| M1i–O1–Dy1 | 101.83 (19) | 98.39 (6) | 101.28 (7) | 101.44 (7) |
| M1–O1–Dy1 | 101.30 (16) | 101.55 (7) | 100.90 (6) | 100.85 (7) |
| M1–O2–Dy1 | 105.47 (17) | 106.03 (7) | 106.32 (7) | 107.29 (7) |
| M1i–O3–Dy1 | 106.62 (18) | 108.46 (7) | 106.07 (7) | 106.90 (7) |
In all cases, there are μ3-OH hydrogen bonding interactions to lattice solvent molecules but not to other molecules. Compounds 1 {Cr2Dy2} and the doped 8 {Al2(Y/Dy)2} are isomorphous to the previously reported compounds 7 {Al2Dy2} and 5 {Fe2Dy2}.17 There are reasonably strong π–π stacking interactions, with C⋯C distances down to 3.446 Å, linking the molecules into 2-D sheets. For compound 3 {Mn2Dy2}, there are similarly strong π–π interactions (shortest C⋯C 3.411 Å) linking the molecules into 1-D chains. Selected bond lengths and angles for the DyIII-containing complexes are listed in Table 2.
Magnetism
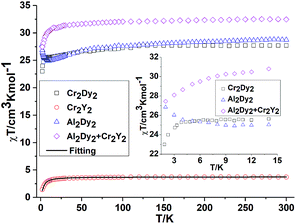
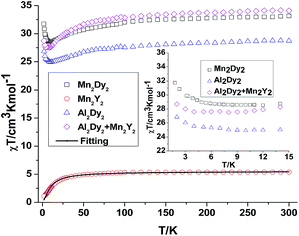
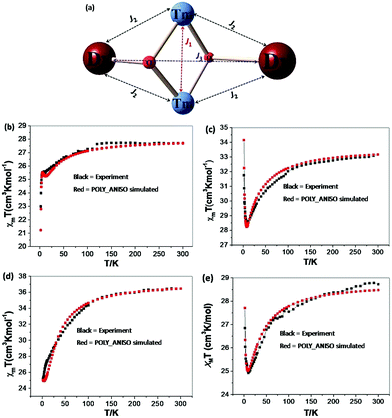
In order to understand how the paramagnetic 3dIII-metal affects the magnetic behaviour of the DyIII in the {MIII2Dy2} clusters, we also describe the yttrium diluted {Al2Dy2} compound, {Al2Dy0.18Y1.82} and the {M2Y2} examples, as we did in the previous study on {Fe2Dy2}.17 This enables us to indirectly assess the 3d–4f interactions in these examples through comparison of the χT vs. T behaviour of {M2Dy2} with the sum of the contributions for the appropriate {M2Y2} and {Al2Dy2} systems. The dc susceptibility data for all the compounds are summarised in Table S2, ESI.†
Effect of deletion of the 4f contributions in {M2Y2}. The magnetic behaviours for {M2Y2} (M = Cr, 2 and Mn, 4) are depicted in Fig. 2 and 3. The χT value for {Cr2Y2} (2) at room temperature is 3.73 cm3 K mol−1 (consistent with two uncoupled S = 3/2 CrIII ions with g = 2.0; see Table S2, ESI† and Fig. 2) decreasing only slowly until about 10 K, below which it quickly drops to 1.44 cm3 K mol−1. This suggests antiferromagnetic coupling between the CrIII ions and the fit of the χT plot of 2 {Cr2Y2} using the PHI software21 gives an antiferromagnetic coupling of JCr–Cr = −0.49 cm−1 for g = 2.0. The molar magnetisation (M) as a function of applied magnetic field at 2 K in the field range 0–7 T does not saturate but does show a value close to the expected saturation value at 7 T for compound 2 {Cr2Y2} of 6.95 μB, which is in line with the result that the exchange between these two CrIII ions is fairly weak (Fig. S2, ESI†).
For {Mn2Y2} (4), the χT value at room temperature is 5.38 cm3 K mol−1 which is lower than what is expected for two uncoupled S = 2 MnIII ions with g = 2.0 (see Table S2† and Fig. 3). The χT value decreases slowly down to about 30 K below which it decreases rapidly to reach 1.10 cm3 K mol−1 at 2 K (Fig. 3). This could be due to antiferromagnetic coupling or significant single ion anisotropy. The χT plot of 4 {Mn2Y2} was also fitted using the PHI software21 and an antiferromagnetic coupling with JMn–Mn = −1.00 cm−1 and g = 1.92 was found – i.e. about twice as strong as for the CrIII compound and in line with the fact that MnIII has four rather than three unpaired electrons. The stronger Mn–Mn AF coupling is more likely to reflect the single electron now in the 3dz2 MnIII orbital, this orbital being empty for CrIII. The Jahn–Teller axis of Mn (and thus this orbital) points towards one of the bridging OH groups, so for each Mn–OH–Mn bridge, one of the two Mn–O interactions involves a 3d orbital with an unpaired electron in it, while for Cr both the 3d orbitals are empty. The reduced magnetisation M–H plots of 4 {Mn2Y2} show a crossover feature at about 2 T (Fig. S2†), which is likely to be the result of significant anisotropy, as previously observed in a {CoII2Y2} compound.15
Inclusion of 4f contribution in {M2Dy2}. For complex 1, {Cr2Dy2}, as shown in Fig. 2, at 300 K, the experimental χT value is 27.70 cm3 K mol−1, which is much lower than the expected value of 32.09 cm3 K mol−1 for two spin-only CrIII ions (S = 3/2, g = 2, C = 1.875 cm3 K mol−1) and two DyIII ions (S = 5/2, L = 5, 6H15/2, g = 4/3, C = 14.17 cm3 K mol−1). The χT product remains almost constant over the whole temperature range, reaching a minimum value of 23.08 cm3 K mol−1 at 2 K. This behaviour is typically observed when both antiferromagnetic interactions between magnetic ions and the thermal depopulation of the DyIII excited states are operative.22,23 In order to probe the interaction between CrIII and DyIII ions in complex 1 {Cr2Dy2}, the χT vs. T curves for {Cr2Dy2} and the addition of {Al2Dy2} data to that of {Cr2Y2} in [{Al2Dy2} + {Cr2Y2}] can be compared (Fig. 2). This makes it possible to gauge any cooperative effects within the 1 {Cr2Dy2} data by seeing whether “the sum of the parts” i.e. addition of the curves for 2 {Cr2Y2} and 7 {Al2Dy2}, differs from the observed data for the actual 1 {Cr2Dy2} compound, since the {Al2Dy2} + {Cr2Y2} data effectively ‘deletes’ the contribution of the Cr–Dy interaction.
As shown in the inset of Fig. 2, the χT value at low temperature for {Cr2Dy2} is lower than the corresponding values for [{Cr2Y2} + {Al2Dy2}], indicating a contribution from antiferromagnetic coupling between the CrIII and DyIII ions.
For complex 3 {Mn2Dy2}, the room temperature χT value of 33.16 cm3 K mol−1 is in good agreement with the expected value of 33.17 cm3 K mol−1 for two uncoupled MnIII ions (S = 2, g = 2.0, C = 2.50 cm3 K mol−1) and two uncoupled DyIII ions (S = 5/2, L = 5, 6H15/2, g = 4/3, C = 14.17 cm3 K mol−1). As the temperature is lowered, the χT product gradually decreases until 15 K, below which it increases to 28.03 cm3 K mol−1 at 2 K. The decrease in χT at higher temperatures can be attributed to the depopulation of the excited states of the DyIII ions, whereas the increase at lower temperature suggests significant ferromagnetic interactions between the MnIII and DyIII ions. Modelling the 3 {Mn2Dy2} data by addition of the curves for 4 {Mn2Y2} and 7 {Al2Dy2}, as shown in the inset of Fig. 3, reveals that the interactions between MnIII and DyIII ions are ferromagnetic.
The field dependence of the magnetisation of 1 {Cr2Dy2} and 3 {Mn2Dy2} were performed at fields ranging from 0 to 7 T at 2 and 5 K. At higher fields, M increases linearly without clear saturation to ultimately reach 16.85 μB (H = 7 T, at 2 K) for 1 {Cr2Dy2} and 11.90 μB (H = 7 T, at 2 K) for 3 {Mn2Dy2}. The lack of saturation on a single master curve of M vs. H data for both complexes suggests the presence of magnetic anisotropy (Fig. S2†).
{Cr2Dy2} 1. No out-of-phase signal (χ′′) was observed even after a static dc field (Fig. S3†) was applied, indicating the absence of SMM behaviour within the measurement parameters of the SQUID.
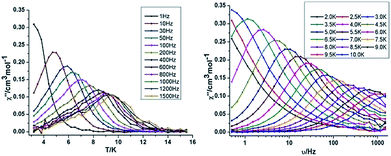
{Mn2Dy2} 3. Both the in-phase (χ′) and out-of-phase (χ′′) susceptibilities display frequency and temperature dependence, signalling the blocking of the magnetisation due to an anisotropy barrier (Fig. 4 and S4, ESI†). The χ′′ vs. ν plots were observed in fields up to 1000 Oe (Fig. S5, ESI†), further suggesting that QTM is inefficient in this system. A plot of χ′′ vs. ν isotherms (Fig. 4, lower right), reveals frequency dependent maxima down to 1.8 K. From these data, Cole–Cole plots (Fig. 5, left) were constructed and fitted to a generalized Debye model using CC-fit24 to determine α values and relaxation times (τ0) in the temperature range 1.8–2.4 K. The plots reveal relatively symmetrical semicircles, indicating a single relaxation process, with α values ranging from 0.067–0.093, indicating a narrow distribution of relaxation times within this single relaxation process. From the frequency-dependent behaviour, it was found that the relaxation follows a thermally activated mechanism from 1.8–2.4 K and plots of ln(τ) vs. 1/T are linear (Fig. 5, right). Fitting to the Arrhenius law [τ = τ0
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ueff/kBT)] afforded values of Ueff = 19.32 K and τ0 = 5.64 × 10−8 s. This result indicates a barrier to thermal relaxation, with the pre-exponential factor consistent with the expected value for an SMM of between 10−6–10−11.25 The energy barrier is comparable with that of the previously reported [NMe4]2[MnIII2DyIII2(tmp)2(O2CMe3)4(NO3)4]·2MeCN·0.5H2O26 (15 K) and [Et3NH]2[MnIII2LnIII2(μ3-O)2(O2CtBu)10] (29 K) complexes.15 The relaxation time, τ, does not become temperature independent at low temperature down to 1.8 K, indicating the absence of a pure quantum regime down to 1.8 K (when the tunnelling rate becomes faster than the activated relaxation). Upon application of a static dc field, a technique used to reduce quantum tunnelling effects, no significant shift in the maximum position of the temperature in the χ′′ vs. ν plots were observed in fields up to 1000 Oe (Fig. S5, ESI†), further suggesting that QTM is inefficient in this system.
exp(Ueff/kBT)] afforded values of Ueff = 19.32 K and τ0 = 5.64 × 10−8 s. This result indicates a barrier to thermal relaxation, with the pre-exponential factor consistent with the expected value for an SMM of between 10−6–10−11.25 The energy barrier is comparable with that of the previously reported [NMe4]2[MnIII2DyIII2(tmp)2(O2CMe3)4(NO3)4]·2MeCN·0.5H2O26 (15 K) and [Et3NH]2[MnIII2LnIII2(μ3-O)2(O2CtBu)10] (29 K) complexes.15 The relaxation time, τ, does not become temperature independent at low temperature down to 1.8 K, indicating the absence of a pure quantum regime down to 1.8 K (when the tunnelling rate becomes faster than the activated relaxation). Upon application of a static dc field, a technique used to reduce quantum tunnelling effects, no significant shift in the maximum position of the temperature in the χ′′ vs. ν plots were observed in fields up to 1000 Oe (Fig. S5, ESI†), further suggesting that QTM is inefficient in this system.
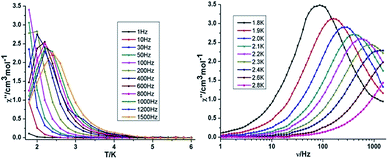 | ||
| Fig. 4 Temperature (left) and frequency (right) dependence under zero dc field of the out-of-phase (χ′′) for compound 3 {Mn2Dy2}. | ||
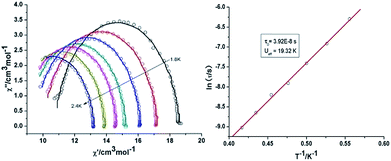 | ||
| Fig. 5 Cole–Cole plots at indicated temperature (left) and τ vs. T−1 plot in zero dc field (right) for 3 {Mn2Dy2}. | ||
{Al2Dy0.18Y1.82} 8. Under zero dc field, quantum tunnelling of the magnetisation (QTM) was observed, preventing the occurrence of clear peaks for 8 (Fig. S6, ESI†) which can be compared with the situation found for our previously reported complex 7 {Al2Dy2}17 where typical SMM behaviour could be observed without application of a dc field with Ueff = 38.7 K and τ0 = 1.06 × 10−6 s. In ref. 17, we specifically targeted the “Fe(III) knockout” for the {Fe2Dy2} compound through replacement with diamagnetic Al(III) in order to investigate the cooperativity between the Dy and Fe ions within this butterfly system. Since we were also able to investigate this system using 57Fe Mössbauer spectroscopy, we could also gauge the influence of the strongly antiferromagnetically coupled central dinuclear Fe2 unit on the uniaxial anisotropy directions of the wingtip Dy(III) ions through a consideration of the multiple hyperfine interactions which could be observed. An important conclusion from this work was the major roles played by the local magnetic fields of the ions involved. By deleting Fe(III) from the compound we could suggest that the uniaxial directions of the magnetic anisotropy on the wingtip Dy(III) ions changed orientation once the influence of the Fe(III) ions was taken away. This helps to explain the rather good SMM behaviour of the pure {Al2Dy2} compound. Now it seems that reducing the Dy(III) influence within the {Al2Dy2} system through dilution with diamagnetic Y(III) leads to a “loss of direction” for the dipolarly coupled Dy(III) ions and a breakdown in suppression of QTM for 8 {Al2Dy0.18Y1.82}. Thus, only through application of a dc field to 8 {Al2Dy0.18Y1.82} could clear peaks be observed in the out of phase (χ′′) data (Fig. S7, ESI†), indicating field-induced SMM behaviour. Since this behaviour is observed only upon application of a static field we can attribute it to suppression of the quantum tunnelling of the magnetisation between sublevels, which is very fast under zero dc field and is observed when the single 4f ion properties become important (achieved here through dilution) and the geometry of the ligand field is sub-optimal for inducing a strong uniaxial, i.e. Ising type of anisotropy. Such activity is known for many lanthanide SMMs.27–29
Temperature and frequency dependent in phase (χ′) and out of phase (χ′′) ac measurements were performed using an applied dc field of 1000 Oe (Fig. 6 and S8, ESI†). This field was chosen to allow for comparisons with previously reported systems. A fitting of the data extracted from the frequency dependent out of phase (χ′′) signals using the Arrhenius equation (τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ueff/kBT)) gives an energy barrier of Ueff = 69.26 K and pre-exponential factor of τ0 = 1.18 × 10−7 s (Fig. S9, ESI†). Cole–Cole plots (χ′′ vs. χ′) for the temperature range 3.5–9.0 K (Fig. S9, ESI†) can be fitted for a single relaxation process using the Debye model to give α parameters in the range 0.14–0.28, indicating a wider distribution of relaxation times than seen for the non-diluted compound 7 {Al2Dy2}. This result indicates that the dipolar interaction between the two distant wingtip DyIII ions plays a key role in suppressing the QTM.30 The comparison data are summarized in Table 3.
exp(Ueff/kBT)) gives an energy barrier of Ueff = 69.26 K and pre-exponential factor of τ0 = 1.18 × 10−7 s (Fig. S9, ESI†). Cole–Cole plots (χ′′ vs. χ′) for the temperature range 3.5–9.0 K (Fig. S9, ESI†) can be fitted for a single relaxation process using the Debye model to give α parameters in the range 0.14–0.28, indicating a wider distribution of relaxation times than seen for the non-diluted compound 7 {Al2Dy2}. This result indicates that the dipolar interaction between the two distant wingtip DyIII ions plays a key role in suppressing the QTM.30 The comparison data are summarized in Table 3.
 | ||
| Fig. 6 Temperature (left) and frequency (right) dependence under 1000 Oe dc field of the out-of-phase (χ′′) for compound 8 {Al2Dy0.18Y1.82}. | ||
| 3d–3d | 3d–Dy | Dy–Dy | SMMs (field/Oe) | |
|---|---|---|---|---|
| 1 {Cr2Dy2} | AF | AF | F | No |
| 3 {Mn2Dy2} | AF | F | F | Yes (0) |
| 5 {Fe2Dy2} | AF | AF | F | Yes (1000) |
| 7 {Al2Dy2} | — | — | F | Yes (0) |
| 8 {Al2Dy0.18Y1.82} | — | — | F | Yes (1000) |
The energy gap between the ground to first-excited state KDs is found to be 27.0 cm−1 (33.9 cm−1), 50.2 cm−1 (50.2 cm−1), 39.9 cm−1 (44.0 cm−1), 47.0 cm−1 (43.5 cm−1), for Dy1 (Dy2) in complexes 1 {Cr2Dy2}, 3 {Mn2Dy2}, 5 {Fe2Dy2} and 7 {Al2Dy2} respectively (see Table 4). For complex 3 {Mn2Dy2}, both Dy1 and Dy2 are equivalent and therefore the ground to first excited state gap and the g-anisotropies are the same while in other cases, both the anisotropy and the gaps are different for the Dy1 and Dy2 ions. In particular, the ground to first excited state energy gaps are significantly larger for complexes 3 {Mn2Dy2} and 7 {Al2Dy2}, while it is computed to be slightly smaller for complex 5 {Fe2Dy2} (Dy1) and much smaller for complex 1 {Cr2Dy2}. Since the energy gap is correlated to the crystal-field splitting energy, this suggests relatively weaker splitting of the mJ levels in 1 {Cr2Dy2} compared to complexes 3 {Mn2Dy2}, 5 {Fe2Dy2} and 7 {Al2Dy2}.
| Dy1 | E KD1 − EKD2 (cm−1) | Angle | Dy2 | E KD1 − EKD2 (cm−1) | Angle | ||
|---|---|---|---|---|---|---|---|
| 1 {Cr2Dy2} | g x1/ g x2 | 0.28/0.22 | 27.0 | 21.8 | 0.18/0.10 | 33.9 | 20.4 |
| g y1/ g y2 | 0.47/0.45 | 0.30/0.26 | |||||
| g z1/ g z2 | 18.13/18.10 | 18.67/17.90 | |||||
| 3 {Mn2Dy2} | g x1/ g x2 | 0.13/1.78 | 50.2 | 52.1 | 0.13/1.78 | 50.2 | 52.2 |
| g y1/ g y2 | 0.36/5.93 | 0.36/5.92 | |||||
| g z1/ g z2 | 19.35/12.16 | 19.34/12.16 | |||||
| 5 {Fe2Dy2} | g x1/ g x2 | 0.25/1.26 | 39.9 | 25.4 | 0.18/0.88 | 44.0 | 17.3 |
| g y1/ g y2 | 0.47/1.40 | 0.35/0.97 | |||||
| g z1/ g z2 | 18.01/15.18 | 18.09/15.79 | |||||
| 7 {Al2Dy2} | g x1/ g x2 | 0.00/1.02 | 47.0 | 35.9 | 0.00/0.70 | 43.5 | 28.3 |
| g y1/ g y2 | 0.00/1.62 | 0.00/0.98 | |||||
| g z1/ g z2 | 19.05/16.56 | 19.00/16.98 | |||||
SHAPE 2.1 analysis18–20 yields a DyMn > DyFe ∼ DyAl > DyCr trend for the distortion of DyIII ions with respect to the idealised spherical-capped square anti-prismatic geometry and this trend matches with the computed energy gap between ground to first excited state.
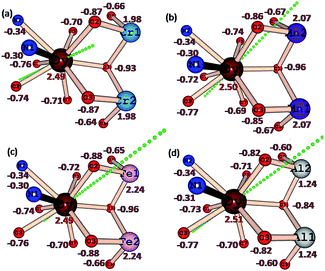
The LoProp computed charges38 obtained from CASSCF calculations for complexes 1 {Cr2Dy2}, 3 {Mn2Dy2}, 5 {Fe2Dy2} and 7 {Al2Dy2} are shown in Fig. 8. For the DyIII ion, the oblate anisotropy ellipsoid means that the density is expected to lie along the plane with the least repulsion. The charge on the μ-alkoxo and μ3-OH are found to be very large in all four cases as they are connected to the trication which tend to polarise the oxygen atom charges significantly. Thus the oblate density lies perpendicular to this direction and the gzz axis lies along the O–Dy–O direction where the oxygen atoms possess the largest negative charges39,40 In complex 1 {Cr2Dy2}, the gzz axis lies in the direction defined by the oxygen atom of one of the carboxylates and the μ-alkoxo oxygen connected to the CrIII ion. While this is found to be similar for complexes 1 {Cr2Dy2}, 3 {Mn2Dy2}, 5 {Fe2Dy2} and 7 {Al2Dy2}, clearly there are structural variations. For example, the Cr–O (alkoxo) bridging distance is 1.963(4) Å, while in complex 3 {Mn2Dy2}, the Mn–O distance is much shorter (1.896(16) Å) in line with the Jahn–Teller distortion. A shorter bond distance is expected to lead to a greater polarisability of the oxygen and resulting the gzz aligning closest to the μ-alkoxo oxygen with a deviation of only 18°.This is much smaller compared to the case in complex 1 {Cr2Dy2} (25°). This significant variation in the orientation of the gzz axis caused by the electronic structure of the trication at the body of the butterfly apparently leads to the variation in the ground-state to excited-state gaps. A similar scenario is noted also for complexes 5 {Fe2Dy2} and 7 {Al2Dy2}, where the ground state gzz axis is found to align along the μ-alkoxo oxygen atom (with deviations of 18.5° for 5 {Fe2Dy2} and 15.4° for complex 7 {Al2Dy2}). Another important result from the analysis of the charges concerns the charge found at the equatorial position of the DyIII ion, as this is reflected in the transverse anisotropy. For complex 7 {Al2Dy2}, significant reduction of charge on the μ3-OH group lying in the equatorial plane is noted and this leads to a drastic reduction of transverse anisotropy at −0.84 in 7 {Al2Dy2} rather than −0.93 in 1 {Cr2Dy2} or −0.96 in 3 {Mn2Dy2} and 5 {Fe2Dy2}.
In all the complexes, mJ = ±15/2 is found to be stabilized as the ground state (see Fig. S10, ESI†). This can be attributed to the stronger axial interactions compared to transverse interactions. However, significant transverse anisotropy is present for the ground state KD of complexes 1 {Cr2Dy2} and 5 {Fe2Dy2} gxx = 0.28/0.18, gyy = 0.47/0.30, gzz = 18.13/18.67 for Dy1/Dy2 of complex 1 {Cr2Dy2} and gxx = 0.25/0.18, gyy = 0.47/0.35, gzz = 18.01/18.09 for Dy1/Dy2 of complex 5 {Fe2Dy2} (Table 4), as a result of the strong mixing of the mJ = ±15/2, ±13/2, ±11/2 and ±9/2 states (see Fig. S10, ESI†). The transverse components for both the complexes are found to be larger for Dy1, and the effect on the measured χT values for both compounds, and in particular for the {Cr2Dy2} one, is a substantial decrease in the value expected considering the summation of the Y and Al analogues with the deleted 4f/3d contributions respectively. This at first sight surprising reduction in the χT value has also been observed for a recently reported {Cr2Dy3} system41 where this was attributed to the changes in the anisotropies of the Dy(III) ions. It should also be noted that the magnetisation plots for the {Cr2Y2} compound indicate that the contribution of the coupled Cr(III) ions is far from isotropic in nature.
In complexes 3 {Mn2Dy2} and 7 {Al2Dy2}, the mixing of KD1 with KD2 is relatively smaller compared to the two complexes 1 {Cr2Dy2} and 5 {Fe2Dy2} because of the larger energy separation between them. Significant axial anisotropy is present for the ground state KD of complex 3 {Mn2Dy2}. A clear Ising nature is observed for the DyIII ions in complex 3 {Mn2Dy2} (gxx = 0.13/0.13, gyy = 0.36/0.36, gzz = 19.35/19.34 for Dy1/Dy2) and even more markedly in complex 7 {Al2Dy2} (gxx = 0.00/0.00, gyy = 0.00/0.00, gzz = 19.05/19.00 for Dy1/Dy2) see Table 4.
To analyse the various possible relaxation processes associated with the single-ion DyIII anisotropy, the mechanisms of the magnetic relaxation were computed and these are shown in Fig. S10, ESI.†
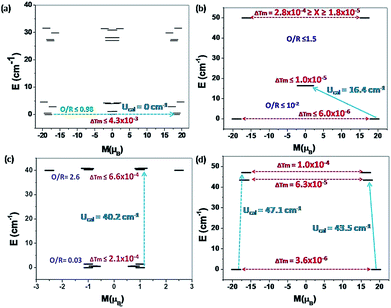
In complexes 1 {Cr2Dy2} and 5 {Fe2Dy2}, the ground state tunnelling probability is large for the Dy1 ion (1.2 × 10−1μB). For the Dy ions in the other compounds, the ground state tunnelling probability is found to be smaller (5.0 × 10−2 to 8.8 × 10−2μB). In complexes 1 {Cr2Dy2} and 5 {Fe2Dy2}, the tunnelling probability at the single ion level in the ground state is larger than in 3 {Mn2Dy2} and 7 {Al2Dy2} and the calculations predict the absence of SMM behaviour. This is in accord with the experimental measurements. If we consider relaxation processes beyond those of the single-ion, then factors such as DyIII–DyIII exchange coupling may play a role in quenching the observed QTM. Therefore, the DyIII–DyIII, DyIII–3dIII and 3dIII–3dIII exchange couplings were taken into account using the POLY_ANISO suite. These gave the 3dIII single ion isotropic g-tensors (see Table S3 in ESI†) which have values too small to significantly influence the magnetic anisotropy of the DyIII centres apart from for complex 3 {Mn2Dy2} where the single-ion zero-field splitting, D, values of the MnIII ions are relatively large at −3.35 cm−1, see Table S3 in ESI.†
 | (1) |
| Complex | J values (Lines model) | J 1 (DFT) | ||||
|---|---|---|---|---|---|---|
| J 1 | J 2 | J 3 | zJ | |||
| 1 {Cr2Dy2} | J Tot | −0.65 | −1.15 | 0.405 | −0.045 | −0.81 |
| J Exc | −0.50 | −0.80 | 0.370 | |||
| J Dip | −0.15 | −0.35 | 0.035 | |||
| 3 {Mn2Dy2} | J Tot | −3.20 | 0.15 | 0.035 | — | −2.10 |
| J Exc | −2.10 | 0.09 | −0.001 | |||
| J Dip | −1.10 | 0.06 | 0.036 | |||
| 5 {Fe2Dy2} | J Tot | −4.20 | −0.12 | 0.060 | — | −4.92 |
| J Exc | −3.00 | −0.05 | 0.025 | |||
| J Dip | −1.20 | −0.07 | 0.035 | |||
| 7 {Al2Dy2} | J Tot | — | — | 0.049 | — | — |
| J Exc | — | — | 0.025 | |||
| J Dip | — | — | 0.024 | |||
For complexes 1 {Cr2Dy2}, 3 {Mn2Dy2} and 5 {Fe2Dy2}, magnetic interactions between the transition metals (J1) are found to be antiferromagnetic in nature with complex 5 {Fe2Dy2} having the largest magnitude of J1 followed by complex 3 {Mn2Dy2} and complex 1 {Cr2Dy2}. To ascertain the J1 values independently, DFT calculations were performed on {Cr2La2} and {Mn2La2} models and these values reproduce the sign as well as the magnitude trend for the J1 interaction. For complexes 1 {Cr2Dy2} and 5 {Fe2Dy2}, the magnetic interaction between Dy–3dIII (J2) is found to be antiferromagnetic whereas for complex 3 {Mn2Dy2}, it is found to be ferromagnetic in nature. All these values are in accord with the earlier literature reports.40,42 The weak CrIII–CrIII (J1) interaction in complex 1 {Cr2Dy2} causes the relaxation to occur via the ground state with very high QTM probability.
For complexes 1 {Cr2Dy2} and 5 {Fe2Dy2}, the tunnelling (Δtun) parameters of the exchange coupled ground state are computed to be large (≤4.3 × 10−3 and ≤2.1 × 10−4 respectively, see Fig. 10a and c respectively, see Fig. S11 in ESI† for low lying exchange spectra for complexes 1 {Cr2Dy2}, 3 {Mn2Dy2}, 5 {Fe2Dy2} and 7 {Al2Dy2}), whereas for complexes 3 {Mn2Dy2} (6.0 × 10−6, see Fig. 10b) and 7 {Al2Dy2} (3.6 × 10−6, see Fig. 10d) the same is computed to be very small. Thus in complex 1 {Cr2Dy2}, the magnetic relaxation occurs via the ground state. In complex 3 {Mn2Dy2}, the first excited state possesses relatively high tunnel splitting (Δtun = 1.0 × 10−5 cm−1) suggesting relaxation via the first excited state with Ucal value of 16.4 cm−1 (see Fig. 10b). This picture is consistent with the experimental data where a relaxation process is observed with a barrier height of 13.5 cm−1 (Ueff). For complex 5 {Fe2Dy2}, the tunnelling probability of the exchange coupled ground state is found to be large which suggests a possible relaxation pathway via the ground state.
Other excited states are found to be below 1.3 cm−1 so applying an external magnetic field can overcome this energy barrier and relaxation can occur through the next higher excited state with a barrier height of 40.2 cm−1. This picture is consistent with the experimental data, where in the presence of an external magnetic field relaxation occurs through an excited state with a barrier height of 11.3 cm−1 (Ueff). Since the tunnelling probability is high, one can expect a reduction in the Ueff value compare to the Ucal value, where this probability is not taken in to consideration.
For complex 7 {Al2Dy2}, the tunnelling probability of the exchange coupled ground state is almost negligible (Δtun = 3.6 × 10−6). This places the estimate of Ucal for this molecule as 43.5 cm−1 and relaxation via the exchange coupled first excited state (Δtun = 6.3 × 10−5, see Fig. 10d). This picture is consistent with the experimental data where in absence of an external field relaxation occurs with a barrier height of 26.9 cm−1.
It is important to note here that there are some deviations in the experimental and theoretically estimated barrier heights. This is essentially due to the fact that our relaxation mechanism has not factored other possibilities such as intermolecular interaction, hyperfine coupling of the metal ions/nitrogen atoms etc., that are likely to contribute the overall relaxation process and thus this difference between Ueff and Ucal is inevitable.
Conclusions
Five new butterfly complexes: [MIII2LnIII2(μ3-OH)2(p-Me-PhCO2)6(L)2] (H2L = 2,2′-((pyridin-2-ylmethyl)azanediyl)bis(ethan-1-ol), M = Cr, Ln = Dy (1) or Y (2), M = Mn, Ln = Dy (3) or Y (4)) and the diluted complex [AlIII2DyIII2]:[AlIII2DyIII0.18Y1.82(μ3-OH)2(p-Me-PhCO2)6(L)2] 8 have been synthesised, characterised and their magnetic slow relaxation properties investigated. This has allowed us to set these compounds into the context of the properties of our previously reported {FeIII2LnIII2}, Ln = Dy 5 or Y 6 and {AlIII2DyIII2} 7 analogues. The nature of the 3d metal ion sitting at the body positions of the butterfly motif steers the slow magnetic relaxation properties of the whole molecule by “tempering” the relaxation of the wingtip Dy ions. This is the first systematic study on changing the nature of the 3dIII body ions from Cr(d3), Mn(d4), Fe(d5) and diamagnetic AlIII within this motif.Ac susceptibility measurements indicate no SMM behaviour was observed for any of the analogues using diamagnetic yttrium at the wingtips instead of Dy. This reveals that the SMM behaviour is intrinsic to the presence of the DyIII ions. Furthermore, for the {Al2Dy2} analogue, the weak (+0.049 cm−1) dipolar interaction between the two far away DyIII ions plays a key role in suppressing the zero-field QTM of the individual DyIII ions as revealed by this compound showing SMM behaviour under zero dc field. Thus the weak but key cooperative interaction plays a significant role for the performance of the system in terms of the dynamic and thus SMM behaviour. Changing from Cr to Mn in the {MIII2LnIII2} motif, the anisotropy of the DyIII ion can be utilised to improve the performance of the SMM through tuning the suppression (quenching) of the QTM processes of the DyIII ions. The SMM behaviour for the four complexes follows the trend, {Al2Dy2} > {Mn2Dy2} > {Fe2Dy2} > {Cr2Dy2}. Ab initio calculations performed on all DyIII-containing molecules reveal similar results. It is clear that the strength and maybe the sign of the 3d–4f exchange interaction plays a key role in directing the nature of the SMM properties observed.
Experimental
General information
All chemicals and solvents used for synthesis were obtained from commercial sources and used as received without further purification. All reactions were carried out under aerobic conditions. N-(2-Pyridylmethyl)iminodiethanol was prepared according to the literature procedure.43 The elemental analyses (C, H, and N) were carried out using an Elementar Vario EL analyser. Fourier transform IR spectra (4000 to 400 cm−1) were measured on a PerkinElmer Spectrum GX spectrometer with samples prepared as KBr discs. Powder X-ray diffraction was carried out on a STOE STADI-P diffractometer, using Cu-Kα radiation with λ = 1.5406 Å.[CrIII2Dy2(μ3-OH)2(L)2(p-Me-PhCO2)6]·2MeCN (1)
H2L (100 mg, 0.5 mmol) in MeCN (5 ml) was added to a solution of CrCl3·6H2O (66 mg, 0.25 mmol), DyCl3·6H2O (94 mg, 0.25 mmol) and 4-methylbenzoic acid (136 mg, 1 mmol) in a mixture of MeCN (20 ml) and MeOH (5 ml). After 10 min of stirring, Et3N (0.42 ml, 3 mmol) was added, leaving the solution stirring for a further 1 min. The final solution was filtered and left undisturbed. After three days, pale green crystals suitable for X-ray analysis were collected and air dried. Yield: 50% (145.4 mg, based on 4-methylbenzoic acid). Anal. calcd for Cr2Dy2C68H72N4O18·2MeCN: C, 49.57; H, 4.51; N, 4.82. Found: C, 49.44; H, 4.37; N, 5.02. Selected IR data (KBr, cm−1) for 1: 3493 (br), 3062 (w), 2978 (w), 2856 (m), 1595 (s), 1542 (s), 1097 (s), 908 (s), 719 (s), 673 (s), 593 (s).[CrIII2Y2(μ3-OH)2(L)2(p-Me-PhCO2)6]·2MeCN (2)
The same reaction conditions as used for compound 1, substituting DyCl3·6H2O with YCl3·6H2O produced compound 2. Yield: 55% (based on 4-methylbenzoic acid). Cr2Y2C68H72N4O18·2MeCN: C, 54.14; H, 4.92; N, 5.26. Found: C, 54.24; H, 4.87; N, 5.00. The IR spectrum is similar to that of compound 1.[MnIII2Dy2(μ3-OH)2(L)2(p-Me-PhCO2)6]·2MeCN·2MeOH (3)
The same reaction conditions used for compound 1 replacing CrCl3·6H2O with MnCl2·4H2O and halving the amount of Et3N produced compound 3. Yield: 61% (187.5 mg, based on 4-methylbenzoic acid). Anal. calcd for Mn2Dy2C68H72N4O18·2MeCN (lose two MeOH): C, 49.41; H, 4.49; N, 4.80. Found: C, 49.29; H, 4.51; N, 4.59. Selected IR data (KBr, cm−1) for 3: 3503 (br), 3058 (w), 2975 (w), 2854 (m), 1593 (s), 1541 (s), 1099 (s), 906 (s), 722 (s), 672 (s), 593 (s).[MnIII2Y2(μ3-O)2(L)2(p-Me-PhCO2)6]·2MeCN·2MeOH (4)
The same reaction conditions as used for compound 3 replacing DyCl3·6H2O with YCl3·6H2O produced compound 4. Mn2Y2C68H72N4O18·2MeCN (with the loss of two MeOH): C, 53.94; H, 4.90; N, 5.24. Found: C, 53.79; H, 4.91; N, 5.30. The IR spectrum is similar to that of compound 4.[AlIII2Dy0.18Y1.82(μ3-OH)2(L)2(p-Me-PhCO2)6]·2MeCN (8)
H2L (100 mg, 0.5 mmol) in MeCN (5 ml) was added to a solution of AlCl3·6H2O (66 mg, 0.25 mmol), DyCl3·6H2O (9.4 mg, 0.025 mmol), YCl3·6H2O (68.3 mg, 0.225 mmol) and 4-methylbenzoic acid (136 mg, 1 mmol) in a mixture of MeCN (20 ml) and MeOH (5 ml). After 10 min of stirring, NEt3 (0.42 ml, 3 mmol) was added and the solution stirred for a further 1 min. The final solution was filtered and left undisturbed. After three days, white crystals suitable for X-ray analysis were collected and air dried. Yield: 45.1% (101.2 mg, based on 4-methylbenzoic acid). Al2Dy0.18Y1.82C68H72N4O18·2MeCN: C, 55.42; H, 5.04; N, 5.39. Found: C, 55.59; H, 4.97; N, 5.20. The IR is similar to that of the reported 7 {Al2Dy2}.Magnetic measurements
The magnetic susceptibility measurements were obtained using a Quantum Design SQUID magnetometer MPMS-XL in the temperature range 1.8–300 K. Measurements were performed on polycrystalline samples restrained in eicosane and placed in sealed plastic bags. Magnetisation isotherms were collected at 2, 5 K between 0 and 7 T. Alternating current (ac) susceptibility measurements were performed with an oscillating field of 3 Oe and ac frequencies ranging from 0.05 to 1500 Hz. The magnetic data were corrected for the sample holder and the diamagnetic contribution.X-ray analysis
The X-ray data were collected on an Oxford Diffraction Supernova E diffractometer, using Mo-Kα radiation (λ = 0.71073 Å) from a microfocus source. Structures were solved by dual-space direct methods using SHELXT44 and refined against Fo2 using SHELXL-2014![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 with anisotropic displacement parameters for all non-hydrogen atoms. Organic hydrogen atoms were placed in calculated positions; the coordinates of H(1) were refined. Crystallographic data (excluding structure factors) for the structures in this paper have been deposited with the Cambridge Crystallographic Data Centre as supplementary publication nos.†
45 with anisotropic displacement parameters for all non-hydrogen atoms. Organic hydrogen atoms were placed in calculated positions; the coordinates of H(1) were refined. Crystallographic data (excluding structure factors) for the structures in this paper have been deposited with the Cambridge Crystallographic Data Centre as supplementary publication nos.†
Computational details
We performed ab initio CASSCF31 + RASSI-SO32 + SINGLE_ANISO33–36 calculations on all paramagnetic ions using the single crystal structure data in MOLCAS 8.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46–50 suite by substituting all the paramagnetic ions with diamagnetic ions (LaIII/ScIII) except for the one of interest as attempted earlier by keeping other parts unchanged. We used the [C.ANO-RCC…3s2p], [N.ANO-RCC…3s2p1d], [O.ANO-RCC…3s2p1d], [H.ANO-RCC…2s], [Al.ANO-RCC…4s3p1d], [Sc.ANO-RCC…5s4p2d1f], [Fe.ANO-RCC…5s4p2d1f], [Cr.ANO-RCC…5s4p2d1f], [Mn.ANO-RCC…5s4p2d1f], [Lu.ANO-RCC…7s6p4d2f1g] and [Dy.ANO-RCC…8s7p5d3f2g1h] basis set for our ab initio calculations.51 For our CASSCF calculations on Dy-mononuclear fragment, nine electrons in seven active 4f orbitals were considered. Further, here in the RASSI-SO step, 21 roots for sextet spin multiplicity were considered.52 For the Cr-mononuclear fragment, the active space of the CASSCF method was constructed considering three electrons in five active 3d orbitals with 10 and 40 roots for quadruplet and doublet spin multiplicities respectively. For the Mn-mononuclear fragment, the active space of the CASSCF method was constructed considering four electrons in five active 3d orbitals. Further, here in the RASSI-SO step, we considered only 5 and 35 roots for pentet and triplet spin multiplicities respectively. For the Fe-mononuclear fragment, five electrons in five active 3d orbitals are considered. For the next RASSI-SO step we only considered 1 and 17 roots for sextet and quadruplet spin multiplicities respectively.33–36 The resultant spin–orbit multiplet has been further used to compute local magnetic properties via SINGLE_ANISO approach. The magnetic exchange interactions (Js) have been computed between all paramagnetic ions for all complexes by fitting ab initio POLY_ANISO with the experimental data.37
46–50 suite by substituting all the paramagnetic ions with diamagnetic ions (LaIII/ScIII) except for the one of interest as attempted earlier by keeping other parts unchanged. We used the [C.ANO-RCC…3s2p], [N.ANO-RCC…3s2p1d], [O.ANO-RCC…3s2p1d], [H.ANO-RCC…2s], [Al.ANO-RCC…4s3p1d], [Sc.ANO-RCC…5s4p2d1f], [Fe.ANO-RCC…5s4p2d1f], [Cr.ANO-RCC…5s4p2d1f], [Mn.ANO-RCC…5s4p2d1f], [Lu.ANO-RCC…7s6p4d2f1g] and [Dy.ANO-RCC…8s7p5d3f2g1h] basis set for our ab initio calculations.51 For our CASSCF calculations on Dy-mononuclear fragment, nine electrons in seven active 4f orbitals were considered. Further, here in the RASSI-SO step, 21 roots for sextet spin multiplicity were considered.52 For the Cr-mononuclear fragment, the active space of the CASSCF method was constructed considering three electrons in five active 3d orbitals with 10 and 40 roots for quadruplet and doublet spin multiplicities respectively. For the Mn-mononuclear fragment, the active space of the CASSCF method was constructed considering four electrons in five active 3d orbitals. Further, here in the RASSI-SO step, we considered only 5 and 35 roots for pentet and triplet spin multiplicities respectively. For the Fe-mononuclear fragment, five electrons in five active 3d orbitals are considered. For the next RASSI-SO step we only considered 1 and 17 roots for sextet and quadruplet spin multiplicities respectively.33–36 The resultant spin–orbit multiplet has been further used to compute local magnetic properties via SINGLE_ANISO approach. The magnetic exchange interactions (Js) have been computed between all paramagnetic ions for all complexes by fitting ab initio POLY_ANISO with the experimental data.37
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding through the TRR/SFB 88 “3MET” is gratefully acknowledged as is support via the Helmholtz Foundation POF STN (Y. P., C. E. A. and A. K. P.). G. R. thanks the SERB (CRG/2018/000430) and AvH Foundation for funding. M. K. S. thanks UGC-India and IIT Bombay for a fellowship.Notes and references
- C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369–2387 CrossRef CAS.
- R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328–2341 CrossRef CAS.
- J. S. Miller and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3076–3091 RSC.
- L. Rosado Piquer and E. C. Sañudo, Dalton Trans., 2015, 44, 8771–8780 RSC.
- D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224–1225 CrossRef CAS PubMed.
- N. Ishikawa, Polyhedron, 2007, 26, 2147–2153 CrossRef CAS.
- J. L. Liu, Y. C. Chen, Y. Z. Zheng, W. Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. L. Tong, Chem. Sci., 2013, 4, 3310–3316 RSC.
- N. E. Chakov, M. Soler, W. Wernsdorfer, K. A. Abboud and G. Christou, Inorg. Chem., 2005, 44, 5304–5321 CrossRef CAS PubMed.
- P. King, W. Wernsdorfer, K. A. Abboud and G. Christou, Inorg. Chem., 2005, 44, 8659–8669 CrossRef CAS PubMed.
- F. Pointillart, K. Bernot, R. Sessoli and D. Gatteschi, Chem.–Eur. J., 2007, 13, 1602–1609 CrossRef PubMed.
- J. L. Liu, J. Y. Wu, Y. C. Chen, V. Mereacre, A. K. Powell, L. Ungur, L. F. Chibotaru, X. M. Chen and M. L. Tong, Angew. Chem., Int. Ed., 2014, 53, 12966–12970 CrossRef CAS PubMed.
- S. K. Langley, D. P. Wielechowski, N. F. Chilton, B. Moubaraki and K. S. Murray, Inorg. Chem., 2015, 54, 10497–10503 CrossRef CAS PubMed.
- B. Moubaraki, S. K. Langley, C. Le, B. F. Abrahams, L. F. Chibotaru, L. Ungur and K. S. Murray, Inorg. Chem., 2015, 54, 3631–3642 CrossRef.
- S. K. Langley, D. P. Wielechowski, B. Moubaraki and K. S. Murray, Chem. Commun., 2016, 52, 10976–10979 RSC.
- E. Moreno-Pineda, N. F. Chilton, F. Tuna, R. E. P. Winpenny and E. J. L. McInnes, Inorg. Chem., 2015, 54, 5930–5941 CrossRef CAS PubMed.
- A. Baniodeh, Y. Lan, G. Novitchi, V. Mereacre, A. Sukhanov, M. Ferbinteanu, V. Voronkova, C. E. Anson and A. K. Powell, Dalton Trans., 2013, 42, 8926–8938 RSC.
- Y. Peng, V. Mereacre, C. E. Anson and A. K. Powell, Phys. Chem. Chem. Phys., 2016, 18, 21469–21480 RSC.
- D. Casanova, P. Alemany, J. M. Bofill and S. Alvarez, Chem.–Eur. J., 2003, 9, 1281–1295 CrossRef CAS PubMed.
- S. Alvarez, D. Avnir, M. Llunell and M. Pinsky, New J. Chem., 2002, 26, 996–1009 RSC.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- M. L. Kahn, J. P. Sutter, S. Golhen, P. Guionneau, L. Ouahab, O. Kahn and D. Chasseau, J. Am. Chem. Soc., 2000, 122, 3413–3421 CrossRef CAS.
- M. L. Kahn, R. Ballou, P. Porcher, O. Kahn and J. Sutter, Chem.–Eur. J., 2002, 8, 525–531 CrossRef CAS.
- http://www.nfchilton.com/phi.html .
- D. Gattenschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford, New York, 2006 Search PubMed.
- A. Mishra, W. Wernsdorfer, S. Parsons, G. Christou and E. K. Brechin, Chem. Commun., 2005, 2086–2088 RSC.
- A. Yamashita, A. Watanabe, S. Akine, T. Nabeshima, M. Nakano, T. Yamamura and T. Kajiwara, Angew. Chem., Int. Ed., 2011, 50, 4016–4019 CrossRef CAS PubMed.
- H. L. C. Feltham, R. Clérac, L. Ungur, L. F. Chibotaru, A. K. Powell and S. Brooker, Inorg. Chem., 2013, 52, 3236–3240 CrossRef CAS PubMed.
- H. L. C. Feltham, F. Klöwer, S. A. Cameron, D. S. Larsen, Y. Lan, M. Tropiano, S. Faulkner, A. K. Powell and S. Brooker, Dalton Trans., 2011, 40, 11425–11432 RSC.
- E. Moreno-Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S. D. Jiang, D. Collison, J. Van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 1–7 Search PubMed.
- B. Swerts, L. F. Chibotaru, R. Lindh, L. Seijo, Z. Barandiaran, S. Clima, K. Pierloot and M. F. A. Hendrickx, J. Chem. Theory Comput., 2008, 4, 586–594 CrossRef CAS PubMed.
- P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- L. F. Chibotaru, A. Ceulemans and H. Bolvin, Phys. Rev. Lett., 2008, 101, 4–7 CrossRef.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112–064122 CrossRef CAS PubMed.
- L. F. Chibotaru and L. Ungur, Program SINGLE_ANISO, KU Leuven, Leuven, Belgium, 2006 Search PubMed.
- L. Ungur and L. F. Chibotaru, http://www.molcas.org/documentation/manual/node105.html.
- L. F. Chibotaru and L. Ungur, Program POLY_ANISO, KU Leuven, Leuven, Belgium, 2007 Search PubMed.
- L. Gagliardi, R. Lindh and G. Karlström, J. Chem. Phys., 2004, 121, 4494–4500 CrossRef CAS PubMed.
- K. R. Vignesh, S. K. Langley, K. S. Murray and G. Rajaraman, Inorg. Chem., 2017, 56, 2518–2532 CrossRef CAS PubMed.
- T. Gupta and G. Rajaraman, Chem. Commun., 2016, 52, 8972–9008 RSC.
- X.-Q. Zhao, S. Xiang, J. Wang, D.-X. Bao and Y.-C. Li, ChemistryOpen, 2018, 7, 192–200 CrossRef CAS PubMed.
- A. Chakraborty, J. Goura, P. Kalita, A. Swain, G. Rajaraman and V. Chandrasekhar, Dalton Trans., 2018, 47, 8841–8864 RSC.
- K. Sundaravel, M. Sankaralingam, E. Suresh and M. Palaniandavar, Dalton Trans., 2011, 40, 8444–8458 RSC.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- J. A. Duncan, J. Am. Chem. Soc., 2009, 131, 2416 CrossRef CAS PubMed.
- V. Veryazov, P. O. Widmark, L. Serrano-Andrés, R. Lindh and B. O. Roos, Int. J. Quantum Chem., 2004, 100, 626–635 CrossRef CAS.
- G. Karlström, R. Lindh, P. Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P. O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239 CrossRef.
- F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, M. Reiher, B. O. Roos, L. Serrano- Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–227 CrossRef CAS PubMed.
- B. O. Roos, R. Lindh, P. Å. Malmqvist, V. Veryazov, P. O. Widmark and A. C. Borin, J. Phys. Chem. A, 2008, 112, 11431–11435 CrossRef CAS PubMed.
- K. Bernot, J. Luzon, L. Bogani, M. Etienne, C. Sangregorio, M. Shanmugam, A. Caneschi, R. Sessoli and D. Gatteschi, J. Am. Chem. Soc., 2009, 131, 5573–5579 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1880458, 1880459, 1880460 and 1902469. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc05362f |
| This journal is © The Royal Society of Chemistry 2019 |