Open Access Article
Open Access ArticleHalogenated building blocks for 2D crystal engineering on solid surfaces: lessons from hydrogen bonding†
Arijit
Mukherjee‡
 a,
Ana
Sanz-Matias‡
a,
Ana
Sanz-Matias‡
 b,
Gangamallaiah
Velpula
b,
Gangamallaiah
Velpula
 a,
Deepali
Waghray
a,
Oleksandr
Ivasenko
a,
Deepali
Waghray
a,
Oleksandr
Ivasenko
 a,
Nerea
Bilbao
a,
Nerea
Bilbao
 a,
Jeremy N.
Harvey
a,
Jeremy N.
Harvey
 *b,
Kunal S.
Mali
*b,
Kunal S.
Mali
 *a and
Steven
De Feyter
*a and
Steven
De Feyter
 *a
*a
aDivision of Molecular Imaging and Photonics, Department of Chemistry, KU Leuven, Celestijnenlaan, 200F, B-3001 Leuven, Belgium. E-mail: kunal.mali@kuleuven.be; steven.defeyter@kuleuven.be
bQuantum Chemistry and Physical Chemistry, Department of Chemistry, KU Leuven, BE-3001 Leuven, Belgium. E-mail: jeremy.harvey@kuleuven.be
First published on 6th March 2019
Abstract
Halogen bonding has emerged as a promising tool in two-dimensional (2D) crystal engineering. Since halogen bonds are similar to hydrogen bonds in a number of aspects, the existing knowledge of hydrogen bonded systems can be applied to halogenated systems. Here we evaluate the applicability of a retrosynthetic approach based on topological similarity between hydrogen and halogen bonds to obtain predictable halogen bonded networks. The self-assembly of 1,3-dibromo-5-alkoxybenzene derivatives was studied in analogy with well-explored alkoxy isophthalic acids using a combination of experimental and theoretical tools. Scanning tunneling microscopy (STM) characterization of the networks formed at the liquid–graphite interface revealed that while the retrosynthetic approach works at the level of small clusters of molecules within the 2D network, the overall structure of the network deviates from the anticipated structure. The monolayers consist of fractured rows of halogen-bonded modules instead of the expected continuous lamellar structure. Each module consists of a discrete number of halogen-bonded molecules. The interactions responsible for the stabilization of halogen bonded dimers are delineated through detailed density functional theory (DFT) calculations coupled with natural bonding orbitals (NBO) and perturbation analysis. A modified force field that includes an extra charged site to imitate the σ hole on the halogen atom was developed and applied to extract total potential energies of the anticipated and observed networks. Plausible reasons for the deviation from the anticipated structure are discussed. Finally, a modified molecular design that allows successful application of the hydrogen bond–halogen bond analogy was tested experimentally.
Introduction
Crystal engineering deals with rational assembly of molecules into crystals by logical selection of supramolecular interactions. Originally aimed at unravelling the guidelines that lead to crystal structure formation, crystal engineering has now matured into a massive field of scientific inquiry that aims to control the structure and properties of functional molecular solids.1 Two-dimensional (2D) crystal engineering on the other hand, concerns the design and fabrication of single molecule thick crystalline layers of organic and metal organic building blocks physisorbed on solid surfaces.2 Such physisorbed monolayers are of considerable interest due to their importance in bottom-up nanofabrication methods. Unlike bulk crystal structures, which are primarily governed by intermolecular interactions and the principle of close packing, the outcome of 2D crystallization is often dependent on the nature of the solid surface. Despite this difference, a number of concepts central to bulk crystal engineering can be readily employed for rationalizing 2D crystallization on surfaces thereby providing precise control on the fabrication of 2D networks.3,4One such concept is that of supramolecular synthons. “A supramolecular synthon is a structural unit within a supermolecule which can be formed and/or assembled by known or conceivable synthetic operations involving intermolecular interactions.”4 The synthon approach, which relies on the identification of discrete assembly patterns from a collection of crystal structures and using that information to deliberately organize molecules in pre-designed structures, is central to modern crystal engineering. The supramolecular synthons are thus ‘structure-directing’ entities which allow us to apply a retrosynthetic approach to crystal engineering. The concept was introduced with the dual objective of reducing the complexity and enhancing the predictability of supramolecular synthesis and is currently being increasingly employed in the design and synthesis of novel crystalline materials with desired properties.5
Despite its proven efficacy in the formulation of new design strategies for bulk crystalline materials, the application of supramolecular synthon approach has been limited to a few strong synthons in 2D crystal engineering on solid surfaces.6 Especially, halogen bonds as supramolecular synthons in 2D surface self-assembly have rarely been studied.3 Furthermore, while the number of robust supramolecular synthons exploited in bulk crystal engineering is quite large, 2D crystal engineering has largely relied on hydrogen bonding (H-bonding) and van der Waals interactions for the fabrication of complex multicomponent nanopatterns.7 A somewhat recent addition to the repertoire of non-covalent interactions employed in 2D crystal engineering is halogen bonding (X-bonding).8,9 While the surface self-assembly of halogenated compounds has been studied for many years, only recently halogen-bonding in its true sense (vide infra) has been employed as a tool for 2D crystal engineering.8 Heavier halogens (Cl, Br, I) in organic molecules have strongly polarizable electron density which causes anisotropy in the electronic distribution. This anisotropic electronic distribution often gives rise to an electrophilic region along the C-halogen axis, also known as sigma (σ) hole. The interaction of such electrophilic region with another nucleophile (such as O, N, or nucleophilic region of other halogen atoms) gives rise to a new class of net attractive interaction called the halogen bond. Due to the localized nature of the σ-hole along the C-halogen axis, halogen bonds are highly directional. They are typically weaker than strong hydrogen bonds but stronger than van der Waals interactions. Thus, a halogen bond is a unique intermolecular interaction with moderate strength and strong directionality.10,11
Not all interactions involving halogens, however, are halogen bonds, as their formation requires the presence of an electrophilic halogen. This is important to note since halogens are also involved in halogen–halogen interactions which, depending on their geometry, are classified as either type-I (symmetrical) or type-II (bent). Only type-II contacts qualify as halogen bonds as they involve the interaction of the electrophilic region of one halogen atom with the nucleophilic region of the other. Type-I contacts, on the other hand, originate from close-packing and are mainly van der Waals-like in nature. Although the ideal geometry for type-II interactions as defined by the angle C–X⋯X is around 90°, recently it has been shown that the angular range for type-II contacts is quite broad (30° ≤ |θ1 − θ2|).12
Halogen bonds share a number of similarities with hydrogen bonds. Both are attractive interactions that involve donation of electron density from a nucleophilic moiety (halogen/hydrogen bond acceptor) to an electrophilic moiety (halogen/hydrogen bond donor). Both interactions are highly directional. The strength of hydrogen as well as halogen bonds can be readily tuned by changing the functional group attached to the halogen/hydrogen atom. Therefore, many halogen bond-based synthons share close topological similarity with known H-bonding synthons. Consequently, the two synthons have been used in analogy with each other in bulk crystal engineering.13 Given that the use of X-bonding in 2D crystal engineering is still relatively nascent, there is plenty of room to apply the existing knowledge of H-bonding synthons14 to halogenated systems. Such an approach will also help to evaluate whether or not the surface self-assembly of halogenated building blocks is predictable and thus can be used reliably for 2D crystal engineering.
In this work, we employ a known H-bonding synthon based on carboxyl groups to design the self-assembly strategy of halogenated building blocks on the surface of highly oriented pyrolytic graphite (HOPG). Using the self-assembly of alkoxy substituted isophthalic acids (ISA) as a model H-bonded system, several 1,3-dibromo-5-alkoxybenzene derivatives were synthesized (Fig. 1a). The appropriateness of the proposed analogy was evaluated by carrying out density functional theory (DFT) calculations on dimers of 1,3-dibromo-5-methoxybenzene which predicted the formation of the expected X-bonded dimer synthons. We also note that the structure-directing ability of Br⋯Br interactions is known from bulk crystal engineering15 as well as from theoretical studies.16 The self-assembly of these building blocks was then characterized using scanning tunneling microscopy (STM) at the 1-phenyloctane/HOPG interface. STM revealed that, while the halogen-bond/hydrogen-bond synthon strategy (vide infra) appears to work at the level of small clusters of molecules, the overall structure of the monolayer deviated from the anticipated lamellar pattern. Molecular mechanics calculations of periodic 2D models were employed to understand the main contributions to the relative stabilities of the anticipated and the observed structures.
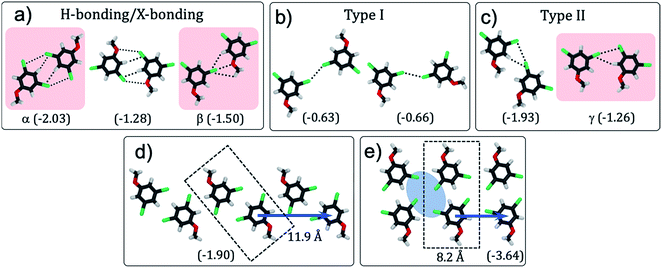
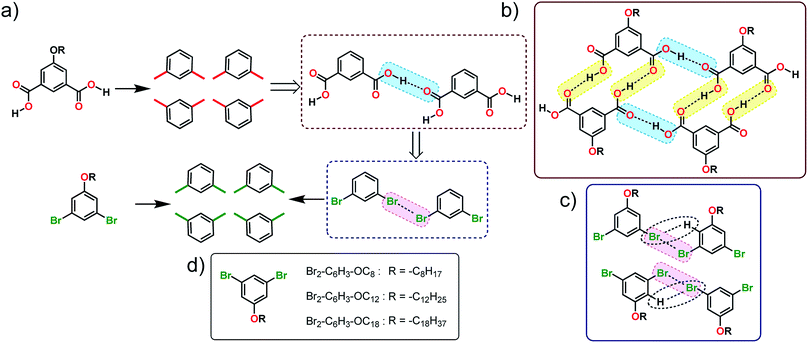 | ||
| Fig. 1 (a) Schematic showing how the H-bonding/X-bonding analogy can be used in a retrosynthetic approach. The hydrogen bonded O–H⋯O synthon is highlighted in blue while halogen bonded Br⋯Br synthon is highlighted in pink. (b and c) Schematics showing the outcome of self-assembly for alkoxy-substituted isophthalic acid derivatives17–19 and the corresponding dibromophenyl derivatives (this work), respectively. The inter-row dimeric H-bonds are highlighted in yellow. We note that alkoxy isophthalic acids with relatively short alkoxy chains form 6 membered cyclic hexagonal structures both in 3D20 as well as in 2D.17 (d) Molecular structures of the 1,3-dibromo-5-alkoxybenzene derivatives. | ||
Results and discussion
The H-bond/X-bond analogy
The supramolecular synthon strategy originates from the analogy that crystals are supramolecular equivalents of molecules and thus crystal engineering is the supramolecular equivalent of organic synthesis.4 In the following, we use this equivalence to dissect the self-assembled patterns formed by alkoxy substituted ISA derivatives on the graphite surface. The self-assembly of alkoxy substituted ISA derivatives at the solution–solid interface has been intensively studied using STM in the recent past. Under typical experimental conditions, ISA derivatives with sufficiently long alkoxy chains form a double row lamellar structure at the solution–HOPG interface.17–19 This structure can be dissected into two types of H-bonding synthons: intra-row catemeric H-bonds (blue rectangle, Fig. 1b) and inter-row dimeric H-bonds (yellow rectangle, Fig. 1b).As synthons are probabilistic in nature, one needs to choose a retrosynthetic strategy based on the robustness of synthons. Intra-row catemer synthons are more probable than the inter-row ones. Hence, the double row patterns in alkoxy carboxylic acids were dissected accordingly. The directionality of catemers formed by the 5-alkoxyisophthalic acid derivatives can, in principle, be mimicked with type II halogen bonds formed by 1,3-dibromobenzene (Fig. 1a). Since long alkyl chains are known to stabilize self-assembled networks on the graphite surface, a series of 1,3-dibromo-5-alkoxybenzene derivatives (Br2-C6H3-OCnFig. 1d) were synthesized. Before scrutinizing their surface self-assembly, the foundation of the proposed analogy was evaluated using DFT calculations.
DFT calculations: possible structures
To evaluate whether 1,3-dibromo-5-alkoxybenzene is capable of forming the anticipated synthon, DFT calculations were carried out on 1,3-dibromo-5-methoxybenzene (Br2-C6H3-OMe). This model compound allowed us to characterize not only the structural features arising due to the brominated head groups and their relative stabilities, but also the role of halogen bonding in the stabilization of the synthon without the convoluting contribution of the alkyl chains.Several hypothetical dimer structures of Br2-C6H3-OMe encompassing a range of possible supramolecular interactions were optimized (Fig. 2). The modelled dimers can be broadly classified into three categories: those stabilized by a combination of H- and X-bonding (Fig. 2a), those involving type-I X⋯X interactions (Fig. 2b) and finally, those stabilized by type-II X⋯X interactions (Fig. 2c). A Br⋯Y (Y = Br, O, H) distance shorter than the sum of van der Waals radii of the individual atoms, and an acceptable C–Br⋯Y angle were used as criteria in the classification presented in Fig. 2. Intermolecular interactions between partially halogenated benzene moieties imply that the same halogen atom can act as halogen bond donor and unconventional hydrogen bond acceptor.21–23 The dimers sustained by H- and/or X-bonding are the most stable together with those featuring type II X⋯X interactions. As anticipated, dimers based on type-I X⋯X bonding are the least stable amongst the structures considered here.
To further confirm the presence of X-bonding and its approximate contribution to the overall stabilization of the dimers, natural bond orbital (NBO) calculations24 were carried out focusing on second-order perturbation theory analysis. This type of analysis allows to identify the individual (natural) orbital contributions to the overall interaction energy in a given structure. Halogen and hydrogen bonds are represented as donor–acceptor interactions between lone pairs of electrons (LP) in the HB/XB acceptor moiety and empty antibonding orbitals (BD*) in the HB/XB donor moiety. The second-order contributions to the interaction energy of each LP–BD* pair can provide insight into the relative importance of each donor–acceptor interaction. We note that NBO is known to overestimate charge-transfer,25 and hence the energies presented here are qualitative descriptors.
Dimers designated as α, β and γ were selected for detailed NBO analysis in view of their structure and stability (structures highlighted in pink in Fig. 2). In dimer α, the Br atoms are at 2.77 Å from the H atom of the phenyl ring indicating formation of unconventional C–H⋯Br H-bonds.23 This is the main stabilizing interaction, according to the much larger contribution of hydrogen bonding to the second order interaction energy as compared to Br⋯Br interactions. Dimer β on the other hand features a close contact (3.03 Å) between the ether oxygen of one molecule and the Br atom of the other molecule indicating formation of a typical X-bond based on halogen–heteroatom interaction. In this dimer, hydrogen and halogen bonding contribute broadly equally to the second order interaction energy, since there is an intermolecular interaction between the Br lone pair and the nearby hydrogen BD* orbital. In the case of dimer γ, the bromine atom of one molecule approaches that of the other within 3.44 Å such that the C–Br⋯Br angle is approximately 90°. Such arrangement is conducive for X-bonding based on type-II X⋯X interactions. The outcome of the NBO analysis presented in Table 1 clearly reveals a sizable contribution of H-bonding to the stabilization of the dimers apart from the anticipated X-bonding interactions. In Table 1, Br: → Br–C σ* indicates the interaction between a lone pair of electrons on the bromine atom of one molecule with the C–Br σ* orbital (amounting to X-bond via type-II Br⋯Br interactions). Br: → H–C σ* indicates the interaction between lone pair of electrons on the bromine atom atom of one molecule with the C–H σ* orbital (amounting to H-bond) (also see Fig. S1 and Table S1 in ESI†).
| System | Method | a (Å) | b (Å) | γ (°) |
|---|---|---|---|---|
| a Calculated considering repeating hexamers only and NOT alternating hexamer–tetramer. | ||||
| Br2-C6H3-OC8 | Experimental | 23 ± 1 | 27 ± 1 | 68 ± 2 |
| Theoretical | 23.5 | 27.4 | 66 | |
| Br2-C6H3-OC12 | Experimental | 30 ± 1 | 29 ± 1 | 62 ± 1 |
| Theoretical | 28.3 | 27.3 | 68 | |
| Br2-C6H3-OC18 | Experimental | 36 ± 1 | 31 ± 1 | 68 ± 2 |
| Theoretical | 35.7 | 27.5 | 69 | |
| Br2-C6H3-OC12O-C6H3-Br2 | Experimental | 24 ± 1 | 14 ± 1 | 92 ± 2 |
| Theoretical | 24.2 | 14.1 | 96 | |
| ISA-OC12O-ISA | Experimental | 24 ± 1 | 17 ± 1 | 90 ± 2 |
| Theoretical | 26.2 | 16.6 | 83 | |
With the exception of one (Fig. 2c, left), all the stable structures are susceptible to appearing on a 1D periodic arrangement. Based on these results, several one-dimensional infinite chains of Br2-C6H3-OMe were designed and their structures optimized using DFT, with periodic boundary conditions in one dimension, along the axis of the chain (see Fig. S2 and Table S2 in ESI†). The outcome reveals that a double row type structure (Fig. 2e), formed by tetrameric synthons is the most stable followed by a zigzag structure (Fig. 2d). Chains involving bromine⋯oxygen halogen bonding (as in β) and type I halogen bonding (Fig. 2b) are considerably less stable. These structures, if they are to be reproduced in two-dimensional monolayers, also allow predictions to be made concerning the relative orientation of the head group chains and the alkyl chains. The alkyl chain angle with respect to the ring to ring vector is expected to be close to 138° for the double row structure (Fig. 2e) and close to 109° for the zigzag structure (Fig. 2d). According to these calculations, the zig-zag structure can be dissected into intra-row catemeric type-II X⋯X and H-bonding interactions, and inter-row dimeric H-bonding interactions, which result in a tetrameric synthon. The double row structure, on the other hand, can be dissected into inter-row dimeric H-bonding interactions and intra-row dimeric XB interactions.
STM of 1,3-dibromo-5-alkoxybenzene derivatives
After the computational assessment of the possible dimeric structures, the surface self-assembly of the Br2-C6H3-OCn derivatives was scrutinized at the liquid/HOPG interface. The objective is to test if they form double row patterns as hypothesized earlier using the H-bond/X-bond analogy and as predicted by DFT calculations presented above.
Fig. 3a shows a representative large-scale STM image obtained after dropcasting a 1-phenyloctane solution of Br2-C6H3-OC18 (C = 2 × 10−3 M) on the HOPG surface. At this concentration, a long-range ordered monolayer is formed which is reminiscent of a bricklayer (particularly similar to the “Flemish bond”, see Fig. S3 in the ESI†). The high resolution STM image presented in Fig. 3d shows that the bright bricks represent clusters of phenyl rings of Br2-C6H3-OC18 separated by striped features which arise from the octadecyloxy chains. Adjacent clusters contain unequal number of molecules. The octadecyloxy chains are fully extended, interdigitated and are aligned along one of the main symmetry axes of the graphite lattice. Unit cell parameters obtained from calibrated STM images are provided in Table 1. A molecular model built using these parameters is provided in Fig. 3g. The model reveals that discrete clusters of six and four molecules, hereafter called hexamers and tetramers, respectively, alternate regularly within the monolayer. An overview of a number of large-scale STM images clearly indicates that the hexamers and tetramers alternate on the surface thus keeping a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 proportion in the number of hexamers and tetramers.
1 proportion in the number of hexamers and tetramers.
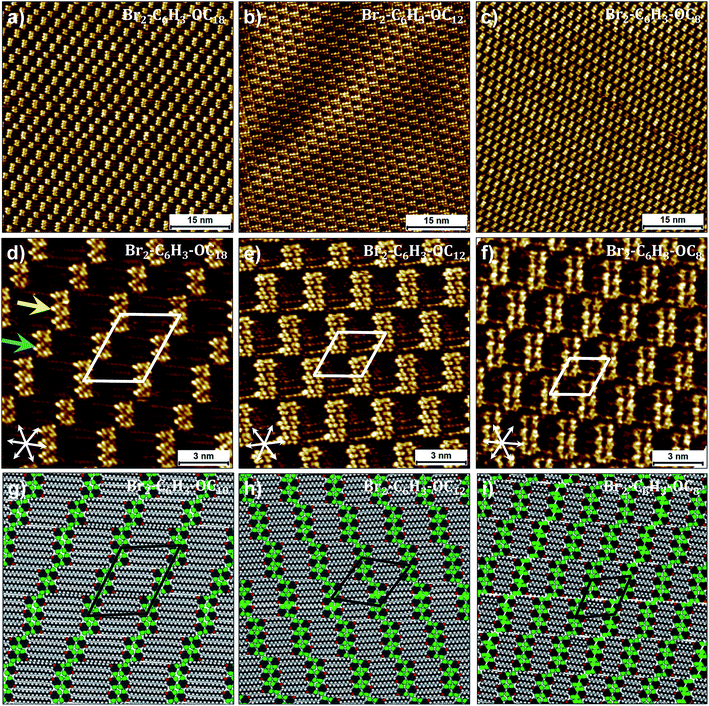 | ||
| Fig. 3 Self-assembly of Br2-C6H3-OCn derivatives at the liquid–solid interface. (a–c) Large-scale and (d–f) small-scale STM images of Br2-C6H3-OCn derivatives. Corresponding molecular models are presented in panels (g–i). While (g) was optimized based on the experimental lattice parameters, (h) and (i) represent the optimized structures at the calculated equilibrium lattice parameters. Both Br2-C6H3-OC8 and Br2-C6H3-OC12 are liquids and the STM images presented above were obtained by directly dropcasting the neat liquids on the HOPG surface, whereas the self-assembly of Br2-C6H3-OC18 was studied at the 1-phenyloctane/HOPG interface (C = 2 × 10−3 M). Graphite symmetry axes are displayed in the lower left corner of small-scale STM images. The arrows in (d) indicate a hexamer (yellow) and a tetramer (blue). Unit cell parameters are provided in Table 2. For additional STM data see Fig. S3 in the ESI.† | ||
Based on the analogy with the self-assembly of alkoxy ISA derivatives and as predicted by DFT calculations, a double row pattern stabilized by intra-lamellar type II X-bonds was expected. It is obvious from the STM data that although the anticipated double rows are formed, they do not lead to continuous lamellae. The fractured arrangement of the hexamers and tetramers is rather unexpected and the possible reasons for such discrete arrangement of molecules are discussed later in the text. Nevertheless, from a strictly geometrical point of view, the H-bond/X-bond analogy as depicted in Fig. 1 appears to be valid at the primary synthon level. The formation of such breaks or gaps indicates that the stabilization offered by X-bonding to the double rows is weak, such that the gaps do not contribute to a large energy penalty. Furthermore, it also appears that the highest contribution to the self-assembly comes from van der Waals interactions between the alkoxy chains which are known to have a dominating influence on the self-assembly of alkylated compounds.
We reasoned that reduction in the length of the alkoxy chains might change the balance of interactions in the self-assembled networks thus allowing us to observe the influence of X-bonding interactions on network formation. To this end, self-assembly of Br2-C6H3-OC12 and Br2-C6H3-OC8 was studied at the liquid–solid interface. Both these compounds exist as liquids at room temperature and hence initial STM experiments were carried out by depositing a drop of neat liquid on the HOPG surface. Fig. 3b and c display representative large-scale STM images showing the self-assembly of Br2-C6H3-OC12 and Br2-C6H3-OC8 on the graphite surface, respectively. Both images clearly show bricklayer type networks similar to that observed in the case of Br2-C6H3-OC18. A major difference however is that in contrast to the alternating arrangement of hexamers and tetramers observed for Br2-C6H3-OC18, the surface appears to be almost exclusively covered by hexamers. Detailed statistical analysis carried out on large-scale STM images indicates that tetramers do exist in these monolayers but their percentage surface coverage for both compounds is less than 5%. Furthermore, the distribution of rows of tetramers is rather random unlike the alternating arrangement observed for Br2-C6H3-OC18. The high-resolution STM images and corresponding molecular models for the two shorter chain length compounds provided in Fig. 2 clearly reveal that despite the reduction in the length of alkoxy chains, the arrangement of molecules within the clusters remains the same. The gaps exist even for Br2-C6H3-OC8, indicating that the observed packing arrangement is intrinsic to these building blocks irrespective of the alkoxy chain length for the chain lengths examined here.
The difference in the surface coverage and the arrangement of hexamers and tetramers for Br2-C6H3-OC18, and the shorter chain length compounds may arise due to the different physical states of the compounds. As noted earlier, Br2-C6H3-OC18 is a solid at room temperature whereas both Br2-C6H3-OC12 and Br2-C6H3-OC8 are liquids. Since Br2-C6H3-OC12 and Br2-C6H3-OC8 were deposited as neat liquids, the self-assembled network is formed from a liquid with relatively high concentration of molecules. On the other hand, the self-assembly of Br2-C6H3-OC18 occurs from a 2 × 10−3 M solution in 1-phenyloctane. Thus, the difference between the two types of arrangements plausibly originates from the concentration of the building blocks. Such concentration effects are routinely observed for 2D crystallization at the liquid–solid interface.26–29 To test this hypothesis, surface self-assembly of Br2-C6H3-OC12, and Br2-C6H3-OC8 was studied using 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) solutions in 1-phenyloctane. Monolayers formed from these dilute solutions indeed show the same alternating arrangement of hexamers and tetramers as observed for Br2-C6H3-OC18 (ESI Fig. S4†). Furthermore, when Br2-C6H3-OC12 and Br2-C6H3-OC8 samples prepared using corresponding neat liquids were subjected to ex situ annealing at 80 °C, the proportion of tetramers in the monolayers increased significantly yielding alternating hexamer/tetramer arrangement observed from dilute solution in 1-phenyloctane. Thus, alternating hexamers and tetramers is the most favourable structure formed for all three compounds. It must be noted that such discontinuity in the molecular rows is neither ideal for halogen bonding nor for the van der Waals interactions between interdigitating alkoxy chains. This is suggestive of a third factor, namely the molecule–substrate interactions, which are known to be critical for self-assembly on solid surfaces.30–32
1 (v/v) solutions in 1-phenyloctane. Monolayers formed from these dilute solutions indeed show the same alternating arrangement of hexamers and tetramers as observed for Br2-C6H3-OC18 (ESI Fig. S4†). Furthermore, when Br2-C6H3-OC12 and Br2-C6H3-OC8 samples prepared using corresponding neat liquids were subjected to ex situ annealing at 80 °C, the proportion of tetramers in the monolayers increased significantly yielding alternating hexamer/tetramer arrangement observed from dilute solution in 1-phenyloctane. Thus, alternating hexamers and tetramers is the most favourable structure formed for all three compounds. It must be noted that such discontinuity in the molecular rows is neither ideal for halogen bonding nor for the van der Waals interactions between interdigitating alkoxy chains. This is suggestive of a third factor, namely the molecule–substrate interactions, which are known to be critical for self-assembly on solid surfaces.30–32
The influence of molecule–substrate interactions was previously invoked for explaining the fractured self-assembly of 4-alkoxybenzoic acid derivatives at the 1-phenyloctane/HOPG interface.33 The self-assembled networks of 4-alkoxybenzoic acids show periodic kinks along the lamella axis which repeat after every three carboxylic acid dimers. It was argued that the kinks arise due to the mismatch in the optimal spacing between carboxyphenyl head groups and the alkoxy chains of the molecules on the graphite surface. Given that the alkoxybenzoic acids form lamellae with end to end arrangement of alkyl chains, the optimal interchain distance of ∼4.4 Å cannot be maintained due to the bulky carboxyphenyl head groups. It was proposed that this mismatch possibly leads to built-up strain in the monolayer. The kinks in the monolayer could thus be the means of relieving such strain. In the present case, however, the alkoxy chains interdigitate thereby reversing the packing requirements compared to the alkoxybenzoic acids. For interdigitating chains, the optimal distance between the chains of molecules adsorbed in the same column is ∼8.8 Å. This number is larger than the optimal spacing of 8.2 Å between the dibromophenyl head groups predicted by periodic DFT calculations (Fig. 2e). Thus, in the present case as well there is a probably slight mismatch between the optimal spacing required by different parts of the assembling molecules. Given the fact that the X-bonding interactions holding the head groups in place are relatively weak, it is plausible that such mismatch may introduce strain in the monolayer which may account for the formation of a discontinuous monolayer. We note that the method used for calculating the optimal spacing between head groups is not quantitative given the relatively weak Br⋯Br interactions and hence the exact number may differ slightly from what is predicted. In order to further determine whether the net interaction energies are indeed any different for the experimentally observed discontinuous structures and the hypothetical continuous lamellae, molecular mechanics (MM) calculations were carried out on Br2-C6H3-OCn assemblies on graphene surface.
Continuous versus discontinuous lamellae: MM calculations
Since the evaluation of potential energies of the different self-assembled structures involves calculations on large models, MM calculations were favoured as the computational method. Standard MM force fields in which atoms are represented as point charges are not adequate to model halogen bonding. Hence, a modified force field that includes an extra charged site to mimic the σ hole on the halogen atom was developed (Fig. 4a).34 This modified force field was tested so as to reproduce the halogen bonded structures and relative energies obtained in the dimer DFT calculations, and hence is expected to provide better results than conventional force-fields. In fact, the interaction energy of a Br2-C6H3-OC8 molecule within a hexamer was found to become more negative by at least 3.4 kcal per mol per molecule with the inclusion of an extra charged site on the halogen atom, turning the total charge–charge interactions from repulsive to attractive (see ESI Tables S3–S5†).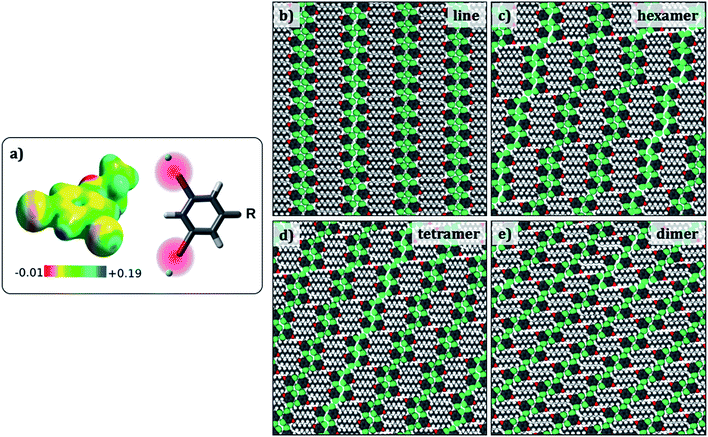 | ||
| Fig. 4 (a) Electrostatic potential map of 1,3-dibromo-5-ethoxybenzene. The sigma hole appears as blue coloured region together with a scheme showing the positive x-site approach used to modify the force field. (b–e) Simulated packings (Br2-C6H3-OC8) for estimating the difference in the total potential energies provided in Table 3. Similar structures were optimized for the other Br2-C6H3-OCn derivatives. | ||
Preliminary molecular mechanics calculations of a single molecule of Br2-C6H3-OC8 on 80 × 80 Å2 sheet of graphene reveal a strong preference for the alkyl chains to align along the zig-zag axis of the substrate (Fig. S6 in the ESI†), as described in the Groszek model,35 and also in agreement with the experimental results. In order to gain insight into the role of periodic separations observed between discrete molecular clusters, four different cluster structures were considered: hexamers, tetramers, dimers, and finally a continuous lamellar (line) structure (Fig. 4). The separation between the clusters is referred to as a ‘gap’ hereon. Periodic models built from each cluster structure resulted in four phases, which possess respectively, 1/6, 1/4, 1/2 and 0 gaps per molecule. Comparison between pure cluster phases allowed us to create a dataset including two extremes (two and zero halogen bonds per molecule for the continuous lamellar structure and the dimer phase) and two intermediate points (the hexamer and the tetramer-based phases) with the intention of finding an energetic trend that explains the experimentally observed gaps.
To this end, the aforementioned geometries were generated and optimized for all three Br2-C6H3-OCn. Atomic positions were optimized together with the lattice parameters (a, b and gamma) and the angle the unit cell vector makes with one of the principal symmetry axes of graphite (see Fig. S7 in the ESI†). The structures selected present the minimum potential energy per unit cell area. Fig. 4 shows optimized packing arrangements for the Br2-C6H3-OC8 derivative. It can be readily noticed that all the packing arrangements with the exception of the dimer structure are based on the tetrameric synthon (Fig. 2e). The alkoxy chains are interdigitated and are aligned along one of the main symmetry axes of graphite. It appears that type-I Br⋯Br interactions may be responsible for the stabilization of the gap structure, since Br⋯Br distances in the optimized structures (3.6 Å to 3.9 Å) match closely with the sum of van der Waals radii of the two atoms (3.8 Å).
Table 3 shows total potential energies per molecule, and per unit area for the simulated geometries displayed in Fig. 4 for all three derivatives of Br2-C6H3-OCn. The energies of all the simulated structures for a given Br2-C6H3-OCn derivative are similar, clearly indicating that the introduction of the gap in the supramolecular structure does not cause a significant energy penalty. Thus, the reason for the appearance of the gaps in the monolayers cannot be ascertained from the total potential energies alone and the origin of the gaps may lie in a much subtle structural factor.
| System | Structure | A/n (nm2) | ΔE/n (kcal mol−1) | ΔE/A (kcal mol−1 nm−2) |
|---|---|---|---|---|
| Br2-C6H3-OC8 | Line | 0.993 | −35.1 | −35.3 |
| Hexamer | 0.980 | −34.4 | −35.1 | |
| Tetramer | 0.966 | −34.3 | −35.5 | |
| Dimer | 0.968 | −33.7 | −34.8 | |
| Br2-C6H3-OC12 | Line | 1.201 | −43.8 | −36.5 |
| Hexamer | 1.202 | −42.6 | −35.5 | |
| Tetramer | 1.193 | −42.4 | −35.5 | |
| Dimer | 1.190 | −42.1 | −35.4 | |
| Br2-C6H3-OC18 | Line | 1.529 | −56.9 | −37.2 |
| Hexamer | 1.520 | −55.2 | −36.3 | |
| Tetramer | 1.519 | −54.8 | −36.1 | |
| Dimer | 1.489 | −52.9 | −35.6 |
We propose that the fractured structures are formed as a result of the competition between the stabilization offered by molecule–substrate interactions and that by lateral Br⋯Br interactions. For instance, in Br2-C6H3-OC8 and Br2-C6H3-OC12 the alkyl chains contribute to roughly 50 and 60% of the overall stabilization energy, respectively (see Fig. S8 in the ESI†). It can be noticed from the table that the area per molecule for each system decreases slightly but consistently in going from the hypothetical line structure to the experimentally observed hexamer structure and the hypothetical structures with higher degrees of fracture. This may indicate that the experimentally observed hexamer structure is relatively more compact compared to the hypothetical line structure. Also note that the line structure has no gaps, whereas the hexamer structure has a gap every six molecules. That is, in the hexamer structure there is an interruption in the intra-row X-bonding every six molecules, while there is none in the case of the linear structure. Such ‘break’ in the X-bonding however appears to lead to a more compact arrangement as described above. Given that the adsorption energy of the molecules is much higher than the type-II Br⋯Br interactions involved here, the gaps may be developed in the monolayer in order to achieve a higher density of molecules on the surface.
The complex yet very subtle interfacial interactions described above can be simplified by considering an alternative design where the influence of alkyl chain interdigitation is minimized and the contribution of halogen atoms in directing the assembly process is increased. To this end, 1,3-dibromo-5-[12-(3,5-dibromophenoxy)dodecyloxy]benzene (Br2-C6H3-OC12O-C6H3Br2, Fig. 5a) was synthesized. This compound is structurally similar to the Br2Ph-OCn derivatives discussed earlier but it has two 1,3-dibromophenoxy head groups instead of one, separated by a dodecyl chain. The corresponding isophthalic acid derivative (ISA-OC12O-ISA, Fig. 5d) was also synthesized for the sake of comparison. The STM image provided in Fig. 5b reveals that Br2-C6H3-OC12O-C6H3-Br2 forms a continuous lamellar network at the 1-phenyloctane/HOPG interface. Single molecules could not be identified unambiguously in the STM images. However, the experimentally obtained unit cell parameters show a good agreement with the computationally obtained ones. A molecular model presented in Fig. 5c reveals that the alkyl chains are neither interdigitated nor close-packed. The 1,3-dibromophenoxy head groups form close-packed rows orthogonal to the orientation of alkyl chains. This packing arrangement leads to the formation of periodic voids in the supramolecular network which are most likely occupied by 1-phenyloctane molecules. The co-adsorbed solvent molecules could not be resolved due to their high mobility. The molecular model reveals that the network is stabilized by Br⋯H–C hydrogen bonding. We note that unit cell vector ‘a’ of this network is in reasonable agreement with the zig-zag structure (Fig. 2d) which was obtained computationally. The formation of the zig-zag structure instead of the relatively compact double row structure appears to be driven by the additional stabilization provided by (transiently) co-adsorbed solvent molecules (see Fig. S10 and Table S9 in the ESI†). The corresponding isophthalic acid derivative forms two different networks at the octanoic acid/HOPG interface. One of them is structurally similar to the supramolecular network formed by Br2-C6H3-OC12O-C6H3-Br2. Octanoic acid was chosen as a solvent in the case of ISA-OC12O-ISA due to its poor solubility in 1-phenyloctane. A representative STM image presented in Fig. 5e clearly shows the different packing arrangements. In one case, the ISA-OC12O-ISA molecules are arranged in the form of the double row structure whereas in the other, a zig-zag network is formed. The zigzag network is structurally similar to that formed by Br2-C6H3-OC12O-C6H3-Br2. A molecular model presented in Fig. 5f shows that the isophthalic acid ‘head groups’ form zig-zag rows stabilized by hydrogen bonding between the carboxylic groups. We note that similar type of zigzag network has been observed for a quaterphenyl based tetracarboxylic acid.36 We also note that comparison of results obtained using different solvents must be treated with caution since solvents are known to influence the outcome of self-assembly processes at the solution–solid interface.37
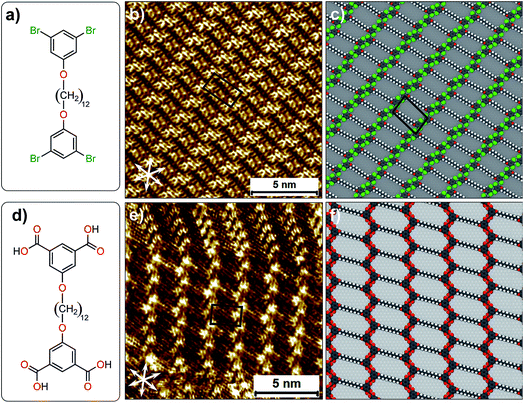 | ||
| Fig. 5 (a) Molecular structure of Br2-C6H3-OC12O-C6H3-Br2. (b) STM image of monolayer formed by Br2-C6H3-OC12O-C6H3-Br2 at the 1-phenyloctane/HOPG interface. (c) A molecular model for the packing arrangement of Br2-C6H3-OC12O-C6H3-Br2. (d) Molecular structure of ISA-OC12O-ISA. (e) STM image of monolayer formed by ISA-OC12O-ISA at the octanoic acid/HOPG interface. (f) A molecular model for the packing arrangement of ISA-OC12O-ISA (see Fig. S5 in the ESI for additional STM data†). | ||
Conclusions and outlook
Halogen bonding, an intermolecular interaction with moderate strength and high directionality, offers an interesting alternative to (2D) crystal engineers. Due to the moderate strength of X-bonds however, the 2D networks formed by halogenated building blocks are often stabilized by a number of other weak interactions. This aspect reduces the predictability of supramolecular synthesis using halogenated building blocks. As a way forward, we have proposed a qualitative guideline based primarily on molecular geometry and topological similarities between hydrogen and halogen bonds. A retrosynthetic approach that uses the existing knowledge of hydrogen-bonded synthons was employed to design a halogen-bonded supramolecular network. Although the approach seems justified at the primary synthon level, the overall structure of halogen-bonded network differs from the anticipated structure based on the H-bond/X-bond analogy. DFT and molecular mechanics calculations provide insight into the different interactions that stabilize the halogen-bonded dimers and the supramolecular network, respectively. While the total potential energies of the anticipated and observed networks do not differ significantly, subtle differences in the packing densities appear to be responsible for the observed behavior. This indicates that although X-bonding may be partly responsible for stabilization of halogenated building blocks in general, other intermolecular and interfacial interactions must be considered in the description of such supramolecular networks.Based on the observations noted above, it may appear as if controlling supramolecular interactions at the solution–solid interface is akin to herding cats. As it stands, it is possible to employ the supramolecular synthon approach to associate small clusters of molecules in a pre-programmed fashion within a crystalline matrix but there is little control over how the small aggregates propagate further. It remains to be seen if halogen bonding interactions are indeed structure directing i.e. if they actually control the outcome of self-assembly on surfaces or if they result as a consequence of global considerations pertaining intermolecular and interfacial interactions of which halogen bonding represents a significant but not determining contribution. The particular example presented above indicates that the latter is the case. We conclude that when competing weak interactions are at play (for instance, packing density vs. Br–Br interactions) then apparently minor effects (in this case, the tiny differences in molecule–substrate) will become structure determining. To get general answers to these questions, it is necessary to explore halogenated systems using a combination of experimental and theoretical tools.
Experimental methods
The synthesis and characterization of Br2-C6H3-OCn, Br2-C6H3-OC12O-C6H3-Br2 and ISA-OC12O-ISA derivatives is described in detail in the ESI.† 1-Phenyloctane (Sigma 99%) and octanoic acid (Sigma ≥99%) were used without further purification. For STM experiments, Br2-C6H3-OC8 and Br2-C6H3-OC12 were used as neat liquids and also as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dilute solutions in 1-phenyloctane. Stock solutions (1 mg mL−1) of the solid compounds (Br2-C6H3-OC18, Br2-C6H3-OC12O-C6H3-Br2) were prepared in 1-phenyloctane. For ISA-OC12O-ISA octanoic acid was used as the solvent. The stock solutions were diluted further to test concentration dependence of self-assembly. All STM experiments were performed at room temperature (21–23 °C) using a PicoLE (Keysight Technologies) machine operating in constant-current mode with the tip immersed in the supernatant liquid. STM tips were prepared by mechanically cutting a Pt/Ir wire (80%/20%, diameter 0.2 mm). Prior to imaging, a drop of neat liquid or solution was placed onto a freshly cleaved surface of highly oriented pyrolytic graphite (HOPG, grade ZYB, Advanced Ceramics Inc., Cleveland, USA). The experiments were repeated in 2–3 sessions using different tips to check for reproducibility and to avoid experimental artefacts, if any. For analysis purposes, recording of a monolayer image was followed by imaging the graphite substrate under the same experimental conditions, except for increasing the current and lowering the bias. The images were corrected for drift via Scanning Probe Image Processor (SPIP) software (Image Metrology ApS), using the recorded graphite images for calibration purposes, allowing a more accurate unit cell determination. The unit cell parameters were determined by examining at least 4 images and only the average values are reported. The images are Gaussian filtered. The imaging parameters are indicated in the figure caption: tunneling current (Iset), and sample bias (Vbias).
1 dilute solutions in 1-phenyloctane. Stock solutions (1 mg mL−1) of the solid compounds (Br2-C6H3-OC18, Br2-C6H3-OC12O-C6H3-Br2) were prepared in 1-phenyloctane. For ISA-OC12O-ISA octanoic acid was used as the solvent. The stock solutions were diluted further to test concentration dependence of self-assembly. All STM experiments were performed at room temperature (21–23 °C) using a PicoLE (Keysight Technologies) machine operating in constant-current mode with the tip immersed in the supernatant liquid. STM tips were prepared by mechanically cutting a Pt/Ir wire (80%/20%, diameter 0.2 mm). Prior to imaging, a drop of neat liquid or solution was placed onto a freshly cleaved surface of highly oriented pyrolytic graphite (HOPG, grade ZYB, Advanced Ceramics Inc., Cleveland, USA). The experiments were repeated in 2–3 sessions using different tips to check for reproducibility and to avoid experimental artefacts, if any. For analysis purposes, recording of a monolayer image was followed by imaging the graphite substrate under the same experimental conditions, except for increasing the current and lowering the bias. The images were corrected for drift via Scanning Probe Image Processor (SPIP) software (Image Metrology ApS), using the recorded graphite images for calibration purposes, allowing a more accurate unit cell determination. The unit cell parameters were determined by examining at least 4 images and only the average values are reported. The images are Gaussian filtered. The imaging parameters are indicated in the figure caption: tunneling current (Iset), and sample bias (Vbias).
Computational methods
DFT geometry optimizations were performed with Gaussian 09 (ref. 38) at the M06-2X/6-31G(d,p) level of theory, using Cs symmetry restriction, on 9 different dibromobenzene methyl ether dimers. The electrostatic potential of a single optimized molecule was computed on 0.001 au contour of the electron density. M06-2X39 functional was chosen due to its accuracy at low computational cost for depicting halogen bonding.40 Natural Bond Orbital (NBO) perturbation analysis was carried out at the same level of theory on three selected dimer optimized structures. The self-assembled structures of Br2-C6H3-OCn derivatives were optimized using molecular mechanics with Tinker.41 Information obtained from test calculations using large supermolecular models including up to 72 molecules on large (160 × 160 Å2) graphene molecules was used to produce and compute infinite periodic systems, all in vacuum. Optimization was performed until the RMS gradients fell below 0.1 kcal mol−1 Å−1. The forcefield used was a modified form of the X-site OPLS-AA forcefield model,34 with the magnitude of the partial positive charge positioned near the Br atom adjusted to 0.035e so as to reproduce the structures and energetics obtained in the DFT calculations. No charge was placed on the graphene atoms to keep the overall charge of the system neutral. The HOPG substrate was modelled by a graphene monolayer, which was held fixed throughout, a choice justified by test calculations suggesting that substrate relaxation contributes less than 0.5 kcal per mol per molecule to graphene–monolayer binding energies. Construction of a periodic model is challenging due to incommensurability between the monolayer and graphene repeating units, the details of the novel procedure used to tackle this problem are discussed in ESI.† Typical supercell sizes reach up to 249 × 186 Å2.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
JNH and ASM would like to thank the KU Leuven for financial support. G. V. acknowledges award of Marie Sklodowska-Curie individual fellowship (number 706314, GRAPHIL). This work is supported by the Fund of Scientific Research–Flanders (FWO), KU Leuven-Internal Funds, and European Research Council under the European Union's Seventh Framework Programme (FP7/2007–2013)/ERC Grant Agreement No. 340324.References
- G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967 CrossRef CAS PubMed.
- K. S. Mali, N. Pearce, S. De Feyter and N. R. Champness, Chem. Soc. Rev., 2017, 46, 2520–2542 RSC.
- A. Mukherjee, J. Teyssandier, G. Hennrich, S. De Feyter and K. S. Mali, Chem. Sci., 2017, 8, 3759–3769 RSC.
- G. R. Desiraju, Angew. Chem., Int. Ed., 1995, 34, 2311–2327 CrossRef CAS.
- A. Mukherjee, Cryst. Growth Des., 2015, 15, 3076–3085 CrossRef CAS.
- A. G. Slater, L. M. A. Perdigão, P. H. Beton and N. R. Champness, Acc. Chem. Res., 2014, 47, 3417–3427 CrossRef CAS PubMed.
- J. A. A. W. Elemans, S. Lei and S. De Feyter, Angew. Chem., Int. Ed., 2009, 48, 7298–7332 CrossRef CAS PubMed.
- Q.-N. Zheng, X.-H. Liu, T. Chen, H.-J. Yan, T. Cook, D. Wang, P. J. Stang and L.-J. Wan, J. Am. Chem. Soc., 2015, 137, 6128–6131 CrossRef CAS PubMed.
- M. Sacchi, A. Y. Brewer, S. J. Jenkins, J. E. Parker, T. Friščić and S. M. Clarke, Langmuir, 2013, 29, 14903–14911 CrossRef CAS PubMed.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- M. Saccone, V. Dichiarante, A. Forni, A. Goulet-Hanssens, G. Cavallo, J. Vapaavuori, G. Terraneo, C. J. Barrett, G. Resnati, P. Metrangolo and A. Priimagi, J. Mater. Chem. C, 2015, 3, 759–768 RSC.
- S. Tothadi, S. Joseph and G. R. Desiraju, Cryst. Growth Des., 2013, 13, 3242–3254 CrossRef CAS.
- A. Mukherjee, S. Tothadi and G. R. Desiraju, Acc. Chem. Res., 2014, 47, 2514–2524 CrossRef CAS PubMed.
- O. Ivasenko and D. F. Perepichka, Chem. Soc. Rev., 2011, 40, 191–206 RSC.
- A. Mukherjee and G. R. Desiraju, IUCrJ, 2014, 1, 49–60 CrossRef CAS PubMed.
- M. E. Brezgunova, E. Aubert, S. Dahaoui, P. Fertey, S. Lebègue, C. Jelsch, J. G. Ángyán and E. Espinosa, Cryst. Growth Des., 2012, 12, 5373–5386 CrossRef CAS.
- K.-W. Park, J. Adisoejoso, J. Plas, J. Hong, K. Müllen and S. De Feyter, Langmuir, 2014, 30, 15206–15211 CrossRef CAS PubMed.
- S. De Feyter, A. Gesquière, M. Klapper, K. Müllen and F. C. De Schryver, Nano Lett., 2003, 3, 1485–1488 CrossRef CAS.
- P. N. Dickerson, A. M. Hibberd, N. Oncel and S. L. Bernasek, Langmuir, 2010, 26, 18155–18161 CrossRef CAS PubMed.
- J. Yang, J.-L. Marendaz, S. J. Geib and A. D. Hamilton, Tetrahedron Lett., 1994, 35, 3665–3668 CrossRef CAS.
- O. Navon, J. Bernstein and V. Khodorkovsky, Angew. Chem., Int. Ed., 1997, 36, 601–603 CrossRef CAS.
- L. Brammer, E. A. Bruton and P. Sherwood, Cryst. Growth Des., 2001, 1, 277–290 CrossRef CAS.
- Y. Lu, S. Zhang, C. Peng and H. Liu, J. Phys. Chem. C, 2017, 121, 24707–24720 CrossRef CAS.
- F. Weinhold and C. R. Landis, Valency and Bonding: A Natural Bond Orbital Donor–Acceptor Perspective, Cambridge University Press, Cambridge, 2005 Search PubMed.
- A. J. Stone, J. Phys. Chem. A, 2017, 121, 1531–1534 CrossRef CAS PubMed.
- S. Ahn and A. J. Matzger, J. Am. Chem. Soc., 2010, 132, 11364–11371 CrossRef CAS PubMed.
- S. Lei, K. Tahara, F. C. De Schryver, M. Vander Auweraer, Y. Tobe and S. De Feyter, Angew. Chem., Int. Ed., 2008, 47, 2964–2968 CrossRef CAS PubMed.
- B. Zha, X. Miao, P. Liu, Y. Wu and W. Deng, Chem. Commun., 2014, 50, 9003–9006 RSC.
- C. Meier, M. Roos, D. Künzel, A. Breitruck, H. E. Hoster, K. Landfester, A. Gross, R. J. Behm and U. Ziener, J. Phys. Chem. C, 2009, 114, 1268–1277 CrossRef.
- T. Balandina, K. Tahara, N. Sändig, M. O. Blunt, J. Adisoejoso, S. Lei, F. Zerbetto, Y. Tobe and S. De Feyter, ACS Nano, 2012, 6, 8381–8389 CrossRef CAS PubMed.
- C. Liu, L. Yang, Y. Wang, S. Lei and W. Hu, J. Phys. Chem. C, 2018, 122, 12307–12314 CrossRef CAS.
- J. M. MacLeod, J. A. Lipton-Duffin, D. Cui, S. De Feyter and F. Rosei, Langmuir, 2015, 31, 7016–7024 CrossRef CAS PubMed.
- K. S. Mali, K. Lava, K. Binnemans and S. De Feyter, Chem. – Eur. J., 2010, 16, 14447–14458 CrossRef CAS PubMed.
- W. L. Jorgensen and P. Schyman, J. Chem. Theory Comput., 2012, 8, 3895–3901 CrossRef CAS PubMed.
- A. J. Groszec, Proc. R. Soc. A, 1970, 314, 473 CrossRef.
- M. Blunt, X. Lin, M. d. C. Gimenez-Lopez, M. Schroder, N. R. Champness and P. H. Beton, Chem. Commun., 2008, 2304–2306 RSC.
- Y. Yang and C. Wang, Curr. Opin. Colloid Interface Sci., 2009, 14, 135–147 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. B.01, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- L. P. Wolters, P. Schyman, M. J. Pavan, W. L. Jorgensen, F. M. Bickelhaupt and S. Kozuch, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 523–540 Search PubMed.
- J. W. Ponder and F. M. Richards, J. Comput. Chem., 1987, 8, 1016–1024 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc04499f |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |