Open Access Article
Open Access ArticleSynthesis and structure of a family of rhodium polystannide clusters [Rh@Sn10]3–, [Rh@Sn12]3–, [Rh2@Sn17]6– and the first triply-fused stannide, [Rh3@Sn24]5–†
Chao
Liu
ab,
Xiao
Jin
c,
Lei-Jiao
Li
d,
Jun
Xu
 a,
John E.
McGrady
a,
John E.
McGrady
 *c and
Zhong-Ming
Sun
*c and
Zhong-Ming
Sun
 *ab
*ab
aSchool of Materials Science and Engineering & National Institute for Advanced Materials, Tianjin Key Lab for Rare Earth Materials and Applications, Center for Rare Earth and Inorganic Functional Materials, State Key Laboratory of Elemento-Organic Chemistry, Nankai University, Tianjin 300350, China. E-mail: sunlab@nankai.edu.cn; Web: http://zhongmingsun.weebly.com
bState Key Laboratory of Rare Earth Resource Utilization, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, 5625 Renmin Street, Changchun, Jilin 130022, China. E-mail: szm@ciac.ac.cn
cDepartment of Chemistry, University of Oxford, South Parks Road, Oxford OX1 3QR, UK. E-mail: john.mcgrady@chem.ox.ac.uk
dSchool of Chemistry & Environmental Engineering, Changchun University of Science & Technology, Changchun 130022, China
First published on 11th March 2019
Abstract
Through relatively subtle changes in reaction conditions, we have been able to isolate four distinct Rh/Sn cluster compounds, [Rh@Sn10]3−, [Rh@Sn12]3−, [Rh2@Sn17]6− and [Rh3@Sn24]5–, from the reaction of K4Sn9 with [(COE)2Rh(μ-Cl)]2(COE = cyclooctene). The last of these has a hitherto unknown molecular topology, an edge-fused polyhedron containing three Rh@Sn10 subunits, and represents the largest endohedral Group 14 Zintl cluster yet to have been isolated from solution. DFT has been used to place these new species in the context of known cluster chemistry. ESI-MS experiments on the reaction mixtures reveal the ubiquitous presence of {RhSn8} fragments that may play a role in cluster growth.
Introduction
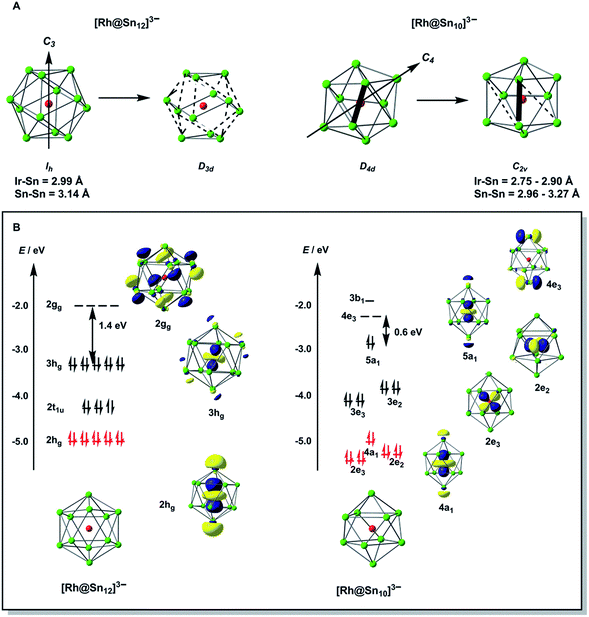
Over the past decade, Zintl phases and Zintl clusters have attracted a great deal of attention in the literature, in part due to their potential applications in cluster assembled materials, but also because of the great challenge they present to conventional models of bonding.1,2 Much of this research activity has been focused on the construction of ligand-free clusters, [Mx@En]q– (E = Ge, Sn, Pb),3 which may in turn provide access to even larger endohedral clusters with nanometer dimensions. The evolution of topology and electronic structure in these larger discrete clusters has the potential to bridge the gap between molecular gas-phase chemistry and the related binary alloys.4 Several clusters with up to 12 vertices have now been structurally characterized, including the smallest endohedral examples with 9-vertices [Co@Sn9]q–,5 [Ni@E9]4– (E = Ge, Sn),6 and [Cu@E9]3– (E = Sn, Pb).7 10-vertex analogues include bicapped square antiprismatic [Ni@Pb10]2−,8 pentagonal prismatic [M@Ge10]3– (M = Co, Fe),9 and also [Fe@Sn10]3–, which adopts an approximately C2v-symmetric structure that can be viewed as intermediate between the two.10 In the 12-vertex family the icosahedral structure is the most common,11 and is adopted by a range of late transition metal clusters including [M@Pb12]2– (M = Ni, Pd, Pt)12 and [Ir@Sn12]3–.13 Further to the left in the periodic table, the [Mn@Pb12]3–![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14a and [Co@Ge12]3–
14a and [Co@Ge12]3–![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14b clusters are also recognizably icosahedral, but are strongly elongated along one 2-fold axis and one 5-fold axis, respectively while the [Ru@Ge12]3– anion adopts a completely different bicapped pentagonal prismatic architecture with D2d point symmetry.15 A third structure type, the hexagonal prism (D6h), has not yet been reported in the crystalline phase, although there is compelling evidence that it is the most stable isomer for silicon clusters such as Cr@Si12 and [Mn@Si12]+.16 The extension of Zintl ion chemistry to clusters of higher nuclearity remains rather limited, and there are only a few known examples of endohedral germanium or tin clusters with two interstitial metal atoms. These include [Co2@Ge16]4–,17 [M2@Sn17]q– (M = Ni,18a Co,5a,5b Pt18b), [Ni2@Sn16Ge]4–,6a [Pd2@E18]4– (E = Ge, Sn)19 and [Ni3@Ge18]4–.6b In addition, a multiply endohedral structure [Sn@Cu12@Sn20]12− has been characterized in the intermetallic phases A12Cu12Sn21.20 Large tetrel clusters with contiguous polyhedral cages have also been isolated from solution, including [Ni6Ge13(CO)5]4–,21 [Sn14NiCO]4–,22 [Ti4Sn15Cp5]q–,23 [Pd3Ge18(EiPr3)6]2– (E = Si, Sn)24 and [Au3Ge45]9−,25 which is the largest heterometallic Zintl cluster known to date.
14b clusters are also recognizably icosahedral, but are strongly elongated along one 2-fold axis and one 5-fold axis, respectively while the [Ru@Ge12]3– anion adopts a completely different bicapped pentagonal prismatic architecture with D2d point symmetry.15 A third structure type, the hexagonal prism (D6h), has not yet been reported in the crystalline phase, although there is compelling evidence that it is the most stable isomer for silicon clusters such as Cr@Si12 and [Mn@Si12]+.16 The extension of Zintl ion chemistry to clusters of higher nuclearity remains rather limited, and there are only a few known examples of endohedral germanium or tin clusters with two interstitial metal atoms. These include [Co2@Ge16]4–,17 [M2@Sn17]q– (M = Ni,18a Co,5a,5b Pt18b), [Ni2@Sn16Ge]4–,6a [Pd2@E18]4– (E = Ge, Sn)19 and [Ni3@Ge18]4–.6b In addition, a multiply endohedral structure [Sn@Cu12@Sn20]12− has been characterized in the intermetallic phases A12Cu12Sn21.20 Large tetrel clusters with contiguous polyhedral cages have also been isolated from solution, including [Ni6Ge13(CO)5]4–,21 [Sn14NiCO]4–,22 [Ti4Sn15Cp5]q–,23 [Pd3Ge18(EiPr3)6]2– (E = Si, Sn)24 and [Au3Ge45]9−,25 which is the largest heterometallic Zintl cluster known to date.
The intimate pathways by which these larger clusters form from smaller component parts have not proven easy to establish for a number of reasons. First, there is rarely a precise stoichiometric relationship between reactants and products, and extensive fragmentation and recombination is clearly an integral feature of cluster growth.26,27 In addition, the under-coordinated nature of the intermediates leads to facile rearrangements that frustrate attempts to follow their formation and decay in real time. Finally, even when species can be crystallized, it is not clear whether the stability of the salt really reflects any intrinsic stability of the cluster anion or simply the favorable lattice enthalpies afforded by the most highly charged anions. Significant insights into the growth of Ti/Sn clusters have, however, been made by Fässler and co-workers who crystallized [Ti(η4-Sn8)Cp]3–, [TiCp2(η1-Sn9)(NH3)]3– and [Ti4Sn15Cp5]q– from the reactions of K4Sn9 and K12Sn17 with [TiCp2Cl2] in liquid ammonia under different conditions.23 The [Sn8Ti] unit in [Ti(η4-Sn8)Cp]3– resembles a fragment of a Ti@Sn12 icosahedron, and may therefore constitute an intermediate in cluster growth.
Herein we describe the rich chemistry that emerges from the reaction of K4Sn9 with a source of rhodium (in this case [(COE)2Rh(u-Cl)]2) in ethylenediamine (en) or dimethylformamide (DMF) solution. Apparently subtle changes in the reaction conditions allow for the isolation of four distinct crystalline products containing the [Rh@Sn10]3– (1), [Rh@Sn12]3– (2a/b) and [Rh2@Sn17]6– (3) anions as well as a triply-fused macropolyhedral cluster, [Rh3@Sn24]5− (4). The structure of the 24-vertex cluster 4 is unprecedented in Zintl chemistry, and is the largest metalated polystannide cluster yet to be isolated from solution. We use density functional theory to explore the electronic structure of all four new products, and to place them in the context of known Zintl ion chemistry. By monitoring the reaction mixtures by electrospray ionization mass spectrometry (ESI-MS), we can identify smaller cluster units present in solution that may play a role in the agglomeration of the larger clusters.
Results and discussion
[Rh@Sn10]3– (1) and [Rh@Sn12]3– (2a)
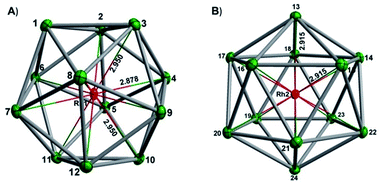
In our initial experiments, the reactants, K4Sn9 and [(COE)2Rh(u-Cl)]2, were stirred for two hours at room temperature. The ESI-MS of the resulting mixture shows a dominant peak corresponding to [RhSn10]– along with smaller peaks due to [RhSn12]–, [RhSn8]– and [RhSn9]– (Fig. 1, top). Filtration of the resultant dark brown solution followed by layering with toluene (Tol) yielded crystals of [K(2,2,2-crypt)]3[Rh@Sn10]·2en along with a smaller amount of crystals of [K(2,2,2-crypt)]3[Rh@Sn12]·2Tol, the total yield being ∼45% based on K4Sn9. X-ray diffraction revealed that the latter contains two crystallographically distinct [Rh@Sn12]3– anions in the unit cell (Fig. 2). One of these is almost perfectly icosahedral (Ih) with twelve Rh–Sn bond lengths of 2.915(5) Å. The structure of the second [Rh@Sn12]3– anion in the unit cell is more interesting, in so much as it is distinctly elongated along one 3-fold axis, giving a D3d-symmetric structure with six long (2.950(5) Å) and six short (2.878(5)Å) Rh–Sn bond lengths. These values represent a distortion of ∼±1.2% about the mean, which is almost identical to that in the perfectly icosahedral anion. The prolate distortion is strikingly reminiscent of that in [Mn@Pb12]3–, and we explore its electronic origins in our electronic structure analysis (vide infra). The presence of [Rh@Sn12]3– in solution was corroborated by ESI-MS of crystalline sample of 2a: negative and positive ion mode spectra revealed mass envelopes corresponding to [RhSn12]– and {[K(2,2,2-crypt)]4[RhSn12]}+, respectively (Fig. S36–S39†). In addition, crystals of 2a dissolved in en display one sharp 119Sn NMR resonance signal at 460.0 ppm at room temperature (Fig. S41†).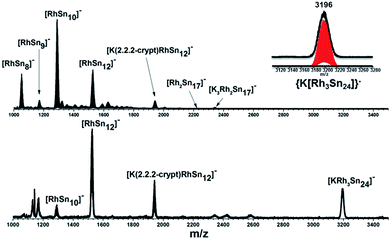 | ||
| Fig. 1 ESI-MS (m/z: 1000–3500) in negative ion mode of en(bottom) and DMF (up) reaction mixtures. The inset show the [KRh3Sn24]− peak and its simulated pattern. | ||
All attempts to refine the X-ray diffraction data for compound 1 were frustrated by positional disorder in the anionic core: there are two distinct [Rh@Sn10]3– components in a 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 ratio. Seven of the Sn positions are common to the two components but the other three differ and this, ultimately, prevents us from assigning specific bond lengths (Fig. S2†). Nevertheless, it is clear from the data that the crystal contains a 10-vertex Rh@Sn10 unit along with three charge balancing [K(2,2,2-crypt)]+ cations, and moreover that the anion is significantly distorted away from the ideal D4d structure adopted by isoelectronic [Ni@Pb10]2–. ESI-MS of the single crystal of 1 confirms that the [Rh@Sn10] unit remains intact in the gas phase (Fig. S30–S34†). The 119Sn NMR spectrum of 1 in en displays a single resonance at −1313.6 ppm at room temperature, indicating that all Sn atoms are time-averaged in solution (Fig. S42†).28
38 ratio. Seven of the Sn positions are common to the two components but the other three differ and this, ultimately, prevents us from assigning specific bond lengths (Fig. S2†). Nevertheless, it is clear from the data that the crystal contains a 10-vertex Rh@Sn10 unit along with three charge balancing [K(2,2,2-crypt)]+ cations, and moreover that the anion is significantly distorted away from the ideal D4d structure adopted by isoelectronic [Ni@Pb10]2–. ESI-MS of the single crystal of 1 confirms that the [Rh@Sn10] unit remains intact in the gas phase (Fig. S30–S34†). The 119Sn NMR spectrum of 1 in en displays a single resonance at −1313.6 ppm at room temperature, indicating that all Sn atoms are time-averaged in solution (Fig. S42†).28
To gain further insight into the structural chemistry of 1 and 2, we have used density functional theory to explore the potential energy surfaces of both anions. The most stable structure for the isolated [Rh@Sn12]3– anion proves to be a perfect icosahedron with optimized Rh–Sn and Sn–Sn bond lengths of 2.99 Å and 3.14 Å, respectively. These compare favourably with the average values of 2.915 Å and 3.06 Å in the more symmetric of the two anions in the unit cell of 2a. All attempts to locate a stable local minimum corresponding to the alternative D3d-symmetric isomer were unsuccessful: the calculations converged instead on the icosahedral structure identified previously, and a single-point calculation performed at a D3d-symmetric geometry where the Rh–Sn bond lengths are distorted by 1.2% of the equilibrium value (2.99 Å) indicates that the distortion seen in the crystal structure destabilises the cluster by only ∼0.004 eV (0.1 kJ mol−1). The Bürgi–Dunitz structural correlation model29 holds that the energy associated with ‘crystal packing’ will distort a molecule along its lowest-frequency vibrational modes, where the energetic cost of the distortion is least. Substantial distortions away from the gas-phase minimum are therefore indicative of a very flat potential surface along the mode in question. Conversely, if the global minimum on the gas-phase potential energy surface is deep (i.e. the bonds are intrinsically strong), the steric pressure of counter-ions in the solid state should not be a strong enough perturbation to distort the structure to any great extent. The negligible energetic cost of the D3d distortion in [Rh@Sn12]3– is therefore consistent with the crystallographic observations. The driving force for such a distortion is apparent in the Kohn–Sham array in Fig. 3B. The 3hg HOMO is an out-of-phase combination of Rh 4d orbitals (19%) and cage-based orbitals of the same symmetry. The corresponding in-phase combination, 2hg, lies ∼1.8 eV lower in energy, and carries the majority of the Rh 4d character (61%, shown in red). In contrast the LUMO, with gg symmetry, is localized entirely on the cage. The mismatch in symmetry of the HOMO and LUMO means that a distortion of the icosahedron to some lower symmetry, where one or more of the components of the hg HOMO shares a common irreducible representation with one or more component of the gg LUMO, is required to allow electron density to flow from the electron-rich metal into the LUMO of the Sn12 cage (a so-called second-order Jahn–Teller distortion). A reduction in symmetry from Ih to D3d achieves precisely this: hg → {a1g + 2eg} and gg → {a1g + a2g + eg}. In the case of [Rh@Sn12]3– the HOMO–LUMO gap is clearly sufficiently large to prevent this charge transfer from occurring in the gas-phase minimum structure, but nevertheless it softens the potential surface along the D3d-symmetric distortion mode, such that the steric pressure in the solid state can drive the cluster anion along this valley.
Turning to the smaller [Rh@Sn10]3– cluster, we have already noted that all attempts to establish the topology of the cluster have been frustrated by disorder. However, the computed potential energy surface indicates that the global minimum is in fact a C2v-symmetric structure with two square faces, although a D4d-symmetric bi-capped square antiprism lies only 0.16 eV higher in energy. These two structures are in fact closely related, and only a small rotation of one Sn–Sn edge (shown as bold in Fig. 3A) is required to interconvert the D4d and C2v-symmetric forms. In such circumstances, the Bürgi–Dunitz structural correlation model again suggests that a range of intermediate structures linking the D4d- and C2v-symmetric limits should be accessible in the solid state, and this is the most likely source of crystallographic disorder in [Rh@Sn10]3–. The potential energy surface of [Rh@Sn10]3– is strikingly similar to that reported for [Fe@Sn10]3–,10 and it is perhaps no coincidence that the crystallography of this iron cluster was also beset by problems of disorder. The electronic origins of the distortion away from perfect D4d symmetry in [Fe@Sn10]3– were discussed at some length in ref. 10, and are in fact very similar to those identified for the Ih → D3d distortion in [Rh@Sn12]3– in the previous section. In short, in the D4d-symmetric isomer there is a very small gap between the HOMO, with 23% Rh 4d character, and the LUMO which is localised entirely on the Sn10 cage. A second-order Jahn–Teller distortion will again allow the transfer of electron density from the electron-rich metal to the cage. The potential energy surfaces of [Rh@Sn10]3– and [Rh@Sn12]3– are therefore qualitatively very similar, in so much as both feature a highly symmetric isomer (Ih or D4d) that is easily distorted along a low-symmetry mode (D3d or C2v). In [Rh@Sn10]3– this distortion is energetically favourable whereas in [Rh@Sn12]3– it is marginally unfavourable, but the underlying cause is the same in both cases.
[Rh2@Sn17]6– (3)
The synthesis of 3 followed exactly the same initial protocol described above for 1 and 2a. However, after the solution is completely depleted of 1 and 2a, crystals of {K3[K(2,2,2-crypt)]3[Rh2@Sn17]}·4en are obtained in lower yields (10%) from dilute solutions over the course of ca. two weeks. The ESI-MS of the original reaction mixture also confirmed the presence of the ion [Rh2Sn17]– (Fig. S23†) along with [K3Rh2Sn17]– (Fig. S24†) in solution. Furthermore, analysis of a DMF solution of the salt showed mass envelopes for the monoanions [K3Rh2Sn17]– and [K5Rh2Sn17]– (Fig. S40 and S41†). Unfortunately, the 119Sn NMR data shows no signal due either to the low concentration in solution or to the intrinsic instability of the anion. The cluster is based on two fused Rh@Sn9 units sharing a single vertex, and three tightly bound K+ ions along with three isolated [K(2,2,2-crypt)]+ units provide charge balance (Fig. 4, top). Rh–Sn bond lengths lie in a narrow range around 2.72 Å (from 2.696(5) Å to 2.761(5) Å) with the exception of those to the bridging Sn(9) which are somewhat shorter, at 2.497(5) Å. The basic structural features of the Rh2Sn17 unit are strikingly similar to those in isostructural [Ni2@Sn17]4–, and [Co2@Sn17]5–. There is a distinct bending at the central Sn atom (Rh–Sn–Rh = 163.9°) which is present in one of the two characterized isomers of [Co2@Sn17]5–,5b but not in the Ni analogue which is almost perfectly D2d-symmetric. The structure of the isoelectronic Pt cluster, [Pt2@Sn17]4–, in contrast appears very different – it adopts a C2-symmetric structure based on a single ellipsoidal Sn17 cage. The four structures can, however, be considered as a continuum linked by a progressive decrease in the M-Sn9-M angle, from 180° in [Ni2@Sn17]4– to 163.9° which, in turn, leads to a short Sn–Sn contact between the two hemispheres (Sn7–Sn13 in Fig. 4, bottom).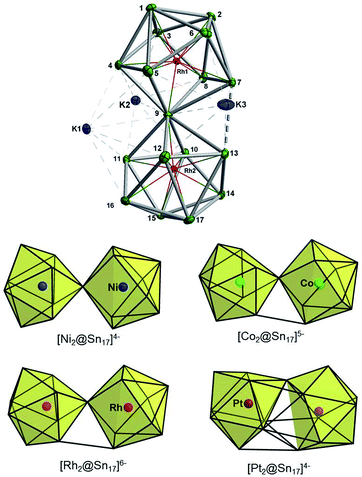 | ||
| Fig. 4 Top: Thermal ellipsoid plots of the [Rh2Sn17]6– anion and its three tightly bound K+ cations (drawn at 50% probability). Bottom: Comparison of the known structures of M2Sn17 anions, M = Ni,18a Co,5b Rh and Pt.18b | ||
The DFT-optimized structure of [Rh2@Sn17]6– is perfectly D2d symmetric, and is topologically identical to the Ni analogue (ESI†). When the three tightly-bound K+ ions are included in the computational model ({K3[Rh2@Sn17]}3–), however, the optimized structure is distinctly bent, with a Rh–Sn9–Rh angle of 164° compared to the value of 163.9° in the X-ray structure. Like clusters 1 and 2a, it appears, therefore, that the potential energy surface for the gas-phase anion [Rh2@Sn17]6– is soft enough to allow the crystalline environment to distort the structure away from the gas-phase minimum. The tightly-bound nature of the K+ ions means that they represent a significant perturbation, and as a result the distortion is much more pronounced that was the case in either [Rh@Sn10]3– or [Rh@Sn12]3– where the cations were sequestered in (2,2,2-crypt) ligands.
[Rh3@Sn24]5– (4)
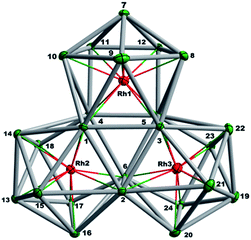
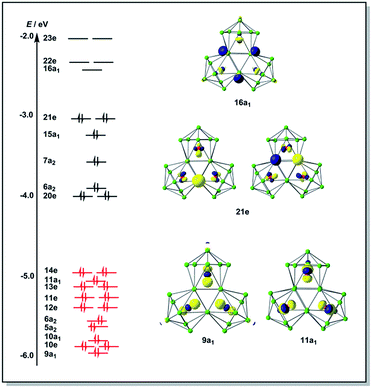
The final product [K(2,2,2-crypt)]5[Rh3@Sn24]·2DMF·Tol was also prepared by treating an en solution of K4Sn9 with [(COE)2Rh(u-Cl)]2. After removal of the en solvent, the residue was re-dissolved in DMF and heated at 50 °C for five hours. Layering with toluene yields small quantities of crystals of 4, along with [K(2,2,2-crypt)]3[Rh@Sn12]·2DMF, 2b, in approximately 25% yield in total. ESI-MS experiments on the DMF reaction mixture (Fig. 1, bottom) indicate that the potassium adduct {K[Rh3Sn24]}– is stable in solution. The other dominant species in the ESI-MS is [RhSn12]– along with smaller amounts of [RhSn10]–. In an attempt to shed some light on possible formation mechanisms for 4, we have also established an alternative synthetic route starting from a preformed crystalline sample of 1, which was re-dissolved in DMF. The resulting solution was processed following the same procedure as for the original synthesis of 4, and crystals were again obtained as the sole product from the solution, this time in a reproducible 30% yield. The increased yield in this second reaction provides circumstantial evidence that [Rh@Sn10]3– or one of its decomposition products may be an intermediate in the formation of the larger complex [Rh3@Sn24]5–. All attempts to characterize the crystalline product 4 further by ESI-MS or 119Sn NMR spectroscopy were frustrated by rapid decomposition of the anion in solution.The structure of the anion 4 is unprecedented in Zintl-ion chemistry (Fig. 5), and merits a detailed discussion. The cluster is composed of three fused Rh@Sn10 units arranged in an approximately C3v-symmetric geometry around an almost perfectly trigonal prismatic Sn6 unit (Fig. 6A). The three Rh@Sn10 subunits are topologically equivalent, and each is very similar to the C2v-symmetric minimum of [RhSn10]3– itself. Within each 10-vertex subunit, a Sn4 square is topped by a capped pentagonal ring: a comparable arrangement is also found in the cluster core in the metalloid clusters {Sn10[Si(SiMe3)3]4}2−,30 and [Ge10{Fe(CO)4}8]6−.31 The Rh–Sn distances range from 2.657(10) to 3.059 (11) Å, comparable to those observed in 1–3, and the Sn–Sn contacts (2.967(11) − 3.190(10) Å) are also consistent with related clusters. The lower face of the cluster (Fig. 6B) has three squares surrounding the central triangle (atoms 4-5-6), forming a slightly concave surface. The upper surface (Fig. 6C), in contrast, has three triangles surrounding the central Sn3 unit (1–2–3). Although the overall symmetry of 4 is close to C3v, subtle differences between three subunits are apparent, particularly on the upper surface (Fig. 6D). Our DFT calculations, however, converge on a perfectly C3v-symmetric structure, very similar to that found in the X-ray experiment, suggesting once again that these subtle distortions are most likely a consequence of crystal packing effects rather than any intrinsic instability of the symmetric structure. The gross features of the cluster are highly reminiscent of the triply-fused icosahedral B28 unit in β-rhombohedral boron32 and, most strikingly, with the ‘triply nido’ defect Ga28 unit in the ternary gallium phase Na13K4Ga47.45.33 It is useful also to highlight the structural relationship between triply fused 4 and the β-isomer of [Co2@Ge16]4–.17b The latter contains two fused Co@Ge10 units with identical topology to those in 4, sharing a single square face rather than the three faces of a trigonal prism. [Co2@Ge16]4– and [Rh3@Sn24]5– can therefore be viewed as the dimer and trimer, respectively, of a common ME8 unit. The doubly-degenerate HOMO of [Rh3@Sn24]5– (Fig. 7) is localised primarily on the three Sn atoms of the trigonal prism on the convex face (Sn1, Sn2, Sn3 in Fig. 5 and 6). The LUMO is also localised on the same three Sn atoms and the cluster is therefore isolobal with a Sn atom, suggesting that this face may be a possible site for further cluster growth.
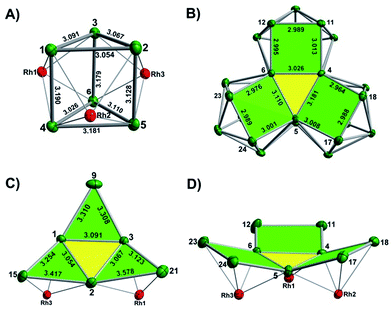 | ||
| Fig. 6 (A) The Sn6 prism of the [Rh3@Sn24]5− structure; (B) the backside view of cluster [Rh3@Sn24]5–; (C) and (D) the upper and lower faces of the [Rh3@Sn24]5– cluster. | ||
Possible growth mechanisms
The results summarized in the previous paragraphs provide a framework for a discussion of possible cluster growth mechanisms. The early stages of cluster growth involve the formation of the clusters containing a single transition metal, [Rh@Sn10]3– and [Rh@Sn12]3–, possibly via an intermediate such as [L2RhSn9]3–, where L = COE or a solvent molecule and the RhL2 fragment sits on the surface of a 10-vertex cluster. Fässler has observed an analogous [(COD)IrSn9]3– species and proposed its intermediacy in the formation of [Ir@Sn12]3–.13 The subsequent steps that lead to the [Rh2@Sn17]6– and [Rh3@Sn24]5– clusters are more difficult to establish, a point that has been highlighted by recent work from Dehnen and co-workers where they speculated that fusion of smaller preformed components may provide a pathway to complex species.27a Our synthetic strategy indicates that progressively increasing the temperature from room temperature to 50 °C, along with prolonged reaction times, allows the Rh/Sn system to evolve from products containing a single transition metal centre to two, and finally three. Further increases in temperature, however, result in decomposition to elemental tin. We have also shown that somewhat higher yields of [Rh3@Sn24]5– can be achieved by starting from a solution of pre-formed [Rh@Sn10]3– rather than from K4Sn9 and a source of rhodium, offering circumstantial evidence that [Rh@Sn10]3– or one of its fragmentation products may play an important role in cluster growth. Given the many uncertainties surrounding the composition and charges of the dominant species in solution as well as the difficulties in accounting for any elemental Sn formed in the reaction, we have chosen not to attempt to compute a reaction pathway that connects the clusters of different size and charge. We can, however, use the experimental data to speculate on the species that may be important in this process. Specifically, the ESI-MS of the solution of the dissolved crystalline sample of 1 in DMF reveals a complex reaction mixture containing, in addition to [Rh@Sn10]– and {K(2,2,2-crypt)[Rh@Sn10]}–, prominent peaks due to [Rh@Sn8]– (Fig. S33†) and {K[Rh@Sn8]}– (Fig. S34†), respectively. The K+-free anion [Rh@Sn8]– was also present in substantial quantities in the ESI-MS of the original reaction mixture (Fig. 1, top), and its appearance in two independent spectra suggests that the [Rh@Sn8]– fragment may represent an island of stability in the Rh@Snx family. A survey of the potential energy surface for [Rh@Sn8]– has identified the most stable isomer as a C2v-symmetric singlet with the Rh atom sitting on the surface of the cluster in approximately square-planar coordination (Fig. S35†). The structure is, in fact, strikingly reminiscent of the TiSn8 fragment in [Ti(η4-Sn8)Cp], which has been proposed as a an intermediate in the growth of the Ti/Sn cluster family.23 A [RhSn8] fragment would most likely arise through loss of Sn from a larger poly-stannide cluster, and this appears to be an entirely general phenomenon: Eichhorn and co-workers have identified a series of anions {K(2,2,2-crypt)[Ni2@Snx]}–, x = 12–17, in their ESI-MS study of the parent [Ni2@Sn17]– cluster.18a The loss of Sn from a stable [Rh@Sn10]z– or [Rh@Sn12]z– unit followed by coalescence of two fragments therefore offers a plausible pathway for cluster growth: for example, a bimolecular reaction between [Rh@Sn8]– and [Rh@Sn9]– may be the source of the small amounts of 3 generated in the reaction. Alternatively, coalescence of [Rh@Sn8]z– + [Rh@Sn10]z–, or of two [Rh@Sn10]z– units, followed by loss of Sn from putative {Rh2Sn18} or {Rh2Sn20} intermediates cannot be ruled out, given the precedent for extensive Sn loss from [Ni2@Sn17]–. Further loss of Sn before or after a bimolecular reaction then offers a route into species of higher nuclearity: for example [Rh2@Sn17]z– → [Rh2@Sn16]z– → [Rh3@Sn24]z–.Conclusions
In summary, we have reported a synthetic protocol based on the reaction of K4Sn9 with a source of low-valent rhodium which, with subtle modifications, can be used to generate four distinct clusters with Rh encapsulated in deltahedral polystannide anions. The initial products, [Rh@Sn12]3– and [Rh@Sn10]3–, contain a single Rh center but prolonged heating at moderate temperatures generates high nuclearity species including an unprecedented [Rh3@Sn24]5– cluster based on three RhSn8 units fused around a central Sn6 trigonal prism. DFT suggests that all four clusters can be viewed, to a first approximation, as containing closed-shell Rh(–I) ions. The Rh 4d orbitals are not, however, completely core-like, and their mixing with orbitals on the Snx cluster results in structural flexibility that has not been observed in isoelectronic analogues containing later transition metal such as [Ni@Pb10/12]2–. ESI-MS measurements, both on the initial reaction mixture and on solutions of pre-formed [Rh@Sn10]3–, indicate that loss of Sn atoms to form [Rh@Sn8] fragments is facile, and indeed there are precedents for similar loss of Sn from Ni2@Sn17 clusters in the literature. We propose tentatively that this fragment may play a role in the nucleation process. Although we have seen no evidence for coalescence beyond the Rh3@Sn24 stoichiometry, the [Rh3@Sn24]5− anion represents a possible intermediate stage in the growth of even larger group 14 intermetalloid clusters.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (21722106, 21571171, and 21871246), Youth Foundation project of Jilin Province 20180520009JH, and Jilin Province innovative research program (20160519004JH).Notes and references
- (a) S. Scharfe, F. Kraus, S. Stegmaier, A. Schier and T. F. Fässler, Angew. Chem., Int. Ed., 2011, 50, 3630 CrossRef CAS PubMed; (b) S. C. Sevov and J. M. Goicoechea, Organometallics, 2006, 25, 5678 CrossRef CAS; (c) R. S. P. Turbervill and J. M. Goicoechea, Chem. Rev., 2014, 114, 10807 CrossRef CAS PubMed; (d) N. Korber, Angew. Chem., Int. Ed., 2009, 48, 3216 CrossRef CAS PubMed; (e) K. Mayer, J. Weßing, T. F. Fässler and R. A. Fischer, Angew. Chem., Int. Ed., 2018, 57, 14372 CrossRef CAS PubMed; (f) R. J. Wilson, B. Weinert and S. Dehnen, Dalton Trans., 2018, 47, 14861 RSC; (g) C. Liu and Z.-M. Sun, Coord. Chem. Rev., 2019, 382, 32 CrossRef CAS.
- (a) M. J. Moses, J. C. Fettinger and B. W. Eichhorn, Science, 2003, 300, 778 CrossRef CAS PubMed; (b) Y. Wang, M. Moses-DeBusk, L. Stevens, J. Hu, P. Zavalij, K. Bowen, B. I. Dunlap, E. R. Glaser and B. W. Eichhorn, J. Am. Chem. Soc., 2017, 139, 619 CrossRef PubMed; (c) Y. Wang, P. Zavalij and B. Eichhorn, Chem. Commun., 2017, 53, 11600 RSC; (d) J. M. Goicoechea and S. C. Sevov, Angew. Chem., Int. Ed., 2006, 45, 5147 CrossRef CAS PubMed; (e) K. Mayer, L. A. Jantke, S. Schulz and T. F. Fässler, Angew. Chem., Int. Ed., 2017, 56, 2350 CrossRef CAS PubMed; (f) F. S. Geitner, W. Klein and T. F. Fässler, Angew. Chem., Int. Ed., 2018, 130, 14717 CrossRef; (g) R. J. Wilson, L. Broeckaert, F. Spitzer, F. Weigend and S. Dehnen, Angew. Chem., Int. Ed., 2016, 55, 11775 CrossRef CAS PubMed; (h) R. J. Wilson, F. Hastreiter, K. Reiter, P. Büschelberger, R. Wolf, R. Gschwind, F. Weigend and S. Dehnen, Angew. Chem., Int. Ed., 2018, 57, 15359 CrossRef CAS PubMed.
- (a) T. F. Fässler and S. D. Hoffmann, Angew. Chem., Int. Ed., 2004, 43, 6242 CrossRef PubMed; (b) T. F. Fässler, Struct. Bonding, 2011, 140, 91 CrossRef; (c) B. Weinert and S. Dehnen, Struct. Bonding, 2017, 174, 99 CrossRef.
- (a) R. B. King, Struct. Bonding, 2011, 140, 1 CAS; (b) V. Arcisauskaite, X. Jin, J. M. Goicoechea and J. E. McGrady, Struct. Bonding, 2016, 169, 181 CrossRef CAS.
- (a) V. Hlukhyy, H. He, L. A. Jantke and T. F. Fässler, Chem.–Eur. J., 2012, 18, 12000 CrossRef CAS PubMed; (b) H. He, W. Klein, L. A. Jantke and T. F. Fässler, Z. Anorg. Allg. Chem., 2014, 640, 2864 CrossRef CAS; (c) V. Hlukhyy, S. Stegmaier, L. Wüllen and T. F. Fässler, Chem.–Eur. J., 2014, 20, 12157 CrossRef CAS PubMed.
- (a) M. M. Gillett-Kunnath, J. I. Paik, S. M. Jensen, J. D. Taylor and S. C. Sevov, Inorg. Chem., 2011, 50, 11695 CrossRef CAS PubMed; (b) J. M. Goicoechea and S. C. Sevov, Angew. Chem., Int. Ed., 2005, 44, 4026 CrossRef CAS PubMed.
- S. Scharfe, T. F. Fässler, S. Stegmaier, S. D. Hoffmann and K. Ruhland, Chem.–Eur. J., 2008, 14, 4479 CrossRef CAS PubMed.
- E. N. Esenturk, J. Fettinger and B. Eichhorn, Chem. Commun., 2005, 247 RSC.
- (a) J. Q. Wang, S. Stegmaier and T. F. Fässler, Angew. Chem., Int. Ed., 2009, 48, 1998 CrossRef CAS PubMed; (b) B. B. Zhou, M. S. Denning, D. L. Kays and J. M. Goicoechea, J. Am. Chem. Soc., 2009, 131, 2802 CrossRef CAS PubMed.
- T. Krämer, J. C. A. Duckworth, M. D. Ingram, B. B. Zhou, J. E. McGrady and J. M. Goicoechea, Dalton Trans., 2013, 42, 12120 RSC.
- (a) L. F. Cui, X. Huang, L. M. Wang, D. Y. Zubarev, A. I. Boldyrev, J. Li and L. S. Wang, J. Am. Chem. Soc., 2006, 128, 8390 CrossRef CAS PubMed; (b) L. F. Cui, X. Huang, L. M. Wang, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2007, 46, 742 CrossRef CAS PubMed; (c) L. F. Cui, X. Huang, L. M. Wang, J. Li and L. S. Wang, J. Phys. Chem. A, 2006, 110, 10169 CrossRef CAS PubMed.
- (a) E. N. Esenturk, J. Fettinger, Y. F. Lam and B. Eichhorn, Angew. Chem., Int. Ed., 2004, 43, 2132 CrossRef CAS PubMed; (b) E. N. Esenturk, J. Fettinger and B. Eichhorn, J. Am. Chem. Soc., 2006, 128, 9178 CrossRef CAS PubMed.
- J. Q. Wang, S. Stegmaier, B. Wahl and T. F. Fässler, Chem.–Eur. J., 2010, 16, 1793 CrossRef CAS PubMed.
- (a) B. B. Zhou, T. Kramer, A. L. Thompson, J. E. McGrady and J. M. Goicoechea, Inorg. Chem., 2011, 50, 8028 CrossRef CAS PubMed; (b) C. Liu, L. J. Li, I. A. Popov, R. J. Wilson, C. Q. Xu, J. Li, A. I. Boldyrev and Z. M. Sun, Chin. J. Chem., 2018, 36, 165 Search PubMed.
- G. Espinoza-Quintero, J. C. A. Duckworth, W. K. Myers, J. E. McGrady and J. M. Goicoechea, J. Am. Chem. Soc., 2014, 136, 1210 CrossRef CAS PubMed.
- (a) S. N. Khanna, B. K. Rao and P. Jena, Phys. Rev. Lett., 2002, 89, 016803 CrossRef CAS PubMed; (b) W. Zheng, J. M. Nilles, D. Radisic and K. H. Bowen, J. Chem. Phys., 2005, 122, 071101 CrossRef PubMed.
- (a) X. Jin, G. Espinoza-Quintero, B. Below, V. Arcisauskaite, J. M. Goicoechea and J. E. McGrady, J. Organomet. Chem., 2015, 792, 149 CrossRef CAS; (b) C. Liu, I. A. Popov, L. J. Li, N. Li, A. I. Boldyrev and Z. M. Sun, Chem.–Eur. J., 2018, 24, 699 CrossRef CAS PubMed.
- (a) E. N. Esenturk, J. C. Fettinger and B. W. Eichhorn, J. Am. Chem. Soc., 2006, 128, 12 CrossRef CAS PubMed; (b) B. Kesanli, J. E. Halsig, P. Zavalij, Y. F. Lam and B. W. Eichhorn, J. Am. Chem. Soc., 2007, 129, 4567 CrossRef CAS PubMed.
- (a) J. M. Goicoechea and S. C. Sevov, J. Am. Chem. Soc., 2005, 127, 7676 CrossRef CAS PubMed; (b) Z. M. Sun, H. Xiao, J. Li and L. S. Wang, J. Am. Chem. Soc., 2007, 129, 9560 CrossRef CAS PubMed; (c) F. S. Kocak, P. Zavalij, Y. F. Lam and B. W. Eichhorn, Inorg. Chem., 2008, 47, 3515 CrossRef CAS PubMed; (d) F. K. Sheong, W.-J. Chen, J.-X. Zhang, Y. Li and Z. Y. Lin, Dalton Trans., 2017, 46, 2214 RSC.
- S. Stegmaier and T. F. Fässler, J. Am. Chem. Soc., 2011, 133, 19758 CrossRef CAS PubMed.
- E. N. Esenturk, J. Fettinger and B. Eichhorn, Polyhedron, 2006, 25, 52 CrossRef.
- L. G. Perla and S. C. Sevov, Angew. Chem., Int. Ed., 2016, 55, 6721 CrossRef CAS PubMed.
- C. B. Benda, M. Waibel and T. F. Fässler, Angew. Chem., Int. Ed., 2015, 54, 522 CAS.
- (a) L. G. Perla and S. C. Sevov, J. Am. Chem. Soc., 2016, 138, 9795 CrossRef CAS PubMed; (b) L. G. Perla, A. Muñoz-Castro and S. C. Sevov, J. Am. Chem. Soc., 2017, 139, 15176 CrossRef CAS PubMed.
- A. Spiekermann, S. D. Hoffmann, T. F. Fässler, I. Krossing and U. Preiss, Angew. Chem., Int. Ed., 2007, 46, 5310 CrossRef CAS PubMed.
- B. Weinert, S. Mitzinger and S. Dehnen, Chem.–Eur. J., 2018, 24, 8470 CrossRef CAS PubMed.
- (a) S. Mitzinger, L. Broeckaert, W. Massa, F. Weigend and S. Dehnen, Nat. Commun., 2016, 7, 10480 CrossRef CAS PubMed; (b) F. Lips, R. Clérac and S. Dehnen, J. Am. Chem. Soc., 2011, 133, 14168 CrossRef CAS PubMed; (c) R. Ababei, W. Massa, K. Harms, X. L. Xie, F. Weigend and S. Dehnen, Angew. Chem., Int. Ed., 2013, 52, 13544 CrossRef CAS PubMed; (d) F. Lips and S. Dehnen, Angew. Chem., Int. Ed., 2009, 48, 6435 CrossRef CAS PubMed.
- B. Eichhorn and S. Kocak, Struct. Bonding, 2011, 140, 59 CrossRef CAS.
- P. Murray-Rust, H. B. Bürgi and J. D. Dunitz, J. Am. Chem. Soc., 1975, 97, 921 CrossRef CAS.
- (a) C. Schrenk, F. Winter, R. Pottgen and A. Schnepf, Chem.–Eur. J., 2015, 21, 2992 CrossRef CAS PubMed; (b) C. Schrenk, B. Gerke, R. Pottgen, A. Clayborne and A. Schnepf, Chem.–Eur. J., 2015, 21, 8222 CrossRef CAS PubMed.
- A. Schnepf and C. Schenk, Angew. Chem., Int. Ed., 2006, 45, 5373 CrossRef CAS PubMed.
- T. Ogitsu, E. Schwegler and G. Galli, Chem. Rev., 2013, 113, 3425 CrossRef CAS PubMed.
- M. Tillard-Charbonnel, A. Manteghetti and C. Belin, Inorg. Chem., 2000, 39, 1684 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: X-ray crystallographic file in CIF format, full experimental, computational details and 119Sn NMR as well as ESI-MS spectra are available. CCDC 1847077–1847080, 1811035. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc03948h |
| This journal is © The Royal Society of Chemistry 2019 |