Open Access Article
Open Access ArticleSingle-molecule photoredox catalysis†
Josef
Haimerl
a,
Indrajit
Ghosh
b,
Burkhard
König
 b,
Jan
Vogelsang
a and
John M.
Lupton
b,
Jan
Vogelsang
a and
John M.
Lupton
 *a
*a
aInstitut für Experimentelle und Angewandte Physik, Universität Regensburg, 93040 Regensburg, Germany. E-mail: john.lupton@ur.de
bInstitut für Organische Chemie, Universität Regensburg, 93040 Regensburg, Germany
First published on 22nd October 2018
Abstract
The chemistry of life is founded on light, so is it appropriate to think of light as a chemical substance? Planck's quantization offers a metric analogous to Avogadro's number to relate the number of particles to an effective reaction of single molecules and photons to form a new compound. A rhodamine dye molecule serves as a dehalogenating photocatalyst in a consecutive photoelectron transfer (conPET) process which adds the energy of two photons, with the first photon inducing radical formation and the second photon triggering PET to the substrate molecule. Rather than probing catalytic heterogeneity and dynamics on the single-molecule level, single-photon synthesis is demonstrated: the light quantum constitutes a reactant for the single substrate molecule in a dye–driven reaction. The approach illustrates that molecular diffusion and excited-state internal conversion are not limiting factors in conPET reaction kinetics because of catalyst–substrate preassociation. The effect could be common to photoredox catalysis, removing the conventional requirement of long excited-state lifetimes.
Introduction
Photosynthesis is the archetypal photocatalytic process. Having evolved from primordial life over billions of years, the conversion of sunlight into chemical energy remains enigmatic at once in its elegance and complexity. Whereas nature combines the energy of multiple photons to drive the conversion of carbon dioxide and water into carbohydrates, even the simplest artificial models of consecutive photoelectron transfer (conPET) synthesis have proven challenging to realize in the laboratory.1–7 Most photocatalysts involve expensive heavy-metal elements, but recently, the potential of hydrocarbon dyes in organic photocatalysis has emerged.8–11 First reports have shown that even common organic dyestuffs such as perylene12 or rhodamine13–15 function as effective organic photocatalysts. Since one of the goals of photocatalysis is to achieve cheap large-scale conversion of materials, single-molecule techniques have received only limited attention as an avenue to exploring and optimizing catalytic efficiency.16 But since, ultimately, photocatalysis is a molecular process, only microscopic spectroscopic techniques can provide truly mechanistic insights for quantum-chemical models.17–19 The main focus to date of the technique in the context of photocatalysis has been on exploring the spatial and temporal heterogeneity of reactions20–25 involving either single-photon mediated processes,26 or using chemical conversion of a dye molecule to track catalytic activity.27–30 In addition, single-molecule techniques have proven versatile in imaging protein-based reactions,31–35 and single-electron transfer events in general.36,52 Little attention has been paid to actually driving chemical reactions on the single-molecule level, with most prior interest directed at the potential of scanning-probe techniques in electrically catalysed reactions for lithographic applications.37–41Few experiments illustrate the particle nature of light more directly than single-photon counting. Passing the fluorescence of a single molecule through a semi-transparent mirror, a beam splitter, with single-photon detectors on either side will give rise to a pronounced anticorrelation in time between the two detectors: photon antibunching occurs, since the same photon cannot be picked up by both detectors.42 This antibunching arises on timescales of the excited-state lifetime of the molecule, i.e. typically several nanoseconds. On longer timescales, the opposite effect occurs: the fluorescent molecule undergoes quantum jumps between bright and dark states, for example between the singlet and the triplet manifolds of the excited state, leading to bunching of photons in time.43 This cycling between emissive and non-emissive states of the fluorophore provides crucial insight into the molecular quantum jumps responsible for the photosynthetic reaction.44
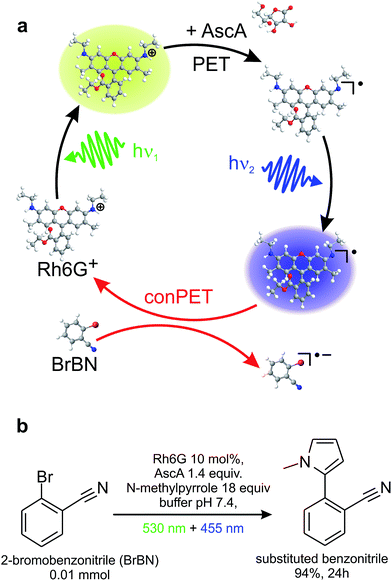
Here, we exploit the versatile method of single-molecule spectroscopy to probe the conPET process, one photon at a time. Fig. 1a illustrates a prototypical model process of aqueous organic photocatalysis exploiting consecutive photoelectron transfer (conPET).13 Absorption of a photon of energy hν1 by a rhodamine-6G (Rh6G) dye molecule leads to the formation of an excited singlet state. This singlet can undergo either radiative relaxation to the ground state by fluorescing, convert into a triplet by intersystem crossing, or interchange charge with reductants to form a radical. If the latter two processes occur, the dye molecule will cease to fluoresce for a short period of time, on the order of a few microseconds up to milliseconds.52 Addition of a reducing agent, ascorbic acid, promotes formation of the rhodamine radical from either the singlet or the triplet state. Since Rh6G in water is cationic,45 electron transfer from the reducing agent will form the neutral Rh6G radical R˙. This radical is characterised by a certain lifetime, and will ultimately relax to the cationic ground state by shedding the additional electron to the environment. The reduction potential of the R˙ ground state of −1 V vs. SCE13 is too low for electron transfer to occur to a substrate molecule to cleave stable bonds in aryl halides, such as in the dehalogenation of 2-bromobenzonitrile. Such a reaction requires a reduction potential of −1.9 V vs. SCE.13,46,47 The additional energy necessary to achieve this is made available by re-exciting the radical with a second photon of energy hν2. The reduction potential of the excited radical state of Rh6G, R˙*, is −2.4 V vs. SCE,13 which is sufficient for dehalogenation of the substrate. The second photon, in combination with the electron transfer to the substrate, therefore removes the additional electron from the dye radical, returning the dye to the ground state and thereby reactivating the S1 → S0 fluorescence cycle. The water-based mechanism proposed here is, in principle, analogous to reaction cycles recently described in organic solvents.13Fig. 1b states the synthetic-scale C–H aromatic substitution reaction of 2-bromobenzonitrile in water, using a reaction mixture containing the dye, substrate, and reducing agent, along with an additional trapping agent, N-methylpyrrole. The reaction occurs under continuous illumination with two light-emitting diodes (LEDs). The conversion yield after 24 hours determined by gas chromatography (GC) is 94%. Chromatograms of the product of this reaction and several control reactions are shown in Fig. S1 of the ESI.† This simple cycle constitutes one of the first reports of a C–H arylation by an organic dye in water and is therefore likely to be of interest in a range of aqueous biochemical reactions.13 Note that the additional trapping agent is only required in the ensemble reaction, where the product yield is monitored, and not in the single-molecule experiments, where the dye acts as the reporter on the reaction. Since the absorption spectrum of the radical is broad, the conPET cycle appears to work with a range of different photon energies. For experimental reasons, different light sources and wavelengths are used for the single-molecule and synthetic-scale reactions.
Even though this conPET cycle apparently works, it is not at all clear how a conventional dye molecule actually enables consecutive photoredox catalysis. Internal conversion is the most efficient process of energy dissipation from higher-lying states in molecules, and a photoexcited radical is expected to shed excess energy to the environment within a few hundred femtoseconds, as documented by transient absorption spectroscopy.48 Such ultrafast energy dissipation inhibits intermolecular photoreactions and would certainly prevent any diffusion-driven process from occurring in solution.
Results and discussion
Single-molecule imaging
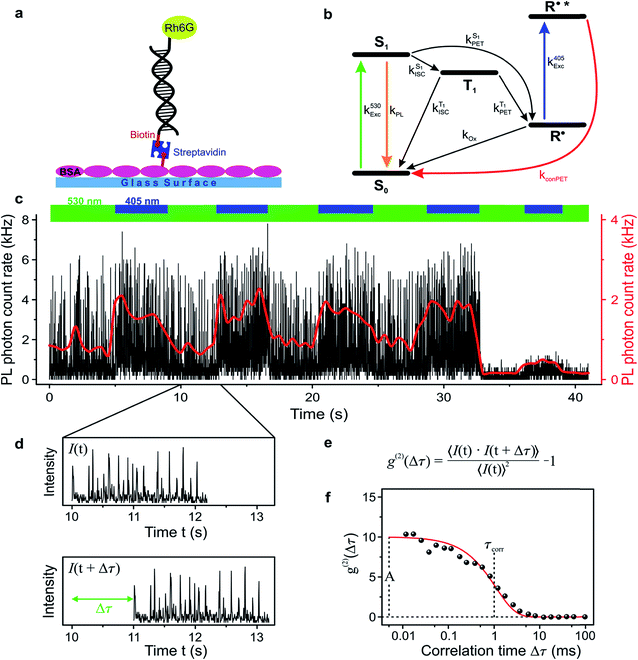
In order to study the conPET mechanism on the single-molecule single-photon level, the photocatalytically active dye molecules have to be immobilized on a surface to prevent diffusion in the solvent.49 We therefore tether the dyes to DNA oligomers, functionalised with biotin–streptavidin linkers, as sketched in Fig. 2a. These linkers bind to biotinylated bovine serum albumin (BSA) covered glass substrates at sufficiently low concentration so that they can be resolved individually in a confocal fluorescence microscope. Fig. 2b indicates the anticipated level scheme of the Rh6G dye molecules. Fluorescence is observed from the single molecules as long as they cycle between S0 and S1 states. Excursions to the triplet or the radical state lead to a disruption of this cycle and inhibit fluorescence. The triplet can relax back to the ground state by reverse intersystem crossing with a rate of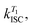 or else be reduced to form the radical of the dye molecule. In the presence of a reducing agent, the singlet can also be reduced to form the radical, which can re-oxidise at an intrinsic rate, returning the dye molecule to its ground state; or else the radical can be photoexcited again to form R˙*, which can transfer its electron to the substrate molecule 2-bromobenzonitrile.
or else be reduced to form the radical of the dye molecule. In the presence of a reducing agent, the singlet can also be reduced to form the radical, which can re-oxidise at an intrinsic rate, returning the dye molecule to its ground state; or else the radical can be photoexcited again to form R˙*, which can transfer its electron to the substrate molecule 2-bromobenzonitrile.
To test the feasibility of tracking the conPET cycle on the single-molecule level, we plot the fluorescence of a single tethered Rh6G molecule in Fig. 2c as a function of time, binned in intervals of 5 ms, with alternating application of hν2. The fluorescence intensity, stated in terms of the photon count rate, appears as bursts of approximately equal strength, separated by prolonged intervals of darkness. The average photon count rate, binned over intervals of 0.5 s, is superimposed in the plot as a red line. As the dye radical is re-excited by hν2, the number of fluorescence spikes increases and the average brightness of the single molecule (red line) doubles. The height of the individual spikes remains almost constant, implying that it is not the number of photons absorbed by the dye which increases upon simultaneous excitation at two wavelengths. Rather, the intermittency between bursts is shortened. Panel d plots a two-second interval of the fluorescence trace of panel c, revealing distinct “on” and “off” periods of the molecular fluorescence. Such intermittency can be used to analyse the fluorescence to extract characteristic timescales τon and τoff. Fitting directly to fluorescence intermittency traces is cumbersome and limited in time resolution by the finite photon count rate. A versatile quantification of the fluorescence dynamics is instead offered by a single-photon correlation analysis of the fluorescence intensity.50 As indicated in panel e, the correlation is computed by calculating the self-convolution, i.e. the time average of the product of the trace with itself, shifted by a temporal offset of Δτ. Fig. 2f shows the result of such a typical cross-correlation, plotted on a logarithmic time axis. The correlation can be fitted with a single-exponential function of the form 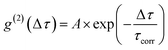 , where A is the correlation amplitude, τcorr is the characteristic decay time of the correlation, and the “on” and “off” times of the molecular fluorescence are related by τon = τcorr (1 + 1/A) and τoff = τcorr (1 + A).50 By adding up τon and τoff, we determine the single-molecule turnover frequency TOFSM = 1/(τon + τoff). This number of cycles which one single dye molecule undergoes through the dark state sets the upper limit for synthetic-scale TOF. Details of the fluorescence microscopy, including the background correction procedure, are summarized in the ESI.†
, where A is the correlation amplitude, τcorr is the characteristic decay time of the correlation, and the “on” and “off” times of the molecular fluorescence are related by τon = τcorr (1 + 1/A) and τoff = τcorr (1 + A).50 By adding up τon and τoff, we determine the single-molecule turnover frequency TOFSM = 1/(τon + τoff). This number of cycles which one single dye molecule undergoes through the dark state sets the upper limit for synthetic-scale TOF. Details of the fluorescence microscopy, including the background correction procedure, are summarized in the ESI.†
Single-molecule photon-correlation spectroscopy
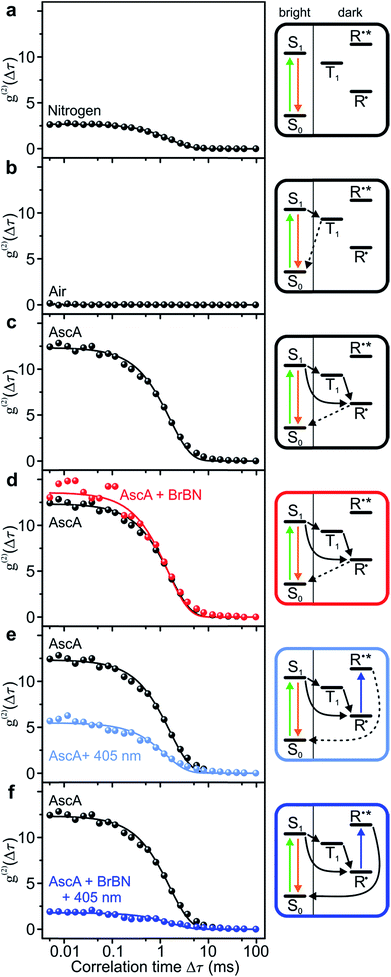
We analyse the photocatalytic cycle using fluorescence intensity correlation spectroscopy. We stress that this analysis is only possible on the single-molecule level, since in the ensemble the molecular excursions to the dark state and the associated fluctuations in fluorescence intensity are averaged out. Each single-molecule fluorescence-intensity trace gives an individual photon correlation curve. To account for the statistical variation between different single molecules, we consider the median value of one hundred single-molecule correlation curves for each value of Δτ, plotted with exponential fits in Fig. 3. We begin in panel a by examining the fluorescence correlation in nitrogen-saturated phosphate-buffered saline (PBS) for the case of excitation with photon energy hν1. Under these conditions, the regular transitions of the dye molecule to the triplet manifold give rise to a well-defined “off” time, which can be attributed to the triplet-state lifetime or the lifetime of a radical formed out of the triplet. The temporal excursions to such a dark state are indicated in the cartoon to the right, with τon = 2.22 ± 0.02 ms, τoff = 5.99 ± 0.09 ms, and TOFSM = 123 s−1. The Rh6G triplet state is quenched by molecular oxygen, by saturating the solvent with air. When this quenching occurs, the dye molecule cycles solely between ground and excited singlet state: no amplitude exists in the photon correlation signal in panel b, implying the absence of a dark state.To monitor the molecular dynamics relating to PET, we carry out the following experiments under conditions where the dark state is stabilised, i.e. under nitrogen saturation. Panel c plots the photon correlation with addition of the reducing agent ascorbic acid. Now, the molecular dark state must be attributed to the radical with τon = 1.73 ± 0.03 ms, τoff = 21.3 ± 0.5 ms, and TOFSM = 44 s−1. Adding the substrate compound 2-bromobenzonitrile in panel d has no effect on the correlation and the associated timescales. In contrast, exciting the radical with hν2 in the absence of the substrate in panel e promotes depopulation of the radical state, shortening the dark-state lifetime to τoff = 8.4 ± 0.3 ms, with τon = 1.5 ± 0.05 ms, and TOFSM = 100 s−1.53 The dramatic effect arises upon simultaneous addition of the two reactants – hν2 photons and 2-bromobenzonitrile molecules – to the dye catalyst. The correlation amplitude in panel f is suppressed almost entirely, but characteristic “on” and “off” times can still be determined as τon = 2.6 ± 0.2 ms, τoff = 4.7 ± 0.4 ms, and TOFSM = 137 s−1. The additional 37 photocycles per second undergone by the catalyst in the presence of the substrate provide a metric for the overall upper limit of the dehalogenation reaction efficiency. Under these reaction conditions, each single Rh6G molecule dehalogenates 37 2-bromobenzonitrile molecules per second.
In order to prove chemical specificity of the microscopic photocatalytic conPET cycle, it is necessary to demonstrate that the dark state of the dye is not quenched for substrate molecules which cannot be dehalogenated. The obvious material to test this is the non-halogenated compound benzonitrile. Fig. 4a plots the single-molecule correlation signal for the four conditions used in Fig. 3c–f, but with benzonitrile added as the substrate. As before, the correlation is identical with only the reducing agent ascorbic acid added (black curve) and with ascorbic acid and benzonitrile combined (red curve) in the solution. Excitation of the Rh6G radical with hν2 shortens the dark-state lifetime by returning the dye from the radical state to the ground state (light–blue curve). However, in contrast to the situation in Fig. 3, addition of benzonitrile has no effect on the photon correlation trace (dark–blue curve). We conclude that benzonitrile does not interact with the photocatalyst since addition of it to the solution has no effect on the fluorescence cross-correlation. This conclusion is crucial since otherwise product inhibition of the catalyst would occur by the dehalogenated substrate, disrupting the photon cycling process. Once bromine is cleaved from 2-bromobenzonitrile, the molecule disassociates from the catalyst of Fig. 1. An alternative test of the reaction is performed with 4-chloroanisole, as summarized in Fig. 4b. This substrate is energetically not expected to undergo bond cleavage by the excited radical R˙*, as the reduction potential necessary amounts to −2.9 V vs. SCE.45 Indeed, in Fig. 4b no effect is seen on the correlation curves of addition of the 4-chloroanisole substrate at the same concentration as that used in Fig. 3.
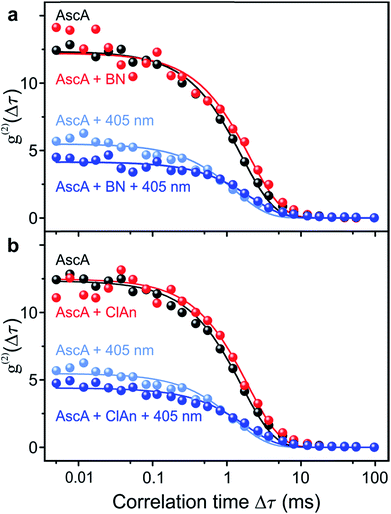 | ||
| Fig. 4 Control measurements of the fluorescence intensity correlation with non-reacting substrate molecules for the four conditions in Fig. 3c–f. (a) Non-halogenated substrate benzonitrile (BN). (b) Substrate 4-chloroanisole (ClAn). The reduction potential of this compound is too high for the photoexcited Rh6G radical. | ||
Discussion
The single-molecule conPET cycle demonstrated here effectively constitutes a single-photon chemical reaction: the first photon hν1, in combination with a reducing agent, generates the photocatalyst – the rhodamine radical – which subsequently reacts the two “compounds”, the substrate 2-bromobenzonitrile and the photon hν2. An appealing aspect of the single-molecule single-photon double-excitation scheme is the potential ability to resolve in time the consecutive excitation processes. In a double-pulse experiment, for example, it should be possible to measure directly the lifetime of the photoexcited radical by varying the duration of the hν2 pulse. In addition, tuning the energy hν2 in a “photocatalytic action” experiment may even allow time-resolved probing of conformational relaxation dynamics of the catalytically active dye which would offer crucial insight for quantum-chemical modelling of the molecular dynamics of the catalyst–substrate interaction. In this context, we derive two conclusions from the observations. First, the photocatalytic reaction is not fundamentally diffusion limited. Since the lifetime of the photoexcited radical R˙* is expected to be extremely short,48 the conPET process can only occur if the substrate molecule is preassociated with the dye catalyst. Second, to prevent product inhibition of the catalyst and enable continued observation of the photocatalytic cycle in fluorescence, the reacted species must dissociate from the catalyst to allow the reaction to begin anew. We propose that the radical exerts an attractive force on the substrate, promoting preassociation, and speculate that such an effect may be more common to photocatalytic processes than previously thought. While we cannot conclusively prove that preaggregation does not occur in the dye ground state, we reiterate the observed reduction in turnover number upon dehalogenation of the substrate, implying that interaction with either form of the dye must be weakened. We note that the substrate is an aromatic system with two electron-withdrawing substituents. The interaction of such an electron-poor aromatic should be stronger with the neutral dye radical than with the cationic dye ground state. As discussed above, depending on the protonation balance, the rhodamine ground state may actually be neutral. In this case, the interaction of the dye with the electron-poor substrate would also be stronger in the anionic radical state than in the neutral ground state. Without precise determination of the different contributions from van der Waals interactions, pi-stacking and electrostatics, such arguments, however, remain qualitative. To further explore the microscopic origins of this phenomenon will necessitate the development of time-dependent density functional theory (TD-DFT) techniques which can take into account the strong polarization effects of the surrounding medium.51 This can be achieved by implementing new theoretical methods to account for the complex excited-state geometry optimization arising from the non-adiabatic molecular dynamics. To arrive at such a microscopic theory of organic photocatalysis it is imperative to have access to truly microscopic experimental data, which only become available on the single-molecule level. An open question is whether the trapping agent N-methylpyrrole used in the ensemble experiments also sticks to the photocatalyst. This could conceivably be expected since dispersive interactions should be of a comparable nature to those of the substrate, but such an association could in turn block the photocatalyst. Given near-unity conversion yields found in the ensemble, such blocking is apparently unlikely.Our crucial conclusion is that in mechanisms which involve preassociation of substrate and photocatalyst, diffusion no longer appears to be the limiting factor so that long excited-state lifetimes are not necessary to ensure effective photocatalytic transformation. This is an important point since most photoredox catalytic cycles involve long-lived triplet states. Triplets, however, limit the overall catalytic potential since electronic energy is inherently lost to the quantum–mechanical exchange interaction by satisfying Pauli's exclusion principle. Our work therefore encourages a renewed search for materials supporting singlet-based photoredox cycles. The dehalogenation reaction demonstrated here on the single-molecule single-photon level constitutes a precursor to more complex photocatalytic mechanisms. We expect the cycle to work equally well in forming carbon–carbon bonds, opening up the possibility of multicolour directed synthesis13 on the single-molecule level.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Research Training Group 1626 of the German Science Foundation.References
- N. A. Romero and D. A. Nicewicz, Chem. Rev., 2016, 116, 10075–10166 CrossRef CAS PubMed.
- C. K. Prier, D. A. Rankic and D. W. C. MacMillan, Chem. Rev., 2013, 113, 5322–5363 CrossRef CAS PubMed.
- D. M. Arias-Rotondo and J. K. McCusker, Chem. Soc. Rev., 2016, 45, 5803–5820 RSC.
- D. M. Schultz and T. P. Yoon, Science, 2014, 343, 985–988 CrossRef CAS PubMed.
- J. Xuan and W. J. Xiao, Angew. Chem., Int. Ed., 2012, 51, 6828–6838 CrossRef CAS PubMed.
- D. A. Nicewicz and D. W. C. MacMillan, Science, 2008, 322, 77–80 CrossRef CAS PubMed.
- H. Kim and C. Lee, Angew. Chem., Int. Ed., 2012, 51, 12303–12306 CrossRef CAS PubMed.
- M. H. Shaw, J. Twilton and D. W. C. MacMillan, J. Org. Chem., 2016, 81, 6898–6926 CrossRef CAS PubMed.
- Y. Du, R. M. Pearson, C. H. Lim, S. M. Sartor, M. D. Ryan, H. S. Yang, N. H. Damrauer and G. M. Miyake, Chem.–Eur. J., 2017, 23, 10962–10968 CrossRef CAS PubMed.
- I. Ghosh, L. Marzo, A. Das, R. Shaikh and B. König, Acc. Chem. Res., 2016, 49, 1566–1577 CrossRef CAS PubMed.
- D. Ravelli, M. Fagnoni and A. Albini, Photoorganocatalysis. What for?, Chem. Soc. Rev., 2013, 42, 97–113 RSC.
- I. Ghosh, T. Ghosh, J. I. Bardagi and B. König, Science, 2014, 346, 725–728 CrossRef CAS PubMed.
- I. Ghosh and B. König, Angew. Chem., Int. Ed., 2016, 55, 7676–7679 CrossRef CAS PubMed.
- E. Yoshioka, S. Kohtani, T. Jichu, T. Fukazawa, T. Nagai, A. Kawashima, Y. Takemoto and H. Miyabe, J. Org. Chem., 2016, 81, 7217–7229 CrossRef CAS PubMed.
- E. Yoshiokaa, S. Kohtani, T. Jichu, T. Fukazawa, T. Nagai, Y. Takemoto and H. Miyabe, Synlett, 2015, 26, 265–270 Search PubMed.
- M. Orrit, Angew. Chem., Int. Ed., 2015, 54, 8004–8005 CrossRef CAS PubMed.
- M. Marchini, G. Bergamini, P. G. Cozzi, P. Ceroni and V. Balzani, Angew. Chem., Int. Ed., 2017, 56, 12820–12821 CrossRef CAS PubMed.
- J. W. Tucker and C. R. J. Stephenson, J. Org. Chem., 2012, 77, 1617–1622 CrossRef CAS PubMed.
- I. Ghosh, J. I. Bardagi and B. König, Angew. Chem., Int. Ed., 2017, 56, 12822–12824 CrossRef CAS PubMed.
- M. B. J. Roeffaers, B. F. Sels, H. Uji-i, F. C. De Schryver, P. A. Jacobs, D. E. De Vos and J. Hofkens, Nature, 2006, 439, 572–575 CrossRef CAS PubMed.
- M. B. J. Roeffaers, G. De Cremer, J. Libeert, R. Ameloot, P. Dedecker, A. J. Bons, M. Buckins, J. A. Martens, B. F. Sels, D. E. De Vos and J. Hofkens, Angew. Chem., Int. Ed., 2009, 48, 9285–9289 CrossRef CAS PubMed.
- F. C. Hendriks, S. Mohammadian, Z. Ristanovic, S. Kalirai, F. Meirer, E. T. C. Vogt, P. C. A. Bruijnincx, H. C. Gerritsen and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2018, 57, 257–261 CrossRef CAS PubMed.
- K. Naito, T. Tachikawa, M. Fujitsuka and T. Majima, J. Phys. Chem. B, 2005, 109, 23138–23140 CrossRef CAS PubMed.
- T. Tachikawa and T. Majima, Chem. Soc. Rev., 2010, 39, 4802–4819 RSC.
- N. Wang, T. Tachikawa and T. Majima, Chem. Sci., 2011, 2, 891–900 RSC.
- B. de Nijs, F. Benz, S. J. Barrow, D. O. Sigle, R. Chikkaraddy, A. Palma, C. Carnegie, M. Kamp, R. Sundararaman, P. Narang, O. A. Scherman and J. J. Baumberg, Nat. Commun., 2017, 8, 994 CrossRef PubMed.
- B. Hulsken, R. Van Hameren, J. W. Gerritsen, T. Khoury, P. Thordarson, M. J. Crossley, A. E. Rowan, R. J. M. Nolte, J. Elemans and S. Speller, Nat. Nanotechnol., 2007, 2, 285–289 CrossRef CAS PubMed.
- T. Adachi, J. Vogelsang and J. M. Lupton, J. Phys. Chem. Lett., 2014, 5, 573–577 CrossRef CAS PubMed.
- P. Chen, X. C. Zhou, H. Shen, N. M. Andoy, E. Choudhary, K. S. Han, G. K. Liu and W. L. Meng, Chem. Soc. Rev., 2010, 39, 4560–4570 RSC.
- T. Christ, F. Kulzer, P. Bordat and T. Basché, Angew. Chem., Int. Ed., 2001, 40, 4192–4195 CrossRef CAS PubMed.
- M. B. J. Roeffaers, G. De Cremer, H. Uji-i, B. Muls, B. F. Sels, P. A. Jacobs, F. C. De Schryver, D. E. De Vos and J. Hofkens, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 12603–12609 CrossRef CAS PubMed.
- K. P. F. Janssen, G. De Cremer, R. K. Neely, A. V. Kubarev, J. Van Loon, J. A. Martens, D. E. De Vos, M. B. J. Roeffaers and J. Hofkens, Chem. Soc. Rev., 2014, 43, 990–1006 RSC.
- H. Yang, G. B. Luo, P. Karnchanaphanurach, T. M. Louie, I. Rech, S. Cova, L. Y. Xun and X. S. Xie, Science, 2003, 302, 262–266 CrossRef CAS PubMed.
- T. J. Ha, A. Y. Ting, J. Liang, W. B. Caldwell, A. A. Deniz, D. S. Chemla, P. G. Schultz and S. Weiss, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 893–898 CrossRef CAS.
- R. D. Smiley and G. G. Hammes, Chem. Rev., 2006, 106, 3080–3094 CrossRef CAS PubMed.
- H. P. Lu and X. S. Xie, J. Phys. Chem. B, 1997, 101, 2753–2757 CrossRef CAS.
- W. Ho, J. Chem. Phys., 2002, 117, 11033–11061 CrossRef CAS.
- L. Lafferentz, F. Ample, H. Yu, S. Hecht, C. Joachim and L. Grill, Science, 2009, 323, 1193–1197 CrossRef CAS PubMed.
- S. W. Hla, L. Bartels, G. Meyer and K. H. Rieder, Phys. Rev. Lett., 2000, 85, 2777–2780 CrossRef CAS PubMed.
- D. G. de Oteyza, P. Gorman, Y. C. Chen, S. Wickenburg, A. Riss, D. J. Mowbray, G. Etkin, Z. Pedramrazi, H. Z. Tsai, A. Rubio, M. F. Crommie and F. R. Fischer, Science, 2013, 340, 1434–1437 CrossRef CAS PubMed.
- I. Swart, L. Gross and P. Liljeroth, Chem. Commun., 2011, 47, 9011–9023 RSC.
- T. Basché, W. E. Moerner, M. Orrit and H. Talon, Phys. Rev. Lett., 1992, 69, 1516–1519 CrossRef PubMed.
- T. Basché, S. Kummer and C. Bräuchle, Nature, 1995, 373, 132–134 CrossRef.
- M. Vester, T. Staut, J. Enderlein and G. Jung, J. Phys. Chem. Lett., 2015, 6, 1149–1154 CrossRef CAS PubMed.
- T. Slanina and T. Oberschmid, ChemCatChem, 2018, 10, 4182–4190 CrossRef CAS.
- M. Neumeier, D. Sampedro, M. Majek, V. A. de la Peña O'Shea, A. Jacobi von Wangelin and R. Pérez-Ruiz, Chem.–Eur. J., 2018, 24, 105–108 CrossRef CAS PubMed.
- S. Doose, H. Neuweiler and M. Sauer, ChemPhysChem, 2009, 10, 1389–1398 CrossRef CAS PubMed.
- D. Gosztola, M. P. Niemczyk, W. Svec, A. S. Lukas and M. R. Wasielewski, J. Phys. Chem. A, 2000, 104, 6545–6551 CrossRef CAS.
- M. Heilemann, R. Kasper, P. Tinnefeld and M. Sauer, J. Am. Chem. Soc., 2006, 128, 16864–16875 CrossRef CAS PubMed.
- W. T. Yip, D. H. Hu, J. Yu, D. A. Vanden Bout and P. F. Barbara, J. Phys. Chem. A, 1998, 102, 7564–7575 CrossRef CAS.
- Z. Zheng, D. A. Egger, J.-L. Brédas, L. Kronik and V. Coropceanu, J. Phys. Chem. Lett., 2017, 8, 3277–3282 CrossRef CAS PubMed.
- J. Vogelsang, R. Kasper, C. Steinhauer, B. Person, M. Heilemann, M. Sauer and P. Tinnefeld, Angew. Chem., Int. Ed., 2008, 47, 5465–5469 CrossRef CAS PubMed.
- S. van de Linde, I. Krstić, T. Prisner, S. Doose, M. Heilemann and M. Sauer, Photochem. Photobiol. Sci., 2011, 10, 499–506 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc03860k |
| This journal is © The Royal Society of Chemistry 2019 |