Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Visualization of the effect of additives on the nanostructures of individual bio-inspired calcite crystals†
Johannes
Ihli‡
 *a,
Jesse N.
Clark
b,
Nasima
Kanwal
c,
Yi-Yeoun
Kim
*a,
Jesse N.
Clark
b,
Nasima
Kanwal
c,
Yi-Yeoun
Kim
 a,
Mark A.
Holden
a,
Mark A.
Holden
 a,
Ross J.
Harder
d,
Chiu C.
Tang
e,
Sharon E.
Ashbrook
a,
Ross J.
Harder
d,
Chiu C.
Tang
e,
Sharon E.
Ashbrook
 c,
Ian K.
Robinson
fg and
Fiona C.
Meldrum
c,
Ian K.
Robinson
fg and
Fiona C.
Meldrum
 *a
*a
aSchool of Chemistry, University of Leeds, Leeds LS2 9JT, UK. E-mail: Johannes.Ihli@materials.ox.ac.uk; F.Meldrum@leeds.ac.uk
bStanford PULSE Institute, SLAC National Accelerator, Menlo Park, California 94025, USA
cSchool of Chemistry and EaStCHEM, University of St. Andrews, North Haugh, St. Andrews, KY16 9ST, UK
dAdvanced Photon Source, Argonne, Illinois 60439, USA
eDiamond Light Source, Harwell Science and Innovation Campus, Didcot, Oxfordshire OX11 0DE, UK
fLondon Centre for Nanotechnology, University College London, London WC1H 0AH, UK
gCondensed Matter Physics and Materials Science, Brookhaven National Lab. Upton, NY 11973-5000, USA
First published on 9th November 2018
Abstract
Soluble additives provide a versatile strategy for controlling crystallization processes, enabling selection of properties including crystal sizes, morphologies, and structures. The additive species can also be incorporated within the crystal lattice, leading for example to enhanced mechanical properties. However, while many techniques are available for analyzing particle shape and structure, it remains challenging to characterize the structural inhomogeneities and defects introduced into individual crystals by these additives, where these govern many important material properties. Here, we exploit Bragg coherent diffraction imaging to visualize the effects of soluble additives on the internal structures of individual crystals on the nanoscale. Investigation of bio-inspired calcite crystals grown in the presence of lysine or magnesium ions reveals that while a single dislocation is observed in calcite crystals grown in the presence of lysine, magnesium ions generate complex strain patterns. Indeed, in addition to the expected homogeneous solid solution of Mg ions in the calcite lattice, we observe two zones comprising alternating lattice contractions and relaxation, where comparable alternating layers of high magnesium calcite have been observed in many magnesium calcite biominerals. Such insight into the structures of nanocomposite crystals will ultimately enable us to understand and control their properties.
Introduction
Soluble additives are frequently used in the precipitation of crystalline materials to control properties including the particle size, morphology, and even polymorph.1–3 There is also growing recognition that this process can be accompanied by the occlusion of the additives within the crystal lattice,4–7 where this provides an attractive means of tuning the properties of functional materials. Indeed, this has been used to introduce color8–11 and magnetism,12,13 enhancing mechanical properties,14–16 and changing the optical properties and bandgap of semiconductors.4,17,18 Quantum dots have also been incorporated into a range of single crystals as a route to producing stable, and highly luminescent nanocomposites,19–21 and introducing additional functionality to metal organic frameworks (MOFs).22 One of the best examples of the potential of this strategy is provided by the formation of biominerals such as the calcite prisms in mollusc shells23–25 and echinoid skeletal elements.26,27 Additives including magnesium ions and organic macromolecules modulate the crystallisation process, resulting in modified morphologies and occlusion of the additives within the crystal lattice.28,29 The result is single crystals with a substantial increase in hardness and fracture resistance when compared to synthetic calcite.15,30–32In order to fully exploit soluble additives to control crystal properties, we need a detailed understanding of their influence on the internal structures of individual crystals, with nanoscale resolution. While techniques such as powder X-ray diffraction (P-XRD) and vibrational spectroscopies are ideal for determining the average effect of additives on crystal structures,33,34 they provide no information on low-frequency inhomogeneities such as defects or compositional zoning. These can arise from the interaction of the additives with the crystal surface during growth and their occlusion in the crystal lattice, and can have a significant impact on the physical properties of crystals. Transmission electron microscopy (TEM) is making significant advances in this regard, where it is now even possible to image the displacement of thousands of individual atoms from their ideal lattice positions in 3D, with picometer resolution.35 Yet, electron microscopy is limited to nanoscale objects, and the preparation of thin sections and the imaging process itself can lead to the formation of artefacts.36–38 While common X-ray microscopy methods also show great potential, they as yet fail in one of the required criteria of spatial-resolution, dimensionality or chemical sensitivity.39,40
Emerging coherent X-ray diffraction imaging (CDI) methods can potentially overcome these limitations,25,41,42 where these techniques eliminate common X-ray optics and replace them with an iterative phase retrieval algorithm for image generation.43 This article describes the use of Bragg Coherent Diffraction Imaging (BCDI) to visualize the inhomogeneities present in individual micron-sized calcite crystals precipitated in the presence of organic and inorganic additives with nanoscale resolution. Investigating amino acids and magnesium ions as important additives, we demonstrate that crystals incorporating low levels of lysine (Lys-calcite) and magnesium ions (Mg-calcite) both alter the internal structures of the crystals. While lysine creates dislocations within the Lys-calcite crystals, Mg ions generate multi-component strain profiles. Further, alternating layers of high magnesium calcite are observed that are comparable to those observed in many magnesium calcite biominerals.26,27 This work provides unique insight into the mechanisms by which additives control material structures and suggests that crystals with specific strain profiles – and thus physical properties – can be generated by judicious selection of additives.
Results
Calcite crystals incorporating either lysine or magnesium ions were precipitated using a vapor diffusion method,44 where droplets of a 5 mM CaCl2 solution containing 2 mM Lys or 2 mM Mg2+ were deposited on hydroxyl-terminated self-assembled monolayers (SAMs). These surfaces support the preferential alignment of the calcite crystals on {104} faces, minimize sample drift during the coherent imaging experiments, and facilitate the experimental alignment. Calcium carbonate precipitation was then induced by exposure to ammonium carbonate vapour for 30 minutes. Crystals were primarily calcite, with a minor fraction of vaterite, as demonstrated by Raman spectroscopy and synchrotron high resolution Powder XRD (HR-PXRD) (Fig. 1). The product crystals were also analysed using scanning electron microscopy (SEM) (Fig. 1a), where pure calcite crystals are rhombohedral in morphology and express six {104} facets. Calcite crystals grown in the presence of lysine (Lys-calcite) were also rhombohedral with very minor edge truncations, while magnesium ions induced a much greater morphological change due to their preferential interaction with the acute step edges. This resulted in magnesian calcite crystals (Mg-calcite) that are elongated along the crystallographic c-axis, and capped with {104} facets.45,46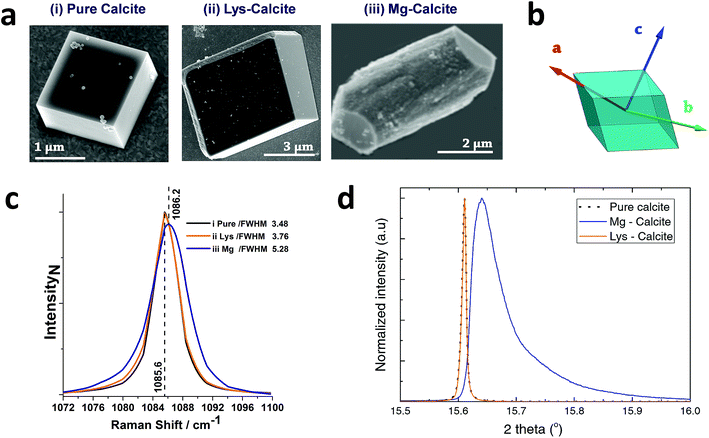 | ||
| Fig. 1 General sample characterization. (a) SEM images of calcite crystals precipitated from a 5 mM CaCl2 solution using the ammonia diffusion method (i) pure calcite, (ii) calcite grown in the presence of 2 mM lysine and (iii) calcite grown in the presence of 2 mM magnesium. (b) Calcite crystal showing a rhombohedral morphology bounded by {104} faces, and indicating the crystallographic axes. (c) The 1086 cm−1 Raman peak (normalized Intensity) of pure calcite, Lys-calcite and Mg-calcite crystals, emphasizing the effect of these additives on the crystal lattice. Full spectra are presented in the ESI.† (d) HR-PXRD patterns, showing the profiles of {104} reflections of the three types of calcite crystals. | ||
Analysis of the average compositions of the crystals showed that they comprised ≈1.8 mol% Mg, as determined by atomic absorption, and ≈0.3 mol% Lys, as shown by fluorescence derivatization of the amino acids released on dissolution of the crystals.47 Raman spectroscopy was used to assess the influence of these additives on the calcite crystal lattice (Fig. 1c and S1†). The main Raman peak at 1086 cm−1, which arises from the symmetric stretch of the carbonate group, shifted from 1085.6 cm−1 to 1086.2 cm−1 on occlusion of Mg2+, where these smaller ions substitute for Ca2+ in the lattice. The full width half maximum (FWHM) peak width also increased by 50% as compared to pure calcite, where this can be attributed to a decrease in the coherent scattering domain size, chemical inhomogeneity in the crystal and an increase in dislocation/defect density.48 The Lys-calcite crystals, in contrast, showed no shift in the 1086 cm−1 peak, and only an 8% increase in the FWHM peak width.
Synchrotron HR-XRD (Fig. 1d) supported these analyses, where Rietveld refinement and line profile analysis of the diffraction patterns revealed virtually no change in the coherent scattering domain size or the lattice parameters for Lys-calcite as compared with pure calcite. In contrast, the diffraction patterns from the Mg-calcite samples revealed a shift and asymmetric broadening in the dominant peak positions (blue arrow) towards smaller d-spacings, as exemplified by a change of the {104} Bragg reflection from 0.011° to 0.086° (integral breadth). Analysis of the patterns revealed a reduction in the domain size from 650 nm to 106 nm, and large lattice distortions of Δc/c = 0.0028 and Δa/a = 0.0017. The higher lattice distortion along the c-axis is consistent with the greater elasticity of calcite in this crystallographic direction.15 An average occlusion level of 2.1–2.3 mol% Mg within the calcite lattice was calculated using the lattice parameters obtained.49
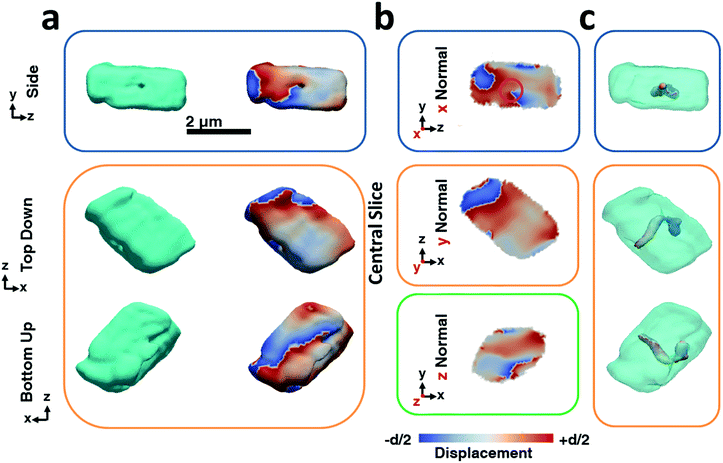
These measurements give information about the average changes in the crystal lattice (P-XRD) and the carbonate ion environment (Raman) on occlusion of these additives. BCDI, in contrast, provides a unique opportunity to determine the local effects of the additives, generating three-dimensional visualizations of the morphology, internal structure, strain fields and associated dislocation network within individual crystals.50,51 In BCDI, the 3D diffraction pattern corresponding to a selected Bragg peak (here {104}) of an isolated crystal is measured. This is achieved by gradually rocking a coherently illuminated sample through a selected Bragg peak during which a series of 2D diffraction patterns are acquired. Inversion of the 3D diffraction pattern by means of a phase retrieval algorithm yields a complex-valued 3D image of the sample (Fig. S2†). The reconstructed amplitude provides a representation of the electron density distribution in the specimen with nanometre resolution (here ≈100 nm), while phase shifts in the complex amplitude provide a 3D visualization of lattice strains with sub-Ångström sensitivity, i.e. the displacement of atoms from the ideal lattice points and scattering vector Q.42,52 Using both types of image contrast, this technique can also be used to visualize selected crystallographic defects.50,51 Details regarding BCDI experiments, image reconstruction and spatial resolution estimation are provided in the ESI Methods and Fig. S3.†
Fig. 2 shows BCDI image reconstructions of a pure calcite crystal that is ≈2.5 μm in diameter. The reconstructed electron densities (amplitudes) provide a visualization of the crystal morphology (Fig. 2a), where this is comparable to the SEM images shown in Fig. 1a. The projected displacements (phase), in turn, correspond to lattice strains and are represented by a cyclic colour map projected onto the recorded electron density (Fig. 2a). A colour shift towards red (+d/2) corresponds to a lattice contraction, while a shift towards blue (−d/2) equates to lattice dilation, where d is equal to the spacing between two adjacent {104} lattice planes. Sections through the centre of the crystal of the displacement maps normal to each major axis x, y, z are shown in Fig. 2b. The crystal can be seen to experience lattice contractions in the order of ≈0.5 Å perpendicular to the substrate, where these are visible up to 300 nm normal to the substrate. The solution-facing {104} facets experience surface relaxation (ESI Movie 1†). No dislocations could be identified, where these are characterized by the combination of a spiral displacement and a low electron density core.50,51,53
The BCDI reconstructions show that precipitation in the presence of Lys causes marked differences in the calcite crystals (Fig. 3). While the image reconstructions are again in morphological agreement with the SEM images and confirm single crystal character, analysis of the strain within the crystal reveals the presence of a single dislocation. The iso-renderings displayed in Fig. 3c show that this is positioned such that it originates at the SAM/crystal interface and then loops over to terminate on one of the larger side faces. (ESI Movie 2†). The spiral displacement associated with the dislocation is clearly visible in the section shown in Fig. 3b (highlighted with a pink circle) and in the side projection given in Fig. 3a. Interestingly, the atomic displacement associated with the tail of the screw dislocation facing the growth solution is visible over the entirety of the crystal face, which indicates that crystal growth is dominated by this single screw dislocation at this stage of its development. Looking further at the strain, it is seen that the crystal is divided along the dislocation line into a heavily strained top half and a nearly undisturbed bottom half. The top half undergoes multiple phase wraps i.e. experiences an accumulated lattice displacement greater than a unit cell from the dislocation line centre towards the crystal faces. ESI Movie 2† further illustrates this, providing slices through the displacement maps parallel and perpendicular to the dislocation line. It is noted, however, that as our data were recorded from the {104} reflection only, we would not necessarily have been able to image any dislocations lying parallel to {104} planes.50 Measurements from a further two reflections would be required to sample the full scale tensor.54 While successful reconstruction of data from a further crystal also revealed the presence of a single dislocation, we would expect this to vary across a population of crystals such that some may exhibit no, or multiple dislocations. Indeed, the number of dislocations will also vary according to the crystal growth conditions.50
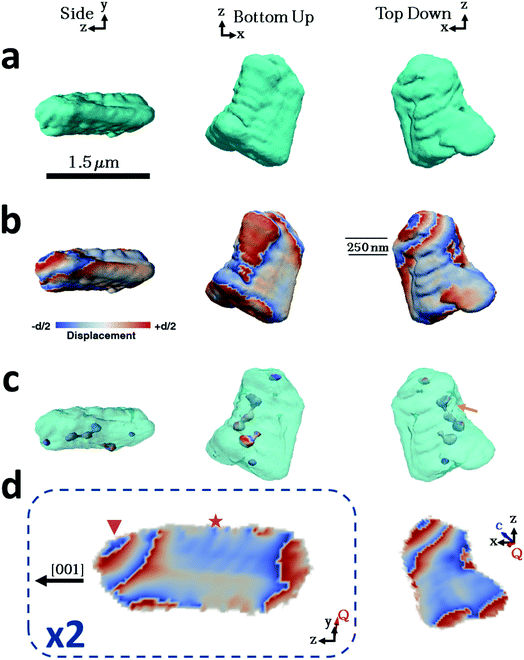
Considering then the Mg-calcite crystals, the diffraction patterns used in the construction of the iso-surface renderings of the crystal shown in Fig. 4a were collected at a d-spacing of 3.031 Å, as compared to 3.035 Å for pure calcite. Application of Vegard's law55 yields a homogenous magnesium content in this particular crystal of ≈1.6 mol%. This is slightly less than the 1.8 mol% obtained as an average of the population of crystals using atomic absorption or 2.1% as determined using HR-PXRD. Unlike the pure calcite and Lys-calcite examined, the iso-surface renderings of the reconstructed electron density do not resemble the crystals observed in the electron microscope. The imaged crystal is significantly smaller (≈1.5 μm) and exhibits a layered structure with curved facets on one side of the crystal when compared to the 4 μm, well-faceted crystals observed by SEM. The corresponding 3D diffraction pattern was also highly distorted. This is not surprising when the increased defect density and the decreased domain size (as determined via Raman and P-XRD) are considered.56 Parts of the crystal that do not satisfy the selected Bragg condition – such as twin domains or “miss-oriented grains” – will be invisible in the retrieved electron density maps.53 A similar discrepancy between the morphology and iso-surface rendering was observed in the reconstruction of a magnesium-rich calcitic prism found in the shell of the mollusc Pinctada margaritifera by Bragg ptychography.25
The iso-surface renderings of the projected displacements reveal that the layered structure is translated into the atomic displacement (Fig. 4b). The crystal examined additionally possesses one major dislocation that runs approximately parallel to the long axis of the reconstructed crystal, and perpendicular to the layers (Fig. 4c, orange arrow). In the absence of a well-defined crystal morphology, the knowledge that the scattering vector Q in the image reconstruction lies nearly parallel to the y axis, and that the orientation of a dislocation is governed by the preferential calcite slip system of {104} and {012} planes and 〈![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif)
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1〉 slip, can be used to determine that the dislocation lies approximately parallel to a {104} facet and that the layers are preferentially oriented with respect to a growth direction of the calcite crystal (ESI Movie 3†).
1〉 slip, can be used to determine that the dislocation lies approximately parallel to a {104} facet and that the layers are preferentially oriented with respect to a growth direction of the calcite crystal (ESI Movie 3†).
Further examination of this repeated lattice contraction and relaxation using slices cut through the centre of the atomic displacement maps (Fig. 4d) reveals that this pattern comprises two components at different length scales. The first comprises localized lattice relaxations (≈50 nm in thickness and 200 nm in length) which are roughly parallel to the long axis of the crystal and run along its whole length. These are marked with a star in Fig. 4d and exhibit average displacements in the d-spacing of 20% or ≈0.6 Å. Considering the possibility that these displacements solely arise from compositional differences, this displacement would correspond to a change in the local Mg concentration of 20 mol% from the average value of 1.6 mol%. It is therefore more likely that it arises from a combination of increased point defect density and elemental substitution. The second component is repeated on a larger scale and is tilted at ≈45° with respect to the long axis of the crystal (indicated with a triangle). This appears as a repeated contraction/relaxation of multiple phase wraps spanning the width of the crystal. Again, data were obtained from a further four crystals, of which one was reconstructed and showed comparable structures. The others were too strained to enable successful reconstruction.
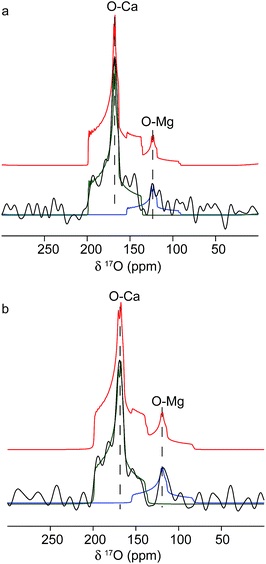
The origins of these different strain components within the Mg-calcite lattice were then investigated further using 17O solid-state NMR spectroscopy57,58 to determine whether they were associated with different local chemical environments. Conventional Magic-Angle Spinning (MAS) NMR spectra57,59 were recorded for calcium carbonate samples that had been precipitated by combining solutions of 17O-enriched carbonate and calcium/magnesium ions, at calcium/magnesium ratios of 10/2 and 10/4. Fig. 5 shows the 17O MAS NMR spectrum of the sample produced at 10/4 Ca/Mg, acquired at 20.0 T. Two distinct resonances centred at about 165 ppm and 120 ppm are observed, with features characteristic of second-order quadrupolar broadening. The spectrum can be fitted with two 17O sites with isotropic chemical shifts of 199 ppm and 155 ppm and quadrupolar coupling constants (CQ) of 7 MHz and 7.5 MHz. These can be attributed to Ca–O and lattice substitutional Mg–O environments, respectively. The fits were obtained by simulating initial powder-pattern lineshapes with NMR parameters from CASTEP density functional theory (DFT) calculations60,61 on calcite, magnesite and a Mg-substituted calcite model system, and then adjusting the parameters to fit the experimental spectrum. Identical shifts were observed with the sample produced at 10/2 Ca/Mg, although the contribution at lower shift (i.e., the Mg-substituted environments) was less pronounced. While these data provide direct evidence for Mg substitution in calcite, it is not possible to differentiate different types of Mg environment, given the low intensity of the 17O signal associated with Mg ions.
Discussion
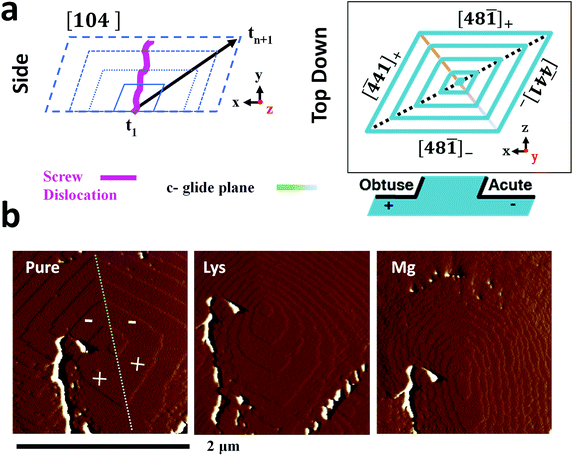
The additive-induced strain profiles observed within the individual calcite crystals provide a unique signature of the interaction between the crystal and the additive, and of the incorporation of the additives within the crystal lattice. Under the low supersaturation conditions employed, crystal growth is dominated by screw dislocations operating on {104} faces (Fig. 6a).46,62 Due to the symmetry of the calcite lattice, these steps lie at acute (designated [![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 41]− and [48
41]− and [48![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ]−) or obtuse (designated [
]−) or obtuse (designated [![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 41]+ and [48
41]+ and [48![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ]+) angles to the {104} planes.63 As calcite growth is dominated by the availability of kink sites on the step edges,64,65 additive-directed crystal growth must be considered in terms of molecular recognition at these distinct step edges, where the acute and obtuse step edges each present a unique environment. Smaller ions such as Mg2+66 and amino acids62 preferentially bind at the acute steps, while larger species such as Sr2+67 often show a preference for the obtuse edges. This inequivalent binding to the step edges then translates into macroscopic changes in the crystal morphologies and variations in the local composition of the crystal.
]+) angles to the {104} planes.63 As calcite growth is dominated by the availability of kink sites on the step edges,64,65 additive-directed crystal growth must be considered in terms of molecular recognition at these distinct step edges, where the acute and obtuse step edges each present a unique environment. Smaller ions such as Mg2+66 and amino acids62 preferentially bind at the acute steps, while larger species such as Sr2+67 often show a preference for the obtuse edges. This inequivalent binding to the step edges then translates into macroscopic changes in the crystal morphologies and variations in the local composition of the crystal.
Evidence of these step-specific interactions can be obtained from atomic force microscopy (AFM). Fig. 6b shows images of a calcite growth hillock after overgrowth in (i) an additive-free, low supersaturation (0.25 mM) calcium carbonate solution, and in the presence of (ii) 0.1 mM Lys, and (iii) 0.1 mM Mg2+. Lysine demonstrates a clear preference for the acute steps, where its addition to the growth solution causes a roughening of the two acute steps on the well-faceted hillock, while the obtuse steps remain unaffected. A decrease in terrace width – which is indicative of step pinning – is seen disproportionately for the acute steps. The ratio of terrace widths changes upon addition of lysine from 1obtuse![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1acute to 1obtuse
1acute to 1obtuse![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.22acute. These microscopic changes in crystal growth cause the truncations of the calcite rhombohedron seen in Fig. 1.
0.22acute. These microscopic changes in crystal growth cause the truncations of the calcite rhombohedron seen in Fig. 1.
The interaction of magnesium ions with calcite has been the subject of considerable interest.45,46,68–71 Like lysine, magnesium ions also preferentially bind to the acute over the obtuse steps. Under the growth conditions employed here, both the acute and the obtuse steps roughen, but the effect on the acute steps is greater, which causes the hillock to adopt an elliptical form. The greatest specificity is typically observed at lower supersaturations, and lower Mg/Ca ratios.46,68 On a macroscopic scale this results in a pile-up of {104} step edges, and the formation of roughened, pseudo-{hk0} faces, as shown in Fig. 1. The retardation of calcite growth by Mg2+ ions is typically attributed to the high dehydration energy of these ions,70,72 and the higher solubility of Mg-calcite.46
In this system, the stronger interaction of Mg2+ ions with calcite, than Lys with calcite, also translates into higher incorporation levels, with the crystals comprising 1.8 mol% Mg2+ and 0.3 mol% Lys. It is noted, however, that this relationship is not universal; additives can exert a strong morphological effect and yet be poorly occluded, while others that exhibit high occlusion efficiencies have little effect on morphology.15,73 The relationship between the growth conditions and Mg occlusion is complex. There is a strong correlation between the Mg/Ca ratio in solution and Mg occlusion, where this can be independent of,65,72 or increase with the crystallisation rate,69,74 depending on the supersaturation regime.
The different occlusion levels in the Lys-calcite and Mg-calcite crystals, together with the changes in the crystal growth that occur in the presence of these additives, necessarily contribute to the contrasting strain profiles present in the crystals. Considering first the Lys-calcite crystals, strain is concentrated along the dislocation line, and then rapidly relaxes away from this. This relaxation is particularly effective along the c-axis (where this can be identified from the crystal morphology), as was also observed in the HR-PXRD data. This is readily rationalised based on the anisotropic crystal structure of calcite, where the layers of carbonate ions parallel to the c-axis render it more elastic along this direction.33,34
Looking then at the Mg-calcite crystals, magnesium readily incorporates into the calcite lattice.45 The majority of the magnesium is homogenously distributed throughout the crystal lattice as a solid solution, which generates the macrostrain (average lattice distortions) observed in PXRD. As this strain is homogeneous, it is not observed in the BCDI image reconstructions. The inhomogeneous strains observed are instead indicative of local variations in the elemental composition in the crystal. A range of phenomena can give rise to this effect. Geological and synthetic calcite crystals occluding Mg2+ ions often exhibit intra-sectorial zoning,67 where only a sub-volume of a single growth sector (that associated with symmetry-related crystal faces) takes up the additive. Preferential association with the acute step edges results in higher Mg concentrations in the equatorial zone of the crystal. This cannot be seen here due to the inhomogeneous strains present within the crystal, which dominate the strain profile. Magnesium ions are also known to accumulate in nano-domains in high-Mg biological calcite crystals, as observed using high resolution transmission electron microscopy (HR-TEM),26 electron diffraction27 and Bragg ptychography,25 and in geological calcite crystals, as seen using X-ray absorption fine structure (XAFS).75 The strain profile in our crystals gives no evidence for this phenomenon, which is expected based on their low Mg contents.
Considering the two types of inhomogeneous strains observed, the first (marked with a triangle in Fig. 4d) appears as micron-spaced phase wraps across the width of the crystal. The tilt angles of the planes containing the phase wraps lie at 40–50° to the c-axis of the crystal (its long axis),46 such that the layers of equal displacement lie approximately parallel to a {104} face (which lies at 45° to the c-axis). These can be attributed to oscillatory zoning, which occurs due to local fluctuations in the solution composition, and gives rise to zones of higher/lower impurity concentrations and defect density at specific time-points in the evolution of a crystal.76 Such zones of equal composition therefore lie in a plane parallel to the crystal growth front. Interestingly, similar alternating layers of high magnesium calcite have previously been observed in magnesium calcite biominerals.24,25,77
The second feature (starred in Fig. 4d) comprises localized lattice relaxations, where zones of equal displacement lie approximately perpendicular to the long axis of the crystal. These cannot be attributed to oscillatory zoning as the strains observed are maintained throughout crystal growth. A possible explanation for this effect can be found in the so-called “template effect” in which topographic features present on the crystal surface are reproduced in subsequent lattice layers.70 This has been observed in AFM studies of the growth of magnesium calcite on pure calcite,70 where it was suggested that incorporation of magnesium ions gives rise to a local strain profile which then influences the occlusion of further foreign ions in subsequent layers. Following the initial random occlusion of magnesium ions at early stages of growth, where lower levels of occlusion are expected,78 more concentrated domains may therefore propagate during subsequent crystal growth.
Conclusions
In summary, this work demonstrates that BCDI offers a unique tool for visualizing the internal structures of individual calcite crystals grown in the presence of soluble additives. It therefore complements common methods such as P-XRD and vibrational spectroscopies that provide data averaged over a population of crystals. BCDI of a calcite crystal precipitated in the presence of lysine revealed that the amino acid was uniformly distributed throughout the crystal, and that its interaction with the growing crystal resulted in the formation of a single screw dislocation that dominated crystal growth. The magnesium ions, in contrast, exerted a much stronger effect on the calcite crystal lattice. In addition to a homogenous solid solution of magnesium ions in the calcite lattice, two distinct inhomogeneous strain features were also present, where these arise from zones of high magnesium calcite. Magnesium ions are therefore expected to have a much greater effect on the mechanical properties of calcite than amino acids, as is observed experimentally. Future work will determine how such crystal dopants control mechanical properties, where this will be achieved using in situ measurements and anomalous scattering effects to determine the individual contributions of elemental and structural inhomogeneities.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by an FP7 advanced grant from the European Research Council (JNC and IKR), by an Engineering and Physical Sciences Research Council (EPSRC) Leadership Fellowship (FCM and JI, EP/H005374/1) and EPSRC grants EP/N002423/1 (FCM, YYK and MAH), and EP/M003027/1 (FCM and MAH). SEA would like to thank the ERC (EU FP7 Consolidator Grant 614290 “EXONMR”) and the Royal Society and Wolfson Foundation for a merit award. Parts of the experimental work was carried out at Advanced Photon Source Beamline 34-ID-C, built with funds from the US National Science Foundation under Grant DMR-9724294 and operated by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract DE-AC02-06CH11357. We thank Diamond Light Source for access to Beamline I-13-1 where this contributed to the results presented here. Work at Brookhaven National Laboratory was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-SC0012704. The UK 850 MHz solid-state NMR Facility used in this research was funded by the EPSRC and BBSRC (contract reference PR140003), as well as the University of Warwick including part funding through Birmingham Science City Advanced Materials Projects 1 and 2 supported by Advantage West Midlands (AWM) and the European Regional Development Fund (ERDF). Collaborative assistance from the 850 MHz Facility Manager (Dinu Iuga, University of Warwick) is acknowledged. We would also like to thank Dr Assaf Gal and Prof. Lia Addadi for their advice with preliminary experiments.Notes and references
- R. Q. Song and H. Colfen, CrystEngComm, 2011, 13, 1249–1276 RSC.
- F. C. Meldrum and H. Colfen, Chem. Rev., 2008, 108, 4332–4432 CrossRef CAS PubMed.
- A. G. Shtukenberg, M. D. Ward and B. Kahr, Chem. Rev., 2017, 117, 14042–14090 CrossRef CAS PubMed.
- A. Brif, G. Ankonina, C. Drathen and B. Pokroy, Adv. Mater., 2014, 26, 477–481 CrossRef CAS PubMed.
- D. C. Green, J. Ihli, Y. Y. Kim, S. Y. Chong, P. A. Lee, C. J. Empson and F. C. Meldrum, Cryst. Growth Des., 2016, 16, 5174–5183 CrossRef CAS.
- B. Kahr and R. W. Gurney, Chem. Rev., 2001, 101, 893–951 CrossRef CAS PubMed.
- A. Berman, L. Addadi, A. Kvick, L. Leiserowitz, M. Nelson and S. Weiner, Science, 1990, 250, 664–667 CrossRef CAS PubMed.
- B. Marzec, D. C. Green, M. A. Holden, A. S. Coté, J. Ihli, S. Khalid, A. Kulak, D. Walker, C. Tang, D. M. Duffy, Y.-Y. Kim and F. C. Meldrum, Angew. Chem., Int. Ed., 2018, 57, 8623–8628 CrossRef CAS PubMed.
- A. N. Kulak, P. C. Yang, Y. Y. Kim, S. P. Armes and F. C. Meldrum, Chem. Commun., 2014, 50, 67–69 RSC.
- B. Kahr and A. G. Shtukenberg, CrystEngComm, 2016, 18, 8988–8998 RSC.
- Y. J. Liu, W. T. Yuan, Y. Shi, X. Q. Chen, Y. Wang, H. Z. Chen and H. Y. Li, Angew. Chem., Int. Ed., 2014, 53, 4127–4131 CrossRef CAS PubMed.
- A. N. Kulak, R. Grimes, Y. Y. Kim, M. Semsarilar, C. Anduix-Canto, O. Cespedes, S. P. Armes and F. C. Meldrum, Chem. Mater., 2016, 28, 7528–7536 CrossRef CAS.
- A. N. Kulak, M. Semsarilar, Y. Y. Kim, J. Ihli, L. A. Fielding, O. Cespedes, S. P. Armes and F. C. Meldrum, Chem. Sci., 2014, 5, 738–743 RSC.
- E. Seknazi and B. Pokroy, Adv. Mater., 2018, 30, 6 CrossRef PubMed.
- Y. Y. Kim, J. D. Carloni, B. Demarchi, D. Sparks, D. G. Reid, M. E. Kunitake, C. C. Tang, M. J. Duer, C. L. Freeman, B. Pokroy, K. Penkman, J. H. Harding, L. A. Estroff, S. P. Baker and F. C. Meldrum, Nat. Mater., 2016, 15, 903–912 CrossRef CAS PubMed.
- Y. Y. Kim, K. Ganesan, P. C. Yang, A. N. Kulak, S. Borukhin, S. Pechook, L. Ribeiro, R. Kroger, S. J. Eichhorn, S. P. Armes, B. Pokroy and F. C. Meldrum, Nat. Mater., 2011, 10, 890–896 CrossRef CAS PubMed.
- Z. Ning, X. Gong, R. Comin, G. Walters, F. Fan, O. Voznyy, E. Yassitepe, A. Buin, S. Hoogland and E. H. Sargent, Nature, 2015, 523, 324–328 CrossRef CAS PubMed.
- M. A. H. Muhammed, M. Lamers, V. Baumann, P. Dey, A. J. Blanch, I. Polishchuk, X. T. Kong, D. Levy, A. S. Urban, A. O. Govorov, B. Pokroy, J. Rodriguez-Fernandez and J. Feldmann, J. Phys. Chem. C, 2018, 122, 6348–6356 CrossRef CAS.
- M. Adam, Z. Y. Wang, A. Dubavik, G. M. Stachowski, C. Meerbach, Z. Soran-Erdem, C. Rengers, H. V. Demir, N. Gaponik and A. Eychmuller, Adv. Funct. Mater., 2015, 25, 2638–2645 CrossRef CAS.
- A. Benad, C. Guhrenz, C. Bauer, F. Eichler, M. Adam, C. Ziegler, N. Gaponik and A. Eychmuller, ACS Appl. Mater. Interfaces, 2016, 8, 21570–21575 CrossRef CAS PubMed.
- Y. J. Liu, H. D. Zang, L. Wang, W. F. Fu, W. T. Yuan, J. K. Wu, X. Y. Jin, J. S. Han, C. F. Wu, Y. Wang, H. L. L. Xing, H. Z. Chen and H. Y. Li, Chem. Mater., 2016, 28, 7537–7543 CrossRef CAS.
- G. Lu, S. Li, Z. Guo, O. K. Farha, B. G. Hauser, X. Qi, Y. Wang, X. Wang, S. Han, X. Liu, J. S. DuChene, H. Zhang, Q. Zhang, X. Chen, J. Ma, S. C. J. Loo, W. D. Wei, Y. Yang, J. T. Hupp and F. Huo, Nat. Chem., 2012, 4, 310–316 CrossRef CAS PubMed.
- F. Nudelman, H. H. Chen, H. A. Goldberg, S. Weiner and L. Addadi, Faraday Discuss., 2007, 136, 9–25 RSC.
- Y. Dauphin, J. P. Cuif, J. Doucet, M. Salome, J. Susini and C. T. Williams, Mar. Biol., 2003, 142, 299–304 CrossRef.
- F. Mastropietro, P. Godard, M. Burghammer, C. Chevallard, J. Daillant, J. Duboisset, M. Allain, P. Guenoun, J. Nouet and V. Chamard, Nat. Mater., 2017, 16, 946–952 CrossRef CAS PubMed.
- I. Polishchuk, A. A. Bracha, L. Bloch, D. Levy, S. Kozachkevich, Y. Etinger-Geller, Y. Kauffmann, M. Burghammer, C. Giacobbe, J. Villanova, G. Hendler, C. Y. Sun, A. J. Giuffre, M. A. Marcus, L. Kundanati, P. Zaslansky, N. M. Pugno, P. Gilbert, A. Katsman and B. Pokroy, Science, 2017, 358, 1294–1298 CrossRef CAS PubMed.
- S. J. Tsipursky and P. R. Buseck, Am. Mineral., 1993, 78, 775–781 CAS.
- J. Aizenberg, J. Hanson, T. F. Koetzle, L. Leiserowitz, S. Weiner and L. Addadi, Chem.–Eur. J., 1995, 1, 414–422 CrossRef CAS.
- U. Magdans and H. Gies, Eur. J. Mineral., 2004, 16, 261–268 CrossRef CAS.
- Y. Y. Kim, L. Ribeiro, F. Maillot, O. Ward, S. J. Eichhorn and F. C. Meldrum, Adv. Mater., 2010, 22, 2082–2086 CrossRef CAS PubMed.
- M. E. Kunitake, S. P. Baker and L. A. Estroff, MRS Commun., 2012, 2, 113–116 CrossRef CAS.
- M. E. Kunitake, L. M. Mangano, J. M. Peloquin, S. P. Baker and L. A. Estroff, Acta Biomater., 2013, 9, 5353–5359 CrossRef CAS PubMed.
- B. Pokroy, A. N. Fitch, F. Marin, M. Kapon, N. Adir and E. Zolotoyabko, J. Struct. Biol., 2006, 155, 96–103 CrossRef CAS PubMed.
- S. Borukhin, L. Bloch, T. Radlauer, A. H. Hill, A. N. Fitch and B. Pokroy, Adv. Funct. Mater., 2012, 22, 4216–4224 CrossRef CAS.
- R. Xu, C. C. Chen, L. Wu, M. C. Scott, W. Theis, C. Ophus, M. Bartels, Y. Yang, H. Ramezani-Dakhel, M. R. Sawaya, H. Heinz, L. D. Marks, P. Ercius and J. W. Miao, Nat. Mater., 2015, 14, 1099–1103 CrossRef CAS PubMed.
- P. Lu, L. Zhou, M. J. Kramer and D. J. Smith, Sci. Rep., 2014, 4, 3945 CrossRef PubMed.
- F. Hofmann, E. Tarleton, R. J. Harder, N. W. Phillips, P.-W. Ma, J. N. Clark, I. K. Robinson, B. Abbey, W. Liu and C. E. Beck, Sci. Rep., 2017, 7, 45993 CrossRef CAS PubMed.
- L. M. Gordon and D. Joester, Nature, 2011, 469, 194–197 CrossRef CAS PubMed.
- J. Ihli, R. R. Jacob, M. Holler, M. Guizar-Sicairos, A. Diaz, J. C. da Silva, D. Ferreira Sanchez, F. Krumeich, D. Grolimund, M. Taddei, W. C. Cheng, Y. Shu, A. Menzel and J. A. van Bokhoven, Nat. Commun., 2017, 8, 809 CrossRef CAS PubMed.
- F. Meirer, D. T. Morris, S. Kalirai, Y. J. Liu, J. C. Andrews and B. M. Weckhuysen, J. Am. Chem. Soc., 2015, 137, 102–105 CrossRef CAS PubMed.
- D. A. Shapiro, Y. S. Yu, T. Tyliszczak, J. Cabana, R. Celestre, W. L. Chao, K. Kaznatcheev, A. L. D. Kilcoyne, F. Maia, S. Marchesini, Y. S. Meng, T. Warwick, L. L. Yang and H. A. Padmore, Nat. Photonics, 2014, 8, 765–769 CrossRef CAS.
- R. Harder and I. K. Robinson, JOM, 2013, 65, 1202–1207 CrossRef.
- J. R. Fienup, Appl. Opt., 1982, 21, 2758–2769 CrossRef CAS PubMed.
- J. Ihli, P. Bots, A. N. Kulak, L. G. Benning and F. C. Meldrum, Adv. Funct. Mater., 2013, 23, 1965–1973 CrossRef CAS.
- K. J. Davis, P. M. Dove and J. J. De Yoreo, Science, 2000, 290, 1134 CrossRef CAS PubMed.
- K. J. Davis, P. M. Dove, L. E. Wasylenki and J. J. De Yoreo, Am. Mineral., 2004, 89, 714 CrossRef CAS.
- H. Brückner, S. Haasmann, M. Langer, T. Westhauser, R. Wittner and H. Godel, J. Chromatogr. A, 1994, 666, 259–273 CrossRef.
- G. Gouadec and P. Colomban, Am. Mineral., 2007, 53, 1–56 CAS.
- E. Zolotoyabko, E. N. Caspi, J. S. Fieramosca, R. B. Von Dreele, F. Marin, G. Mor, L. Addadi, S. Weiner and Y. Politi, Cryst. Growth Des., 2010, 10, 1207–1214 CrossRef CAS.
- J. N. Clark, J. Ihli, A. S. Schenk, Y. Y. Kim, A. N. Kulak, J. M. Campbell, G. Nisbet, F. C. Meldrum and I. K. Robinson, Nat. Mater., 2015, 14, 780–784 CrossRef CAS PubMed.
- J. Ihli, J. N. Clark, A. S. Cote, Y. Y. Kim, A. S. Schenk, A. N. Kulak, T. P. Comyn, O. Chammas, R. J. Harder, D. M. Duffy, I. K. Robinson and F. C. Meldrum, Nat. Commun., 2016, 7, 11878 CrossRef CAS PubMed.
- Y. C. K. Chen-Wiegart, R. Harder, D. C. Dunand and I. McNulty, Nanoscale, 2017, 9, 5686–5693 RSC.
- A. Ulvestad, J. N. Clark, R. Harder, I. K. Robinson and O. G. Shpyrko, Nano Lett., 2015, 15, 4066–4070 CrossRef CAS PubMed.
- F. Hofmann, E. Tarleton, R. J. Harder, N. W. Phillips, P. W. Ma, J. N. Clark, I. K. Robinson, B. Abbey, W. J. Liu and C. E. Beck, Sci. Rep., 2017, 7, 45993 CrossRef CAS PubMed.
- F. Zhang, H. Xu, H. Konishi and E. E. Roden, Am. Mineral., 2010, 95, 1650–1656 CrossRef CAS.
- A. S. Cote, R. Darkins and D. M. Duffy, Phys. Chem. Chem. Phys., 2015, 17, 20178–20184 RSC.
- S. E. Ashbrook and M. E. Smith, Chem. Soc. Rev., 2006, 35, 718–735 RSC.
- S. E. Ashbrook and M. E. Smith, eMagRes, 2011 DOI:10.1002/9780470034590.emrstm1213.
- S. E. Ashbrook, D. M. Dawson and J. M. Griffin, Local Structure Characterisation, John Wiley & Sons Ltd, 1st edn, 2014 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- C. A. Orme, A. Noy, A. Wierzbicki, M. T. McBride, M. Grantham, H. H. Teng, P. M. Dove and J. J. DeYoreo, Nature, 2001, 411, 775–779 CrossRef CAS PubMed.
- H. H. Teng, P. M. Dove, C. A. Orme and J. J. De Yoreo, Science, 1998, 282, 724–727 CrossRef CAS PubMed.
- J. J. De Yoreo, L. A. Zepeda-Ruiz, R. W. Friddle, S. R. Qiu, L. E. Wasylenki, A. A. Chernov, G. H. Gilmer and P. M. Dove, Cryst. Growth Des., 2009, 9, 5135–5144 CrossRef CAS.
- L. C. Nielsen, J. J. De Yoreo and D. J. DePaolo, Geochim. Cosmochim. Acta, 2013, 115, 100–114 CrossRef CAS.
- J. Paquette and R. J. Reeder, Geology, 1990, 18, 1244–1247 CrossRef CAS.
- J. Paquette and R. J. Reeder, Geochim. Cosmochim. Acta, 1995, 59, 735–749 CrossRef CAS.
- J. Xu, J. H. Wang, M. Hong and H. H. Teng, Am. Mineral., 2016, 101, 1104–1112 CrossRef.
- I. Sethmann, J. W. Wang, U. Becker and A. Putnis, Cryst. Growth Des., 2010, 10, 4319–4326 CrossRef CAS.
- J. M. Astilleros, L. Fernandez-Diaz and A. Putnis, Chem. Geol., 2010, 271, 52–58 CrossRef CAS.
- L. E. Wasylenki, P. M. Dove and J. J. De Yoreo, Geochim. Cosmochim. Acta, 2005, 69, 4227–4236 CrossRef CAS.
- A. Mucci and J. W. Morse, Geochim. Cosmochim. Acta, 1983, 47, 217–233 CrossRef CAS.
- Y. Y. Kim, M. Semsarilar, J. D. Carloni, K. R. Cho, A. N. Kulak, I. Polishchuk, C. T. Hendley, P. J. M. Smeets, L. A. Fielding, B. Pokroy, C. C. Tang, L. A. Estroff, S. P. Baker, S. P. Armes and F. C. Meldrum, Adv. Funct. Mater., 2016, 26, 1382–1392 CrossRef CAS.
- R. A. Berner, J. T. Westrich, R. Graber, J. Smith and C. S. Martens, Am. J. Sci., 1978, 278, 816–837 CrossRef CAS.
- A. A. Finch and N. Allison, Mineral. Mag., 2007, 71, 539–552 CrossRef CAS.
- M. Shore and A. D. Fowler, Can. Mineral., 1996, 34, 1111–1126 CAS.
- Y. Dauphin, J. Biol. Chem., 2003, 278, 15168–15177 CrossRef CAS PubMed.
- Y. Y. Kim, C. L. Freeman, X. Q. Gong, M. A. Levenstein, Y. W. Wang, A. Kulak, C. Anduix-Canto, P. A. Lee, S. B. Li, L. Chen, H. K. Christenson and F. C. Meldrum, Angew. Chem., Int. Ed., 2017, 56, 11885–11890 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc03733g |
| ‡ Current affiliation: Department of Materials, University of Oxford, Oxford OX2 6HT, UK. |
| This journal is © The Royal Society of Chemistry 2019 |