Open Access Article
Open Access ArticleNegative area compressibility of a hydrogen-bonded two-dimensional material†
Guoqiang
Feng
abc,
Wei-Xiong
Zhang
 d,
Liyuan
Dong
c,
Wei
Li
d,
Liyuan
Dong
c,
Wei
Li
 *ac,
Weizhao
Cai
*ac,
Weizhao
Cai
 *e,
Wenjuan
Wei
c,
Lijun
Ji
c,
Zheshuai
Lin
*f and
Peixiang
Lu
*cg
*e,
Wenjuan
Wei
c,
Lijun
Ji
c,
Zheshuai
Lin
*f and
Peixiang
Lu
*cg
aSchool of Materials Science and Engineering, Nankai University, Tianjin 300350, China. E-mail: wl276@nankai.edu.cn
bDepartment of Physics and Mechanical & Electrical Engineering, Hubei University of Education, Wuhan 430205, China
cSchool of Physics, Huazhong University of Science and Technology, Wuhan 430074, China. E-mail: lupeixiang@hust.edu.cn
dSchool of Chemistry and Chemical Engineering, Sun Yat-Sen University, Guangzhou 510275, China
eDepartment of Physics and Astronomy, University of Utah, Salt Lake City, Utah 84112, USA. E-mail: wzhcai@gmail.com
fCenter for Crystal R&D, Key Lab of Functional Crystals and Laser Technology of Chinese Academy of Sciences, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing 100190, China. E-mail: zslin@mail.ipc.ac.cn
gLaboratory for Optical Information Technology, Wuhan Institute of Technology, Wuhan 430205, China
First published on 4th December 2018
Abstract
Very few materials expand two-dimensionally under pressure, and this extremely rare phenomenon, namely negative area compressibility (NAC), is highly desirable for technological applications in pressure sensors and actuators. Hitherto, the few known NAC materials have dominantly been limited to 2D crystals bonded via coordination interactions while other 2D systems have not been explored yet. Here, we report the large NAC of a hydrogen-bonded 2D supramolecular coordination complex, Zn(CH3COO)2·2H2O, with a synergistic microscopic mechanism. Our findings reveal that such an unusual phenomenon, over a wide pressure range of 0.15–4.44 GPa without the occurrence of any phase transitions, arises from the complex cooperation of intra-layer coordination and hydrogen-bonding interactions, and inter-layer van der Waals forces. In addition, we propose that these NAC crystals could have important applications as pressure-converting materials in ultrasensitive pressure sensing devices.
Introduction
Materials that possess large mechanical anisotropy to external pressure are highly desirable due to their potential for technological application in next-generation microscale or nanoscale pressure sensors and actuators.1,2 Recently, new classes of materials, such as coordination polymers,3–7 metal–organic frameworks (MOFs)8–10 and molecular crystals,11,12 were found to show negative linear compressibility (NLC) properties, i.e. they expand along one direction when compressed uniformly.13 This counterintuitive behaviour is generally associated with the wine-rack-like geometric motif: horizontal expansion couples with shrinkage in the vertical direction during framework hinging. It is well known that all materials must fulfil the thermodynamic requirement: their intrinsic volumes should decrease under hydrostatic compression. Hence, the most extreme and counterintuitive response to pressure is negative area compressibility (NAC): an expansion of a plane is perpendicular to the direction of strongest contraction. The uncommon NAC effect is extremely rare, and only very few compounds have been experimentally observed.14–17 For example, the recently reported porous MOF [Zn(L)2(OH)2]n·H2O, where L is 4-(1H-naphtho[2,3-d]imidazole-1-yl)benzoate with tetragonal symmetry, shows the strongest NAC response so far, its giant piezo-mechanical response arising from cooperation of the flexible [–Zn–O(H)–]n coordination helices and puckered [–Zn–L–]4 quadrangular rings.17Recently, two dimensional (2D) materials have been found to show remarkable physical properties under pressure which include structural reorganization,18 semiconductor-to-metal transition,19 enhanced tunneling magnetoresistance20 and superconductivity.21 More interestingly, NAC phenomena have also been found in 2D materials. For example, the layered silver(I) tricyanomethanide framework, which has orthorhombic symmetry, exhibits weak NAC along the ac plane below 0.62 GPa due to the flattening of puckered honeycomb-like layers.15 This mechanism has also been found to be the driving force for a few inorganic NAC materials, such as KBBF,22 TlGaSe2 (ref. 23) and NaV2O5.14 Despite the emerging interest in the NAC effects on the aforementioned 2D materials bonded via coordination interactions, hydrogen-bonded 2D systems have not attracted much attention. As hydrogen-bonding is fundamentally different from coordination bonds in terms of electronic nature,24 this virgin field could widen the territory of NAC materials. To explore this possibility, here we report the discovery of the large negative area compressibility (NAC) phenomenon over a wide pressure range up to 4.44 GPa in zinc acetate dihydrate (Zn(CH3COO)2·2H2O), a commonly used food supplement and drug for treating cold.25 Our high-pressure synchrotron powder X-ray diffraction (HP-PXRD) experiments and first-principles calculations reveal that the intrinsic NAC in Zn(CH3COO)2·2H2O arises from the concerted opposite-rotating of the ‘fan-shaped’ [Zn(CH3COO)·H2O]+ coordination unit.
Results and discussion
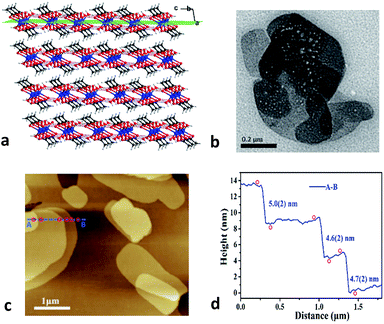
Zn(CH3COO)2·2H2O is a coordination complex and crystallizes in the monoclinic system with space group C2/c as shown in Fig. S1.† Within the complex, the Zn atom is coordinated by two water molecules and four O atoms of two acetate ligands to form a distorted octahedral geometry. The adjacent zinc complexes are linked through O–H⋯O hydrogen bonds with distances of 2.608 and 2.638 Å along the b and c axes to generate a layered supramolecular architecture (Fig. 1a and S1†).26 The neighboring layers are stacked down the a-axis with a skewed angle of 76°, via van der Waals interactions with an interlayer spacing of 7.090 Å. As expected for a 2D material, (100) is the major face of the formed crystals.Considering the 2D nature of this molecular material, we characterized the crystals using transmission electron microscopy (TEM) and atomic force microscopy (AFM). The bulk crystals were ground gently in ethanol, and then the resulting suspension was deposited on a holey carbon support film prior to TEM testing. Bright-field images show nanosheets having good morphology with lateral sizes of about 200–800 nm (Fig. 1b). Moreover, the thickness of the nanosheets was quantified using AFM. As shown in Fig. 1c, the AFM image of a typical multi-layered nanosheet exhibits a thickness of about 4–5 nm (Fig. 1d), which corresponds to the height of ∼7 layers. The ease of exfoliation indicates the significant mechanical anisotropy in the crystal structure of Zn(CH3COO)2·2H2O, which has been further probed via a single-crystal nanoindentation experiment.27 The (100) and (001) faces were indented with a Berkovich tip with a radius of ∼50 nm in the quasi-static mode and the load-indentation depth (P–h) curves are displayed in Fig. S2.† There are several discrete displacement bursts (‘pop-ins’) in the loading portion on both faces, which indicate the fragile nature of hydrogen-bonding and layered packing motif in Zn(CH3COO)2·2H2O, similar to other molecular crystals.28 The average values of the elastic modulus (E) are 5.8(3) and 4.3(2) GPa for the (001) and (100) planes, respectively, giving an anisotropy ratio (E(001)/E(100)) of 1.35.
To explore the pressure effect on the structure of Zn(CH3COO)2·2H2O, we carried out high-pressure powder X-ray diffraction (HP-PXRD) experiments in diamond anvil cells at room temperature.29Fig. 2a and b show the evolution of the relative lattice parameters with respect to the pressure from ambient pressure to 4.44 GPa (Table S1†). It is apparent that no phase-transition was detected in the whole measured pressure range and the crystal retains its monoclinic symmetry (Fig. S3–S5†). Both the unit-cell volume (V) and lattice parameter a undergo pronounced reductions of about 18% and 20% up to 4.44 GPa, while the c-axis and β angle decrease only by about 1.9% and 7.1%, respectively. However, the b-axis expands by about 2.3%, giving anomalous negative linear compressibility behavior. This abnormal behavior can be clearly evidenced by the (001) Bragg peak's shift to the low diffraction angle region (high d-spacing) under compression (Fig. S5†). As Zn(CH3COO)2·2H2O crystallizes in the monoclinic space group C2/c, its strain eigenvectors are not exactly along the crystallographic axes. To more clearly investigate the anomalous expansion of Zn(CH3COO)2·2H2O, the principal compressibilities converted from variable-pressure lattice parameters are calculated using PASCal software30 and the results are summarized in Table S2.† The relative changes for the principal axes and the corresponding principal compressibilities as a function of pressure are plotted in Fig. 2c and d (Tables S2 and S3†), where KX1 = 40.4(15), KX2 = −2.1(4), and KX3 = −6.0(7) TPa−1. Strikingly, the compressibility is negative along the (X2, X3)-plane, with the magnitude of K(X2, X3) = KX2 + KX3 = −8.1(8) TPa−1. The (X2, X3)-plane with NAC behavior expands approximately within the (b, c)-plane located in an individual layer of the structure and the X1 principal axis is approximately parallel to the layer-stacking direction [100] (Fig. 1a and Table S2†). As summarized in Table 1, Zn(CH3COO)2·2H2O ranks the third among all hitherto known 8 NAC materials, and ranks the first if excluding those with phase transitions and metastable high-pressure NAC. Specifically, the NAC of Zn(CH3COO)2·2H2O is about an order of magnitude larger than that of the recently reported deep-UV nonlinear crystal KBe2BO3F2 (KBBF),22 and about 4.5 times larger than that of NaV2O5.14 Though the NAC effect of the molecular framework Ag(tcm) (tcm = tricyanomethanide)15 is similar to that of Zn(CH3COO)2·2H2O, its phase transition at around 0.62 GPa would dramatically narrow down the applicable window to only about 1/7 that of Zn(CH3COO)2·2H2O. In addition, under practical application circumstances, single-crystals or single-crystalline films with oriented NAC faces are required, and any pressure-induced phase transitions will inevitably lead to significant structural reconstruction and corresponding destruction of the crystal morphology (e.g. twinning induced cracking), hence being detrimental to the key NAC functionality. In this context, the non-emergence of a pressure-induced transition in compound Zn(CH3COO)2·2H2O is critically advantageous. Compared with 2-MeBzIm (2-methylbenzimidazole)16 and [Zn(L)2(OH)2]n·guest (L = 4-(1H-naphtho[2,3-d]imidazole-1-yl)benzoate; the guest is water),17 which exhibit stronger NAC effects but only in their metastable high-pressure phases, the ease of growing oriented single crystals and fabricating devices using complex Zn(CH3COO)2·2H2O and similar NAC materials under ambient conditions would be significantly more favorable as well.
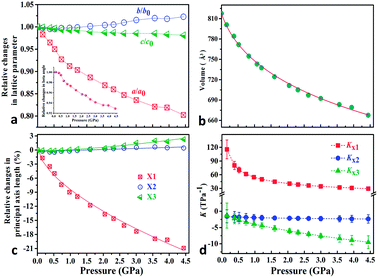 | ||
| Fig. 2 (a) Relative changes of lattice parameters as a function of pressure; the beta angle changes are shown as an inset in (a). (b) The third order Birch–Murnaghan EoS fits31 for cell volume vs. pressure (Fig. S3†). (c) Pressure-dependent relative changes in length for the three principal axes and (d) the corresponding principal compressibility KX1, KX2 and KX3. | ||
| Materials | Pressure range (GPa) | NAC (TPa−1) | Phase transition (P–T) |
|---|---|---|---|
| KBBF22 | 0.22–6.39 | −1.0(2) | Non P–T |
| NaV2O5 (ref. 14) | 4–10 | −1.5 | Non P–T |
| Ag(tcm)15 | 0–0.62 | −7.5(8) | Non P–T |
| 2-MeBzIm16 | 0.24–2.40 | −15(6) | 0.22 GPa |
| [Zn(L)2(OH)2]n·guest17 | 1.0–2.6 | −72(6) | 1.0, 2.6 GPa |
| TlGaSe2 (ref. 23) | — | Indirect method | — |
| 2-(3′-Chlorophenyl) imidazoline36 | 0.0001–0.08 | — | — |
| Zn(CH3COO)2·2H2O | 0.15–4.44 | −8.1(8) | Non P–T |
In a second series of measurements, we collected the powder X-ray data of Zn(CH3COO)2·2H2O up to 7.53 GPa to check its phase stability at room temperature. Fig. S6† displays the raw two-dimensional X-ray diffraction images and diffraction peaks as a function of pressure. Below 4.28 GPa, the results are well consistent with previous measurements. However, further compression led to the disappearance of most sharp diffraction peaks and the prominent broadening of residual peaks, which indicates that the title compound loses its crystallinity. It is well-known that hybrid organic–inorganic compounds have low resistance to hydrostatic stress and amorphization often occurs at medium pressure (usually only a few GPa).32,33 For example, the photovoltaic hybrid perovskite (CH3NH3)PbI3 undergoes a gradual amorphization after the structural phase transformation takes place at 2.5 GPa.34
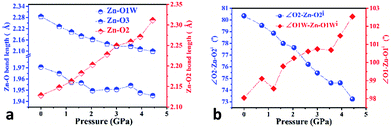
In order to elucidate the microscopic mechanism of the NAC behavior, the atomic geometries of the Zn(CH3COO)2·2H2O crystal were calculated, at intervals of about 0.5 GPa from ambient pressure to 4.44 GPa, using the first-principles geometry optimization based on the experimental lattice parameters.35 The extracted NAC mechanism and details of structural evolution at ambient pressure, 2.05 and 4.44 GPa are shown in Fig. 3 and S7.† The variations of bond lengths and angles are shown in Fig. 4 and Table S4.† Owing to the relatively weak van der Waals interactions between adjacent layers, the supramolecular structure contracts considerably along the a-axis with increasing pressure. However, the bc-plane which is linked by stronger O–H⋯O bonds experiences fewer but unusual changes within the layer. The opposite rotating ‘fan-shaped’ unit, shown in Fig. 3, is utilized to schematically demonstrate the alterations of the coordination geometry and the corresponding NAC mechanism under pressure. The purple ‘fan-shaped’ unit represents the plane that includes Zn, C1, O3 and O2 of the acetate ligands, and water oxygen O1W within the half coordination geometry [Zn(CH3COO)·(H2O)]+, and the green ‘fan-shaped’ unit is comprised of counterpart atoms from the other half coordination geometry. Before we reveal the structural mechanism responsible for the NAC behavior, we need to stress the fact that two ‘fan-shaped’ [Zn(CH3COO)·(H2O)]+ units in each coordination geometry are confined by four O1Wvi–H1vi⋯O2 and O1Wvii–H2vii⋯O3 bonds approximately along the b- and c-axis in the layer, which allow the structure to respond uniquely to pressure. In the purple [Zn(CH3COO)·(H2O)]+ unit, the Zn–O2 and Zn–O1W bonds elongate and contract by about 8.6% and 1.3% from ambient pressure to 4.44 GPa, respectively. In addition, the O1Wvi–H1vi⋯O2 bond shrinks by about 3.0% with an angle decrease of about 1.4% up to 4.44 GPa. Meanwhile, the intersectional angle O2–Zn–O2i of the two ‘fan-shaped’ units concurrently decreases from 80.35° to 73.24° (8.8%), accompanied by the increase of the O1W–Zn–O1Wi angle from 98.05° to 102.54° (4.6%) as shown in Fig. 4 and S7.† The less significant contraction of the O1Wvi–H1vi⋯O2 distance and Zn–O1W bond is compensated for by the substantial increase of the Zn–O2 bond along the b-axis. And the dramatic closure of the angle between the two ‘fan-shaped’ structural units increases the elongated projection of the coordination geometry along the b-axis (X3 direction), hence leading to significant expansion of KX3 = −6.0(7) TPa−1. For understanding the expansion along X2 (approximately along the c-axis), we also need to take into account both the coordination bonding and hydrogen-bonding. The O1Wvii–H2vii⋯O3 bond length expands by about 0.4% with a bond angle decrease of about 0.2%, while the Zn–O3 bond length shrinks significantly by about 8.1%. Nevertheless, the slightly larger angle closure of the two ‘fan-shaped’ units can counterbalance the coupled contraction of the Zn–O3 and O1Wvii–H2vii⋯O3 bonds, which consequently leads to a small expansion along X2 with KX2 = −2.1(4) TPa−1. In addition, we need to take into account the synergistic contribution from the methyl group of the acetate ligand. During compression, it is forced to tilt and rotate along both X2 and X3 directions, hence facilitating the NAC (Fig. S7 and S8†). Such a complex cooperation process under pressure can be understood from the model cartoons in Fig. 3b and structural evolution in Fig. S7 and S8.†
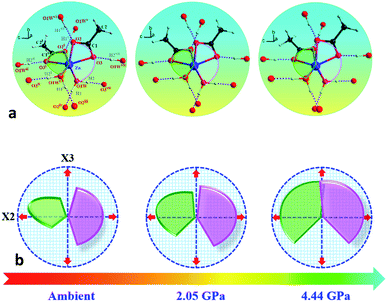 | ||
| Fig. 3 (a) Schematic structural evolution mechanism responsible for the NAC behavior in Zn(CH3COO)2·2H2O. Purple and green rotating ‘fan-shaped’ units represent the two half zinc coordination geometries in the crystal structure which lie approximately within planes through Zn, C1, O1W, O3, O2 and Zn, C1i, O1Wi, O3i, O2i, respectively. (b) The generic mechanical response stimulating the expansion of X3 and X2 directions to the opposite rotation of the two ‘fan-shaped’ units under compression. The rotation and expansion of the ‘fan-shaped’ planes are exaggerated for illustrative purposes. Note: the X2 principal axis is approximately oppositely along the c-axis, and the X3 principal axis is oppositely along the b-axis (Table S2†). Atoms are colored as in Fig. 1. Symmetry codes: (i) −x, y, 0.5 − z; (ii) x, −y, 0.5 + z; (iii) x, −1 + y, z; (iv) −x, −1 + y, 0.5 − z; (v) x, 1 + y, z; (vi) −x, 1 + y, 0.5 − z; (vii) −x, −y, −z. | ||
Notably, though the NAC mechanism in Zn(CH3COO)2·2H2O is broadly reminiscent of the ‘Lifshitz’ scenario,13,37 the cooperative involvement of coordination interactions, hydrogen-bonding and van der Waals forces in it extends beyond the singular molecular force in known materials. The underlying NAC mechanism in KBBF is primarily attributed to the flattening of the Be2BO3F2 layer induced by the shrinkage of the Be–F bond under compression.22 In molecular frameworks Ag(tcm)15 and [Zn(L)2(OH)2]n·guest,17 the NAC effects respectively arise from rippling of the honeycomb-like architecture and compression of flexible helices, which are both mainly caused by coordination bond flexing.
The above large NAC and compensating substantial shrinkage along the orthogonal axis in Zn(CH3COO)2·2H2O and similar materials could lead to many important technical applications under high-pressure working environments, such as precise pressure sensing materials.38 A typical example is the pressure-converting material used in a Fabry–Perot interferometer pressure sensor, as schematically depicted in Fig. 5. To facilitate the discussion, we refer to the formula describing the refractive optical path difference (Δ) below:
Δ = 2nh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ |
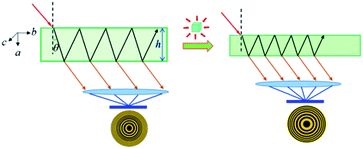 | ||
| Fig. 5 Proposed schematic illustration of using Zn(CH3COO)2·2H2O crystals as a sensing medium in a Fabry–Perot interferometer pressure sensor by taking advantage of its large NAC. | ||
Conclusions
In summary, we have revealed that a 2D molecular material, Zn(CH3COO)2·2H2O, shows the extremely rare NAC effect over a wide pressure range via a combined approach of high-pressure experiments and first-principles calculations. Compared with other known NAC materials, Zn(CH3COO)2·2H2O exhibits a synergistic NAC mechanism which arises from a complex cooperation of in-plane coordination and hydrogen-bonding, and out-of-plane van der Waals interactions in its supramolecular structure. Moreover, we propose that Zn(CH3COO)2·2H2O and other NAC crystals could have important applications as pressure-converting materials for fabricating ultrasensitive pressure sensors. Considering the intrinsic electronic difference between hydrogen-bonding and other bonding forces, 2D materials assembled via hydrogen-bonding will offer a new materials platform for exploring pressure stimuli in quantum confined solids. More broadly, we envisage that the rich structural diversity in coordination compounds and other molecular materials in extreme environments will undoubtedly facilitate the discovery of new electronic, optical and magnetic functionalities from hybrid 2D materials by considering hydrogen-bonding and other supramolecular interactions.Experimental
General information and synthesis
All chemicals and solvents were of reagent grade and used as received. Zinc salt Zn(CH3COO)2·2H2O was synthesized according to a literature method.26High-pressure synchrotron powder X-ray diffraction measurements (HP-PXRD)
The high-pressure synchrotron powder XRD experiments were performed at the 4W2 beamline of the Beijing Synchrotron Radiation Facility (BSRF). An X-ray beam with a wavelength of 0.6199 Å was focused on a 36 × 12 μm2 spot using Kirkpatrick–Baez mirrors. The hydrostatic pressure was exerted by the systematic diamond anvil cells (DACs) with a culet diameter of 400 μm. The samples in well ground powder form were placed in a hole of about 120 μm diameter in a pre-indented stainless steel gasket with a thickness of about 40 μm. Silicone oil served as the pressure-transmitting medium and ruby chips were placed for pressure calibration by measuring the fluorescence shift as a function of pressure.39 The diffraction patterns were collected using a Pilatus 2M detector and integrated via the Fit2d suite of programs.40 The cell parameters under different pressures were refined by the Pawley method using the whole profile fitting program implemented in Materials Studio.First-principles calculations
The first-principles calculations were performed by using CASTEP,41,42 a total energy package based on plane-wave pseudopotential density functional theory (DFT).41 The local density approximation (LDA)43,44 was adopted to describe the exchange–correlation energy. Optimized ultrasoft pseudopotentials were adopted.45 A kinetic energy cutoff of 500 eV and a Monkhorst–Pack k-point mesh of 6 × 6 × 2 spanning less than 0.04 Å−1 were chosen.46 The atomic positions at intervals of about 0.5 GPa in the 0–4.44 GPa range were calculated by first-principles geometry optimization. In this geometry optimization, the cell parameters were fixed at the experimental values, and only the atomic positions at each pressure were optimized.Atomic force microscopy (AFM)
The surface topographies and the corresponding height profiles of different thickness nanosheets were collected using a Digital Instrument Multimode SPM in the tapping mode with a BRUKER RTESPA-300 tip. The bulk crystals were ground gently, and the nanosheets were prepared by dispersing the ground Zn(CH3COO)2·2H2O powder in ethanol and sonicating it for about 30 min in a KQ3200DE ultrasonic cleaner. Then the milky suspension in the vial was centrifuged at a rate of 4000 rpm. After keeping the tube still for a few minutes, the top suspension containing exfoliated nanosheets was deposited on a clean silicon substrate (1 × 1 cm2). After the solvent on the substrate was evaporated completely, the as-prepared nanosheets were scanned at a rate of 1.00 Hz. The images were taken with a resolution of 256 × 256 pixels.2Transmission electron microscopy (TEM)
The bulk crystals were ground gently and dispersed in ethanol, and then the resulting suspension was deposited on a holey carbon support film prior to TEM testing. A Titan 60-300 Cs corrected transmission electron microscope operating at 300 kV was used to capture the bright-field images on the high dynamic range image plates. The nanosheets were very sensitive to the electron beam and lost their crystallinity within 5 s.Nanoindentation
The nanoindentation experiments were performed on the (100) and (001) facets using a nanoindenter (Triboindenter from Hysitron, Minneapolis, USA) with in situ imaging capability.47 The machine continuously monitors and records the load (P) and displacement (h) of the indenter with force and displacement resolutions of 1 mN and 0.2 nm, respectively. A three-sided pyramidal Berkovich diamond indenter with a sharp tip radius of about 50 nm was used to indent the crystals. A standard fused silica sample with a reduced modulus of 72 GPa and hardness of 9 GPa was adopted for calibration. The raw data were analysed using the Oliver and Pharr method.48,49Conflicts of interest
There are no conflicts to declare.Acknowledgements
All authors are grateful for the funding support from the National Natural Science Foundation of China (Grant No. 21571072 and No. 11474292) and the support from the 4W2 beam line of Beijing Synchrotron Radiation Facility (BSRF). G. F. acknowledges the funding support from the Science Research Project of Hubei Provincial Department of Education, China (Grant No. B2018198).Notes and references
- R. H. Baughman, S. Stafström, C. Cui and S. O. Dantas, Science, 1998, 279, 1522–1524 CrossRef CAS PubMed.
- X. X. Jiang, Y. Yang, M. S. Molokeev, P. F. Gong, F. Liang, S. H. Wang, L. Liu, X. Wu, X. D. Li, Y. C. Li, S. F. Wu, W. Li, Y. C. Wu and Z. S. Lin, Adv. Mater., 2018, 30, 1801313 CrossRef PubMed.
- A. L. Goodwin, D. A. Keen and M. G. Tucker, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18708–18713 CrossRef CAS PubMed.
- A. B. Cairns, A. L. Thompson, M. G. Tucker, J. Haines and A. L. Goodwin, J. Am. Chem. Soc., 2011, 134, 4454–4456 CrossRef PubMed.
- A. B. Cairns, J. Catafesta, C. Levelut, J. Rouquette, A. van der Lee, L. Peters, A. L. Thompson, V. Dmitriev, J. Haines and A. L. Goodwin, Nat. Mater., 2013, 12, 212–216 CrossRef CAS PubMed.
- H. J. Shepherd, T. Palamarciuc, P. Rosa, P. Guionneau, G. Molnár, J.-F. Létard and A. Bousseksou, Angew. Chem., Int. Ed., 2012, 51, 3910–3914 CrossRef CAS PubMed.
- C. H. Woodall, C. M. Beavers, J. Christensen, L. E. Hatcher, M. Intissar, A. Parlett, S. J. Teat, C. Reber and P. R. Raithby, Angew. Chem., Int. Ed., 2013, 52, 1–5 CrossRef PubMed.
- W. Li, M. R. Probert, M. Kosa, T. D. Bennett, A. Thirumurugan, R. P. Burwood, M. Parinello, J. A. K. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2012, 134, 11940–11943 CrossRef CAS PubMed.
- W. Cai and A. Katrusiak, Nat. Commun., 2014, 5, 4337 CrossRef CAS PubMed.
- Q. Zeng, K. Wang and B. Zou, J. Am. Chem. Soc., 2017, 139, 15648–15651 CrossRef CAS PubMed.
- A. D. Fortes, E. Suard and K. S. Knight, Science, 2011, 331, 742–746 CrossRef CAS PubMed.
- W. Cai, J. He, W. Li and A. Katrusiak, J. Mater. Chem. C, 2014, 2, 6471–6476 RSC.
- A. B. Cairns and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 20449–20465 RSC.
- I. Loa, K. Syassen, R. K. Kremer, U. Schwarz and M. Hanfland, Phys. Rev. B, 1999, 60, R6945–R6948 CrossRef CAS.
- S. A. Hodgson, J. Adamson, S. J. Hunt, M. J. Cliffe, A. B. Cairns, A. L. Thompson, M. G. Tucker, N. P. Funnell and A. L. Goodwin, Chem. Commun., 2014, 50, 5264–5266 RSC.
- W. Zieliński and A. Katrusiak, Cryst. Growth Des., 2014, 14, 4247–4253 CrossRef.
- W. Cai, A. Gładysiak, M. Anioła, V. J. Smith, L. J. Barbour and A. Katrusiak, J. Am. Chem. Soc., 2015, 137, 9296–9301 CrossRef CAS PubMed.
- S. M. Clark, K.-J. Jeon, J.-Y. Chen and C.-S. Yoo, Solid State Commun., 2013, 154, 15–18 CrossRef CAS.
- A. P. Nayak, S. Bhattacharyya, J. Zhu, J. Liu, X. Wu, T. Pandey, C. Q. Jin, A. K. Singh, D. Akinwande and J.-F. Lin, Nat. Commun., 2014, 5, 3731 CrossRef CAS PubMed.
- T. Kmura, A. Asamitsu, Y. Tomioka and Y. Tokura, Phys. Rev. Lett., 1997, 79, 00319007 Search PubMed.
- P. Cervantes, Z. Slanic, F. Bridges, E. Knittle and Q. Williams, J. Phys. Chem. Solids, 2002, 63(10), 1927–1933 CrossRef CAS.
- X. X. Jiang, S. Y. Luo, L. Kang, P. F. Gong, W. J. Yao, H. W. Huang, W. Li, R. J. Huang, W. Wang, Y. C. Li, X. D. Li, X. Wu, P. X. Lu, L. F. Li, C. T. Chen and Z. S. Lin, Adv. Mater., 2015, 27, 4851–4857 CrossRef CAS PubMed.
- M. Y. Seyidova and R. A. Suleymanov, J. Appl. Phys., 2010, 108, 063540 CrossRef.
- A. M. Sweetman, S. P. Jarvis, H. Q. Sang, I. Lekkas, P. Rahe, Y. Wang, J. B. Wang, N. R. Champness, L. Kantorovich and P. Moriarty, Nat. Commun., 2014, 5, 3931 CrossRef CAS PubMed.
- G. A. Eby, Med. Hypotheses, 2010, 74, 482–792 CrossRef CAS PubMed.
- T. Ishioka, A. Murata, Y. Kitagawa and K. T. Nakamura, Acta Crystallogr., 1997, C53, 1029 CAS.
- G. Q. Feng, D. Gui and W. Li, Cryst. Growth Des., 2018, 18, 4890–4895 CrossRef CAS.
- S. Varughese, M. S. R. N. Kiran, U. Ramamurty and G. R. Desiraju, Angew. Chem., Int. Ed., 2013, 52, 2701–2712 CrossRef CAS PubMed.
- D. Gui, L.-J. Ji, A. Muhammad, W. Li, W.-Z. Cai, Y.-C. Li, X.-D. Li, X. Wu and P.-X. Lu, J. Phys. Chem. Lett., 2018, 9(4), 751–755 CrossRef CAS PubMed.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329 CrossRef CAS.
- R. J. Angel, J. Gonzalez-Platas and M. Alvaro, Z. Kristallogr., 2014, 229, 405–419 CAS.
- S. Sobczak and A. Katrusiak, Cryst. Growth Des., 2018, 18(2), 1082–1089 CrossRef CAS.
- Q. Li, S. Li, K. Wang, Z. W. Quan, Y. Meng and B. Zou, J. Phys. Chem. Lett., 2017, 8(2), 500–506 CrossRef CAS PubMed.
- M. Szafrański, A. Katrusiak and J. Phys, Chem. Lett., 2016, 7(17), 3458–3466 Search PubMed.
- G. Q. Feng, X. X. Jiang, W. J. Wei, P. F. Gong, L. Kang, Z. H. Li, Y. C. Li, X. D. Li, X. Wu, Z. S. Lin, W. Li and P. X. Lu, Dalton Trans., 2016, 45, 4303–4308 RSC.
- M. Anioła, A. Katrusiak and R. Kia, CrystEngComm, 2012, 14, 6424–6427 RSC.
- I. M. Lifshitz, Zh. Eksp. Teor. Fiz., 1952, 22, 475–486 Search PubMed.
- R. H. Baughman, S. Stafstrom, C. X. Cui and S. O. Dantas, Science, 1998, 279, 1522–1524 CrossRef CAS PubMed.
- H. K. Mao, J. Xu and P. M. Bell, J. Geophys. Res., 1986, 91, 4673–4676 CrossRef CAS.
- J. Hammersley, Fit2d User Manual, ESRF, Grenoble, France, 1996 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Prob ert, K. M. Refson and C. Z. Payne, Kristallografiya, 2005, 220, 567–570 CAS.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter, 1981, 23, 5079 CrossRef.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter, 1990, 41(2), 1227 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- L.-Y. Dong, S.-J. Sun, Z.-Y. Deng, W. Li, F.-X. Wei, Y.-J. Qi, Y.-C. Li, X.-D. Li, P.-X. Lu and U. Ramamurty, Comput. Mater. Sci., 2018, 141, 49 CrossRef CAS.
- W. C. Oliver and G. M. Pharr, J. Mater. Res., 1992, 7, 1564–1583 CrossRef CAS.
- W. C. Oliver and G. M. Pharr, J. Mater. Res., 2004, 19, 3–20 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc03291b |
| This journal is © The Royal Society of Chemistry 2019 |