Mapping the conceptual space formed by students’ understanding of coordination number of a transition metal complex: an exploratory study

Abstract

We report here on an exploratory study done with a sample of university students (N = 140) which sought to explore their understanding of the term ‘coordination number’, a concept encountered in the topic of transition metals chemistry, through a simple open-ended question. The findings show that the conceptual space related to the conceptions students harbour span the interval from non-canonical to canonical limits. That is, the responses from the students include incorrect, partially correct and correct answers. Additionally, instructor commentary, based on teaching experience acquired with a number of cohorts of students, is provided for the range of conceptions encountered, a departure somewhat from the traditional approach, and among the very few, if any, studies, which use such an approach. Those conceptions that are partially correct cannot strictly be labelled as alternative conceptions as it is argued that these can still be used by students to solve problems set in certain contexts on the topic.

---

Introduction

Alternative conceptions

In the common ‘alternative conceptions’ (ACs) framework, it is assumed that students harbour a number of misconceptions related to a topic and that these have to be addressed in order for effective learning to occur. The presence of ACs comes in the way of students achieving good conceptual understanding of a topic. Depending on the nature of the ACs, some can reside in very sturdy conceptual frameworks (Gilbert and Watts, 1983) while others can have a fleeting existence as these are contextually generated (Claxton, 1993). A distinction ought to be made between the terms ‘concept’ and ‘conception’. Though there is no general consensus on their similarities and differences, Duit and Treagust (1995) view concepts as having scientific robustness while conceptions depart from normative scientific frameworks. We use this interpretation in this study.

Sfard (2008) regards that it is concepts that are learnt and that these are anchored in the learner's mental framework. “Concepts are to be understood as basic units of knowledge that can be accumulated, gradually refined and combined to form ever richer cognitive structures” (p. 3). “The understanding of a concept is always an individual understanding, that is, a conception, and the quality of this understanding is decided upon by the extent to which the individual can communicate with experts in the field” (Larsson and Halldén, 2010). A large number of studies have thus focused on identifying students’ ACs as these can be used by instructors to promote proper conceptual understanding. The ‘alternative conceptions’ framework is very much in line with the constructivist perspective, which emphasizes the importance of existing knowledge of the learner in interpreting new knowledge. However, a common criticism is that the way some of the ACs are framed is a matter of terminology (Hammer, 1996), which reflects a chasm between students’ and scientists’ ways of thinking. Another point is that the framework is not able to shed light on the genesis of the gamut of the ACs uncovered (Taber, 2010).

Studies on ACs in chemistry at the undergraduate level have received relatively less attention than those at the school level. For example, Luxford and Bretz (2014) developed a bonding representations inventory to document a number of ACs about covalent and ionic bonding representations among undergraduate students. In another study, McClary and Bretz, (2012) developed and used a 4-tier diagnostic instrument to identify students’ ACs related to acid strength in organic chemistry. Cooper et al. (2010) explored undergraduates’ difficulties in developing representational competencies on Lewis structures. Recognizing the importance of exploring undergraduate students’ understanding, the US National Research Council's report on discipline-based educational research has a chapter on identifying and improving college students’ conceptual understanding in science and engineering (Singer et al., 2012). Specifically, it has been noted that “Chemistry education could benefit from additional measures that specifically target students’ conceptual understanding because only a few such measures exist – to date, chemistry education researchers have used a variety of other tools to uncover and document incorrect ideas and beliefs” (p. 74).

Clearly, more work needs to be done in exploring the understanding of chemistry undergraduates on a number of topics. The present study is an attempt in this direction.

Rationale for study

Why focus on a concept not in the ‘big ideas’ topic in chemistry?

A large number of studies in the misconceptions literature have focused on ACs harboured by students on various topics in the sciences and at different academic levels. Most of the studies have focused on school-level students (for example, Gurcay and Gulbas, 2015; Supasorn, 2015) and relatively fewer have been done on university students (for example, McClary and Bretz, 2012; Sreenivasulu and Subramaniam, 2013). Studies on misconceptions in the sciences have contributed immensely towards understanding the nature of ACs harboured by students as well as providing instructors valuable resources for use in teaching and learning.

Studies on chemistry in the mainstream science (and chemistry) education journals have generally focussed on classical or ‘big ideas’ topics – for example, chemical bonding (Peterson and Treagust, 1989); nuclear chemistry (Tekin and Nakiboglu, 2006); atomic structure (Griffiths and Preston, 1992); electrochemistry (Sanger and Greenbowe, 1997); chemical equilibria (Hackling and Garnett, 1985); and reaction kinetics (Yan and Subramaniam, 2018). There are relatively fewer studies which have focused on topics encountered in the university chemistry curriculum (for example, chemical thermodynamics (Sreenivasulu and Subramaniam, 2013) and organic chemistry (Zoller, 1990). Studies in the literature have also generally focused on topics rather than solely on unitary concepts in these topics. Where unitary concepts have been explored in university chemistry education, it has been within the framework of the relevant topic – for example, acid strength in organic chemistry (McClary and Bretz, 2012).

There is also a need for researchers to focus on concepts that are not included in the ‘big ideas’ topics. As indicated earlier, there has already been a lot of research studies that have been conducted on various ‘big ideas’ topics in the sciences, and we feel there is a need to also focus on other topics or concepts within the latter. This can possibly help to open up further research endeavours on these topics or concepts, thus providing university instructors with further resources for use in their teaching. This is a key driver for the current study.

We were interested in the range of conceptions harboured by university students when asked for their understanding of a singular entity – coordination number, a term encountered in the topic of transition metals chemistry. The latter is a very important topic in the university chemistry curriculum but there is a scarcity of studies on misconceptions in this topic. There is one recent study (Sreenivasulu and Subramaniam, 2014) on this topic, and the authors documented 23 ACs on this topic. However, there was no ACs reported on ‘coordination number’ in their study.

By probing students’ responses on their understanding of coordination number, we wished to explore to what extent a range of conceptions exist for this term at the group level and assess the relative accuracy of these conceptions. The range of conceptions harboured by students on a concept can have instructional implications on how the concept can be better taught.

Why generate the conceptual space about a unitary concept

In the science misconceptions literature, it has been noted that students have varying conceptualizations of a term – for example, limiting reagent (Mammen, 1996) and oxidation number (Brandriet and Bretz, 2014). The varying conceptualizations of the term represent a spectrum of understandings and these may demarcate the diverse interpretations of the term between canonical and non-canonical limits. We label this as ‘conceptual space’ in the context of this paper. From an instructional perspective, we feel that it is desirable for instructors to know the elements of this conceptual space as it can help to promote the transitioning towards normative understanding. This would be an additional objective of our study.

Why focus on instructor commentary on student responses?

In most studies on ACs, the emphasis has been on eliciting students’ views, often through diagnostic instruments, tests, interviews, etc. There are very few, if any, studies that have focused on eliciting teachers’ views on why students harbour ACs. By virtue of their experience in teaching various topics, interactions with students over a period of time and marking of test papers, teachers are likely to possess useful insights on students’ understanding of various topics, the misconceptions harboured by them and perhaps why these misconceptions occur in the first place. Tapping on their perspectives can possibly shed further light on students’ thinking, and can provide a useful lens that appears to be generally lacking in the literature. This will be an additional focus of our study.

Indeed, reflections based on teaching practice are important in developing a teacher's knowledge and beliefs (Clarke and Hollingsworth, 2002). Shulman's model of pedagogical reasoning and action (Shulman, 1987, p. 15) emphasizes that teachers need to be aware of students’ understanding of a particular topic as this has instructional implications, and this can come about by teaching a number of cohorts of students. Van Driel and Berry (2012) also reiterate the point that ‘pedagogical content knowledge includes teachers’ understanding of how students learn, or fail to learn, specific subject matter’.

The views of teachers on the conceptions of students and why these arise come from experience with teaching a number of cohorts over a period of time, and such views are likely to be relatively more representative at the group level when consolidated – that is, it can uncover the common ACs that tend to recur across cohorts and provide some pointers for the basis of these. Thus, we feel that teachers’ views have more generalizability as compared to interviews of students. Interviews are usually restricted to a limited number of students and the views emerging, though useful, cannot be taken as being unequivocally representative of their cohort. We also feel that there is a need to go beyond interviews, especially in studies involving a large sample size where a single open-ended question is used to probe student understanding.

This motivation is another driver for the current study.

Problems with understanding concept of coordination number

There is hardly any literature that explores students’ understanding of the term ‘coordination number’ though it is an important term in transition metals chemistry at high school and undergraduate levels. From our teaching experience, we note that the topic of transition metals chemistry is fraught with several ACs, and the term ‘coordination number’ poses some barriers towards proper conceptual understanding. The term requires conceptual integration of ideas across different domains in chemistry – for example, chemical bonding, periodic table, and stoichiometry.

We have observed that the primary source of students’ problems with understanding and interpreting of the term ‘coordination number’ is due to their confusion with appropriate usage and application of the terms coordination number, oxidation number, and valence. Based on the first author's teaching experience of the topic and based on information from text books, the difficulties, ambiguities, and sources of confusion arise mostly where coordinate (often used interchangeably with coordinate covalent) or dative bonds are involved. Also, students’ prior knowledge on the concept of ‘valence’, which refers to the number of bonds it forms in its compounds/molecular formula in question, will not be applicable with coordination compounds and, hence, they may not be able to relate it to the modern terms.

The first author has also observed during tutorial discussions that some students tend to apply the concept of valence and coordination number interchangeably. He has further noted that a number of students tend to apply the concept of oxidation number interchangeably when interpreting the term ‘coordination number’ of the metal ion in complex ions. Such interpretations are highly misleading. For example, in instances where they view that Mn²⁺ forms two bonds with Cl⁻ (MnCl₂) and Mn⁷⁺ forms seven bonds with Cl⁻ (MnCl₇), these were thought to have coordination numbers of 2 and 7 respectively. When the students start to learn about coordination number in the metal complexes, it has also been noted that this confusion leads to a serious misconception that di, tri, tetra, penta-, hexa-, and heptavalent metal ions would have coordination numbers of 2, 3, 4, 5, 6 and 7 respectively.

It is important to note that valence is a classical concept which may not clearly accommodate coordinate bonds or dative bonds as it is based on a molecular view of chemistry and is studied prior to electronic theories of bonding. Thus, along with modern bonding theories and clear definitions of terms about coordination compounds, basic Werner's terminology about primary valence and secondary valence of the central metal ions in complexes needs to be emphasized as a fundamental conceptualization during instruction although these two terms are replaced by oxidation number (or oxidation state) and coordination number respectively.

Concept of coordination number in transition metals chemistry

In metal complexes, the central metal ion is surrounded by two or more molecules or ions, called ligands, which form coordinate covalent bonds with the metal centre. The coordinate covalent bonds between the central metal ion and the ligands can be considered as σ-bonds. According to Lewis acid–base theory, ligands act as electron pair donors and hence are considered as Lewis bases while the central metal ion acts as an electron pair acceptor, that is, a Lewis acid. An atom in the ligand that can donate an electron pair and directly bond to the metal centre is called the donor atom.

Since coordinate bond formation results from a Lewis acid–base reaction, coordination number can also be viewed as being equal to the number of electron pairs donated by ligand donor atoms or accepted by the metal in the formation of a coordination compound since the number of such electron pairs shared represent the number of bonds between the metal ion and ligand.

By way of example, CoCl₃·6NH₃ can be described as having a strongly bound unit called a complex ion [Co(NH₃)₆]³⁺. This unit within the square bracket is considered as a complex entity or ion formed by coordination of NH₃ to the central Co³⁺ (Fig. 1). There are three other Cl⁻ counter ions (as they balance the charge on the complex ion) which are located outside the square bracket (not shown). The neutral [Co(NH₃)₆]Cl₃ can be termed as a coordination compound, in which the metal is bonded to the ligands through a coordinate covalent bond (σ-bond).

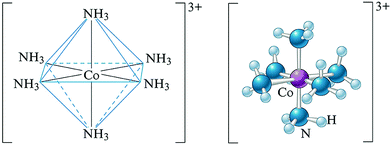Fig. 1 Structural formula of a complex ion, [Co(NH₃)₆]³⁺ showing central metal ion and ligands (left: octahedral geometry around cobalt ion; right: ball and stick model).

The coordination number of a metal ion is not always evident from the composition of the solid metal complex as solvent molecules and species that are potentially ligands may simply fill spaces within the structure and do not always have any direct bonds to the central metal ion. For instance, X-ray diffraction studies show that CoCl₂·6H₂O contains the neutral complex [CoCl₂(H₂O)₄]·2H₂O, which has two uncoordinated H₂O molecules occupying well-defined positions in the crystal as water of crystallization.

The central metal ion forms a certain number of bonds with the ligands based on the number of donor atoms it can be bonded to. Basically, the term coordination number is related to this number of bonds. Thus, the coordination number of a metal ion in a complex refers to the number of bonds between the ligand donor atoms and the central metal ion. In an inorganic coordination entity, it is also the number of σ-bonds between ligands and the central metal ion. For example, in [Ag(NH₃)₂]⁺, [Pt(NH₃)₄]²⁺ and [Co(NH₃)₆]³⁺, the number of bonds between the ligands and the central metal ion (that is, the coordination number) is 2, 4 and 6 respectively, where each ammonia molecule acts as a monodentate ligand, with a lone pair of electrons on the nitrogen atom, and is bonded to the central metal ion via a nitrogen donor atom. In these examples, it can be noted that the number of bonds around the central metal ion in the complex is the same as the number of ligands bonded to it as the ligand is monodentate (each ligand forms one bond to the metal ion through one donor atom).

Organometallic compounds and, hence, π-bonds, are not considered for this study in determining coordination number. Further, in view of non-carbon or non-organic pi-bonding ligands such as oxides and nitrides that give rise to potential multiple ligand–metal bonds, chemistry of complexes containing such pi-donors are out of scope of the course and hence not considered in this study.

Research questions

The specific research questions that we wished to better understand were:

(1) What is the range of conceptions harboured by university students on the term ‘coordination number’ in relation to a transition metal complex?

(2) How accurate are the conceptions harboured by these students?

(3) From the point of view of the course instructor, what is the basis for the students harbouring the reported conceptions?

(4) What are the elements of the conceptual space related to the term ‘coordination number’, based on students’ responses?

We report on the findings of the above in this exploratory study.

Methodology

Sample

Undergraduate students (N = 140) from the first author's university participated in this study after being briefed on the purpose of the study.

Permission to conduct the study was obtained from the first author's university, and participating students provided informed consent. They were enrolled in the second year of the BSc program in chemistry. Their ages ranged from 19–23, with most being females.

Instrument

A simple open-ended question, framed as follows, was used to elicit the undergraduates’ understanding of the term ‘coordination number’:

What do you understand by the term ‘coordination number’, as applied to a transition metal complex. (What is required here is not a textbook definition but an elaboration that shows your understanding)

Half an A-4 size page was allocated for students to write their responses.

Such an approach, of course, lacks the rigor of in-depth interviews which, in any case, can usually be done on only a limited number of students. However, the approach has the advantage of tapping on the responses of a large sample of students (N = 140) to uncover conceptions at the group level. The level of detail that can be obtained from such an approach is unlikely to approach those from interviews but nevertheless, there is scope for analysing the responses, which are in students’ own handwriting, to probe their understanding of this term.

An additional reason for using just a single question is that recent research has shown that such an approach can be useful for probing students’ understanding at the group level when the sample size is large (for example, Seoh et al., 2016; Loh and Subramaniam, 2018). In the latter study, high school students’ ACs on galvanic cells was documented, among other things, and no interviews were used. There is a need for more studies of this nature so as to contribute further to the utility of using such types of questions to document ACs. This is another driver for the current research.

Procedure

Students sat for the ‘test’ after having completed a one-semester course on transition metals chemistry, where the term ‘coordination number’ is encountered. They took less than 15 minutes to answer this question.

As part of the course, students were instructed about ‘coordination number’ through various examples of mono-, bi-, tri- and polydentate ligands, including EDTA which is hexadentate, and their modes of bonding to metal ions with the help of illustrations to show how the term ‘coordination number’ can be viewed with respect to different types of ligands. They were also taught about the concept of ‘chelation’ (formation of ring structures around the central metal ion) while illustrating the coordination modes of bidentate ligands such as ethylenediamine and ethanedioate as well as other polydentate ligands with the central metal ion.

Data analysis

The responses of students were keyed into an Excel file. A simple coding approach was used to classify the responses. In this approach, the categories emerged naturally from the data set rather than being imposed from a pre-conceived viewpoint. Students’ responses which share commonalities were placed into a particular category and the common understanding emanating in these responses was framed as a statement broadly representing their understanding. Those responses that are semantically congruent were also placed in the same category. The frequencies of the responses for each category were added up and expressed as percentages.

A research assistant (who was doing his PhD in a different area in Chemistry but who has previously done a course on transition metals chemistry as part of his course requirements) helped to do the classification of the responses after being briefed by the authors on the steps needed. Both authors later independently examined the classifications. There were no major disagreements between them but minor differences in opinions were resolved by dialogue. There was full agreement between both authors on the final classification of the responses into the various categories and the category labels assigned.

Students’ responses were compared with the standard IUPAC definition of the term ‘coordination number’ – “the number of σ-bonds (sigma bonds) between ligands and the central atom.” for identifying and categorizing the students’ conceptions as incorrect, partially correct or correct. A student's response about ‘coordination number’ is categorized as correct if it meets the above scientific and standard IUPAC definition. Apart from this, any response that implies the number of secondary valencies or number of electron pairs donated by ligand donors or accepted by the central metal ion are also considered to be valid definitions (note that our study is not about organometallic compounds where pi-bonds also exist between the ligands and the central metal and, hence, definitions including pi bonds are excluded).

The conceptual space was framed by arranging the students' responses in increasing order of conceptualization – that is, from incorrect to partially correct to correct.

Results and discussion

Students’ interpretation of the term ‘coordination number’

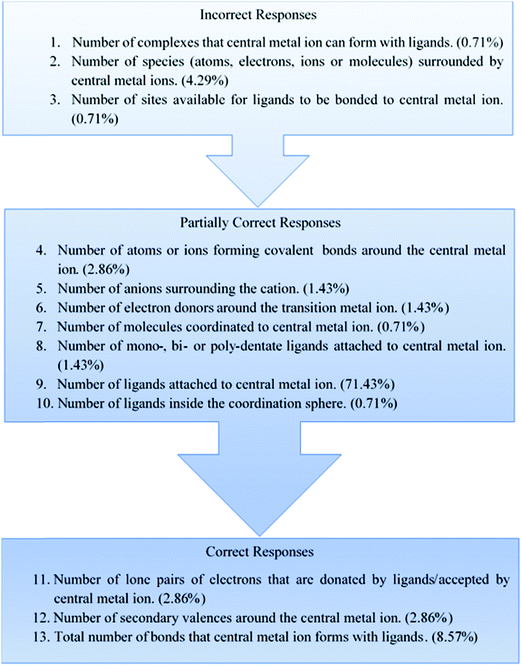
Students expressed various degrees of conceptualizations and interpretations of the term ‘coordination number’, based on the grouping of their responses into various categories which emerged from the coding (Table 1).

It can be seen that students’ responses can be arranged into 13 different categories, representing various degrees of conceptualization of the term ‘coordination number’. A possible reason for the emergence of a large number of categories is that the sample size itself is large, thus permitting multifarious conceptions to emerge at the group level.

Some students (5.71%) gave a variety of responses (1–3 in Table 1), which ranged from incorrect responses to ACs. In this 5.71%, about 4.3% of the sample interpreted ‘coordination number’ incorrectly as ‘number of species (electrons, ions and molecules) surrounded by central metal ions’. It is surprising that these students have the incorrect idea that there are central metal ions around the ions or electrons or molecules in a metal complex, and that the number of such central metal ions will be equal to the coordination number. It can be considered as an AC. One of the students (0.71%) provided an incorrect definition of coordination number in that it is equal to the ‘number of complexes that the central metal ion can form with ligands’. This can also be regarded as an AC. Another student (0.71%) thought that the coordination number is equal to the ‘number of sites available for ligands to be bonded to central metal ion’. This conveys a misinterpretation that the central metal ion would have a certain number of bonding sites available for ligands and that this is equal to the coordination number. Though this meaning is ambiguous and incomplete, it can be considered as fragmented understanding comprising some important knowledge elements suitable for the construction of the meaning of ‘coordination number’. More likely, they might have appropriated such terminologies for expression without adequate understanding of the underlying nuances (Clough and Driver, 1985).

Table 1 Students’ interpretations of the term ‘coordination number’ (arranged in increasing order of correct conceptualization)

S. no.	Students’ conception	Sample verbatim response of students	Number	%
1	Number of complexes that central metal ion can form with ligands.	Coordination number is the number of complexes which the transition metal is able to form with the ligands	1	0.71
2	Number of species (atoms, electrons, ions and molecules) surrounded by central metal ions.	Coordination number is the number of different atoms, molecules, ions or electrons surrounded by metal ions.	6	4.29
3	Number of sites available for ligands to be bonded to central metal ion.	Coordination number is the number of sites that are available for the ligands that are able to be bonded to the central metal ion.	1	0.71
4	Number of atoms or ions forming covalent bonds around the central metal ion	It is the number of atoms or ions surrounding a central metal atom or ion forming non-ionic but directional covalent bonds with the metals.	4	2.86
5	Number of anions surrounding the cation.	Coordination number shows the ions or secondary valence. It shows how-many ions are around the central metal ion in coordination sphere.	2	1.43
6	Number of electron donors around the transition metal ion.	Coordination number refers to the number of donors (ligands) to the transition metal ion	2	1.43
7	Number of molecules coordinated to central metal ion.	Coordination number tells the size of the metal ion, whether it can accommodate more molecules or ligands or not.	1	0.71
8	Number of mono-, bi- or poly-dentate ligands attached to central metal ion.	In [CoCl4]^2+ the coordination number is 4 with mono-, bi- or poly-dentate ligand.	2	1.43
9	Number of ligands attached to central metal ion.	Number of ligands attached to the metal centre	100	71.43
10	Number of ligands inside the coordination sphere.	Coordination number is the number of ligands that is attached to the metal ion. It is directional (unlike primary valency also known as oxidation state). In general, only ligands in the inner sphere are included as the coordination number.	1	0.71
11	Number of lone pairs of electrons that are donated by ligands/accepted by central metal ion.	Coordination number is the number of lone pair of electrons that the central metal ion accepts from its ligands due to partially filled d-orbitals.	4	2.86
12	Number of secondary valencies around the central metal ion.	Coordination number = secondary valency	4	2.86
13	Total number of bonds that central metal ion forms with ligands.	Coordination number is the number of bonds that the metal ion is able to form. It is the number of bonds that the metal ion can form in a complex.	12	8.57

---

About 6.43% of the sample explained the term coordination number as the number of atoms, ions, anions, electron donors or molecules around the central metal ion or atom (4–7 in Table 1). Interestingly, these conceptions are not considered to be completely correct. Under this category, 2.86% of the sample indicated the coordination number as the number of atoms or ions forming covalent bonds around the central metal ion. A definition in terms of anions such as the number of anions surrounding the cation is provided by 1.43% of the sample. The other two definitions such as: number of electron donors around the transition metal ion and number of molecules coordinated to central metal ion, are expressed respectively by 1.43% and 0.71% of the sample under this category of the sample. However, these interpretations are not completely correct but can be considered as ambiguous and hence are partially correct when compared with the correct definition.

It has to be noted that for each of the foregoing responses, the percentage selection is less than 10%. There is little guidance in the literature on the percentage frequency of incorrect responses from open-ended questions that can be considered as ACs. As one of the foci of our study is to explore the conceptual space of the term ‘coordination number’ we shall study such responses by the students since it can provide potentially useful insights on students’ mental models and thinking.

It has to be noted that in the misconceptions literature, selections below 10% for questions in diagnostic instruments are generally not regarded as ACs. Though there is no consensus on this norm, since it is regarded as somewhat arbitrary (Taber and Tan, 2011), nevertheless it is still useful from a parsimonious standpoint to sieve the more important responses from the larger data set and the approach is generally used by researchers when identifying ACs from diagnostic tests. However, for a study of this nature, which also seeks to frame the conceptual space formed by students’ conceptualization of the term ‘coordination number’, responses below 10% cannot be overlooked, especially if these have also occurred in previous cohorts of students. It is for this reason that we have included such responses as well.

The majority of the students attempted to explain the coordination number of a central metal ion in terms of the number of ligands in general. In fact, it is also expected that most of the students try to map the concept of coordination number in a metal complex with the number of ligands. Thus, 73.54% (103 out of 140 students) of the sample explained coordination number in terms of the number of ligands, as shown in student's conceptions 8–10 in Table 1. The definitions under this category are partially correct. Interestingly, 71.4% of the sample expressed their understanding of coordination number as: the number of ligands attached to the central metal ion. A few students (about 1.43%) indicated the same type of definition but tried to include the type of ligands (denticity of ligands) as in: number of mono-, bi- or poly-dentate. ligands attached to central metal ion. Another 0.71% of the sample interpreted the term coordination number as being equivalent to ‘the number of ligands inside the coordination sphere’. Again, both these interpretations of the term ‘coordination number’ can also be considered to be partially correct.

Thus, altogether 73.54% of the sample interpreted the term ‘coordination number’ partially correctly in terms of the number of ligands or groups in general. This group of students seem to have strongly believed that the number of ligands around the central metal ion or atom and the coordination number are one and the same. But this conception can be considered correct only in some contexts when there are mono-dentate ligands in the coordination complex. This might be an indication that most of the students have not completely achieved proper understanding of the term, coordination number, and defining it with respect to the nature of ligands, possibly because they have not been able to achieve adequate conceptual integration of the various domain knowledge needed to appreciate this term.

Some of the students defined the coordination number correctly (concepts 11–13 in Table 1). Under this category, 14.29% of the sample interpreted it correctly as equal to the number of electron pairs donated by ligands (2.86%) (or) number of secondary valencies (2.86%) (or) total number of bonds between the metal ion or atom and the ligands (8.57%). Besides those correct responses matching that of the IUPAC definition, the responses – number of electron pairs donated by ligands or the number of secondary valencies around the central metal ion, can also be accepted as correct responses as both these imply the number of bonds between the ligands and central metal ion and also in light of classical Werner's theory of coordination compounds (Kauffman (1967) (Werner's concept of ‘secondary valence’ is replaced by ‘coordination number’ in modern coordination chemistry).

Responses 11–13 are considered correct definitions of coordination number, as taught in class. It also reveals the students’ ability to interpret the meaning and correct definition of coordination number as it was taught during classroom instruction, and is applicable to several types of metal complexes containing different types of ligands, ranging from simple mono-dentate to poly-dentate.

Among the students’ responses, some excerpts indicated more information than just a definition of coordination number. For example:

‘Coordination number depends on the geometry of the metal complex. For example, when the coordination number is 4 it gives tetrahedral complexes. It depends on the size of the metal ion, ligand and steric effects.’

‘Coordination number decides the geometry around the metal ion. In [Fe(H₂O)₆] it is 6. In [CrCl₄] it is equal to 4.’

Some of them answered very briefly:

‘Inner sphere, [M(L)₆]’

Students’ responses displayed different forms of answers, ranging from a single sentence to elaborated ones, and either with graphical or non-graphical examples or without both, as categorized in Table 2. Most of the students (108 out of 140) answered through just a single sentence without providing any graphic or non-graphic examples. Some of the students' responses (6), including drawings, are provided in Fig. 2.

Table 2 Frequencies of students’ responses according to level of elaboration to open ended question

No. of samples with single sentence responses			No. of samples with elaborated responses
108	7	4	14	1	6
Note: In view of space constraints, graphics are not shown.
Without any graphic or non-graphic example	With graphic example	With non-graphic example	Without any graphic or non-graphic example	With graphic example	With non-graphic example
Example	Example	Example	Example	Example	Example
Coordination number is the number of ligands around the metal ion.	Coordination number is the number of sites available for ligands to be bonded to central metal ion.	Coordination number is equal to the secondary valence.	Coordination number is the number of ligands that is attached to the metal ion. It is directional (unlike primary valency also known as oxidation state). In general, only ligands in the inner sphere are included as the coordination number.	Coordination number is the number of ligands bonded to the central metal ion via coordinate bonds.	Coordination number is the number of ligands that are in the coordination sphere. For example, coordination number in [Cu(H 2 O) 6 ] ^2+ is 6 and 3 in [Cu(en) 3 ] ^2+ . Even though ‘en’ forms bidentate bonds with Cu ^2+ , the coordination number is 6.
		In [Cr(H 2 O) 4 ] ^2+ coordination number is 4.		Coordination number depends on the size of the metal ion, nature of the ligand and size of the ligand.

---

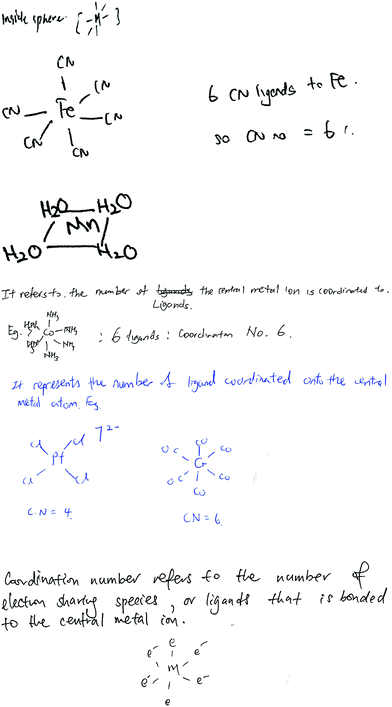Fig. 2 Examples of students’ responses for the term ‘coordination number’, expressed with aid of diagrams.

Table 3 presents instructor commentary on the various conceptions of the term’coordination number’ from the lens of the first author's teaching experience with a number of cohorts of students.

Table 3 Instructor commentary on students’ understanding of the term ‘coordination number’

S. no.	Students’ response	Instructor evaluation based on teaching experience
1	Number of complexes that central metal ion can form with ligands.	This is incorrect. A transition metal ion can form various complexes with different types of ligands. The number of such complexes can be several. Depending on the nature of the ligand, the coordination number can be different. It is incorrect to attribute the number of complexes formed by a complex that can be potentially formed with various ligands as being equivalent to the coordination number.
		For example, if a transition metal ion, M forms ‘n’ number of different types of coordination compounds, then ‘n’ does not represent the coordination number of the metal ion ‘M’.
2	Number of species (atoms, electrons, ions and molecules) surrounded by central metal ions.	This is incorrect. It is conceptually irrelevant and meaningless to define the term ‘coordination number’ in a metal complex in this way. Students misconceptualized it since structurally it is not possible for electrons, ions and molecules to be surrounded by a pool of central metal ions in a coordination compound. It is likely that students have appropriated such terminologies for expression without integrating their understanding of this term.
3	Number of sites available for ligands to be bonded to central metal ion.	This is incorrect. There is no clear indication of what is meant by ‘number of sites’ and no proper articulation of its meaning. This indicates students’ confusion about whether the ligand will have some sites for bonding with the central metal ion or whether there are sites from the central metal ion for ligands to be bonded with. Either way, this is incorrect.
4	Number of atoms or ions forming covalent bonds around the central metal ion	This can be considered to be partially correct.
		There is no indication whether the ion is an anion. It also does not refer to whether the atom is a monoatomic donor atom or a donor atom of a polyatomic molecular ligand. It shows lack of understanding of the term ‘ligand’, which could be either a molecular species with one or more donor atoms such as H2O (with one oxygen as donor atom) or an anion that can donate an electron pair to the central metal ion.
		For example, in the case of [CoF6]^3−, the ligand is F^− but not F atom as such. Students could have thought that monoatomic anions such as halides (F^−, Br^−, Cl^− and I^−) that are bonded to the central metal ion are atoms, but these species are acting as monoatomic anionic ligands. Students could have also viewed donor atoms of a ligand simply as atoms bonded to the central metal ion.
		In certain contexts, such an approach can lead to the correct answer. For example, if students assume [Co(H2O)6]^3+ as having 6 oxygen atoms (from the 6 aqua ligands that take part in bond formation with the central metal ion) that are bonded to Co^3+, then 6 is the coordination number, which is the same as the number of oxygen atoms bonded.
		Students seem to have conceptualized it partially, perhaps by reading and referring to a few standard text books as well – for example, Cotton et al. (1995); Kotz et al. (2010), which allude to this.
5	Number of anions surrounding the cation.	This can also be considered to be partially correct as it does not specify the number of bonds and, as such, is limited to only certain complexes where the ligand is an anion.
		For example, in [CoF6]^3−, the coordination number is 6 since there are six anions (F^−) surrounding the cation (Co^3+). As it can be appropriate for such cases of monodentate anionic ligands, it cannot be generalized for bi-dentate anionic ligands such as ethanedioate ions (C2O4^2−) or other multidentate anions.
		It is possible that students might have been influenced by reading some standard general chemistry text books (for example, Kotz et al. (2010), which allude to this.
6	Number of electron donors around the transition metal ion.	This can be considered to be partially correct.
		This is similar to defining coordination number as the number of ligands (which are electron pair donors) around the metal ion – however, there is no mention of the number of bonds around the central metal ion.
		For example, in [Co(H2O)6]^3+ there are six oxygen donor atoms bonded with the central Co^3+ from the six aqua ligands. From this viewpoint, the coordination number is 6 for central Co^3+.
		Again, students might have been influenced by reading some text books on transition metals (for example, Jones (2001), which allude to this.
7	Number of molecules coordinated to central metal ion.	This can be considered to be partially correct. The number of molecules bonded to the central metal ion will not necessarily be the same as the number of bonds between the molecules and the central metal ion.
		For example, in metal complexes containing bidentate ligands, such as ethylene diamine (en), that is, [Ni(en)3]^2+, the number of molecules coordinated to the central Ni^2+ is 3 but the number of sigma bonds or coordinate bonds (coordination number) is 6. Similarly, for example, in [Ni(C2O4)3]^4− containing the bidentate ethanedioate ions (C2O4^2−), the number of ethanedioate anions surrounding the central Ni^2+ is 3 but the coordination number is 6.
		However, in some complex ions, for instance, [Ni(NH3)6]^2+ as well as [Cu(H2O6)]^2+ containing neutral monodentate ligand molecules such as NH3 or H2O respectively, the coordination number becomes equal to the number of molecules coordinated to the central metal ion (6 in this case).
		Students might have also been influenced by reading some standard inorganic chemistry text books as well (for example, Cotton et al. (1995); Rodgers (2012), which allude to this.
8	Number of mono-, bi- or poly-dentate ligands attached to central metal ion.	This can be considered to be partially correct.
		However, at the very basic level, this can be an acceptable meaning of the term ‘coordination number’ with respect only to monodentate ligands. For example, in the case of NH3 or H2O, the coordination number is equal to the number of such ligands (and hence coordination bonds) bonded to the central metal ion, as in [Ni(NH3)6]^2+ or [Ni(H2O))6]^2+, where the coordination number is 6.
		However, this is a loose and partially correct explanation. As students learn more about ligands, for example, denticity (polydentate nature), chelation and chelating effect, they would start to think about differentiating ligands as mono- bi- tri- or polydentate, based on their denticity. They should then be able to relate denticity or the number of donor atoms a ligand contains with coordination number. For example, three bidentate ligands are sufficient to get a coordination number of 6 or, in general when there are multidentate ligands, the number of ligands attached to the central metal ion will be less than the actual number of bonds formed with it. As an example, in [Ni(en)3]^2+ containing a bidentate ‘en’ ligand, the number of ligands coordinated to the central Ni^2+ is 3 but the number of sigma bonds or coordinate bonds (coordination number) is 6.
9	Number of ligands attached to central metal ion.	This interpretation can be considered to be partially correct.
		If the ligand is monodentate, as in NH3, the number of ligands attached to the central metal ion is equal to the number of bonds since each bond arises from one ligand. However, the number of ligands bonded to the central metal ion will not necessarily be the same as the coordination number. For example, if the ligands are multidentate, then the number of ligands attached to the central metal ion will be less than the actual number of bonds attached to it, that is, the coordination number.
		Again, as an example, in [Ni(en)3]^2+ containing a bidentate ‘en’ ligand, the number of ligands coordinated to the central Ni^2+ is 3 but the number of sigma bonds or coordinate bonds (coordination number) is 6.
		Such partially correct definitions can also arise possibly when students are influenced by self-reading of some standard text books, for example, Kotz et al. (2010), Rodgers (2012), which allude to this.
10	Number of ligands inside the coordination sphere.	This can be considered to be partially correct, and similar to conception 9.
		According to Werner's theory of coordination compounds, a metal complex is regarded as a primary coordination sphere or inner-sphere in which the ligands are attached directly to the central metal ion or atom and their number is called the secondary valency (coordination number in modern terminology).
		However, this response is as good as the previous one as the number of ligands inside the coordination sphere and having bonded to the central metal ion will not necessarily be the same as the coordination number unless the ligand is monodentate.
		For example, in [Ni(en)3]^2+ containing a bidentate ‘en’ ligand, the number of these ligands coordinated to the central Ni^2+ inside the coordination sphere is 3 but the number of sigma bonds or coordinate bonds (coordination number) is 6 as each ‘en’ ligand can form two bonds.
		Students might have also been influenced by self-reading some standard inorganic chemistry textbooks, for example, Atkins and Overton (2010), which allude to this.
11	Number of lone pairs of electrons that are donated by ligands/accepted by central metal ion.	This interpretation can be considered to be correct, based on Lewis acid base concept applied to coordination bond formation and also based on Werner's theory of coordination compounds as the number of electron pairs donated by ligands will be the same as number of secondary valencies around the metal ion. This interpretation by the students implies an alternative meaning of the term ‘coordination number’. A donor atom of a ligand donates an electron pair to get bonded to the metal ion in a complex.
		Students would have conceptualized and interpreted that the number of electron pairs donated by ligands or those accepted by the central metal ion as equal to the number of bonds (coordination number) formed between the ligands and the central metal ion.
		For example, in the case of [Ni(NH3)6]^2+ or [Ni(H2O))6]^2+ the coordination number is equal to 6 because there are six lone pairs of electrons donated by six NH3 or H2O ligands. These six lone pairs correspond to six bonds to the central Ni^2+ ion, which is equal to the coordination number 6.
		This definition can also be applicable to complexes containing multidentate ligands. For example, in [Ni(en)3]^2+ each bidentate ‘en’ ligand donates two lone pairs and, hence, there are six lone pairs donated by the three ‘en’ ligands which would represent six bonds that corresponds to the coordination number of 6 for the central Ni^2+.
		Through this response, students seem to apply the concept of Lewis-acid base theory in the formation of coordinate covalent bonds between the ligand donor atoms and the central metal ion. Along these lines, this response can be very much valid.
12	Number of secondary valencies around the central metal ion.	This is correct.
		According to Werner's theory of coordination compounds, a complex ion, for example, [Ni(NH3)6]^2+ is either considered as coordination sphere or inner sphere which contains six bonds between the central Ni^2+ and six NH3 ligands. The bonds between the metal ion and ligand donor atoms are considered as ‘secondary valencies’ and number of secondary valencies is equal to the ‘coordination number’ in modern terminology.
		Through this response, students seem to apply Werner's theory of coordination compounds, where the term ‘secondary valence’ is encountered and represents the number of coordinate bonds between the central metal ion and the ligands (Kauffman (1967). However, in modern terminology, the term ‘coordination number’ has replaced the idea of ‘secondary valence’.
13	Total number of bonds that central metal ions form with ligands.	This is correct.
		This definition removes any ambiguity pertaining to the nature of the ligands- whether or not it is monodentate or polydentate. With this definition, students seem to have also correctly conceptualized the fact that if there are multidentate ligands attached to the central metal ion, then the number of such ligands will not be the same as the coordination number.
		For example, in [Ni(NH3)6]^2+ or [Ni(H2O))6]^2+, as the ligands NH3 and H2O are mono-dentate, and as there are 6 such ligands, there will be 6 sigma bonds around the Ni^2+ and the coordination number is 6. On the other hand, in [Ni(en)3]^2+, where there is a bidentate ‘en’ ligand, the number of ligands coordinated to the central Ni^2+ is 3 but the number of bonds (and thus coordination number) is 6.

---

A key point emerging from the instructor commentary in Table 3 is that even though there are instances of ACs in the students’ responses, a number of these responses can be considered to be partially correct as these are applicable in certain contexts. This presents some evidence for the existence of stable and fruitful conceptions as these can allow students to correctly answer questions set in certain contexts. The terms ‘stable’ and ‘fruitful are not related to aspects commonly encountered in longitudinal studies. By ‘stable’, we mean that the AC in question seems to be ensconced in the mental schemata of the students while by ‘fruitful’, we mean that it can be harnessed to correctly answer questions set in certain contexts. These conceptions are probably a carry-over from the students’ high school days, and thus these seem to be stable and fruitful because they have explanatory relevance in certain contexts. However, we have to acknowledge that our claims here are not supported by the data presented, and it is just based on the pedagogical content knowledge of the first author acquired by teaching previous cohorts of students. Not presenting meaningful application problems to the students in this study to extract evidence in support of our claims is a limitation of our study, and can be the basis for further work. Our key objective in this study was, however, to uncover the range of conceptions harboured by them of coordination number.

Proper conceptual understanding of a concept is linked to the extent to which students can accurately cognize the relevant scientific models inherent in that concept (Glynn and Duit, 1995). This means students need proper conceptual integration of the various knowledge elements in that concept at the theory or model level during learning and also be able to make use of this understanding to make predictions and provide explanations (NRC, 1996).

It can be noted that the term ‘coordination number’ is encountered by students when they are taught introductory transition metals chemistry at grade 12 level. The topic is developed in further depth when students take up chemistry at university. This means that some of the conceptions related to coordination number reported in this study are likely to have been developed in the students at the grade 12 level and may have remained somewhat resistant to instruction in some of them even at university. Owing to the extensive content that is covered in transition metals chemistry at the university level, there is a limit to the amount of time that can be allocated for covering the concept of ‘coordination number’ in depth. Students at university are expected to have some prior knowledge on the topic and take further responsibility for their own learning after attending lectures and tutorials on the topic.

Conceptual space for coordination number

When the responses are lined up from the incorrect to the correct, they span a range (Fig. 3). It can be seen that the responses increase in their degree of conceptualization when moving from the incorrect to the correct, with the intermediate ones being partially correct.

Fig. 3 Conceptual space for the term ‘coordination number’.

The responses of students, when placed from the incorrect to the correct, illuminate diverse interpretations of the term ‘coordination number’. It is suggested that this typology offers a useful lens for exploring the conceptualization of the term ‘coordination number’ at the group level and that this has instructional implications, which we will elaborate later. The intermediate conceptual elements might also represent the barriers needed for transitioning from non-canonical to canonical understandings.

The genesis of the conceptions can also be better appreciated from an instructor's perspective. As mentioned earlier, one of the aims of the present study is to explore why students hold on to such conceptions. A large body of literature exists on this, with interviews of students largely used to advance useful insights. While this is appropriate, the perspectives from an instructor, which is grounded in the pedagogical content knowledge acquired by teaching a number of cohorts of students, can also be important, and seem to be missing in the literature. For example, in relation to this study, the first author has not only extensive experience in teaching the topic of transition metals chemistry at the undergraduate level as well as interacting with students over tutorials but has also content research interests in this topic, among others. The insights and experiences that can be offered for some of the incorrect and partially correct responses from the lens of the instructor can add a valuable perspective in better understanding the responses of the students.

It is clear that students have some understanding of ‘coordination number’ that is reasonably based on the idea of ‘attachment point’ but it needs to be developed further by a refined concept of ligand to include polydenticity. The partially correct conceptions cannot be strictly labelled as incorrect or invalid since they possess explanatory significance in some contexts. These can be considered as ACs but not genuine mistakes. From the standpoint of Posner et al. (1982), the conceptions can be considered to be ‘fruitful’ since these can be used to correctly solve some problems. However, the latter authors used the term ‘fruitful’ for concepts – that is, in the process of conceptual change; students are more likely to abandon conceptions for concepts if they find the concepts useful for solving problems. In this regard, our finding that some conceptions can also be fruitful from the point of view of students (and instructor) is of significance. Also, the conception may have more explanatory coherence (Thagard, 1992) for the student and thus tends to be used. This could be the reason why it would appear to be anchored somewhat firmly in the cognitive framework of the students.

Implications for instruction

Textbooks generally present the normative content of a topic. Seldom do they include misconceptions on science topics or variations of a conception. This is understandable as these are usually based on research in educational settings, and the textbook is not really a platform for including such content. Thus, educational research is very important for enhancing teaching and learning. If the diversity and range of conceptions that students have on a topic or concept can be documented, instructors can have useful resources to promote greater cognitive engagement with the content taught. In this way, the transitioning from incorrect or partially correct to correct conceptualization can be made more effectively. Also, any of the conceptions can be used as a precursor to refine understanding of the concept or show their inadequacies with respect to normative understanding across contexts. The various conceptions reported in this study can be used by instructors as conceptual resources (Hammer, 1996) in the pathway to promote meaningful understanding (Ausubel, 1968), thus addressing possible ACs or pre-empting these from taking root in students.

In transition metals chemistry, the term ‘coordination number’, along with terms like primary valence and secondary valence, has been in use for many years and are adequately presented or defined in many freshman general chemistry texts. However, the way that this concept is being presented in different chemistry texts (see some sample definitions given in Discussion section) reveal some inconsistencies of usage or present some loose or incomplete explanations that may appear to confuse students as well as instructors. While describing the coordination compounds of both main group and transition metals, the oxidation number and coordination number terminology are to be preferred respectively without discarding the original ideas of structure and bonding concepts, for example, the concept of secondary valency (which is replaced by coordination number in modern descriptions), introduced by Werner's theory.

The current research shows that a considerable number (73.54%) of undergraduate students explained the term ‘coordination number’ partially correctly but inadequately. Such inadequate responses provided by the students can be seen as partial and fragmented understanding of the term ‘coordination number’ rather than labelling these as wrong conceptions. Some pieces of these knowledge can make reasonable sense to the students as these can be used to answer questions framed in certain contexts, as illustrated earlier. Such ‘viable’ conceptions are rooted in the students’ mental frameworks and can remain ensconced there if these are not refuted (Posner et al., 1982; von Glaserfeld, 1989).

The current sample of students were taught the term ‘coordination number’ with proper definitions along with diagrammatic illustrations of metal complexes containing several types of ligands ranging from mono-dentate to polydentate so that they can differentiate the number of bonds around the central metal ion and the number of ligands. They were also taught the term ‘coordination number’ as associated conceptually with several relevant terms such as ‘central ion’, ligands, coordination compound, primary valence, secondary valence (through Werner's theory of coordination compounds), Lewis acid–base adduct (metal ion as electron pair acceptor or Lewis acid and ligand as electron pair donor or Lewis base), coordination sphere or inner sphere, complex ion, coordination species/entity, coordination bonds (dative bonds), coordination geometry around central metal ion i.e. linear, tetrahedral, square planar and octahedral metal complexes etc. Despite this, the majority of the students (71.4%) indicated rather loosely and partially correctly that coordination number is the ‘number of ligands attached to the central metal ion’. This definition goes well only when monodentate ligands are considered to be bonded. This implies students’ difficulty in relating how the number of ligands bonding to the metal varies, based on the multiplicity of bonds formed by multidentate ligands as they seemed to generalize the definition of coordination number as ‘number of ligands around the metal ion’ for all ligands, irrespective of whether they are mono-, bi- or poly-dentate.

Thus, it is highly essential to further refine the instructional strategy that would ensure that students are able to clearly make conceptual connections with these interrelated terms. Informed by this study, we suggest an exploratory instructional strategy for this term. Besides just definitions and meaning of the term coordination number, instructors could highlight various examples of multidentate ligands and their modes of bonding to metal ions with the help of illustrations to show how the term ‘coordination number’ can be viewed with respect to different types of ligands. Along these lines, we propose the following elements of an instructional strategy when the term ‘coordination number’ is introduced:

• Recapitulate that transition metals can form ions of more than one oxidation state.

• Explain what a ligand is and introduce the various types of ligands – from simple mono-dentate ligands (such as molecules like NH₃ and H₂O or anions such as CN⁻) to bidentate ligands (such as ethylenediamine and ethanedioate) to polydentate ligands (such as EDTA, which is hexadentate).

• Explain what a coordination compound is and how coordinate covalent bonds are formed between the donor atom of a ligand and the central metal ion in a transition metal complexes.

• Explain the formation of coordination compounds as the bonding between a Lewis acid (central metal ion as electron pair acceptor) and a Lewis base (ligand as electron pair donor).

• Identify the ligands in a few complexes and their donor atoms used in bond formation with the central metal ion. Show that each donor atom of a ligand donates a lone pair of electrons to the central metal ion to form a coordinate covalent bond (sigma bond) with it.

• Determine both oxidation number and coordination number of the central metal ion in a complex so that both can be differentiated in terms of numerical values.

• Depending on the type and number of ligands attached to the central metal ion, show via examples that the coordination number can be the same or different.

• Draw the structural formulae of a few transition metal complexes, given the name or molecular formula, and study how ligands are coordinated to the central metal ion.

• Elaborate on other interpretations of coordination number encountered in contexts such as ionic solids and lattices so that students can know the distinction between these.

Appendix 1 shows a suggested instructional strategy and sequencing of lesson development for introducing the term ‘coordination number’. We also elaborate there on how the relevant aspects are informed by the present study.

The proposed teaching approach is only a suggestion, based on insights from our findings, and can be the basis for future work. Within the framework of a ‘progressive research programme’ (Taber, 2008), this can be considered to be appropriate.

Students should have learnt specific terms and words such as complex ions, coordination number, ligands, mono-dentate ligands, polydentate ligands, lone-pairs, coordination bonds, central atom, etc., but they may have not have constructed a firm meaning while attempting to interpret the canonical meaning of the term ‘coordination number’ pertinent to situations in coordination chemistry. One way to overcome such learning difficulties is in addition to having them learn the definition and meaning of the term coordination number, they need to be also encouraged to explain this term with the help of drawing of molecular structures of complexes and the bonding involved rather than written formats without using words so that they can get the correct interpretation of the term. It is also important to pay attention to the way students interpret and monitor their usage of language while doing so, particularly in situations where there are imprecise phrasings.

Students can also be asked to explain what they think is going on in the formation of various complex compounds and the bonding between the metal ions and the various types of ligands ranging from mono-dentate to poly-dentate ligands. Accordingly, it is necessary to show counter-examples and logical flaws in any inappropriate explanations while actively engaging the students in discussions and work through those inappropriate and inadequate conceptions. It is also necessary to reiterate the authentic and accurate meanings and explanations of the term ‘coordination number’ where necessary.

Furthermore, it is also useful and important to include examples to illustrate some basic ideas that a coordination compound may consist of a complex cation with simple anionic counter ions (e.g., [Co(NH₃)₆]Cl₃); a complex anion with simple cationic counter ions (e.g., K₄(Fe(CN)₆]); or a complex cation with complex anion as counter ion, for example, as in [Co(NH₃)₆][FeCl₄]₃.

In addition to teaching methods and content to teach, instructors need to appropriately choose the contexts presented to students carefully, so as to facilitate them to interpret things in different possible ways, to compare their explanations to different possible contexts and learn from examples. This would help them to identify differences and similarities of the term coordination number. For example, it would be useful to present students with all the possible different contexts for the same topic or concept. As an example, the term ‘coordination number’ can be explained in relation to different contexts and its connection to the structure of ionic solids and solid state chemistry, molecular geometry using the concept of steric number, and to coordination chemistry. Instructors can ask students to notice the conceptual similarities or differences while using the term ‘coordination number’.

Besides the IUPAC definition for coordination number in inorganic coordination entities such as transition metal complexes and that we have considered for this study for comparison, there is also another IUPAC definition of coordination number: “The coordination number of a specified atom in a chemical species is the number of other atoms directly linked to that specified atom”. For example, the coordination number of carbon in methane is four, and it is five in protonated methane, CH₅⁺. (The term is used in a different sense in the crystallographic description of ionic crystals.) Thus, it very important for instructors to carefully use those relevant to the context and topic while teaching this term to avoid confusion and misconceptualization by the students. Hence, the concept of coordination number can be explicitly illustrated with various examples covering the complex ions containing various types of ligands ranging from simple mono-dentate ligands (such as NH₃, H₂O, CN⁻, etc.) to bidentate ligands (such as ethylene diamine (en), oxalato, acetylacetonato (acac), 2,2′-bipyridine (bpy) etc.) and polydentate ligands such as EDTA which is hexadentate.

Limitations

The study is based on a sample of university students’ responses to an open-ended question. Students were required to express their understanding in writing beyond just the definition or meaning of the term coordination number. However, a number of responses were rather brief, which did not permit us to get further insights from these responses. The findings cannot be generalized to the entire population of chemistry undergraduates in the university nor taken as a proxy for their proficiency in chemistry.

No interviews were carried out to probe the nuances of students’ understanding as the intent was to leverage on instructor experience to provide useful insights on students’ thinking behind their responses to the open-ended question – an approach that seems to be lacking in the literature as compared to the numerous studies using interviews and diagnostic instruments to probe students’ understanding. Further, responses from interview data based on a small group of students (say, 6–8) might add some supporting evidence to the student's conceptions but it may not completely represent the views of the whole sample under study. However, it can be assumed that such small percentages of conceptions from the interview data may fall into one of the categories found. This study suggests that having an adequately large sample size of students working on an open-ended question about a unitary concept can be a promising model or approach to map the conceptual space about it. This study could also be seen as exemplifying an effective approach while attempting to demonstrate how a single open-ended question in combination with a large sample size can also be useful to generate a range of conceptions as compared to administering a diagnostic test with multiple questions but to a limited sample size.

Notwithstanding the foregoing, other researchers may wish to interview students in similar studies on this or other topics in order to gain further insights on students’ thinking as well as triangulate findings.

Conclusions

The findings from this study can be summarized as follows:

(a) A range of conceptions harboured by university students of a unitary concept ‘coordination number’ has been documented through the analyses of their responses to an open-ended question.

(b) The responses form a conceptual space which ranges from incorrect to partially correct to correct interpretations, thus showing the varying conceptualizations of the term ‘coordination number’ at the group level.

(c) The study has incorporated an instructor's interpretation on why a range of conceptions are harboured by the undergraduates – such a perspective seems to be lacking in the science education literature, where responses to diagnostic instruments and interviews of students seem to be the dominant mode for ‘unpacking’ the range of conceptions harboured by students in a topic.

(d) A number of the conceptions cannot be considered to be totally inaccurate as these partially correct conceptions have some explanatory coherence in certain contexts.

(e) Based on the conceptions documented, we have suggested a pedagogical approach that can be used to teach the concept of ‘coordination number’ from a research-informed perspective.

Conflicts of interest

There are no conflicts to declare.

Appendix 1

Exploratory instructional strategy for lesson development on ‘coordination number’

Teaching approach	Content/concept	Learning outcomes
Section A
Introduce concept of ‘coordination number’.	Coordination number of a metal ion in a complex gives an idea about the number of bonds between the donor atoms of ligands and the central metal ion. According to IUPAC, the coordination number in an inorganic coordination entity is defined as the number of σ-bonds between ligands and the central atom. (Organometallic compounds containing pi-bonds are out of scope here)	Understand the concept of the terms ‘coordination number’ in a coordination compound, electron pair donor, and ligand.
	Illustrate coordination number of 6 using some simple examples, for instance (Co(NH3)6]^3+ and [Fe(CN)6]^4−.
Formation of coordinate bond as the reaction between Lewis acid (central metal ion as electron pair acceptor) and Lewis base (ligand as electron pair donor)	Determine oxidation number and coordination numbers	Apply and verify the concept of coordinate bond formation between the donor atom of a ligand and central metal ion. Apply and extend the knowledge of the concept of Lewis acids and bases to identify the central metal ion as Lewis acid and ligand and Lewis base.
Determine the oxidation number and coordination number of the central metal ion.	The ligands of a complex ion are molecules (neutral species such as NH3) or anions (such as CN^−) with one or more donor atoms.	Identify the number of donor atoms coordinating to the central metal ion.
Explain the terms primary valency and secondary valency based on Werner's Theory of Coordination compounds	Each donor atom of a ligand donates a lone pair of electrons to the central metal ion to form a coordinate covalent bond (sigma bond) with it.	Determine the coordination number by looking at the number of sigma bonds between the central metal ion and the donor atoms of the ligands bonded.
		Determine oxidation number and differentiate it with coordination number.
		Apply the concept of central metal ion and hence the number of electron pairs donated.
Section B
Types of ligands vs. coordination number	Introduce various types of ligands from simple mono-dentate ligands (such as NH3, H2O, CN^−, etc.) to bidentate ligands (such as ethylene diamine (en), oxalato, acetylacetonato (acac), 2,2′-bipyridine (bpy) etc.), and polydentate ligands such as EDTA which is hexadentate.	Differentiate between monodenate and multidentate ligands up to hexadentate ligand such as EDTA.
	Discuss meaning of the denticity of a ligand. Monodentate ligands have one donor atom per ligand and hence can donate one lone pair of electrons to the central metal ion; thus they can form one coordinate covalent bond per donor atom with the central metal ion. Thus, students can start to think that bidentate ligand will have two donor atoms per ligand, each of which bonds to the metal ion; tridentate ligand will have three donor atoms per ligand and each of it bonds to the metal ion, and so on. If the ligand is hexadentate, it will have six donor atoms and coordination number of the central metal ion bonded to hexadentate ligand would be six.
	Monodentate ligands are either anions (e.g., Cl^−, CN^−etc.) or neutral molecules (e.g., NH3, H2O etc.) that can donate a single pair of electrons through their donor atom. If the ligands are all monodentate, then the number of such ligands attached to the central metal ion will be the same as the number of bonds formed by those ligands with the central metal ion.	Apply the concept of denticity of ligands to determine the coordination number of the central metal ion in a complex ion.
	Based on this, coordination number of a metal ion in a complex gives an idea about the number of bonds between the donor atoms of ligands and the central metal atom of ion.
Section C
Examples of complex ions in which the central metal ion is bonded to different types of ligands (bidentate to multidentate ligands), and examining the coordination number.	[Cr(en)3]^3+: complex ion containing a bidentate ligand ethylene diamine	Coordination number is the same as the number of ligands if the ligands are all monodentate (each ligand with one donor atom coordinating to the central metal ion).
	(en = H2NCH2CH2NH2)	Verify and interpret that coordination number is not always equal to the number of ligands attached to the central metal atom/ion.
	[Co(EDTA)]^−, cobalt complex containing a single hexadentate EDTA^4− ligand with six donor atoms which form six coordinate bonds with the central Co^3+ to give coordination number of 6 for Co^3+.	Examine the coordination number based on the type of ligand attached.
		Understand how to formulate metal complex ions and neutral metal coordination compounds containing different ligands.
		Draw structural formulae of the complex ions.

Section A is intended to address the incorrect conceptions (1, 2 and 3), as explored and observed in this study. Through the topical lessons and examples suggested, it also attempts to address the basic meaning of the terms such as primary valency and secondary valency as well as how these are relevant to oxidation number and coordination number respectively in modern terminology. Students are expected to define the term ‘coordination number’ correctly and basically first with respect to monodentate ligands by integrating the concepts of Lewis acid–base theory and Werner's theory of coordination compounds.

Section B is intended to address the difficulties of students while defining the term coordination number with respect to the number of ligands. As explored in this study, the majority of students (71.4%) indicated rather loosely but partially correctly that coordination number is the ‘number of ligands attached to the central metal ion’. This definition goes well only when monodentate ligands are considered to be bonded. This section aims to address the conceptual difficulties associated with defining coordination number in relation to multidentate ligands and partially correct conceptions such as other responses (4–10) observed in this study. Students are expected to gain more insights into the term coordination number through various examples of ligands – from monodenate to multidenate ligands.

Section C is intended to offer higher order thinking about defining coordination numbers and also through drawing structural formulae of various types of complexes.

Acknowledgements

We are most thankful to the referees and editors for their careful reading of our manuscript and for offering detailed and constructive, yet encouraging, comments on our study. This is gratefully appreciated, and have permitted us to clarify our own thinking further as well as significantly helped us in revising our manuscript. We acknowledge financial support in the form of a Teaching Enhancement Grant (C-143-000-019-001) from the Center for Development of Teaching and Learning (CDTL), National University of Singapore, for this study.

References

1. Atkins P. W., Overton T., Rourke J., Weller M. and Armstrong F. A., (2010), Shriver and Atkins’ Inorganic Chemistry, Oxford: Oxford University Press, pp. 199–208.
2. Ausubel D. P., Novak J. D. and Hanesian H., (1968), Educational Psychology: A Cognitive View, New York: Holt, Rinehart and Winston.
3. Brandriet A. R. and Bretz S. L., (2014), Measuring meta-ignorance through the lens of confidence: examining students' redox misconceptions about oxidation numbers, charge, and electron transfer, Chem. Educ. Res. Pract., 15(4), 729–746.
4. Clarke D. and Hollingsworth H., (2002), Elaborating a model of teacher professional growth, Teach. Teach. Educ., 18(8), 947–967.
5. Claxton G., (1993), The interplay of values and research in science education, in Black P. J. and Lucas A. M. (ed.), Children's Informal Ideas in Science, London: Routledge, pp. 190–207.
6. Clough E. E. and Driver R., (1985), Secondary students' conceptions of the conduction of heat: Bringing together scientific and personal wiews, Phys. Educ., 20(4), 176–82.
7. Cooper M. M., Grove N., Underwood S. M. and Klymkowsky M. W., (2010), Lost in Lewis structures: an investigation of student difficulties in developing representational competence, J. Chem. Educ., 87(8), 869–874.
8. Cotton F. A., Wilkinson G. and Gaus P. L., (1995), Basic Inorganic Chemistry, New York: John Wiley & Sons, Inc., pp. 165–170.
9. Duit R. and Treagust D. F., (1995), Students’ conceptions and constructivist teaching approaches, in Fraser B. J. and Walberg H. J. (ed.), Improving science education, Chicago, Illinois: University of Chicago Press, pp. 49–60.
10. Gilbert J. K. and Watts D. M., (1983), Concepts, misconceptions and alternative conceptions: changing experiences in science education, Studies in Science Education, 10, 61–98.
11. Glynn S. M. and Duit R., (1995), Learning science meaningfully: Constructing conceptual models, in Glynn S. M. and Duit R. (ed.), Learning science in the schools: Research reforming practice, Mahwah, New Jersey: Lawrence Erlbaum Associates, pp. 3–33.
12. Griffiths A. K. and Preston K. R., (1992), Grade-12 students' misconceptions relating to fundamental characteristics of atoms and molecules, J. Res. Sci. Teach., 29(6), 611–628.
13. Gurcay D. and Gulbas E., (2015), Development of three-tier heat, temperature and internal energy diagnostic test, Res. Sci. Technol. Educ., 33(2), 197–217.
14. Hackling M. W. and Garnett P. J., (1985), Misconceptions of chemical equilibrium, Eur. J. Sci. Educ., 7(2), 205–214.
15. Hammer D., (1996), Misconceptions or p-prims: how may alternative perspectives of cognitive structure influence instructional perceptions and intentions, J. Learn. Sci., 5(2), 97–127.
16. Jones C. J., (2001), d-and f-Block Chemistry, Cambridge, UK: Royal Society of Chemistry, pp. 54–70.
17. Kauffman G. B., 1967, Alfred Werner's Co-ordination Theory, Educ. Chem., 4(1), 11.
18. Kotz J. C., Treichel P. M. and Townsend J. R., (2010), Chemistry and Chemical Reactivity, Belmont, CA: Brooks/Cole, Cengage Learning, pp. 1029–1035.
19. Larsson Å. and Halldén O., (2010), A structural view on the emergence of a conception: Conceptual change as radical reconstruction of contexts, Sci. Educ., 94(4), 640–664.
20. Loh A. L. S. and Subramaniam R., (2018), Mapping the knowledge structure exhibited by a cohort of students based on their understanding of how a galvanic cell produces energy, J. Res. Sci. Teach., 55(6), 777–809.
21. Luxford C. J. and Bretz S. L., (2014), Development of the bonding representations inventory to identify student misconceptions about covalent and ionic bonding representations, J. Chem. Educ., 91(3), 312–320.
22. Mammen K. J., (1996), Chemistry students' erroneous conceptions of limiting reagent, S. Afr. J. High. Educ., 10(1), 188–195.
23. McClary L. M. and Bretz S. L., (2012), Development and assessment of a diagnostic tool to identify organic chemistry students’ alternative conceptions related to acid strength, Int. J. Sci. Educ., 34(15), 2317–2341.
24. National Research Council (1996), National science education standards, Washington, DC: National Academy Press.
25. Peterson R. F. and Treagust D. F., (1989), Grade-12 students' misconceptions of covalent bonding and structure, J. Chem. Educ., 66(6), 459.
26. Posner G. J., Strike K. A., Hewson P. W. and Gertzog W. A., (1982), Accommodation of a scientific conception: toward a theory of conceptual change, Sci. Educ., 66(2), 211–227.
27. Rodgers G. E., (2012), Descriptive Inorganic, Coordination and Solid State Chemistry, Belmont, CA; Brooks/Cole, Cengage Learning, pp. 9–20.
28. Sanger M. J. and Greenbowe T. J., (1997), Common student misconceptions in electrochemistry: Galvanic, electrolytic, and concentration cells, J. Res. Sci. Teach., 34(4), 377–398.
29. Seoh K. H. R., Subramaniam R. and Hoh Y. K., (2016), How humans evolved according to Grade 12 Students in Singapore, J. Res. Sci. Teach., 53(2), 291–323.
30. Sfard A., (2008), Thinking as Communication, Cambridge: Cambridge University Press.
31. Shulman L. S., (1987), Knowledge and teaching: foundations of the new reform, Harvard Educ. Rev., 57(1), 1–23.
32. Singer S. R., Nielsen N. R. and Schweingruber H. A. (ed.), (2012), Identifying and improving students’ conceptual understanding in science and engineering, in Discipline-based education research: understanding and improving learning in undergraduate science and engineering, Washington: National Academies Press.
33. Sreenivasulu B. and Subramaniam R., (2013), University students’ understanding of chemical thermodynamics, Int. J. Sci. Educ., 35(4), 601–635.
34. Sreenivasulu B. and Subramaniam R., (2014), Exploring undergraduates’ understanding of transition metals chemistry with the use of cognitive and confidence measures, Res. Sci. Educ., 44(6), 801–828.
35. Supasorn S., (2015), Grade 12 students' conceptual understanding and mental models of galvanic cells before and after learning by using small-scale experiments in conjunction with a model kit, Chem. Educ. Res. Pract., 16(2), 393–407.
36. Taber K. S., (2008), Conceptual resources for learning science: Issues of transience and grain?size in cognition and cognitive structure, International Journal of Science Education, 30(8), 1027–1053.
37. Taber K. S., (2010), Straw men and false dichotomies: Overcoming philosophical confusion in chemical education, J. Chem. Educ., 87(5), 552–558.
38. Taber K. S. and Tan K. C. D., (2011), The insidious nature of ‘hard-core’ alternative conceptions: implications for the constructivist research programme of patterns in high school students’ and pre-service teachers’ thinking about ionisation energy, Int. J. Sci. Educ., 33(2), 259–297.
39. Tekin B. B. and Nakiboglu C., (2006), Identifying students' misconceptions about nuclear chemistry. A study of Turkish high school students, J. Chem. Educ., 83(11), 1712.
40. Thagard P., (1992), Conceptual Revolutions, Princeton University Press.
41. Van Driel J. H. and Berry A., (2012), Teacher professional development focusing on pedagogical content knowledge, Educ. Res., 41(1), 26–28.
42. Von Glaserfeld E., (1989), Learning as a Constructivist Activity, in Murphy P. and Moon (ed.), Developments in Learning and Assessment, London: Hodder & Stoughton.
43. Yan Y. K. and Subramaniam R., (2018), Using a multi-tier diagnostic test to explore the nature of students’ alternative conceptions on reaction kinetics, Chem. Educ. Res. Pract., 19(1), 213–226.
44. Zoller U., (1990), Students' misunderstandings and misconceptions in college freshman chemistry (general and organic), J. Res. Sci. Teach., 27(10), 1053–1065.

---

Footnote

† Current address: Residential College 4, 6 College Ave East, University Town, National University of Singapore, Singapore 138614, Singapore. E-mail: rc4bs@nus.edu.sg

---