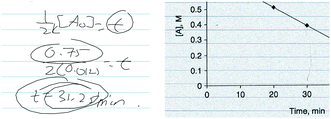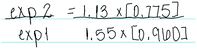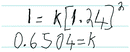Productive features of problem solving in chemical kinetics: more than just algorithmic manipulation of variables

Abstract

Problem solving is a critical feature of highly quantitative physical science topics, such as chemical kinetics. In order to solve a problem, students must cue into relevant features, ignore irrelevant features, and choose among potential problem-solving approaches. However, what is considered appropriate or productive for problem solving is highly context-dependent. This study is part of a larger project centered on students’ integration of chemistry and mathematics knowledge and skills. The data for this study came from semi-structured interviews with 40 general chemistry students using a think-aloud protocol. Interview prompts involved students working through two chemical kinetics problems, one involving a second-order system and one involving a zero-order system. In both cases, students could solve the problem using the data provided and relevant equations, or by taking a conceptual approach and considering the relationship between quantities. Using the resource-based model of cognition as our theoretical framework, analysis focused on characterizing the productive and unproductive problem-solving routes used by students. Findings emphasize the role of using conceptual reasoning and reflecting on one's work during problem solving, which have implications for instructors as they guide students to think about chemical kinetics and to solve problems across quantitative topics in science, technology, engineering, and mathematics.

---

Introduction

Previous work that has investigated various facets of problem solving is pervasive in the literature, particularly in the context of both chemistry and physics (Gabel and Bunce, 1994; Bodner and Herron, 2002; Hsu et al., 2004; Cooper and Stowe, 2018). The representation of problem-solving in previous work is likely a reflection of chemistry faculty and national-level organization's (i.e., American Chemical Society) desire for students to engage in critical thinking and problem solving (Bruck et al., 2010; Wenzel et al., 2012, 2015; Bretz et al., 2013; Bruck and Towns, 2013; Holme et al., 2015); however, both of these terms are not well-defined, which is a challenge for instruction and assessment (Stowe and Cooper, 2017; Cooper and Stowe, 2018). Furthermore, although problem solving could be defined as “what chemists do” (Bodner, 2015), typical textbook-style problems that dominate chemistry courses do not reflect the work done by scientists (Cooper and Stowe, 2018).

Thus, increasingly more work has been carried out to emphasize tasks that move beyond rote memorization and simple algorithmic processing, promoting student engagement in science practices (Brandriet et al., 2015; Laverty et al., 2016; Reed et al., 2017; Stowe and Cooper, 2017; Underwood et al., 2018). Science practices reflect the set of tools scientists use to engage in inquiry, including: asking questions; developing and using models; planning and carrying out investigations; analyzing and interpreting data; using mathematics and computational thinking; constructing explanations; engaging in argument from evidence; obtaining, evaluating, and communicating information (National Research Council, 2012).

The emphasis that the science practices attribute to experimental considerations (e.g., analyzing and interpreting data) is particularly well-suited for highly quantitative contexts such as chemical kinetics, which deals to a great extent with developing models from empirical evidence (Becker et al., 2017; Brandriet et al., 2018). Within the context of the undergraduate chemistry curriculum, chemical kinetics is a key topic, with ideas central to chemical kinetics spanning general chemistry and upper-level physical chemistry courses (Holme and Murphy, 2012; Holme et al., 2015; Holme et al., 2017), but more discipline-based education research is needed that moves beyond identifying students’ alternative conceptions in chemical kinetics (Justi, 2002; Bain and Towns, 2016).

Here we describe the results from a study that shares a dataset with a larger project interested in how students use conceptual and mathematical reasoning to solve chemical kinetics problems. Using this data corpus, our research group recently published work that characterized student engagement in modeling (Bain et al., 2018a), and we analyzed how students reasoned about catalysts and half-lives in relation to a zero-order system (Bain et al., 2018b). Building on these findings, this work investigated the various problem-solving routes used by students, focusing on the nature of different problem-solving approaches and their role in helping the student reach an answer. Our analysis addresses the following research question: What characterizes successful problem solving in typical general chemistry problems (e.g., chemical kinetics)?

Review of related literature

Expert vs. novice

When reviewing education literature there is a clear distinction made between expert and novice problem solvers, with the intention of supporting novices in developing expertise. One of the key differences reported between experts and novices is the extent in which experts utilize their meaningfully organized knowledge to reason qualitatively about a problem, in contrast to novices, who primarily focus on more algorithmic approaches involving equations and expressions (Larkin and Reif, 1979; Chi et al., 1981; Reif, 1983; Van Heuvelen, 1991). In addition, another distinction between experts and novices is that although experts have access to a large body of knowledge that helps them reason about problems, novices must rely on surface features because they lack this knowledge (Chi et al., 1981). As discussed by Reif and Heller (1982), although it is beneficial for novices to learn and understand the techniques that experts use when problem solving, simply mirroring experts is not always productive, suggesting the importance of focusing on “effective” rather than “expert” problem-solving. According to Wheatley's (1984) definition of a problem, “what you do when you don’t know what to do”, a true problem is something that the student would not have experienced before; therefore, attempting to reproduce the procedure utilized by an expert would not be useful.

Instructional support for students

Given the distinction made above between how novices solve problems in contrast to experts, previous work has investigated how instruction can support students in engaging in problem solving, such as the incorporation of working in groups (Keith and Anderson, 1992; Heller et al., 1996; Ge and Land, 2003; Cooper et al., 2008; Sandi-Urena et al., 2011) or explicit instruction on problem solving (Reif and Heller, 1982; Bunce, et al., 1991; Huffman, 1997; Yuriev et al., 2017). A significant body of literature has attempted to improve problem solving through the use of specific problem-solving models. According to Woods (2000), there are over 150 strategies and models for solving problems reported across the literature in a myriad of disciplinary fields (e.g., Polya, 1945; Mettes et al., 1980; Reif and Heller, 1982; Gick, 1986; Bunce et al., 1991; Shahat et al., 2012; Bodner, 2015; Yuriev et al., 2017). As discussed by Yuriev et al. (2017), problem-solving models typically encompass similar steps, such as problem identification, problem representation, planning, implementation, and evaluation. However, problem-solving models have the tendency to be used by students as a series of linear steps to follow and often do not reflect the process followed by experts when solving unfamiliar or novel problems (Woods, 2000; Bodner, 2015). Furthermore, although explicit instruction using a problem-solving model may improve student ability to algorithmically work through a problem, this does not guarantee that students are able to make conceptual connections (Bunce et al., 1991).

In comparison to conceptual problems, research overwhelmingly indicates students perform better on algorithmic problems (Nurrenbern and Pickering, 1987; Pickering, 1990; Sawrey, 1990; Nakhleh, 1993; Nakhleh and Mitchell, 1993; Zoller et al., 1995; Nakhleh et al., 1996; Stamovlasis et al., 2005; Cracolice et al., 2008; Sanger et al., 2013). Much of this body of research involved comparing student responses on algorithmic problems and analogous conceptual problems; however, this does not adequately address the idea that instruction and assessment should emphasize the ability to combine or blend mathematical and conceptual reasoning during problem solving (Kuo et al., 2013; Bain et al., 2018a, 2018b).

Theoretical perspectives

Data analysis and subsequent framing of results was theoretically grounded in the resource-based model of cognition. The resources perspective describes a model for the cognitive organization of ideas, asserting that knowledge is a network composed of units (“resources”) that are activated in specific contexts (Hammer and Elby, 2003; Hammer et al., 2005). This framework builds on and encompasses diSessa's (1993) discussion of fine-grained knowledge units that are based in experience (“phenomenological primitives”) and are structured dynamically with respect to the variation in the connections among knowledge elements.

One of the useful features of the resource-based model of cognition is its explanatory power in describing the inconsistency often observed in student responses (Hammer and Elby, 2003). The context-dependence attributed to student reasoning in the resources perspective acknowledges that students may have access to productive resources for approaching a problem, but the prompt may not have cued students into using these resources. Thus, student application of ideas from one context to another does not involve “transferring” unitary, stable concepts; rather, it involves activating productive resources and deactivating unproductive resources in a way that allows students to address a problem (Hammer et al., 2005).

Within the context of this study, the resources perspective provided the language to think about how students approached problem solving. When reading the interview prompts, students cued into different features and different resources were activated. We view each problem-solving strategy as a student's response to the activation of resources; that is, the implementation of a given problem-solving route represents how students made use of the resources that were activated. These activated resources constitute different types of information (e.g., epistemological, procedural, conceptual), but our intention was not to identify and categorize the individual resources utilized by the students (Becker et al., 2017). The decision not to focus on the fine-grained resources associated with each problem-solving strategy was based on limitations in the data (activated resources related to problem-solving strategies tended to be more implicit and not readily observable), as well as an effort to simplify our discussion and frame our results in a way that is relevant for instruction. This builds on the sentiment expressed by Wittmann (2006), in which he discussed that student reasoning is often observed at a level that is smaller than large-scale concepts, but bigger than fine-grained resources—a “mesoscopic” middle-ground between macroscopic and microscopic cognitive systems that serves as a practical scope for researchers and practitioners to consider student reasoning.

Our dataset involved a variety of problem-solving approaches used by the students to reach a final answer, some of which moved students closer to the correct answer and others that were less useful for problem-solving in this context. Focusing on the problem-solving strategies that were utilized provides insight regarding how students view quantitative problems. By analyzing the nature of students’ problem-solving routes, it allows us to consider how instructors can support students in a way that builds on students’ knowledge and encourages the use of context-appropriate resources (Heisterkamp and Talanquer, 2015; Becker et al., 2017).

Methods

Participants

Over the course of two semesters (fall 2015 and spring 2016), participants for this study were sampled from a second-semester general chemistry course intended for engineering majors at a midwestern research university (n = 40). The participants were recruited before instruction on chemical kinetics, interviewed after tested on the relevant material, and compensated with a $10 iTunes gift card for their participation (completed with the approval of our university's Institutional Review Board). As indicated earlier, this study shares a data corpus with a larger project (previously reported in this journal) that characterized students’ ability to integrate chemistry and mathematics when reasoning about chemical kinetics (Bain et al., 2018a, 2018b). For the study discussed herein we present a detailed analysis of the specific problem-solving approaches utilized by students in our sample.

Data collection and analysis

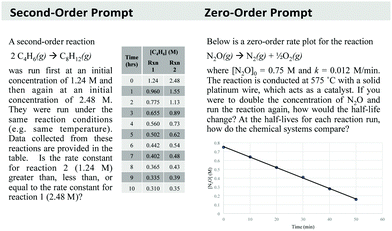
The primary source of data for this project came from semi-structured interviews, using a think-aloud protocol, in which students were encouraged to explain their reasoning and were asked probing questions in order make their thought process more explicit (King and Horrocks, 2010; Becker and Towns, 2012). Provided in Fig. 1 are the two interview prompts that are relevant for this study. The first prompt asked the students to consider how concentration affects the rate constant of a second-order reaction, and the second prompt asked the students to think about the half-life of a zero-order reaction. The questions posed in the interview prompts could be solved algorithmically using related equations and the data provided; alternatively, they were designed so that they could also be solved conceptually by drawing a connection between relevant quantities.

Fig. 1 Second- and zero-order chemistry prompts.

During the interviews students used a Livescribe™ smartpen to work through the problems, allowing digital synchronization of each student's written work with the audio recording of their interview (Linenberger and Bretz, 2012; Harle and Towns, 2013; Cruz-Ramirez de Arellano and Towns, 2014). Following transcription of the interviews, the data were organized into interpreted narratives, which were documents with two columns; one column had the verbatim student transcript and other column contained a description of the passage that summarized what the student was discussing or tersely described their problem-solving step (Page, 2014; Bain et al., 2018a, 2018b). The interpreted narratives were then coded using inductive analysis, focusing on the problem-solving routes students used to address the interview prompts. Data analysis involved two researchers coding in tandem with the assignment of codes requiring 100% agreement, which was paired with a constant comparison methodology to refine the codes (Strauss and Corbin, 1990; Campbell et al., 2013). This process resulted in the list of problem-solving approaches described in Table 1.

Table 1 Description of student problem-solving routes (in order of highest frequency)

Problem-solving route	Description	Example
Conceptual reasoning	Addresses prompt or attempts to answer the prompt by predicting and/or providing justification involving a conceptual understanding (non-algorithmic approach to solving the problem), which may involve recalling related content/information	Russel: “They were run under the same reaction conditions, same temperature, so the rate constant will be the same. So just initially I would think it'd be equal… because if you're holding temperature the same, and the initial concentration I didn't think had an effect on the rate constant.”
Reflection	Considers the feasibility of an answer or problem-solving approach, which may influence them to change their answer or try a different approach; distinct from conceptual reasoning in the way that content or ideas are used to evaluate a previous response or approach	Nate: “I thought it [the rate constants] would be the same… Because I assumed that the initial concentration of the reaction does not affect the rate constant of the reaction.”
Equation & data	Uses an equation and the provided data from the table/graph to solve; typically preceded by the problem-solving route equation recall	Trip: “And then, then you just plug in numbers and solve for k for both reactions.”
Equation recall	Provides an appropriate equation to solve the prompt; although often followed by the problem-solving route equation & data, in some cases students simply provided the equation and did not use it to solve the problem	Damien: “So I know that it's a second-order reaction so it follows one over concentration is equal to one over concentration, plus kt.”
Graphical approach	Reasons graphically, which may involve generating values or abstracting information from a graph	Rufus: “I don't know if I did the wrong, but I mean, you can just look at the graph and see. If you go from 0.6 to 0.3… That's going to take 30 seconds. If you go from 0.75, half that is 0.375, it would be 35 seconds.”
Ratio calculation	Quantitatively compares numbers in the provided data table/graph by dividing and/or subtracting numbers to identify a pattern (typically involves calculations, but not a formal equation/formula)	Ivy: “I feel like I remember going from the time, and you do 8 minus 1, so that'd be 7 hours. Then, you take 0.365 minus 0.960, or you divide it, to find the rate constant…If this is the right thing that I'm thinking of.”
Slope calculation	Reasons about the slopes in a graph or performs calculations related to the slope of a line	Walter: “I did 1 over the concentration, since it's second order, if we graph… to get the linear relationship it should be 1 over A versus time. I picked just the first two points so I did 0 over 1 over 1.24, and …1 over 0.960 because this would be the two points on the graph. I'm going to find y2 minus y1 over x2 minus x1. That answer would the be the slope, which is k.”
Patterns & trends	Qualitatively compares numbers in the provided data table, making generalizations to identify patterns or trends	Georgina: “Just looking at the data right now, I would expect reaction 1 to have a lower rate constant reaction because … For time 0 on reaction 1 it's 1.24 moles. For reaction 2, it's 2.48. It's basically double reaction one. For their final time here for both of them, they're almost the same. It's 0.31 for reaction 1 and 0.35 for reaction 2.”
Data to check	Checks answer by using data presented in table/graph or uses data to check the validity of an equation they proposed	Vanya: “Then, solve for time by doing 0.75 over 2 times 0.012 is going to be time… Doing that calculation, 0.75 divided by 1.024. t is equal to 31.25. Which from the graph makes reasonable sense [uses graph to estimate answer].”
Method of initial rates	Reasons or performs calculations using the method of initial rates	Lily: “Then from here, I kind of want to think that you compare two different experiments like one at time two or one at hour two and one at hour one and then you can plug in… if I do experiment 2 at hour two over experiment 1 at hour one then you … See, this confuses me. I think it must be 1.13, so times your two reactions together… Then divide that over Experiment 1 which is 1.55 times 0.960.”
Rate calculation	Reasons or performs calculations using the rate law	Jonathan: “I know my rate for, or it took an hour. Then, I'm looking for my rate constant… one [hour] equals rate constant times my concentration squared. So, I would use, I believe that you would need a higher rate constant for the first one. Since I'm going to use, for example, 1.24 squared, then 1 equals k, 2.48 squared. Then it's k in reaction one would be 1.24 squared, which I calculated before, and then 1 divided by that.”

---

For clarity, our definition of the problem-solving route conceptual reasoning was influenced in part by the description provided by Holme et al. (2015), which emphasizes different skills such as the ability to make predictions and explain phenomena. Furthermore, when students were characterized as using the reflection problem-solving route, they incorporated content in a way that was different from the conceptual reasoning problem-solving route in the sense that students were using conceptual reasoning to evaluate a problem-solving route or an answer generated from a problem-solving route.

Influenced by our theoretical framework, analysis involved an additional layer of coding in which each problem-solving route was coded as productive or unproductive in the context in which it was used (generally, problem-solving approaches are not inherently productive or unproductive, and it depends on the context whether or not a particular approach is useful). In characterizing a problem-solving route (PSR) as productive, we considered if the answer/calculation that resulted from a PSR was correct and the extent in which it moved the student closer to the final correct answer. In addition, we also characterized each student based on whether their final answer was correct, incorrect, or if the student was unsure about the final answer (undecided).

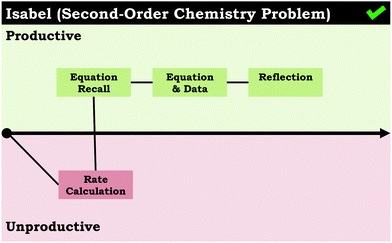
After assigning all relevant PSR and productive/unproductive codes, we created “problem-solving maps” to summarize students’ responses for both of the chemistry prompts. The problem-solving maps visually represent each student's chronological movement through an interview prompt. An example of a problem-solving map is provided in Fig. 2, in which we can see that Isabel initially began with an unproductive problem-solving route (rate calculation), which was followed by three productive problem-solving routes (equation recall, equation & data, and reflection), and Isabel ultimately answered the question correctly (indicated by the green check-mark symbol in the upper right-hand corner of the problem-solving map). The final stage of data analysis involved comparing students’ problem-solving maps to find trends.

Fig. 2 Isabel's problem-solving map for the second-order chemistry problem chronologically displays the problem-solving routes used and characterizes the problem-solving routes based on how productive they were for answering the prompt; the green check-mark symbol in the upper right-hand corner indicates that the student's final answer was correct.

Findings

Students across our sample exhibited a range of problem-solving approaches in response to the chemistry prompts. Here we describe the trends observed when comparing each student's problem-solving map, discussing the features that made problem-solving trajectories productive or unproductive.

Student difficulty with reasoning about the data

One of the themes that emerged during data analysis was a cluster of problem-solving routes that were typically only used when students worked through the second-order chemistry problem and were consistently characterized as unproductive, including: patterns & trends, ratio calculation, rate calculation, and method of initial rates. Each of these problem-solving routes was an attempt made by the students to make use of the data table provided; however, these routes did not move the students closer to the final answer. In the case of patterns & trends and ratio calculation, the students reasoned about the data qualitatively and quantitatively, respectively, trying to get a general idea about the data without using a formal equation. Within this prompt, the students were unable to productively analyze and interpret the data, with students that began their problem solving with patterns & trends typically ending up with an incorrect or undecided final answer. Although this suggests the students had difficulty connecting the data provided to relevant equations or problem-solving approaches, it also illustrates students were trying to draw conclusions directly from the data, a competency that has been emphasized in the literature (National Research Council, 2012; Heisterkamp and Talanquer, 2015; Becker et al., 2017).

When approaching the problem using method of initial rates and rate calculation, students plugged values into expressions without considering the nature of the data presented in the tables. For example, when students attempted to solve the problem using an approach that was reminiscent of the method of initial rates (a common task in introductory general chemistry courses, such as the course from which the students were sampled), it seemed that the students simply associated tables of data with the method of initial rates, without considering the type of data the table contained (i.e., concentration and time values, as opposed to concentration and initial rate values). On a similar note, the rate calculation problem-solving route involved students inappropriately plugging in concentration and time values from the table directly into the rate law.

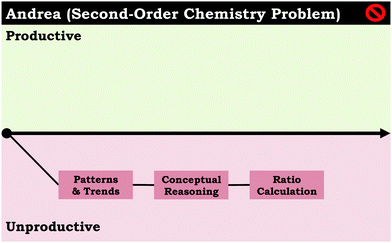
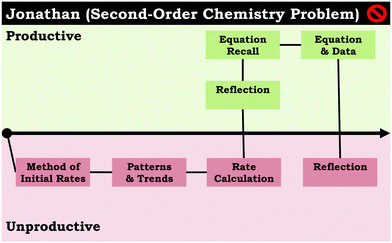
We also noted this group of problem-solving routes were often used together. Across the student responses for the second-order chemistry prompt, eight students displayed three or more unproductive problem-solving routes in a row, which typically involved a combination of patterns & trends, ratio calculation, rate calculation, and method of initial rates. In most cases, this resulted in students working through multiple unproductive problem-solving routes and then arriving at a final incorrect or undecided answer. This is illustrated in Fig. 3 with Andrea's problem-solving map, in which patterns & trends is paired with ratio calculation. Moreover, Jonathan's problem-solving map (Fig. 4) follows a similar trend, in which he initially had difficulty solving the problem, beginning with the less productive problem-solving routes described above; however, after some reflection he was able to solve the problem (correctly) using the second-order integrated rate law. It is interesting to note that in this instance the reason why Jonathan got the final answer wrong was because of how he interpreted his calculations. The second-order chemistry problem asked the students to think about how running a reaction at two different initial concentrations influenced the rate constant. Jonathan solved for the rate constant for each reaction (equation & data), but the values he calculated were slightly different, and he concluded that one rate constant was larger than the other (unproductive reflection). We see this as another example of students having difficulty reasoning about the data; in this case the issue is rooted in thinking about the nature of empirical data, which is limited in its precision.

Fig. 3 Andrea's problem-solving map for the second-order chemistry problem chronologically displays the problem-solving routes used and characterizes the problem-solving routes based on how productive they were for answering the prompt; the red circle-backslash symbol in the upper right-hand corner indicates that the student's final answer was incorrect.

Fig. 4 Jonathan's problem-solving map for the second-order chemistry problem chronologically displays the problem-solving routes used and characterizes the problem-solving routes based on how productive they were for answering the prompt; the red circle-backslash symbol in the upper right-hand corner indicates that the student's final answer was incorrect.

The sentiment that students had difficulty reasoning about the data is summarized with the following statement made by one of the students:

Lily: “You're just given a lot and you feel overwhelmed after reading the question. The question is several sentences long. You're given a table, which doesn't really intimidate me because you can use whatever information at the table that you need to or that you want. You can pick and choose what you want out of that, but interpreting what the question is asking is kind of a struggle and knowing what equation you need to set up exactly from the information given because sometimes they give you more information than what you actually need to solve the problem.”

Lily began solving the problem using method of initial rates, realized this was not helping her solve the answer, and then indicated she was unable to solve the problem, despite it being similar to what was presented in class. In the quote above, Lily talks about the key problem at hand—being able to connect an appropriate problem-solving route to the data provided, which requires more than using rehearsed algorithmic approaches that are based in recognition of surface features. We argue that students such as Lily would benefit from incorporating more conceptual reasoning into their problem solving.

The role of conceptual reasoning

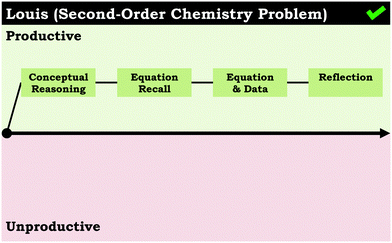
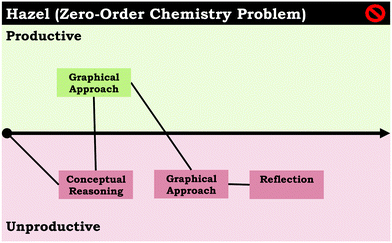
Analysis of student problem-solving routes for the second-order chemistry problem indicated students that began with conceptual reasoning were more likely to get the answer correct. Out of the 16 students that had conceptual reasoning as their first problem-solving step, only two students did not have the correct final answer. Similarly, within our sample, among the nine students that exclusively used productive problem-solving routes for the second-order chemistry problem, most began with conceptual reasoning and followed a straightforward, linear progression similar to Louis’ problem-solving map in Fig. 5. Here, Louis initially answered the prompt correctly and then supported his initial claim mathematically. These results support the utility of conceptual reasoning in problem solving, particularly in a context similar to this prompt, in which students were given data that they may not have initially known how to use. The role conceptual reasoning has on influencing the problem-solving routes used cannot be understated; however, it is important to note—and it is perhaps unsurprising—that the incorporation of non-normative ideas in problem solving does more harm than good. That is, in order for the integration of conceptual ideas to be productive, the concepts must be scientifically correct. This was particularly evident when looking at the student responses for the zero-order chemistry problem, where students incorporated (non-normative) conceptual reasoning in their problem solving, which conflicted with the data provided. In this case, the primary problem for students seemed to be the lack of alignment of the data with the students’ conceptual understanding of half-life.

Fig. 5 Louis’ problem-solving map for the second-order chemistry problem chronologically displays the problem-solving routes used and characterizes the problem-solving routes based on how productive they were for answering the prompt; the green check-mark symbol in the upper right-hand corner indicates that the student's final answer was correct.

In Bain et al. (2018b), we previously reported that students in our larger data corpus tended to discuss first-order half-life ideas (i.e., constant half-life) as features that define half-life in general, which negatively influenced their ability to reason about the zero-order chemistry prompt. Consistent with these results, a closer look at students’ problem-solving approaches used in the zero-order chemistry problem reveals that although students used conceptual reasoning as a problem-solving route with the same frequency across both chemistry prompts, conceptual reasoning was characterized as unproductive for the zero-order prompt almost three times as much as the second-order prompt. Thus, students used non-normative ideas to interpret the data provided, guide problem solving, and reason about calculations. Further illustrating the students’ difficulty with reasoning about half-lives in a zero-order system, nine students in our sample had the incorrect final answer for the zero-order chemistry prompt, all of which began with incorrect conceptual reasoning. For example, in Hazel's problem-solving map in Fig. 6, she started off by answering conceptually (incorrectly) by saying that the half-life should be constant, so concentration should not influence the half-life. This ended up influencing how she approached the problem, because she attempted to recall an equation (it was clear she was thinking of the first-order half-life equation). Ultimately, Hazel was unable to mathematically support her reasoning, but persisted with her initial reasoning.

Fig. 6 Hazel's problem-solving map for the zero-order chemistry problem chronologically displays the problem-solving routes used and characterizes the problem-solving routes based on how productive they were for answering the prompt; the red circle-backslash symbol in the upper right-hand corner indicates that the student's final answer was incorrect.

The results for the zero-order prompt mirror those pertaining to the second-order prompt, representing how conceptual reasoning influences the trajectory of problem solving, regardless of whether the conceptual reasoning is consistent with a more normative understanding of chemical kinetics. We observed similar trends in our data when we consider how students reflected or did not reflect on their answers throughout the problem-solving process. In the next section, we illustrate this by focusing on students that used reflections productively, unproductively, or did not use reflections at all.

Reflecting on the feasibility of an answer or approach

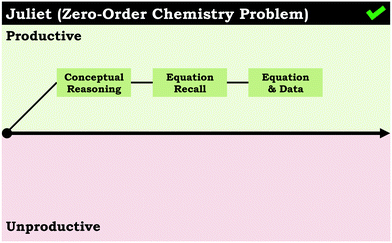
Generally, student engagement in reflection occurred with the same frequency across both prompts. For the group of students that did not use the reflection problem-solving route (11 for the second-order prompt and 13 for the zero-order prompt), we noted that their problem-solving maps tended to be polarized with either all unproductive or all productive problem-solving routes. For example, consider Juliet's problem-solving map for the zero-order chemistry problem (Fig. 7) and Andrea's problem-solving map for the second-order chemistry problem (Fig. 3), both of which did not involve the reflection problem-solving route.

Fig. 7 Juliet's problem-solving map for the zero-order chemistry problem chronologically displays the problem-solving routes used and characterizes the problem-solving routes based on how productive they were for answering the prompt; the green check-mark symbol in the upper right-hand corner indicates that the student's final answer was correct.

Although having a reflection does not necessarily mean a student will have a problem-solving trajectory that oscillates between productive and unproductive problem-solving routes, this pattern of one-sided problem-solving routes suggests that reflections help change the problem-solving direction when students are unsatisfied with their answers (such as both of Jonathan's reflections in Fig. 4). In addition, reflections at the end of a problem-solving map suggest a student was satisfied with their answer, cuing the student that they are done solving the problem (such as Isabel's reflection in Fig. 2 and Louis’ reflection in Fig. 5). Moreover, as was the case with the conceptual reasoning problem-solving route, reflecting on work during problem solving depends largely on the use of normative chemistry ideas. By definition, unproductive reflections move students away from the correct answer, which is illustrated across both prompts. Students that had unproductive reflections (10 students for each prompt) tended to have incorrect or undecided final answers, whereas students with productive reflections (19 for the second-order prompt and 17 for zero-order prompt) tended to have correct final answers.

Limitations

The generalizability of the results discussed is limited due to the nature of our sample (a small group of students majoring in engineering) and the context-dependent nature of problem solving. We would also like to note that characterizing each student based on their final answer, although simplifies analysis, does not adequately capture students’ problem-solving; however the problem-solving maps do help express the dynamic problem-solving approaches displayed in a given interview. Additionally, analysis of reflections in a clinical context is both artificial (to some extent) and challenging because of the role of the interviewer. Probing questions may serve as a catalyst for students to engage in reflection, which the students may not have done if problem-solving on their own. Nevertheless, as previously mentioned in this work, not every student engaged in reflection, suggesting that some students may be more competent in this skill, which was illustrated in this work to be critical for problem solving, supporting the need to investigate the role of reflections during problem-solving to provide insight for practitioners and researchers.

Conclusions and implications

Our analysis of problem-solving routes indicates that students have access to a variety of approaches that they can use to reason about data and solve problems. We assert that these problem-solving strategies reflect students making use of and responding to the resources that were activated by the prompt. Although not all of the problem-solving approaches were useful for this context and were likely the result of the activation of unproductive resources, they may aid students in reasoning about other problems they come across (e.g., method of initial rates task). For the second-order chemistry prompt, the primary trend observed was the difficulty students had with reasoning about the data, which cued students into using multiple unproductive problem-solving routes. Based on student responses, it is possible that students viewed the prompt as an exercise instead of a problem, utilizing approaches they have routinely used to answer questions on related material. As discussed by Bodner and McMillen (1986), an exercise involves following a rehearsed procedure to reach an answer (i.e., standard textbook examples that have a clear approach and solution), whereas solving a problem requires working through a process that is unfamiliar. Thus, students that attempted to use problem-solving approaches such as method of initial rates incorrectly identified the prompt as a typical textbook method of initial rates exercise and applied the associated procedure to reach an answer. Central to this observed trend is the ability to reason about the information provided and think about how that data can be used to address the prompt. However, when students tried to think more generally about the data provided (qualitatively or quantitatively) we observed this negatively influenced their problem-solving trajectories. Stated differently, focusing on surface features resulted in the activation of unproductive resources that cued students into using problem-solving approaches that did not help them adequately address the prompt.

Our results suggest students need more direct support and opportunities to reason about data, which requires students to incorporate conceptual reasoning in a meaningful way to help move beyond surface features and identify relationships (National Research Council, 2012; Heisterkamp and Talanquer, 2015). Heisterkamp and Talanquer (2015) asserted that opportunities to reason about data should encompass a variety of contexts, drawing attention to contrasting ideas that students may associate with one another based on surface features. This could involve explicitly discussing various approaches to solving a problem—why certain problem-solving approaches are appropriate and others are not—and emphasizing what information can be elicited from data. Thus, by providing students varied contexts and making them aware of relevant features and ideas, students can have a more comprehensive understanding of target concepts (Bussey et al., 2013; Bain et al., 2018b).

In the case of the zero-order chemistry prompt, students tended to generalize first-order reasoning about half-lives, which led to the use of unproductive problem-solving routes. One way to frame the unproductive problem-solving approaches observed in our dataset is that their implementation suggests a lack of conceptual reasoning or the presence of unproductive conceptual ideas, such as considerations of the values that can be inserted into expressions (e.g., method of initial rates, rate calculation), understanding the conclusions that can be reached by comparing values (e.g., ratio calculation, patterns & trends), or applying first-order reasoning to other chemical systems (e.g., conceptual reasoning, reflection). Thus, (scientifically normative) conceptual reasoning could help students transform unproductive problem-solving routes into tools that can be used to reach a solution. This is perhaps best illustrated in the problem-solving route patterns & trends, which, if better integrated with chemistry concepts, would be reminiscent of problem-solving strategies used by effective problem-solvers, in the sense that it is based on qualitative reasoning in contrast to an overemphasis on algorithmic manipulations, which has been associated with less sophisticated reasoning (Larkin and Reif, 1979; Chi et al., 1981; Reif and Heller, 1982; Reif, 1983; Becker et al., 2017; Brandriet et al., 2018).

As previously discussed, Bodner (2015) asserted that when experts solve unfamiliar problems they do not follow the simple linear sequence implied by most problem-solving models; rather, he described expert reasoning as anarchistic, in which their trajectories tend to lack order. Thus, we assert that what makes an expert better at solving problems is not the process they employ, but rather the combination of meaningfully connected and productive resources they have available. Reif and Heller (1982) made a similar argument, stating that studying experts as a means to better understand effective problem solving is challenging and problematic, since many of the features and cognitive processes that define expert problem solving are tacit and are not readily observable. In the study by Bunce et al. (1991) they found that although explicit instruction using a problem-solving model improved students’ ability to work through typical chemistry problems, students exhibited difficulty in reasoning conceptually and incorporating concepts while problem solving. Perhaps part of the issue with problem solving models is that they can become just another equation or algorithm students utilize without thinking about the underlying chemistry. Therefore, rather than proposing yet another problem-solving model, we assert that instructional support to improve students’ problem solving is best addressed through an emphasis on conceptual reasoning.

The previously discussed definition of conceptual reasoning provided by Holme et al. (2015) emphasized that conceptual reasoning is more than definitions of laws and principles; it involves productively making use of chemistry to accomplish different tasks. In the context of problem solving, Reif (1983) discussed the role of domain knowledge, stating that definitions of concepts are not enough; students need ancillary knowledge that makes foundational concepts useful, that is, a productive working knowledge of chemistry principles—something that is implicitly and tacitly utilized by experts, but often not conveyed to students. In order to improve student ability to work through problems and reason conceptually, instruction must be intentional and changes must be made to better support learning (Reif and Heller, 1982; Reif, 1983; Nakhleh et al., 1996; Zoller and Pushkin, 2007; Cooper, 2015). Instructors need to create opportunities to intentionally draw attention to the supporting ideas, demonstrating the utility of chemistry principles in solving problems and fostering a more meaningful understanding of chemistry. In the case of chemical kinetics, students may be provided the Arrhenius equation (which describes the factors that affect the rate constant), but in what ways are they expected to leverage the implications of this equation to solve problems, make predictions, and provide explanations on assessments? Students study what is assessed (Cooper, 2015); thus, if we want students to develop a deeper understanding of relevant concepts, exams and corresponding grading rubrics must include the criterion that student responses incorporate conceptual reasoning (Hull et al., 2013). Assessment should be built around core ideas and require students to make connections between finer-grained ideas, which serves as the context for students to engage in science practices, such as constructing explanations and engaging in argument from evidence (e.g., data) (Cooper et al., 2017). However, assessing students’ ability to integrate concepts and engage in science practices does not have to involve developing a completely new curriculum and exam questions; as suggested by Underwood et al. (2018), one practical way to do this is to modify existing assessment questions and tasks through the use of the criteria developed by Laverty et al. (2016).

In the context of our data, students used conceptual reasoning as a means to evaluate problem-solving routes and solutions, in which students considered the feasibility of their work. In the field of psychology, reasoning that is fast and intuitive is characterized as type 1 reasoning, whereas reasoning that is more slow and deliberate is characterized as type 2 reasoning (Evans, 2012; Kruglanski, 2013; Varga and Hamburger, 2014). Although we do not make any claims about classifying students in our data based on type 1 or type 2 reasoning, we assert that more successful problem solving can occur when students do not attempt to quickly plug values into the first equation that comes to mind—students need to engage in more deliberate self-regulating behavior, which is more consistent with the type 2 end of the cognitive processing spectrum. Our discussion of students reflecting on their work during problem solving encompasses actions related to the regulation of cognition, which is part of metacognitive thinking (Brown, 1987; Schraw et al., 2006). According to Schraw and Moshman (1995), the regulation of cognition involves controlling one's learning and thinking through planning, monitoring, and evaluation. Asserting the importance of engaging in these self-regulating behaviors, Cooper and Sandi-Urena (2009) developed an instrument to measure student ability to engage in the regulation of cognition during chemistry problem solving. In one study involving the use of the metacognitive skillfulness instrument, Sandi-Urena et al. (2011) demonstrated that working through problems in a collaborative setting, combined with subsequent instructional prompting, improved students’ ability to engage in self-regulating behavior. However, it is important to note that the problems utilized by Sandi-Urena et al. (2011) were intentionally selected to create “cognitive imbalance”, in which the problems encouraged reflections because of the nature of the counter-intuitive and unexpected solutions to the problems.

Thus, here we reiterate the importance of intentionality in instruction. If we want students to be able to engage in self-regulating behavior, instruction must reflect this goal, which involves more than just having students work with their peers; students must be provided problems that require them to engage in critical thinking and ask questions. As practitioners and researchers, one of the problems we need to solve is how we can improve the teaching and learning of chemistry. Our study focused on characterizing students’ problem solving by analyzing different approaches utilized, which provided insight regarding the importance of conceptual reasoning and reflection during the problem-solving process. In the spirit of metacognition, we encourage our readers to reflect on their work, what they want students to know, what they want their students to be able to do, and what metrics can be used to assess if these goals are being reached.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The National Science Foundation under grant DUE-1504371 supported this work. Any opinions, conclusions, or recommendations expressed in this article are those of the authors and do not necessarily reflect the views of the National Science Foundation. We wish to thank Tom Holme and the Towns research group for their support and helpful comments on the manuscript.

References

1. Bain K. and Towns M. H., (2016), A review of research on the teaching and learning of chemical kinetics, Chem. Educ. Res. Pract., 17(2), 246–262.
2. Bain K., Rodriguez J. G., Moon A. and Towns M. H., (2018a), The characterization of cognitive processes involved in chemical kinetics using a blended processing framework, Chem. Educ. Res. Pract., 19, 617–628.
3. Bain K., Rodriguez J. G. and Towns M. H., (2018b), Zero-Order Chemical Kinetics as a Context To Investigate Student Understanding of Catalysts and Half-Life, J. Chem. Ed., 95(5), 716–725.
4. Bodner G. M., (2015), Research on Problem Solving in Chemistry, in Garcia-Martinez J. and Serrano-Torregrosa E., (ed.), Chemistry Education: Best Practices, Opportunities and Trends, Weinheim, Germany: Wiley-VCH Verlag GmbH & Co. KGaA, pp. 181–201.
5. Bodner G. M. and Herron J. D., (2002), Problem Solving in Chemistry, in Gilbert J. K., De Jong O., Justi R., Treagust D. F. and Van Driel J. H., (ed.), Chemical Education: Towards Research-based Practice, Dordecht: Kluwer Academic Publishers, pp. 235–266.
6. Bodner G. M. and McMillen T. L. B., (1986), Cognitive Restructuring As an Early Stage in Problem Solving, J. Res. Sci. Teach., 23(8), 727–737.
7. Becker N. and Towns M. H., (2012), Students’ understanding of mathematical expressions in physical chemistry contexts: an analysis using Sherin's symbolic forms, Chem. Educ. Res. Pract., 13(3), 209–220.
8. Becker N. M., Rupp C. A. and Brandriet A., (2017), Engaging students in analyzing and interpreting data to construct mathematical models: an analysis of students’ reasoning in a method of initial rates task, Chem. Educ. Res. Pract., 18(4), 798–810.
9. Brandriet A., Reed J. J. and Holme T., (2015), A Historical Investigation into Item Formats of ACS Exams and Their Relationships to Science Practices, J. Chem. Educ., 92(11), 1798–1806.
10. Brandriet A., Rupp C. A., Lazenby K. and Becker N., (2018), Evaluating students’ abilities to construct models from data using latent analysis, Chem. Ed. Res. Pract., 19, 375–391.
11. Bretz S., Fay M., Bruck L. B. and Towns M. H., (2013), What faculty interviews reveal about meaningful learning in the undergraduate laboratory, J. Chem. Educ., 90(3), 5–7.
12. Brown, A., (1987), Metacognition, executive control, self-regulation, and other more mysterious mechanisms, in Weinert F. and Kluwe R., (ed.) Metacognition, Motivation, and Understanding, Hilldale, NJ: Erlbaum, pp. 65–116.
13. Bruck A. D. and Towns, M., (2013), Development, Implementation, and Analysis of a National Survey of Faculty Goals for Undergraduate Chemistry Laboratory, J. Chem. Educ., 90, 685–693.
14. Bruck L. B., Towns M. and Bretz S. L., (2010), Faculty perspectives of undergraduate chemistry laboratory: goals and obstacles to success, J. Chem. Educ., 87(12), 1416–1424.
15. Bunce D. M., Gabel D. L. and Samuel J. V., (1991), Enhancing chemistry problem-solving achievement using problem categorization, J. Res. Sci. Teach., 28, 505–521.
16. Bussey T. J., Orgill M., Crippen K. J., (2013), Variation Theory: A Theory of Learning and a Useful Theoretical Framework for Chemical Education Research, Chem. Educ. Res. Pract., 14, 9–22.
17. Campbell J. L., Quincy C., Osserman, J. and Pedersen O. K., (2013), Coding In-depth Semistructured Interviews: Problems of Unitization and Intercoder Reliability and Agreement, Sociol. Methods Res., 42(3), 294–320.
18. Chi M. T. H., Feltovich P. J. and Glaser R., (1981), Categorization and representation of physics problems by experts and novices, Cog. Sci., 5(2), 121–152.
19. Cooper M., (2015), Why Ask Why? J. Chem. Educ., 92(8), 1273–1279.
20. Cooper M. M. and Sandi-Urena S., (2009), Design and Validation of an Instrument To Assess Metacognitive Skillfulness in Chemistry Problem Solving, J. Chem. Educ., 86(2), 240–245.
21. Cooper M. M. and Stowe R. L., (2018), Chemistry Education Research—From Personal Empiricism to Evidence, Theory, and Informed Practice, Chem. Rev., 118(12), 6053–6087.
22. Cooper M. M., Cox C. T., Nammouz M., Case E. and Stevens R., (2008), An assessment of the effect of collaborative groups on students’ problem-solving strategies and abilities, J. Chem. Educ., 85(6), 866–872.
23. Cooper M. M., Posey L. A. and Underwood S. M., (2017), Core Ideas and Topics: Building Up or Drilling Down? J. Chem. Educ., 94(5), 541–548.
24. Cracolice M. S., Deming J. C. and Ehlert B., (2008), Concept learning versus problem solving: a cognitive difference, J. Chem. Educ., 85(6), 873–878.
25. Cruz-Ramirez de Arellano D. and Towns M. H., (2014), Students’ understanding of alkyl halide reactions in under-graduate organic chemistry, Chem. Educ. Res. Pract., 15, 501–515.
26. diSessa A. A., (1993), Toward an Epistemology of Physics, Cognition and Instruction, 10(2–3), 105–225.
27. Evans J. S. B. T., (2012), Dual-process theories of deductive reasoning: facts and fallacies, in Holyoak K. and Morrison R., (ed.), The Oxford Handbook of Thinking and Reasoning, New York, NY: Oxford University Press, pp. 115–133.
28. Gabel D. L. and Bunce D. M., (1994), Research on problem solving: chemistry, in Gabel D. L., (ed.), Handbook of Research on Science Teaching and Learning, A project of the National Science Teachers Association, New York: Macmillan.
29. Ge X. and Land S. M., (2003), Scaffolding students’ problem-solving processes in an ill-structured task using question-prompts and peer interactions, Educ. Technol. Res. Dev., 51, 21–38.
30. Gick M. L., (1986), Problem-solving strategies, Educ. Psychol., 21, 99–120.
31. Hammer D. and Elby A., (2003), Tapping epistemological resources for learning physics, J. Learn. Sci., 12(1), 53–90.
32. Hammer D., Elby A., Scherr R. E. and Redish E. F., (2005), Resources, framing, and transfer, in Mestre J. P., (ed.), Transfer of learning from a modern multidisciplinary perspective, Greenwich, CT: Information Age Publishing.
33. Heisterkamp K. and Talanquer V., (2015), Interpreting Data: The Hybrid Mind, J. Chem. Educ., 92(12), 1988–1995.
34. Holme T. and Murphy K., (2012), The ACS Exams Institute Undergraduate Chemistry Anchoring Concepts Content Map I: General Chemistry, J. Chem. Educ., 89(4), 721–723.
35. Holme T., Luxford C. and Brandriet A., (2015), Defining conceptual understanding in general chemistry, J. Chem. Educ., 92(9), 1477–1483.
36. Holme T., Luxford C. and Murphy K., (2015), Updating the General Chemistry Anchoring Concepts Content Map, J. Chem. Educ., 92, 1115–1116.
37. Holme T., Reed J., Raker J. and Murphy K., (2017), The ACS Exams Institute Undergraduate Chemistry Anchoring Concepts Content Map IV: Physical Chemistry, J. Chem. Educ., 95(2), 238–241.
38. Huffman D., (1997), Effect of Explicit Problem Solving Instruction on High School Students’ Problem-Solving Performance and Conceptual Understanding of Physics, J. Res. Sci. Teach., 34(6), 551–570.
39. Harle M. and Towns M. H., (2013), Students’ understanding of primary and secondary protein structure: drawing secondary protein structure reveals student understanding better than simple recognition of structures, Biochem. Mol. Biol. Educ., 41(6), 369–376.
40. Heller P., Keith R. and Anderson S., (1992), Teaching problem solving through cooperative grouping—Part 1: group versus individual problem solving, Am. J. Phys., 60, 627–636.
41. Hsu L., Brewe E., Foster T. M. and Harper, K. A., (2004), Resource letter RPS-1: research in problem solving, Am. J. Phys., 72(9), 1147–1156.
42. Hull M. M., Kou E., Gupta A. and Elby A., (2013), Problem-solving Rubrics Revisited: Attending to Blending of Informal Conceptual and Formal Mathematical Reasoning, Physical Review Special Topics – Physics Education Research, 9, 010105.
43. Justi R., (2002), Teaching and learning chemical kinetics, in Gilbert J. K., De Jong O., Justi R. Treagust D. and Van Driel J. H., (ed.), Chemical Education: Towards Research-based Practice, Dordrecht: Kluwer, pp. 293–315.
44. King N. and Horrocks C., (2010), Interviews in qualitative research, London: SAGE Publications, Ltd.
45. Kruglanski A., (2013), Only one? The default interventionist perspective as a unimodel–commentary on Evans & Stanovich (2013), Perspect. Psychol. Sci., 8, 242.
46. Kuo E., Hull M. M., Gupta A. and Elby A., (2013), How students blend conceptual and formal mathematical reasoning in solving physics problems, Sci. Educ., 97(1), 32–57.
47. Larkin, J. H. and Reif F., (1979), Understanding and teaching problem-solving in physics, Eur. J. Sci. Educ., 1(2), 191–203.
48. Laverty J. T., Underwood S. M., Matz R. L., Posey L. A., Jardeleza E. and Cooper M. M., (2016), Characterizing College Science Assessments: The Three-Dimensional Learning Assessment Protocol, PLoS One, 11(9), 1–21.
49. Linenberger K. J. and Bretz S. L., (2012), A novel technology to investigate students’ understandings of enzyme representations, J. Coll. Sci. Teach., 42(1), 45–49.
50. Mettes C. T. C. W., Pilot A., Roossink H. J. and Kramers-Pals H., (1980), Teaching and Learning Problem Solving in Science, J. Chem. Educ., 57(12), 883–885.
51. Nakhleh M. B., (1993), Are Our Students Conceptual Thinkers or Algorithmic Problem Solvers? Identifying Conceptual Students in General Chemistry, J. Chem. Educ., 70(1), 53–55.
52. Nakhleh M. B. and Mitchell R. C., (1993), Concept Learning versus Problem Solving: There is a Difference, J. Chem. Educ., 70(3), 191–192.
53. Nakhleh M. B., Lowrey K. A. and Mitchell R. C., (1996), Narrowing the Gap between Concepts and Algorithms in Freshmen Chemistry, J. Chem. Educ., 70(8), 758–762.
54. Nurrenbern S. C. and Pickering M., (1987), Concept Learning versus Problem Solving: Is There a Difference? J. Chem. Educ., 64(6), 508–510.
55. National Research Council, (2012), A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas, Washington, D.C.: National Academies Press.
56. Page J. M., (2014), Childcare choices and voices: using inter-preted narratives and thematic meaning-making to analyse mothers’ life histories, Int. J. Qual. Stud. Educ., 27(7), 850–876.
57. Pickering M., (1990), Further studies on concept learning versus problem solving, J. Chem. Educ., 67(3), 254–255.
58. Polya G., (1945), How to solve it; a new aspect of mathematical method, Princeton, NJ: Princeton University.
59. Reed J. J., Brandriet A. R. and Holme T. A., (2017), Analyzing the Role of Science Practices in ACS Exam Items, J. Chem. Educ., 94(1), 3–10.
60. Reif F., (1983), How can chemists teach problem solving? Suggestions derived from studies of cognitive processes, J. Chem. Educ., 60(11), 948–953.
61. Reif F. and Heller J. I., (1982), Knowledge Structure and Problem Solving in Physics, Educ. Psychol., 17(2), 102–127.
62. Sandi-Urena, S., Cooper M. M. and Stevens R. H., (2011), Enhancement of metacognition use and awareness by means of a collaborative intervention. Int. J. Sci. Educ., 33(3), 323–340.
63. Sanger M. J., Vaughn C. K. and Binkley D. A., (2013), Concept learning versus problem solving: evaluating a threat to the validity of a particulate gas law question, J. Chem Educ., 90, 700–709.
64. Sawrey B. A., (1990), Concept learning versus problem solving: revisited, J. Chem. Educ., 67(3), 253–254.
65. Schraw G. and Moshman D., (1995), Metacognitive Theories, Educational Psychology Review, 7(4), 351–371.
66. Schraw G., Crippen K. J. and Hartley K., (2006), Promoting Self-Regulation in Science Education: Metacognition as Part of a Broader Perspective on Learning, Res. Sci. Educ., 36, 111–139.
67. Shahat M. A., Ohle A., Treagust D. F. and Fischer H. E., (2012), Design, Development, and Validation of a Model of Problem solving for Egyptian Science Classes, International Journal of Science and Mathematics Education, 11, 1157–1181.
68. Stamovlasis D., Tsaparlis G., Kamilatos C., Papaoikonomou D. and Zarotiadou, E., (2005). Conceptual understanding versus algorithmic problem solving: further evidence from a national chemistry examination. Chem Educ. Res. Pract., 6(2), 104–118.
69. Stowe R. and Cooper M. (2017), Practicing What We Preach: Assessing “Critical Thinking” in Organic Chemistry, J. Chem. Educ., 94, 1852–1859.
70. Strauss A. and Corbin J., (1990), Basics of Qualitative Research: Grounded Theory Procedures and Techniques, Newbury Park, CA: SAGE Publications, Ltd.
71. Underwood S., Posey L., Herrington D., Carmel J. and Cooper M., (2018), Adapting Assessment Tasks to Support Three-Dimensional Learning, J. Chem. Educ., 95, 207–217.
72. Van Heuvelen A., (1991), Learning to think like a physicist: a review of research-based instructional strategies, Am. J. Phys., 59, 891–897.
73. Varga A. L. and Hamburger K., (2014), Beyond type 1 and type 2 processing: the tridimensional way, Front. Psychol., 5, 993.
74. Wenzel T. J., Larive C. K. and Frederick K. A., (2012), Role of Undergraduate Research in an Excellent and Rigorous Chemistry Curriculum, J. Chem. Educ., 89(1), 7–9.
75. Wenzel T. J., Mccoy A. B. and Landis C. R., (2015), An Overview of the Changes in the 2015 ACS Guidelines for Bachelor's Degree Programs, J. Chem. Educ., 92, 965–968.
76. Wheatley, G. H., (1984), Problem solving in school mathematics. MEPS Technical Report 84.01, School Mathematics and Science Center, West Lafayette, IN: Purdue University.
77. Wittmann M. C., (2006), Using Resource Graphs to Represent Conceptual Change, Phys. Rev. ST Phys. Educ. Res., 2, 020105.
78. Woods D., (2000), An evidence-based strategy for problem solving, J. Eng. Educ., 89(4), 443–459.
79. Yuriev E., Naidu S., Scehmbri L. S. and Short J. L., (2017), Scaffolding the development of problem-solving skills in chemistry: guiding novice students out of dead ends and false starts, Chem. Educ. Res. Pract., 18, 486–504.
80. Zoller U. and Pushkin D., (2007), Matching Higher-Order Cognitive Skills (HOCS) promotion goals with problem-based laboratory practice in a freshman organic chemistry course, Chem. Educ. Res. Pract., 8(2), 153–171.
81. Zoller U., Lubezky A., Nakhleh M. B., Tessier B. and Dori Y. J., (1995), Success on algorithmic and LOCS vs. conceptual chemistry exam questions, J. Chem. Educ., 72(11), 987–989.

---