Covariational reasoning and mathematical narratives: investigating students’ understanding of graphs in chemical kinetics

Abstract

Graphical representations are an important tool used to model abstract processes in fields such as chemistry. Successful interpretation of a graph involves a combination of mathematical expertise and discipline-specific content to reason about the relationship between the variables and to describe the phenomena represented. In this work, we studied students’ graphical reasoning as they responded to a chemical kinetics prompt. Qualitative data was collected and analyzed for a sample of 70 students through the use of an assessment involving short-answer test items administered in a first-year, non-majors chemistry course at a Swedish university. The student responses were translated from Swedish to English and subsequently coded to analyze the chemical and mathematical ideas students attributed to the graph. Mathematical reasoning and ideas related to covariation were analyzed using graphical forms and the shape thinking perspective of graphical reasoning. Student responses were further analyzed by focusing on the extent to which they integrated chemistry and mathematics. This was accomplished by conceptualizing modeling as discussing mathematical narratives, characterizing how students described the “story” communicated by the graph. Analysis provided insight into students’ understanding of mathematical models of chemical processes.

---

Introduction

Chemical kinetics is concerned with the rates of chemical processes, where experimental conditions influencing rate are often studied and inferences about the associated reaction mechanism are often made, typically through the construction of mathematical models using differential calculus. Mathematical operations and graphical reasoning centered around the derivative provide useful tools for modeling systems that change over time. However, a review of the literature indicates that undergraduate students lack a clear understanding of rate and rate-related ideas, with ample evidence supporting the claim that students struggle with a conceptual understanding of functions, covariational reasoning, and assignment of meaning to variables (White and Mitchelmore, 1996; Castillo-Garsaw et al., 2013; Moore et al., 2013; Aydin, 2014; Moore, 2014; Rasmussen et al., 2014; Bain and Towns, 2016).

Given this backdrop, it is not surprising students have difficulty using and applying calculus in other contexts, such as modeling physical systems (Becker and Towns, 2012). The act of modeling, which often requires processes to be translated into mathematical formalisms, is a common practice in the sciences, and it has been identified as a foundational scientific practice that students should engage in at all levels of education (National Research Council, 2012; Bruce, 2013; Posthuma-Adams, 2014; Edwards and Head, 2016). Modeling in the physical sciences can be particularly challenging because it often requires the integration of (scientific) knowledge with a student's mathematical knowledge, a problem that is further compounded when considering that chemistry requires students to think abstractly at the particulate-level, which is not readily observable or accessible (Kozma and Russell, 1997; Becker and Towns, 2012; Bain et al., 2018). Nevertheless, researchers agree that making connections across different domains of knowledge through modeling is necessary to promote a deeper understanding of chemistry (Talanquer, 2011; Taber, 2013; Sjostrom and Talanquer, 2014; Cooper et al., 2015; Laverty et al., 2016; Becker et al., 2017).

Previous work has investigated student understanding of mathematical expressions and their relationship to chemical phenomena, with many studies placed in the context of chemical kinetics (Jasien and Oberem, 2002; Justi, 2002; Greenbowe and Meltzer, 2003; Hadfield and Wieman, 2010; Becker and Towns, 2012; Bain and Towns, 2016; Becker et al., 2017). In their review paper, Bain and Towns (2016) comment on the highly quantitative nature of chemical kinetics, which heavily relies on the use of graphs and representations, making it an excellent context to investigating graphical reasoning. In addition, Bain and Towns (2016) echo the call of the National Research Council for more discipline-based education research (DBER) that focuses on studies at the undergraduate level and emphasizes interdisciplinary work, such as collaborations between chemistry and mathematics communities (Singer et al., 2012). This study seeks to contribute to the body of knowledge related to graphical reasoning in the physical sciences by bridging the gap between research done in chemistry and mathematics. To this end, our guiding research question is the following: In what ways do students use mathematics in combination with their knowledge of chemistry and chemical kinetics to interpret concentration versus time graphs?

Review of related literature

Graphical reasoning in physical science

Among the reviewed literature, few studies focus on the overlap of chemical and graphical reasoning, and among the chemical kinetics studies reviewed, none focus exclusively on reasoning related to graphical representations. However, student difficulties with graphs are discussed briefly as part of larger studies situated in chemical kinetics. The general consensus from the literature is that students are often unable to make conclusions about the chemical mechanism that is implied in graphical representations of chemical processes, and the use of graphs in chemical kinetics may even be a source of anxiety for students (Cakmakci et al., 2006; Cakmakci, 2010; Tastan et al., 2010; Cakmakci and Aydogdu, 2011; Kolomuc and Tekin, 2011; Secken and Seyhan, 2015). Furthermore, research suggests that the presentation of chemical kinetics and its graphical representation in textbooks can be a source of confusion for students and may not adequately promote a conceptual understanding (Quisenberry and Tellinghuisen, 2006; Gegios et al., 2017; Seethaler et al., 2018).

More generally, studies that involved prompting students to reason about physical science graphs along with parallel, decontextualized (math-only) graphs have discussed the role of mathematical ability (Potgieter et al., 2007) and the increased complexity associated with contextualized graphs (Planinic et al., 2013; Phage et al., 2017), in which different contexts may cue students to utilize less-productive problem-solving strategies to reason about the graphs (Ivanjeck et al., 2016). Collectively, the body of literature on graphical reasoning in the physical sciences provides insight regarding the complex factors that interact when students reason about graphs. In the section that follows, we build on this body of literature by focusing more explicitly on the role of mathematical reasoning, considering the role of covariational reasoning in understanding the information represented in a graph.

Covariational reasoning

A useful working definition of covariational reasoning is tersely provided by Saldanha and Thompson (1998), in which they frame covariation as “holding in mind a sustained image of two quantities (magnitudes) simultaneously.” Building on this conceptualization, covariational reasoning focuses on the relationship between two variables and how they change (Carlson et al., 2002; Thompson and Carlson, 2017). Across the literature, covariational reasoning has been emphasized as fundamental for understanding advanced topics in mathematics, modeling dynamic processes, and thinking about graphs (Thompson, 1994; Confrey and Smith, 1995; Carlson et al., 2002; Habre, 2012; Ellis et al., 2016).

Using covariational reasoning as a resource to interpret graphs is highlighted in the process–object distinction, which is framed in the mathematics community as involving complementary perspectives regarding how a mathematical function can be viewed (Even, 1990; Schwartz and Yerushalmy, 1992; Sfard, 1992; Moschkovich et al., 1993; Potgieter et al., 2007). According to Moschkovich et al. (1993) the process perspective of a graph emphasizes the underlying covariation and relationship between the variables (viewing the graph as a mapping of all possible input and output values), whereas the object perspective of a graph draws attention to the graph as a whole (viewing it as an entity with properties). This characterization of considering a graph as a process or an object is at the core of Moore and Thompson's (2015) conceptualization of shape thinking. Within the shape thinking framework, reasoning is characterized as emergent, which more explicitly considers the relationship between the varying quantities (framing the graph as a process), and static, which focuses on the overall shape of the curve (framing the graph as an object). We would like to emphasize that static reasoning or viewing the graph as an object is not inherently unproductive; both conceptualizations of a graph are resources that may be useful for solving problems in different contexts, and students should be able to reason using both perspectives (Even, 1990; Schwartz and Yerushalmy, 1992; Sfard, 1992; Potgieter et al., 2007).

In the context of chemical kinetics, we are not simply mapping all possible inputs to outputs in the sense of a function with respect to x, rather, there are physical meanings attached. In particular, the independent variable time t is directional, so the individual points on the graph are not independent of all others, but rather there is a “history”. The story “unfolds” and unlike in pure mathematical settings, students need to be able to imagine and follow this “unfolding” with time. Therefore, covariation takes on an interesting new meaning from the perspective of an expert reasoning with chemistry concepts, in which a point in the Cartesian coordinate system becomes an event and a group of meaningfully connected points becomes a story. The relationship between the variables that define an event and the coordination of what Saldanha and Thompson (1998) refer to as “simultaneous continuous variation” affords the ability to make interferences about the process, which serves as the basis for a descriptive account informed by chemistry ideas. For this reason, we frame modeling as engaging in mathematical narratives, which involves discussing the “story” communicated by a graph, or engaging in “narratives that fuse aspects of events and situations with properties of symbols and notations,” (Nemirovsky, 1996). This affords us the language to think about how students integrated chemistry ideas to interpret graphs.

Theoretical perspectives

Our approach toward investigating graphical reasoning is a combination of multiple frameworks and is described in more detail in a forthcoming paper (Rodriguez et al., 2018). From a theoretical perspective, the resources framework informed the design, implementation, and analysis of our study (Hammer et al., 2005). Knowledge is conceptualized within the resources framework as being defined by a coordinated and dynamic system of cognitive units, with varying levels of complexity in terms of the connections between the individual cognitive units (i.e., resources) (Hammer and Elby, 2002, 2003). Furthermore, the context in which a task is situated influences the resources that are activated by a student; however, activated resources are not necessarily productive and may be better suited for other contexts (Richards et al., 2018).

As discussed by Becker et al. (2017), resources can be characterized as procedural, epistemological, or conceptual in nature. In this work we focus on students’ conceptual resources related to chemistry and mathematics. In the case of mathematical resources, we build on Sherin's (2001) symbolic forms framework. Symbolic forms are mathematical resources that involve attributing intuitive mathematical ideas to a pattern in an equation (Sherin, 2001). Although the symbolic forms framework was originally developed to characterize how physics students think about equations during quantitative problem solving, it has proven useful for investigating mathematical reasoning across discipline-based education fields, including chemistry (Sherin, 2001; Izak, 2004; Becker and Towns, 2012; Hu and Rebello, 2013; Jones, 2013, 2015a, 2015b; Von Korff and Rubello, 2014; Dorko and Speer, 2015). In our forthcoming paper, we describe how symbolic forms can be adapted for the analysis of graphical reasoning, in which we frame reasoning involving “graphical forms” as attributing mathematical ideas (conceptual schema) to a registration (region in the graph); for example, the graphical form steepness as rate involves associating the steepness of a graphical region with ideas related to rate (Rodriguez et al., 2018). A summary of graphical forms described in Rodriguez et al. (2018) is provided in Table 1. It is worth drawing attention to the dynamic nature of graphical forms, which may involve multiple conceptual schemas potentially being associated with a single registration. This can be illustrated by considering the distinction between a straight line with a zero gradient (which indicates constant concentration in a concentration vs. time curve) or a straight line with a non-zero slope (which indicates a constant rate of change in the concentration values in a concentration vs. time curve).

Table 1 Examples of graphical forms (reproduced or adapted from Rodriguez et al., 2018)

Graphical form	Registration and conceptual schema
Steepness as rate	Varying levels of steepness in a graph correspond to different rates
Straight means constant	A straight line indicates a lack of change/constant rate
Curve means change	A curve indicates continuous change/changing rate

---

For the study discussed herein, we used graphical forms to characterize and analyze the intuitive mathematical ideas students used to reason about graphs. Furthermore, our approach to analyzing students’ mathematical reasoning involved characterizing graphical forms using the emergent and static designations from the shape thinking framework, meaning we categorized students’ intuitive mathematical ideas about graphs based on whether they focused more on its process or object nature (Moore and Thompson, 2015). Our use of multiple frameworks during data analysis was an effort to address the themes that emerged from the data, which lead us to consider literature from different communities. The graphical forms framework afforded the ability to characterize mathematical resources activated by students, the shape thinking perspective provided insight regarding students’ engagement in covariational reasoning, and framing our discussion around mathematical narratives allowed us to consider the integration of mathematics and chemistry ideas. Thus, our combination of frameworks allowed us to focus on the mathematical resources students used and draw conclusions regarding how students combined mathematical reasoning with chemistry ideas to explain the process modeled.

Methods

Data collection

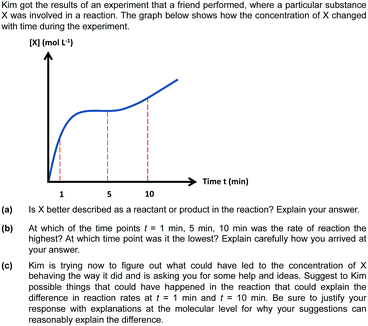
The primary source of data was an assessment administered to 109 students following the chemical kinetics unit in a first-year non-majors chemistry course at a Swedish university (F. M. H. as instructor, exams were administered in Swedish). Student responses submitted for examination are legally matters of public record under the Swedish system and are freely available to the public upon request. The responses used for this study were accessed as digitally scanned copies. All grading had been completed and the student results finalised before any translation or data analysis commenced. The scanned exam responses were identified only by anonymous codes and no decoding was performed at any point during the study. Thus, the identity of each participant was protected and unknown to the researchers.

The final sample that we report is comprised of 70 students (more information regarding our final sample size is provided below). To provide context, the prerequisites for students in this course involved senior high school (gymnasium) chemistry and a mathematics series that encompassed differential and integral calculus, including concepts such as the limit definition of the derivative and its relationship to the slope of a tangent line. The prompt given to the students provided a concentration vs. time graph, along with three short-answer questions related to the graph (provided in Fig. 1). Content validity of the assessment items was achieved by discussing and co-developing this prompt among a group of four researchers, and the wording in the prompt was refined after initially being piloted (in both English and Swedish) with a group of participants that included three professors, a postdoctoral researcher, and two PhD students. One of the learning objectives for the kinetics unit was for students to be able to extract information about what is happening at the molecular level from a graphical representation of a reaction. This is reflected in the design of the prompt, which focuses on conceptual understanding and requires students to integrate chemical and mathematical knowledge. Furthermore, the prompt supports students to reason conceptually by scaffolding the students to first consider what is happening and then consider why this is happening. The first two items in the prompt ask the students to think about (a) what is being modeled and (b) the rate at different points in the graph (what); the last item (c) asks the students to explain why the rate changed (why). This is in line with the notion that in order to elicit a deeper level of thinking, instructors must ask what (descriptive, surface-level questions) before they ask why (mechanistic, explanatory questions) (Cooper, 2015).

Fig. 1 Prompt used to assess students’ chemical and mathematical reasoning.

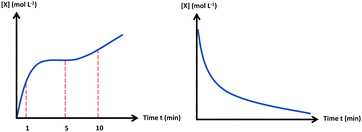
This emphasis on conceptual understanding led the researchers to consider how students apply knowledge to unfamiliar situations, which has been identified as a key component of conceptual understanding (Holme et al., 2015). Within the resources framework, in order for students to be able to use knowledge in novel situations, resources related to the task need to be coherently organized in such a way that they are not dependent on a single context (Hammer et al., 2005). The prompt was designed, in part, to evaluate the extent in which students are able to use the appropriate knowledge in a different context. The graph in the prompt did not reflect the concentration vs. time graphs normally depicted in textbooks, and although chemically possible, it exhibited deviations from empirical results one would observe in typical laboratory work done in an introductory general chemistry course (see Fig. 2). In addition to representing a somewhat unfamiliar problem-solving scenario, the last item in the prompt reflects what is described as an “ill-defined” problem, in which the question is open-ended and does not have one correct answer (Singer et al., 2012). For this problem, students are prompted to suggest a plausible explanation for the observed graph shape, which could encompass a myriad of possible justifications. This requires students to attend to features in the graph, draw conclusions using intuitive mathematical ideas, and subsequently connect their mathematical reasoning to chemistry concepts.

Fig. 2 Graph used in the prompt (left) and a graph used in a typical chemistry textbook (right).

Moreover, we would also like to note the nature of the prompt we developed incorporated considerations discussed in the National Research Council's (2012) conceptualization of “three-dimensional learning”, which encompasses: science practices (combination of skill and knowledge utilized by scientists); crosscutting concepts (unifying ideas that have applicability across science fields); and core ideas (fundamental principles relevant to a discipline). Using the criteria provided in the Three-Dimensional Learning Assessment Protocol (3D-LAP; Laverty et al., 2016) to evaluate whether our prompt elicited student engagement in these three dimensions, we concluded that our prompt was “three-dimensional”. It required students to engage in developing and using models (science practice), reason about patterns/cause and effect (crosscutting concepts), and consider ideas related to stability in chemical systems (core idea).

Data analysis

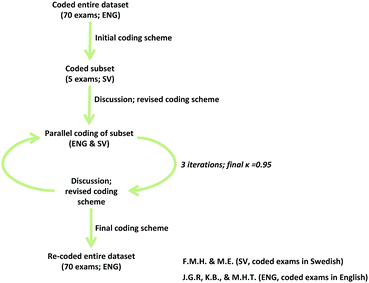
Student exam responses were analyzed using open coding, which was informed by the graphical forms, shape thinking, and mathematical narratives perspectives. Due to the role of language in shaping meaning and our understanding of the student responses, coding and considerations of inter-rater reliability across languages were closely intertwined. Our data analysis process is best reflected in the multi-step workflow presented in Fig. 3.

Fig. 3 Coding and considerations of inter-rater reliability involved an iterative process with multiple rounds of coding followed by discussion between the two teams of researchers. F. M. H. and M. E. have research and technical expertise in chemistry (in Swedish and English) and coded the data in Swedish (SV); J. G. R., K. B., and M. H. T. have research and technical expertise in chemistry (in English only) and coded the data in English (ENG).

The first stage involved developing and refining the coding scheme for the students’ exam responses (J. G. R. and K. B.). Prior to coding, the exams were translated from Swedish into English by one of the authors (F. M. H.) and a random sample of the exams were subsequently back-translated by a different author (M. E.) to confirm the accuracy and quality of the translations. After analyzing responses for 50 (of the 109) students, it was thought data saturation was reached because all student responses could be classified using existing codes. To confirm data saturation, 20 additional exams were coded, making the final sample that we report comprised of 70 students. Initial analysis of the 70 exams was done through the process of constant-comparison, with two researchers (J. G. R. and K. B.) coding in tandem and requiring 100% agreement for assignment of codes (Strauss and Corbin, 1990; Campbell et al., 2013). Following the coding of the translated dataset, two different researchers (F. M. H. and M. E.) applied the coding scheme to five students’ original (untranslated) exams and discussed their code assignments with the other authors (J. G. R., K. B., and M. H. T.). Based on this discussion, both teams (J. G. R./K. B. and F. M. H./M. E.) re-coded the same five exams (English and Swedish, respectively) using the refined coding scheme. Once again, all the authors met and discussed the code assignments; subsequently both teams re-coded the same five exams, as well as another five exams, which yielded a Cohen's Kappa of 0.92. Both teams then coded an additional four exams to reach a final Cohen's Kappa of 0.95 for 20% of the data corpus (14 out of 70 exams). This iterative process of both teams coding and discussing helped to refine and modify the coding scheme and the assignment of codes, which was ultimately used in the final stage of data analysis to re-code the entire dataset (J. G. R. and K. B.).

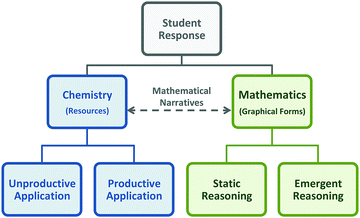
The coding scheme developed into a multi-tier categorization system that was used to characterize student responses, as shown in Fig. 4. Although not depicted in the coding scheme, we also coded student responses based on whether it was correct or incorrect, that is, whether students would have received credit for their response to the item on the exam. To be clear, our primary focus involved elucidating the resources activated by students in this context. Our use of an additional layer of coding involving the correct/incorrect designation was not to catalog students’ misconceptions; instead, it served as a metric to gauge how productive student responses were and provide a way to frame the resources that were inappropriately activated or applied in this context. We were attempting to address the practical consideration regarding grading, in which responses characterized as more productive would earn students more credit on the exam and would simultaneously reflect a more normative understanding of chemistry ideas.

Fig. 4 The multi-tiered coding scheme involved characterizing student responses based on the chemistry ideas (resources, categorized based on application to context) and mathematical ideas (mathematical resources/graphical forms, categorized using the shape thinking framework) that were used to solve the prompt. The dotted line in diagram indicates potential integration of chemistry and mathematics ideas (discussing mathematical narratives).

As shown in Fig. 4, we characterized the student responses based on the discipline-specific (chemistry vs. mathematics) resources, such as the content and reasoning the students used. This was developed through a combination of inductive and deductive analysis; the chemistry categories developed as a result of the observed student responses and the mathematical reasoning categories were modeled after the graphical forms framework and the delineation of emergent vs. static reasoning. For the chemistry categories, an “Unproductive Application” sub-category was created to encompass instances in which students activated or utilized resources in a manner that were less useful for problem-solving in this context, and a “Productive Application” sub-category was created to encompasses ideas and reasoning that more appropriately addressed the prompt. It is also important to note that chemical and mathematical reasoning categories were not mutually exclusive, in which examples involving both types of reasoning could qualify as engaging in mathematical narratives (the dotted line in Fig. 4). However, for the purpose of this study, our characterization of mathematical narratives focused primarily on instances in which student descriptions involved a more normative understanding of chemical kinetics. Thus, our discussion of mathematical narratives in the next section encompasses the criterion that students provided a chemically plausible explanation of the graph provided. This was an effort to narrow the scope of analysis, emphasizing reasoning that more closely reflected that of experts, in the sense of the ability to productively combine different domains of knowledge (Hull et al., 2013; Bain et al., 2018).

Findings

Analysis of the data revealed that students employed multiple different types and combinations of chemical and mathematical reasoning when interpreting concentration vs. time graphs. We have organized the following sections based on the student answers to each item in the prompt.

Item (a): is X better described as a reactant or product?

In the prompt the students were presented with a graph showing concentration as a function of time, and in the first item students were asked to specify if the y-axis corresponded to reactants or products. Students tended not to explicitly employ mathematical reasoning to respond to this item, focusing instead on the nature of chemical reactions. With few exceptions in our sample, students overwhelmingly provided the correct answer, stating that the graph showed the concentration of the products. Among students that answered this item correctly, the most common justification provided was the idea that “products increase, reactants decrease”. This is reflected in Benjamin's response to item (a):

Benjamin: “A product, since the concentration rises. This suggests that more molecules of the substance is formed, contrary to a reactant where the substance is consumed.”

One of the limitations of our sample is that we were not able to ask probing follow-up questions to clarify students’ reasoning. However, based on how students such as Benjamin responded to item (a) we can draw some inferences about their mathematical reasoning. In order to be able to connect the graph with the idea that the amount of product increases during a reaction, it is implied that the students are able to elicit the general trend or directionality of the graph, namely, that the graph is increasing. This is a basic reasoning skill that is foundational for interpreting graphs, and we characterize this intuitive mathematical idea as the graphical form trend from shape directionality, in which the students looked at the graph as a whole and reached a conclusion regarding the graph's overall tendency to increase or decrease. In terms of classifying graphical forms as static or emergent using the shape thinking framework conceptualized by Moore and Thompson (2015), we view trend from shape directionality as an example of static reasoning. In this case, the entire graph is the registration attended to by the students, where they focused more on the general shape of the overall graph and assigned ideas to this “object”, as opposed to using emergent reasoning and conceptualizing the graph as a process or mapping of all possible input and output values. We would like to emphasize that static reasoning is not inherently unproductive, and in this context students used it effectively as a resource to solve the problem.

Given that Benjamin reasoned using the graphical form trend from shape directionality, we assert that his approach to answering the question began with intuitive mathematical ideas about the graph, followed by the assignment of chemistry ideas that are consistent with conclusions reached using mathematical reasoning. Thus, Benjamin, who represents a typical student response for item (a), described the general story communicated by the graph by integrating mathematics and chemistry ideas. This type of reasoning that seemed to involve mathematics as a starting point for engaging in modeling (i.e., discussing mathematical narratives) is consistent with what was previously observed when students engage in quantitative problem-solving (Bain et al., 2018). We argue that anchoring reasoning in mathematical ideas is particularly important for interpreting graphs, because it is through the use of intuitive mathematical reasoning that we can determine trends in the data—e.g., how rate changes in item (b)—and subsequently attribute a chemically plausible explanation for these observed trends—e.g., a particulate-level explanation of the graph's shape in item (c).

Item (b): at which point is the rate highest/lowest?

In the second item students were prompted to reason about the rate at different points in the reaction. In comparison to item (a) where students tended to respond primarily by referencing chemistry concepts, in item (b) students frequently responded in purely mathematical terms. As before, few students answered this item incorrectly, with a majority of students addressing the prompt by using the graphical form steepness as rate. This graphical form involved students attending to a region of the graph, drawing inferences, and registering ideas about the relative magnitude of the rate. Within our dataset we characterized reasoning involving the steepness as rate graphical form as static or emergent, once again operationalizing the distinction made by Moore and Thompson (2015). To illustrate an example of static steepness as rate, consider Rosalynn's discussion of slope below:

Rosalynn: “The reaction rate is the greatest after 1 minute. The slope of the curve is the steepest here and the slope shows the reaction rate. The reaction rate is the lowest after 5 minutes. The curve is flat here, and the flatter the slope the slower the rate.”

In this example, Rosalynn equated the slope of the graph to the reaction rate, with her description utilizing general terms that emphasized the general shape of specific registrations (e.g., “steepness” and “flat”). Our conceptualization of static reasoning encompasses student responses that consider the graph (or a region of the graph) as a whole by drawing attention to its shape or framing it as an object with descriptive features. This is in contrast to how others, such as Hillary, reasoned using the steepness as rate graphical form:

Hillary: “At t = 1 min the curve has the highest slope, in other words there is the greatest difference in conc. per time, the derivative gives the exact answer. Quickest. At t = 5 min the rate was the lowest since the derivative is 0, in other words time passes but the conc. does not increase, no reaction occurs.”

Similar to Rosalynn's response, Hillary used the steepness of the graph to reason about rate; however, rather than simply attending to the general shape of regions in the graph, Hillary's discussion of rate made use of reasoning that incorporated ideas related to the derivative. In this sense, we consider Hillary's reasoning to be emergent, which more explicitly considers the relationship between both variables, “conc. per time”. Comparing the static and emergent characterizations of steepness as rate, aspects of covariational reasoning are more prominent when thinking about the derivative or the formal definition of slope, because they inherently involve drawing a connection between both variables. However, the presence of words such as “derivative” in a student's response does not necessarily indicate their reasoning is emergent, rather, the defining feature of emergent reasoning is the incorporation of ideas related to covariation or the process described by correlated variables.

Since the second item dealt with thinking about the rate of change, it readily lent itself to reasoning using the derivative, which led to our observation of emergent reasoning. However, in comparison to emergent reasoning, twice as many students engaged in static reasoning to address item (b). As mentioned previously, static reasoning is not necessarily unproductive; on the contrary, reasoning that focused on the shape of different regions of the curve to determine the relative slope was sufficient for responding to this question.

Item (c): explain the observed differences in the graph

In the final prompt, students were asked to reason about the chemistry that gave rise to this particular graph shape, which explicitly required students to discuss the story that is communicated by the graph. In our analysis of this item, we observed significantly more variation in the student responses. This was expected given the “ill-defined” nature of the item, which made the question open to a range of answers. Therefore, we classified the student responses to item (c) as extraneous, relevant, and chemically plausible, which represents movement toward more productive reasoning (Fig. 5). The distinction made between these categories of reasoning is based on the conceptualization of argumentation as involving a claim, evidence, and reasoning, where the reasoning is the explanation that connects how the evidence supports the initial claim (Toulmin, 1958; Becker et al., 2017). In each of the cases observed in our study (extraneous, relevant, chemically plausible) a claim was made about what was happening, the graph was used as evidence, and reasoning was provided to connect the explanation of what was happening to the graph. The distinction made between the extraneous, relevant, and chemically plausible categories was an attempt to organize and sort our data in order to aid analysis, and ultimately, support our primary focus regarding understanding the resources used by students and characterizing students’ application of these resources. In the sections that follow we provide examples of each of these cases.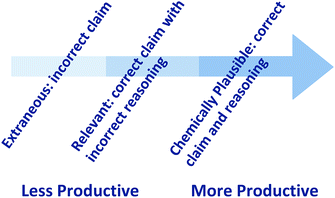

Fig. 5 Student responses were characterized as extraneous, relevant, and chemically plausible depending on how productive the statement was for addressing item (c), adapted from Toulmin's (1958) conceptualization of argumentation.

Extraneous. For statements characterized as extraneous, student responses typically involved an incorrect claim in which they discussed content that was unrelated to the topic of chemical kinetics and did not adequately explain the graph provided (within our dataset it is implied that if students had an incorrect claim, then the reasoning was incorrect as well). For example, a number of students described the graph by bringing in ideas about acid–base chemistry and titrations, as in Bess’ response to item (c):

Bess: “The solution is a diprotic acid which means that protolysis occurs in two steps: the reaction rate has two ‘spikes’ A diprotic acid, e.g. carbonic acid donates 2 protons after complete protolysis. Because protolysis occurs when carbonic acid and its conjugate base has a solution the pKa value of which is pKa1: 6.35 and pKa2: 10.33.”

Other students even explicitly used the word “titration” in their description of the graph. This was likely based on students associating the shape of the concentration vs. time graph with a titration curve's sigmoidal shape. In this case, the prompt activated resources that may be useful for problem solving in other contexts, but was not useful for thinking about this graph. The discussion of titrations and related content can be thought of as an extreme example of viewing the graph as an object, in which students simply associated chemistry ideas with the shape.

Relevant. When students made claims that involved ideas related to chemical kinetics, but justified their claim with incorrect reasoning, we classified their responses as relevant. In these instances, students referenced ideas (resources) that were related to chemical kinetics and could potentially explain the graph provided (e.g., complex reaction mechanism, equilibrium, factors that affect rate, etc.), but their reasoning did not connect the graph to their initial claim. The most common reason students were placed in this category was when they attributed the shape of the graph to a complex mechanism with multiple reactions. However, they did not correctly explain how this corresponded to the process modeled by the graph. Consider James’ response to item (c):

James: “R = k[A]^a[B]^b– at the beginning there was a lot of reactants that could form products – high reaction rate. The fact that it later increased again could be due to another reaction. The products themselves became reactants and formed new product.”

Initially, James provided a reasonable explanation that the initial rate of a reaction was fast because there were more reactants available (productively applying the resource more reactant, higher rate), but when describing the point in the graph where the rate increases again (t = 10), he stated that it was the result of a second reaction. If it were the case that a second reaction occurred this would not be communicated with the graph provided because the y-axis has not changed. The graph shows how a specific product changes over time, and a different reaction that forms a different product would not be represented on the graph (if the product did start to react, the concentration shown in the graph would begin to drop). Although while James activated a chemistry resource relevant for this problem (the resource complex reaction mechanism), its application was less productive and led to a result that was inconsistent with the graph provided. As shown in James’ response, the extraneous, relevant, and chemically plausible designations are not mutually exclusive, and different portions of a student's response could be classified into different categories (i.e., the first sentence was chemically plausible, but the remainder of the passage was only relevant).

Chemically plausible. In contrast to relevant statements, chemically plausible statements involved correct reasoning that connected chemical kinetics concepts to the graph. In these cases, the explanations provided by the students reflected reasonable descriptions of the process; in most cases this involved relating factors that affect rate to the different regions in the graph. In the previous section, we saw an example where James provided a chemically plausible description of the beginning portion of the graph, which was a common explanation provided by the students to explain what was happening at t = 1. Other common explanations regarding what could have resulted in the observed graph shape involved a discussion of how changing the reaction conditions could have resulted in the observed variation in rate (e.g., addition of more reactant, addition of catalyst, changing temperature, changing volume), or a discussion of equilibrium. For example, below Zachary described what could have happened at t = 5 and t = 10:

Zachary: “What could have happened is that at t = 5 the reaction reached equilibrium but more reactant was added and according to Le Chatelier's principle the reaction forms more products to reduce the stress in the system. At t = 10, product is constantly being removed which results in a constant and even formation of the products.”

In the example provided Zachary connected the flat region in the graph to equilibrium, discussing how Le Chatelier's principle provided insight into what could have resulted in the observed shape of the graph. From the perspective of an expert, a simpler explanation could explain the constant rate of the reaction at t = 10; nevertheless, Zachary's description is not outside the realm of possibility, with his reasoning reflecting a deeper and detailed level of thinking that attempted to account for the distinct features of the graph.

Mathematical narratives: the complete story

Taken as a whole, the graph provided in the prompt tells a story about a reaction that initially proceeded quickly, slowed, and then sped up again. Although a majority of students did provide a chemically plausible explanation for at least one region of the graph, in some cases we observed students providing a chemically plausible description to explain each of the three distinct regions of the graph: t = 1, characterized by a high reaction rate; t = 5, characterized by a low or nearly zero reaction rate (the “flat” region); and t = 10, characterized by a moderate reaction rate. In Fig. 6, we provide an example from our data of a student engaging in discussing mathematical narratives. Using Nancy's responses from item (b) and item (c) we are able to map her mathematical and chemical ideas onto the graph, which together comprise the story she discussed. In this instance, Nancy used graphical forms to draw inferences about the rate at different points on the graph, to which she was then able to attribute a chemically plausible explanation; thus, graphical forms supported her ability to reason about the phenomenon modeled in the graph. Furthermore, Nancy's use of the graphical form steepness as rate could be classified as static, emphasizing that the distinction between emergent and static is not based on productivity, since both can be useful for reasoning about a given context. This type of reasoning that attended to each of the regions represented a smaller portion of the student sample, which can be attributed in part to the prompt in item (c) that only explicitly asks the students to reason about the beginning and the end of the graph (t = 1 and t = 10). Nevertheless, some students such as Nancy “walked” along the graph and discussed what happened at each main event represented.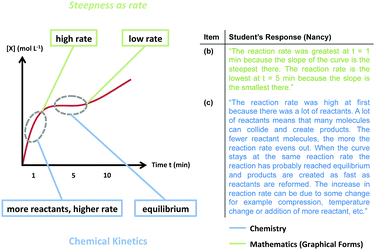

Fig. 6 Student engagement in discussing mathematical narratives (for clarity, the graph shown above has been modified from the original version that was provided in the exam).

Language considerations

Young and Temple (2004) discussed the role of language as more than simply communicating meaning or ideas, emphasizing that language constructs meaning, which has implications for research involving translated data, “Without talking to interpreters about their views on the issues being discussed the researcher will not be able to begin to allow for differences in understandings of words, concepts and worldviews across languages”. Aligning with this perspective, we would like to discuss some of the unexpected considerations regarding language and culture that emerged as we discussed the data with our co-researchers that worked with the untranslated data (F. M. H. and M. E.). In Swedish, the standard mathematical term for the gradient of a line in two-dimensional space is lutning, which is the noun form of the verb luta, “to lean”. Both words are of general, everyday usage, but are nevertheless used in Swedish to describe the characteristics of a line in the more specialized, mathematical context. Furthermore, this description of the derivative is dynamic in the way that it connotes action. For instance, from its grammatical construction, the word lutning is literally “leaning-ness” or the act of leaning. Also, a line can luta skarpt, “lean strongly”, as opposed to the more static description of a line having a steep gradient/slope, as is the norm in English. This suggests some level of cultural and colloquial familiarity or association for the students affording a nuanced understanding of the derivative and rate-related ideas, which may influence students’ graphical reasoning.

Limitations

Our method of data collection afforded us a relatively large sample of students’ responses that would be less feasible with other methods such as interviews. However, the fixed nature of written responses prevented us from gaining clarification or additional information from the students regarding their responses. Moreover, given the limited information provided by our sample, we cannot make any claims about a student's ability to engage in reasoning characterized as static or emergent; we can only discuss whether or not a particular type of reasoning was elicited with our prompt.

We also acknowledge the complex role of language in our study, which prompted us to analyze the untranslated data in addition to the translated data. First-year chemistry courses are taught around the globe and international collaborations require devising methods to handle translation of language and attentiveness to the general nature of language. Future work involves further investigating the relationship between our results and language by continuing to work through our data in its original language.

Conclusions

The role of covariation in graphical reasoning

In our work we discussed graphical forms as descriptions of intuitive mathematical ideas that serve as tools to draw conclusions from a graph. These graphical forms were further characterized based on the process–object distinction, which involved operationalizing Moore and Thompson's (2015) shape thinking framework and their conceptualization of emergent and static reasoning. Across our sample we observed students utilizing reasoning both types of reasoning in a single passage, and we suggest that if students are able to engage in emergent and static reasoning, both types of reasoning may inform one another. Furthermore, based on our analysis, we propose that demarcation between emergent and static reasoning is more fluid and may be better viewed as a spectrum within the shape thinking perspective. Sometimes it seemed as though reasoning characterized as static may have elements of covariation. For example, the graphical form trend from shape directionality was classified as static, since it focuses on the shape as a whole and the general trend of the graph. Although not as explicit as other instances involving emergent reasoning, covariation is implied to a lesser extent in the sense that it involves “coordinating the direction of change of one variable with changes in the other”, a mental action that Carlson et al. (2002) listed along with many behaviors they asserted exemplify covariational reasoning. The potentially flexible boundaries of shape thinking does not negate the utility inherent in emergent and static reasoning, it simply brings to the forefront the critical role of covariation in reasoning about graphs. The importance and relevance of engaging in both types of reasoning derives from their productive role as resources that have broad applicability in thinking about graphs in a various contexts.

Moreover, although both static and emergent conceptualizations can be productive in some situations, this does not mean they are equally productive in all situations. In particular, there are situations where a lack of emergent reasoning would be highly limiting in terms of understanding dynamic processes. This was exemplified in our dataset when students only viewed the graph as an object, focusing primarily on the representation as a static image that had associated properties (e.g., “titration curve”). If we were to consider the example of a student who can only see (or memorize) an exponential decay (concentration vs. time) curve as one entity representing “consumption” or “first order reaction”, then the entire graph is just one static object and the dynamic and continuous processes embedded in even such a simple graph are unavailable. From an instructional perspective, we need to help students think about the whole process, “walk along the curve”, and ask themselves what is happening and how it is changing.

Promoting engagement in discussing mathematical narratives

In order for students to interpret representations of dynamic processes they must be able to attend to features of the graph and make connections to relevant concepts (McDermott et al., 1987). In practice, this involves the integration of intuitive mathematical ideas and chemistry concepts to describe the phenomena being modeled (i.e., discussing mathematical narratives). We view engaging in mathematical narratives as a target for instruction. However, in order to ensure students are meeting this objective instructors have to be intentional about assessment, because assessment shapes how and what students study (Cooper, 2015; Bain et al., 2018). The prompt used in this study can be used to guide the development of assessments and assignments that scaffold students to engage in mathematical narratives using Cooper's (2015)what-then-why model. Supporting students in interpreting graphs involves first asking what questions that direct students to focus on specific features of the graph (the axes, distinct regions of the curve, etc.) and encourage students to make mathematical inferences about the slope or trends, and then ask why questions that require students to provide an explanation of the graph by connecting chemistry ideas to the mathematical inferences they previously made. In this way, instruction can more explicitly guide students toward using mathematical resources productively.

Additionally, we would like to emphasize the value in getting students to critique statements and reflect on the plausibility of responses, since this may help support students in making connections and reasoning mathematically (Becker et al., 2017). For example, following an exam (such as the one discussed herein), the instructor could provide some examples of students’ “less productive” reasoning and prompt the students to critique the responses and reason why they may or may not be chemically plausible. As we observed in our dataset, students frequently discussed ideas that are relevant to chemical kinetics, but in some cases it seemed as though students may simply be using the correct “vocabulary” associated with this context; a closer reading of their responses indicated an incomplete understanding of related concepts, suggesting the need for more support in how to use the resources they have more productively to better reflect an expert's understanding of phenomena.

Moreover, student engagement in discussing mathematical narratives is dependent on their ability to reason mathematically about graphs, which, as mentioned previously, is largely influenced by their ability to use covariational reasoning. In their work Carlson et al. (2002) provided a framework that described different behaviors that when exhibited afford the classification of a learner into different developmental stages (in a Piagetian sense) in terms of their ability to consider the different facets of covariation in the context of graphical reasoning. At the lower levels of the covariation progression is the ability to think more generally about the relationship between variables and the associated trends, and at the higher levels of the progression is the ability to apply calculus concepts such as instantaneous rate-of-change to reason about graphs. Considering the progressive levels of sophistication proposed by Carlson et al. (2002) regarding the ability to use different mathematical tools such as calculus to reason covariationally, our working definitions of static and emergent reasoning suggests that static reasoning may be more accessible to a larger group of students that are less proficient in mathematics; however, additional work is needed to better establish a relationship between static/emergent conceptualizations and mathematical proficiency. Although we reaffirm that more expert-like graphical reasoning encompasses both the process and the object perspective of viewing a graph, it is important to be cognizant of the mathematical resources available to students and to understand that students may not be able to move fluidly between both perspectives.

Language as a productive resource

Song and Carheden (2016) noted that dual-meaning vocabulary (words that have both an “everyday” and a scientific/technical definition) is often a barrier for student learning and a source of confusion because of the conflicting or unrelated meanings. For example, the colloquial use of the word base (bottom layer, foundation) differs to a large extent from the chemical definition (electron pair donor, compound that increases the pH of an aqueous solution). Within our dataset we briefly discussed the connection between the Swedish language and the notion of slope. In contrast to the examples discussed by Song and Carheden (2016) (and references therein), the everyday associations with the Swedish word lutning informs and constructively shapes the understanding of the technical, mathematical usage of the word. Framed in this way, language serves as a productive resource for students, but the extent in which we can leverage this type of knowledge to better support student learning requires further work (Warren et al., 2001; Gee, 2008).

Future work

Within the context of this study, future work involves diving deeper into the dataset in Swedish. We are interested in exploring the intricacies of language and its role in students’ graphical understanding. Based on our international collaboration we were able to develop a coding scheme that allowed for the characterization and analysis of student responses across languages; however, an additional layer of inductive coding that is specific to the untranslated data is necessary to provide a more rich description of the data, potentially providing insight into how we can use language to support students’ learning and connect technical language to culture (Markic and Childs, 2016).

The results presented herein illustrate the use of our approach toward investigating students’ understanding of a graphical representation of a dynamic process. The graphical forms framework afforded a way to characterize students’ reasoning and consider the extent in which the students engaged in covariational reasoning, providing insight regarding the mathematical resources utilized by students. We encourage the community to continue to add to the literature on graphical reasoning and investigate how we can promote students to provide deeper, mechanistic explanations of phenomena. Based on the extensive review of the literature done by the National Research Council, we assert studies that investigate graphical reasoning should be placed in contexts that have little representation, such as advanced topics in biochemistry or physical chemistry, which likely involve the use of distinct combinations of the resources described herein (Singer et al., 2012).

Our investigation of graphical reasoning involved synthesizing constructs and frameworks from educational research done in physics (graphical forms, mathematical narratives) and mathematics (covariation, process–object reasoning, shape thinking). We find tremendous value in moving outside the limits of our discipline and considering how other fields approach thinking about the many facets of education and learning. We advocate for work that moves not just beyond our disciplinary fields, but also crosses international boundaries to expand our collective knowledge.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We wish to thank Casey Wright, Jocelyn Nardo, and the Towns research group for their support and helpful comments on the manuscript. F. M. H. and M. E. would like to acknowledge the financial support of the Centre for Discipline-based Education Research in Mathematics, Engineering, Science and Technology, Uppsala University.

References

1. Aydin Y., (2014), The effects of problem based approach on student's conceptual understanding in a university mathematics classroom, Procd. Soc. Behv., 152, 704–707.
2. Bain K. and Towns M. H., (2016), A review of research on the teaching and learning of chemical kinetics, Chem. Educ. Res. Pract., 17(2), 246–262.
3. Bain K., Rodriguez J. G., Moon A. and Towns M. H., (2018), The characterization of cognitive processes involved in chemical kinetics using a blended processing framework, Chem. Educ. Res. Pract., 19, 617–628.
4. Becker N. and Towns M. H., (2012), Students’ understanding of mathematical expressions in physical chemistry contexts: an analysis using Sherin's symbolic forms, Chem. Educ. Res. Pract., 13(3), 209–220.
5. Becker N. M., Rupp C. A. and Brandriet A., (2017), Engaging students in analyzing and interpreting data to construct mathematical models: an analysis of students’ reasoning in a method of initial rates task, Chem. Educ. Res. Pract., 18(4), 798–810.
6. Bruce C., (2013), Beyond the syllabus: using the first day of class in physical chemistry as an introduction to the development of macroscopic, molecular-level, and mathematical models, J. Chem. Educ., 90(9), 1180–1185.
7. Cakmakci G., (2010), Identifying alternative conceptions of chemical kinetics among secondary school and undergraduate students in Turkey, J. Chem. Educ., 87(4), 449–455.
8. Cakmakci G. and Aydogdu C., (2011), Designing and evaluating an evidence-informed instruction in chemical kinetics, Chem. Educ. Res. Pract., 12(1), 15–28.
9. Cakmakci G., Leach J. and Donnelly J., (2006), Students’ ideas about reaction rate and its relationship with concentration or pressure, Int. J. Sci. Educ., 28(15), 1795–1815.
10. Campbell J. L., Quincy C., Osserman J. and Pedersen O. K., (2013), Coding In-depth Semistructured Interviews: Problems of Unitization and Intercoder Reliability and Agreement, Sociol. Methods Res., 42(3), 294–320.
11. Carlson M., Jacobs S., Coe E., Larsen S. and Hsu E., (2002), Applying covariational reasoning while modeling dynamic events: a framework and a study, J. Res. Math. Educ., 33(5), 252–378.
12. Castillo-Garsaw C., Johnson H. and Moore K., (2013), Chunky and smooth images of change, For the Learning of Mathematics, 33(3), 31–37.
13. Confrey J. and Smith E., (1995), Splitting, covariation, and their role in the development of exponential functions, J. Res. Math. Educ., 26(1), 66–86.
14. Cooper M., (2015), Why ask why? J. Chem. Educ., 92(8), 1273–1279.
15. Cooper M. M., Caballero M. D., Ebert-May D., Fata-Hartley C. L., Jardeleza S. E., Krajcik S., et al., (2015), Challenge faculty to transform STEM learning, Science, 350(6258), 281–282.
16. Dorko A. and Speer N., (2015), Calculus students’ understanding of area and volume units, Invest. Math. Learn., 8(1), 23–46.
17. Edwards A. and Head M., (2016), Introducing a culture of modeling to enhance conceptual understanding in high school chemistry courses, J. Chem. Educ., 93(8), 1377–1382.
18. Ellis A., Ozgur Z., Kulow T., Dogan M. and Amidon J., (2016), An exponential growth learning trajectory: students’ emerging understanding of exponential growth through covariation, Math. Think. Learn., 18(3), 151–181.
19. Even, R., (1990), Subject matter knowledge for teaching and the case of functions, Educ. Stud. Math., 21, 551–544.
20. Gee J., (2008), What is academic language? in Rosebery A. S. and Warren B., (ed.), Teaching science to English Language Learners: Building on Students’ Strengths, Arlington, VA: National Science Teachers Association Press, pp. 57–69.
21. Gegios T., Salta K. and Koinis S., (2017), Investigating high-school chemical kinetics: the Greek chemistry textbook and students’ difficulties, Chem. Educ. Res. Pract., 18(1), 151–168.
22. Greenbowe T. J. and Meltzer D. E., (2003), Student learning of thermochemical concepts in the context of solution calorimetry, Int. J. Sci. Educ., 25(7), 779–800.
23. Habre S., (2012), Students’ challenges with polar functions: covariational reasoning and plotting in the polar coordinate system, Int. J. Math. Educ. Sci. Technol., 48(1), 48–66.
24. Hadfield L. C. and Wieman C. E., (2010), Student interpretations of equations related to the first law of thermodynamics, J. Chem. Educ., 87(7), 750–755.
25. Hammer D. and Elby A., (2002), On the form of a personal epistemology, in Hofer B. K. and Pintrich P. R. (ed.), Personal Epistemology: The Psychology of Beliefs about Knowledge and Knowing, Mahwah, NJ: Erlbaum, pp. 169–190.
26. Hammer D. and Elby A., (2003), Tapping epistemological resources for learning physics, J. Learn. Sci., 12(1), 53–90.
27. Hammer D., Elby A., Scherr R. E. and Redish E. F., (2005), Resources, framing, and transfer, in Mestre J. P. (ed.), Transfer of learning from a modern multidisciplinary perspective, Greenwich, CT: Information Age Publishing.
28. Holme T., Luxford C., and Brandriet A., (2015), Defining conceptual understanding in general chemistry, J. Chem. Educ., 92(9), 1477–1483.
29. Hu D. and Rebello N. S., (2013), Understanding student use of differentials in physics integration problems, Phys. Rev. Spec. Top.-Ph., 9(20108), 1–14.
30. Hull M. M., Kuo E., Gupta A. and Elby A., (2013), Problem-solving rubrics revisited: attending to the blending of informal conceptual and formal mathematical reasoning, Phys. Rev. Spec. Top.-Ph., 9(10105), 1–16.
31. Ivanjeck L., Susac A., Planinic M., Andrasevic A. and Milin-Sipus Z., (2016), Student reasoning about graphs in different contexts, Phys. Rev. Phys. Educ. Res., 12(1), 010106.
32. Izak A., (2004), Students’ coordination of knowledge when learning to model physical situations, Cognit. Instruct., 22(1), 81–128.
33. Jasien P. and Oberem G., (2002), Understanding of elementary concepts in heat and temperature among college students and K-12 teachers, J. Chem. Educ., 79(7), 889–895.
34. Jones S., (2013), Understanding the integral: students’ symbolic forms, J. Math. Behav., 32(2), 122–141.
35. Jones S., (2015a), The prevalence of area-under-a-curve and anti-derivative conceptions over Riemann sum-based conceptions in students’ explanations of definite integrals, Int. J. Math. Educ. Sci. Tech., 46(5), 721–736.
36. Jones S., (2015b), Areas, anti-derivatives, and adding up pieces: definite integrals in pure mathematics and applied science contexts, J. Math. Behav., 38, 9–28.
37. Justi R., (2002), Teaching and learning chemical kinetics, in Gilbert J. K., De Jong O., Justi R. Treagust D. and Van Driel J. H. (ed.), Chemical Education: Towards Research-based Practice, Dordrecht: Kluwer, pp. 293–315.
38. Kolomuc A. and Tekin S., (2011), Chemistry teachers’ misconceptions concerning concept of chemical reaction rate, Eurasian J. Phys. Chem. Educ., 3, 84–101.
39. Kozma R. B. and Russell J., (1997), Multimedia and understanding: expert and novice responses to different representations of chemical phenomena, J. Res. Sci. Teach., 34, 949–968.
40. Laverty J. T., Underwood S. M., Matz R. L., Posey L. A., Jardeleza E. and Cooper M. M., (2016), Characterizing College Science Assessments: The Three-Dimensional Learning Assessment Protocol, PLoS One, 11(9), 1–21.
41. Markic S. and Childs P. E., (2016), Language and the teaching and learning of chemistry, Chem. Educ. Res. Pract., 17(3), 434–438.
42. McDermott L., Rosenquist M., and van Zee E., (1987), Investigation of student understanding of the concept of acceleration in one dimension, Am. J. Phys., 55, 503–513.
43. Moore K. C., (2014), Signals, symbols, and representational activity, in Steffe L., Moore K., Hattfield L. and Belbase S. (ed.), Epistemic Algebraic Students: Emerging Models of Students' Algebraic Knowing, Laramie, WY: University of Wyoming, pp. 211–235.
44. Moore K. C. and Thompson P. W., (2015), Shape thinking and students’ graphing activity, in Fukawa-Connelly T., Infante N., Keene K. and Zandieh M. (ed.), Proceedings of the 18th Annual Conference on Research in Undergraduate Mathematics Education, Pittsburgh, PA, pp. 782–789.
45. Moore K. C., Paoletti T. and Musgrave, S., (2013), Covariational reasoning and invariance among coordinate systems, Journal of Mathematical Behavior, 32(3), 461–473.
46. Moschkovich J., Schoenfeld A. H., and Arcavi A., (1993), Aspects of understanding: on multiple perspectives and representations of linear relations and connections among them, in Romberg T.A., Fenemma E. and Carpenter T.P. (ed.), Integrating Research on the Graphical Representation of Functions, New York: Erlbaum, pp. 69–100.
47. National Research Council, (2012), A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas, Washington, DC: National Academies Press.
48. Nemirovsky R., (1996), Mathematical narratives, modeling, and algebra, in Bednarz N., Kiernan C. and Lee L. (ed.), Approaches to Algebra: Perspectives for Research and Teaching, Dordecht, The Netherlands: Kluwer Academic Publishers, pp. 197–223.
49. Phage I. B., Lemmer M. and Hitage M., (2017), Probing Factors Influencing Students’ Graph Comprehension Regarding Four Operations in Kinematics Graphs, Afr. J. Res. Math., Sci., Technol. Educ., 21(2), 200–210.
50. Planinic M., Ivanjeck L., Susac A. and Millin-Sipus Z., (2013), Comparison of university students’ understanding of graphs in different contexts, Phys. Rev. Spec. Top.-Ph., 9, 020103.
51. Posthuma-Adams E., (2014), How the chemistry modeling curriculum engages students in seven science practices outlines by the college board, J. Chem. Educ., 91(9), 1284–1290.
52. Potgieter M., Harding A. and Engelbrecht J., (2007), Transfer of algebraic and graphical thinking between mathematics and chemistry, J. Res. Sci. Teach., 45(2), 297–218.
53. Quisenberry K. and Tellinghuisen J., (2006), Textbook deficiencies: ambiguities in chemical kinetics rates and rate constants, J. Chem. Educ., 83(3), 510–512.
54. Rasmussen C., Marrongelle K. and Borba M. C., (2014), Research on calculus: what do we know and where do we need to go? ZDM Math. Educ., 46, 507–515.
55. Richards A. J., Jones D. C. and Etkina E., (2018), How Students Combine Resources to Make Conceptual Breakthroughs, Res. Sci. Educ., 1–23,  DOI:10.1007/s11165-018-9725-8.
56. Rodriguez J. G., Bain K. and Towns M. H., (2018), Graphical forms: the adaption of Sherin's symbolic forms for the analysis of graphical reasoning across disciplines, manuscript in preparation.
57. Saldanha L. and Thompson P., (1998), Re-thinking covariation from a quantitative perspective: simultaneous continuous variation, Proceedings of the Annual Meeting of the Psychology of Mathematics Education – North America, Raleigh, NC: North Carolina University, pp. 298–304.
58. Schwartz J. and Yerushalmy M., (1992), Getting students to function in and with algebra, in Harel G. and Dubinsky E. (ed.), The Concept of Function: Aspects of Epistemology and Pedagogy (MAA Notes, Vol. 25, pp. 261–289), Washington, DC: Mathematical Association of America.
59. Secken N. and Seyhan H., (2015), An analysis of high school students’ academic achievement and anxiety over graphical chemistry problems about the rate of a reaction: the case of the Sivas Province, Procd. Soc. Behv., 174, 347–354.
60. Seethaler S., Czworkowski J. and Wynn L., (2018), Analyzing general chemistry texts’ treatment of rates of change concepts in reaction kinetics reveals missing conceptual links, J. Chem. Educ., 95(1), 28–36.
61. Sfard A., (1992), Operational Origins of mathematical objects and the quandary of reification – the case function, in Harel G. and Dubinsky E. (ed.), The Concept of Function: Aspects of Epistemology and Pedagogy (MAA Notes, Vol. 25, pp. 59–84), Washington, DC: Mathematical Association of America.
62. Sherin B. L., (2001), How students understand physics equations, Cognit. Instruct., 19, 479–541.
63. Singer S. R., Nielson N. R. and Schweingruber H. A., (2012), Discipline-Based Education Research: Understanding and Improving Learning in Undergraduate Science and Engineering, Washington, DC: National Academies Press.
64. Sjostrom J. and Talanquer V., (2014), Humanizing Chemistry Education: From Simple Contextualization to Multifaceted Problematization, J. Chem. Educ., 91(8), 1125–1131.
65. Song Y. and Carheden S., (2016), Dual meaning vocabulary (DMV) words in learning chemistry, Chem. Educ. Res. Pract., 15(2), 128–141.
66. Strauss A. and Corbin J., (1990), Basics of Qualitative Research: Grounded Theory Procedures and Techniques, Newbury Park, CA: SAGE Publications, Ltd.
67. Taber K. S., (2013), Revisiting the chemistry triplet: drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education, Chem. Educ. Res. Pract., 14, 156–168.
68. Talanquer V., (2011), Macro, Submicro, and Symbolic: the many faces of the chemistry “ triplet”, Int. J. Sci. Educ., 33(2), 179–195.
69. Tastan O., Yalcinkay E. and Boz Y., (2010), Pre-service chemistry teachers' ideas about reaction mechanism, J. Turk. Sci. Educ., 7, 47–60.
70. Thompson P., (1994), Images of rate and operational understanding of the fundamental theorem of calculus, Educ. Stud. Math., 26, 229–274.
71. Thompson P. W. and Carlson M. P., (2017), Variation, Covariation, and Functions: Foundational Ways of Thinking Mathematically, in Cai J. (ed.), Compendium for Research in Mathematics Education, Reston, VA: National Council of Teachers of Mathematics, pp. 421–456.
72. Toulmin S., (1958), The Uses of Argument, Cambridge, MA: Cambridge University Press.
73. Von Korff J. and Rubello N. S., (2014), Distinguishing between “change” and “amount” infinitesimals in first-semester calculus-based physics, Am. J. Phys., 82, 695–705.
74. Warren B., Ballenger C., Ogonowski M. and Rosebery A. S., (2001), Rethinking diversity in learning science: the logic of everyday sense-making, J. Res. Sci. Teach., 38(5), 529–552.
75. White P. and Mitchelmore M., (1996), Conceptual knowledge in introductory calculus, J. Res. Math. Educ., 27, 79–95.
76. Young B. and Temple A., (2004), Qualitative research and translation dilemmas, Qual. Res., 4(2), 161–178.

---