Open Access Article
Open Access ArticleA two-step modelling approach for plasma reactors – experimental validation for CO2 dissociation in surface wave microwave plasma
Sergio H.
Moreno
a,
Andrzej I.
Stankiewicz
a and
Georgios D.
Stefanidis
 *b
*b
aIntensified Reaction & Separation Systems, Process & Energy Laboratory, Delft University of Technology, Leeghwaterstraat 39, 2628 CB, Delft, The Netherlands
bChemical Engineering Department, Katholieke Universiteit Leuven, Celestijnenlaan 200f, 3001 Leuven (Heverlee), Belgium. E-mail: georgios.stefanidis@kuleuven.be
First published on 24th April 2019
Abstract
Plasma reactors have the potential to enable CO2 utilization technologies and so there is need to investigate their performance from a chemical or process engineering perspective. Multiphysics models are excellent tools to carry out this analysis; however, practical engineering models of plasma reactors are limited. Herein a two-step modelling approach for plasma reactors is presented. In the first step, a 2D plasma reactor model with a simple chemistry is used to characterize the discharge. The result of this step is used in the second step to develop a global (volume averaged) model of the reactor with the actual chemistry. The approach is applied in the case of CO2 dissociation in a non-thermal surface wave microwave plasma reactor. Preliminary calculations reveal the need to include the vibrationally enhanced dissociation of CO2 in the chemistry of the model. Reduced vibrational kinetics are employed for this purpose by introducing the fictitious species  . The model predictions are compared to experimental results to validate the model and obtain insight into the performance of the reactor. In comparison to the experimental results the conversions obtained with the model are underestimated between 11% and 25%. The dominant dissociation paths in the plasma reactor are also identified. Further calculations are performed to show the importance of an approximate description of the power deposition. Limitations of the approach are discussed as well, especially those with major contribution to the discrepancies between experimental and modelling results.
. The model predictions are compared to experimental results to validate the model and obtain insight into the performance of the reactor. In comparison to the experimental results the conversions obtained with the model are underestimated between 11% and 25%. The dominant dissociation paths in the plasma reactor are also identified. Further calculations are performed to show the importance of an approximate description of the power deposition. Limitations of the approach are discussed as well, especially those with major contribution to the discrepancies between experimental and modelling results.
1. Introduction
The utilization of CO2 emerges as a promising approach in the blend of solutions to cope with two major challenges confronted by human society nowadays, global warming and low-carbon circular economy. Among the CO2 utilization alternatives, the concept of solar fuels stands out, as the surplus in green electricity is used to produce synthetic fuels from CO2. Thus, the limitations of renewable sources with respect to their unsteady nature are removed by storing the surplus of green electricity as a fuel that can be used in high demand periods.Microwave plasma has the potential to enable this technology due to its particular characteristics that allow for efficient splitting of the CO2 molecule, reaching energy efficiencies up to 90%.1 The mechanism behind the efficient dissociation of CO2 is the vibrationally enhanced dissociation, in which the vibrational energy of highly excited states in the asymmetric vibrational mode can decrease the activation energy of the dissociation reaction. That way, the endothermic reaction is carried out efficiently, breaking the very stable CO2 molecule. The importance of vibrational excitation for achieving an efficient dissociation in diatomic and triatomic molecules has already been known for decades.2,3 In a nutshell, under adequate conditions, the low-lying asymmetric vibrational states get excited by electron collisions and they transfer their energy to higher vibrational states thus creating an overpopulation of highly energetic states that can easily dissociate. This is claimed to be the most efficient dissociation mechanism; a detailed description can be found elsewhere.1,4
After some years in the shadows, the CO2 dissociation by means of non-thermal plasma has recently been brought back to the spotlight, mainly due to the crucial need to find solutions to the aforementioned challenges.5 From the modelling point of view, research groups in Antwerp, Bari and Lisbon have been working on the fundamental understanding of the physical and chemical processes taking place in the plasma. For this purpose, the Boltzmann equation for the electrons is solved together with detailed kinetic models that involve specific interactions between distinct energy states of the molecules.6–11 From the experimental point of view, various techniques have recently been used to gain new insights into the effect of different plasma configurations, operating conditions and gas compositions on the behaviour of CO2-containing plasmas.12–21 Despite these efforts, not all processes taking place inside the plasma, or involved in the dissociation, are fully understood and crucial data required for modelling, such as cross sections or rate constants, are not available.
Given the potential of the technology, it is beneficial to investigate its performance from a chemical or process engineering point of view. Thus, there is need for practical engineering plasma models that consider dimensionality and transport, and ultimately allow for integration of a plasma reactor to a process system. In this document, we describe a two-step modelling approach for plasma reactors, applied to the specific case of CO2 dissociation in a non-thermal surface wave microwave plasma reactor. The work is continuation of our previous published research on the matter.12,13,22 In the first step, the two-dimensional axisymmetric Argon plasma model, developed in ref. 13, is used to characterize the discharge by identifying the power losses, the deposited power density patterns and the time and length scales as well as by performing a qualitative analysis of the plasma and process variables. These results are then used in the second step to develop the model of the CO2 plasma reactor. During the process, the need to include the vibrationally enhanced dissociation in the chemistry of the model is identified. For this purpose, the methodology for the reduction of vibrational kinetics in non-equilibrium microwave plasma presented in ref. 22 is used. The final model predictions are compared to our previously published experimental results12 to validate the model and get insight into the performance of our lab-scale reactor. The reader is referred to ref. 12, 13 and 22 for further details on the reduction methodology, the experimental setup and the Argon model.
2. First step: power deposition and discharge characterization
The energy required for the CO2 dissociation comes from the microwave power, which is transferred to the electrons and from these to other species. It reaches the highest values inside the surface wave launcher (Surfatron), where most of the microwave power is deposited, and decreases downstream. An estimate of the power deposition per unit volume (deposited power density) can be obtained from our previously developed two-dimensional model of an Argon plasma.13The physics of this self-consistent model involve variables whose times and lengths scales differ widely in magnitude, making the non-linear system of equations numerically challenging to solve. Simple chemistries, such as Argon, are preferred in this first step as they allow for characterization of the discharge without adding much more complexity to the system of equations. The opposite is true for complex chemistries, such as CO2 dissociation, for which vibrationally excited states must be included in the non-thermal plasma model. The kinetics of vibrationally excited states lead to very high gradients and rates during the solution of the system of equations as well as numerical instabilities early in the simulation that impede the solution of equations.
The Argon model was slightly modified to account for the heat removal from the reactor. In our experimental setup the cooling system consisted of cooling water at 5 °C flowing inside the Surfatron and compressed air at 20 °C blowing inside the cavity (between the Surfatron and the quartz tube). A detailed modelling of the cooling system is outside the scope of the present work. Thus, for the sake of simplicity the inner wall temperature of the quartz tube was fixed to a specific value.
Simulations at the experimental conditions of the pure CO2 dissociation reported in ref. 12 were performed in the Argon model to investigate the power deposition in the reactor. In the experiments, the microwave power input was 150 W, the pressure 20 mbar, the inlet temperature 300 K and the inlet flowrate 100, 200 and 300 sccm. The simulations were carried out in a time dependent solver until 0.02 s, which is sufficient time for the process to reach steady state. The results of the simulation for an inlet flowrate of 300 sccm and a tube inner wall temperature of 300 K are shown in Fig. 1–3. Qualitatively similar results were obtained for the other flowrates. The analysis of the results is only performed in the axial direction due to its relevance with the second step of the approach.
 | ||
Fig. 1 Electron density (top), electron temperature (middle) and gas temperature (bottom) profiles at steady state (0.006 s). These profiles were obtained using the Argon model13 for a flowrate of 300 sccm, inlet temperature of 300 K, inner wall temperature of 300 K, outlet pressure of 20 mbar and a microwave power input of 150 W. (1 eV ≈ 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 K). 600 K). | ||
 | ||
| Fig. 2 Velocity (top) and pressure (bottom) profiles at steady state (0.016 s). Argon model at the same conditions given in Fig. 1. | ||
 | ||
| Fig. 3 Deposited power density profile at steady state (0.006 s). Argon model at the same conditions given in Fig. 1. The power density peak seen at 116 mm is related to the intense electric field formed at this point due to the Surfatron design (see small protrusion at the bottom of Fig. 4). | ||
Fig. 1 shows the steady state average values of the electron density, electron temperature and gas temperature as a function of z (axial coordinate). These profiles are obtained by integrating the variables in the radial and angular directions and dividing the result over the cross section of the quartz tube. The steady state for these variables is obtained at ∼0.006 s, given their direct relation with the electron kinetics, which are characterized by very short timescales. The steady state for the average velocity and the pressure is reached later, at 0.016 s (profiles shown in Fig. 2).
The steady state of the average deposited power density is shown in Fig. 3. This profile remains constant after 0.006 s, when the plasma variables have also reached their steady states. However, the portion of the profile corresponding to the Surfatron body (between 38 and 118 mm) stabilizes earlier in the simulation, at ∼0.001 s. In this zone, the plasma is ignited and most of the power is deposited.
In a surface wave discharge, the generated plasma serves as a propagating medium for the surfaces waves that are created and shaped inside the surface wave launcher. These electromagnetic waves travel axially in both directions inside the plasma while feeding it with their power.23 This can be easily seen in Fig. 3, where the power density decreases as the electromagnetic waves travel through the plasma and completely vanishes when the plasma does as well (see Fig. 1). The power density oscillations, also observed in Fig. 3, are related to the variations in the magnitude of the surface wave electric field and, particularly, its axial component. Inside the plasma the axial component of the electric field dominates over the radial component, thus having a larger contribution to the power deposition. Outside of the plasma, the radial component dominates.24 It can also be seen that all variables exhibit fluctuations driven by the power deposition fluctuations inside the Surfatron body.
Electrons are the driving force in a plasma, they take energy form the microwaves before transferring it to the heavy species. The behaviour of the variables in Fig. 1 and 2 can be explained in simple terms from the variations seen in Fig. 3. The microwave power energizes the electrons, increasing their mean energy, which is proportional to the electron temperature. High ionization rates are obtained at high electron temperatures and therefore high electron densities are located at zones of high deposited power densities. Conversely, more power can be deposited in zones of high electron densities. The electrons subsequently transfer their energy to the Argon species via elastic and inelastic collisions, which ultimately leads to a local increase of the gas temperature where high electron densities are located. Similarly, the velocity increases at zones of high temperatures due to the local expansion of the gas. For this ideal gas, the variation between the temperature and the velocity is roughly linear given the very low pressure drop. At higher local velocities the pressure drop increases, but for the entire reactor it remains low and almost linear with the tube length, as expected for this laminar flow.
The total power deposited in the plasma is 121.8 W, which corresponds to the area below the curve of Fig. 3 multiplied by the quartz tube cross section. This value is smaller than the 150 W of microwave power input to the Surfatron due to the leakage of microwaves. Fig. 4 shows the time average power flow in the positive radial and z directions at the edge of the Surfatron body, where most of the microwave leak takes place. The addition of a waveguide at the Surfatron outlet has proven to be successful in limiting these power losses, thereby increasing the overall performance of the reactor for the case of CO2 reduction with hydrogen.13
 | ||
| Fig. 4 Time average power flow (0 to 0.02 s) in the positive radial direction (left) and positive z direction (right). Argon model at the same conditions given in Fig. 1. | ||
Another important quantity is the 89.4 W of power that is deposited inside the Surfatron body, within a length of approximately 8 cm. This gives an average power density of 8.9 × 107 W m−3, which is enough to ignite and sustain the plasma. The remaining 32.4 W are deposited at considerably lower power densities, with an average power density of 9.5 × 106 W m−3 over 27 cm of plasma (approximately 35 cm of total Argon plasma length according to Fig. 1).
Fig. 5 shows the evolution of the power deposition in time, distinguishing the total deposited power from the power deposited inside the Surfatron body. These two quantities reach their steady state values at approximately the same time as the plasma variables do (0.006 s) and their difference is established at the early stages of the discharge.
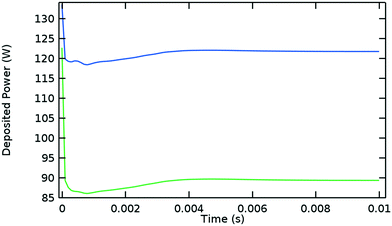 | ||
| Fig. 5 Deposited microwave power over time. Blue: Total deposited power, green: deposited power inside the Surfatron body (at high power densities). Argon model at the same conditions given in Fig. 1. | ||
Additional simulations were performed for the lowest experimental inlet flowrate and a higher wall temperature (results summarized in Table 1). It is concluded that in our setup for an Argon plasma at the conditions of the CO2 dissociation experiments, approximately 80% of the power input is deposited into the plasma and 20% in lost to the surroundings. Moreover, 60% of the power input is deposited effectively at high power densities, while 20% is gradually deposited at low power densities. The latest plays a role in sustaining the plasma, although its effectiveness in this regard is considerably inferior for a molecular plasma, due to the internal degrees of freedom of the molecules (mainly vibration at low electron temperatures). Molecular plasmas are highly collisional in comparison to atomic plasmas; consequently the electron temperature is lower and decays faster in space and time. Therefore, in the so-called afterglow, the small amount of energy gained by the electrons at low power densities is predominantly transferred to vibrational states (of CO2, CO and O2 molecules in a CO2 plasma) and ultimately to heat, further increasing the temperature and the relaxation rates.
| Flowrate (sccm) | T w (K) | Total Pdep (W) | Deposition eff. (%) | P dep,SB (W) | SB-deposition eff. (%) |
|---|---|---|---|---|---|
| 100 | 300 | 123.1 | 82% | 91.1 | 61% |
| 100 | 600 | 126.0 | 84% | 92.7 | 62% |
| 300 | 300 | 121.8 | 81% | 89.4 | 60% |
| 300 | 600 | 125.9 | 84% | 92.6 | 62% |
The quartz tube temperature has a minor effect on the power deposition according to the results shown in Table 1. The real temperature of the inner wall is clearly not uniform along the reactor, but measurements indicated that it ranged from 50 to 90 °C downstream of the Surfatron.12 A rough estimation of the surface plasma/inner reactor wall temperature was also done by means of thermal imaging, showing temperatures as high at 600 K at the Surfatron outlet.13 The variation of the deposited power is shown to be small within the range of these temperatures.
To illustrate the approach, a profile similar to that of Fig. 3 is used as input to the global model for CO2 dissociation. Using a profile based on the results of the Argon model is more descriptive than a power input value as it gives information on where and how the power is deposited into the plasma. This information is necessary for the modelling of the reactor, given its direct relation with the plasma variables. Furthermore, it is also closer to reality than assuming, for instance, a uniform power deposition in the plasma.
The simplified deposited power density profile used in the CO2 model is designed to be easier to construct and adjust to the CO2 plasma, while retaining the main characteristics of the profile shown in Fig. 3 that is, a high and oscillating power density inside the Surfatron body and a lower and approximately linearly decaying power density outside of it. The deposited power density profile, Pd,den (z), can be computed using the following equation, in which ri is the inner radius, Lp is the length of the plasma and Pdep is the total deposited power computed from the power input and the deposition efficiency.
 | (1) |
3. Second step: global model in a Lagrangian approach
In a so-called global model the variables are averaged over the reactor volume, removing the spatial dependence in the equations. Thus, the equations to solve are simplified to the much simpler rate equations, such as the following equation for the conservation of species: | (2) |
The electron temperature is computed by the following equations
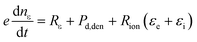 | (3) |
 | (4) |
![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) the mean electron energy and ne the electron density, which is computed from the electroneutrality assumption.
the mean electron energy and ne the electron density, which is computed from the electroneutrality assumption.
These time-dependent equations can be used in a Lagrangian description to obtain a one-dimensional model of the plasma reactor. In this approach, it is assumed that the reactor behaves as a plug flow reactor and a perfectly mixed volume element is tracked in the time domain as it flows throughout the reactor. There is no flow entering or leaving the volume element. The microwave power is deposited in the volume element depending on its position according to the profile computed from eqn (1). The velocity of the element is computed from the flowrate and process conditions, and it is integrated to find its position. This also allows to transform the results of the global model from the time domain into the space domain, i.e. the axial coordinate. In section 4 all results are conveniently given in the space domain, as functions of z and not time. Fig. 6 illustrates the approach.
 | ||
| Fig. 6 Approach for modelling CO2 dissociation in a microwave plasma reactor. Top: Experimental setup used in ref. 12, middle: two-dimensional axisymmetric sketch of the reactor,13 bottom: approach used in this work. | ||
Radial and angular variations of the variables inside the reactor are neglected by using this approach. The volume element is axisymmetric, with a radius equal to the inner radius of the quartz tube used in the experimental setup, 2 mm. The length of the quartz tube is approximately 40 cm from the starting point of the surface wave launcher to the sampling point for the mass spectroscopy analysis used for the quantification of the gas composition. Tubing of 3 mm inner radius and 2.5 m length connects the sampling point to the mass spectrometer.
This simple model can predict the plasma and process variables within reasonable agreement while using much less computational resources than a two-dimensional model. The COMSOL Multiphysics' Plasma Module was used for the implementation of the global model. A detailed explanation of the equations solved in this module can be found elsewhere,25 herein only brief explanations are provided when needed. The following subsections describe the most relevant aspects of the global model.
3.1. Species
The species included in the CO2 model are listed in Table 2. These consist of neutral, excited and charged species. CO2 and the products of its dissociation comprise the neutral species. Excited states refer to the internal degrees of freedom of CO2 used in the calculation of the electron temperature and the fictitious species ,22 which groups all levels in the asymmetric vibrational mode of the CO2 molecule. As mentioned before, highly excited states in this vibrational mode are involved in the vibrationally enhanced dissociation of CO2.
,22 which groups all levels in the asymmetric vibrational mode of the CO2 molecule. As mentioned before, highly excited states in this vibrational mode are involved in the vibrationally enhanced dissociation of CO2.
Vibrational and electronically excited states are only included for CO2, considering that it is the initial and dominant species in the discharge and therefore it has the highest influence in the electron kinetics. Table 3 lists the excited states along with their energy levels and statistical weights. The vibrational state of a CO2 molecule is given by three quantum numbers (i j k) describing the vibrational levels in the symmetric stretching, symmetric bending and asymmetric stretching modes, respectively. The symmetric bending levels are degenerate as the bending can take place in orthogonal planes, having, for a vibrational level j a degeneracy of j + 1. In addition, the symmetric levels ((i + 1) j k) and (i (j + 2) k) are coupled due to the proximity of their energy levels, implying that they coexist and therefore are usually grouped into a single species. The statistical weights given in Table 3 refer to the total degeneracy of the species. In the case of CO2v8, the statistical weight was computed considering the coupled symmetric levels with a maximum energy slightly lower than the energy threshold of the excitation cross section. The electronically excited species are assumed to be non-degenerate. Lastly, two charged species besides electrons are considered, the positive ion CO2+ and the negative ion O−. The production/consumption of these two species is coupled to the electron density due to the electroneutrality assumption. Lower electron densities are obtained at a higher production of O− and the opposite is true for CO2+.
| Species | Vibrational states | Threshold (eV) | Statistical weight |
|---|---|---|---|
| CO2v1 | (0 1 0) | 0.083 | 2 |
| CO2v2a | (0 2 0) | 0.167 | 3 |
| CO2v2b | (1 0 0) | 0.167 | 1 |
| CO2v3 | (0 3 0) + (1 1 0) | 0.252 | 6 |
| CO2v4 | (0 0 1) | 0.291 | 1 |
| CO2v5a | (2 0 0) | 0.339 | 1 |
| CO2v5b | (0 4 0) + (1 2 0) + (0 1 1) | 0.339 | 10 |
| CO2v6 | (0 5 0) + (2 1 0) + (1 3 0) + (0 2 1) + (1 0 1) | 0.422 | 12 |
| CO2v7a | (3 0 0) | 0.505 | 1 |
| CO2v7b | (0 6 0) + (2 2 0) + (1 4 0) | 0.505 | 15 |
| CO2v8 | (0 n 0) + (n 0 0) | 2.500 | 256 |
| CO2e1 | — | 7.0 | 1 |
| CO2e2 | — | 10.5 | 1 |
3.2. Reactions
The set of reactions is based on our previous work and has been updated according to the species, which now include a negative ion and more excited states. The reactions are mainly elementary two-body reactions and few three-body reactions. They are further divided into electron impact reactions, vibrational energy transfer reactions, reactions between neutral species, reactions involving charged species and surface reactions. Tables 4–8 show these reactions.| No | Process | Reaction | Ref | Note |
|---|---|---|---|---|
| Notesa Computed from the cross section set of the reference.b The total cross section referred as the sum of partial cross sections is used here.c Rate constant given by 2.0 × 10−11Te−0.5Tg−1 (m3 s−1).d http://www.lxcat.net, retrieved on November 1, 2017.e Assuming a direct dissociation into ground state oxygen atoms (3P) from electronic states A3Σu+, A3Δu and c1Σu− with threshold energy of 6 (eV).f Assuming a direct dissociation into ground state oxygen atoms from the electronic state B3Σu− with threshold energy of 8.4 (eV).g http://www.lxcat.net, retrieved on August 9, 2018.h Rate constant given by 10−43 (m6 s−1). M = CO2, CO, O2 or O. | ||||
| RX1 | Elastic scattering | e + CO2 → e + CO2 | 10 | |
| RX2 | Dissociative attachment | e + CO2 → CO + O− | 10 | |
| RX3a | Vibrational excitation | e + CO2 → e + CO2v1 | 10 | |
| RX3b | Superelastic deexcitation | e + CO2v1 → e + CO2 | 10 | |
| RX4a | Vibrational excitation | e + CO2 → e + CO2v2a | 10 | |
| RX4b | Vibrational excitation | e + CO2 → e + CO2v2b | 10 | |
| RX5 | Vibrational excitation | e + CO2 → e + CO2v3 | 10 | |
| RX6 | Vibrational excitation | e + CO2 → e + CO2v4 | 10 | |
| RX7a | Vibrational excitation | e + CO2 → e + CO2v5a | 10 | |
| RX7b | Vibrational excitation | e + CO2 → e + CO2v5b | 10 | |
| RX8 | Vibrational excitation | e + CO2 → e + CO2v6 | 10 | |
| RX9a | Vibrational excitation | e + CO2 → e + CO2v7a | 10 | |
| RX9b | Vibrational excitation | e + CO2 → e + CO2v7b | 10 | |
| RX10 | Vibrational excitation | e + CO2 → e + CO2v8 | 10 | |
| RX11 | Electronic excitation | e + CO2 → e + CO2e1 | 10 | |
| RX12 | Electronic excitation | e + CO2 → e + CO2e2 | 10 | |
| RX13 | Total ionization | e + CO2 → 2e + CO2+ | 10 | |
| RX14a | Vibrational excitation | e + CO2 → e +  |
22 | |
| RX14b | Superelastic deexcitation | e +  → e + CO2 → e + CO2 |
22 | |
| RX15 | Electron impact dissociation | e + CO2 → e + CO + O | 26 | |
| RX16 | Dissociative recombination | e + CO2+ → CO + O | 27 | |
| RX17 | Elastic scattering | e + CO → e + CO | 28 | |
| RX18 | Elastic scattering | e + O2 → e + O2 | 29 | |
| RX19 | Dissociative attachment | e + O2 → O + O− | 29 | |
| RX20a | Electron impact dissociation | e + O2 → e + O + O | 29 | , |
| RX20b | Electron impact dissociation | e + O2 → e + O + O | 29 | , |
| RX21 | Elastic scattering | e + O → e + O | 29 | |
| RX22 | Three-body electron attachment | e + O + M → O− + M | 30 | |
| No | Reaction | Rate constant | Ref |
|---|---|---|---|
| RV1 |
 + M → νl + M → νl + (1 − νl) CO2 + M + (1 − νl) CO2 + M |
f(TV/T) | 22 |
| RV2 |
 + CO2 → νl + CO2 → νl + (1− νl) CO2 + CO2 + (1− νl) CO2 + CO2 |
f(TV/T) | 22 |
| RV3 | CO2vi + M ↔ CO2 + M | 7.14 × 10−14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−177T−1/3 + 451T−2/3) exp(−177T−1/3 + 451T−2/3) |
31 |
| RV4 | CO2v4 + CO2 ↔ CO2 + CO2 | 0.43 × 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−407T−1/3 + 824T−2/3) + 0.86 × 10−6 exp(−407T−1/3 + 824T−2/3) + 0.86 × 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−404T−1/3 + 1096T−2/3) + 1.43 × 10−11 exp(−404T−1/3 + 1096T−2/3) + 1.43 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−252T−1/3 + 685T−2/3) + 2 × 2.13 × 10−11 exp(−252T−1/3 + 685T−2/3) + 2 × 2.13 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−242T−1/3 + 633T−2/3) exp(−242T−1/3 + 633T−2/3) |
31 |
| RV5 | CO2v4 + M ↔ CO2 + M (M = CO, O2) | 0.43 × 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−407T−1/3 + 824T−2/3) + 0.86 × 10−6 exp(−407T−1/3 + 824T−2/3) + 0.86 × 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−404T−1/3 + 1096T−2/3) + 1.43 × 10−11 exp(−404T−1/3 + 1096T−2/3) + 1.43 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−252T−1/3 + 685T−2/3) exp(−252T−1/3 + 685T−2/3) |
31 |
| No | Reaction | Rate constant | Ref |
|---|---|---|---|
| RN1 | CO2 + M → CO + O + M | 4.39 × 10−13 exp(−65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/T) 000/T) |
1 |
| RN2 | CO2 + O → CO + O2 | 7.77 × 10−18 exp(−16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600/T) 600/T) |
1 |
| RN3 |
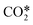 + M → CO + O + M + M → CO + O + M |
f(TV/T) | 22 |
| RN4 |
 + O → CO + O2 + O → CO + O2 |
f(TV/T) | 22 |
| RN5 | CO + O + M → CO2 + M | 8.2 × 10−46 exp(−1510/T) | 32 |
| RN6 | CO + O2 → CO2 + O | 1.23 × 10−18 exp(−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800/T) 800/T) |
1 |
| RN7 | O + O + M → O2 + M | 1.27 × 10−44 (T/300)−1 exp(−170/T) | 33 |
| No | Reaction | Sticking coefficient | Correction factor | Diffusion length |
|---|---|---|---|---|
| RS1 | CO2vi → CO2 | 1 | 1 | Λ eff,cyl |
| RS2 | CO2ei → CO2 | 1 | 1 | Λ eff,cyl |
| RS3 | CO2+ → CO2 | 1 | h l,hr | N/A |
The energy gained by the electrons from the electromagnetic fields is transferred to other species through electron impact reactions. Their rate constants are given as functions of the mean electron energy in the form of tabulated data. The cross sections used for the calculations are given in the references of Table 4. These cross sections were integrated with a Maxwellian electron energy distribution function (EEDF) for mean electron energies up to 10 eV. It is known that the EEDF is in general non-Maxwellian and the rate constants of electron impact processes can be overestimated due to this assumption, particularly for high energy processes. To illustrate this, the rate constant for the direct electron impact dissociation (RX15 in Table 4) can be overestimated up to an order of magnitude for low electron temperatures (∼0.7 eV), when compared to the result obtained by solving the two-term approximation of the Boltzmann equation. For higher electron temperatures (∼2 eV), the rate constant is overestimated by less than 40%. The same comparison for the vibrational excitation of the first asymmetric level (low energy process, RX6 in Table 4) gives an overestimation of around 20% for an electron temperature of 0.7 eV. For higher electron temperatures (>1.8 eV), the deviation is only 1%. Nevertheless, it is very important to remark that different values of the mean electron energy are obtained when the energy conservation equation for the electrons (eqn (3)) is solved with rates computed with a Maxwellian EEDF and a non-equilibrium EEDF. Therefore, the overestimations mentioned before do not represent the error induced in the rates of the electron impact processes by assuming a Maxwellian EEDF. Indeed, the error is expected to be smaller considering the higher mean electron energies required for a non-equilibrium EEDF to achieve an ionization rate comparable to that obtained with a Maxwellian EEDF. The electron temperature determining the Maxwellian EEDF is computed using eqn (3) and (4).
The reactions in Table 4 are: 1) collision processes from a complete and consistent cross section set for CO2 (RX1–13), 2) additional processes for CO2 that make no contribution to eqn (3) (RX14, 15) and 3) elastic scattering and processes leading to electron losses for the other species. An elastic scattering cross section is computed by subtracting the cross sections of inelastic processes (attachment, excitation and ionization) from the effective momentum transfer cross section.
Vibrationally excited states created by electron impact reactions are mostly deexcited by collisional processes at moderate and high pressures. In the case of symmetric vibrational states (CO2vi, i ≠ 4), the deexcitation takes place via vibrational–translational (VT) relaxation, i.e. the energy stored in the vibrational degree of freedom is transferred to the translational degree of freedom i.e., as heat. The probability of this energy transfer is highest for processes in which one vibrational quantum is transferred and the rate increases as the vibrational level increases. It is therefore assumed that the process takes place in a cascade fashion and the limiting rate is the VT relaxation of the first symmetric vibrational level. The rate constant of the latter is assumed for the VT relaxation reactions of all symmetric vibrational levels (reaction RV3) and all collision partners M.
For purely asymmetric vibrational levels (CO2v4,  ), the deexcitation takes place via VT relaxation and intermode vibrational–vibrational relaxation (VV′), where vibrational energy is transferred to the symmetric vibrational modes. However, the vibrational relaxation of the symmetric modes is much faster than the same in the asymmetric mode; it is therefore assumed that any symmetric level formed in the VT or VV′ relaxation is immediately relaxed. Purely asymmetric vibrational states are thus involved in their vibrational relaxation processes and the VV′ relaxation acts as an additional VT relaxation process. Therefore, the rate constant for the reaction RV4 is the sum of the VT and VV′ relaxation rate constants of the reference. Specifically, the first three terms in the expression correspond to the VT relaxation reactions CO2v4 + M ↔ CO2vi + M ↔ CO2 + M with M = CO2 and the symmetric levels CO2v1, CO2v2a + CO2v2b and CO2v3 as respective intermediate states. Reaction RV5 corresponds to the analogous VT relaxation reactions for M = CO and O2. The last term in the expression for the rate constant of reaction RV4 corresponds to the VV′ relaxation reactions CO2v4 + CO2 ↔ CO2vi + CO2vj ↔ CO2 + CO2 with the symmetric levels CO2v1, CO2v2a + CO2v2b or CO2v2a + CO2v2b, CO2v1 as intermediate states.
), the deexcitation takes place via VT relaxation and intermode vibrational–vibrational relaxation (VV′), where vibrational energy is transferred to the symmetric vibrational modes. However, the vibrational relaxation of the symmetric modes is much faster than the same in the asymmetric mode; it is therefore assumed that any symmetric level formed in the VT or VV′ relaxation is immediately relaxed. Purely asymmetric vibrational states are thus involved in their vibrational relaxation processes and the VV′ relaxation acts as an additional VT relaxation process. Therefore, the rate constant for the reaction RV4 is the sum of the VT and VV′ relaxation rate constants of the reference. Specifically, the first three terms in the expression correspond to the VT relaxation reactions CO2v4 + M ↔ CO2vi + M ↔ CO2 + M with M = CO2 and the symmetric levels CO2v1, CO2v2a + CO2v2b and CO2v3 as respective intermediate states. Reaction RV5 corresponds to the analogous VT relaxation reactions for M = CO and O2. The last term in the expression for the rate constant of reaction RV4 corresponds to the VV′ relaxation reactions CO2v4 + CO2 ↔ CO2vi + CO2vj ↔ CO2 + CO2 with the symmetric levels CO2v1, CO2v2a + CO2v2b or CO2v2a + CO2v2b, CO2v1 as intermediate states.
For reactions RV1, 2 the rate constants are computed according to the methodology of the reference, i.e. from the state-specific normalized populations and rate constants of the vibrational levels lumped within the fictitious species  . In addition, the symmetric levels are replaced by ground state CO2 for the reasons previously explained. Rate constants for reverse reactions are computed by using the detailed balancing principle. No reverse reactions are considered for reactions RV1, 2 as the highly energetic fictitious species
. In addition, the symmetric levels are replaced by ground state CO2 for the reasons previously explained. Rate constants for reverse reactions are computed by using the detailed balancing principle. No reverse reactions are considered for reactions RV1, 2 as the highly energetic fictitious species 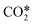 can only be produced by electron collisions.
can only be produced by electron collisions.
Thermal dissociation of CO2 takes place through reactions RN1 and RN2, whereas vibrationally enhanced dissociation takes place through the analogous reactions RN3 and RN4. The rate constants for the reactions RN3, 4 are computed by following the approach of the given reference. This approach is also used to compute the enthalpy change in these reactions, as exemplified here for RN3. Fig. 7 illustrates the enthalpy change in the dissociation reaction RN1 for specific levels of the asymmetric vibrational mode of CO2. For this reaction and this vibrational mode, the vibrational energy decreases the activation energy, which is also the enthalpy change of the reaction.
The enthalpy change of the lumped reaction RN3 is computed by adding the heat of the dissociation reactions for all asymmetric vibrational levels (grouped inside  ) and the result is made equal to the heat of reaction of the lumped reaction, as follows
) and the result is made equal to the heat of reaction of the lumped reaction, as follows
Therefore, the expression for the enthalpy change of reaction RN3 is
 | (5) |
The brackets denote concentration, ni is the normalized population of the asymmetric vibrational level i, k is the rate constant, ΔHr the enthalpy change and Ei the vibrational energy of the asymmetric vibrational level i. The enthalpy change of reaction RN4 is computed likewise, from its analogous reaction RN2 and considering that only half of the vibrational energy decreases the activation energy.1 Any vibrational energy surplus in this case becomes heat of the products.
The remaining reactions between neutrals are recombination reactions producing O2 and CO2. Reactions involving charged species are limited to three detachment reactions, releasing electrons from the negative ions O−.
Ions can also recover a neutral charge in a collision with a wall, as well as excited states can also return to their ground state through the same action. Given the low temperature of heavy species (neutrals, excited and ions), it is assumed that the probability of this grounding event is 1, i.e. every time an excited or charged species collides with a wall it returns to the neutral ground state. This probability is also referred to as the sticking coefficient and is given in Table 8 along with the surface reactions of the model. No surface reaction is considered for the negative ions O− as they are confined in the plasma core due the action of the ambipolar field.
The rate constants can be computed from the sticking coefficients by using the following expression37
 | (6) |
 | (7) |
 | (8) |
Surface recombination reactions for neutral species are neglected. The sticking coefficients of these reactions cannot be determined intuitively and are difficult to estimate; they are functions of the gas and wall temperatures and strongly depend on the material of the wall and its surface properties.38 Experimentally obtained values are also scarce and not in agreement.39,40 In addition, no significant carbon deposition was observed during the CO2 dissociation experiments in our setup.
3.3 Transport effects
The effects of transport on energy and mass conservation are treated globally. Momentum conservation is not solved for, viscous effects are disregarded and the pressure is assumed uniform and constant throughout the reactor (see Fig. 2 for the negligible pressure loss of order 10−3 in the Argon model).Diffusion effects are only considered for the surface reactions as the concentration of the reacting species at the wall is not equal to their average concentration. Regarding the excited states, the diffusion coefficients Dk,m and the effective diffusion length Λeff are needed to compute their diffusion rates from eqn (8). The calculation of the former is based on the kinetic gas theory and is included in COMSOL's Plasma Module.25 The latter, for a cylindrical reactor of length Lr and inner radius ri can be estimated as follows41
 | (9) |
The positive ion diffuses to the walls at a higher rate due to the action of the ambipolar field. The correction factors hl,hr for the surface reaction of CO2+ are the wall to centre ratios of the species concentration in the z and r dimensions, respectively, and are computed, based on ref. 42, from
 | (10) |
 | (11) |
In the above expressions, J1 is the Bessel function of the first order, λi is the ion-neutral mean free path, uB the Bohm velocity and Da the ambipolar diffusion coefficient, computed as follows
 | (12) |
 | (13) |
 | (14) |
Regarding heat transfer, it is assumed that heat conduction is the dominant heat transfer mechanism in the plasma.44 The heat transfer equation therefore corresponds to that of a cylinder with heat generation inside and a constant wall temperature. It can be easily shown than in this case a parabolic temperature profile is obtained and the heat losses and maximum temperature are
 | (15) |
| Tmax = 2T − Tw | (16) |
The heat losses are included in the following heat transfer equation to calculate the temperature of the gas in the plasma
 | (17) |
The acceleration induced by the ambipolar field leads to higher kinetic energies in the positive ions. This kinetic energy is εi = Vs + 0.5Te, with the sheath voltage Vs computed as in ref. 38
 | (18) |
The contribution of the asymmetric vibrational states to the specific heat of the fictitious species  is computed from their vibrational energy. The following equations are used for the calculation
is computed from their vibrational energy. The following equations are used for the calculation
 | (19) |
 | (20) |
 | (21) |
 , R the universal gas constant, Evib the mean vibrational energy, and ni and Ei are the population and vibrational energy of the level i, respectively. The reader is referred to ref. 22 for the details regarding the calculation of the energies and populations of the vibrational levels grouped within
, R the universal gas constant, Evib the mean vibrational energy, and ni and Ei are the population and vibrational energy of the level i, respectively. The reader is referred to ref. 22 for the details regarding the calculation of the energies and populations of the vibrational levels grouped within  . The calculation of the enthalpy change in deexcitation reactions of
. The calculation of the enthalpy change in deexcitation reactions of  is performed using the computed specific heat for this species.
is performed using the computed specific heat for this species.
4. Modelling results and experimental validation
The simplified profile used as input for the CO2 model is shown in Fig. 8. This profile is based on Fig. 3 and consists of three peaks of the same magnitude distributed uniformly inside the Surfatron body and a declining power density downstream. The plasma obtained in the CO2 experiments is shorter than the Argon plasma at the same process conditions, with a total length of approximately 20 cm.12,13 Assuming this value for the plasma length as well as deposition efficiencies of 62% inside the Surfatron body and 21% for the surface wave (refer to Table 1, the value corresponding to TW = 600 K is assumed for the former), the piecewise linear profile is calculated using eqn (1). It is also assumed that the power deposition starts inside the Surfatron body and the profile remains constant within the range of studied flowrates as it was observed in the Argon model.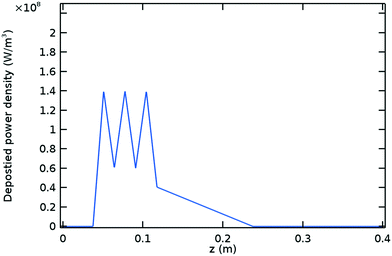 | ||
| Fig. 8 Deposited power density profile for the CO2 model. Refer to Fig. 3 for the power density profile obtained with the Argon model. | ||
The simulations in the CO2 model are performed at the same process conditions of the experiments for three different values of the inlet flowrate, 100, 200 and 300 sccm. The pressure is fixed at 20 mbar, the initial (inlet) temperature and the wall temperature are both 300 K and the input power is 150 W. CO2 is ∼100% of the initial composition and the initial mass fractions of the excited species are computed by assuming a Boltzmann distribution. In addition, thermal equilibrium is initially assumed for the electrons and the initial ionization degree (electrons to neutrals ratio) is 10−10. A direct solver is used for the fully coupled system of equations and the solution time is optimized using Anderson acceleration with a dimension of iteration space of 10.
The CO2 conversion in the plasma reactor as a function of the axial position can be computed with the following expression, where nCO2 is the total density of the CO2 species and v is the flow velocity.
 | (22) |
Several reactions in the model can contribute to the dissociation of the CO2 molecule. These can be arranged into 5 different paths:
1. Dissociative attachment (RX2, Table 4).
2. Ionization + dissociative recombination (RX13 + RX16, Table 4).
3. Direct electron impact dissociation (RX15, Table 4).
4. Thermal dissociation (RN1, 2, Table 6).
5. Vibrationally enhanced dissociation (RX14a, Table 4 + RN3, 4, Table 6).
The dashed lines in Fig. 9 show the CO2 conversion computed when the vibrationally enhanced dissociation of CO2 is not considered. In this case, the conversion at the reactor outlet (x = 0.4 m) is 11%, 16% and 31% for 300, 200 and 100 sccm, respectively. In these calculations the direct electron impact dissociation is the dominant path, forming approximately 92% of CO. Dissociative recombination after ionization and dissociative attachment also contribute, forming 5.5% and 2.5% of CO, respectively. Thermal dissociation is orders of magnitude smaller than the other paths due to the relatively low temperatures in the plasma.
These conversion values are clearly far from the experimental values of 18%, 32% and 66% obtained for the same flowrates, indicating that the vibrationally enhanced dissociation could play a significant role in the dissociation of CO2. It is worth mentioning that the CO2 recombination from the reactor outlet to the measuring device is, in all cases, estimated to be less than 1% and is therefore neglected. Hereinafter, conversion refers to the conversion at the outlet of the reactor unless otherwise stated.
It is possible to estimate the CO2 dissociation via vibrational excitation by including the fictitious species  in the model. The stoichiometric coefficients, reaction rates, enthalpy of reactions and specific heat required to include this species in the model are computed from the non-thermal degree by following the methodology presented in ref. 22 (see previous sections 3.2 and 3.3). This reduction methodology is based on 1) lumping all asymmetric vibrational levels within the fictitious species
in the model. The stoichiometric coefficients, reaction rates, enthalpy of reactions and specific heat required to include this species in the model are computed from the non-thermal degree by following the methodology presented in ref. 22 (see previous sections 3.2 and 3.3). This reduction methodology is based on 1) lumping all asymmetric vibrational levels within the fictitious species 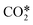 , 2) assuming a Treanor distribution of these levels, 3) using an algebraic approximation based on the Landau–Teller formula to compute the evolution of non-thermal degree in the discharge and 4) employing weighted algebraic expressions to compute the rate constants of reactions involving
, 2) assuming a Treanor distribution of these levels, 3) using an algebraic approximation based on the Landau–Teller formula to compute the evolution of non-thermal degree in the discharge and 4) employing weighted algebraic expressions to compute the rate constants of reactions involving  . The application of this methodology results in a substantial simplification regarding the number of reactions and species required to describe the vibrationally enhanced dissociation of CO2.
. The application of this methodology results in a substantial simplification regarding the number of reactions and species required to describe the vibrationally enhanced dissociation of CO2.
The non-thermal degree is an implicit comparison between VV and VT relaxation and is given by the ratio between the vibrational temperature TV and the gas temperature T. The vibrational temperature is based on the population density of the first vibrational level of the asymmetric mode and is computed from TV = E1/ln(n0/n1). An efficient dissociation of CO2 is possible at low temperatures and high non-thermal degrees, when the vibrational energy is predominantly exchanged between vibrational levels (VV relaxation) instead of being lost as heat (VT relaxation).
The CO2 model without the fictitious species 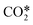 is used to estimate the non-thermal degree at the characteristic time of the VT relaxation, i.e. the time at which VT relaxation kicks in and the evolution of TV/T follows the trend described in ref. 22. This characteristic time is approximately 1.6 × 10−4 s and it is computed at the initial conditions of the discharge from τVT = (kRV4nCO2)−1, where kRV4 is the rate constant of the VT relaxation reaction RV4 and nCO2 is the population density of CO2. The non-thermal degree is then computed at 1.6 × 10−4 s after the power deposition starts, giving the approximate values of 3.5, 3.1 and 2.6 for 300, 200 and 100 sccm, respectively.
is used to estimate the non-thermal degree at the characteristic time of the VT relaxation, i.e. the time at which VT relaxation kicks in and the evolution of TV/T follows the trend described in ref. 22. This characteristic time is approximately 1.6 × 10−4 s and it is computed at the initial conditions of the discharge from τVT = (kRV4nCO2)−1, where kRV4 is the rate constant of the VT relaxation reaction RV4 and nCO2 is the population density of CO2. The non-thermal degree is then computed at 1.6 × 10−4 s after the power deposition starts, giving the approximate values of 3.5, 3.1 and 2.6 for 300, 200 and 100 sccm, respectively.
The results of the full model, including  , are shown in the solid lines of Fig. 9. The conversion in the plasma reactor is now 16%, 24% and 52% for 300, 200 and 100 sccm, respectively. The absolute increase in the conversion by considering the vibrationally enhanced dissociation is 5%, 8% and 21%, which also correspond to a relative increase of 45%, 50% and 68%, respectively. These numbers confirm that this path plays a significant role and must be considered when modeling the CO2 dissociation in non-thermal plasmas. In these calculations, the dominant paths for the dissociation are now the direct electron impact dissociation and the vibrationally enhanced dissociation. The dissociative recombination after ionization and dissociative attachment also have minor contributions, whereas thermal dissociation is still negligible.
, are shown in the solid lines of Fig. 9. The conversion in the plasma reactor is now 16%, 24% and 52% for 300, 200 and 100 sccm, respectively. The absolute increase in the conversion by considering the vibrationally enhanced dissociation is 5%, 8% and 21%, which also correspond to a relative increase of 45%, 50% and 68%, respectively. These numbers confirm that this path plays a significant role and must be considered when modeling the CO2 dissociation in non-thermal plasmas. In these calculations, the dominant paths for the dissociation are now the direct electron impact dissociation and the vibrationally enhanced dissociation. The dissociative recombination after ionization and dissociative attachment also have minor contributions, whereas thermal dissociation is still negligible.
Table 9 gives the percentage of CO molecules formed by each of the dissociation paths. The direct electron impact dissociation accounts for approximately 55% of the dissociation, while 40% is due to the vibrationally enhanced dissociation. Although not shown in the table, there is an absolute increase in the dissociation for each path as the flowrate decreases, due to an increase in the electron density. However, the dissociation rate for all paths increase differently as the electron temperature increases, modifying the rate constant of the electron impact reactions.
| CO2 dissociation path | ||||
|---|---|---|---|---|
| Flowrate (sccm) | 1 DA | 2 I + DR | 3 DEID | 5 VED |
| 100 | 1.4% | 3.0% | 53.2% | 42.4% |
| 200 | 1.5% | 2.8% | 54.0% | 41.7% |
| 300 | 1.6% | 2.8% | 56.2% | 39.4% |
The conversions obtained with the full model are still lower than the experimental values, having relative errors of 11%, 25% and 21%. These deviations can be seen in Fig. 10, where the experimental and modelling results are plotted as functions of the flowrate. Given the complexity of modelling plasma and the simplifications taken in the process, the results are considered in fair agreement. Indeed, various elements have influence on the lower conversions obtained in the model, particularly the power deposition. The power deposition efficiencies were characterized from a model of an atomic plasma and are assumed to remain the same for a molecular plasma. However, this is not necessarily true since molecules have more degrees of freedom and have chemical bonds that can be broken (or formed); therefore, molecular plasmas are more reactive and have more energy channels through which the energy given by the electrons can flow or be stored. In other words, this means that the power deposition in the CO2 plasma is expected to be higher than the value taken from the Argon model. The calculation of a correction factor for the power deposition in the CO2 plasma can be problematic due to the complexity of the physics involved in the 2D self-consistent model, e.g. the electromagnetic wave equation inside and outside of the reactor. The formulation of the power deposition depends on the type discharge and the presence of electric arcs can simplify the treatment.46
The dashed line of Fig. 10 illustrates the influence of the deposition efficiencies in the conversion. For these calculations, it is assumed that all 150 W of power input are deposited in the plasma, with 75% of it being deposited inside the Surfatron body (approximate ratio of 62/83). The non-thermal degrees are kept constant, implying that these conversions are slightly underestimated. Nevertheless, these results serve as a limiting case, proving that this uncertainty alone can explain the lower conversions in the model. It is to be noted that the power deposition remains lower than 100% in the CO2 plasma. As we proved experimentally, the addition of a waveguide reduces the power losses and increases the performance of the reactor for the case of CO2 reduction with hydrogen.13
The portion of power deposited inside the Surfatron body can also vary, having further influence on the conversion, as most of the CO2 dissociation takes place there. Fig. 11 shows the densities and mole fractions of the neutral species as functions of the axial position in the plasma reactor. The oscillations seen in the graph at the top are partially caused by expansions due to the increase in the gas temperature when power is deposited. This effect is not present in the mole fractions shown in the graph at the bottom, where the remaining fluctuations are then related to the reacting system. In the bottom graph, it is seen that most of the CO2 dissociation takes place inside the Surfatron body, forming mainly CO and O. O2 is subsequently formed by the recombination of two O atoms, or in the reaction of  and O.
and O.
 | ||
| Fig. 11 Densities (top) and mole fractions (bottom) of neutral species as functions of the axial position in the reactor for a flowrate of 100 sccm. Blue: CO2, green: CO, cyan: O, red: O2. | ||
The fluctuations still seen in O2 are located at the peaks of the power deposition profile and are related to electron impact dissociation reactions of O2. The maximum dissociation of CO2, corresponding to a maximum conversion of 56%, is slowly reached downstream of the Surfatron; afterwards, recombination takes place and the final conversion of 54% is achieved. O atoms also recombine into O2 downstream of the Surfatron, notably past the end of the plasma. The final products are then CO2, CO and O2, as expected.
The energy efficiency of the reactor can be computed from the CO2 conversion, considering that a minimum of 2.93 eV per CO2 molecule are required for the reaction CO2 → CO + 1/2 O2 to take place. The energy input per particle in the plasma, commonly known as specific energy input (SEI), is also used in the calculation, as follows
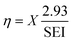 | (23) |
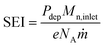 | (24) |
| Flowrate (sccm) | SEI, model (eV/molecule) | E. Efficiency, model (%) | E. Efficiency, exp. (%) |
|---|---|---|---|
| 100 | 17.3 | 8.8 | 8.3 |
| 200 | 8.7 | 8.1 | 8.3 |
| 300 | 5.8 | 7.9 | 6.8 |
Assuming 100% of power deposition in the model, as before, the energy efficiencies for the same flowrates increase to approximately 10%, which is still a low value. The reason for this is that the experimental conditions and the reactor itself were not optimized for an efficient dissociation of CO2, which is achieved at low values of SEI (<2 eV per molecule). At high values of the SEI, such as the ones in Table 10, relatively high electron densities and electron temperatures are obtained, shifting the EEDF away from the vibrational excitation reactions. An efficient dissociation of CO2 should take place mostly through vibrational excitation, not direct electron impact dissociation with a higher energy requirement. As mentioned before, the latter is the main dissociation path in the Surfatron reactor, leading to low energy efficiencies.
The effect of the SEI is clearly seen in the top and middle graphs of Fig. 12, showing that both the electron density and electron temperature increase as the SEI increases (flowrate decreases). Nonetheless, the results for the different flowrates are quite similar and within the range of typical values for non-thermal CO2 microwave plasmas: Te ≈ 0.5–2 eV and ne ≈ 1018–20 1/m3. The ionization degree in the plasma is then 10−5 inside the Surfatron body and 10−6 outside.
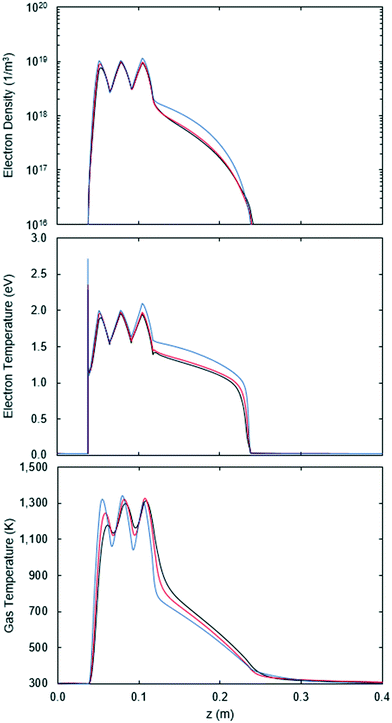 | ||
| Fig. 12 Electron density (top), electron temperature (middle) and gas temperature (bottom) as a function of the axial position in the reactor for 100 (blue), 200 (red) and 300 sccm (black). | ||
Experimental values of the electron density and electron temperature in this reactor were determined downstream of the Surfatron for gas mixtures of H2 and CO2.12 Electron densities in the order of 1021 and 1020 1/m3 were estimated for H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratios of 4 and 3, respectively. Likewise, electron temperatures of 1.3 and 0.7 eV were estimated for H2
CO2 ratios of 4 and 3, respectively. Likewise, electron temperatures of 1.3 and 0.7 eV were estimated for H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratios of 3 and 1, respectively. Lower electron densities and temperatures are expected for lower mixing ratios.11 These reference values suggest that the computed electron densities are within the expected order of magnitude while the electron temperatures are slightly overestimated (see below discussion on lack of electron transport).
CO2 ratios of 3 and 1, respectively. Lower electron densities and temperatures are expected for lower mixing ratios.11 These reference values suggest that the computed electron densities are within the expected order of magnitude while the electron temperatures are slightly overestimated (see below discussion on lack of electron transport).
A qualitative match between Fig. 1 and 12 is also observed, confirming that these variables follow the power deposition profile. Therefore, given that the variables in Fig. 1 and 12 determine the rate of the electron impact reactions, it can be inferred that not only the deposited power, but also the density at which it is deposited has an influence on the results.
The lack of electron transport in the CO2 model is also evident by comparing the electron densities and electron temperatures of Fig. 1 and 12. In the Argon model, a smaller difference is seen between the values inside and outside of the Surfatron body. Furthermore, the slope at which they decrease in the low power density zone is flatter, being virtually horizontal for the electron temperature. Thus, the lack of electron transport in the CO2 model results in a less uniform plasma with a reduced reactivity due to the rapid decay in the number of electrons.
The average gas temperature, shown at the bottom of Fig. 12, does not vary much with the flowrate, except in the first and last peaks of the power deposition. The variations seen in the first peak are related to the electron density, while the CO2 dissociation explains the variations in the last peak. The CO2 dissociation is also related to the electron temperature and density variations seen for a flowrate of 100 sccm in Fig. 12.
Despite the variations, the maximum average temperature for the flowrates is the same, reaching around 1300 K inside the Surfatron body. Hence, according to eqn (16), the maximum gas temperature at the center of the plasma is 2300 K, which is within the range of our previously estimated values for the gas temperature, 2200–2400 K.12
It is also possible to verify the previous assumption regarding the electropositive behavior of the plasma. Fig. 13 shows that the maximum electronegativity is around 0.2 as the power deposition begins. However, it promptly decays and for most of the plasma, it is in the order of magnitude of 10−3, which agrees with the assumption of a very low electronegativity (α = nO−/ne ≪ 1). This means that there are few negative ions, which are confined at the core of the plasma and their effect on the positive ions can be neglected.
 | ||
| Fig. 13 Electronegativity as a function of the axial position in the reactor for 100 (blue), 200 (red) and 300 sccm (black). | ||
Even though the positive ions are not held back in their movement towards the walls, the rate of surface recombination is two orders of magnitude smaller than the collisional counterpart (dissociative recombination, RX16 Table 4). Thus, most electrons are lost inside the plasma instead of being lost to the walls.
Contrarily, the rates of collisional and surface deexcitation of vibrationally excited species are comparable, with the surface process becoming more important as the vibrational level increases due to the limiting rate assumed for the collisional process. Moreover, the reverse collisional process intensifies the relevance of the surface deexcitation, making its contribution to vibrational deexcitation larger than the collisional counterpart.
The importance of surface reactions in this model is expected from the characteristic diffusion time, which, depending on the computed gas temperature, is estimated in the order of 0.1–1 ms. This characteristic time is shorter than the residence time in the plasma reactor, which for 20 cm of plasma is approximately 3.7, 5.7 and 11.6 ms for 300, 200 and 100 sccm, respectively. Therefore, for such a small reactor and relatively low operating pressure, the species have sufficient time to diffuse and possibly collide with the walls.
For larger reactors, the surface reactions can be neglected considering that their rates scale as 1/r compared to the gas phase reactions. In addition, longer characteristic diffusion times are also obtained and fewer species would reach the walls during the short residence times in the reactor.
5. Conclusions
We have developed a two-step modelling approach for plasma reactors, consisting of a plasma characterization step using simple chemistry and a global modelling step using the actual chemistry of interest. Specifically, in the first step, we used a self-consistent two-dimensional axisymmetric Argon plasma model of a laboratory surface wave microwave plasma reactor to characterize the discharge, particularly the power deposition along the reactor. In the second step, the outcome of the first step was used to develop a zero-dimensional volume-averaged CO2 plasma model, under a Lagrangian description, which represents a one-dimensional model of our experimental setup.With the global model we showed that the vibrationally enhanced dissociation is a relevant process taking place in the reactor and must be included in the model. For this purpose, we have used the fictitious species  that groups all levels in the asymmetric vibrational mode of the CO2 molecule. We also pointed out the significant role of the surface reactions in the deactivation of excited species at the investigated conditions in our plasma reactor. The relevance of the surface reactions should be evaluated according to the reactor design and operating conditions before deciding whether to include them in the modelling process.
that groups all levels in the asymmetric vibrational mode of the CO2 molecule. We also pointed out the significant role of the surface reactions in the deactivation of excited species at the investigated conditions in our plasma reactor. The relevance of the surface reactions should be evaluated according to the reactor design and operating conditions before deciding whether to include them in the modelling process.
The results of the simulations showed CO2 conversions of 16%, 24% and 52%, for inlet flowrates of 300, 200 and 100 sccm, respectively. The relative increase in the conversion when the vibrationally enhanced dissociation is considered was 45%, 50% and 68%, respectively. With the model we also identified the direct electron impact dissociation and the vibrationally enhanced dissociation as the dominant paths for the CO2 dissociation in our plasma reactor, accounting for approximately 55% and 40% of CO formation, respectively.
The experimental conversions for the corresponding flowrates of 300, 200 and 100 sccm are 18%, 32% and 66%, respectively. Thus, the agreement between the modelling and experimental values, mentioned in the previous paragraph, is good in view of the complexity involved in modelling non-thermal CO2 plasma reactors. The experimental validation of the CO2 plasma variables indicates that the electron densities are close to the expected order of magnitude and the gas temperature is in agreement with the experimentally estimated values. The electron temperatures are slightly overestimated, mainly due to the lack of electron transport in the global model.
The power deposition profile determined with the Argon model was identified as the major source of error, due to the uncertainty of its variation when the plasma is generated in a CO2 flow, e.g. higher power depositions are expected in a molecular plasma. Despite this, the profile obtained from the Argon model was adopted as it is more descriptive than a power input value and closer to reality than an arbitrarily shaped profile. Using the Argon model, it was determined that 17% of the power input is lost to the surroundings and the remaining power is deposited into the plasma. Moreover, it was identified that 75% of the power deposition occurs inside the Surfatron body, whereas 25% is gradually deposited by the surface waves as they travel axially along the plasma.
Additional simulations showed that the uncertainties regarding the power deposition profile can explain the error obtained in the CO2 conversion. It is therefore essential to have an approximate description of the power deposition profile, including the deposited power inside the Surfatron reactor, the power of the surface wave, the length of the plasma and the power deposition densities (shape of the profile). It was also shown with both models that the latter can be particularly important as the plasma variables have a fast response and closely follow the same variations.
Further limitations of the global model were also discussed, especially those that can contribute to the discrepancies in the results. Among these are the simplified treatment of the heat transfer inside the reactor body, the simplified treatment of the heat and mass transfer in the radial direction (due to averaging) and the lack of heat and mass transfer (plug flow assumption) in the axial direction (due to the Lagrangian approach).
Despite these limitations, we believe that the two-step modelling approach is valuable for process engineering applications involving design, optimization and verification of plasma reactors and their performance.
Conflicts of interest
There are no conflicts to declare.References
- A. Fridman, Plasma chemistry, Cambridge University Press, 2008 Search PubMed.
- V. D. Rusanov, A. a. Fridman and G. V. Sholin, Usp. Fiz. Nauk, 1981, 134, 185 CrossRef CAS.
- M. Capitelli, M. Dilonardo and E. Molinari, Chem. Phys., 1977, 20, 417–429 CrossRef CAS.
- M. Capitelli, C. M. Ferreira, B. F. Gordiets and A. I. Osipov, Plasma Kinetics in Atmospheric Gases, Springer Berlin Heidelberg, Berlin, Heidelberg, 2000, vol. 31 Search PubMed.
- R. Snoeckx and A. Bogaerts, Chem. Soc. Rev., 2017, 46, 5805–5863 RSC.
- T. Kozák and A. Bogaerts, Plasma Sources Sci. Technol., 2014, 23, 045004 CrossRef.
- T. Kozák and A. Bogaerts, Plasma Sources Sci. Technol., 2015, 24, 015024 CrossRef.
- L. D. Pietanza, G. Colonna, G. D'Ammando, A. Laricchiuta and M. Capitelli, Plasma Sources Sci. Technol., 2015, 24, 042002 CrossRef.
- L. D. Pietanza, G. Colonna, G. D'Ammando, A. Laricchiuta and M. Capitelli, Phys. Plasmas, 2016, 23, 013515 CrossRef.
- M. Grofulović, L. L. Alves and V. Guerra, J. Phys. D: Appl. Phys., 2016, 49, 395207 CrossRef.
- P. Diomede, M. C. M. van de Sanden and S. Longo, J. Phys. Chem. C, 2017, 121, 19568–19576 CrossRef CAS.
- J. F. de la Fuente, S. H. Moreno, A. I. Stankiewicz and G. D. Stefanidis, Int. J. Hydrogen Energy, 2016, 41, 21067–21077 CAS.
- J. F. de la Fuente, S. H. Moreno, A. I. Stankiewicz and G. D. Stefanidis, Int. J. Hydrogen Energy, 2017, 42, 12943–12955 CrossRef CAS.
- W. Bongers, H. Bouwmeester, B. Wolf, F. Peeters, S. Welzel, D. van den Bekerom, N. den Harder, A. Goede, M. Graswinckel, P. W. Groen, J. Kopecki, M. Leins, G. van Rooij, A. Schulz, M. Walker and R. van de Sanden, Plasma Processes Polym., 2017, 14, 1600126 CrossRef.
- T. Silva, N. Britun, T. Godfroid and R. Snyders, Plasma Sources Sci. Technol., 2014, 23, 025009 CrossRef.
- L. F. Spencer and A. D. Gallimore, Plasma Sources Sci. Technol., 2013, 22, 015019 CrossRef.
- B. L. M. Klarenaar, M. Grofulović, A. S. Morillo-Candas, D. C. M. van den Bekerom, M. A. Damen, M. C. M. van de Sanden, O. Guaitella and R. Engeln, Plasma Sources Sci. Technol., 2018, 27, 045009 CrossRef.
- B. Hrycak, M. Jasiński and J. Mizeraczyk, Acta Phys. Pol., A, 2014, 125, 1326–1329 CrossRef.
- M. Jasiński, M. Dors and J. Mizeraczyk, Int. J. Environ. Sci. Technol., 2008, 2, 134–139 Search PubMed.
- L. M. Martini, S. Lovascio, G. Dilecce and P. Tosi, Plasma Chem. Plasma Process., 2018, 38, 707–718 CrossRef CAS.
- L. M. Martini, N. Gatti, G. Dilecce, M. Scotoni and P. Tosi, Plasma Phys. Controlled Fusion, 2018, 60, 014016 CrossRef.
- J. F. de la Fuente, S. H. Moreno, A. I. Stankiewicz and G. D. Stefanidis, React. Chem. Eng., 2016, 1, 540–554 RSC.
- M. Jimenez-Diaz, E. A. D. Carbone, J. van Dijk and J. J. a. M. van der Mullen, J. Phys. D: Appl. Phys., 2012, 45, 335204 CrossRef.
- M. Selby and G. M. Hieftje, Spectrochim. Acta, Part B, 1987, 42, 285–298 CrossRef.
- COMSOL, Plasma Module User's Guide, COMSOL 5.3, 2017 Search PubMed.
- L. S. Polak and D. I. Slovetsky, Int. J. Radiat. Phys. Chem., 1976, 8, 257–282 CrossRef CAS.
- R. E. Beverly, Opt. Quantum Electron., 1982, 14, 501–513 CrossRef CAS.
- Phelps database, www.lxcat.net, retrieved on October 24, 2017 Search PubMed.
- L. L. Alves, J. Phys.: Conf. Ser., 2014, 565, 012007 CrossRef.
- H. Shields, A. L. S. Smith and B. Norris, J. Phys. D: Appl. Phys., 1976, 9, 1587–1603 CrossRef CAS.
- J. A. Blauer and G. R. Nickerson, A survey of vibrational relaxation rate data for processes important to CO2–N2–H2O infrared plume radiation, Irvine, California, 1973 Search PubMed.
- A. Cenian, A. Chernukho, V. Borodin and G. Śliwiński, Contrib. Plasma Phys., 1994, 34, 25–37 CrossRef CAS.
- S. Hadj-Ziane, B. Held, P. Pignolet, R. Peyrous and C. Coste, J. Phys. D: Appl. Phys., 1992, 25, 677–685 CrossRef CAS.
- T. G. Beuthe and J.-S. Chang, Jpn. J. Appl. Phys., 1997, 36, 4997–5002 CrossRef CAS.
- J. T. Gudmundsson and E. G. Thorsteinsson, Plasma Sources Sci. Technol., 2007, 16, 399–412 CrossRef CAS.
- H. Hokazono and H. Fujimoto, J. Appl. Phys., 1987, 62, 1585–1594 CrossRef CAS.
- R. J. Kee, M. E. Coltrin and P. Glarborg, Chemically Reacting Flow, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2003 Search PubMed.
- M. A. Lieberman and A. J. Lichtenberg, Principles of Plasma Discharges and Materials Processing, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2005 Search PubMed.
- A. F. Kolesnikov, I. S. Pershin, S. A. Vasil'evskii and M. I. Yakushin, J. Spacecr. Rockets, 2000, 37, 573–579 CrossRef CAS.
- N. G. Bykova, S. A. Vasil'evskii, A. N. Gordeev, A. F. Kolesnikov, I. S. Fershin and M. I. Yakushin, Fluid Dyn., 1997, 32, 876–886 CrossRef CAS.
- P. J. Chantry, J. Appl. Phys., 1987, 62, 1141–1148 CrossRef.
- C. Lee and M. A. Lieberman, J. Vac. Sci. Technol., A, 1995, 13, 368–380 CrossRef CAS.
- L. A. Viehland and E. A. Mason, At. Data Nucl. Data Tables, 1995, 60, 37–95 CrossRef CAS.
- C. M. Ferreira, B. F. Gordiets and E. Tatarova, Plasma Phys. Controlled Fusion, 2000, 42, B165–B188 CrossRef CAS.
- L. I. Stiel and G. Thodos, AIChE J., 1964, 10, 26–30 CrossRef CAS.
- G. Trenchev, S. Kolev, W. Wang, M. Ramakers and A. Bogaerts, J. Phys. Chem. C, 2017, 121, 24470–24479 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |