Making better decisions during synthetic route design: leveraging prediction to achieve greenness-by-design†
Abstract
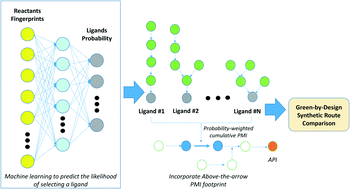
Modern pharmaceuticals are becoming increasingly complex. Incorporating knowledge of a route's holistic sustainability during the route design process could be a critical enabler to minimizing the environmental impact of pharmaceutical manufacturing. The pursuit of the optimal synthesis has historically been characterized by disconnection strategy, or things like step count, however, the optimal synthesis of a molecule may also be assessed through environmentally relevant metrics. The synthesis with the lowest possible cumulative process mass intensity (cPMI) could be considered optimal, a route which may not necessarily be the shortest, but has the best holistic sustainability (for example, considering the synthesis of all reagents and reactants). Previously, we demonstrated the importance of assessing the entire synthetic network by including “above-the-arrow” reagents/reactants into cPMI, to reflect the impact of reagents, such as ligands, on the overall sustainability of the route. Here we present the development of a machine learning approach, using substrate fingerprints, to build a multiclass predictive model to identify which ligands will likely function in a Pd-catalyzed C–N coupling reaction. The resulting predicted multiclass probabilities were then linked to the corresponding ligand cPMIs to yield a probability-weighted predicted holistic PMI for the transformation, integrating the synthesis of the ligand. This proof-of-confidence study may extend our ability to holistically assess different synthetic route options, considering their full impact, to aid decision-making during route ideation. This may lead to greener outcomes in the development of synthetic routes in the pharmaceutical sector and beyond.
- This article is part of the themed collections: Synthesis 4.0: Towards an Internet of Chemistry and Celebrating our 2019 Prize and Award winners


 Please wait while we load your content...
Please wait while we load your content...