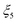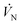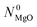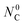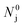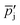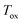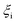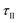Open Access Article
Open Access ArticleOn the prevailing reaction pathways during magnesium production via carbothermic reduction of magnesium oxide under low pressures†
Adrian
Coray
and
Zoran R.
Jovanovic
 *
*
Department of Mechanical and Process Engineering, ETH Zürich, 8092 Zürich, Switzerland. E-mail: zjovanovic@ethz.ch
First published on 13th February 2019
Abstract
In this work we identify the prevailing reaction pathways of carbothermic reduction of MgO for the temperature and pressure ranges of 1375–1450 °C and 1–2 kPa, respectively, and normalized reduction extents of up to 0.4. It has been previously suggested that Mg(g) is produced by either (i) MgO dissociation forming O2 as the reaction intermediate or (ii) MgO(s)–C(s) boundary reaction producing CO that then reduces MgO while forming CO2 as the reaction intermediate. Either of the intermediates (O2 or CO2) are then consumed by C, which is necessary to sustain further Mg(g) production. To identify the prevailing pathways, O2 or CO2 was co-fed with Ar to sweep reacting MgO–C blends with the intent to shift the equilibrium of one of the suspected Mg(g)-producing reactions. After accounting for envisaged effects of both the C/MgO ratio in the reacting blends and the CO concentration in the reaction atmosphere, it is demonstrated that Mg(g) is produced via (1) MgO thermal dissociation and (2) MgO reduction with CO that take place in parallel. At 1375 °C and 1400 °C, roughly twice as much Mg(g) was produced via pathway (1) as compared to pathway (2). There is no evidence supporting the relevance of a direct MgO(s)–C(s) boundary reaction.
1 Introduction
The automotive industry has been considering magnesium (Mg) as an attractive substitute for the 50% denser aluminum (Al) to decrease the fuel consumption of vehicles by lowering their weight.1–3 Commercially, Mg is produced mainly by the Pidgeon process, which is based on the reduction of magnesium oxide (MgO) by ferrosilicon (FexSi).1,3,4 However, compared to the process for making Al this process consumes more than twice the energy (133 versus 54 MJ kg−1)‡ and releases as much as three times more CO2 (25.4 versus 8.7 kg CO2eq per kg).5,6 Therefore, in order to exploit the potential for the fuel efficiency benefit owing to lightweighting of vehicles, the embedded energy content in Mg must be reduced.7 One way to achieve this goal is to circumvent the need for the energy-intensive production of ferrosilicon by using carbon (C) as the reducing agent and produce Mg via carbothermic reduction (CTR) of MgO.2,8,9The carbothermic reduction of MgO constitutes a myriad of elementary reaction steps that can be summarized by the following overall reaction (1):8–13
 | (1) |
Thermodynamic calculations indicate that the temperature required for the forward reaction (1) to proceed is dependent on the partial pressures of the products.8,9,13,14 Reducing these from 50 to 0.5 kPa decreases the onset temperature of the forward reaction from ∼1750 °C to ∼1350 °C, thereby reducing heat losses and the energy required to preheat the reactants. In addition, it has been demonstrated that lower CO partial pressures drastically decrease the severity of the reverse reaction (1), which takes place during cooling of the product mixture.14,15 These benefits thus present a strong incentive for investigating the CTR under vacuum, as they may compensate for the additional pumping work required to maintain low reaction pressures.
In spite of the extensive research dedicated to understanding the constituent steps of reaction (1),14,16,17 at present there is no consensus on the prevailing mechanism of the carbothermic reduction. The reported findings gravitate around two hypotheses. The first one has been advocated by Komarek et al.16 who have proposed that MgO first dissociates into Mg(g) and O and that the latter then diffuses to the C-surface where it reacts to form CO. The authors have not commented on excluding the recombination of the atomic oxygen from consideration, which is believed to be very fast at the temperatures of interest. This recombination transforms their proposed mechanism into its equivalent, summarized as follows:
 | (2) |
 | (3) |
On the other hand, Rongti et al.17 and Chubukov et al.14 have advocated the mechanism according to which MgO is directly reduced by both C and CO. Specifically, the Mg(g) production is initiated by the MgO(s)–C(s) boundary reaction (1) that prevails up to MgO conversions of  = 0.2 (ref. 14)–0.25 (ref. 17). At conversions higher than these, the MgO is reduced mainly by CO
= 0.2 (ref. 14)–0.25 (ref. 17). At conversions higher than these, the MgO is reduced mainly by CO
 | (4) |
 | (5) |
Experimental evidence supporting the significance of reaction (4) has been provided by Rongti et al.17 and Chubukov et al.14 Rongti et al.17 investigated the effect of CO concentration on the kinetics of MgO reduction by graphite. Exploiting non-isothermal thermogravimetry at atmospheric pressure, these authors have observed an increase in the Mg(g) production rate upon switching the reaction atmosphere from pure Ar to CO–Ar mixtures containing 10 or 20% CO. The authors have attributed this observation to the facilitating effect of an increase in the CO concentration on reaction (4). However, the reduction in pure CO was much slower than in pure Ar which has been attributed to the suppressing effect of high CO concentrations on the removal of CO2 from the reduction site viareaction (5). Chubukov et al.14 studied the kinetics of MgO reduction with carbon black under isothermal/isobaric conditions at temperatures and total pressures in the range of 1350–1650 °C and 0.1–100 kPa, respectively. Depending on the MgO conversion, these authors observed a dual effect of decreasing the total pressure on the Mg(g) production rate that they explained as follows:
1. At  < 0.2, a decrease in the total pressure increases the reaction rate, which was attributed to favoring the MgO(s)–C(s) boundary reaction (1).
< 0.2, a decrease in the total pressure increases the reaction rate, which was attributed to favoring the MgO(s)–C(s) boundary reaction (1).
2. At  > 0.35, reducing the total pressure decreases the reaction rate, which was attributed to higher removal rates of CO and CO2 from the reaction zone. It, however, remains unclear why an increased removal rate of CO2 from the reaction zone would decrease the rate of CTR as it should actually favor reaction (4).
> 0.35, reducing the total pressure decreases the reaction rate, which was attributed to higher removal rates of CO and CO2 from the reaction zone. It, however, remains unclear why an increased removal rate of CO2 from the reaction zone would decrease the rate of CTR as it should actually favor reaction (4).
In spite of the limited experimental evidence supporting the contribution of the reaction pathway comprising reaction steps 4 and 5,14,17 the current literature12,14,17–20 neither conclusively proves its prevalence in the overall reaction nor justifies ruling out the contribution of the alternative pathway comprising reactions (2) and (3). The objective of this work is to reconcile previously reported findings and conclusively discriminate prevailing reaction pathways that dominate the Mg(g) production.
2 Methodology
2.1 The principle
The candidates for the prevailing reaction pathways discussed in the previous section may be distinguished by the gaseous intermediates they involve:I. If Mg(g) is produced by the thermal dissociation of MgO viareaction (2), O2 acts as the key intermediate.
II. If Mg(g) is produced by the MgO reduction with CO viareaction (4), CO2 acts as the key intermediate.
III. If Mg(g) is produced by the MgO(s)–C(s) boundary reaction (1), no gaseous intermediate is formed.
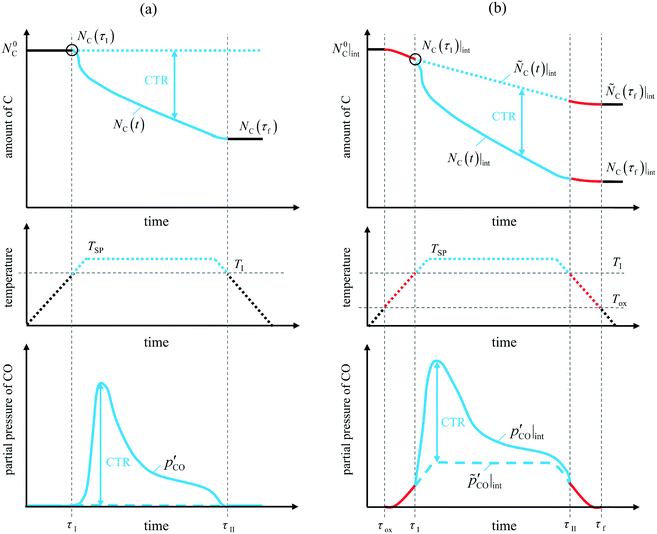
It should be noted that in cases I and II involving the formation of gaseous intermediates the Mg(g) production is sustained by the removal of those intermediates from the reaction site by the reactions with C. This means that the Mg(g) production should be suppressed if the partial pressures of those intermediates were increased above the values shown in section S1 of the ESI,† thereby shifting the equilibria of both reactions (2) and (4) towards the reactants. Therefore, the prevailing reaction pathway(s) may be discriminated by comparing the extents of CTR in the case when a reacting C/MgO blend is swept with an O2–Ar mixture and a CO2–Ar mixture with the extents of CTR in the cases when the same blend is reacted without adding any oxidants to the sweep and then implementing the logic outlined in Fig. 1 as follows:
• The MgO dissociation is the prevailing pathway if the CTR is suppressed with the O2–Ar but not with the CO2–Ar sweep.
• The MgO reduction with CO is the prevailing pathway if the CTR is suppressed with the CO2–Ar but not with the O2–Ar sweep.
• The MgO(s)–C(s) boundary reaction is the prevailing pathway if the CTR remains unaffected by the presence of either O2 or CO2 in the sweep gas.
• If the CTR were suppressed with both the O2–Ar and the CO2–Ar sweeps, it would appear that both MgO dissociation and MgO reduction with CO pertain to the Mg production. However, this conclusion may be confounded by an extra CO2 production under the O2–Ar sweep via reactions
 | (6) |
 | (7) |
 , thereby shifting the equilibrium of reaction (4) towards the reactants. It would therefore be unclear whether the suppression of the CTR under the O2–Ar sweep was the result of the equilibrium shifts of reaction (2) or (4) without information about the effective partial pressures of CO2, CO, and Mg(g) in the reaction atmosphere.
, thereby shifting the equilibrium of reaction (4) towards the reactants. It would therefore be unclear whether the suppression of the CTR under the O2–Ar sweep was the result of the equilibrium shifts of reaction (2) or (4) without information about the effective partial pressures of CO2, CO, and Mg(g) in the reaction atmosphere.
It should be noted, however, that compared to the reference cases in which no oxidant is added into the gas sweeping a reacting C/MgO blend, the addition of O2 or CO2 into the sweep gas introduces two side effects: (i) it increases consumption of C viareactions (3), (5), and (6) and (ii) it affects the effective  in the reacting atmosphere because of the additional CO production viareactions (3) and (5) and/or its consumption viareaction (7). Previous research has suggested that the rate of CTR decreases with a decrease in C/MgO molar ratio11,17 while it may either increase or decrease with an increase in
in the reacting atmosphere because of the additional CO production viareactions (3) and (5) and/or its consumption viareaction (7). Previous research has suggested that the rate of CTR decreases with a decrease in C/MgO molar ratio11,17 while it may either increase or decrease with an increase in  .14,17 In addition, it has also been reported that the rate of CTR decreases with time, which has been attributed to a gradual sintering of MgO particles14 that may proceed at different rates depending on the reaction atmosphere. Therefore, the addition of either of the suspected intermediates into the sweep gas may affect the Mg(g) production not only because of favoring reverse reaction (2) or (4) but also because of (i) the differences in the effective C/MgO ratios and CO partial pressures and (ii) the atmosphere-assisted sintering of the MgO particles.
.14,17 In addition, it has also been reported that the rate of CTR decreases with time, which has been attributed to a gradual sintering of MgO particles14 that may proceed at different rates depending on the reaction atmosphere. Therefore, the addition of either of the suspected intermediates into the sweep gas may affect the Mg(g) production not only because of favoring reverse reaction (2) or (4) but also because of (i) the differences in the effective C/MgO ratios and CO partial pressures and (ii) the atmosphere-assisted sintering of the MgO particles.
2.2 Accounting for the effects of side reactions
Fig. 2 qualitatively illustrates the expected temporal amounts of C in a MgO–C blend (top) and CO partial pressures over the same blend (bottom) when the blend is swept with Ar (Fig. 2a) or Ar diluted with a suspected intermediate (Fig. 2b) while subjected to a temperature program indicated by the dotted lines (middle) comprising three stages: (i) heat up ramp from ambient to a setpoint reaction temperature , (ii) hold at
, (ii) hold at  , and (iii) cool-down ramp from
, and (iii) cool-down ramp from  to the ambient temperature. As shown in the top part of Fig. 2a, when pure Ar is used as the sweep gas the amount of C remains at its initial value
to the ambient temperature. As shown in the top part of Fig. 2a, when pure Ar is used as the sweep gas the amount of C remains at its initial value 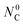 until
until  when the blend reaches the onset temperature of CTR
when the blend reaches the onset temperature of CTR  , thus
, thus  for
for  . With the further progress of the temperature program, C is consumed solely by CTR until
. With the further progress of the temperature program, C is consumed solely by CTR until  when the temperature drops below
when the temperature drops below  during the cool-down ramp. Therefore the amount of C remains at
during the cool-down ramp. Therefore the amount of C remains at  for
for  . However, if either O2 or CO2 is added to the sweep gas, it starts oxidizing C at a temperature
. However, if either O2 or CO2 is added to the sweep gas, it starts oxidizing C at a temperature  that is generally lower than
that is generally lower than  . This is illustrated by the top part of Fig. 2b illustrating that within the time interval
. This is illustrated by the top part of Fig. 2b illustrating that within the time interval  C is consumed by the reaction with the added oxidant before
C is consumed by the reaction with the added oxidant before  is reached, implying that the amount of C at the onset of CTR
is reached, implying that the amount of C at the onset of CTR  is lower than the initial amount
is lower than the initial amount . After this point of time, i.e.,
. After this point of time, i.e.,  , C is consumed both by the reaction with the added oxidant and by CTR until the temperature drops below
, C is consumed both by the reaction with the added oxidant and by CTR until the temperature drops below  . As the temperature decreases from
. As the temperature decreases from  to
to 
 the amount of C continues to decrease because of the reaction with the oxidant to eventually stabilize at
the amount of C continues to decrease because of the reaction with the oxidant to eventually stabilize at  for
for 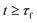 . Due to likely high rates of the oxidation reactions at the temperatures in question, the consumption of C by the added oxidant is expected to be mass-transfer limited, thereby occurring at a constant rate owing to a constant gas velocity and an insignificantly decreasing particle size.21 Accordingly, the amount of C that would be observed in the absence of CTR, i.e. in the absence of MgO, is designated by the straight dashed line in the top sketch of Fig. 2b
. Due to likely high rates of the oxidation reactions at the temperatures in question, the consumption of C by the added oxidant is expected to be mass-transfer limited, thereby occurring at a constant rate owing to a constant gas velocity and an insignificantly decreasing particle size.21 Accordingly, the amount of C that would be observed in the absence of CTR, i.e. in the absence of MgO, is designated by the straight dashed line in the top sketch of Fig. 2b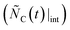 . Therefore, the amount of C consumed by CTR only is represented by
. Therefore, the amount of C consumed by CTR only is represented by . The analogous description applies for the discussion of temporal CO partial pressures illustrated in the bottom parts of Fig. 2. Again, the constant partial pressure of CO that would be observed in the absence of CTR
. The analogous description applies for the discussion of temporal CO partial pressures illustrated in the bottom parts of Fig. 2. Again, the constant partial pressure of CO that would be observed in the absence of CTR  stems from the assumption that the consumption of C by the added intermediate is mass-transfer limited.
stems from the assumption that the consumption of C by the added intermediate is mass-transfer limited.
In general, the rates of C consumption and the resulting CO production by the side reactions of the suspected intermediates with C are specific to the oxidant added to the sweep gas. The dependence of these rates on the total sweep gas flow rate and/or the partial pressure of the oxidants can be assessed through a series of tests with pure C and/or C-(inert solid) blends swept with O2–Ar and CO2–Ar mixtures. The equal amounts of C available for CTR regardless of which oxidant is fed with the sweep, i.e.,
 | (8) |
 , (ii) the flow rates of the O2–Ar and CO2–Ar sweep gas mixtures, and (iii) the partial pressures of O2 and CO2 in the sweep gas mixtures.
, (ii) the flow rates of the O2–Ar and CO2–Ar sweep gas mixtures, and (iii) the partial pressures of O2 and CO2 in the sweep gas mixtures.
However, even when the feed rates and compositions of the O2–Ar and the CO2–Ar sweep gas mixtures are adjusted to ensure the same consumption rates of C, the corresponding CO production rates are different because the oxidation of C with CO2 produces twice as much CO per mole of C. This results in  , which may affect the extent of CTR through the effect of the CO partial pressure on the onset temperature of CTR and/or its rate. Moreover, even though satisfying the equation set (8) ensures that the amounts of C available for CTR under the O2–Ar and CO2–Ar sweeps are roughly the same at all times, the amount of C decreases with time faster in these cases than if no oxidant is added to the sweep. Therefore, the presence of oxidants in the sweep may result in a lower extent of the CTR merely because of a lower amount of C available for CTR but not because of suppressing forward reactions (2) and/or (4). To account for the effects of the differences in both the amounts of C available for CTR and the effective CO partial pressures, one thus needs to establish a reference for comparing the extents of CTR obtained under sweep gas mixtures containing O2 or CO2 with those measured in the absence of either of the oxidants in the sweep. Such a reference range of the extents may be determined by using the initial amounts of C set at
, which may affect the extent of CTR through the effect of the CO partial pressure on the onset temperature of CTR and/or its rate. Moreover, even though satisfying the equation set (8) ensures that the amounts of C available for CTR under the O2–Ar and CO2–Ar sweeps are roughly the same at all times, the amount of C decreases with time faster in these cases than if no oxidant is added to the sweep. Therefore, the presence of oxidants in the sweep may result in a lower extent of the CTR merely because of a lower amount of C available for CTR but not because of suppressing forward reactions (2) and/or (4). To account for the effects of the differences in both the amounts of C available for CTR and the effective CO partial pressures, one thus needs to establish a reference for comparing the extents of CTR obtained under sweep gas mixtures containing O2 or CO2 with those measured in the absence of either of the oxidants in the sweep. Such a reference range of the extents may be determined by using the initial amounts of C set at
 | (9) |
 | (10) |
 . This choice of the reaction conditions encompasses the expected effects of the extra consumption of C by the oxidants added to the sweep on the C/MgO ratios and CO partial pressures during the CTR. The pertinent reaction pathway(s) may then be conclusively identified if adding an oxidant to the sweep (i) has no effect on the extent of CTR or (ii) it results in a CTR extent that is below the reference range of the CTR extents. If, however, adding an oxidant to the sweep suppresses the Mg production but the corresponding CTR extent is higher than that obtained with no oxidant in the sweep and with
. This choice of the reaction conditions encompasses the expected effects of the extra consumption of C by the oxidants added to the sweep on the C/MgO ratios and CO partial pressures during the CTR. The pertinent reaction pathway(s) may then be conclusively identified if adding an oxidant to the sweep (i) has no effect on the extent of CTR or (ii) it results in a CTR extent that is below the reference range of the CTR extents. If, however, adding an oxidant to the sweep suppresses the Mg production but the corresponding CTR extent is higher than that obtained with no oxidant in the sweep and with  , the decision cannot be made without considering the effective species partial pressures in the reaction atmosphere and/or the effect of the initial C/MgO ratio on the extent of CTR.
, the decision cannot be made without considering the effective species partial pressures in the reaction atmosphere and/or the effect of the initial C/MgO ratio on the extent of CTR.
3 Experimental
3.1 Program
The methodology presented in the previous section was implemented through the experimental program comprising three phases as outlined in Table S1 of section S2 of the ESI.† The first phase involves experiments exploiting a standard temperature program under an O2–Ar sweep having the total inlet molar rate and composition set at and
and  , respectively. It starts with comparison experiment #1 which represents the reaction of
, respectively. It starts with comparison experiment #1 which represents the reaction of  moles of MgO blended with
moles of MgO blended with  moles of C to determine temporal amounts of the residual carbon in the blend
moles of C to determine temporal amounts of the residual carbon in the blend  indicated by the solid line in the top sketch of Fig. 2b. In the next step of this phase, the same initial amount of C
indicated by the solid line in the top sketch of Fig. 2b. In the next step of this phase, the same initial amount of C  was oxidized under the same sweep gas mixture in the absence of MgO to quantify the C consumption in the absence of CTR, i.e., to determine the values of
was oxidized under the same sweep gas mixture in the absence of MgO to quantify the C consumption in the absence of CTR, i.e., to determine the values of 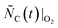 indicated by the dashed line in the top sketch of Fig. 2b. With
indicated by the dashed line in the top sketch of Fig. 2b. With  and
and  at hand, one can determine
at hand, one can determine  and
and  and, therefore,
and, therefore,  and
and  , as well as the extent of CTR during comparison experiment #1.
, as well as the extent of CTR during comparison experiment #1.
Phase 2 repeats the same steps of phase 1 under the standard 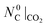 ,
,  , and
, and  that ensures the same C consumption in the absence of MgO, as observed in phase 1 (i.e.,
that ensures the same C consumption in the absence of MgO, as observed in phase 1 (i.e.,  A for
A for  ). The reaction of
). The reaction of 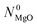 moles of MgO blended with
moles of MgO blended with  moles of C under the CO2–Ar sweep gas mixture having the molar rate and CO2 composition adjusted to satisfy the equalities imposed by eqn (8) represents comparison experiment #2.
moles of C under the CO2–Ar sweep gas mixture having the molar rate and CO2 composition adjusted to satisfy the equalities imposed by eqn (8) represents comparison experiment #2.
Phase 3 involves the reference CTR experiments performed under the standard temperature program in the absence of either O2 or CO2 in the sweep. The reacting blends comprised  moles of MgO and C in the amounts set according to eqns (9) and (10), with
moles of MgO and C in the amounts set according to eqns (9) and (10), with  and
and  determined in phases 1 and 2. Each of these blends is then reacted under both (i) an Ar sweep and (ii) the CO–Ar sweep having the flow rate and composition adjusted to ensure that the CO partial pressures during the experiments resemble those observed during comparison experiment #2
determined in phases 1 and 2. Each of these blends is then reacted under both (i) an Ar sweep and (ii) the CO–Ar sweep having the flow rate and composition adjusted to ensure that the CO partial pressures during the experiments resemble those observed during comparison experiment #2  .
.
The conclusive discrimination among the reaction pathways under consideration is based on establishing that the extent of CTR observed in the comparison experiments (#1 and/or #2) is either (i) unaffected by the presence of the oxidants in the sweep or (ii) lower than the lowest extent of the CTR observed in the reference experiments of phase 3. The former would imply the relevance of the MgO(s)–C(s) boundary reaction while the latter would point to reactions (2) and/or (4) as the prevailing pathway(s).
3.2 Materials
Table 1 lists the sources, specific surface areas (Micromeritics TriStar 3000 N2 adsorption analyzer), volume-based mean particle sizes (HORIBA LA-950 laser scattering analyzer), and impurities contained in the as-received solid raw materials used in this study: MgO and C as reactants and Al2O3 as the inert diluent for the C oxidation experiments in the absence of MgO. The discrepancy between the ratios of the BET areas and the mean particle sizes of MgO and C implies that these materials were either highly porous or that they comprised agglomerates of finer particles.MgO and Al2O3 powders contained H2O and CO2 as impurities adsorbed from the surroundings. The MgO powder additionally contained both of these impurities chemically bonded in the forms of Mg(OH)2 and MgCO3. The as-received charcoal contained moisture, volatile matter, and ash. The weight fractions of the impurities in the as-received MgO and Al2O3 powders ( and
and  , respectively) and charcoal (
, respectively) and charcoal ( ,
, 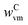 , and
, and  ) were determined as described in section S3 of the ESI.†
) were determined as described in section S3 of the ESI.†
3.3 Apparatus
Fig. 3 shows a schematic of the experimental apparatus. The reactant bed ② (a MgO–C blend, an Al2O3–C blend, or C alone) was placed into the assembly shown in more detail on the left side of the figure. The reactant bed was poured over the graphite felt (Sigratherm® GFA5) ④ protected with a C layer of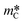 = 0.23 g ③ to prevent the infiltration of MgO into the felt, thereby allowing the complete recovery of the residual MgO after the reaction. Seven Al2O3 tubes (∅10 × 2 mm, l = 10 mm) ⑤ separated the felt bottom from the support ⑥ (Schupp Ceramics, Ultraboard, mullite fibers, ∅58 mm, l = 20 mm) in order to prevent a reaction of the SiO2 from the mullite support with the graphite felt. Seven boreholes (∅4 mm) in the support allowed the removal of sweep and product gases. The packed bed assembly was placed into a reactor tube ⑦ (Al2O3, ∅70 × 5 mm, l = 1200 mm) and held in place at the location of the hot zone by five support tubes ⑧ (Al2O3, ∅58 × 5 mm, l = 100 mm). Heat was provided by an electrically heated tube furnace ⑨ (Carbolite STF 16-450) equipped with an R-type thermocouple ⑩ measuring the temperature in the furnace chamber at the height of the hot zone (the location is indicated by a dot in Fig. 3). The part of the reactor tube below the furnace was cooled by surrounding air via natural convection and provided a cooling zone for precipitating the Mg(g) product. Sweep gas flow rates were controlled by calibrated mass flow controllers
= 0.23 g ③ to prevent the infiltration of MgO into the felt, thereby allowing the complete recovery of the residual MgO after the reaction. Seven Al2O3 tubes (∅10 × 2 mm, l = 10 mm) ⑤ separated the felt bottom from the support ⑥ (Schupp Ceramics, Ultraboard, mullite fibers, ∅58 mm, l = 20 mm) in order to prevent a reaction of the SiO2 from the mullite support with the graphite felt. Seven boreholes (∅4 mm) in the support allowed the removal of sweep and product gases. The packed bed assembly was placed into a reactor tube ⑦ (Al2O3, ∅70 × 5 mm, l = 1200 mm) and held in place at the location of the hot zone by five support tubes ⑧ (Al2O3, ∅58 × 5 mm, l = 100 mm). Heat was provided by an electrically heated tube furnace ⑨ (Carbolite STF 16-450) equipped with an R-type thermocouple ⑩ measuring the temperature in the furnace chamber at the height of the hot zone (the location is indicated by a dot in Fig. 3). The part of the reactor tube below the furnace was cooled by surrounding air via natural convection and provided a cooling zone for precipitating the Mg(g) product. Sweep gas flow rates were controlled by calibrated mass flow controllers  and
and  (Bronkhorst EL-Flow Select series). The low-pressure environment was provided by a vacuum pump
(Bronkhorst EL-Flow Select series). The low-pressure environment was provided by a vacuum pump  (Adixen ACP15) protected by a particle filter
(Adixen ACP15) protected by a particle filter  (Whatman, GF/F grade glass fiber filter). The pressure inside the reactor tube was monitored using a pressure sensor
(Whatman, GF/F grade glass fiber filter). The pressure inside the reactor tube was monitored using a pressure sensor  (Kistler Instrumente AG, type 4045A1) positioned in the cold zone above the furnace and controlled via a globe valve
(Kistler Instrumente AG, type 4045A1) positioned in the cold zone above the furnace and controlled via a globe valve  positioned in front of the vacuum pump. An overpressure relief valve
positioned in front of the vacuum pump. An overpressure relief valve  was set at 30 kPa overpressure relative to ambient pressure. The product gas composition was measured every 65 seconds using a gas chromatograph
was set at 30 kPa overpressure relative to ambient pressure. The product gas composition was measured every 65 seconds using a gas chromatograph  (Agilent M200).
(Agilent M200).
3.4 Procedure
The MgO–C blends were prepared by stirring grams of as-received MgO powder and
grams of as-received MgO powder and  grams of as-received charcoal powder with a spatula in a pill glass and occasionally breaking agglomerates until the blends appeared homogeneous. To investigate the reaction of C with O2 added to the sweep gas, MgO was substituted with
grams of as-received charcoal powder with a spatula in a pill glass and occasionally breaking agglomerates until the blends appeared homogeneous. To investigate the reaction of C with O2 added to the sweep gas, MgO was substituted with  grams of as-received Al2O3 powder that does not react with C within the pressure and temperature ranges investigated.22 The effective amounts of the MgO, Al2O3 and C in the blends (
grams of as-received Al2O3 powder that does not react with C within the pressure and temperature ranges investigated.22 The effective amounts of the MgO, Al2O3 and C in the blends ( ,
,  and
and  , respectively) were calculated as
, respectively) were calculated as | (11) |
The reaction of C with CO2 added to the sweep gas was investigated using  grams of as-received charcoal powder without diluting it with Al2O3.
grams of as-received charcoal powder without diluting it with Al2O3.
The reactant beds (MgO–C, Al2O3–C, or C alone) were poured into the packed bed assembly after which the apparatus was sealed and the vacuum pump was started. Then, the globe valve in front of the vacuum pump was opened and the total pressure inside the reactor was reduced to 0.8–1.9 kPa under 0.16–0.39 LN min−1 of Ar sweep (Messer 4.6). After pressure equilibration, the furnace was heated under a continuing Ar flow to 1000 °C at a 20 °C min−1 ramp rate and held at 1000 °C for 15 minutes to ensure the complete dissociation of Mg(OH)2 and MgCO3 contained in the starting MgO and the evaporation of volatile matter contained in the starting charcoal. In some experiments, the gas flow was then switched to one of the bottled gas mixtures – 5% O2–Ar (Messer 5.0), 5% CO2–Ar (Messer 4.8), or 5% CO–Ar (Messer 4.7) flowing at rates in the range of 0.16–0.39 LN min−1 which resulted in a total pressure of 0.8–1.9 kPa and therefore initial partial pressures of O2, CO2 and CO of 40–95 Pa. The furnace was then ramped at 20 °C min−1 to the desired setpoint temperature  of 1375, 1400 or 1450 °C and held there for 30 minutes, after which the furnace was shut off and allowed to cool off. When a gas mixture was used as the sweep, it was replaced by Ar when the furnace temperature reached 1250 °C.
of 1375, 1400 or 1450 °C and held there for 30 minutes, after which the furnace was shut off and allowed to cool off. When a gas mixture was used as the sweep, it was replaced by Ar when the furnace temperature reached 1250 °C.
A possible deposition of C in the cooling zone via reverse Boudouard reaction (5)23 was tested by feeding a 5% CO–Ar mixture into the empty reactor maintained at 1450 °C under a CO partial pressure of ∼95 Pa and measuring the amount of produced CO2 in the product gas.
3.5 Calculations
 and
and  , respectively. The extent
, respectively. The extent  refers to the extent of the reverse reaction (5), i.e.,
refers to the extent of the reverse reaction (5), i.e.,  .
.
 and (b) in the cooling zone
and (b) in the cooling zone  when C is swept with O2–Ar and CO2–Ar mixtures in the absence of MgO. Note: the extent
when C is swept with O2–Ar and CO2–Ar mixtures in the absence of MgO. Note: the extent  ≥ 0 refers to the extent of the reverse reaction (5).
≥ 0 refers to the extent of the reverse reaction (5).
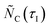 and
and  (see Fig. 2) were estimated combining balance eqns (12), (14), and (16) for the O2–Ar sweep and eqns (13) and (15) for the CO2–Ar sweep as
(see Fig. 2) were estimated combining balance eqns (12), (14), and (16) for the O2–Ar sweep and eqns (13) and (15) for the CO2–Ar sweep as
 | (18) |
 | (19) |
In eqns (18) and (19),  represents the total molar amount of species i entrained with the product gas up to the point of time
represents the total molar amount of species i entrained with the product gas up to the point of time  calculated as
calculated as
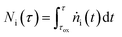 | (20) |
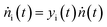 | (21) |
 and
and  representing the temporal mole fractions of species i determined by gas chromatography and the temporal total molar rates of the product gas, respectively. The latter was calculated as
representing the temporal mole fractions of species i determined by gas chromatography and the temporal total molar rates of the product gas, respectively. The latter was calculated as | (22) |
 | (23) |
 | (24) |
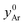 represents the mole fraction of Ar in the inlet sweep gas mixture and
represents the mole fraction of Ar in the inlet sweep gas mixture and  is the total molar flow rate of the sweep gas
is the total molar flow rate of the sweep gas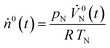 | (25) |
 standardized with a flow definer (MesaLabs, Bios DryCal Definer 220) at
standardized with a flow definer (MesaLabs, Bios DryCal Definer 220) at  = 101.3 kPa and
= 101.3 kPa and  = 0 °C for a given output to the mass-flow controller MFC 2.
= 0 °C for a given output to the mass-flow controller MFC 2.
The only remaining variables needed to calculate the temporal amounts of carbon viaeqns (18) and (19) are the extents of Boudouard reaction (5) . As these extents scale with the CO concentration in the cooling zone, they were evaluated by flowing a pilot CO–Ar stream through the setup kept under typical reaction conditions. This evaluation demonstrated the absence of CO2 in the effluent at a CO partial pressure of 95 Pa, thereby allowing to consider that
. As these extents scale with the CO concentration in the cooling zone, they were evaluated by flowing a pilot CO–Ar stream through the setup kept under typical reaction conditions. This evaluation demonstrated the absence of CO2 in the effluent at a CO partial pressure of 95 Pa, thereby allowing to consider that  for
for  ≤ 95 Pa.
≤ 95 Pa.
Under the CO2–Ar sweep, temporal partial pressures of CO in the hot zone expected in the absence of CTR were approximated by the values that were observed during the C oxidation experiments in the absence of MgO as
 | (26) |
Under the O2–Ar sweep, however, the outlet rate of CO may not be representative of the CO rate coming from the hot zone because of CO oxidation viareaction (7) that may have proceeded in the cooling zone. However, as reaction (7) produces a mole of CO2 per mole of CO, the rate of CO in the hot zone  may be bounded as
may be bounded as
 | (27) |
Owing to the high dilution of the product gas with Ar ( ≈ 0.9–0.95) the total molar rate was not significantly different between the hot zone and the outlet, i.e.
≈ 0.9–0.95) the total molar rate was not significantly different between the hot zone and the outlet, i.e.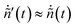 , which results in
, which results in  . Therefore, the partial pressure of CO in the hot zone is estimated as
. Therefore, the partial pressure of CO in the hot zone is estimated as
 | (28) |
The composition and the flow rate of the CO–Ar sweep in the reference CTR experiments was selected such that the resulting 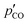 observed in the absence of CTR matched the highest CO partial pressures observed during the C oxidation experiments performed under O2–Ar and CO2–Ar sweeps in the absence of MgO.
observed in the absence of CTR matched the highest CO partial pressures observed during the C oxidation experiments performed under O2–Ar and CO2–Ar sweeps in the absence of MgO.
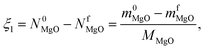 | (29) |
 is the mass of the unreacted MgO in the residual reactant blend that was determined by thermogravimetry, as described in section S4 of the ESI.†
is the mass of the unreacted MgO in the residual reactant blend that was determined by thermogravimetry, as described in section S4 of the ESI.†
The presence of O2 or CO2 in the sweep gas, however, precludes direct calculation of 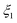 viaeqn (29) as some of the produced Mg(g) may re-oxidize within the hot zone via reverse reactions (2) and (4) to the extent that is not known. For this reason, the extents of CTR for the comparison runs of phases 1 and 2 were estimated exploiting the overall C balance and assuming that the amount of C removed by the CTR is approximately equal to the amount of the reduced MgO, as suggested by the overall reaction (1). Based on the reactions listed in Table 4, this amount of C corresponds to the molar extent of reaction (1) expressed as
viaeqn (29) as some of the produced Mg(g) may re-oxidize within the hot zone via reverse reactions (2) and (4) to the extent that is not known. For this reason, the extents of CTR for the comparison runs of phases 1 and 2 were estimated exploiting the overall C balance and assuming that the amount of C removed by the CTR is approximately equal to the amount of the reduced MgO, as suggested by the overall reaction (1). Based on the reactions listed in Table 4, this amount of C corresponds to the molar extent of reaction (1) expressed as
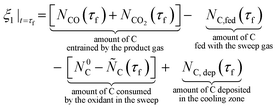 | (30) |
 | (31) |
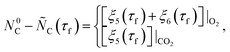 | (32) |
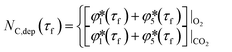 | (33) |
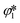 ≥ 0 and
≥ 0 and  ≥ 0 refer to the extents of the reverse reactions (1) and (5).
≥ 0 refer to the extents of the reverse reactions (1) and (5).
The total amount of fed CO2 was determined as
 | (34) |
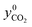 represents the mole fraction of CO2 in the inlet sweep gas mixture. However, if either O2 or CO2 is present in the sweep gas, the five reaction extents listed in Table 4 cannot be calculated based on the measured CO and CO2 outlet mole rates as the only information available. While the need for extents
represents the mole fraction of CO2 in the inlet sweep gas mixture. However, if either O2 or CO2 is present in the sweep gas, the five reaction extents listed in Table 4 cannot be calculated based on the measured CO and CO2 outlet mole rates as the only information available. While the need for extents  and
and  can be conveniently circumvented by calculating the final amount of C in the absence of CTR
can be conveniently circumvented by calculating the final amount of C in the absence of CTR  according to eqns (18) and (19), respectively, the final amount of deposited C
according to eqns (18) and (19), respectively, the final amount of deposited C  ranging as
ranging as | (35) |
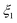 is determined via the MgO balance eqn (29). As in this case
is determined via the MgO balance eqn (29). As in this case  =
=  = 0 and
= 0 and | (36) |
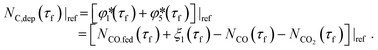 | (37) |
As the amount of C deposited in the cooling zone increases with the increase in the partial pressures of Mg and CO, one of the reference experiments should be performed under conditions ensuring the highest  within the range of the conditions investigated. Using this value as the estimate of the higher limit for the amount of C deposited during the comparison runs of phases 1 and 2 will only inflate the extents of the CTR in those runs. Since the CTR mechanism can be discriminated if one of the CTR extents from the comparison runs is lower than the lowest CTR extent observed in the reference experiments of phase 3, this approach should make the decision only more conservative.
within the range of the conditions investigated. Using this value as the estimate of the higher limit for the amount of C deposited during the comparison runs of phases 1 and 2 will only inflate the extents of the CTR in those runs. Since the CTR mechanism can be discriminated if one of the CTR extents from the comparison runs is lower than the lowest CTR extent observed in the reference experiments of phase 3, this approach should make the decision only more conservative.
4 Results and discussion
4.1 Phase 1: O2–Ar sweep
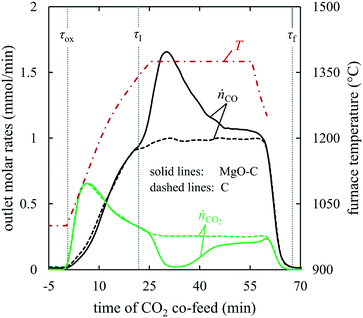
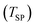 : 1375, 1400, and 1450 °C. Fig. 4 shows a comparison of the outlet CO, CO2, and O2 molar flow rates in the product gas from the experiments with the MgO–C and Al2O3–C blends at 1375 °C; the results for the remaining two setpoint temperatures are shown in section S5 of the ESI.† The onset of the CTR was identified at
: 1375, 1400, and 1450 °C. Fig. 4 shows a comparison of the outlet CO, CO2, and O2 molar flow rates in the product gas from the experiments with the MgO–C and Al2O3–C blends at 1375 °C; the results for the remaining two setpoint temperatures are shown in section S5 of the ESI.† The onset of the CTR was identified at 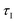 ≈ 22 min by the inflection point of the CO molar rate observed with the MgO–C blend. The amount of Al2O3 for the Al2O3–C blend (20.1 mmol) was selected to match the heat capacity of the substituted MgO, thereby providing an equal sink for the heat released by the exothermic reaction (3). This resulted in a good agreement between the CO production rates with these two blends prior to the onset of CTR. This agreement could not be achieved with C alone (see Fig. S2 of section S5 of the ESI†) which has been attributed to the increase in the local temperature of the C bed due to exothermic reaction (3) (
≈ 22 min by the inflection point of the CO molar rate observed with the MgO–C blend. The amount of Al2O3 for the Al2O3–C blend (20.1 mmol) was selected to match the heat capacity of the substituted MgO, thereby providing an equal sink for the heat released by the exothermic reaction (3). This resulted in a good agreement between the CO production rates with these two blends prior to the onset of CTR. This agreement could not be achieved with C alone (see Fig. S2 of section S5 of the ESI†) which has been attributed to the increase in the local temperature of the C bed due to exothermic reaction (3) ( = −110.5 kJ mol−1 (ref. 24)). The CO2 observed in the outlet was attributed to reaction (6) taking place in the hot zone and/or reaction (7) taking place in the hot and/or cooling zone. Lower CO2 and O2 product flows in the test with MgO–C compared to those observed with Al2O3–C implied the re-oxidation of (i) Mg(g/l/s)via reverse reactions (2) and (4) taking place in the hot and/or cooling zone and (ii) deposited C viareactions (3) and (6) taking place in the cooling zone only.
= −110.5 kJ mol−1 (ref. 24)). The CO2 observed in the outlet was attributed to reaction (6) taking place in the hot zone and/or reaction (7) taking place in the hot and/or cooling zone. Lower CO2 and O2 product flows in the test with MgO–C compared to those observed with Al2O3–C implied the re-oxidation of (i) Mg(g/l/s)via reverse reactions (2) and (4) taking place in the hot and/or cooling zone and (ii) deposited C viareactions (3) and (6) taking place in the cooling zone only.
 = 47.1 ± 0.15 mmol over the entire temperature range investigated. The final amount of C in the absence of CTR
= 47.1 ± 0.15 mmol over the entire temperature range investigated. The final amount of C in the absence of CTR  decreased from 31.6 at 1375 °C to 26.6 mmol at 1450 °C. This decrease was attributed mainly to the increase in the durations of the heating and cooling temperature ramps that increased the total duration of O2 co-feed from 60 min at
decreased from 31.6 at 1375 °C to 26.6 mmol at 1450 °C. This decrease was attributed mainly to the increase in the durations of the heating and cooling temperature ramps that increased the total duration of O2 co-feed from 60 min at  = 1375 °C to 73 min at
= 1375 °C to 73 min at  = 1450 °C. At the same time, the C consumption in the experiments with the Al2O3–C blend was essentially unaffected by an increase in
= 1450 °C. At the same time, the C consumption in the experiments with the Al2O3–C blend was essentially unaffected by an increase in  (see section S5 of the ESI†). This, together with a roughly constant CO production rate once the temperature stabilized at
(see section S5 of the ESI†). This, together with a roughly constant CO production rate once the temperature stabilized at  , confirms that the oxidation of C in these experiments was controlled by film diffusion which for the typical C conversion of 12–17% implies an essentially constant conversion rate.25 With the total
, confirms that the oxidation of C in these experiments was controlled by film diffusion which for the typical C conversion of 12–17% implies an essentially constant conversion rate.25 With the total  ∼0.8 kPa,
∼0.8 kPa,  was in the range 55–65 Pa and 60–75 Pa at 1375 °C and 1450 °C, respectively.
was in the range 55–65 Pa and 60–75 Pa at 1375 °C and 1450 °C, respectively.
4.2 Phase 2: CO2–Ar sweep
 : 1375, 1400, and 1450 °C. Fig. 5 shows a comparison of the outlet CO, CO2, and O2 molar flow rates in the product gas from the experiments with the MgO–C blend and C alone at 1375 °C; the results for the remaining two setpoint temperatures are shown in section S5 of the ESI† and the repeatability of the experiments is demonstrated in section S6 of the ESI.† The onset point of CTR was identified at
: 1375, 1400, and 1450 °C. Fig. 5 shows a comparison of the outlet CO, CO2, and O2 molar flow rates in the product gas from the experiments with the MgO–C blend and C alone at 1375 °C; the results for the remaining two setpoint temperatures are shown in section S5 of the ESI† and the repeatability of the experiments is demonstrated in section S6 of the ESI.† The onset point of CTR was identified at  ≈ 22 min as the time stamp of the inflection point of the CO molar flow rate obtained with the MgO–C blend. Markedly, good agreement between the data sets for
≈ 22 min as the time stamp of the inflection point of the CO molar flow rate obtained with the MgO–C blend. Markedly, good agreement between the data sets for  was achieved even without diluting C with Al2O3. This was attributed to the endothermic consumption of C by CO2viareaction (5) (
was achieved even without diluting C with Al2O3. This was attributed to the endothermic consumption of C by CO2viareaction (5) ( = +172.4 kJ mol−1 (ref. 24)). As was the case for the O2–Ar sweep, once the temperature stabilized at
= +172.4 kJ mol−1 (ref. 24)). As was the case for the O2–Ar sweep, once the temperature stabilized at 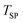 the production of CO due to the consumption of C with co-fed CO2 was approximately constant and essentially independent of
the production of CO due to the consumption of C with co-fed CO2 was approximately constant and essentially independent of  (see section S5 of the ESI†). A decrease in the molar rate of CO2 observed with the C–MgO during CTR compared to that observed during C oxidation experiments with C alone was attributed to the oxidation of Mg(g/l/s) and via reverse reaction (4) taking place in the hot and/or cooling zone.
(see section S5 of the ESI†). A decrease in the molar rate of CO2 observed with the C–MgO during CTR compared to that observed during C oxidation experiments with C alone was attributed to the oxidation of Mg(g/l/s) and via reverse reaction (4) taking place in the hot and/or cooling zone.
 = 47.8 ± 0.05 mmol over the entire temperature range investigated. As was the case for the tests under an O2–Ar sweep, the final amount of C in the absence of CTR
= 47.8 ± 0.05 mmol over the entire temperature range investigated. As was the case for the tests under an O2–Ar sweep, the final amount of C in the absence of CTR  decreased with increasing
decreased with increasing 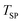 from 32.6 mmol at 1375 °C to 31.8 and 27.5 mmol at 1400 °C and 1450 °C, respectively, mainly because of the prolonged duration of the CO2 co-feed. Compared to the O2–Ar sweep experiments, the relative differences between the calculated values of
from 32.6 mmol at 1375 °C to 31.8 and 27.5 mmol at 1400 °C and 1450 °C, respectively, mainly because of the prolonged duration of the CO2 co-feed. Compared to the O2–Ar sweep experiments, the relative differences between the calculated values of  and of
and of  were ≤2% and ≤4%, respectively (see section S7 of the ESI†). The set of conditions listed in Table 6 therefore provided that
were ≤2% and ≤4%, respectively (see section S7 of the ESI†). The set of conditions listed in Table 6 therefore provided that  and
and 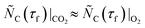 (see eqn (8)) thus no iterations with different CO2–Ar sweep flow rates and/or compositions mentioned in section 2.2 and Table S1 of section S2 in the ESI† were needed. With
(see eqn (8)) thus no iterations with different CO2–Ar sweep flow rates and/or compositions mentioned in section 2.2 and Table S1 of section S2 in the ESI† were needed. With  ,
,  was approximately constant at
was approximately constant at  and ranged from 94 Pa (
and ranged from 94 Pa ( = 1375 °C) to 97 Pa (
= 1375 °C) to 97 Pa ( = 1450 °C) (see section S7 of the ESI†).
= 1450 °C) (see section S7 of the ESI†).
4.3 Phase 3: Ar and CO–Ar sweeps
The initial conditions selected for the reference CTR experiments under CO–Ar and Ar sweeps are shown in Table 7. The starting amounts of C for the blends with moles of MgO were selected to satisfy
moles of MgO were selected to satisfy 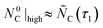 and
and 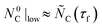 . To account for the observed decrease in
. To account for the observed decrease in  with an increase in
with an increase in  ,
,  was adjusted to 32.9, 31.6, and 26.6 mmol for
was adjusted to 32.9, 31.6, and 26.6 mmol for 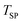 = 1375, 1400, and 1450 °C, respectively. The higher limit of CO partial pressure in the sweep was set to
= 1375, 1400, and 1450 °C, respectively. The higher limit of CO partial pressure in the sweep was set to  = 95 Pa to match
= 95 Pa to match  that ranged from 94 to 97 Pa. This was accomplished by flowing a 5% CO–Ar mixture with a normal flow rate
that ranged from 94 to 97 Pa. This was accomplished by flowing a 5% CO–Ar mixture with a normal flow rate 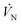 = 0.39 LN min−1, which resulted in
= 0.39 LN min−1, which resulted in 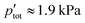 . The total normal flow rate of the Ar sweep was chosen to be the same as that of the CO–Ar sweep (0.39 LN min−1) also resulting in
. The total normal flow rate of the Ar sweep was chosen to be the same as that of the CO–Ar sweep (0.39 LN min−1) also resulting in  .
.
| (°C) | Sweep gas | (LN min−1) | in the sweep (Pa) | Solids | (mmol) | (mmol) | (mmol) | (—) |
|---|---|---|---|---|---|---|---|---|
| 1375 | 5% CO–Ar | 0.390 | 95 | MgO–C | 49.6 | 47.5 | — | 0.96 |
| 5% CO–Ar | 0.390 | 95 | MgO–C | 49.6 | — | 32.9 | 0.67 | |
| Ar | 0.390 | — | MgO–C | 49.6 | 47.5 | — | 0.96 | |
| 1400 | 5% CO–Ar | 0.390 | 95 | MgO–C | 49.6 | 47.5 | — | 0.96 |
| 5% CO–Ar | 0.390 | 95 | MgO–C | 49.6 | — | 31.6 | 0.64 | |
| Ar | 0.390 | — | MgO–C | 49.6 | 47.5 | — | 0.96 | |
| 1450 | 5% CO–Ar | 0.390 | 95 | MgO–C | 49.6 | 47.5 | — | 0.96 |
| 5% CO–Ar | 0.390 | 95 | MgO–C | 49.6 | — | 26.6 | 0.54 | |
| Ar | 0.390 | — | MgO–C | 49.6 | 47.5 | — | 0.96 | |
The outlet gas in all the reference experiments comprised only Ar and CO. Fig. 6 indicates a remarkable similarity between the outlet CO molar rates observed during the comparison experiments under the CO2–Ar sweep and the reference experiments under the CO–Ar sweep with  . As expected, the outlet CO molar rates observed under the O2–Ar sweep were lower. The results of the experiments performed under the Ar sweep with
. As expected, the outlet CO molar rates observed under the O2–Ar sweep were lower. The results of the experiments performed under the Ar sweep with  and the CO–Ar sweep with
and the CO–Ar sweep with  are also available in section S5 of the ESI.†
are also available in section S5 of the ESI.†
 | ||
Fig. 6 CO molar rates observed at (a)  = 1400 °C and (b) 1450 °C with = 1400 °C and (b) 1450 °C with  ≈ ≈  = 47.5 mmol and = 47.5 mmol and  = 49.6 mmol under CO–Ar (black solid line), CO2–Ar (green dashed line) and O2–Ar (blue dotted line). A comparison of the CO molar rates for 1375 °C is shown in section S5 of the ESI.† = 49.6 mmol under CO–Ar (black solid line), CO2–Ar (green dashed line) and O2–Ar (blue dotted line). A comparison of the CO molar rates for 1375 °C is shown in section S5 of the ESI.† | ||
In spite of the absence of CO2 in the outlet gas during the experiments completed under CO–Ar and Ar sweeps, visual inspection of the cooling zone upon these experiments confirmed the presence of deposited C, MgO and/or Mg. This implies that C may have deposited as a consequence of the direct recombination of the products via the reverse reaction (1). The other possibility is that the condensed Mg(l/s) may have catalyzed the Boudouard reaction (as C deposition was not observed at up to 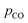 ≤ 95 Pa in the absence of CTR) but that the produced CO2 was completely consumed by the Mg(g/l/s) reoxidation via the reverse reaction (4). This scenario would impose the equality of the extents of the reverse reactions (4) and (5), i.e.
≤ 95 Pa in the absence of CTR) but that the produced CO2 was completely consumed by the Mg(g/l/s) reoxidation via the reverse reaction (4). This scenario would impose the equality of the extents of the reverse reactions (4) and (5), i.e.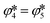 , thereby making the Boudouard reaction only a step of the reverse overall reaction (1), as suggested by Hischier et al.15
, thereby making the Boudouard reaction only a step of the reverse overall reaction (1), as suggested by Hischier et al.15
4.4 Discrimination of the prevailing reaction pathways
The extents of CTR calculated as outlined in section 3.5.3 are normalized by = 49.6 mmol and shown in Fig. 7 as a function of
= 49.6 mmol and shown in Fig. 7 as a function of  . The highest amount of C deposited in the cooling zone, indicating the highest
. The highest amount of C deposited in the cooling zone, indicating the highest  and
and  , is expected to be observed in the experiment performed with the higher initial amount of C
, is expected to be observed in the experiment performed with the higher initial amount of C  = 47.5 mmol under the CO–Ar sweep as this experiment resulted in the highest Mg(g) production and the highest
= 47.5 mmol under the CO–Ar sweep as this experiment resulted in the highest Mg(g) production and the highest  in the cooling zone. Therefore, setting the maximum amount of deposited C to the amount calculated for this particular experiment, i.e.,
in the cooling zone. Therefore, setting the maximum amount of deposited C to the amount calculated for this particular experiment, i.e., | (38) |
 as
as | (39) |
 | ||
Fig. 7 Normalized extents of CTR as a function of 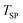 under (I) an Ar sweep with under (I) an Ar sweep with  = 47.5 mmol (open circles), (II) a CO–Ar sweep with = 47.5 mmol (open circles), (II) a CO–Ar sweep with  = 47.5 mmol (filled circles), (III) a CO2–Ar sweep with = 47.5 mmol (filled circles), (III) a CO2–Ar sweep with  = 53.3 mmol corresponding to = 53.3 mmol corresponding to  = 47.8 mmol ≈ = 47.8 mmol ≈  (open diamonds), (IV) a CO–Ar sweep with (open diamonds), (IV) a CO–Ar sweep with  = 32.9 (1375 °C), 31.6 (1400 °C), and 26.6 mmol (1450 °C) (filled squares) and (V) an O2–Ar sweep with = 32.9 (1375 °C), 31.6 (1400 °C), and 26.6 mmol (1450 °C) (filled squares) and (V) an O2–Ar sweep with  = 53.3 mmol corresponding to = 53.3 mmol corresponding to  = 47.1 mmol ≈ = 47.1 mmol ≈ 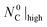 (open triangles). The error bars for the comparison runs (III and V) represent (open triangles). The error bars for the comparison runs (III and V) represent  calculated viaeqn (37) for the experiments from the set (II) as the expected maximum of calculated viaeqn (37) for the experiments from the set (II) as the expected maximum of  . The dotted lines are added only to indicate trends. . The dotted lines are added only to indicate trends. | ||
The results presented in Fig. 7 can be summarized as follows:
(A) The addition of CO to the sweep gas slightly suppresses the Mg(g) production (data set II versus data set I); therefore, the runs performed under the CO–Ar sweep (data sets II and IV) may serve as a conservative reference for the CTR in the absence of the oxidants in the sweep.
(B) The extents of CTR in the comparison experiments performed under the O2–Ar sweep with  (data set V) were up to 60% lower than those obtained under the CO–Ar sweep with
(data set V) were up to 60% lower than those obtained under the CO–Ar sweep with  (data set IV).
(data set IV).
(C) The extents of CTR in the comparison experiments performed under the CO2–Ar sweep with  (data set III) were lower than those obtained under the CO–Ar sweep with
(data set III) were lower than those obtained under the CO–Ar sweep with  (data set II) but higher than those obtained under the CO–Ar sweep with
(data set II) but higher than those obtained under the CO–Ar sweep with  (data set IV).
(data set IV).
As the addition of O2 to the sweep showed no facilitating effect on the sintering of MgO (see Fig. S13 in section S8 of the ESI†), the O2-induced suppression of the Mg(g) production in spite of a more favorable C/MgO ratio (observation B) can be attributed only to the equilibrium shifts of reactions (2) and/or (4) because of the potential increase in both  and the ratio
and the ratio  . The former can be estimated from the outlet O2 molar rates and then used to calculate the equilibrium partial pressures of Mg resulting from the MgO dissociation (reaction (2)) according to the analysis presented in section S10 of the ESI.† These equilibrium partial pressures were five to six orders of magnitude lower than the partial pressures of Mg estimated from the observed Mg(g) productions, as described in section S9 of the ESI.† This implies that at
. The former can be estimated from the outlet O2 molar rates and then used to calculate the equilibrium partial pressures of Mg resulting from the MgO dissociation (reaction (2)) according to the analysis presented in section S10 of the ESI.† These equilibrium partial pressures were five to six orders of magnitude lower than the partial pressures of Mg estimated from the observed Mg(g) productions, as described in section S9 of the ESI.† This implies that at  values of 1375 °C and 1400 °C the MgO dissociation (reaction (2)) essentially did not contribute to the Mg(g) production under the O2–Ar sweep (data set V). It should be noted that this claim cannot be extended to the experiment performed at
values of 1375 °C and 1400 °C the MgO dissociation (reaction (2)) essentially did not contribute to the Mg(g) production under the O2–Ar sweep (data set V). It should be noted that this claim cannot be extended to the experiment performed at 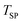 = 1450 °C as the outlet O2 molar rate was essentially zero during a part of this experiment, hence the thermal dissociation could have taken place also. Using analogous reasoning outlined in S10 of the ESI† to estimate
= 1450 °C as the outlet O2 molar rate was essentially zero during a part of this experiment, hence the thermal dissociation could have taken place also. Using analogous reasoning outlined in S10 of the ESI† to estimate  ratios for the experiments under the CO2–Ar sweep (data set III) indicates that the partial pressures of Mg estimated from the observed Mg(g) productions are ∼20 to 4000 times higher than those predicted by the equilibrium of reaction (4). This implies that under the CO2–Ar sweep (data set III) the MgO reduction with CO (reaction (4)) essentially did not contribute to the Mg(g) production.
ratios for the experiments under the CO2–Ar sweep (data set III) indicates that the partial pressures of Mg estimated from the observed Mg(g) productions are ∼20 to 4000 times higher than those predicted by the equilibrium of reaction (4). This implies that under the CO2–Ar sweep (data set III) the MgO reduction with CO (reaction (4)) essentially did not contribute to the Mg(g) production.
A plausible explanation for the observed O2 and CO2 effects is that Mg(g) is produced via both (a) MgO thermal dissociation and (b) MgO reduction with CO that take place in parallel. The role of C is to remove the intermediates O2 and CO2 from the reaction sites, thereby favoring forward reactions (2) and (4). Markedly, at 1375 °C and 1400 °C the sums of the extents obtained under the CO2–Ar (data set III) and O2–Ar sweeps (data set V) are essentially equal to the extents obtained under the Ar–CO sweep (data set II) (see Fig. S14, section S11 of the ESI†); at 1450 °C, the sum slightly exceeds the extent from the data set II which could be attributed to the Mg(g) production under the O2–Ar sweep partly to the MgO dissociation also. This implies that adding O2 or CO2 to the sweep allows the isolation of one of the steps by preventing the other and to determine that at 1375 °C and 1400 °C roughly twice as much Mg(g) was produced via the MgO dissociation compared to the MgO reduction with CO.
The conclusion outlined above appears to contradict the claim by Chubukov et al.14 who have advocated that under the same reaction conditions MgO(s)–C(s) boundary reaction governs the Mg(g) production rather than MgO dissociation. It should be noted that the disagreement may be existing only in the interpretation of the same reaction mechanism. Specifically, the MgO dissociation (reaction (2)) is sustained by the removal of O2 from the MgO surface via oxidation of C (reaction (3)) and the sum of these two steps results in the stoichiometry of the overall reaction (1). However, there is no evidence supporting the relevance of a direct solid–solid reaction. In fact, the results of the comparison experiments presented in Fig. 7 indirectly demonstrate that the contact between the materials is not a factor. In particular, the CTR experiments under the O2–Ar and the CO2–Ar sweeps (data sets III and V, respectively) were performed with the same initial amount of C which was pre-oxidized to essentially the same extent before reaching the onset temperature of CTR (see Fig. S10 of section S7 in the ESI†). Therefore, the pre-oxidation of C with O2 and CO2 should have affected the interfacial contact between the materials in the same way. Yet, the extents of the MgO reduction under the CO2–Ar sweep are roughly twice as high compared to those observed under the O2–Ar sweep.
5 Summary and conclusions
This work discriminates the prevailing reaction pathways of the carbothermic reduction of MgO for normalized reduction extents of up to 0.4 achieved within the temperature and pressure ranges of 1375–1450 °C and 1–2 kPa, respectively. It demonstrates that Mg(g) is produced in the ratio ∼2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 via (1) MgO thermal dissociation and (2) MgO reduction with CO that take place in parallel. These pathways generate O2 (pathway 1) and CO2 (pathway 2) as the intermediates that diffuse and react with C, thereby sustaining the Mg production. It is also argued that the MgO dissociation pathway may have been confused with the MgO(s)–C(s) boundary reaction advocated by previous investigators, which relies on the direct contact of the solid reactants. Therefore, our findings imply that the rate of the overall MgO reduction may be controlled by the diffusion of the intermediates from the MgO(s) surface to the C(s) surface and/or a loss of the MgO surface area due to sintering rather than by the loss of the direct contact between MgO(s) and C(s).
1 via (1) MgO thermal dissociation and (2) MgO reduction with CO that take place in parallel. These pathways generate O2 (pathway 1) and CO2 (pathway 2) as the intermediates that diffuse and react with C, thereby sustaining the Mg production. It is also argued that the MgO dissociation pathway may have been confused with the MgO(s)–C(s) boundary reaction advocated by previous investigators, which relies on the direct contact of the solid reactants. Therefore, our findings imply that the rate of the overall MgO reduction may be controlled by the diffusion of the intermediates from the MgO(s) surface to the C(s) surface and/or a loss of the MgO surface area due to sintering rather than by the loss of the direct contact between MgO(s) and C(s).
Nomenclature
Greek symbols
Subscripts
| imp | Impurity |
| N | Normal (0 °C and 101.3 kPa) |
| tot | Total |
| vm | Volatile matter |

| O2–Ar sweep |
| CO2–Ar sweep |

| Intermediate (O2–Ar sweep or CO2–Ar sweep) |

| High initial amount of C |

| Low initial amount of C |
Abbreviations
| CTR | Carbothermic reduction |
| MFC | Mass flow controller |
| SSA | Specific surface area |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Professor Aldo Steinfeld for providing financial support and allowing the use of the facilities and resources within the Professorship for Renewable Energy Carriers at ETH Zürich and to Simon Ackermann, Brendan Bulfin, Christopher Muhich, Michael Takacs, David Weibel, and Vladimir Paunovic for fruitful discussions.References
- F. Cherubini, M. Raugei and S. Ulgiati, Resour., Conserv. Recycl., 2008, 52, 1093–1100 CrossRef.
- S. Das, JOM, 2008, 60, 63–69 CrossRef CAS.
- J. Du, W. Han and Y. Peng, J. Cleaner Prod., 2010, 18, 112–119 CrossRef CAS.
- F. Gao, Z. Nie, Z. Wang, X. Gong and T. Zuo, Int. J. Life Cycle Assess., 2009, 14, 480–489 CrossRef CAS.
- S. Ehrenberger, H. Dieringa and H. Friedrich, Life Cycle Assessment of Magnesium Components in Vehicle Construction, I. o. V. Concepts, German Aerospace Center DLR, Stuttgart, Germany, 2013 Search PubMed.
- Environmental Profile Report for the European Aluminium Industry - Reference Year 2010, European Aluminum Association, Brussels, 2013 Search PubMed.
- A. Tharumarajah and P. Koltun, J. Cleaner Prod., 2007, 15, 1007–1013 CrossRef.
- G. Brooks, S. Trang, P. Witt, M. N. H. Khan and M. Nagle, JOM, 2006, 58, 51–55 CrossRef CAS.
- I. Vishnevetsky and M. Epstein, Sol. Energy, 2015, 111, 236–251 CrossRef CAS.
- M. E. Gálvez, A. Frei, G. Albisetti, G. Lunardi and A. Steinfeld, Int. J. Hydrogen Energy, 2008, 33, 2880–2890 CrossRef.
- L. Hong, H. Y. Sohn and M. Sano, Scand. J. Metall., 2003, 32, 171–176 CrossRef CAS.
- M. Nusheh, H. Yoozbashizadeh, M. Askari, N. Kuwata, J. Kawamura, J. Kano, F. Saito, H. Kobatake and H. Fukuyama, ISIJ Int., 2010, 50, 668–672 CrossRef CAS.
- M. Halmann, A. Frei and A. Steinfeld, Miner. Process. Extr. Metall. Rev., 2011, 32, 247–266 CrossRef CAS.
- B. A. Chubukov, A. W. Palumbo, S. C. Rowe, I. Hischier, A. J. Groehn and A. W. Weimer, Thermochim. Acta, 2016, 636, 23–32 CrossRef CAS.
- I. Hischier, B. A. Chubukov, M. A. Wallace, R. P. Fisher, A. W. Palumbo, S. C. Rowe, A. J. Groehn and A. W. Weimer, Sol. Energy, 2016, 139, 389–397 CrossRef CAS.
- K. L. Komarek, A. Coucoulas and N. Klinger, J. Electrochem. Soc., 1963, 110, 783–791 CrossRef CAS.
- L. Rongti, P. Wei and M. Sano, Metall. Mater. Trans. B, 2003, 34, 433–437 CrossRef.
- Y. Tian, B.-Q. Xu, C.-B. Yang, B. Yang, T. Qu, H.-X. Liu, Y.-N. Dai and D.-C. Liu, Metall. Mater. Trans. B, 2014, 45, 1936–1941 CrossRef CAS.
- G. Levêque and S. Abanades, Thermochim. Acta, 2015, 605, 86–94 CrossRef.
- W.-D. Xie, J. Chen, H. Wang, X. Zhang, X.-D. Peng and Y. Yang, Rare Met., 2016, 35, 192–197 CrossRef CAS.
- S. Yagi and D. Kunii, Symp. (Int.) Combust., [Proc.], 1955, 5, 231–244 CrossRef.
- M. Kruesi, M. E. Galvez, M. Halmann and A. Steinfeld, Metall. Mater. Trans. B, 2011, 42, 254–260 CrossRef CAS.
- M. Kogler, E.-M. Köck, B. Klötzer, T. Schachinger, W. Wallisch, R. Henn, C. W. Huck, C. Hejny and S. Penner, J. Phys. Chem. C Nanomater. Interfaces, 2016, 120, 1795–1807 CrossRef CAS PubMed.
- A. Roine, Outokumpu HSC Chemistry for Windows 5.0, Outokumpu Research Oy, Finland, 2002 Search PubMed.
- O. Levenspiel, Chemical reaction engineering, John Wiley & Sons, New York, 3rd edn, 1999 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8re00295a |
| ‡ Exclusive upstream processes. |
| This journal is © The Royal Society of Chemistry 2019 |