Open Access Article
Open Access ArticleRevealing quantum mechanical effects in enzyme catalysis with large-scale electronic structure simulation†
Zhongyue
Yang
 a,
Rimsha
Mehmood
ab,
Mengyi
Wang
ac,
Helena W.
Qi
ab,
Adam H.
Steeves
a,
Rimsha
Mehmood
ab,
Mengyi
Wang
ac,
Helena W.
Qi
ab,
Adam H.
Steeves
 a and
Heather J.
Kulik
a and
Heather J.
Kulik
 *a
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: hjkulik@mit.edu; Tel: +617 253 4584
bDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
cDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 29th November 2018
Abstract
Enzymes have evolved to facilitate challenging reactions at ambient conditions with specificity seldom matched by other catalysts. Computational modeling provides valuable insight into catalytic mechanism, and the large size of enzymes mandates multi-scale, quantum mechanical-molecular mechanical (QM/MM) simulations. Although QM/MM plays an essential role in balancing simulation cost to enable sampling with the full QM treatment needed to understand electronic structure in enzyme active sites, the relative importance of these two strategies for understanding enzyme mechanism is not well known. We explore challenges in QM/MM for studying the reactivity and stability of three diverse enzymes: i) Mg2+-dependent catechol O-methyltransferase (COMT), ii) radical enzyme choline trimethylamine lyase (CutC), and iii) DNA methyltransferase (DNMT1), which has structural Zn2+ binding sites. In COMT, strong non-covalent interactions lead to long range coupling of electronic structure properties across the active site, but the more isolated nature of the metallocofactor in DNMT1 leads to faster convergence of some properties. We quantify these effects in COMT by computing covariance matrices of by-residue electronic structure properties during dynamics and along the reaction coordinate. In CutC, we observe spontaneous bond cleavage following initiation events, highlighting the importance of sampling and dynamics. We use electronic structure analysis to quantify the relative importance of CHO and OHO non-covalent interactions in imparting reactivity. These three diverse cases enable us to provide some general recommendations regarding QM/MM simulation of enzymes.
1. Introduction
Enzymes have evolved to facilitate challenging reactions at ambient temperature and pressure often with exquisite specificity seldom matched in industrial synthesis.1,2 Nevertheless, the role of the enzyme environment in either statically or dynamically promoting these characteristics remains challenging to understand. Although protein crystallography and spectroscopy provide foundational knowledge of protein structure, atomistic simulation of enzymes3 represents a crucial component in our understanding of how the protein environment contributes to rate enhancement and reaction specificity. Unlike their molecular catalyst counterparts or the unit cells of heterogeneous catalysts, enzymes are usually thousands of atoms in size. Low computational cost, e.g., with molecular mechanics (MM) force fields, is required to enable sampling, whereas quantum mechanical (QM) treatment is needed to describe bond rearrangement, polarization, and charge transfer. These complementary strengths have motivated the development of a multilevel approach known as QM/MM.4–12In QM/MM, the region of primary interest is treated with QM and the remainder is treated at the MM level of theory, making the computationally demanding QM simulation the bottleneck. As a result, typical QM region sizes were until recently on the order of tens of atoms (i.e. ligands and a few residues).12–14 The use of small QM regions has motivated method development10,15–24 to minimize QM/MM boundary effects and to evaluate25 how moving beyond conventional electrostatic embedding to advanced, polarizable,18,25–30 force field treatments may improve QM/MM descriptions. Even with these advances, larger QM region sizes may be necessary in order to describe charge transfer between MM residues and the QM active site.31,32
A key question in QM/MM modeling is how to best choose residues to include in the QM region. When small QM regions or clusters are employed, it is possible to predict physically reasonable mechanisms,33 but one may also not be aware of missing critical residues needed to describe the essential enzyme action.34,35 Despite the successes of force fields in capturing much of globular protein structure, there are notable cases where even fundamental properties of loop structure36 or disordered proteins37 are qualitatively described incorrectly, casting doubt on the ability of present MM force fields to reveal the mechanistic significance of residues in these contexts. Although conventional QM methods employed, e.g., semi-local or hybrid density functional theory (DFT) have their own shortcomings,38 treating more of the enzyme with DFT implicitly imparts more physics and makes fewer assumptions than a conventional fixed point charge force field.39 Significant advances31,36,40–46 in computational efficiency over the past decade have made it possible to carry out fully ab initio, quantum chemical simulation of polypeptides36,47 as well as QM/MM treatments of enzymes with large (>100 atoms) QM regions.
Numerous researchers35,48–56 have leveraged these advances to identify how sensitive mechanistic predictions are to QM region size in QM/MM calculations. The majority of resulting studies have revealed an exceptionally slow approach to asymptotic limits (ca. 500–1000 atoms) for radial convergence: NMR shieldings,48,49 proton transfer,57 solvation effects,50 barrier heights,35,51,52 forces,53 excitation energies,54,58,59 partial charges,55 bond critical points,60 and redox potentials.56 There are cases where smaller QM regions have been motivated (e.g., in DNA models61 and the cytochrome P450cam metalloenzyme62), so there is increasing consensus that it is important to determine the extent to which a given property is sensitive to the QM region size.
Over the years, numerous systematic approaches have been developed for QM region construction based on perturbation or evaluation of properties at the MM51,63 or QM35,62,64,65 level. Incorporating essential residues in this way can reveal fundamental, quantum mechanical aspects of enzyme mechanism, such as environment-mediated charge separation of neutralizing substrates or essential charge-assisted, low-barrier hydrogen bonds that would be impossible to accurately describe with only MM or across the QM/MM boundary.34 In this work we use the phrase “quantum mechanical effects” to focus on classical treatment of nuclei but explicit modeling of the electronic wavefunction. In addition, the quantum mechanical nature of such interactions can change as a function of the reaction coordinate. Although efficient sampling methods are under development,66 challenges remain in how to pair large QM regions from systematic QM/MM region construction with the sampling needed to understand the role of protein conformational dynamics in enzyme mechanism. Indeed, although static QM/MM simulations with over 1000 QM atoms have become increasingly routine, hundreds of thousands of such energy evaluations are required to compute a potential of mean force. Thus, identification of the relationship of dynamical and free energy properties to QM region size has primarily been studied with semi-empirical methods,53,67–71 and this effort has only recently been extended to fully-first principles DFT.34
Given this tension between the need for sampling and for first-principles modeling of the electronic structure of the active site in order to develop mechanistic insight into enzyme action, it is important to continue to develop an understanding of when large scale electronic structure simulation is essential and what insight it can bring. The rest of this article is outlined as follows. In section 2, we provide the computational details of the calculations employed in this work. In section 3, we show how QM region selection impacts the insights obtained from QM/MM simulation of three representative enzymes with diverse structures: Mg2+-dependent catechol O-methyltransferase72 (COMT), the metal-free glycyl radical enzyme choline trimethylamine lyase (CutC),73–75 and a structural Zn-metal binding site in the DNA methyltransferase DNMT1.76 Finally, in section 4, we provide our conclusions.
2. Computational details
Protein structure and preparation
CutC holoenzyme with choline substrate (PDB ID: 5FAU73) and DNMT1 with a 19 base-pair DNA strand and S-adenosyl homocysteine (SAH) inhibitor (3PTA76) were obtained from the PDB. SAH in DNMT1 was modified to the S-adenosyl methionine (SAM) cofactor with Avogadro,77 and 54 missing residues were added and refined using loop refinement with Modeller78 (ESI,† Table S1). Protonation states of apoenzyme residues were assigned using the H++ webserver79–82 assuming a pH of 7.0 with all other defaults applied. Protonation states of residues adjacent to cofactors or substrates were manually assigned (ESI,† Tables S2 and S3). The two resulting holoenzymes (CutC −19 net charge, DNMT −22 net charge) were used as starting points for subsequent force field file preparation with the tleap utility in AMBER83 prior to simulation (ESI,† Tables S4 and S5). All standard residues were simulated with the AMBER ff14SB84 force field. The zinc Amber force field (ZAFF)85 was employed for Zn2+ and coordinating residues in DNMT, and DNMT DNA base pairs were described by the parmBSC1 force field86 (ESI,† Table S6). Due to our focus on fixed tetrahedral coordination of Zn2+ with protein residues, we used the original ZAFF rather than newer forms87,88 that have improved descriptions of variable coordination, e.g., in aqueous solvent. Force fields for remaining organic non-standard residues were generated using the generalized AMBER force field (GAFF)89 with partial charges assigned from restrained electrostatic potential (RESP) charges90 obtained with GAMESS-US91 at the Hartree-Fock/6-31G*92 level, as implemented by the R.E.D.S. web server.93–95 The proteins were solvated with 10–15 Å of TIP3P96 water in a periodic rectangular prism box and neutralized with Na+ counterions. Starting AMBER topology and coordinate files for the 151![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 473-atom DNMT1 and 111
473-atom DNMT1 and 111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 741-atom CutC systems are provided in the ESI.†
741-atom CutC systems are provided in the ESI.†
MM equilibration and dynamics
Protein molecular dynamics (MD) equilibration and production steps in AMBER were as follows: i) restrained (1000 steps) and unrestrained (2000 steps) minimizations were carried out, ii) 10 ps NVT heating to 300 K with a Langevin thermostat with collision frequency of 1.0 ps−1 and a random seed, iii) 1 ns NPT equilibration using the Berendsen barostat with a pressure relaxation time of 2 ps, and iv) 250 ns (100 ns for CutC) of production dynamics. All MD employed SHAKE97 with a 2 fs timestep and a 10 Å electrostatic cutoff.QM/MM calculations
In QM/MM simulations, TeraChem42,98 was used for the QM portion, and OpenMM99 was used for DNMT1 whereas AMBER83 was used for CutC. In all cases, we employ electrostatic embedding and hydrogen link atoms for passivating covalent bonds that cross the QM to MM border, i.e.:| EQM/MM = EQM + EQM−MM + EMM | (1) |
QM regions were selected systematically for CutC resulting in a QM region containing 281 atoms (0 net charge) for use in QM/MM, and larger 1043 atom snapshots (+2 net charge) were used for electronic structure analysis (ESI,† Table S7). Radial QM regions up to 417 atoms and 0 net charge were studied for Zn2 in DNMT1 as described in the main text. MD snapshots selected for QM/MM were post-processed using the center of mass utility in PyMOL100 to generate the largest possible spherical droplet centered around each protein that was circumscribed by the original rectangular prism periodic box. These snapshots are simulated without electrostatic cutoff and only spherical cap boundary conditions enforced with a restraining potential of 1.5 kcal mol−1 Å−2. This lack of electrostatic cutoff combined with the use of electrostatic embedding means that the point charges of all MM atoms in the systems are explicitly included as one-electron nuclear-electron attraction terms in the QM calculation. For both CutC and DNMT1, the QM region is modeled with DFT using the range-separated exchange-correlation functional ωPBEh101 (ω = 0.2 bohr−1) with an LANL2DZ effective core potential102 on Zn in DNMT1 and 6-31G*92 for the remaining atoms.
For DNMT1, rigid binding energies were computed from single point energies with and without Zn in MD snapshots at around 40, 60, and 100 ns from a 250 ns MD simulation (see ESI†). CutC simulations included 2000 step QM/MM minimizations followed by steered molecular dynamics (SMD). SMD in CutC used a 1000 kcal mol−1 Å−2 harmonic pulling force and 0.5 fs timestep over the reaction coordinate for around 2000 steps. The linear combination of distances (LCOD) reaction coordinates used were: 1) for hydrogen atom transfer the difference between the choline H distance to a C on choline and S(C489); and 2) for cholinyl radical deprotonation the difference between the hydroxyl H atom on cholinyl radical distance to the hydroxyl O atom or to E491 O− (see ESI† for starting configurations).
Analysis
Atom-wise and by-residue sums of Voronoi deformation density (VDD) or Mulliken charges and spins were evaluated on QM/MM SMD snapshots in CutC (every 10 snapshots) or in select MD snapshots for DNMT1, respectively. By-residue sums as well as real-space VDD charges103 were employed to reduce basis set sensitivity as in previous work35,62,64 for CutC. In CutC, hydrogen bonds were identified and quantified using the heuristic half of the potential energy density104 at the bond critical point (BCPs),105 as implemented in Multiwfn.106 Close contacts (<85% of sum of van der Waals radii) were identified and analyzed as described in the main text. For evaluation of pairwise interaction strength with QM or MM, capping H atoms were added on the backbone vector with a scaled bond length (1.09 Å for C–H, 1.01 Å for N–H). These pairs were geometry optimized in TeraChem42,98 at the B3LYP107–109/6-31G*92 level of theory with heavy atoms and capping H atoms frozen and the protein environment was mimicked with the conductor-like implicit solvent model (COSMO)47,110 with ε = 4. Optimizations used the L-BFGS algorithm in Cartesian coordinates, as implemented in DL-FIND,111 to default thresholds of 4.5 × 10−4 hartree per bohr for the maximum gradient and 1 × 10−6 hartree for the change in energy between steps. QM single points for energy decomposition analysis (EDA) were calculated with symmetry adapted perturbation theory (SAPT) at the DF-SAPT0 (ref. 112–114)/jun-cc-pVDZ level of theory, as implemented in Psi4.115 MM EDA was carried out with the generalized Born (GB) and surface area (SA) continuum solvation model approach (MM/GBSA) using the MMPBSA.py116 utility with the GB117 “OBC” model II, as previously motivated.118 The same force fields were employed as described previously, and only gas phase terms were retained for comparison to QM results.3. Results and discussion
3a. COMT: charge transfer in enzyme active sites
To explore QM region dependence in protein simulation, we begin by summarizing several 0 K QM/MM and finite-temperature dynamics studies we have previously carried out34,62,68,119 on the enzyme catechol O-methyltransferase (COMT). COMT is a SAM- and Mg2+-dependent MTase72 that reacts with catecholamine substrates bound in a bidentate fashion to Mg2+ at the active site120 (Fig. 1). The rate-determining121 step is direct SN2 methyl transfer122 from a positively charged SAM123 to a negatively charged, deprotonated catecholate124,125 (CAT) to produce neutral SAH and methylated catechol products (Scheme 1). The free energy barrier for this reaction is estimated from experimental kinetic studies to be 18.1 (ref. 126)–19.2 (ref. 127) kcal mol−1. The methyl group transfer process can be well defined by a single linear combination of distances (LCOD) coordinate that is the difference in bond length between the transferring methyl group to the SAM S atom versus the accepting catecholate O− to the methyl group (Fig. 1).COMT represents a challenging test case for simulation methods, beyond difficulties in predicting35,68–70,128–131 the experimental free energy barrier. Although numerous crystal structures of COMT consistently indicate an unusually short 2.6–2.8 Å non-bonded distance between the donating methyl group on SAM and the catecholate acceptor, classical MD simulations seldom, if ever, sample these distances.68,132,133 Instead, it was observed that large QM regions are essential to sampling these distances.35,134 Furthermore, from small QM region and gas phase cluster studies, it was hypothesized that charge neutralization might occur in the transition state.135 However, we have since determined34,35 that a critical role of the enzyme active site is to mediate charge transfer between the substrate and surroundings to increase charge separation at the transition state, an effect that can only be observed with larger QM regions.
Although significant QM region dependence and a mandate for larger QM regions in QM/MM simulation have been noted for numerous properties,35,51–55,58–60 COMT itself may be a good example of more extreme challenges in QM/MM simulation for enzyme catalysis. The substrates, SAM and CAT, themselves are large at already 64 atoms, and the size of SAM (ca. 15 Å end-to-end) as well as number of polar and charged functional groups means it can form numerous non-covalent interactions with the enzyme active site (Fig. 1). In addition to E90, E64, and S72 around SAM, catecholate also has the potential to form strong interactions with a neighboring E199 or K144 (Fig. 1).
Thus we revisit and make a comprehensive comparison of several strategies we have developed to understand how changing the QM region changes predictions of catalytic action both in 0 K reaction coordinates35,62 and in room temperature free energy simulations.34,68 Due in part to the ovoid shape of the substrates, radial convergence is very slow in COMT as judged through 0 K Ea and ΔErxn values.35 Both quantities converge only at around 500 atoms in the QM region, with small QM regions significantly overestimating asymptotically large QM region limits, and even qualitative discrepancies are observed such as endothermic reactions for the smallest QM regions35 (Fig. 2). In such a radial convergence study, residues are included at increasingly large distance cutoffs from a central point in the active site, thus providing limited guidance on which residues are essential to include within a given cutoff. For that reason, we developed methodologies designed to enable systematic QM region construction.
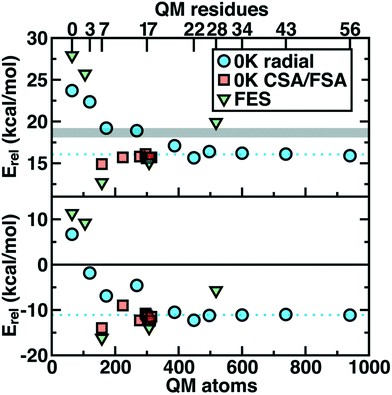 | ||
| Fig. 2 Barrier heights (top) and reaction energies (bottom) in kcal mol−1 for methyl transfer in COMT versus the number of atoms in the QM region obtained three ways: 0 K QM/MM properties from radially increasing distance cutoffs (blue circles, from ref. 35), systematically constructed regions (red squares, from ref. 62) and 300 K QM/MM free energy dynamics (green triangles, from ref. 34). (top) ΔG‡ at 300 K or the 0 K Ea with the experimental ΔG‡ range126,127 indicated as a gray shaded region that should only be compared to the green triangles. (bottom) ΔGrxn at 300 K or the 0 K ΔErxn. In both plots, the asymptotic limit from the average of the three largest 0 K radial QM regions is shown as a blue dotted line and should only be compared to the blue circles and red squares. Approximate protein residue counts for each QM region size are labeled on the x-axis at top. | ||
In charge shift analysis (CSA),35,62 we carry out QM/MM single points with large (ca. 1000 atom) QM regions on the protein once with the substrates/cofactors present and then rigidly removed. We compute the change in by-residue-summed partial charges on surrounding residues and determine them to be essential for a QM treatment if the change is above a threshold (typically, |0.04–0.05e|). Beyond obvious residues (e.g., Mg2+-coordinating D141, D169, and N170 or hydrogen bonding E64), this approach revealed35,62 surprising interactions with nonpolar residues, such as a V42 proximal to the substrates. Conversely, proximal charged residues need not necessarily be detected by this method if charge transfer to the substrates is limited.
The limitation of CSA is that it requires a 1000-atom QM calculation, which we circumvent in the complementary Fukui shift analysis (FSA) approach.62,64 In that method, we compute the by-residue condensed Fukui function of the core active site substrates (e.g., in COMT this corresponds to SAM, catecholate, and Mg2+) in the presence and absence of each additional residue one residue at a time, making FSA parallelizable. The Fukui function136 represents a measure of the substrate's electrophilicity or nucleophilicity, and the condensed,137 by-substrate-summed form simply represents what fraction of an added or removed electron is added or removed from the substrates.
Overall, CSA and FSA applied to COMT each reveal around 16 essential residues around the substrates or <300 atoms in comparison to 500 atoms from the radially converged region. The two methods predict 14 residues in common, despite computing fundamentally distinct quantities, with the non-overlapping residues being E64 and A73 for CSA and G66 and Y71 for FSA. The former CSA residues can be rationalized as only interacting with the substrate by mediation through many-body effects absent from FSA, whereas FSA may detect electronic interactions not mediated through charge transfer. Overall, QM/MM Ea and ΔErxn values obtained with CSA and FSA QM regions (ca. 300 atoms) were within <1 kcal mol−1 of the asymptotic limits (ca. 500–1000 atoms) and in significantly improved agreement over radial QM regions of comparable size62 (Fig. 2).
We further developed the charge deletion analysis (CDA) method to determine if any CSA- or FSA-selected residues could be judged as false positives. In CDA, we constructed a QM region consisting of the union of the CSA and FSA residues, and then we moved each residue back to the MM region one by one to determine if this caused a change to the by-residue-summed partial charges on the active site substrates or on neighboring residues. This approach also gave a ranking to residues selected by CSA or FSA and allowed us to identify even smaller QM regions that should contain the most essential residues.62 These 150–200 atom QM regions constructed from CDA-ranked CSA/FSA residues were within approximately 1 kcal mol−1 of the asymptotic limit of Ea and showed slightly poorer agreement for ΔErxn. Overall, agreement was dramatically improved over radial QM regions of equivalent size, and agreement was found to be best when the smaller QM region yielded consistent electronic structure properties (e.g., charge separation in the transition state) with the larger QM regions.
In a recent study,34 we sought to address whether these observations applied to first-principles QM/MM free energy simulations. Thus, we selected 5 QM regions that merged the principles of the radial study with the systematic methods we introduced: 1) a minimal QM region, 2) including the Mg2+-coordination sphere, 3) including the top-ranked residues from CDA, 4) the consensus residue set from CSA/FSA, and 5) a 0 K-asymptotically converged, 518 atom QM region. Similar trends of overestimating barrier heights and predicting endergonic reactions are observed for the smallest QM regions (Fig. 2). However, more variability is observed34 in the larger (ca. 150–500 atom) QM regions for free energy simulation than at 0 K62 (Fig. 2). Although the CSA/FSA region is by far in the best agreement with region 5, the discrepancy between the two regions is much larger than that for the equivalent at 0 K (Fig. 2). This discrepancy arose because i) differing QM regions led to sampling different trajectories and dynamics and ii) during dynamics residue proximity to the active site changed and sampled orientations that were not considered during CSA/FSA analysis. Understanding how this electronic structure evolves is essential to developing methods that go beyond CSA35,62 or FSA62,64 by incorporating dynamics.65 It is thus also useful to understand what electronic properties give rise to such slow convergence of energetics in the COMT active site.
From our recent study of QM/MM free energy simulation convergence,34 we now examine the residue-residue coupling of electronic properties from the largest QM region in that work (518 non-link atoms, 28 protein residues plus substrates, see Fig. 1). Specifically, we compute the by-residue Mulliken partial charge sums at every timestep of the 210 ps dynamics. If partial charge sums on each residue show little variation, an MM description with a fixed point-charge force field should adequately describe such residues. Thus, we investigate potential couplings by computing the covariance matrix of the by-residue partial charge sums (Fig. 3). To compare the three types of residues (i.e., with zero, one, or two bonded QM residues on either side along the protein chain) in this QM region on equal footing, the by-residue sum always includes both sidechain and backbone atoms. Isolating one example residue, E90, which is coordinated by the two I89 and I91 QM residues, reveals a comparable standard deviation of the charge for the sidechain-only by-residue sum (0.023e over 0.25 ps) in comparison to the full by-residue sums (0.028e over 0.25 ps) reported here. Further comparison of backbone and sidechain-derived effects will be the focus of future work.
Since the matrix is computed over the full reaction coordinate, SAM and catecholate have the largest individual variances and pairwise covariance as methyl transfer is associated with redistribution of their charges (Fig. 3). The Mg2+ cation, which is essential for COMT catalysis,72 has more moderate variance and is most strongly coupled to the catecholate charge, which is reasonable since catecholate remains doubly coordinated to Mg2+ throughout the reaction (see Fig. 1 and 3).
Somewhat surprisingly, D141, D169, N170, and water which all also coordinate the Mg2+ have overall low covariance with Mg2+, each other, and other protein residues (Fig. 3). The only exception to this observation is the neighboring residues D169 and N170, which exhibit significant covariation that is still less than other adjacent residue pairs (e.g., W143/K144), including those with neutral residues (e.g., A67/Y68 or Y71/S72, see Fig. 3). The observation of enhanced covariance between neighboring residues suggests some component of backbone participation in the overall factors that determine charge coupling. This confirms our earlier suggestions34 of reduced individual charge fluctuation for the Mg2+-coordinating residues in comparison to even non-polar residues more distant from the active site. These observations in COMT point to potentially reduced fluctuations and coupling between residues immobilized by binding to metals or co-factors, a common feature of metalloenzymes.
Although couplings between core active site residues and the Mg2+ coordination sphere are quite low, there are significant charge couplings between SAM/catecholate and other protein residues. Most of these residues reside in regions 3 and 4, including V42, E64, S72, and E199, reinforcing not just expected hydrogen bonding interaction partners but the surprising (i.e., V42) interactions noted through static CSA/FSA results62 (Fig. 3). These observations highlight that distance-based determination of QM region, which is frequently used in convergence studies,35,53 is an incomplete guide with regard to whether residues are coupled to each other or the active site. The region 3 and 4 residues also have among the strongest covariance within the individual region subset (Fig. 3). For intra-region coupling in the 10 residues designated as region 4, E64-Y71/S72 and E64/S119 covariances are observed, consistent with these residues forming hydrogen bonds during the reaction. Interestingly, covariances between substrate-adjacent, nonpolar M40 and charged E64 are nearly as high as some of these polar/charged hydrogen-bonding interactions (Fig. 3). In contrast, region 5 covariances are small both internally and with the other regions (Fig. 3). The most notable exceptions to this analysis for region 5 are i) L198, which is backbone adjacent to the high-variance, charged E199 and ii) similarly the E90-adjacent I89 (Fig. 3). When we observed differences in QM/MM free energy barriers between simulations with only region 4 vs. region 5 residues in the QM region, we attributed34 this difference to specific residues such as K144 that were missing from region 4. Interestingly, analysis of the covariance on the overall reaction coordinate, however, does not reveal a critical coupling between K144 or other region 5 residues and the core substrates (Fig. 3).
In addition to overall covariance across the reaction coordinate, we computed individual covariance matrices for reactant-(R), transition-state-(TS), and product-(P) like windows from the umbrella sampling simulations that individually correspond to 15 ps of dynamics. The R and P windows are the extrema from our umbrella-sampling path, with the methyl group fully on SAM in the former and a fully methylated catechol in the latter. To select the TS window, we determined the 0.1 Å LCOD region around the maximum of the QM/MM free energy surface to be Δ = d(S–C)–d(C–O) = 0.28–0.38 Å. We then determined that the window with a target Δ = 0.30 Å sampled this range of Δ values 95% of the time and selected it as our TS region. Comparison of R, TS, and P covariance matrices reveals notable differences in the three points along the reaction coordinate, reinforcing the significant reorganization of electronic structure in the enzyme active site along the reaction coordinate (Fig. 4).
Although SAM has one of the largest variances and couplings with other residues (e.g., E64 and S72) in the R window, as SAH in the P window its couplings and variance are among the lowest of all residues (Fig. 4). Conversely, CAT variance is highest in the product state, with strong coupling to S119 as well as E199 likely due to the formation of a low barrier, charge-assisted hydrogen bond in the product34 (Fig. 4). In the TS window, the core substrates have markedly decreased covariance with each other or with any other residues in comparison to R or P (Fig. 4). As a result, covariance of region 5 residue pairs such as W143/K144 or K144/L198 in the TS are of similar magnitudes to the strongest observed in other QM regions. Comparing R to P windows, it is evident that, although both covariance matrices have larger covariance magnitudes than the TS window, the contributions from more remote residues decrease across the reaction coordinate, with strong coupling of E64 and S72 in the R window absent in the P window (Fig. 4). Instead in the product state, E199 interactions dominate with reduced coupling of residues to E64 and S119 (Fig. 4).
Overall, covariance of charges sampled in different portions of the reaction coordinate, computed here for the first time on range-separated hybrid DFT QM/MM free energy simulation dynamics, provides distinct insight into how electronic structure evolves across a reaction coordinate. Sensitivity of the COMT reaction coordinate to QM region is likely related to the fact that the electronic structure evolves so significantly both during dynamics and across the reaction coordinate.
3b. CutC: electronic and geometric structure in radical reactions.
CutC (ref. 138) is an abundant glycyl radical enzyme (GRE)139,140 that catalyzes degradation of choline to trimethylamine (TMA) and acetaldehyde in the human gut microbiome (Scheme 2). After formation of a stable α-carbon glycyl radical at G821 by an activating enzyme, CutD,74 the formation of a short-lived and reactive cysteine radical, C489, has been proposed73,74 that can then initiate choline decomposition via C–H abstraction. The resulting cholinyl α-hydroxyalkyl radical likely undergoes deprotonation by an adjacent general base E491, weakening the C–N bond and leading to cleavage, in contrast to the 1,2-migration pathway suggested for other radical enzymes.141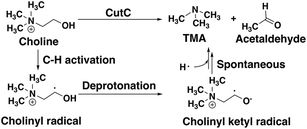 | ||
| Scheme 2 Putative reaction pathway for CutC-catalyzed choline degradation to trimethylamine (TMA) and acetaldehyde. | ||
Although the crystal structure of CutC with bound choline substrate73 can be used to infer the mechanism, QM/MM simulation can provide valuable insight to the dynamic and electronic rearrangements that occur during catalysis in the CutC active site. We focus on the two most essential and poorly understood steps in the CutC reaction mechanism: 1) short-lived cholinyl radical formation and 2) cholinyl radical (Cho˙) deprotonation (Scheme 2). Alternative mechanisms besides direct elimination for Cho˙ were ruled out based on stability of the relevant intermediates in both the gas phase and an implicit solvent environment that approximates the enzyme active site (ESI,† Table S8 and Fig. S1). The MD equilibration of CutC sampled choline dihedral configurations in the active site not expected to be reactive, although the reactive orientation was the predominant species (ESI,† Fig. S2 and S3).
Candidate QM region residues were determined using the systematic35 CSA method.34,62,64 With CSA, electronic reorganization was assessed in a large QM region that contained all residues within 6.5 Å of the choline substrate (i.e., 925 atoms) after C489A mutation and choline removal, as outlined in sec. 2 (ESI,† Table S4). For this CSA step, no geometry optimization is carried out of the greater protein except of the replaced methyl hydrogen atoms in the C489A mutation. Mutagenesis studies had identified138 Y208, D216, F395, E491, T502, and Y506 as relevant for catalysis. Due to the less polar substrate and active site, CutC charge shifts are lower than those observed in COMT and are largest for N393, E491, and D216 (Fig. 5 and ESI,† Fig. S4 and Table S7). After setting a reduced threshold of |0.02 e| for the charge shift to account for reduced polarity, 10 residues (ca. 200 atoms), including charged (E491, D216), polar (Y208, Q333, Q393), and nonpolar (W501, M336, G488, C489, V490) residues, are selected for the QM region. This includes D216 and E491 as well as Y208, but not the less-choline-proximal T502 and Y506 residues suggested by experimental mutagenesis138 (ESI,† Fig. S4). In addition to CSA selected residues, the loop (i.e., V819–S823) containing G821 responsible for forming the C489 radical was also included (ESI,† Table S7). Residues not detected by CSA are treated at the MM level of theory during SMD, which is expected to be sufficient due to the absence of charge transfer between the residues and the substrate, and subsequent electronic structure analysis was carried out on >1000 atom QM region snapshots (ESI,† Table S7).
To study the essential reaction steps for CutC, we map reaction coordinates with LCODs in SMD for C–H abstraction (i.e., the difference of S(C489)⋯H and C (Cho)–H distances) and O–H deprotonation (i.e., the difference of O–(E491)⋯H and O(Cho)–H distances), as described in the Computational details. These LCODs correspond to mapping the transfer of H atom and H+, respectively, but any spontaneous events that occur during these processes can also be observed during our SMD run. Because our SMD pulling speeds are too high to provide quantitative estimates of barrier heights,142 we focus instead on qualitative geometric rearrangements and on electronic structure (i.e., spin and charge transfer) changes that occur across the reaction coordinate.
For the C–H abstraction step, the H atom is transferred to the thiyl radical of C489 (Fig. 6). The Cho and C489 donor/acceptor atom separation is reduced to around 2.9 Å at the moment of transfer in comparison to a 3.9 Å separation in reactants and products (Fig. 6). At this point of minimum separation, the C–H distance is slightly shorter than the S–H distance (1.37 Å vs. 1.56 Å), consistent with the fact that the equilibrium C–H bond (1.09 Å) is shorter than the equilibrium S–H bond (1.33 Å) (Fig. 6). Across this reaction coordinate, we also observe spontaneous proton transfer from the hydroxyl group of choline to the carboxylate group of E491 (Fig. 6). In this case, the proton is shared between Cho˙ and E491, with oscillation consistent with a low barrier, charge-assisted hydrogen bond143 observed in the reaction. Here, the longer 1.6 Å O(Cho˙)–H distances correspond to the proton residing predominantly on E491 (Fig. 6). This observation of spontaneous proton transfer is consistent with the expected increased acidity of the hydroxyl proton on a radical, as it is known that the pKa values of α-hydroxy radicals can be reduced144 due to the formation of a stable ketyl radical anion.
For the deprotonation of the Cho˙ hydroxyl, we studied proton transfer from the hydroxyl to E491, increasing the separation of E491 and Cho˙ during deprotonation to ensure that the proton is fully transferred and no longer shared (Fig. 6). Starting from an initial structure where E491 O- is nearly 2.0 Å from the Cho˙ hydroxyl, driving forward separation and full transfer of the proton to E491 causes spontaneous cleavage of the deprotonated Cho˙ C–N bond (Fig. 6). Although oscillations in C–N bond length occur over the full reaction coordinate, C–N bond cleavage initiates at LCOD values beyond 0.5 Å, which corresponds to full localization of the proton on E491 and Cho˙ O−⋯H distances of slightly greater than the longest distances (i.e., >1.5 Å) observed in the previous reaction coordinate (Fig. 6). As soon as the C–N bond cleaves, it reaches a value greater than 2.0 Å, leading to unambiguous formation of trimethylamine (TMA) and acetaldehyde radical. Although direct elimination has been hypothesized,73 this is the first computational observation of spontaneous C–N cleavage in CutC. Slower pulling speeds or alternative sampling schemes are needed in future work to quantify the energy barrier in this step. During the trajectory, the acetaldehyde radical also rearranges, with formation of a planar geometry at the carbonyl oxygen and a shortening of the C–O distance to a double bond (Fig. 6 and ESI,† Fig. S5). This rearrangement can also be rationalized in terms of the CutC active site, which orients choline such that the radical p orbital is antiperiplanar to the C–N bond. This orientation enables hyperconjugation between the p orbital and C–N σ* orbital to weaken the C–N bond and enable direct TMA elimination. When we separately considered the pathway for protonation of the TMA group in Cho˙ by a protonated D216, we observed inversion of the TMA improper, C–N bond cleavage and acetaldehyde radical formation with a strong hydrogen bond to E491 as well (ESI,† Fig. S6). However, we ruled out this step because the D216 proton starts quite far (∼4 Å) from the N acceptor on Cho˙, requiring significant movement of the substrate for this step to occur (ESI,† Fig. S6).
Mulliken spins of the C489 S and choline C confirm that our SMD approach captures the H atom abstraction (Fig. 7). As the hydrogen bond of the Cho˙ radical forms to E491, spin starts to accumulate on the O atom of Cho˙ (Fig. 7). This indicates ketyl radical anion character with spin delocalization increasing the acidity of the hydroxyl group. Although the spin is split between the carbon and oxygen atom, the total spin on those two species is complementary to the S atom spin, indicating that only those two atoms accept the radical from C489 (Fig. 7). During O–H deprotonation, spin remains on Cho˙ until the TMA elimination begins (Fig. 6 and 7). The cleavage of the C–N bond is accompanied by the rearrangement of the radical: some small amount of spin accumulates on the N atom along with a transition of a significant amount of the spin to the other C atom on the newly formed acetaldehyde radical fragment (Fig. 7). In comparison, the forced TMA protonation step that also produces TMA elimination leads to less net spin on the nitrogen atom of the TMA fragment (ESI,† Fig. S7).
During Cho˙ deprotonation, spins appear delocalized over several species. Analysis of charges on these fragments can help rationalize some of these observations (Fig. 8). The total charge over all of fragments originating from Cho˙ decreases over the course of C–N bond cleavage from around +0.8e to +0.6e, reduced from the nominal +1 charge that would be expected (Fig. 8). We decompose this charge into i) the proton that is transferred to E491, ii) the acetaldehyde radical fragment, and iii) eliminated TMA (Fig. 8). From this decomposition, we observe that the charge on the transferring proton (+0.5e) is relatively constant, suggesting further that the two remaining fragments are nearly neutral after deprotonation (Fig. 8). This deviation is particularly apparent for TMA, which has a reduced partial charge from +0.6e to +0.2e at the end of the reaction step, suggesting that the appearance of the radical spin on the N atom of TMA arises in part because TMA is being eliminated as a neutral species, rather than a cation (Fig. 8). The weak negative net charge on the acetaldehyde radical is not obviously as significant, as it was instead positive in the case of forced TMA protonation following fragmentation, likely due to differences in the degree of hydrogen bonding with E491 (ESI,† Fig. S8).
Finally, we return to the nature of the non-covalent interactions in the active site of CutC that could be responsible for imparting its reactivity. Thus far, we have identified the E491-Cho interaction to be essential for TMA elimination, whereas we found protonation by D216 to be less plausible (ESI,† Fig. S6–S8). Earlier experimental work73 had also suggested that C–H⋯O interactions between TMA and adjacent D216, Y506, and Y208 could play an important role in positioning choline during the reaction. To quantify the relative role of C–H⋯O and O–H⋯O hydrogen bonds (HBs), we evaluate close contacts, defined as cases where two heavy atoms are within 85% or less of the sum of the distance of their van der Waals' radii, in the CutC crystal structure and our SMD trajectories (see Computational details). In the entire CutC crystal structure, 15 close contact residue pairs (12 O⋯O and 3 N⋯O) are observed that represent potential HB interactions, with most (10 of 15) being categorized as sidechain–sidechain (ESI,† Table S9). The interaction energies of the pairs of residues are all favorable, whether calculated with QM or MM methods with minimum total interaction strengths of around 4 kcal mol−1 (ESI,† Text S1). HB energies can also be directly estimated from the quantum theory of atoms in molecules (QTAIM) approach104,105 and are found to be at least 11 kcal mol−1, with the HB energy well correlated to heavy atom distances (Fig. 9). None of the heavy atom distances in putative C–H⋯O HBs were within close contact distance cutoffs (3.2–3.7 Å, vs. <2.7 Å for a C⋯O close contact). As a result, at most weakly favorable interactions are observed between these choline-residue pairs of 2.9 kcal mol−1 evaluated with SAPT0, and some interactions are weakly unfavorable (ESI,† Text S1). QTAIM HB energies for these pairs are also significantly smaller than for their O⋯O counterparts (0.7 to 4.0 kcal mol−1), commensurate with the longer heavy atom separations (Fig. 9).
Examining all C–H⋯O and O–H⋯O interactions sampled during our reaction coordinates confirms the observations made on the crystal structure (Fig. 9). Most C–H⋯O interactions range from 2.25 to 3.50 Å, whereas nearly all O–H⋯O hydrogen bonds have an H⋯O separation that ranges from 1.70 to 2.25 Å (Fig. 9). Due to the high order dependence on separation of hydrogen bond strength energies, C–H⋯O HBs are dramatically weaker than O–H⋯O HBs (i.e., 0–5 kcal mol−1vs. 5–25 kcal mol−1). Notably, the charge assisted O–H⋯O HB between the Cho˙ hydroxyl and E491 is expected to have a significant HB energy (i.e., >15 kcal mol−1) far in excess of the total contribution of the three C–H⋯O HBs (i.e., ∼6–7 kcal mol−1). Thus, while C–H⋯O interactions are expected to be useful for positioning the choline substrate, the E491 hydrogen bonding interaction likely plays the dominant role.
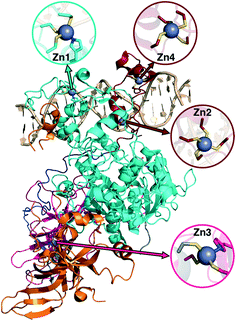
3c. DNMT1: considerations for structural metal cofactors
Metalloproteins present unique challenges for simulation, owing to the need to accurately describe the metalorganic bond at the cofactor site as well as noncovalent interactions in the broader active site. Metals typically play either a catalytic role, e.g., as in the heme in cytochrome P450 (ref. 145) or a structural role.146–148 Here, we study DNMTs, which are members of the broad class of MTases introduced in sec. 3a and are examples where bound metals play a structural role. In humans, DNMTs are responsibly for methylating the 5′ position of cytosine bases in CpG-rich islands using SAM as the methyl donor,149 an essential epigenetic process that is crucial for cell fate determination, gene silencing, and genome stability.150 We focus on DNMT1, which has been structurally characterized76 with its four native Zn metal binding sites intact (Fig. 10). Three of the sites (Zn1, Zn2, and Zn4) are adjacent to the DNA binding domain, whereas the remaining site, Zn3, is more distant (Fig. 10). In all cases, Zn is tetrahedrally coordinated, but in both Zn1 and Zn3 the coordination is 3Cys–1His in contrast to the 4Cys coordination for the other two sites (Fig. 10). Disruption of DNA methylation upon exposure to toxic metals (e.g., Cd, As, and Ni) has been implicated in cancer,151 and there is some evidence that these toxic metals could be replacing native Zn metal.152 QM/MM modeling of the electronic structure around Zn binding sites could provide crucial insight into how substitution by Cd (ref. 153) or As (ref. 151) might occur and disrupt DNMT activity in a Zn-site-dependent manner.Here, we focus on the Zn2 site, which is close to both the DNA-protein interface and the methyltransferase catalytic site (Fig. 10). We carried out 250 ns of MD to observe the sampled Zn–S(Cys) distances at the 4Cys Zn2 binding site (ESI,† Fig. S9). All Zn–S bond lengths between Zn and Cys13, Cys16, Cys19, or Cys51 average around 2.4 Å but sample distances as short as 2.0 and as long as 2.8 Å (ESI,† Fig. S9). Most close contacts observed in the crystal structure are not observed after equilibration (ESI,† Table S9 and Text S1). QM-only geometry optimizations of 300-atom QM cluster models confirm the good performance of ZAFF85 for the covalent Zn–S bond lengths: average MD-sampled bond lengths are in agreement with QM-optimized bond lengths (ESI,† Fig. S9 and Table S10). The 0.8 Å range of sampled Zn–S distances suggests that multiple snapshots should indeed be investigated in the context of computing energetics of Zn2+ displacement from binding sites. The good correspondence of QM and MM bond lengths suggests this sampling can be achieved at the more efficient MM level of theory, unlike COMT where we showed first principles sampling was essential (see sec. 3a).
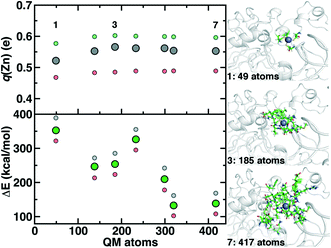
Although we have already discussed QM region convergence in the context of COMT, convergence of properties around the structural Zn2+ ion merits some attention. Here, we define QM regions by including a residue if any of that residue's atoms are within a radial distance cutoff of the Zn2+ ion. Radial convergence studies are carried out because the Zn2 site is near the surface of DNMT1, making the extraction of a large QM sphere for CSA35,62 challenging. Starting from a minimal 3 Å radius QM region 1 that incorporates only Zn2 and the four coordinating Cys residues (net charge: −2, 49 atoms with link H atoms), we constructed six additional QM regions: 5 Å, 6 Å, 7 Å, 8 Å, 9 Å, and 10 Å (Fig. 11 and ESI,† Table S10 and Fig. S10). The largest QM region 7 contains 417 atoms including link H atoms and has zero net charge (ESI,† Table S10 and Fig. S10). Only the three smallest QM regions have a modest net charge of −2 or −1, whereas the remaining four regions are neutral, and most QM regions have 8 or fewer covalent cuts (ESI,† Table S10).
We evaluate key electronic structure and energetic properties with these seven QM regions to determine QM/MM QM region dependence for DNMT1. As a measure of the electronic structure, we evaluate the Mulliken partial charge of Zn2+ in the holoenzyme and focus on its variation with QM region size rather than absolute charges that will be more sensitive to the partial charge scheme. Next, we evaluate a rigid binding energy of Zn2+, which provides an upper bound estimate of the binding strength of Zn2+ to the active site residues and thus how easily it can be displaced by other metals. We evaluate the Zn2+ rigid binding energy, ΔE, as:
| ΔE = E(Zn/DNMT1) − E(DNMT1) − E(Zn2+) | (2) |
We compute both Mulliken partial charges and ΔE values for all 7 QM regions on three uncorrelated snapshots selected from the 1st quartile, median, and 3rd quartile of the Zn–S bond distribution from MD to determine the effect of configuration on QM region convergence. Significant variation is indeed observed among the three snapshots for any given QM region, with the snapshots with generally more positively charged Zn2+ also having higher ΔE values (Fig. 11). Qualitatively, Mulliken charges appear QM region insensitive, with only QM region 1 having slightly more neutral Zn2+ than all other QM regions (Fig. 11). In comparison, QM region 2 adds several residues, including a positively charged Arg12 near the Zn2+ site and adjacent residues to each Cys that could make those residues more electron-withdrawing (ESI,† Table S10). Overall, the variation within a QM region over the three snapshots is at least 0.12e, whereas the variation for a given snapshot by QM region is at most around 0.03e (Fig. 11). Thus, making this comparison allows us to determine that Zn2+ Mulliken charges are more configurationally sensitive than QM-region sensitive.
Repeating this analysis on ΔE, we observe a very different trend: variations of around 50–70 kcal mol−1 across the three snapshots for a fixed QM region are smaller than variations in average ΔE for differing QM regions (i.e., 355 kcal mol−1 for 1 vs. 138 kcal mol−1 for 7) (Fig. 11). Excluding QM region 4, ΔE generally decreases as the QM region increases, with only QM region 6 (320 atoms) within good agreement of region 7 (132 kcal mol−1 for 6 vs. 138 kcal mol−1 for 7) (Fig. 11). Reviewing residues present in QM region 4 but absent in 3 suggests that ΔE increases for 4 because Arg50, proximal to the Zn2+ binding site, is introduced in 4 and interacts strongly with Cys51 altering its binding strength to Zn2+ (ESI,† Table S10).
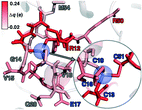
To rationalize why ΔE is so sensitive to the QM region, we examined how by-residue-summed partial charges change in QM region 7 when Zn2+ is removed (Fig. 12). Although most of the charge is gained on the 4 coordinating Cys residues, this gain is highly asymmetric: Cys13 and Cys51 gain 0.24 and 0.18e, whereas Cys16 and Cys19 gain only 0.11 and 0.05e, respectively, likely due to indirect influence of other neighboring QM residues (Fig. 12 and ESI,† Table S11). In addition to the covalently bound residues, Arg12, which is included in QM region 2 and larger QM regions, gains 0.20e, more than most Cys residues (ESI,† Table S6). Other residues have significant shifts in charge, even when further away, such as Gln20 in QM region 3 that is neutral but gains 0.06e when Zn2+ is removed (Fig. 12 and ESI,† Table S11). Overall, no significant difference is observed for charge shift magnitudes between non-polar active site residues (e.g., G14, V15, V18, M54), polar but neutral residues (Q20), or charged residues (e.g., E17, R12, R50), in accordance with previous observations35,62 of charge shifts in COMT (Fig. 12). Significant differences in the electrostatic environment for large QM region simulations thus stabilize Zn2+ removal over minimal QM regions via more physical delocalization of charge.
4. Conclusions
In this work, we have studied the electronic structure and reactivity of three diverse enzymes with QM/MM simulation: i) the Mg2+-dependent catechol O-methyltransferase (COMT), ii) the glycyl radical enzyme choline trimethylamine lyase (CutC), and iii) Zn2+-dependent DNA methyltransferase (DNMT1).In COMT, a system with a catalytic metal ion and a bulky SAM cofactor, we noted large differences in predictions depending on the means by which QM regions were constructed, ranging from minimal regions, to radially enlarged regions, and finally systematic construction methods. This was due to the numerous non-covalent substrate–protein interactions in the active site. To explain why techniques to reduce the sizes of QM regions for 0 K reaction coordinates were less successful when applied to QM/MM free energy simulations, we analyzed covariance matrices of the by-residue-summed partial charges. We observed long-range coupling between active site residue charges and distant residues and found that the pattern of couplings varied dynamically along the reaction coordinate.
We next studied CutC as a case where radical chemistry presents challenges to model both charge transfer and the evolution of spin densities. From systematic QM/MM analysis, fewer non-covalent interactions were observed to play essential roles in the CutC active site. By mapping out reaction coordinates with QM/MM steered MD, we observed that initiating one bond cleavage event triggered other reaction events. Using this approach, we provided evidence for spontaneous decomposition of the substrate into products following deprotonation of the cholinyl substrate radical. Through electronic structure analysis of the non-covalent interactions in the active site, we concluded that the E491 to choline O–H⋯O charge-assisted hydrogen bond likely dominates over weaker but still favorable C–H⋯O interactions.
To illustrate the tradeoffs faced when modeling a transition metal that plays a structural role, we studied the Zn2+ binding site of DNMT1. Here, we noted the important role of sampling and averaging over configurations through a robust MM force field. We also observed rapid convergence in small QM regions of some properties (i.e., Mulliken charge of Zn) dictated by nearest neighbor interactions, whereas others that involve significant perturbations to the electrostatic environment (i.e., rigid Zn binding energy) had slower convergence in line with observations on COMT.
These three diverse cases enable us to provide some general recommendations regarding QM/MM simulation of enzymes. Dynamical sampling of distinct geometric configurations provides essential insight into enzyme catalysis. Nevertheless, the effect of QM region size can dominate over the benefits of extensive sampling in cases where the electrostatic environment provided by the MM treatment is too different from the charge transfer allowed in the QM environment (e.g., with strong, charge-assisted hydrogen bonds or other non-covalent interactions). Systematic QM region construction methods provide useful insight by detecting difficult-to-describe interactions with MM. When properties are dominated by through-bond interactions, small QM regions may be sufficient, especially for select metallocofactor properties. Thus, when studying new proteins, researchers will always benefit from QM region sensitivity analysis of properties being studied, and systematic tools should make this analysis straightforward. Beyond these considerations, outstanding challenges remain for computational enzyme modeling, including: accelerating sampling, improving QM methods along with MM embedding, and improved sampling considerations in systematic QM/MM partitioning, which are underway in our group.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
Support for this research was provided by a core center grant P30-ES002109 from the National Institute of Environmental Health Sciences, National Institutes of Health (for R. M. and H. J. K.) and an NEC Corporation Grant from the MIT Research Support Committee (for Z. Y.). H. J. K. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund, which partially supported the work (H. J. K, H. W. Q., and M. W.). H. W. Q. was supported in part by a Department of Energy Computational Science Graduate Fellowship (DOE-CSGF). This work was carried out in part using computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. This work used the XStream computational resource, supported by the National Science Foundation Major Research Instrumentation program (ACI-1429830).References
- K. M. Koeller and C.-H. Wong, Enzymes for Chemical Synthesis, Nature, 2001, 409, 232 CrossRef CAS PubMed.
- H. E. Schoemaker, D. Mink and M. G. Wubbolts, Dispelling the Myths--Biocatalysis in Industrial Synthesis, Science, 2003, 299, 1694–1697 CrossRef CAS PubMed.
- J. Gao, S. Ma, D. T. Major, K. Nam, J. Pu and D. G. Truhlar, Mechanisms and Free Energies of Enzymatic Reactions, Chem. Rev., 2006, 106, 3188–3209 CrossRef CAS PubMed.
- M. J. Field, P. A. Bash and M. Karplus, A Combined Quantum-Mechanical and Molecular Mechanical Potential for Molecular-Dynamics Simulations, J. Comput. Chem., 1990, 11, 700–733 CrossRef CAS.
- D. Bakowies and W. Thiel, Hybrid Models for Combined Quantum Mechanical and Molecular Mechanical Approaches, J. Phys. Chem., 1996, 100, 10580–10594 CrossRef CAS.
- T. Z. Mordasini and W. Thiel, Combined Quantum Mechanical and Molecular Mechanical Approaches, Chimia, 1998, 52, 288–291 CAS.
- G. Monard and K. M. Merz, Combined Quantum Mechanical/Molecular Mechanical Methodologies Applied to Biomolecular Systems, Acc. Chem. Res., 1999, 32, 904–911 CrossRef CAS.
- J. L. Gao and D. G. Truhlar, Quantum Mechanical Methods for Enzyme Kinetics, Annu. Rev. Phys. Chem., 2002, 53, 467–505 CrossRef CAS PubMed.
- E. Rosta, M. Klahn and A. Warshel, Towards Accurate Ab Initio QM/MM Calculations of Free-Energy Profiles of Enzymatic Reactions, J. Phys. Chem. B, 2006, 110, 2934–2941 CrossRef CAS PubMed.
- H. Lin and D. Truhlar, QM/MM: What Have We Learned, Where Are We, and Where Do We Go from Here?, Theor. Chem. Acc., 2007, 117, 185–199 Search PubMed.
- A. Warshel and M. Levitt, Theoretical Studies of Enzymic Reactions: Dielectric, Electrostatic and Steric Stabilization of the Carbonium Ion in the Reaction of Lysozyme, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, QM/MM Methods for Biomolecular Systems, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- P. Vidossich, G. Florin, M. Alfonso-Prieto, E. Derat, S. Shaik and C. Rovira, On the Role of Water in Peroxidase Catalysis: A Theoretical Investigation of Hrp Compound I Formation, J. Phys. Chem. B, 2010, 114, 5161–5169 CrossRef CAS PubMed.
- P. Carloni, U. Rothlisberger and M. Parrinello, The Role and Perspective of Ab Initio Molecular Dynamics in the Study of Biological Systems, Acc. Chem. Res., 2002, 35, 455–464 CrossRef CAS PubMed.
- K. P. Eurenius, D. C. Chatfield, B. R. Brooks and M. Hodoscek, Enzyme Mechanisms with Hybrid Quantum and Molecular Mechanical Potentials. I. Theoretical Considerations, Int. J. Quantum Chem., 1996, 60, 1189–1200 CrossRef CAS.
- H. M. Senn and W. Thiel, QM/MM Studies of Enzymes, Curr. Opin. Chem. Biol., 2007, 11, 182–187 CrossRef CAS PubMed.
- A. Monari, J.-L. Rivail and X. Assfeld, Advances in the Local Self-Consistent Field Method for Mixed Quantum Mechanics/Molecular Mechanics Calculations, Acc. Chem. Res., 2012, 46, 596–603 CrossRef PubMed.
- Y. Wang and J. Gao, Projected Hybrid Orbitals: A General QM/MM Method, J. Phys. Chem. B, 2015, 119, 1213–1224 CrossRef CAS PubMed.
- P. Slavicek and T. J. Martinez, Multicentered Valence Electron Effective Potentials: A Solution to the Link Atom Problem for Ground and Excited Electronic States, J. Chem. Phys., 2006, 124, 084107 CrossRef PubMed.
- R. B. Murphy, D. M. Philipp and R. A. Friesner, A Mixed Quantum Mechanics/Molecular Mechanics (QM/MM) Method for Large Scale Modeling of Chemistry in Protein Environments, J. Comput. Chem., 2000, 21, 1442–1457 CrossRef CAS.
- Y. Zhang, T.-S. Lee and W. Yang, A Pseudobond Approach to Combining Quantum Mechanical and Molecular Mechanical Methods, J. Chem. Phys., 1999, 110, 46–54 CrossRef CAS.
- G. A. DiLabio, M. M. Hurley and P. A. Christiansen, Simple One-Electron Quantum Capping Potentials for Use in Hybrid QM/MM Studies of Biological Molecules, J. Chem. Phys., 2002, 116, 9578–9584 CrossRef CAS.
- O. A. von Lilienfeld, I. Tavernelli, U. Rothlisberger and D. Sebastiani, Variational Optimization of Effective Atom-Centered Potentials for Molecular Properties, J. Chem. Phys., 2005, 122, 14113 CrossRef PubMed.
- B. Wang and D. G. Truhlar, Combined Quantum Mechanical and Molecular Mechanical Methods for Calculating Potential Energy Surfaces: Tuned and Balanced Redistributed Charge Algorithm, J. Chem. Theory Comput., 2010, 6, 359–369 CrossRef CAS PubMed.
- N. M. Thellamurege and H. Hirao, Effect of Protein Environment within Cytochrome P450cam Evaluated Using a Polarizable-Embedding QM/MM Method, J. Phys. Chem. B, 2014, 118, 2084–2092 CAS.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. DiStasio Jr, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, Current Status of the AMOEBA Polarizable Force Field, J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- T. A. Halgren and W. Damm, Polarizable Force Fields, Curr. Opin. Struct. Biol., 2001, 11, 236–242 CrossRef CAS PubMed.
- L. J. Nåbo, J. M. H. Olsen, T. J. Martínez and J. Kongsted, The Quality of the Embedding Potential Is Decisive for Minimal Quantum Region Size in Embedding Calculations: The Case of the Green Fluorescent Protein, J. Chem. Theory Comput., 2017, 13, 6230–6236 CrossRef PubMed.
- A. Ganguly, E. Boulanger and W. Thiel, Importance of MM Polarization in QM/MM Studies of Enzymatic Reactions: Assessment of the QM/MM Drude Oscillator Model, J. Chem. Theory Comput., 2017, 13, 2954–2961 CrossRef CAS PubMed.
- D. Loco, L. Lagardère, S. Caprasecca, F. Lipparini, B. Mennucci and J.-P. Piquemal, Hybrid QM/MM Molecular Dynamics with AMOEBA Polarizable Embedding, J. Chem. Theory Comput., 2017, 13, 4025–4033 CrossRef CAS PubMed.
- I. S. Ufimtsev, N. Luehr and T. J. Martínez, Charge Transfer and Polarization in Solvated Proteins from Ab Initio Molecular Dynamics, J. Phys. Chem. Lett., 2011, 2, 1789–1793 CrossRef CAS.
- G. Nadig, L. C. Van Zant, S. L. Dixon and K. M. Merz, Charge-Transfer Interactions in Macromolecular Systems: A New View of the Protein/Water Interface, J. Am. Chem. Soc., 1998, 120, 5593–5594 CrossRef CAS.
- F. Himo, Recent Trends in Quantum Chemical Modeling of Enzymatic Reactions, J. Am. Chem. Soc., 2017, 139, 6780–6786 CrossRef CAS PubMed.
- H. J. Kulik and Q. M. Large-Scale, MM Free Energy Simulations of Enzyme Catalysis Reveal the Influence of Charge Transfer, Phys. Chem. Chem. Phys., 2018, 20, 20650–20660 RSC.
- H. J. Kulik, N. Seelam, B. Mar and T. J. Martinez, Adapting DFT+U for the Chemically-Motivated Correction of Minimal Basis Set Incompleteness, J. Phys. Chem. A, 2016, 120, 5939–5949 CrossRef CAS PubMed.
- H. J. Kulik, N. Luehr, I. S. Ufimtsev and T. J. Martinez, Ab Initio Quantum Chemistry for Protein Structure, J. Phys. Chem. B, 2012, 116, 12501–12509 CrossRef CAS PubMed.
- S. Rauscher, V. Gapsys, M. J. Gajda, M. Zweckstetter, B. L. de Groot and H. Grubmüller, Structural Ensembles of Intrinsically Disordered Proteins Depend Strongly on Force Field: A Comparison to Experiment, J. Chem. Theory Comput., 2015, 11, 5513–5524 CrossRef CAS PubMed.
- A. D. Becke, Perspective: Fifty Years of Density-Functional Theory in Chemical Physics, J. Chem. Phys., 2014, 140, 18A301 CrossRef PubMed.
- S. Riniker, Fixed-Charge Atomistic Force Fields for Molecular Dynamics Simulations in the Condensed Phase: An Overview, J. Chem. Inf. Model., 2018, 58, 565–578 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martínez, Quantum Chemistry on Graphical Processing Units. 1. Strategies for Two-Electron Integral Evaluation, J. Chem. Theory Comput., 2008, 4, 222–231 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martinez, Quantum Chemistry on Graphical Processing Units. 2. Direct Self-Consistent-Field Implementation, J. Chem. Theory Comput., 2009, 5, 1004–1015 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martínez, Quantum Chemistry on Graphical Processing Units. 3. Analytical Energy Gradients, Geometry Optimization, and First Principles Molecular Dynamics, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- C. M. Isborn, N. Luehr, I. S. Ufimtsev and T. J. Martinez, Excited-State Electronic Structure with Configuration Interaction Singles and Tamm-Dancoff Time-Dependent Density Functional Theory on Graphical Processing Units, J. Chem. Theory Comput., 2011, 7, 1814–1823 CrossRef CAS PubMed.
- C. Ochsenfeld, J. Kussmann and D. S. Lambrecht, Linear-Scaling Methods in Quantum Chemistry, Rev. Comput. Chem., 2007, 23, 1 CAS.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Auxiliary Basis Sets for Main Row Atoms and Transition Metals and Their Use to Approximate Coulomb Potentials, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Auxiliary Basis Sets to Approximate Coulomb Potentials, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- F. Liu, N. Luehr, H. J. Kulik and T. J. Martínez, Quantum Chemistry for Solvated Molecules on Graphical Processing Units Using Polarizable Continuum Models, J. Chem. Theory Comput., 2015, 11, 3131–3144 CrossRef CAS PubMed.
- D. Flaig, M. Beer and C. Ochsenfeld, Convergence of Electronic Structure with the Size of the QM Region: Example of QM/MM NMR Shieldings, J. Chem. Theory Comput., 2012, 8, 2260–2271 CrossRef CAS PubMed.
- J. D. Hartman, T. J. Neubauer, B. G. Caulkins, L. J. Mueller and G. J. Beran, Converging Nuclear Magnetic Shielding Calculations with Respect to Basis and System Size in Protein Systems, J. Biomol. NMR, 2015, 62, 327–340 CAS.
- S. J. Fox, C. Pittock, T. Fox, C. S. Tautermann, N. Malcolm and C. K. Skylaris, Electrostatic Embedding in Large-Scale First Principles Quantum Mechanical Calculations on Biomolecules, J. Chem. Phys., 2011, 135, 224107 CrossRef PubMed.
- R. Z. Liao and W. Thiel, Convergence in the QM-Only and QM/MM Modeling of Enzymatic Reactions: A Case Study for Acetylene Hydratase, J. Comput. Chem., 2013, 34, 2389–2397 CAS.
- K. Sadeghian, D. Flaig, I. D. Blank, S. Schneider, R. Strasser, D. Stathis, M. Winnacker, T. Carell and C. Ochsenfeld, Ribose-Protonated DNA Base Excision Repair: A Combined Theoretical and Experimental Study, Angew. Chem., Int. Ed., 2014, 53, 10044–10048 CrossRef CAS PubMed.
- I. Solt, P. Kulhanek, I. Simon, S. Winfield, M. C. Payne, G. Csanyi and M. Fuxreiter, Evaluating Boundary Dependent Errors in QM/MM Simulations, J. Phys. Chem. B, 2009, 113, 5728–5735 CrossRef CAS PubMed.
- C. M. Isborn, A. W. Goetz, M. A. Clark, R. C. Walker and T. J. Martinez, Electronic Absorption Spectra from MM and Ab Initio QM/MM Molecular Dynamics: Environmental Effects on the Absorption Spectrum of Photoactive Yellow Protein, J. Chem. Theory Comput., 2012, 8, 5092–5106 CrossRef CAS PubMed.
- D. E. Vanpoucke, J. Oláh, F. De Proft, V. Van Speybroeck and G. Roos, Convergence of Atomic Charges with the Size of the Enzymatic Environment, J. Chem. Inf. Model., 2015, 55, 564–571 CrossRef CAS PubMed.
- T. V. Harris and R. K. Szilagyi, Protein Environmental Effects on Iron-Sulfur Clusters: A Set of Rules for Constructing Computational Models for Inner and Outer Coordination Spheres, J. Comput. Chem., 2016, 37, 1681–1696 CrossRef CAS PubMed.
- S. Roßbach and C. Ochsenfeld, Influence of Coupling and Embedding Schemes on QM Size Convergence in QM/MM Approaches for the Example of a Proton Transfer in DNA, J. Chem. Theory Comput., 2017, 13, 1102–1107 CrossRef PubMed.
- M. R. Provorse, T. Peev, C. Xiong and C. M. Isborn, Convergence of Excitation Energies in Mixed Quantum and Classical Solvent: Comparison of Continuum and Point Charge Models, J. Phys. Chem. B, 2016, 120, 12148–12159 CrossRef CAS PubMed.
- J. M. Milanese, M. R. Provorse, E. Alameda and C. M. Isborn, Convergence of Computed Aqueous Absorption Spectra with Explicit Quantum Mechanical Solvent, J. Chem. Theory Comput., 2017, 13, 2159–2171 CrossRef CAS PubMed.
- A. Morgenstern, M. Jaszai, M. E. Eberhart and A. N. Alexandrova, Quantified Electrostatic Preorganization in Enzymes Using the Geometry of the Electron Charge Density, Chem. Sci., 2017, 8, 5010–5018 RSC.
- S. Das, K. Nam and D. T. Major, Rapid Convergence of Energy and Free Energy Profiles with Quantum Mechanical Size in Quantum Mechanical–Molecular Mechanical Simulations of Proton Transfer in DNA, J. Chem. Theory Comput., 2018, 14, 1695–1705 CrossRef CAS PubMed.
- M. Karelina and H. J. Kulik, Systematic Quantum Mechanical Region Determination in QM/MM Simulation, J. Chem. Theory Comput., 2017, 13, 563–576 CrossRef CAS PubMed.
- S. Sumner, P. Söderhjelm and U. Ryde, Effect of Geometry Optimizations on QM-Cluster and QM/MM Studies of Reaction Energies in Proteins, J. Chem. Theory Comput., 2013, 9, 4205–4214 CrossRef CAS PubMed.
- H. W. Qi, M. Karelina and H. J. Kulik, Quantifying Electronic Effects in QM and QM/MM Biomolecular Modeling with the Fukui Function, Acta Phys.-Chim. Sin., 2018, 34, 81–91 CAS.
- M. P. Waller, S. Kumbhar and J. Yang, A Density-Based Adaptive Quantum Mechanical/Molecular Mechanical Method, ChemPhysChem, 2014, 15, 3218–3225 CrossRef CAS PubMed.
- G. König, P. S. Hudson, S. Boresch and H. L. Woodcock, Multiscale Free Energy Simulations: An Efficient Method for Connecting Classical MD Simulations to QM or QM/MM Free Energies Using Non-Boltzmann Bennett Reweighting Schemes, J. Chem. Theory Comput., 2014, 10, 1406–1419 CrossRef PubMed.
- K. Meier, W. Thiel and W. F. van Gunsteren, On the Effect of a Variation of the Force Field, Spatial Boundary Condition and Size of the QM Region in QM/MM MD Simulations, J. Comput. Chem., 2012, 33, 363–378 CrossRef CAS PubMed.
- N. Patra, E. I. Ioannidis and H. J. Kulik, Computational Investigation of the Interplay of Substrate Positioning and Reactivity in Catechol O-Methyltransferase, PLoS One, 2016, 11, e0161868 CrossRef PubMed.
- J. Lameira, R. P. Bora, Z. T. Chu and A. Warshel, Methyltransferases Do Not Work by Compression, Cratic, or Desolvation Effects, but by Electrostatic Preorganization, Proteins: Struct., Funct., Bioinf., 2015, 83, 318–330 CrossRef CAS PubMed.
- G. Jindal and A. Warshel, Exploring the Dependence of QM/MM Calculations of Enzyme Catalysis on the Size of the QM Region, J. Phys. Chem. B, 2016, 120, 9913–9921 CrossRef CAS.
- M. A. Olsson and U. Ryde, Comparison of QM/MM Methods to Obtain Ligand-Binding Free Energies, J. Chem. Theory Comput., 2017, 13, 2245–2253 CrossRef CAS PubMed.
- J. Axelrod and R. Tomchick, Enzymatic O-Methylation of Epinephrine and Other Catechols, J. Biol. Chem., 1958, 233, 702–705 CAS.
- S. Bodea, M. A. Funk, E. P. Balskus and C. L. Drennan, Molecular Basis of C–N Bond Cleavage by the Glycyl Radical Enzyme Choline Trimethylamine-Lyase, Cell Chem. Biol., 2016, 23, 1206–1216 CrossRef CAS PubMed.
- S. Craciun and E. P. Balskus, Microbial Conversion of Choline to Trimethylamine Requires a Glycyl Radical Enzyme, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 21307–21312 CrossRef CAS.
- G. Kalnins, J. Kuka, S. Grinberga, M. Makrecka-Kuka, E. Liepinsh, M. Dambrova and K. Tars, Structure and Function of Cutc Choline Lyase from Human Microbiota Bacterium Klebsiella Pneumoniae, J. Biol. Chem., 2015, 290, 21732–21740 CrossRef CAS PubMed.
- J. Song, O. Rechkoblit, T. H. Bestor and D. J. Patel, Structure of Dnmt1-DNA Complex Reveals a Role for Autoinhibition in Maintenance DNA Methylation, Science, 2011, 331, 1036–1040 CrossRef CAS PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: An Advanced Semantic Chemical Editor, Visualization, and Analysis Platform, Aust. J. Chem., 2012, 4, 17 CAS.
- N. Eswar, B. Webb, M. A. Marti-Renom, M. Madhusudhan, D. Eramian, M. y. Shen, U. Pieper and A. Sali, Comparative Protein Structure Modeling Using Modeller, Curr. Protoc. Bioinf., 2006, 15, 5.6. 1–5.6. 30 CrossRef PubMed.
- J. Labahn, J. Granzin, G. Schluckebier, D. P. Robinson, W. E. Jack, I. Schildkraut and W. Saenger, Three-Dimensional Structure of the Adenine-Specific DNA Methyltransferase M. Taq I in Complex with the Cofactor S-Adenosylmethionine, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 10957–10961 CrossRef CAS.
- R. Anandakrishnan, B. Aguilar and A. V. Onufriev, H++ 3.0: Automating pK Prediction and the Preparation of Biomolecular Structures for Atomistic Molecular Modeling and Simulations, Nucleic Acids Res., 2012, 40, W537–W541 CrossRef CAS PubMed.
- J. C. Gordon, J. B. Myers, T. Folta, V. Shoja, L. S. Heath and A. Onufriev, H++: A Server for Estimating pKas and Adding Missing Hydrogens to Macromolecules, Nucleic Acids Res., 2005, 33, W368–W371 CrossRef CAS PubMed.
- J. Myers, G. Grothaus, S. Narayanan and A. Onufriev, A Simple Clustering Algorithm Can Be Accurate Enough for Use in Calculations of pKs in Macromolecules, Proteins: Struct., Funct., Bioinf., 2006, 63, 928–938 CrossRef CAS PubMed.
- D. A. Case, J. T. B., R. M. Betz, D. S. Cerutti, T. E. Cheatham, III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, T. Luchko, R. Luo, B. Madej, K. M. Merz, G. Monard, P. Needham, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, R. Salomon-Ferrer, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, D. M. York and P. A. Kollman Amber 2015, University of California, San Francisco, http://www.ambermd.org (accessed August 31, 2018).
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, Ff14sb: Improving the Accuracy of Protein Side Chain and Backbone Parameters from Ff99sb, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- M. B. Peters, Y. Yang, B. Wang, L. s. Füsti-Molnár, M. N. Weaver and K. M. Merz Jr, Structural Survey of Zinc-Containing Proteins and Development of the Zinc Amber Force Field (Zaff), J. Chem. Theory Comput., 2010, 6, 2935–2947 CrossRef CAS PubMed.
- I. Ivani, P. D. Dans, A. Noy, A. Pérez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goñi, A. Balaceanu, G. Portella, F. Battistini, J. L. Gelpí, C. González, M. Vendruscolo, C. A. Laughton, S. A. Harris, D. A. Case and M. Orozco, Parmbsc1: A Refined Force Field for DNA Simulations, Nat. Methods, 2016, 13, 55 CrossRef CAS PubMed.
- P. Li, B. P. Roberts, D. K. Chakravorty and K. M. Merz, Rational Design of Particle Mesh Ewald Compatible Lennard-Jones Parameters for +2 Metal Cations in Explicit Solvent, J. Chem. Theory Comput., 2013, 9, 2733–2748 CrossRef CAS.
- P. Li and K. M. Merz, Taking into Account the Ion-Induced Dipole Interaction in the Nonbonded Model of Ions, J. Chem. Theory Comput., 2014, 10, 289–297 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and Testing of a General Amber Force Field, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- M. S. Gordon and M. W. Schmidt, Advances in Electronic Structure Theory: GAMESS a Decade Later, Theory Appl. Comput. Chem.: First Forty Years, 2005, 1167–1189 CAS.
- P. C. Harihara and J. A. Pople, Influence of Polarization Functions on Molecular-Orbital Hydrogenation Energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef.
- F. Wang, J.-P. Becker, P. Cieplak and F.-Y. Dupradeau, R. E. D. Python: Object Oriented Programming for Amber Force Fields, Université De Picardie-Jules Verne, Sanford|Burnham Medical Research Institute, Nov. 2013. http://q4md-forcefieldtools.org/REDServer-Development/ (accessed August 31, 2018) Search PubMed.
- E. Vanquelef, S. Simon, G. Marquant, E. Garcia, G. Klimerak, J. C. Delepine, P. Cieplak and F.-Y. Dupradeau, R.E.D. Server: A Web Service for Deriving RESP and ESP Charges and Building Force Field Libraries for New Molecules and Molecular Fragments, Nucleic Acids Res., 2011, 39, W511–W517 CrossRef CAS.
- F.-Y. Dupradeau, A. Pigache, T. Zaffran, C. Savineau, R. Lelong, N. Grivel, D. Lelong, W. Rosanski and P. Cieplak, The R.E.D. Tools: Advances in RESP and ESP Charge Derivation and Force Field Library Building, Phys. Chem. Chem. Phys., 2010, 12, 7821–7839 RSC.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of Simple Potential Functions for Simulating Liquid Water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of N-Alkanes, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- Petachem, http://www.petachem.com (accessed August 31, 2018).
- P. Eastman, M. S. Friedrichs, J. D. Chodera, R. J. Radmer, C. M. Bruns, J. P. Ku, K. A. Beauchamp, T. J. Lane, L.-P. Wang, D. Shukla, T. Tye, M. Houston, T. Stich, C. Klein, M. R. Shirts and V. S. Pande, Openmm 4: A Reusable, Extensible, Hardware Independent Library for High Performance Molecular Simulation, J. Chem. Theory Comput., 2013, 9, 461–469 CrossRef CAS PubMed.
- Schrodinger, LLC, The PyMOL Molecular Graphics System, Version 1.7.4.3, http://www.pymol.org (accessed August 31, 2018) Search PubMed.
- M. A. Rohrdanz, K. M. Martins and J. M. Herbert, A Long-Range-Corrected Density Functional That Performs Well for Both Ground-State Properties and Time-Dependent Density Functional Theory Excitation Energies, Including Charge-Transfer Excited States, J. Chem. Phys., 2009, 130, 054112 CrossRef.
- P. J. Hay and W. R. Wadt, Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for the Transition Metal Atoms Sc to Hg, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- C. F. Guerra, J. W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, Voronoi Deformation Density (VDD) Charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD Methods for Charge Analysis, J. Comput. Chem., 2004, 25, 189–210 CrossRef CAS PubMed.
- E. Espinosa, E. Molins and C. Lecomte, Hydrogen Bond Strengths Revealed by Topological Analyses of Experimentally Observed Electron Densities, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- R. F. Bader, A Quantum Theory of Molecular Structure and Its Applications, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- T. Lu and F. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. Klamt and G. Schuurmann, Cosmo: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient, J. Chem. Soc., Perkin Trans. 2, 1993, 2, 799–805 RSC.
- J. Kästner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, DL-FIND: An Open-Source Geometry Optimizer for Atomistic Simulations, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef PubMed.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of Van Der Waals Complexes, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- E. G. Hohenstein and C. D. Sherrill, Density Fitting and Cholesky Decomposition Approximations in Symmetry-Adapted Perturbation Theory: Implementation and Application to Probe the Nature of π-π Interactions in Linear Acenes, J. Chem. Phys., 2010, 132, 184111 CrossRef.
- E. G. Hohenstein, R. M. Parrish, C. D. Sherrill, J. M. Turney and H. F. Schaefer, Large-Scale Symmetry-Adapted Perturbation Theory Computations via Density Fitting and Laplace Transformation Techniques: Investigating the Fundamental Forces of DNA-Intercalator Interactions, J. Chem. Phys., 2011, 135, 174107 CrossRef.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, Psi4 1.1: An Open-Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
- B. R. Miller, T. D. McGee, J. M. Swails, N. Homeyer, H. Gohlke and A. E. Roitberg, Mmpbsa.Py: An Efficient Program for End-State Free Energy Calculations, J. Chem. Theory Comput., 2012, 8, 3314–3321 CrossRef CAS PubMed.
- V. Tsui and D. A. Case, Theory and Applications of the Generalized Born Solvation Model in Macromolecular Simulations, Biopolymers, 2000, 56, 275–291 CrossRef CAS PubMed.
- A. Onufriev, D. Bashford and D. A. Case, Exploring Protein Native States and Large-Scale Conformational Changes with a Modified Generalized Born Model, Proteins: Struct., Funct., Bioinf., 2004, 55, 383–394 CrossRef CAS PubMed.
- H. J. Kulik, J. Zhang, J. P. Klinman and T. J. Martinez, How Large Should the QM Region Be in QM/MM Calculations? The Case of Catechol O-Methyltransferase, J. Phys. Chem. B, 2016, 120, 11381–11394 CrossRef CAS PubMed.
- T. Lotta, J. Vidgren, C. Tilgmann, I. Ulmanen, K. Melen, I. Julkunen and J. Taskinen, Kinetics of Human Soluble and Membrane-Bound Catechol O-Methyltransferase: A Revised Mechanism and Description of the Thermolabile Variant of the Enzyme, Biochemistry, 1995, 34, 4202–4210 CrossRef CAS PubMed.
- M. F. Hegazi, R. T. Borchardt and R. L. Schowen, Alpha-Deuterium and Carbon-13 Isotope Effects for Methyl Transfer Catalyzed by Catechol O-Methyltransferase. Sn2-Like Transition State, J. Am. Chem. Soc., 1979, 101, 4359–4365 CrossRef CAS.
- R. W. Woodard, M. D. Tsai, H. G. Floss, P. A. Crooks and J. K. Coward, Stereochemical Course of the Transmethylation Catalyzed by Catechol O-Methyltransferase, J. Biol. Chem., 1980, 255, 9124–9127 CAS.
- J. Axelrod, J. Methylation Reactions in the Formation and Metabolism of Catecholamines and Other Biogenic Amines, Pharmacol. Rev., 1966, 18, 95–113 CAS.
- J. K. Coward, E. P. Slisz and F. Y. H. Wu, Kinetic Studies on Catechol O-Methyltransferase, Product Inhibition and the Nature of the Catechol Binding Site, Biochemistry, 1973, 12, 2291–2297 CrossRef CAS.
- J. Vidgren, L. A. Svensson and A. Liljas, Crystal Structure of Catechol O-Methyltransferase, Nature, 1994, 368, 354–358 CrossRef CAS PubMed.
- P. Lautala, I. Ulmanen and J. Taskinen, Molecular Mechanisms Controlling the Rate and Specificity of Catechol O-Methylation by Human Soluble Catechol O-Methyltransferase, Mol. Pharmacol., 2001, 59, 393–402 CrossRef CAS PubMed.
- J. Zhang and J. P. Klinman, Enzymatic Methyl Transfer: Role of an Active Site Residue in Generating Active Site Compaction That Correlates with Catalytic Efficiency, J. Am. Chem. Soc., 2011, 133, 17134–17137 CrossRef CAS PubMed.
- T. H. Rod and U. Ryde, Quantum Mechanical Free Energy Barrier for an Enzymatic Reaction, Phys. Rev. Lett., 2005, 94, 138302 CrossRef PubMed.
- T. H. Rod and U. Ryde, Accurate QM/MM Free Energy Calculations of Enzyme Reactions: Methylation by Catechol O-Methyltransferase, J. Chem. Theory Comput., 2005, 1, 1240–1251 CrossRef CAS PubMed.
- M. Roca, V. Moliner, I. Tuñón and J. T. Hynes, Coupling between Protein and Reaction Dynamics in Enzymatic Processes: Application of Grote−Hynes Theory to Catechol O-Methyltransferase, J. Am. Chem. Soc., 2006, 128, 6186–6193 CrossRef CAS PubMed.
- G. D. Ruggiero, I. H. Williams, M. Roca, V. Moliner and I. Tuñón, QM/MM Determination of Kinetic Isotope Effects for COMT-Catalyzed Methyl Transfer Does Not Support Compression Hypothesis, J. Am. Chem. Soc., 2004, 126, 8634–8635 CrossRef CAS PubMed.
- E. Y. Lau and T. C. Bruice, Importance of Correlated Motions in Forming Highly Reactive near Attack Conformations in Catechol O-Methyltransferase, J. Am. Chem. Soc., 1998, 120, 12387–12394 CrossRef CAS.
- E. Y. Lau and T. C. Bruice, Comparison of the Dynamics for Ground-State and Transition-State Structures in the Active Site of Catechol O-Methyltransferase, J. Am. Chem. Soc., 2000, 122, 7165–7171 CrossRef CAS.
- J. Zhang, H. J. Kulik, T. J. Martinez and J. P. Klinman, Mediation of Donor–Acceptor Distance in an Enzymatic Methyl Transfer Reaction, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7954–7959 CrossRef CAS.
- B. Kuhn and P. A. Kollman, QM−Fe and Molecular Dynamics Calculations on Catechol O-Methyltransferase: Free Energy of Activation in the Enzyme and in Aqueous Solution and Regioselectivity of the Enzyme-Catalyzed Reaction, J. Am. Chem. Soc., 2000, 122, 2586–2596 CrossRef CAS.
- R. G. Parr and W. Yang, Density Functional Approach to the Frontier-Electron Theory of Chemical Reactivity, J. Am. Chem. Soc., 1984, 106, 4049–4050 CrossRef CAS.
- W. Yang and W. J. Mortier, The Use of Global and Local Molecular Parameters for the Analysis of the Gas-Phase Basicity of Amines, J. Am. Chem. Soc., 1986, 108, 5708–5711 CrossRef CAS.
- S. Craciun, J. A. Marks and E. P. Balskus, Characterization of Choline Trimethylamine-Lyase Expands the Chemistry of Glycyl Radical Enzymes, ACS Chem. Biol., 2014, 9, 1408–1413 CrossRef CAS PubMed.
- L. R. F. Backman, M. A. Funk, C. D. Dawson and C. L. Drennan, New Tricks for the Glycyl Radical Enzyme Family, Crit. Rev. Biochem. Mol. Biol., 2017, 52, 674–695 CrossRef CAS.
- B. J. Levin, Y. Y. Huang, S. C. Peck, Y. Wei, A. Martínez-del Campo, J. A. Marks, E. A. Franzosa, C. Huttenhower and E. P. Balskus, A Prominent Glycyl Radical Enzyme in Human Gut Microbiomes Metabolizes Trans-4-Hydroxy-L-Proline, Science, 2017, 355, eaai8386 CrossRef.
- B. Kovačević, D. Barić, D. Babić, L. Bilić, M. Hanževački, G. M. Sandala, L. Radom and D. M. Smith, Computational Tale of Two Enzymes: Glycerol Dehydration with or without B12, J. Am. Chem. Soc., 2018, 140, 8487–8496 CrossRef.
- S. Park, F. Khalili-Araghi, E. Tajkhorshid and K. Schulten, Free Energy Calculation from Steered Molecular Dynamics Simulations Using Jarzynski's Equality, J. Chem. Phys., 2003, 119, 3559–3566 CrossRef CAS.
- F. Van Duijneveldt and J. Murrell, Some Calculations on the Hydrogen Bond, J. Chem. Phys., 1967, 46, 1759–1767 CrossRef CAS.
- G. P. Laroff and R. W. Fessenden, Equilibrium and Kinetics of the Acid Dissociation of Several Hydroxyalkyl Radicals, J. Phys. Chem., 1973, 77, 1283–1288 CrossRef CAS.
- I. G. Denisov, T. M. Makris, S. G. Sligar and I. Schlichting, Structure and Chemistry of Cytochrome P450, Chem. Rev., 2005, 105, 2253–2278 CrossRef CAS.
- K. D. Karlin, Metalloenzymes, Structural Motifs, and Inorganic Models, Science, 1993, 261, 701–708 CrossRef CAS.
- B. L. Vallee and D. S. Auld, Zinc Coordination, Function, and Structure of Zinc Enzymes and Other Proteins, Biochemistry, 1990, 29, 5647–5659 CrossRef CAS.
- C. Andreini, I. Bertini, G. Cavallaro, G. L. Holliday and J. M. Thornton, Metal Ions in Biological Catalysis: From Enzyme Databases to General Principles, JBIC, J. Biol. Inorg. Chem., 2008, 13, 1205–1218 CrossRef CAS.
- O. J. Miller, W. Schnedl, J. Allen and B. F. Erlanger, 5-Methylcytosine Localised in Mammalian Constitutive Heterochromatin, Nature, 1974, 251, 636 CrossRef CAS.
- A. Bird, DNA Methylation Patterns and Epigenetic Memory, Genes Dev., 2002, 16, 6–21 CrossRef CAS.
- J. F. Reichard and A. Puga, Effects of Arsenic Exposure on DNA Methylation and Epigenetic Gene Regulation, Epigenomics, 2010, 2, 87–104 CrossRef CAS PubMed.
- D. Bhattacharyya, A. Boulden, R. Foote and S. Mitra, Effect of Polyvalent Metal Ions on the Reactivity of Human O 6-Methylguanine-DNA Methyltransferase, Carcinogenesis, 1988, 9, 683–685 CrossRef CAS.
- T. Dudev and C. Lim, Principles Governing Mg, Ca, and Zn Binding and Selectivity in Proteins, Chem. Rev., 2003, 103, 773–788 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8re00213d |
| This journal is © The Royal Society of Chemistry 2019 |


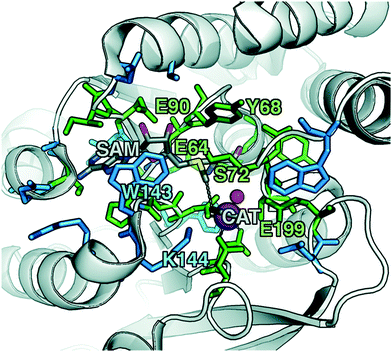
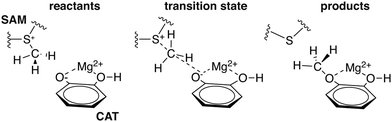


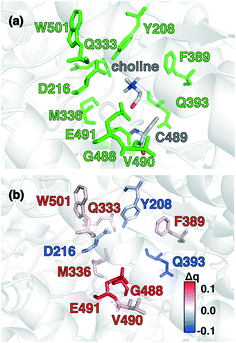
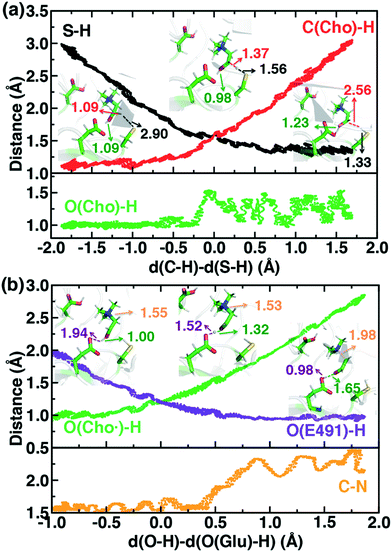
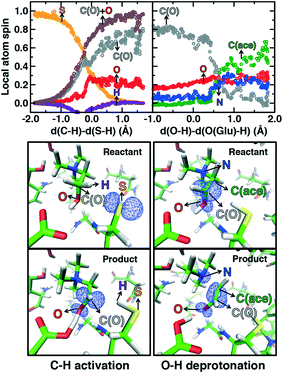
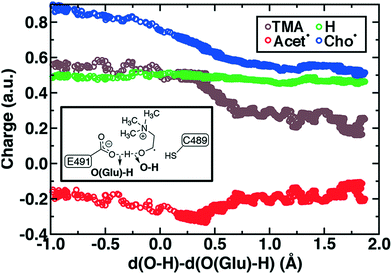
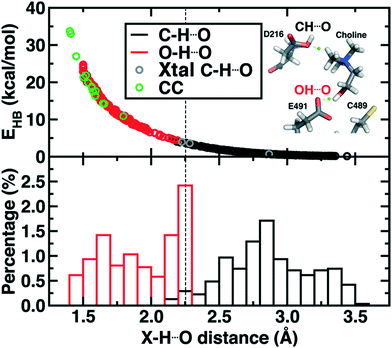
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (red circles), X
O (red circles), X