Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reorientation dynamics and ion diffusivity of neat dimethylimidazolium dimethylphosphate probed by NMR spectroscopy†
Christoph Wiedemann *a,
Günter Hempelb and
Frank Bordusa*a
*a,
Günter Hempelb and
Frank Bordusa*a
aInstitute of Biochemistry and Biotechnology, Charles Tanford Protein Center, Martin Luther University Halle-Wittenberg, Kurt-Mothes-Str. 3a, D-06120 Halle (Saale), Germany. E-mail: christoph.wiedemann@biochemtech.uni-halle.de; frank.bordusa@biochemtech.uni-halle.de
bInstitute of Physics, Martin Luther University Halle-Wittenberg, Betty-Heimann-Str. 7, D-06120 Halle (Saale), Germany
First published on 4th November 2019
Abstract
NMR spectroscopy at two magnetic field strengths was employed to investigate the dynamics of dimethylimidazolium dimethylphosphate ([C1C1IM][(CH3)2PO4]). [C1C1IM][(CH3)2PO4] is a low-melting, halogen-free ionic liquid comprising of only methyl groups. 13C spin–lattice relaxation rates as well as self-diffusion coefficients were measured for [C1C1IM][(CH3)2PO4] as a function of temperature. The rotational correlation times, τc, for the cation and the anion were obtained from the 13C spin–lattice relaxation rates. Although from a theoretical point of view cations and anions are similar in size, they show different reorientation mobilities and diffusivities. The self-diffusion coefficients and the rotational correlation times were related to the radii of the diffusing spheres. The analysis reveals that the radii of the cation and the anion, respectively, are different from each other but constant at temperatures ranging from 293 to 353 K. The experimental results are rationalised by a discrete and individual cation and anion diffusion. The [(CH3)2PO4]− anion reorients faster compared to the cation but diffuses significantly slower indicating the formation of anionic aggregates. Relaxation data were acquired with standard liquid and magic-angle-spinning NMR probes to estimate residual dipolar interactions, chemical shift anisotropy or differences in magnetic susceptibility within the sample.
Introduction
Organic salts with a melting point at ambient temperatures (melting points below 373 K) are commonly referred to as ionic liquids (ILs).1,2 ILs consist almost exclusively of organic cations and in-/organic anions. They are generally characterised by physical and chemical properties different from other molecular or atomic solvents, e.g. negligible vapour pressure, high chemical and thermal stability, high ionic conductivity and non-flammability. Because of their physicochemical characteristics, ILs have attracted wide attention as promising environmental friendly, “green” alternatives for commonly used organic solvents. The possibility of fine-tuning IL properties by an enormous diversity of cation–anion combinations renders ILs as substitute solvents or solvent additives in a wide range of laboratory and industrial applications.1,3–6 In addition to application in chemistry and physics, ILs have attracted considerable attention as solvents or solvent-mixtures in biochemistry.7–12A deeper understanding of IL properties at a molecular or even atomic level is of vital interest with respect to the rational design of novel ILs or the previous knowledge about the suitability of ILs for a desired process. Facing the plethora of various types and classes of ILs, a comprehensive characterization of the physicochemical properties is, realistically seen, only possible for selected cation–anion combinations. The prediction of the physicochemical characteristics, and, maybe even more importantly, the potential performance for novel task-driven ILs based on structure–function relationships of known cation–anion combinations is a great challenge. Hence, a combined approach integrating spectroscopic, experimental and theoretical/computational methods is required to broaden our understanding of ILs and the cationic–anionic interplay among each other and with solutes as well.
Nuclear magnetic resonance (NMR) is a powerful spectroscopic techniques for studying compounds or molecular systems at an atomic level. Despite some experimental limitations (e.g. high IL viscosity, radio frequency absorption due to high concentration of charged particles resulting in sample heating, detuned frequency channels, or with respect to solutes the suppression of IL solvent signals) it has been frequently shown that ILs can be thoroughly investigated by NMR.13–18 By means of NMR spectroscopy different types of information on IL structure and dynamics are readily accessible by probing chemical shifts, nuclear Overhauser effects (NOEs), relaxation times or self-diffusion coefficients. The atomic composition of ILs offers an intrinsic set of NMR active spin-1/2 nuclei, such as 1H, 13C, 15N, 19F, 31P, suitable for investigation. In order to understand IL properties as a whole and the single contributions of the IL cation and anion respectively, to the observable IL properties, the characterization of the molecular dynamics is of great interest. The relaxation properties and diffusivity of selected imidazolium-based ILs have been successfully investigated recently using NMR spectroscopy.19–28
Here, we examine and analyse 13C spin–lattice relaxation times (T1, relaxation rate: R1 = 1/T1) as well as self-diffusion coefficients of the ionic liquid dimethylimidazolium dimethylphosphate ([C1C1IM][(CH3)2PO4], Fig. 1) over a wide temperature range. In contrast to other imidazolium-based ILs, [C1C1IM][(CH3)2PO4] is a low-melting (liquid at room temperature), halogen-free IL comprising only methyl groups. The relaxation data were acquired with standard liquid probes at two magnetic field strengths and compared with data collected with high-resolution magic-angle spinning (HR-MAS) probes.
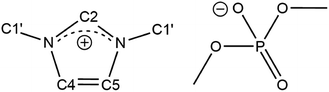 | ||
| Fig. 1 Chemical structure and denotation of dimethylimidazolium dimethylphosphate ([C1C1IM][(CH3)2PO4]). | ||
Materials and methods
Samples
[C1C1IM][(CH3)2PO4] was purchased from IoLiTec GmbH (Heilbronn, Germany) in highest available purity (≥98%) and used without further purification. The purity was confirmed by 1H and 13C NMR spectroscopy. The 1H and 13C NMR spectra [C1C1IM][(CH3)2PO4] are depicted in Fig. S1 and S2 (ESI†). Due to molecular symmetry the chemical shifts of H4/C4 and H5/C5 are respectively equivalent. For each 1H and 13C species of [C1C1IM][(CH3)2PO4] only single resonances were observed. No signals indicating impurities could be observed in the 1H spectrum except a very weak water peak. The water peak intensity was in the range of 13C satellite signal intensity of [C1C1IM][(CH3)2PO4] 1H resonances and originated from H2O traces in the used D2O.NMR measurements
All NMR experiments were acquired on Bruker AvanceIII systems with different magnetic field strengths, 9.35 T and 16.45 T, corresponding to a 13C resonance frequency of 100.6 MHz and 176.2 MHz, respectively. Both systems were equipped with 5 mm room-temperature liquid probes and 4 mm triple resonance HR-MAS probes. Liquid probe samples were fitted with a coaxial insert containing D2O for field frequency locking. All HR-MAS NMR experiments were collected without field frequency locking and the sample spin rate was 6 kHz. The field drift of both magnets was less than 0.3 Hz per hour without field frequency locking. The sample temperatures were controlled by variable temperature units. Temperature calibration was carried out with 4% MeOH in CD3OD for the low temperature range (278.2–300.2 K) and 80% ethylene glycol in DMSO-d6 for the high temperature range (300.2–353.2 K).Inversion recovery experiments (180°–τ–90°) with power gated 1H decoupling were collected and the 13C longitudinal relaxation times (T1) were calculated from signal heights by a single exponential fit. For all experiments the relaxation delay was at least five times the longitudinal relaxation time of the slowest relaxing nucleus.
Diffusion coefficients of [C1C1IM][(CH3)2PO4] were measured at several temperatures using the double stimulated echo bipolar pulse-gradient pulse sequence (dstebpgp3s) for convection compensation and longitudinal eddy current delay implemented in the standard Bruker pulse library. The experimental signal amplitudes S were fitted to the Stejskal–Tanner equation29,30 S/S0 = exp[−γ2δ2g2(Δ − δ/3)D]. γ is the 1H gyromagnetic ratio, δ holds the gradient pulse length, g is the gradient strength, Δ reflects the diffusion time and Dt is the diffusion coefficient. δ was fixed at 3 ms, and Δ was set appropriately. In order to avoid signal attenuation caused by the 1H T1 relaxation timing parameters were kept constant and only the gradient strength g was varied in 32 linear steps from 2 to 95% of the maximum probe gradient strength (4.78 G mm−1). The probe gradient system was calibrated by measuring the diffusion coefficient of a water sample at 298.2 K and compared with the literature value (Dt = 2.299 × 10−9 m2 s−1).31
Data processing was performed with Topspin 3.5.6 (Bruker Biospin GmbH, Rheinstetten) and the relaxation data were analysed with the software Dynamics Center 2.4.4 (Bruker Biospin GmbH, Rheinstetten).
Theoretical background
For any given system, the observed longitudinal relaxation rates are in general caused by a combination of different relaxation mechanisms and can be expressed in total according to eqn (1):
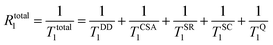 | (1) |
The Bloembergen–Purcell–Pound (BPP) theory, first introduced for dipolar 1H relaxation36 and later extended to other heteronuclei including 13C,37 provides the theoretical basis for describing the observed T1 temperature dependence in terms of rotational correlation time and resonance frequency. Under broadband 1H decoupling and neglecting cross-correlation effects between different interactions, the dipolar longitudinal relaxation rate of proton-attached 13C nuclei is given by eqn (2).
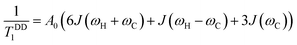 | (2) |
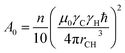 | (3) |
Another source of 13C relaxation is CSA. For an axially-symmetric molecule, the principal components of the chemical shift tensor are parallel (δ∥) and perpendicular (δ⊥) to the symmetry axis and their difference (Δδ) is relevant for relaxation. The longitudinal 13C relaxation due to CSA is given by eqn (4).
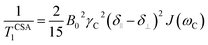 | (4) |
For proton-attached 13C nuclei with only moderately small CSA the contribution of CSA to the overall relaxation rate is one order of magnitude smaller than those for dipole–dipole relaxation and mostly neglected in the discussion of proton-attached 13C relaxation. However, the contribution of CSA to 13C longitudinal relaxation should be taken into account in particular at high magnetic fields and in situations where the nuclei under investigation exhibits large chemical shift ranges. In such a case, the total longitudinal relaxation rate for a proton-attached 13C nuclei is the sum of the rate due to dipolar interaction and CSA (eqn (5)).39
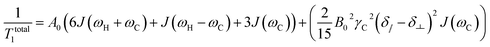 | (5) |
For rigid molecules with isotropic diffusion and a single molecular rotational correlation time (τc) the spectral density J(ω) can be modelled by eqn (6):
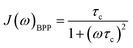 | (6) |
In situations where the 1H–13C dipolar interaction (eqn (2)) is the main source of 13C relaxation and the contribution of CSA is absent or not considered (second term in eqn (5) vanishes) it is worthwhile to note that eqn (2) by applying the BPP spectral density function (eqn (6)) reaches its maximum point, and hence T1 a minimum, at ωCτc = 0.791. Using the relation ωH/ωC ≈ 3.98 and rearranging eqn (2) the theoretical 13C T1 minimum can be calculated by eqn (7):
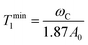 | (7) |
To account for contributions from additional intramolecular motion to relaxation the generalized order parameter S2 (0 < S2 ≤ 1) and an effective internal correlation time (τi) were introduced in the “simple model-free” approach40 (eqn (8)).
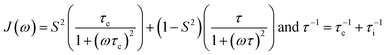 | (8) |
For S2 = 1 or in the slow intramolecular motion regime (τi ≫ τc) eqn (8) reduces to eqn (6). In the fast intramolecular motion limit (τi ≪ τc) eqn (8) reduces to J(ω) = S2J(ω)BPP. One elegant way to extract information about molecular mobility from 13C longitudinal relaxation times under the assumption of fast intramolecular motion and neglecting the CSA contribution is given in great detail in recent publications by Matveev et al.41–43 With the knowledge of the precise 13C T1 minimum it is possible to independently simplify the determination of the value of S2 (S2 = ωC/(1.87A0Tmin1)) and hence to calculate τc for any given T1.
Sometimes the relaxation of viscous liquids, even far above the melting point, is insufficiently described by eqn (6) or (8) and a correlation time distribution should be included into J(ω). For such systems the molecular motion and relaxation properties can be described more efficiently by a distribution of correlation times rather than a single correlation time and an order parameter.44–48 Therefore, the empirical Cole–Davidson (CD) approach49,50 (eqn (9)) is widely used in literature for quantitative analysis of relaxation data with distributed correlation times. In eqn (9) the parameter β (0 < β ≤ 1) describes the width of the distribution and τCD is related to τc by τc = βτCD. For β = 1 eqn (9) simplifies to eqn (6).
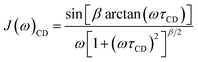 | (9) |
In situations where a molecule undergoes anisotropic tumbling or has moieties with fast internal reorientation compared with the overall molecular motion (e.g. fast rotating methyl groups) the order parameter S2 can be replaced by the expression Si2 = 1/4(3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(φ) − 1)2. Here, the motion of a 13C–1H vector around its rotation axis (symmetry axis) and the azimuthal angle φ is taken into account.23,35,51–54 For a methyl group with tetrahedral geometry (φ = 109.5°) Si2 takes the value 0.11. The motion of the methyl rotation axis itself is considered by setting S2 = 0.11SMet2.
cos2(φ) − 1)2. Here, the motion of a 13C–1H vector around its rotation axis (symmetry axis) and the azimuthal angle φ is taken into account.23,35,51–54 For a methyl group with tetrahedral geometry (φ = 109.5°) Si2 takes the value 0.11. The motion of the methyl rotation axis itself is considered by setting S2 = 0.11SMet2.
It is generally accepted that the temperature dependence of τc follows the Arrhenius form (eqn (10)). EA is the activation energy for rotational diffusion and R the universal gas constant.
| τc = τ0eEA/RT | (10) |
| τc = τVFTeEVFT/R(T − T0) | (11) |
The experimental relaxation data for one 13C nucleus at both magnetic field strengths were simultaneously fitted with different models and parameter sets. Constrained least-square fitting was performed using Python scripts written in-house. Bounds T0 > 0, 0 < S2 ≤1 and 0< β ≤ 1 were imposed. The reduced χ2 value (χred2) was used to assess the validity of the fits.
All mechanisms that contribute to 13C relaxation mainly arise from intramolecular contributions. Therefore, longitudinal 13C relaxation times are a reliable probe of molecular mobility and their analysis renders possible the characterization of molecular mobility in detail.
Results
Comparison HR-MAS vs. liquid probe
Most of the 13C relaxation studies rely on the assumption that after inversion the recovery of the longitudinal part of the magnetisation follows a single exponential process. However, in situations where 13C nuclei are directly attached to a proton, heteronuclear cross-relaxation by dipole–dipole interaction can lead to a non-exponential recovery of 13C longitudinal magnetisation unless the 13C spectra are collected with broadband 1H decoupling.55 The impact of cross-relaxation effects on the 13C–1H dipolar relaxation mechanism was estimated by determining the 13C T1 values under 1H broadband decoupling conditions enabling NOE enhancement and under 1H inverse gated decoupling without NOE enhancement at different magnetic fields and for selected temperatures (Table S1†). There are no or virtually negligible differences between the 13C T1 values measured under broadband and gated 1H decoupling at selected field strength and temperature. Based on these data we conclude that there is no impact of cross-relaxation in the 13C–1H dipole–dipole relaxation mechanism neither for the [C1C1IM]+ cation nor the [(CH3)2PO4]− anion within the observed temperature range. The 13C relaxation by dipole–dipole interaction within [C1C1IM][(CH3)2PO4] can be considered as a single exponential process. This is in agreement with the result presented by Imanari et al.19 for the [C3C1IM]+ cation in [C3C1IM][Br].To reduce residual dipolar interactions or differences in magnetic susceptibility that might be present in the sample, [C1C1IM][(CH3)2PO4] was also studied by HR-MAS NMR. As already shown for the high-resolution liquid probes even under magic-angle spinning there is nor difference in the 13C longitudinal relaxation times determined with broadband or gated 1H decoupling (Table S1†). The 13C T1 values of single carbons obtained by collecting spectra with standard liquid probes and HR-MAS probes are highly comparable at selected field strength and temperature. On one hand this reflects the accuracy of probe temperature calibration. On the other hand the orientational components (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1) of the Hamiltonians for the dipolar interaction, CSA or differences in the magnetic susceptibility due to sample inhomogeneity are averaged to zero by molecular motion without additional sample spinning. Despite the high viscosity of [C1C1IM][(CH3)2PO4], the motional averaging is fast enough to remove the contributions from interactions which would lead to line broadening. This assumption is further confirmed by measuring the 13C line widths at several temperatures with high-resolution liquid and HR-MAS probes with 6 kHz sample spinning rate (Table S2†). There are no differences in the 13C line widths for each carbon at selected temperatures regardless which probe was used.
θ − 1) of the Hamiltonians for the dipolar interaction, CSA or differences in the magnetic susceptibility due to sample inhomogeneity are averaged to zero by molecular motion without additional sample spinning. Despite the high viscosity of [C1C1IM][(CH3)2PO4], the motional averaging is fast enough to remove the contributions from interactions which would lead to line broadening. This assumption is further confirmed by measuring the 13C line widths at several temperatures with high-resolution liquid and HR-MAS probes with 6 kHz sample spinning rate (Table S2†). There are no differences in the 13C line widths for each carbon at selected temperatures regardless which probe was used.
All 13C signals of [C1C1IM][(CH3)2PO4] are attenuated with decreasing temperature due to increasing line broadening, which indicates a restriction in the molecular motion. However, the methyl groups of the [C1C1IM]+ cation and the [(CH3)2PO4]− anion are less attenuated compared with the cation ring carbons. This indicates a less restricted motion of the cationic as well as the anionic methyl groups compared with cation ring carbons.
In conclusion, for [C1C1IM][(CH3)2PO4] a sample spinning at the “magic angle” (θ = 54.7°) is not essential to improve the spectral resolution.
13C relaxation studies
The 13C longitudinal relaxation times of [C1C1IM][(CH3)2PO4] were measured at two magnetic field strengths under broadband proton decoupling within a temperature range from 278.2 K to 353.2 K in the next step. Based on this temperature dependence and the application of different models, characteristic rotational correlation times (τc) were derived for each 13C nuclei in the molecule.The temperature dependence of the 13C longitudinal relaxation times is shown in Fig. 2. At first, with increasing temperature the magnitude of the 13C T1 values decreases for all cation carbons until reaching a minimum. After passing the minimum the magnitude of the 13C T1 values increase with increasing temperature. At a field strength of 9.35 T C2, C4/5 and C1′ of the imidazolium cation show a T1 minimum at approx. 298 K. For C2 and C4/5 the observed T1 minima of 0.231 s and 0.213 s, respectively, are close to the theoretical T1 minimum of 0.158 s for pure dipole–dipole relaxation of a CH group at that field strength assuming a BPP spectral density function (eqn (7)). At 16.45 T the T1 minimum of C2, C4/5 and C1′ is uniformly shifted to 303 K and for C2 and C4/5 the values in the T1 minimum (0.341 s and 0.305 s) closely match the calculated T1 minimum of 0.276 s. The fact that all [C1C1IM]+ cation ring carbons for a given magnetic field strength have a T1 minimum at nearly the same temperature indicates an isotropic reorientation of the cation. The deviation between the measured and the calculated relaxation times can be explained by a distribution of correlation times or additional internal motion of the H–C bond vector, which corroborates the application of “model-free” approach (eqn (8)).
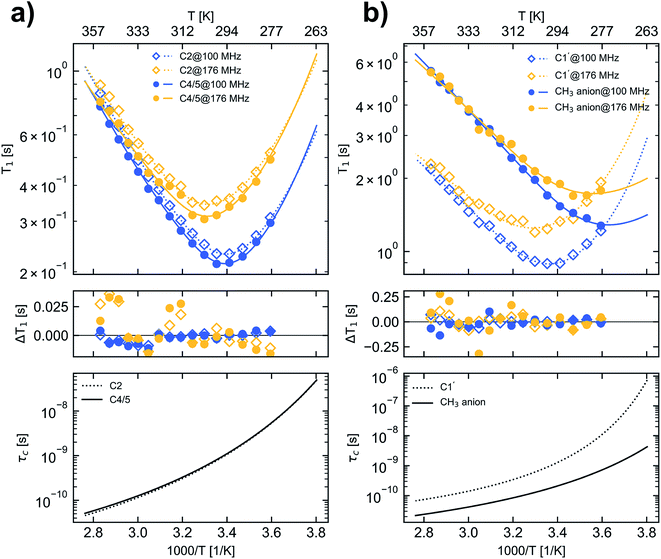 | ||
| Fig. 2 13C longitudinal relaxation times (upper panels), the difference between measured and fitted relaxation times (middle panel) and the calculated τc values (lower panel) for carbons in [C1C1IM][(CH3)2PO4] as a function of temperature. (a) carbon C2 (open squares and dotted lines) and C4/5 (filled circles and solid lines), (b) carbon C1′ (open squares and dotted lines) and CH3 carbons of the anion (filled circles and solid lines). For denotation see Fig. 1. Blue and yellow markers represent data measured at B0 of 9.35 T and 16.45 T corresponding to a 13C resonance frequency of 100.6 MHz and 176.2 MHz, respectively. The lines in the upper panel represent calculated 13C relaxation times according the fit parameters given in Table 2D. | ||
At all temperatures the product of the T1 relaxation times of the C1′ methyl nuclei and the number of attached protons (n = 3) is larger than those of the C2 and C4/5 CH groups (n = 1) by a factor of 9–12. The inverse of this factor is in the order of 0.1 corresponding to the aforementioned expression of S2 for fast rotating methyl groups with tetrahedral geometry. Furthermore, the measured C1′ relaxation times indicate an unrestrained rotational motion of the [C1C1IM]+ methyl groups. The theoretical 13C T1 values for dipole–dipole relaxation of a methyl group with free internal rotation also depend on the selected X–C–H bond angle φ. For φ = 109.5° 13C T1 of a rapidly rotating CH3 group which is 3-times longer than for a CH moiety under the assumption that both have the same effective rotational correlation time. With an increasing bond angle (φ > 109.5°) the longitudinal 13C relaxation time of CH3 theoretically increases further by a factor of ≈4, ≈4.5 and ≈5 for φ values of 112°, 113° and 114°, respectively, compared to a CH group. A rough estimation of the 13C T1 ratio of C1′ and C2 or C4/5 of the [C1C1IM]+ cation suggests that the bond angle φ of the methyl group is slightly greater than 109.5°.
The methyl carbons in the [(CH3)2PO4]− anion only reveal a T1 minimum at 288 K for a field strength of 16.45 T, indicating a much more active motion compared with the carbons of the cation. Within the selected temperature range no T1 minimum could be observed at 9.35 T for the methyl carbons of the [(CH3)2PO4]− anion. It can be assumed that the methyl carbon of the [(CH3)2PO4]− anion would also show a minimum in the 13C T1 relaxation time at 9.35 T, which however would appear only at a lower temperature than accessible in this study. For the methyl carbons in the [(CH3)2PO4]− anion no clear field strength dependence of the T1 relaxation could be observed in the high temperature range (>320 K). Also for the carbons of the cation the differences in the T1 values reduce with increasing temperatures (Fig. 2, Table S3†).
CSA contribution to 13C relaxation
Mostly, the relaxation of proton attached 13C nuclei in the liquid state is solely discussed in terms of dipolar interaction and the contribution of CSA to relaxation is neglected in literature.Measuring 13C T1 relaxation times at different magnetic field strengths in the fast motion limit (ωCτc ≪ 1) directly allows an estimation of the CSA contribution to relaxation. From the data obtained in this study, we can not completely exclude CSA contributions to relaxation for any carbons of [C1C1IM][(CH3)2PO4] but the comparable 13C T1 times at different magnetic field strengths in the high temperature range indicate only a minor effect of CSA to relaxation compared to dipole–dipole interaction. This is in agreement with the observation of Imanari et al.19 who stated also a minor impact of CSA for imidazolium based IL cations. However, in situations where CSA additionally contributes to 13C relaxation eqn (5) should be more suitable to represent the measured 13C T1 relaxation times. Therefore, we analysed our data in two ways: without taking account of CSA and in consideration of CSA.
Calculation of τc and Ea
Considering the above remarks, at first we treated the 13C relaxation times of [C1C1IM][(CH3)2PO4] as a result of the dipole–dipole relaxation mechanism between carbons and directly attached protons which can be described readily by eqn (2) and the modified BPP spectral density function (eqn (8)). We assume that the intramolecular motion is at least one order of magnitude faster than the overall molecular motion (τi≪τc) so that the second term in eqn (8) is negligible. For comparison the CD spectral density (eqn (9)) was also used for fitting. The temperature dependence of τc was modelled with the Arrhenius (eqn (10)) and VFT (eqn (11)) approach, respectively. In the Arrhenius approach one activation energy is assumed for the entire temperature range. However, for viscous liquids a decreasing temperature can correlate with an increasing activation energy. Such a behaviour is sometimes better described by the VFT equation.2,23 For [C1C1IM][(CH3)2PO4] the precise glass transition temperature is not known but it was experimentally shown that for imidazolium based ILs the glass transition temperature is in the range of 180–220 K.56–61 The fit parameters are summarized in Table 1.| S2 | EA (kJ mol−1) | τ0 (s) | τc at 298 K (ns) | χred2 | ||
|---|---|---|---|---|---|---|
| a Fast methyl-group rotation was considered by modifying S2 with the factor 0.11 (S2 = 0.11SMet2). For methyl carbons SMet2 is given.b Reduced χ2 values for data at 9.35 T.c Reduced χ2 values for data at 16.45 T.d Fitted S2 with a C–H bond length of 1.13 Å. | ||||||
| (A) | C2 | 0.70 (0.87d) | 38.18 | 1.67 × 10−16 | 0.82 | 2.98b/6.78c |
| C4/5 | 0.76 | 38.27 | 1.67 × 10−16 | 0.85 | 3.60b/8.26c | |
| C1′ | 0.56a | 32.22 | 2.09 × 10−15 | 0.93 | 4.87b/12.34c | |
| CH3 anion | 0.64a | 18.97 | 6.58 × 10−14 | 0.14 | 1.06b/1.36c | |
Regardless of the type of spectral density function or temperature dependence which is applied, all fits provide comparable results with respect to the order parameter, activation energy and rotational correlation time. Even the obtained T0 parameters are in agreement with values reported in literature. There is no difference in the goodness-of-fit between the application of the Arrhenius or the VFT approximation for the temperature dependence of τc. The same applies for the used spectral density functions. However no reliable fit could be obtained for the methyl carbon of the anion by applying the VFT approach for the τc temperature dependence. It has to be noted that the application of the Arrhenius approach provides very good fits for the methyl carbon of the anion. The experimental data at 9.35 T are obviously better represented by the fit parameters than the relaxation data at 16.45 T potentially indicating a more pronounced CSA contribution at the higher field strength.
In the next step we treated the 13C relaxation as a combination of dipole–dipole interaction and CSA (eqn (5)) under the assumption of fast internal motion. Again the experimental data were fitted to a BPP (eqn (8)) and CD (eqn (9)) type spectral density function and the Arrhenius (eqn (10)) and VFT (eqn (11)) approach for the temperature dependence of τc, respectively. The obtained fit parameters are compiled in Table 2. Taking account of CSA significantly improves the goodness-of-fit and the experimental data at both magnetic field strengths are well represented by the fit parameters. The estimated Δδ values for the IL ring carbons are in the range of 112–142 ppm. This is in agreement with Δδ for aromatic ring carbons reported by others.23,62,63 However, the fitted Δδ values (Table 2) for the methyl carbons are unexpectedly high when the motion of the 13C–1H vector around its rotation axis is considered (S2 = 0.11SMet2). Excluding the factor 0.11 during fitting would result in Δδ values in the range of 40–60 ppm for the methyl carbons.
| S2 | EA (kJ mol−1) | τ0 (s) | τc at 298 K (ns) | Δδ (ppm) | χred2 | ||
|---|---|---|---|---|---|---|---|
| a Fast methyl-group rotation was considered by modifying S2 with the factor 0.11 (S2 = 0.11SMet2). For methyl carbons SMet2 is given.b Reduced χ2 values for data at 9.35 T.c Reduced χ2 values for data at 16.45 T.d Fitted S2 with a C–H bond length of 1.13 Å. | |||||||
| (A) | C2 | 0.60 (0.75d) | 38.26 | 1.79 × 10−16 | 0.92 | 134.28 | 1.54b/1.39c |
| C4/5 | 0.64 | 38.21 | 1.92 × 10−16 | 0.96 | 142.58 | 1.69b/1.77c | |
| C1′ | 0.45a | 32.09 | 2.57 × 10−15 | 1.09 | 280.20 | 1.11b/2.03c | |
| CH3 anion | 0.44a | 22.99 | 2.14 × 10−14 | 0.23 | 207.06 | 0.82b/1.09c | |
| β | S2 | EA (kJ mol−1) | τ0 (s) | τCD/τc at 298 K (ns) | Δδ (ppm) | χred2 | ||
|---|---|---|---|---|---|---|---|---|
| (B) | C2 | 0.60 | 0.72 | 40.89 | 1.02 × 10−16 | 1.50/0.90 | 112.64 | 1.68b/0.72c |
| C4/5 | 0.65 | 0.74 | 40.43 | 1.18 × 10−16 | 1.45/0.94 | 121.37 | 1.85b/1.24c | |
| C1′ | 0.57 | 0.55a | 34.97 | 1.39 × 10−15 | 1.89/1.07 | 280.08 | 0.95b/1.65c | |
| CH3 anion | 0.27 | 0.64a | 28.91 | 6.99 × 10−15 | 0.82/0.22 | 264.62 | 2.04b/1.07c |
| S2 | EVFT (kJ mol−1) | T0 (K) | τ0 (s) | τc at 298 K (ns) | Δδ (ppm) | χred2 | ||
|---|---|---|---|---|---|---|---|---|
| (C) | C2 | 0.61 (0.75d) | 23.63 | 66.82 | 4.10 × 10−15 | 0.89 | 132.84 | 1.22b/1.74c |
| C4/5 | 0.65 | 18.78 | 93.24 | 1.49 × 10−14 | 0.92 | 140.40 | 1.16b/2.24c | |
| C1′ | 0.45a | 17.07 | 84.80 | 6.94 × 10−14 | 1.06 | 277.69 | 1.08b/2.35c | |
| CH3 anion | 0.32a | 4.29 | 191.29 | 3.01 × 10−12 | 0.38 | 279.79 | 0.65b/0.99c |
| β | S2 | EVFT (kJ mol−1) | T0 (K) | τ0 (s) | τCD/τc at 298 K (ns) | Δδ (ppm) | χred2 | ||
|---|---|---|---|---|---|---|---|---|---|
| (D) | C2 | 0.33 | 1.00 | 5.54 | 203.36 | 2.05 × 10−12 | 2.37/0.78 | 125.80 | 0.08b/0.49c |
| C4/5 | 0.37 | 1.00 | 5.26 | 205.03 | 2.44 × 10−12 | 2.20/0.81 | 134.09 | 0.13b/0.85c | |
| C1′ | 0.21 | 1.00a | 2.62 | 236.28 | 2.61 × 10−11 | 4.35/0.90 | 267.22 | 0.31b/0.80c | |
| CH3 anion | 0.12 | 1.00a | 3.52 | 210.58 | 1.12 × 10−11 | 1.42/0.17 | 303.64 | 0.22b/1.13c |
The calculated τc, for example at 298 K, are nearly equal within the selected spectral density approach for all carbons of the [C1C1IM]+ cation characterizing a uniform reorientation and molecular mobility. Moreover, our 13C relaxation measurements at two different magnetic field strengths reveal nearly the same rotational correlation times for all cation carbons (Tables 1 and 2) regardless of the selected type of spectral density function or approach for the temperature dependence of τc. Under this point of view the assumption of isotropic motion for the imidazolium ring is justified at least at room temperature. The activation energies (EA) of molecular reorientation for the imidazolium ring carbons are in the range of 32–38 kJ mol−1 for BPP type spectral density and 39–42 kJ mol−1 for CD approach, respectively. Using VFT approach to model the temperature dependence of τc results in activation energies (EVFT) within 2–8 kJ mol−1. These values are consistent with results obtained by others for imidazolium ring carbons and attached methyl groups.19,23,41,42,64 The fitted EA/EVFT values are nearly unaffected by the inclusion of CSA to the analysis of the relaxation data. Only the combination of BPP spectral density function, including the CSA relaxation mechanism and a VFT type τc temperature dependency results in high EVFT values of 17–23 kJ mol−1 and low T0 values for the [C1C1IM]+ carbons (Table 2C).
It was shown recently that the behaviour of the anion as a whole can be reasonably described by values obtained for methyl groups in carbon containing IL anions.43,64 For the methyl carbons of the anion, the calculated activation energies (EA/EVFT) are considerably lower compared with cation carbons. At 298 K τc is at least three to five times shorter than the corresponding values of the cation indicating a faster reorientation mobility of the anion. Moreover, this emphasises the hypothesis that cation and anion behave independently as dissociated ions and may form rather short-living ion pairs. We wish to point out that the molecular mobilities of [C1C1IM]+ and [(CH3)2PO4]− should be considered as time-weighted averages between the reorientation dynamics of tightly associated [C1C1IM]–[(CH3)2PO4] ion pairs and single dissociated ions.
The S2 of the ring carbons C2 (≈0.6–0.72) and C4/5 (≈0.64–0.78) calculated under the assumption of a C–H bond length of 1.09 Å and a BPP type spectral density would reveal a moderate degree of additional internal motion. The slightly lower S2 of C2 compared to C4/5 suggests accordingly that the proton attached to C2 is not preferentially involved in H-bonding in comparison to the other ring protons. The participation of the cationic H2 in hydrogen bonding with anions should result in a more constrained orientation, and hence higher order parameter of the corresponding C–H vector. The prominent role of the C2 position of imidazolium based IL cations in interacting with anions mainly via hydrogen bonding is extensively described in literature.18,23,65–71 It is well known that the length of a C–H bond can vary depending on the hybridization of the carbon atom and the polarity of the bond.72 In this context, Antony et al.73 postulated for the strong hydrogen bonding donor at position C2 of the imidazolium based cation (in this case 1-butyl-3-methylimidazolium) a C–H bond length of 1.13 Å. Reevaluating the C2 data with an elongated C–H bond length results in higher S2 values. By applying a C–H bond length of 1.13 Å S2 of C2 increases to values up to 0.99. These higher order parameters would corroborate the hypothesis that the proton in C2 position acts in hydrogen bond formation with the anion also for [C1C1IM][(CH3)2PO4]. The H-bond formation mainly between the CH group in position 2 of the cation and the [(CH3)2PO4]− anion is in agreement with existing hypothesis about the cationic–anionic interaction in imidazolium based ILs and the ability of [(CH3)2PO4]− to act as relatively strong H-bond acceptor.71 The order parameters obtained for the methyl groups in C1′ and the anion are slightly smaller compared to the ring carbons when the BPP type spectral density is applied for fitting. This indicates a slightly higher flexibility of the methyl carbons.
With respect to S2 the results are somewhat different when the CD spectral density function is used. Here, the best fits were obtained when the fit parameter S2 takes rather high values which would correlate with no or only very limited internal motion. However, the low β values of all carbons in [C1C1IM][(CH3)2PO4] could point to a broad distribution of correlation times.
The consistency between the fit parameters and the data derived at two magnetic field strengths justifies the chosen theoretical models and the approach of evaluation. The combination of applying the CD type spectral density function, the VFT approach for the τc temperature dependence and taking CSA into account provides the best fit results for our experimental data within the selected temperature range (Fig. 2). Experimental data at lower temperatures or higher magnetic field strengths than accessible in this study would further improve the reliability of the proposed fitting approach mainly for the more mobile IL anion. However, we do not want to conceal that our experimental data are also considerably well represented by the simple assumption of dipolar relaxation and the BPP spectral density function including S2 only (Table 1A).
As already mentioned (see Theoretical background) in situations where the temperature dependence of the 13C T1 values reveals a precise minimum the independent calculation of S2 (S2 = ωC/(1.87A0Tmin1)) and thus τc for any given T1 is possible. For further information we refer to the recent publications by Matveev et al.41,42,64 Since the 13C nuclei in [C1C1IM][(CH3)2PO4] reveal T1 minima, we also calculated S2 and extracted τc values for each temperature for comparison as proposed by the authors. Finally the τc temperature dependence was fitted according the Arrhenius (eqn (10)) and VFT approach (eqn (11)). The motional characteristics of [C1C1IM][(CH3)2PO4] applying this approach are summarized in Table S4 and depicted in Fig. S3 and S4.† Particularly with respect to S2, τc and EA the fit parameters obtained by applying the BPP spectral density function and neglecting any CSA contributions are in remarkable agreement with the values obtained by simultaneous fitting the relaxation data of two magnetic field strengths (Tables 1 and 2). In conclusion, if a clear temperature dependent 13C T1 minimum is observable at one magnetic field strength, the calculation of S2 in that point, and thereafter τc and EA, provides a robust and reliable approach for the extraction of information about molecular motion.
Nuclear Overhauser effect
The nuclear Overhauser effect (NOE) is an import consequence of dipolar relaxation. In addition, to validate that the 13C relaxation proceeds mainly by dipole–dipole interaction with attached protons the NOE enhancement factors η were measured in addition for selected temperatures, field strengths and probe settings (Table S5† and Fig. 3). Depending on the selected field strength comparable enhancement factors were obtained for each temperature using either HR-MAS or liquid probes.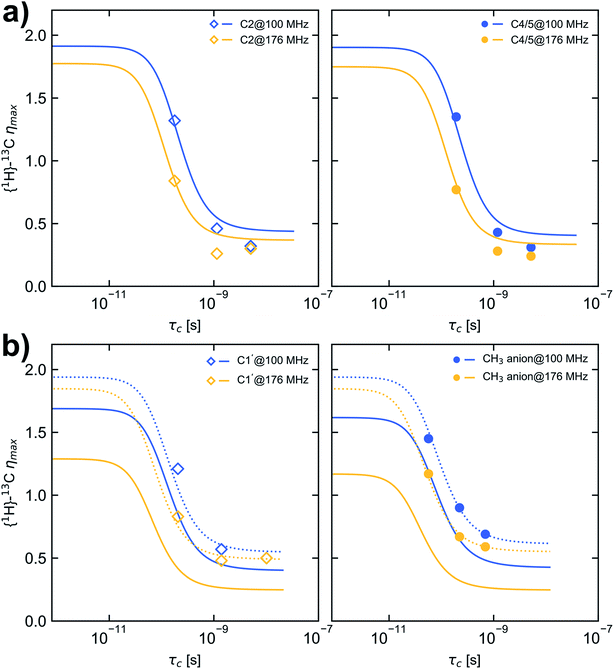 | ||
| Fig. 3 Dependence of maximum {1H}–13C NOE enhancement (ηmax) on τc calculated for a CD spectral density function and considering CSA with the fit parameters given in Table 2D (solid lines). (a) carbon C2 (left, open squares) and C4/5 (right, filled circles), (b) carbon C1′ (left, open squares) and CH3 carbon of the anion (right, filled circles). Dashed lines in (b) are calculated with the fit parameters given in Table 2D but a CSA value of 100 ppm. Blue and yellow markers represent data measured at B0 of 9.35 T and 16.45 T corresponding to a 13C resonance frequency of 100.6 MHz and 176.2 MHz, respectively. | ||
The maximum η observable relies on the rotational correlation time and thus on the molecular motion of the nuclei under investigation. Other relaxation pathways than intramolecular dipole–dipole interaction, which contribute to the longitudinal relaxation rate (e.g. CSA or intermolecular dipole–dipole interaction), can reduce the maximum η (eqn (12)).39 Here we examine the 13C NOE enhancement taking CSA into account. In the case that CSA is not considered the term (Δδ = δ∥ − δ⊥) in eqn (12) is set to 0.
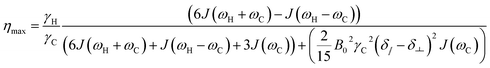 | (12) |
On the basis of the best parameters derived from fitting the relaxation data (Table 2D, CD type spectral density function and CSA contribution) the dependence of ηmax on τc was calculated and depicted in Fig. 3. For comparison also the ηmax dependence on τc was calculated using the fit parameter given in Tables 1A and D (see Fig. S5 and S6†). Because for the selected temperatures (278.2 K, 293.2 K and 323.2 K) the molecular motion of [C1C1IM][(CH3)2PO4] is not in the fast motion limit (ωCτc ≪ 1) and the relaxation by CSA is considered as a leakage term the maximum η observable of 1.98 for pure 1H–13C dipolar interaction can not be reached.
However, an increase in temperature resulting in shorter τc correlates with increased η values as shown in Fig. 3. For carbon C2 and C4/5 the observed enhancement factors η match the theoretical ones reasonably well and higher enhancements are obtained in the motion regime of ωCτc ≈ 1 at 9.35 T compared with 16.45 T. For the methyl carbons the observed enhancement factors deviate substantially from the expected values. The reason could be that the Δδ values for the methyl groups (Δδ = 267 and 303 ppm, respectively) are overestimated in the fitting procedure. Recalculating the dependence of ηmax on τc with a Δδ value of 100 ppm reveal a nearly perfect agreement between measured and expected NOE enhancement factors (Fig. 3b, dashed lines). This confirms that the CD spectral density function and fitted parameters β, EVFT, T0 and τ0 at least are suitable to model the molecular mobility of [C1C1IM][(CH3)2PO4]. From fitting the relaxation data and comparing the measured and calculated η values the 13C relaxation of [C1C1IM][(CH3)2PO4] partially by CSA can't be excluded. Moreover, for Δδ ≈ 100 ppm the maximum relaxation rate due to CSA is 0.4 s−1 (at 9.35 T) and 0.7 s−1 (at 16.45 T). CSA contributes field strength dependent to the overall 13C relaxation (6% and 17% at 9.35 T and 16.45 T, respectively) which is nevertheless dominantly driven by dipolar 1H–13C relaxation. However, the absolute Δδ values, mainly for the methyl groups, needs to be taken with caution and it has to be mentioned that the CSA magnitude can vary with temperature. Additional relaxation data at other magnetic field strengths or the direct measurement of the CSA is necessary to verify the fitted Δδ values.
Diffusion study
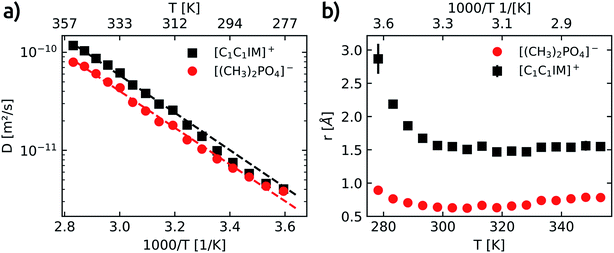
To gain a deeper understanding of cation–anion association/dissociation, formation of ion pairs or the aggregation of ions is of vital interest not only in the description of the IL electrical conductance and mass transport but also to rationalise the individual interaction of cation and anion with potential solute molecules.Each of the four well resolved resonances in the 1H spectrum of [C1C1IM][(CH3)2PO4] has been used to determine the temperature dependence of the translational self-diffusion coefficients (Dt). Three out of the four resonances were assigned to the [C1C1IM]+ cation and the D values obtained for the cation are averaged (see Table S6†). The temperature dependence of D is shown in Fig. 4a and fitted to an Arrhenius-type equation (eqn (10)). The activation energies of translational diffusion, EA, for the neat [C1C1IM][(CH3)2PO4] are 36.5 ± 1.9 kJ mol−1 and 35.8 ± 2.2 kJ mol−1 for the [C1C1IM]+ cation and the [(CH3)2PO4]− anion, respectively. These values are in the same order found for other ILs.59–61,74–76 It is interesting that EA for diffusion and rotational correlation give nearly the same values at least for the cation. The activation energy of the anion for diffusion is slightly higher compared to the rotational correlation.
The increase in the diffusion coefficients for both cation and anion with increasing temperature is to be expected. The diffusion coefficients associated with the [C1C1IM]+ cation are higher than the values obtained for the [(CH3)2PO4]− for the whole temperature range. The apparent cationic transference number and the predicted molar conductivity derived from the self-diffusion coefficients of [C1C1IM][(CH3)2PO4] are calculated and plotted in Fig. S7.† In contrast to other imidazolium based ILs,59–61 here, we observe an increase in the apparent cationic transference number with increasing temperature (Fig. S7a†). This can be rationalised by the slightly lower activation energy for the diffusion of the anion compared to the cation. At higher temperatures the diffusion of [(CH3)2PO4]− increases relatively less compared to the IL cation. The high cationic transference numbers of [C1C1IM][(CH3)2PO4] also reveal a faster diffusion of the cation than the anion, even though both ions are similar in size, and that the difference in cationic and anionic diffusion increases with temperature.
As already reported in earlier studies on several imidazolium59–61,74,75 or piperidinium76 based ILs also in our investigation the anion diffuses at a slower rate than the cation. In most of these previous reports the slower diffusing anion was smaller compared to a larger IL cation. The primary aggregation of IL anions resulting in a lower anionic diffusion constant was proposed to rationalise this surprising observation on the one hand.74,77 On the other hand it was suggested that the diffusion of the IL cation is faster than expected.75
According to the Stokes–Einstein equation (eqn (13)) the self-diffusion coefficient is inversely proportional to hydrodynamic radius (r) and, therefore, to the volume (V) of a spherical particle under investigation.78 For considering the anion and the cation it follow the ratios: 3√Vcation/3√Vanion = rcation/ranion = Danion/Dcation. The calculated van-der-Waals volumes79 (and effective radii74,80) of the [C1C1IM]+ cation and the [(CH3)2PO4]− anion are 89.8 Å3 (2.59 Å) and 96.8 Å3 (2.82 Å), respectively, and, hence, result in a theoretical ratio of the diffusion coefficients of Danion/Dcation = 0.97 and hydrodynamic radii of rcation/ranion = 0.92 for [C1C1IM][(CH3)2PO4]. The experimental ratio Danion/Dcation continuously decreases from 0.95 at 278.2 K to 0.67 at 353.2 K. At lower temperatures the experimental Danion/Dcation is in total agreement with the theoretical ratio and the lower Danion can be explained by the larger anionic volume. However, at higher temperatures the experimental Danion/Dcation deviates clearly from the theoretical ratio.
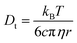 | (13) |
In a classical description the rotational correlation time τc of an isotropically diffusing sphere is given by eqn (14).18,78,81,82 The combination of eqn (13) and (14) by eliminating η, kB and T makes it possible to correlate both NMR accessible values Dt and τc to the hydrodynamic radius r of a particle under investigation (eqn (15)). Applying the fit parameters from Table 2D allowed the calculation of τc for every temperature.
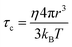 | (14) |
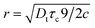 | (15) |
The experimentally acquired r of the cation is slightly smaller than theoretically estimated but in good agreement with other results for imidazolium based IL cations.68,74,82,83 Within limits, this corroborates the Stokes–Einstein approximation made and shows the applicability of eqn (15) for estimating hydrodynamic radii based on τc and D at least for the imidazolium based IL cation.
However, the experimentally based radius of the anion seems to be unrealistic small and deviates significantly from the theoretical value. If the aforementioned consideration (rcation/ranion = Danion/Dcation) holds true, one should expect nearly the same value for both ratios. The experimental ratio of the hydrodynamic radii rcation/ranion is in the range of 1.98–2.52 and reveals a clear contradiction to the experimentally obtained ratio of the diffusion coefficients Danion/Dcation = 0.76 averaged over the temperature range.
Assuming the radius of the anion derived from rotational correlation times, and hence, the ratio rcation/ranion = 1.98–2.52, is correct, this would imply that the measured diffusion coefficients of the [(CH3)2PO4]− anion are too small by a factor of ≈2.6–3.3. However, it is more likely that the calculated radius of the anion based on eqn (15) is too small. Under the premise that the calculated τc values of the anion are correct and that the actual hydrodynamic radius of a single and isolated [(CH3)2PO4]− particle has nearly the same value as the cation (≈2 Å, s. above) the measured diffusion coefficients of the anion are too small by a factor of ≈4 to 6 for this molecular size and τc values. In reverse, if it means that in average 4–6 [(CH3)2PO4]− anions cluster, is subject to speculation. The [(CH3)2PO4]− anion diffuse substantially slower than expected, in particular in the high temperature range. To explain these phenomena the concept of anion-rich aggregates in ILs was recently suggested and experimentally verified.74,77 Along this line, the diffusion coefficients and, thus, the derived hydrodynamic radii of [C1C1IM]+ and [(CH3)2PO4]− and their interpretation presented in this study render the formation of anionic aggregates a suitable model to explain the comparatively low diffusion coefficients of the anion. One should keep in mind the different NMR time scales at which the diffusion (ms to s) and the reorientation (ns) dynamics are studied. Both time scales are too long for the detection of short-living uncharged IL ion pairs. The lifetime of such ion pairs was estimated to be in ≥ps time frame.18 The longitudinal 13C relaxation of [C1C1IM][(CH3)2PO4] may reflects the rotational reorientation of single/not aggregated ionic particles in the ns time regime whereas the diffusion represents a “longtime” averaged clustering/aggregation mainly of the anions. Based on our NMR data presented here no reliable statement about the number of clustering anions is possible. The concept of cooperative hydrogen bonding was introduced to rationalise the cationic aggregates.84,85 The question needs to be resolved how anionic aggregates can overcome the repulsive Coulomb interaction.
Conclusion
Here, we report about the analysis of reorientation mobility of the room temperature IL [C1C1IM][(CH3)2PO4] on the basis of 13C longitudinal relaxation times measured at two magnetic field strengths by means of standard NMR liquid probes and by applying magic angle spinning. In addition, an analysis of the diffusion coefficients measured by PFG-NMR techniques at temperatures ranging from 278 K to 353 K was performed to correlate the rotational correlation times and the diffusion coefficients with the hydrodynamic radii of the [C1C1IM]+ cation and the [(CH3)2PO4]− anion.Despite their high viscosity pure imidazolium based ILs with a melting point at ambient temperatures can be properly studied by standard liquid NMR probe heads. With respect to IL signal line width, and hence resolution no improvement could be obtained by applying HR-MAS probes.
Therefore, the 13C longitudinal relaxation behaviour of the [C1C1IM]+ cation as well as the [(CH3)2PO4]− anion within the tested temperature range is reliably described by the BPP theory, the application of the generalised order parameter and an Arrhenius type τc temperature dependence. However, with regard to the goodness-of-fit (χred2 in Tables 1 and 2) the 13C longitudinal relaxation behaviour is more precisely represented by the application of the CD type spectral density function, VFT type τc temperature dependence and the consideration of CSA to 13C relaxation. This agrees with the findings from others.23,47 Additional relaxation data at a wider range of magnet field strengths and/or temperatures would be necessary to corroborate the distinction between different dynamic models and the total amount of CSA contribution. In this respect, it has to be mentioned that field-cycling NMR relaxometry is a valuable technique to obtain information on molecular dynamics over a broad range of Larmor frequencies (kHz to MHz).48,86 We wish to point out that field-cycling NMR relaxometry is successfully employed to investigate the dynamics of ILs recently.26,45,47,63,87–92
Although from a theoretical point of view similar in size, the [C1C1IM]+ cation and the [(CH3)2PO4]− anion reveal different reorientation mobilities and diffusivities. The [(CH3)2PO4]− anion shows a three to five times faster reorientation at room temperature compared to the cation. This indicates that cation and anion are not tightly associated in their reorientation mobility.
The temperature dependence of the self-diffusion coefficients is sufficiently described by the Arrhenius equation in the selected temperature range. In the course of the diffusion measurements we did not observe any indications of phase separation, and hence structural heterogeneity. It can be speculated that at lower temperatures the translational diffusion don't follow an Arrhenius-type but rather a VFT-type thermally activated process, as already observed for ILs.47,93 Intriguingly, the activation energies derived from relaxation data and diffusion measurements are nearly the same at least for the cation. This suggests that the effective size of the [C1C1IM]+ cation is the same for rotational correlation and diffusion. For the [C1C1IM]+ cation the hydrodynamic radius derived from rotational correlation times and diffusion coefficients fits very well with theoretical considerations and imply the existence of single dissociated cationic particles.
Assuming that the hydrodynamic radius of an isolated [(CH3)2PO4]− anion is similar to the [C1C1IM]+ cation the measured diffusion coefficients of the anion are too small to corroborate the model of single diffusing anionic entities. In contrast, the [(CH3)2PO4]− anion diffuses slower than expected and reveals a diffusion behaviour that indicates the formation of anionic aggregates.
Mainly with respect to IL ions interacting with solute molecules a better understanding of the ionic aggregation state and the dissociated action of IL cation and anion will help to rationalise the effects observed.
It has to be proven further whether and by which way of action the presence of solute molecules (in addition to carbohydrates e.g. peptides or proteins) in pure ILs has a measurable impact on the IL microstructure.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Prof. T. Michael Duncan at Cornell University for his support. Support by the “Institut für Technische Biochemie (ITB) e.V.” affiliated at the Martin Luther University Halle-Wittenberg is gratefully acknowledged. In addition, we acknowledge the financial support of the Martin Luther University Halle-Wittenberg within the funding programme Open Access Publishing by the German Research Foundation (DFG).References
- J. P. Hallett and T. Welton, Room-Temperature Ionic Liquids: Solvents for Synthesis and Catalysis. 2, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- H. Weingärtner, Understanding Ionic Liquids at the Molecular Level: Facts, Problems, and Controversies, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef.
- R. Hayes, G. G. Warr and R. Atkin, Structure and Nanostructure in Ionic Liquids, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS.
- M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Application of Ionic Liquids to Energy Storage and Conversion Materials and Devices, Chem. Rev., 2017, 117, 7190–7239 CrossRef CAS.
- C. Dai, J. Zhang, C. Huang and Z. Lei, Ionic Liquids in Selective Oxidation: Catalysts and Solvents, Chem. Rev., 2017, 117, 6929–6983 CrossRef CAS.
- Z. Zhang, J. Song and B. Han, Catalytic Transformation of Lignocellulose into Chemicals and Fuel Products in Ionic Liquids, Chem. Rev., 2017, 117, 6834–6880 CrossRef CAS.
- N. Wehofsky, C. Wespe, V. Cerovsky, A. Pech, E. Hoess, R. Rudolph and F. Bordusa, Ionic Liquids and Proteases: A Clean Alliance for Semisynthesis, ChemBioChem, 2008, 9, 1493–1499 CrossRef CAS.
- Y. Fukaya, K. Hayashi, M. Wada and H. Ohno, Cellulose dissolution with polar ionic liquids under mild conditions: required factors for anions, Green Chem., 2008, 10, 44–46 RSC.
- D. Diddens, V. Lesch, A. Heuer and J. Smiatek, Aqueous ionic liquids and their influence on peptide conformations: Denaturation and dehydration mechanisms, Phys. Chem. Chem. Phys., 2017, 19, 20430–20440 RSC.
- H. Weingärtner, C. Cabrele and C. Herrmann, How ionic liquids can help to stabilize native proteins, Phys. Chem. Chem. Phys., 2012, 14, 415–426 RSC.
- M. Silva, A. M. Figueiredo and E. J. Cabrita, Epitope mapping of imidazolium cations in ionic liquid–protein interactions unveils the balance between hydrophobicity and electrostatics towards protein destabilisation, Phys. Chem. Chem. Phys., 2014, 16, 23394–23403 RSC.
- T. Takekiyo and Y. Yoshimura, Suppression and dissolution of amyloid aggregates using ionic liquids, Biophys. Rev., 2018, 10, 853–860 CrossRef CAS.
- K. Damodaran, in Annual Reports on NMR Spectroscopy, Elsevier Ltd., 1st edn, 2016, vol. 88, pp. 215–244 Search PubMed.
- R. Nanda and K. Damodaran, A review of NMR methods used in the study of the structure and dynamics of ionic liquids, Magn. Reson. Chem., 2018, 56, 62–72 CrossRef CAS.
- Y. Lingscheid, S. Arenz and R. Giernoth, Heteronuclear NOE Spectroscopy of Ionic Liquids, ChemPhysChem, 2012, 13, 261–266 CrossRef CAS.
- R. Giernoth, D. Bankmann and N. Schlörer, High performance NMR in ionic liquids, Green Chem., 2005, 7, 279 RSC.
- D. Bankmann and R. Giernoth, Magnetic resonance spectroscopy in ionic liquids, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 51, 63–90 CrossRef CAS.
- H. Weingärtner, NMR studies of ionic liquids: Structure and dynamics, Curr. Opin. Colloid Interface Sci., 2013, 18, 183–189 CrossRef.
- M. Imanari, H. Tsuchiya, H. Seki, K. Nishikawa and M. Tashiro, Characterization of the molecular reorientational dynamics of the neat ionic liquid 1-butyl-3-methylimidazolium bromide in the super cooled state using 1H and 13C NMR spectroscopy, Magn. Reson. Chem., 2009, 47, 67–70 CrossRef CAS.
- W. R. Carper, P. G. Wahlbeck, J. H. Antony, D. Mertens, A. Dölle and P. Wasserscheid, A Bloembergen-Purcell-Pound 13C NMR relaxation study of the ionic liquid 1-butyl-3-methylimidazolium hexafluorophosphate, Anal. Bioanal. Chem., 2004, 378, 1548–1554 CrossRef CAS.
- N. E. Heimer, J. S. Wilkes, P. G. Wahlbeck and W. R. Carper, 13C NMR relaxation rates in the ionic liquid 1-ethyl-3-methylimidazolium butanesulfonate, J. Phys. Chem. A, 2006, 110, 868–874 CrossRef CAS.
- J. H. Antony, A. Dölle, D. Mertens, P. Wasserscheid, W. R. Carper and P. G. Wahlbeck, 13C NMR relaxation rates in the ionic liquid 1-methyl-3-nonylimidazolium hexafluorophosphate, J. Phys. Chem. A, 2005, 109, 6676–6682 CrossRef CAS.
- J. H. Antony, D. Mertens, A. Dölle, P. Wasserscheid and W. R. Carper, Molecular reorientational dynamics of the neat ionic liquid 1-butyl-3-methylimidazolium hexafluorophosphate by measurement of 13C nuclear magnetic relaxation data, ChemPhysChem, 2003, 4, 588–594 CrossRef CAS.
- P. G. Gordon, D. H. Brouwer and J. A. Ripmeester, Probing the Local Structure of Pure Ionic Liquid Salts with Solid- and Liquid-State NMR, ChemPhysChem, 2010, 11, 260–268 CrossRef CAS.
- F. Cesare Marincola, C. Piras, O. Russina, L. Gontrani, G. Saba and A. Lai, NMR investigation of imidazolium-based ionic liquids and their aqueous mixtures, ChemPhysChem, 2012, 13, 1339–1346 CrossRef.
- A. Ordikhani Seyedlar, S. Stapf and C. Mattea, Dynamics of the ionic liquid 1-butyl-3-methylimidazolium bis(trifluoromethylsulphonyl)imide studied by nuclear magnetic resonance dispersion and diffusion, Phys. Chem. Chem. Phys., 2015, 17, 1653–1659 RSC.
- T. Endo, M. Imanari, H. Seki and K. Nishikawa, Effects of Methylation at Position 2 of Cation Ring on Rotational Dynamics of Imidazolium-Based Ionic Liquids Investigated by NMR Spectroscopy: [C4mim]Br vs [C4C1mim]Br, J. Phys. Chem. A, 2011, 115, 2999–3005 CrossRef CAS.
- T. Endo, H. Murata, M. Imanari, N. Mizushima, H. Seki, S. Sen and K. Nishikawa, A comparative study of the rotational dynamics of PF 6- anions in the crystals and liquid states of 1-butyl-3-methylimidazolium hexafluorophosphate: Results from 31P NMR spectroscopy, J. Phys. Chem. B, 2013, 117, 326–332 CrossRef CAS.
- E. O. Stejskal and J. E. Tanner, Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient, J. Chem. Phys., 1965, 42, 288–292 CrossRef CAS.
- J. E. Tanner, Use of the Stimulated Echo in NMR Diffusion Studies, J. Chem. Phys., 1970, 52, 2523–2526 CrossRef CAS.
- M. Holz, S. R. Heil and A. Sacco, Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG measurements, Phys. Chem. Chem. Phys., 2000, 2, 4740–4742 RSC.
- G. C. Levy, Carbon-13-spin–lattice relaxation studies and their application to organic chemical problems, Acc. Chem. Res., 1973, 6, 161–169 CrossRef CAS.
- H. W. Spiess, D. Schweitzer and U. Haeberlen, Molecular motion in liquid toluene from a study of 13C and 2D relaxation times, J. Magn. Reson., 1973, 9, 444–460 CAS.
- E. Breitmaier, K.-H. Spohn and S. Berger, 13C Spin–Lattice Relaxation Times and the Mobility of Organic Molecules in Solution, Angew. Chem., Int. Ed. Engl., 1975, 14, 144–159 CrossRef.
- N. Platzer, Carbon-13NMR. The analysis of the relaxation times T1 of benzofuran and of a series of its methyl derivatives. Correlations between molecular motions and structural properties, Org. Magn. Reson., 1978, 11, 350–356 CrossRef CAS.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Relaxation effects in nuclear magnetic resonance absorption, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- I. Solomon, Relaxation Processes in a System of Two Spins, Phys. Rev., 1955, 99, 559–565 CrossRef CAS.
- K. Dill and A. Allerhand, Small errors in carbon–hydrogen bond lengths may cause large errors in rotational correlation times determined from carbon-13 spin–lattice relaxation measurements, J. Am. Chem. Soc., 1979, 101, 4376–4378 CrossRef CAS.
- P. Luginbühl and K. Wüthrich, Semi-classical nuclear spin relaxation theory revisited for use with biological macromolecules, Prog. Nucl. Magn. Reson. Spectrosc., 2002, 40, 199–247 CrossRef.
- G. Lipari and A. Szabo, Model-Free Approach to the Interpretation of Nuclear Magnetic Resonance Relaxation in Macromolecules. 1. Theory and Range of Validity, J. Am. Chem. Soc., 1982, 104, 4546–4559 CrossRef CAS.
- V. V. Matveev, D. A. Markelov, E. A. Brui, V. I. Chizhik, P. Ingman and E. Lähderanta, 13C NMR relaxation and reorientation dynamics in imidazolium-based ionic liquids: revising interpretation, Phys. Chem. Chem. Phys., 2014, 16, 10480–10484 RSC.
- V. V. Matveev and K. V. Tyutyukin, in Modern Problems of Molecular Physics, ed. L. A. Bulavin and A. V. Chalyi, Springer International Publishing AG, 2018, pp. 51–66 Search PubMed.
- V. V. Matveev, D. A. Markelov, A. V. Ievlev, E. A. Brui, K. V. Tyutyukin and E. Lähderanta, Molecular mobility in several imidazolium-based ionic liquids according to data of 1H and 13C NMR relaxation, Magn. Reson. Chem., 2018, 56, 140–143 CrossRef CAS.
- N. Petzold, B. Schmidtke, R. Kahlau, D. Bock, R. Meier, B. Micko, D. Kruk and E. A. Rössler, Evolution of the dynamic susceptibility in molecular glass formers: Results from light scattering, dielectric spectroscopy, and NMR, J. Chem. Phys., 2013, 138, 12A510 CrossRef CAS.
- M. Flämig, M. Hofmann, A. Lichtinger and E. A. Rössler, Application of proton field-cycling NMR relaxometry for studying translational diffusion in simple liquids and polymer melts, Magn. Reson. Chem., 2019, 57, 805–817 CrossRef.
- W. R. Carper, Z. Meng, P. Wasserscheid and A. Dölle, NMR Relaxation Studies and Molecular Modeling of 1-butyl-3-methylimidazolium PF6[BMIM][PF6], Electrochem. Soc. Proc., 2002, 2002–19, 973–982 CrossRef CAS.
- M. Wencka, T. Apih, R. C. Korošec, J. Jenczyk, M. Jarek, K. Szutkowski, S. Jurga and J. Dolinšek, Molecular dynamics of 1-ethyl-3-methylimidazolium triflate ionic liquid studied by1H and 19F nuclear magnetic resonances, Phys. Chem. Chem. Phys., 2017, 19, 15368–15376 RSC.
- D. Kruk, A. Herrmann and E. A. Rössler, Field-cycling NMR relaxometry of viscous liquids and polymers, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 63, 33–64 CrossRef CAS.
- D. W. Davidson and R. H. Cole, Dielectric Relaxation in Glycerol, Propylene Glycol, and n-Propanol, J. Chem. Phys., 1951, 19, 1484–1490 CrossRef CAS.
- P. A. Beckmann, Spectral densities and nuclear spin relaxation in solids, Phys. Rep., 1988, 171, 85–128 CrossRef.
- D. E. Woessner, Nuclear Spin–Lattice Relaxation in Axially Symmetric Ellipsoids with Internal Motion, J. Chem. Phys., 1969, 50, 719 CrossRef CAS.
- J. W. Blunt and J. B. Stothers, The influence of methyl group geometry on methyl rotational barriers as estimated from 13C relaxation data, J. Magn. Reson., 1977, 27, 515–519 CAS.
- S. Ng, R. V Sathasivam, K.-M. Lo, Y. Xie and H. F. Schaefer III, 13C NMR Relaxation Study of Molecular Motions in Tetraphenyltin and Tetra(p-tolyl)tin in Solution, J. Phys. Chem. A, 2005, 109, 12059–12063 CrossRef CAS.
- W. A. Mellink and R. Kaptein, Determination of the methyl group rotation energy barrier in some substituted tricyclo[3.1.0.02,6]hexanes by carbon-13 spinlattice relaxation, Org. Magn. Reson., 1980, 13, 279–281 CrossRef CAS.
- I. D. Campbell and R. Freeman, Influence of cross-relaxation on NMR spin–lattice relaxation times, J. Magn. Reson., 1973, 11, 143–162 CAS.
- J. J. M. Ramos, C. A. M. Afonso and L. C. Branco, Glass Transition Relaxation and Fragility in Two Room Temperature Ionic Liquids, J. Therm. Anal. Calorim., 2003, 71, 659–666 CrossRef.
- G. Jarosz, M. Mierzwa, J. Zioło, M. Paluch, H. Shirota and K. L. Ngai, Glass Transition Dynamics of Room-Temperature Ionic Liquid 1-Methyl-3-trimethylsilylmethylimidazolium Tetrafluoroborate, J. Phys. Chem. B, 2011, 115, 12709–12716 CrossRef CAS.
- O. Yamamuro, Y. Minamimoto, Y. Inamura, S. Hayashi and H. Hamaguchi, Heat capacity and glass transition of an ionic liquid 1-butyl-3-methylimidazolium chloride, Chem. Phys. Lett., 2006, 423, 371–375 CrossRef CAS.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, Physicochemical properties and structures of room temperature ionic liquids. 1. Variation of anionic species, J. Phys. Chem. B, 2004, 108, 16593–16600 CrossRef CAS.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, Physicochemical properties and structures of room temperature ionic liquids. 2. variation of alkyl chain length in imidazolium cation, J. Phys. Chem. B, 2005, 109, 6103–6110 CrossRef CAS.
- H. Tokuda, K. Ishii, M. A. B. H. Susan, S. Tsuzuki, K. Hayamizu and M. Watanabe, Physicochemical properties and structures of room-temperature ionic liquids. 3. Variation of cationic structures, J. Phys. Chem. B, 2006, 110, 2833–2839 CrossRef CAS.
- T. M. Duncan, A Compilation of Chemical Shift Anisotropies, Farragut Press, Chicago, 1990 Search PubMed.
- G. W. Driver, Y. Huang, A. Laaksonen, T. Sparrman, Y. L. Wang and P. O. Westlund, Correlated/non-correlated ion dynamics of charge-neutral ion couples: The origin of ionicity in ionic liquids, Phys. Chem. Chem. Phys., 2017, 19, 4975–4988 RSC.
- V. V Matveev, D. A. Markelov, V. I. Chizhik, P. Ingman and E. Lähderanta, Molecular mobility of counterion functional groups in ionic liquid 1-ethyl-3-methylimidazolium acetate according to 1H and 13C NMR relaxation data, Russ. Chem. Bull., 2013, 62, 1985–1990 CrossRef.
- R. C. Remsing, J. L. Wildin, A. L. Rapp and G. Moyna, Hydrogen bonds in ionic liquids revisited: (35/37)Cl NMR studies of deuterium isotope effects in 1-n-butyl-3-methylimidazolium chloride, J. Phys. Chem. B, 2007, 111, 11619–11621 CrossRef CAS.
- K. Noack, P. S. Schulz, N. Paape, J. Kiefer, P. Wasserscheid and A. Leipertz, The role of the C2 position in interionic interactions of imidazolium based ionic liquids: a vibrational and NMR spectroscopic study, Phys. Chem. Chem. Phys., 2010, 12, 14153–14161 RSC.
- K. Dong, S. Zhang and J. Wang, Understanding the Hydrogen Bonds in Ionic Liquids and their Roles in Properties and Reactions, Chem. Commun., 2016, 52, 6744–6764 RSC.
- J.-F. Huang, P.-Y. Chen, I. W. Sun and S. P. Wang, NMR evidence of hydrogen bonding in 1-ethyl-3-methylimidazolium-tetrafluoroborate room temperature ionic liquid, Inorg. Chim. Acta, 2001, 320, 7–11 CrossRef CAS.
- A. Wulf, K. Fumino, D. Michalik and R. Ludwig, IR and NMR Properties of Ionic Liquids: Do They Tell Us the Same Thing?, ChemPhysChem, 2007, 8, 2265–2269 CrossRef CAS.
- A. D. Headley and N. M. Jackson, The effect of the anion on the chemical shifts of the aromatic hydrogen atoms of liquid 1-butyl-3-methylimidazolium salts, J. Phys. Org. Chem., 2002, 15, 52–55 CrossRef CAS.
- P. A. Hunt, C. R. Ashworth and R. P. Matthews, Hydrogen bonding in ionic liquids, Chem. Soc. Rev., 2015, 44, 1257–1288 RSC.
- C. W. N. Cumper, The relation between carbon-hydrogen bond lengths and bond angles, Trans. Faraday Soc., 1958, 54, 1261 RSC.
- J. H. Antony, D. Mertens, T. Breitenstein, A. Dölle, P. Wasserscheid and W. R. Carper, Molecular structure, reorientational dynamics, and intermolecular interactions in the neat ionic liquid 1-butyl-3-methylimidazolium hexafluorophosphate, Pure Appl. Chem., 2004, 76, 255–261 CAS.
- S. M. Green, M. E. Ries, J. Moffat and T. Budtova, NMR and Rheological Study of Anion Size Influence on the Properties of Two Imidazolium-based Ionic Liquids, Sci. Rep., 2017, 7, 1–12 CrossRef CAS PubMed.
- C. S. Lovell, A. Walker, R. A. Damion, A. Radhi, S. F. Tanner, T. Budtova and M. E. Ries, Influence of Cellulose on Ion Diffusivity in 1-Ethyl-3-Methyl-Imidazolium Acetate Cellulose Solutions, Biomacromolecules, 2010, 11, 2927–2935 CrossRef CAS.
- K. S. Han, S. Li, E. W. Hagaman, G. A. Baker, P. Cummings and S. Dai, Rotational and Translational Dynamics of N-Butyl-N-methylpiperidinium Trifluoromethanesulfonimide Ionic Liquids Studied by NMR and MD Simulations, J. Phys. Chem. C, 2012, 116, 20779–20786 CrossRef CAS.
- J. Hou, Z. Zhang and L. A. Madsen, Cation/Anion Associations in Ionic Liquids Modulated by Hydration and Ionic Medium, J. Phys. Chem. B, 2011, 115, 4576–4582 CrossRef CAS.
- W. R. Carper and C. E. Keller, Direct Determination of NMR Correlation Times from Spin–Lattice and Spin–Spin Relaxation Times, J. Phys. Chem. A, 1997, 101, 3246–3250 CrossRef CAS.
- Y. H. Zhao, M. H. Abraham and A. M. Zissimos, Fast Calculation of van der Waals Volume as a Sum of Atomic and Bond Contributions and Its Application to Drug Compounds, J. Org. Chem., 2003, 68, 7368–7373 CrossRef CAS.
- E. McLaughlin, Viscosity and self-diffusion in liquids, Trans. Faraday Soc., 1959, 55, 28–38 RSC.
- T. Köddermann, R. Ludwig and D. Paschek, On the Validity of Stokes–Einstein and Stokes–Einstein–Debye Relations in Ionic Liquids and Ionic-Liquid Mixtures, ChemPhysChem, 2008, 9, 1851–1858 CrossRef.
- C. K. Larive, M. Lin, B. S. Kinnear, B. J. Piersma, C. E. Keller and W. R. Carper, 13C and 27Al NMR Relaxation, Viscosity, and 1H Diffusion Studies of an Ethylaluminum Dichloride Melt, J. Phys. Chem. B, 1998, 102, 1717–1723 CrossRef CAS.
- A. Martinelli, M. Maréchal, Å. Östlund and J. Cambedouzou, Insights into the interplay between molecular structure and diffusional motion in 1-alkyl-3-methylimidazolium ionic liquids: A combined PFG NMR and X-ray scattering study, Phys. Chem. Chem. Phys., 2013, 15, 5510–5517 RSC.
- A. Strate, T. Niemann, D. Michalik and R. Ludwig, When Like Charged Ions Attract in Ionic Liquids: Controlling the Formation of Cationic Clusters by the Interaction Strength of the Counterions, Angew. Chem., Int. Ed., 2017, 56, 496–500 CrossRef CAS.
- T. Niemann, D. Zaitsau, A. Strate, A. Villinger and R. Ludwig, Cationic clustering influences the phase behaviour of ionic liquids, Sci. Rep., 2018, 8, 14753 CrossRef.
- R. Kimmich and E. Anoardo, Field-cycling NMR relaxometry, Prog. Nucl. Magn. Reson. Spectrosc., 2004, 44, 257–320 CrossRef CAS.
- A. Ordikhani Seyedlar, S. Stapf and C. Mattea, Nuclear magnetic relaxation and diffusion study of the ionic liquids 1-ethyl- and 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide confined in porous glass, Magn. Reson. Chem., 2019, 57, 818–828 CrossRef CAS PubMed.
- D. Kruk, M. Wojciechowski, S. Brym and R. K. Singh, Dynamics of ionic liquids in bulk and in confinement by means of 1H NMR relaxometry-BMIM-OcSO4 in an SiO2 matrix as an example, Phys. Chem. Chem. Phys., 2016, 18, 23184–23194 RSC.
- D. Kruk, M. Wojciechowski, Y. L. Verma, S. K. Chaurasia and R. K. Singh, Dynamical properties of EMIM-SCN confined in a SiO2 matrix by means of 1H NMR relaxometry, Phys. Chem. Chem. Phys., 2017, 19, 32605–32616 RSC.
- K. Pilar, A. Rua, S. N. Suarez, C. Mallia, S. Lai, J. R. P. Jayakody, J. L. Hatcher, J. F. Wishart and S. Greenbaum, Investigation of Dynamics in BMIM TFSA Ionic Liquid through Variable Temperature and Pressure NMR Relaxometry and Diffusometry, J. Electrochem. Soc., 2017, 164, H5189–H5196 CrossRef CAS.
- A. E. Khudozhitkov, P. Stange, A. M. Bonsa, V. Overbeck, A. Appelhagen, A. G. Stepanov, D. I. Kolokolov, D. Paschek and R. Ludwig, Dynamical heterogeneities in ionic liquids as revealed from deuteron NMR, Chem. Commun., 2018, 54, 3098–3101 RSC.
- D. Kruk, R. Meier, A. Rachocki, A. Korpała, R. K. Singh and E. A. Rössler, Determining diffusion coefficients of ionic liquids by means of field cycling nuclear magnetic resonance relaxometry, J. Chem. Phys., 2014, 140, 244509 CrossRef CAS.
- K. Hayamizu, S. Tsuzuki, S. Seki and Y. Umebayashi, Multinuclear NMR studies on translational and rotational motion for two ionic liquids composed of BF4 anion, J. Phys. Chem. B, 2012, 116, 11284–11291 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra07731f |
| This journal is © The Royal Society of Chemistry 2019 |