Open Access Article
Open Access ArticlePrediction of pressure-induced phase transformations in Mg3As2†
Kang Yang,
Jingming Shi *,
Shicong Ding,
Ruiming Su,
Wenwen Cui,
Meiling Xu
*,
Shicong Ding,
Ruiming Su,
Wenwen Cui,
Meiling Xu ,
Jian Hao* and
Yinwei Li
,
Jian Hao* and
Yinwei Li
School of Physics and Electronic Engineering, Jiangsu Normal University, Xuzhou, China. E-mail: jingmingshi@jsnu.edu.cn; jian_hao@jsnu.edu.cn
First published on 25th October 2019
Abstract
Pressure is a fundamental tool that can induce structural and electronic transformations, which is helpful to search for exotic materials not accessible at ambient conditions. Here, we have performed an extensive structural study on cubic Mg3As2 in a pressure range of 0–100 GPa by using a combination of structure predictions and first-principle calculations. Interestingly, two novel structures with space groups C2/m and P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) were uncovered that become energetically most stable at pressures of 12 GPa and 30 GPa, respectively. Phonon dispersions demonstrate that the three phases are dynamically stable in their respective low-enthalpy pressure ranges. The electronic calculations show that Mg3As2 keeps semiconductor properties at pressures up to 100 GPa. The interesting thing is that the direct semi-conducting property of Mg3As2 transforms into indirect semi-conducting when the pressure is above 12 GPa. The current results provide new insights for understanding the behavior of Mg3As2 at high pressures.
were uncovered that become energetically most stable at pressures of 12 GPa and 30 GPa, respectively. Phonon dispersions demonstrate that the three phases are dynamically stable in their respective low-enthalpy pressure ranges. The electronic calculations show that Mg3As2 keeps semiconductor properties at pressures up to 100 GPa. The interesting thing is that the direct semi-conducting property of Mg3As2 transforms into indirect semi-conducting when the pressure is above 12 GPa. The current results provide new insights for understanding the behavior of Mg3As2 at high pressures.
1 Introduction
Pressure is considered as one of the most fundamental thermodynamic variables which can be used to influence the structural configuration, electronic properties and synthesis of unusual stoichiometric materials.1–9 These fruitful results indicate that pressure is a powerful tool for discovering and designing novel materials which possess unique properties, like being super conductive, super hard, and transparent semi-conductive.Group II alkaline metal elements typically form A3B2-type compounds with the elements in group V. These compounds have attracted much attention due to their wide band gaps and can be viewed as good materials in electronic and optoelectronic devices. Mg3N2, a typical A3B2-type compound, has been identified to crystallize in the cubic anti-bixbyite structure of the mineral (Mn,Fe)2O3 (ref. 10) with space group Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) at ambient conditions. Experimental studies have shown that the cubic Mg3N2 undergoes several phase transformations11,12 to C2/m13 and P
at ambient conditions. Experimental studies have shown that the cubic Mg3N2 undergoes several phase transformations11,12 to C2/m13 and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (ref. 13) at high pressure. While for another compound in this group, Ca3N2, numerous phases have been synthesized at the experimental level or predicted in theoretical simulations, namely Ia
m1 (ref. 13) at high pressure. While for another compound in this group, Ca3N2, numerous phases have been synthesized at the experimental level or predicted in theoretical simulations, namely Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ,14,15 R
,14,15 R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c,16,17 Pbcn,18 C2/m,19 P
c,16,17 Pbcn,18 C2/m,19 P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1,19 and I
m1,19 and I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d.20 In 2017, a phase transition of Mg3P2 was found by theoretical simulation when going from ambient conditions to high pressure.21 It reveals that there are four phases of Mg3P2 in the A3B2-type family that are stable in the pressure range from the ambient to 100 GPa. The previous studies have shown that most of the structures of the A3B2-type family possess Ia
3d.20 In 2017, a phase transition of Mg3P2 was found by theoretical simulation when going from ambient conditions to high pressure.21 It reveals that there are four phases of Mg3P2 in the A3B2-type family that are stable in the pressure range from the ambient to 100 GPa. The previous studies have shown that most of the structures of the A3B2-type family possess Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry which is the typical configuration of rare-earth sesquioxides (e.g., Sc2O3,22 Y2O3,23 Er2O3,24 Gd2O3,25 In2O3 (ref. 26)). As, the sister element to N and P elements in group VA, exhibits the similar electron-cloud out of the core and possesses similar chemical properties. In early 1964, Juza and Kroebel experimentally found two phases of Mg3As2, namely Ia
symmetry which is the typical configuration of rare-earth sesquioxides (e.g., Sc2O3,22 Y2O3,23 Er2O3,24 Gd2O3,25 In2O3 (ref. 26)). As, the sister element to N and P elements in group VA, exhibits the similar electron-cloud out of the core and possesses similar chemical properties. In early 1964, Juza and Kroebel experimentally found two phases of Mg3As2, namely Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and P
and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1,27 which were also reported by Ali Mokhtari and Matin Sedighi in 2010 with simulation28 and collected by the Materials Project database.29 However, the As atom has a much larger ionic radius than N and P atoms, which may affect the structural configuration of arsenide and the phase transformation sequence, especially at high pressure. On the other hand, the existent compounds of the A3B2-type family usually have large band gaps, which is beneficial to potential applications. For example, the band gap of Mg3N2 (ref. 13) is about 1.65 eV at ambient conditions and 2.35 eV at about 25 GPa, respectively. While for the Mg3P2 compound,21 the gap is about 1.73 eV and 1.14 eV at ambient conditions and 2.5 GPa, respectively. When the pressure is above 35 GPa, Mg3P2 transforms into a metallic phase. Thus, there is a lot of necessity for us to study the band gap evolution and the potential applications of Mg3As2 from ambient conditions to high pressure. Finally, as an antistructure in comparison to the traditional A2B3-type, accurate structural configuration and the phase transition sequence of Mg3As2 under high pressure can provide important implications for understanding the compressional behavior of related materials like rare-earth sesquioxides.
m1,27 which were also reported by Ali Mokhtari and Matin Sedighi in 2010 with simulation28 and collected by the Materials Project database.29 However, the As atom has a much larger ionic radius than N and P atoms, which may affect the structural configuration of arsenide and the phase transformation sequence, especially at high pressure. On the other hand, the existent compounds of the A3B2-type family usually have large band gaps, which is beneficial to potential applications. For example, the band gap of Mg3N2 (ref. 13) is about 1.65 eV at ambient conditions and 2.35 eV at about 25 GPa, respectively. While for the Mg3P2 compound,21 the gap is about 1.73 eV and 1.14 eV at ambient conditions and 2.5 GPa, respectively. When the pressure is above 35 GPa, Mg3P2 transforms into a metallic phase. Thus, there is a lot of necessity for us to study the band gap evolution and the potential applications of Mg3As2 from ambient conditions to high pressure. Finally, as an antistructure in comparison to the traditional A2B3-type, accurate structural configuration and the phase transition sequence of Mg3As2 under high pressure can provide important implications for understanding the compressional behavior of related materials like rare-earth sesquioxides.
In order to clarify the phase transitions and potential electronic applications of Mg3As2 compounds from ambient conditions to high pressure, we performed systematic structural searches by using a structural prediction method combining with the first-principles method. We predicted two novel structures of Mg3As2 that are unknown in the pressure range from ambient to 100 GPa. The phonon dispersions show that all the novel phases of Mg3As2 were dynamically stable. Electronic property calculations show that all the phases of Mg3As2 can be viewed as semiconductors. Interestingly, with the pressure increasing, the character of direct semiconductor (for P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 and C2/m phases) will turn into an indirect band gap property (P
m1 and C2/m phases) will turn into an indirect band gap property (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase).
phase).
2 Methods
For the structure stability, we used two steps to get the ground state structure at each pressure. Firstly, as the elements with similar electron clouds always form the same structure configuration, we chose the known phases of Mg–N and Mg–P (like Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , C2/m and P
, C2/m and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1) as prototype structures to predict the novel phase of the Mg–As system. Secondly, we performed structure predictions to search all the possible structures in the energy surface. For the structure prediction we used the CALYPSO30,31 method with the cells containing 2 to 4 formula units in a pressure range from 0 to 100 GPa. The underlying ab initio structural relaxations and the electronic band structure calculations were performed in the framework of density functional theory (DFT) using the VASP code.32 The calculations were carried out in the generalized gradient approximation33 for the exchange–correlation potential, using the Perdew–Burke–Ernzerhof34 (PBE) functional. The electronic wave functions were expanded in a plane wave basis set with a cutoff energy of 600 eV. The electron–ion interaction was described by means of projector augmented wave (PAW)35 pseudopotentials with 2p63s2 and 3s23p3 electrons in the valence band for the Mg and As atoms, respectively. Monkhorst–Pack k-point36 meshes with a grid density of 0.03 Å−1 were chosen to achieve a total energy convergence of better than 1 meV per atom. The phonon dispersion curves were computed by the direct supercell calculation method, as implemented in the PHONOPY program.37
m1) as prototype structures to predict the novel phase of the Mg–As system. Secondly, we performed structure predictions to search all the possible structures in the energy surface. For the structure prediction we used the CALYPSO30,31 method with the cells containing 2 to 4 formula units in a pressure range from 0 to 100 GPa. The underlying ab initio structural relaxations and the electronic band structure calculations were performed in the framework of density functional theory (DFT) using the VASP code.32 The calculations were carried out in the generalized gradient approximation33 for the exchange–correlation potential, using the Perdew–Burke–Ernzerhof34 (PBE) functional. The electronic wave functions were expanded in a plane wave basis set with a cutoff energy of 600 eV. The electron–ion interaction was described by means of projector augmented wave (PAW)35 pseudopotentials with 2p63s2 and 3s23p3 electrons in the valence band for the Mg and As atoms, respectively. Monkhorst–Pack k-point36 meshes with a grid density of 0.03 Å−1 were chosen to achieve a total energy convergence of better than 1 meV per atom. The phonon dispersion curves were computed by the direct supercell calculation method, as implemented in the PHONOPY program.37
3 Results and discussions
To investigate the phase transitions of Mg3As2, we performed structural prediction with unit-cell sizes of maximal four formula units (f.u.) at pressures of 0, 20, 50 and 100 GPa, respectively. Due to computational restrictions, we decided to use a suitable unit-cell size to ensure the calculation efficiency. For the next step, we chose at least 5 structures in each prediction for further accurate geometric optimization. The phase transitions of Mg3As2 under high pressure are further illustrated in Fig. 1, where we plot the relative enthalpies per formula unit with respect to the C2/m phase as a function of pressure, including the enthalpies of metastable phases that we predicted. From Fig. 1, we can clearly find that the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase is the ground-state for Mg3As2 at ambient conditions. The crystal structure of this phase is shown in Fig. 2(a). The Ia
phase is the ground-state for Mg3As2 at ambient conditions. The crystal structure of this phase is shown in Fig. 2(a). The Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase has an interesting configuration with Mg–As bond lengths of 2.62–2.73 Å. There are eight formula units in its primitive cell and all the Mg atoms are in the same Wyckoff positions (48e) while two different As atoms possess the (8b) and (24d) positions. In this phase, each Mg atom connects with four As atoms, while each As atom is bonded to six Mg atoms. However, the Ia
phase has an interesting configuration with Mg–As bond lengths of 2.62–2.73 Å. There are eight formula units in its primitive cell and all the Mg atoms are in the same Wyckoff positions (48e) while two different As atoms possess the (8b) and (24d) positions. In this phase, each Mg atom connects with four As atoms, while each As atom is bonded to six Mg atoms. However, the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase is quickly destabilized by pressure, and a novel structure with space group P
phase is quickly destabilized by pressure, and a novel structure with space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 becomes the ground-state at a pressure of 1.3 GPa. The crystal configuration of this phase is shown in Fig. 2(b). This phenomenon also emerges in the similar system of Mg3P2.21 The P
m1 becomes the ground-state at a pressure of 1.3 GPa. The crystal configuration of this phase is shown in Fig. 2(b). This phenomenon also emerges in the similar system of Mg3P2.21 The P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phase has five atoms in its primitive cell. The Mg atoms possess Wyckoff positions of (2d) and (1a), while the As atoms only locate at (2d) positions. The Mg atoms and As atoms form an octahedron and tetrahedron with Mg–As bond lengths of 2.62–2.73 Å. These behaviors are in good agreement with the information that was presented in the Materials Project database.29 When the pressure increases, the C2/m phase becomes energetically favorable at around 12 GPa. The C2/m structure has two formula units in its unit cell, as shown in Fig. 2(c). This is a remarkable structure which is composed of a regular octahedron and a tetrahedron. They connect to each other with a sharing edge formed by two As atoms. The distances between the Mg atom and As atom are 2.47–2.73 Å at 20 GPa. With the pressure increasing to 30 GPa, we predict a novel phase with P
m1 phase has five atoms in its primitive cell. The Mg atoms possess Wyckoff positions of (2d) and (1a), while the As atoms only locate at (2d) positions. The Mg atoms and As atoms form an octahedron and tetrahedron with Mg–As bond lengths of 2.62–2.73 Å. These behaviors are in good agreement with the information that was presented in the Materials Project database.29 When the pressure increases, the C2/m phase becomes energetically favorable at around 12 GPa. The C2/m structure has two formula units in its unit cell, as shown in Fig. 2(c). This is a remarkable structure which is composed of a regular octahedron and a tetrahedron. They connect to each other with a sharing edge formed by two As atoms. The distances between the Mg atom and As atom are 2.47–2.73 Å at 20 GPa. With the pressure increasing to 30 GPa, we predict a novel phase with P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry which is energetically favored in a large range of pressures from about 30 GPa to more than 100 GPa, the maximum pressure we considered. The P
symmetry which is energetically favored in a large range of pressures from about 30 GPa to more than 100 GPa, the maximum pressure we considered. The P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase has an interesting structural configuration with several octahedrons and they connect with each other by sharing one or two faces, as shown in Fig. 2(d). The distances between the Mg and As atoms are around 2.50–2.65 Å under 30 GPa. Thus, we propose a clear phase transformation sequence of Mg3As2 from ambient conditions to high pressure. The sequence is as follows:
phase has an interesting structural configuration with several octahedrons and they connect with each other by sharing one or two faces, as shown in Fig. 2(d). The distances between the Mg and As atoms are around 2.50–2.65 Å under 30 GPa. Thus, we propose a clear phase transformation sequence of Mg3As2 from ambient conditions to high pressure. The sequence is as follows:  . Comparing with the series of phase transitions of Mg3N2
. Comparing with the series of phase transitions of Mg3N2 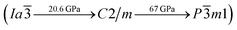 13 and Mg3P2
13 and Mg3P2  ,21 we can find that these three compounds adopt the same ambient structure, while high pressure phases vary accordingly, which is caused by the different ionic radii of N, P and As atoms. The lattice parameters and atomic coordinates which are optimized for the most energetically favorable structures are listed in Table 1. The lattice parameters of Ia
,21 we can find that these three compounds adopt the same ambient structure, while high pressure phases vary accordingly, which is caused by the different ionic radii of N, P and As atoms. The lattice parameters and atomic coordinates which are optimized for the most energetically favorable structures are listed in Table 1. The lattice parameters of Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (a = 12.16 Å) are in good agreement with the data in the Materials Project (a = 12.176 Å),29 which indicates that our calculations are credible. To examine the interactions between Mg and As atoms of the new phases, we calculated the Bader charges, as shown in Table 1. The results show that all the phases of Mg3As2 compound exhibit ionic behavior and each Mg atom will lose about 1.50e while each As atom will gain about 2.25e. To understand the bonding behaviors of these structures, we calculated the electron localization function (ELF) and the charge density difference, as shown in the ESI.† The results show that the charges almost localize around the As atoms that form anions, while Mg atoms act as cations. This is also in good agreement with the results of the Bader analysis.
(a = 12.16 Å) are in good agreement with the data in the Materials Project (a = 12.176 Å),29 which indicates that our calculations are credible. To examine the interactions between Mg and As atoms of the new phases, we calculated the Bader charges, as shown in Table 1. The results show that all the phases of Mg3As2 compound exhibit ionic behavior and each Mg atom will lose about 1.50e while each As atom will gain about 2.25e. To understand the bonding behaviors of these structures, we calculated the electron localization function (ELF) and the charge density difference, as shown in the ESI.† The results show that the charges almost localize around the As atoms that form anions, while Mg atoms act as cations. This is also in good agreement with the results of the Bader analysis.
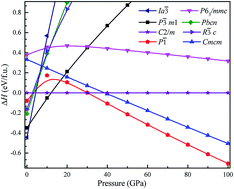 | ||
| Fig. 1 Relative enthalpy per formula unit of the different phases of Mg3As2 with respect to the C2/m phase as a function of pressure. | ||
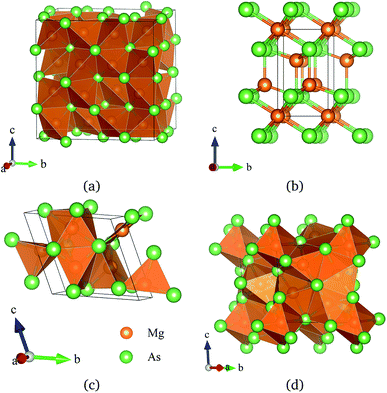 | ||
Fig. 2 Crystal structures of Mg3As2 (orange: Mg and green: As); (a) the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase at ambient pressure, (b) the P phase at ambient pressure, (b) the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phase at 5 GPa, (c) the C2/m phase at 15 GPa and (d) the P m1 phase at 5 GPa, (c) the C2/m phase at 15 GPa and (d) the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase at 30 GPa. phase at 30 GPa. | ||
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , P
, P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1, C2/m and P
m1, C2/m and P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phases at selected pressures. Bader charges of these phases at specific conditions are shown in the last column
phases at selected pressures. Bader charges of these phases at specific conditions are shown in the last column
| Pressure (GPa) | Space group | Lattice parameters | Atomic coordinates (fractional) | Bader charge (e) |
|---|---|---|---|---|
| 0 | Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
a = b = c = 12.46 Å | Mg (48e) (−0.11, −0.36, 0.88) | 1.51 |
| α = β = γ = 90° | As (8b) (−0.25, −0.25, 0.75) | −2.26 | ||
| As (24d) (−0.02, −1.00, 0.25) | −2.26 | |||
| 5 | P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 m1 |
a = b = 4.19 Å | Mg (2d) (0.33, 0.67, 0.36) | 1.50 |
| c = 6.55 Å | Mg (1a) (0.00, 0.00, 0.00) | 1.56 | ||
| α = β = 90°, γ = 120° | As (2d) (0.33, 0.67, 0.77) | −2.28 | ||
| 15 | C2/m | a = 13.84 Å | Mg (4i) (0.34, 0.50, 0.02) | 1.49 |
| b = 3.89 Å | Mg (4i) (0.25, 0.00, 0.66) | 1.52 | ||
| c = 7.15 Å | Mg (2c) (0.50, 0.50, 0.50) | 1.55 | ||
| α = 116.67° | Mg (2b) (0.50, 0.00, 1.00) | 1.53 | ||
| β = 105.80° | As (4i) (0.13, 0.50, 0.74) | −2.29 | ||
| γ = 90° | As (4i) (0.40, 0.50, 0.73) | −2.26 | ||
| 30 | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
a = 6.77 Å | Mg (2i) (0.52, 0.53, 0.72) | 1.56 |
| b = 6.80 Å | Mg (2i) (0.23, 0.23, 0.15) | 1.56 | ||
| c = 7.14 Å | Mg (2i) (0.09, 0.77, 0.61) | 1.54 | ||
| α = 93.32° | Mg (2i) (0.97, 0.67, 0.25) | 1.55 | ||
| β = 97.04° | Mg (2i) (0.50, 0.79, 0.110) | 1.55 | ||
| γ = 65.85° | Mg (1a) (0.00, 0.00, 0.00) | 1.54 | ||
| Mg (1f) (0.50, 0.00, 0.50) | 1.58 | |||
| As (2i) (0.33, 0.95, 0.80) | −2.35 | |||
| As (2i) (0.21, 0.89, 0.32) | −2.31 | |||
| As (2i) (0.79, 0.43, 0.04) | −2.37 | |||
| As (2i) (0.75, 0.61, 0.51) | −2.26 |
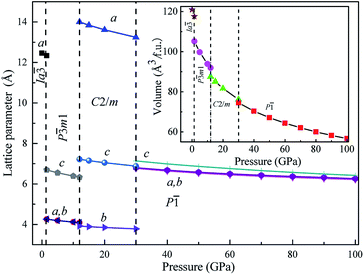
We also calculated the lattice parameters and volumes of these four novel phases of Mg3As2 as a function of pressure, as shown in Fig. 3. It reveals that all the lattice constants will decrease when the pressure increases and detects that the volume collapses at the phase transitions: Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) → P
→ P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (at 1.3 GPa), P
m1 (at 1.3 GPa), P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 → C2/m (at 12 GPa) and C2/m → P
m1 → C2/m (at 12 GPa) and C2/m → P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (at 30 GPa). This indicates that the three phase transitions in Mg3As2 are first-order in nature. This phenomenon is in good agreement with the previous works on Mg3P2.21
(at 30 GPa). This indicates that the three phase transitions in Mg3As2 are first-order in nature. This phenomenon is in good agreement with the previous works on Mg3P2.21
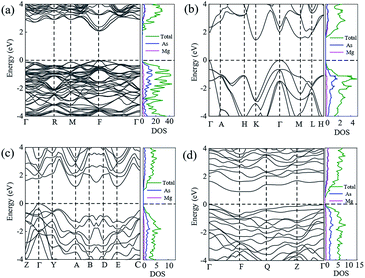
In order to ensure the thermal stability of these novel structures, we calculated the phonon dispersions of Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , P
, P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1, C2/m and P
m1, C2/m and P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) at 0, 1.5, 20 and 30 GPa, respectively, as shown in Fig. 4. As expected, they do not exhibit any imaginary phonon frequencies indicating that all the novel phases are mechanically stable. It is well known that the PBE function systematically underestimates band gaps. Therefore we decided to adopt the hybrid exchange–correlation functional of Heyd, Scuseria, and Ernzerhof (HSE06)38 to obtain reliable band gaps. The calculated electronic band structures (HSE06) and the projected densities of state (HSE06) are shown in Fig. 5. For comparison, the calculated band structures of all structures by using the PBE function are shown in the ESI.† From our calculation, it is evident that all the four phases of Mg3As2 are semiconductors and the band gap will decrease with increasing pressure. For example, at 0 GPa, the band gap of the Ia
at 0, 1.5, 20 and 30 GPa, respectively, as shown in Fig. 4. As expected, they do not exhibit any imaginary phonon frequencies indicating that all the novel phases are mechanically stable. It is well known that the PBE function systematically underestimates band gaps. Therefore we decided to adopt the hybrid exchange–correlation functional of Heyd, Scuseria, and Ernzerhof (HSE06)38 to obtain reliable band gaps. The calculated electronic band structures (HSE06) and the projected densities of state (HSE06) are shown in Fig. 5. For comparison, the calculated band structures of all structures by using the PBE function are shown in the ESI.† From our calculation, it is evident that all the four phases of Mg3As2 are semiconductors and the band gap will decrease with increasing pressure. For example, at 0 GPa, the band gap of the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase is 1.42 eV (PBE) and 2.08 eV (HSE06), which is in good agreement with the previous work,28 while it will become 0.86 eV (PBE) and 1.43 eV (HSE06) for P
phase is 1.42 eV (PBE) and 2.08 eV (HSE06), which is in good agreement with the previous work,28 while it will become 0.86 eV (PBE) and 1.43 eV (HSE06) for P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 at 1.5 GPa, 0.68 eV (PBE) and 1.21 eV (HSE06) for C2/m at 20 GPa and 0.49 eV (PBE) and 0.93 eV (HSE06) for P
m1 at 1.5 GPa, 0.68 eV (PBE) and 1.21 eV (HSE06) for C2/m at 20 GPa and 0.49 eV (PBE) and 0.93 eV (HSE06) for P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) at 30 GPa, respectively. Comparing to another two compounds (Mg3N2 (ref. 13) and Mg3P2 (ref. 21)), Mg3As2 has a larger band gap at ambient conditions and can remain a semiconductor even at high pressure. These good performances can make Mg3As2 compounds act as good potential semiconductors at both ambient conditions and high pressure. The projected densities of state show that the electrons near the Fermi level are almost all contributed by the As atoms, which reveals that the As atoms play an important role in the semiconductor property.
at 30 GPa, respectively. Comparing to another two compounds (Mg3N2 (ref. 13) and Mg3P2 (ref. 21)), Mg3As2 has a larger band gap at ambient conditions and can remain a semiconductor even at high pressure. These good performances can make Mg3As2 compounds act as good potential semiconductors at both ambient conditions and high pressure. The projected densities of state show that the electrons near the Fermi level are almost all contributed by the As atoms, which reveals that the As atoms play an important role in the semiconductor property.
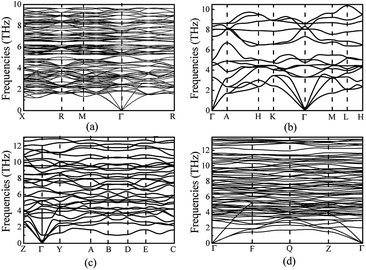 | ||
Fig. 4 Phonon dispersions of Mg3As2 for (a) the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase at ambient pressure, (b) the P phase at ambient pressure, (b) the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phase at 1.5 GPa, (c) the C2/m phase at 20 GPa and (d) the P m1 phase at 1.5 GPa, (c) the C2/m phase at 20 GPa and (d) the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase at 30 GPa. phase at 30 GPa. | ||
4 Conclusions
In summary, using a global structural prediction method we studied systematically the phase transitions and electronic properties of Mg3As2. We identified two novel phases with unexpected structures that might be experimentally synthesizable over a wide range of pressures. The novel phases have C2/m and P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry under high pressure. The transition pressures of the two structures are 12 GPa and 30 GPa, respectively. The Bader charge calculations show that all the phases possess ionic behavior. The phonon dispersions reveal that they are mechanically stable. From the calculations of electronic properties we can indicate that all the phases are semiconductor. These results show remarkable phase transitions of Mg3As2, and can serve as an important guide for further experimental studies of this compound.
symmetry under high pressure. The transition pressures of the two structures are 12 GPa and 30 GPa, respectively. The Bader charge calculations show that all the phases possess ionic behavior. The phonon dispersions reveal that they are mechanically stable. From the calculations of electronic properties we can indicate that all the phases are semiconductor. These results show remarkable phase transitions of Mg3As2, and can serve as an important guide for further experimental studies of this compound.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. S. and W. C. acknowledge the Project Funded by the National Natural Science Foundation of China under Grant No. 11804129 and No. 11804128 and the Jiangsu Normal University under Grant No. 18XLRS003 and No. 18XLRS004. Y. L. and J. H. acknowledge funding from the National Natural Science Foundation of China under Grant No. 11722433 and No. 11404148 and Qing Lan Project of Jiangsu Province. All the calculations were performed using the High Performance Computing Center of the School of Physics and Electronic Engineering of Jiangsu Normal University. The crystal structures were visualized with VESTA.39References
- L. Zhang, Y. Wang, J. Lv and Y. Ma, Nat. Rev. Mater., 2017, 2, 17005 CrossRef CAS.
- Y. Ma, M. Eremets, A. R. Oganov, Y. Xie, I. Trojan, S. Medvedev, A. O. Lyakhov, M. Valle and V. Prakapenka, Nature, 2009, 458, 182–185 CrossRef CAS.
- Y. Li, Y. Wang, C. J. Pickard, R. J. Needs, Y. Wang and Y. Ma, Phys. Rev. Lett., 2015, 114, 125501 CrossRef.
- Y. Li, J. Hao, H. Liu, Y. Li and Y. Ma, J. Chem. Phys., 2014, 140, 899 Search PubMed.
- A. Drozdov, M. Eremets, I. Troyan, V. Ksenofontov and S. Shylin, Nature, 2015, 525, 73 CrossRef CAS.
- D. Duan, Y. Liu, F. Tian, D. Li, X. Huang, Z. Zhao, H. Yu, B. Liu, W. Tian and T. Cui, Sci. Rep., 2014, 4, 6968 CrossRef CAS.
- Y. Li, X. Feng, H. Liu, J. Hao, S. A. Redfern, W. Lei, D. Liu and Y. Ma, Nat. Commun., 2018, 9, 722 CrossRef.
- Y. Li, J. Hao, H. Liu, S. Lu and J. S. Tse, Phys. Rev. Lett., 2015, 115, 105502 CrossRef.
- J. Shi, W. Cui, S. Botti and M. A. L. Marques, Phys. Rev. Mater., 2018, 2, 023604 CrossRef CAS.
- M. Stackelberg and R. Paulus, Z. Phys. Chem. B, 1933, 22, 305–322 Search PubMed.
- D. Partin, D. Williams and M. O’Keeffe, J. Solid State Chem., 1997, 132, 56–59 CrossRef CAS.
- F. Zong, C. Meng, Z. Guo, F. Ji, H. Xiao, X. Zhang, J. Ma and H. Ma, J. Alloys Compd., 2010, 508, 172–176 CrossRef CAS.
- J. Hao, Y. Li, Q. Zhou, D. Liu, M. Li, F. Li, W. Lei, X. Chen, Y. Ma and Q. Cui, et al., Inorg. Chem., 2009, 48, 9737–9741 CrossRef CAS.
- H. Moissan, Compt. Rend., 1898, 127, 497–501 CAS.
- O. Reckeweg and F. J. DiSalvo, Z. Anorg. Allg. Chem., 2001, 627, 371–377 CrossRef CAS.
- H. H. Franck, M. A. Bredig and G. Hoffmann, Naturwissenschaften, 1933, 21, 330–331 CrossRef CAS.
- H. Hartmann and H. J. Fröhlich, Z. Anorg. Allg. Chem., 1934, 218, 190–192 CrossRef CAS.
- R. S. Bradley, D. C. Munro and M. Whitfield, J. Inorg. Nucl. Chem., 1966, 28, 1803–1812 CrossRef CAS.
- J. Hao, Y. Li, J. Wang, C. Ma, L. Huang, R. Liu, Q. Cui, G. Zou, J. Liu and X. Li, J. Phys. Chem. C, 2010, 114, 16750–16755 CrossRef CAS.
- C. Braun, S. L. Börger, T. D. Boyko, G. Miehe, H. Ehrenberg, P. Höhn, A. Moewes and W. Schnick, J. Am. Chem. Soc., 2011, 133, 4307 CrossRef CAS.
- B. Liu, J. Hao, X. Tang and Y. Li, J. Alloys Compd., 2017, 720, 207–211 CrossRef CAS.
- T. Schleid and G. Meyer, J. Less-Common Met., 1989, 149, 73–80 CrossRef.
- B. Antic, P. Oennerud, D. Rodic and R. Tellgren, Powder Diffr., 1993, 8, 216–220 CrossRef CAS.
- Q. Guo, Y. Zhao, C. Jiang, W. L. Mao, Z. Wang, J. Zhang and Y. Wang, Inorg. Chem., 2007, 46, 6164–6169 CrossRef CAS.
- F. Zhang, M. Lang, J. Wang, U. Becker and R. Ewing, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 064114 CrossRef.
- H. Yusa, T. Tsuchiya, J. Tsuchiya, N. Sata and Y. Ohishi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 092107 CrossRef.
- R. Juza and R. Kroebel, Z. Anorg. Allg. Chem., 1964, 331, 187–199 CrossRef CAS.
- A. Mokhtari and M. Sedighi, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 405, 1715–1720 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, et al., APL Mater., 2013, 1, 011002 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra06341b |
| This journal is © The Royal Society of Chemistry 2019 |