Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Experimental evidence for the role of paramagnetic oxygen concentration on the decay of long-lived nuclear spin order†
Bryan
Erriah
and
Stuart J.
Elliott‡
 *
*
School of Chemistry, University of Southampton, Southampton SO17 1BJ, UK. E-mail: stuart-james.elliott@univ-lyon1.fr
First published on 29th July 2019
Abstract
Nuclear singlet lifetimes are often dependent on the quantity of paramagnetic oxygen species present in solution, although the extent to which quenching or removing molecular oxygen has on extending singlet lifetimes is typically an unknown factor. Here we investigate the behaviour of the singlet relaxation time constant as a function of the oxygen concentration in solution. An experimental demonstration is presented for a chemically inequivalent proton pair of the tripeptide alanine–glycine–glycine in solution. We introduce a simple methodology to ensure the solution is saturated with predetermined concentrations of oxygen gas prior to measurements of the singlet lifetime. Singlet lifetimes were measured by using the spin-lock induced crossing pulse sequence. We present a linear relationship between the amount of oxygen dissolved in solution and the singlet relaxation rate constant. Singlet relaxation was found to be ∼2.7 times less sensitive to relaxation induced by paramagnetic oxygen compared with longitudinal relaxation. The relaxation behaviour is described by using a model of correlated fluctuating fields. We additionally examine the extension of singlet lifetimes by doping solutions with the chelating agent sodium ascorbate, which scavenges oxygen radicals in solution.
1 Introduction
The observation of non-equilibrium magnetization in solution is limited by the spin–lattice relaxation time constant T1. Long-lived states (LLS) are protected against the in pair dipole–dipole relaxation mechanism and decay with extended lifetimes,1–25 providing a means of bypassing this limitation. For spin-1/2 pairs, the long-lived state is defined as the mean population imbalance between the exchange-antisymmetric nuclear singlet state and the exchange-symmetric nuclear triplet states.1,2 The long-lived state is referred to as nuclear singlet order, and has a corresponding decay time constant denoted TS. LLS lifetimes dwarfing T1 by a factor of 50 have been observed,26,27 with a LLS lifetime exceeding 1 hour recorded for a 13C2-labelled naphthalene derivative to room temperature solution.28 LLS have applications to ligand-binding,29–32 reaction monitoring33 and imaging contrast.34 The combination of LLS with hyperpolarization techniques has also been proposed.35–41Numerous relaxation mechanisms attenuate singlet lifetimes including: out-of-pair dipole–dipole couplings,42,43 chemical shift anisotropy,28,43 scalar-relaxation-of-the-second-kind,44,45 singlet–triplet leakage43,46 and spin-rotation/spin-internal-motion.28,47 Dissolved paramagnetic impurities in solution additionally contribute to the singlet relaxation rate constant TS−1. A previous study from Tayler and Levitt explored the dependence of nuclear singlet lifetimes on the concentration of transition metal and lanthanide salts present in solution.48 Relaxation caused by paramagnetic oxygen dissolved in solution is also an important singlet decay mechanism. In some cases, expelling dissolved oxygen from solution can dramatically lengthen the observed singlet lifetime.26,27,49,50 To the best of our knowledge, a detailed study regarding the behaviour of singlet relaxation times as a function of paramagnetic oxygen concentration in solution has not been reported.
In this communication, we investigate the singlet lifetime behaviour for a proton pair of the polypeptide alanine–glycine–glycine (Fig. 1a) as a function of the oxygen concentration in solution. A straightforward approach to establish a desired concentration of oxygen in solution is described. Singlet and longitudinal relaxation rate constants were found to have a linear dependence on the concentration of oxygen in solution, with nuclear singlet order observed to be a factor of ∼2.7 less sensitive to paramagnetic oxygen induced relaxation compared with ordinary magnetization. A description of the relaxation behaviour using a model of correlated fluctuating fields is discussed. Singlet lifetimes are additionally measured in solutions containing the oxygen radical scavenging agent sodium ascorbate.
2 Methods
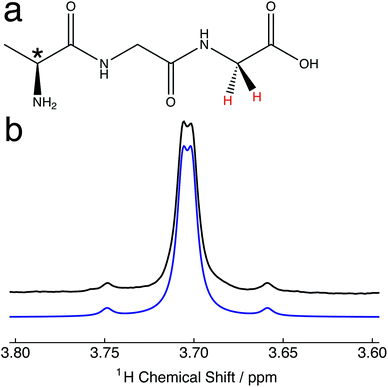
10.2 mg of alanine–glycine–glycine (Ala–Gly–Gly) was dissolved in 2 mL of D2O solvent at a concentration of 25 mM. Samples were transferred to NMR tubes with an outer diameter of 10 mm.The relevant portion of the experimental proton NMR spectrum corresponding to the α-protons of the Gly terminal residue of Ala–Gly–Gly is shown in Fig. 1b. The two central peaks of the AB spectral pattern are resolved, and are separated by an inner splitting of 1.7 Hz. Fig. 1b indicates that the two protons are strongly-coupled, i.e. there is a small chemical shift difference between the two protons sites with respect to the in pair J-coupling. The constituent singlet nuclei are diastereotopic due to the presence of a molecular chiral centre (*, Fig. 1a). The experimental proton NMR spectrum can be well simulated using the following parameters:51JHH = 16.9 ± 0.3 Hz; Δν = 8.8 ± 0.1 Hz, which are in approximate agreement with the literature.52
The small proton chemical shift difference allows access to the long-lived nuclear singlet order, by using pulsed methods,52–54 and their variants,46,55–59 which operate efficiently in the near-chemical equivalence regime. In the current study, we employed a modified version of the spin-locking induced crossing (SLIC) pulse sequence,54 as shown in Fig. 2. Details of the pulse sequence optimization and the T00 filter are given elsewhere.60,61 The sequence converts the spin-locked magnetization into singlet order through the action of the chemical shift difference, with conversion complete in a time τSLIC ≃ 2−1/2Δν−1, where Δν is the proton chemical shift difference in hertz, neglecting relaxation and other complications. The parameters of the SLIC pulse were adjusted to achieve optimal triplet–singlet population conversion: ωSLIC/2π = JHH = 16.9 Hz; τSLIC = 100 ms. The singlet order is allowed to evolve for a variable time interval τEV in the presence of an on resonant continuous wave (CW) radiofrequency field, with nutation frequency ωCW/2π = 300 Hz, which suppresses relaxation contributions from singlet-triplet mixing.43 The maximum integral of the singlet-filtered 1H NMR signal, relative that induced by a single 90° pulse, was found to be 0.37. The loss relative to the theoretical maximum of 2/3 is not yet fully understood but is attributed to radiofrequency field imperfections, static magnetic field inhomogeneities and relaxation.62 Since JHH ∼ 2Δν the performance of the SLIC pulse may not be optimal, which would lead to additional losses in triplet–singlet population conversion.54
A stringent requirement of this study is the accurate determination of the concentration of molecular oxygen dissolved in solution. As such, a key sample preparation step is the exposure of the D2O solution to a predetermined weight percentage (wt%) of O2 gas (via sample bubbling) for a sufficient amount of time as to allow full saturation of the O2 gas in solution.
To achieve a satisfactory saturation of oxygen gas, a sufficient solution bubbling time was determined from a series of calibration experiments. Samples were exposed to three gasses (O2 gas wt% given in brackets); nitrogen (<0.01), compressed air (∼20.95) and oxygen (>99.99), for incremented time periods (up to 180 s) until no discernible changes in the measured singlet or longitudinal relaxation times were observed. J.-Young low pressure/vacuum (LPV) NMR tubes (outer diameter = 10 mm) were connected to gas cylinders via 1/16 inch PTFE tubing and a glass NMR pipette. The gas flow rate was 29 mL min−1. The dead space of the NMR tube above the solution was exposed to gas for 10 s following the solution bubbling process.
For singlet and longitudinal lifetime measurements as a function of the dissolved oxygen concentration in solution, samples were bubbled for 180 s with a range of N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O2 gas mixtures. Cylinders of mixed N2
O2 gas mixtures. Cylinders of mixed N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O2 gases were purchased from BOC Ltd UK. Cylinders were 1.2 L in volume and pressurized to 200 bar. The wt% of O2 gas ranged from 2.5%–17.5% in 2.5% increments. Errors on the wt% of O2 gas in each cylinder were provided by BOC Ltd UK. Singlet relaxation times TS were estimated by using the SLIC pulse sequence described in Fig. 2. Longitudinal relaxation times T1 were measured by using separate inversion-recovery experiments.
O2 gases were purchased from BOC Ltd UK. Cylinders were 1.2 L in volume and pressurized to 200 bar. The wt% of O2 gas ranged from 2.5%–17.5% in 2.5% increments. Errors on the wt% of O2 gas in each cylinder were provided by BOC Ltd UK. Singlet relaxation times TS were estimated by using the SLIC pulse sequence described in Fig. 2. Longitudinal relaxation times T1 were measured by using separate inversion-recovery experiments.
3 Results
Single exponential relaxation curves illustrating the decay of nuclear singlet order after bubbling the solution with nitrogen, compressed air and oxygen gases for 180 s are shown in Fig. 3. Singlet lifetimes TS range from 7.0 s (O2 gas) to 45.6 s (N2 gas). Longitudinal relaxation time constants and ratios of TS to T1 are given in Table 1.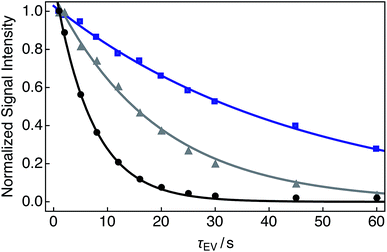 | ||
| Fig. 3 Experimental relaxation curves for 25 mM Ala–Gly–Gly dissolved in D2O solution acquired at 9.4 T (1H nuclear Larmor frequency = 400 MHz) and 298 K with two transients per data point. A delay of 230 s was used between successive transients. Samples were prepared by saturating the D2O solution with the following gases (O2 weight percentage, wt%) for 180 s prior to measurements of the singlet lifetime: black: O2 (>99.99); grey: compressed air (∼20.95); blue: N2 (<0.01). The decay profiles were obtained by implementing the SLIC pulse sequence described in Fig. 2. Singlet lifetimes (TS): black filled circles: 7.0 ± 0.1 s; grey filled triangles: 19.1 ± 0.6 s; blue filled squares: 45.6 ± 0.9 s. All signal intensities were normalized to the first data point. The fitted curves have a single exponential form. | ||
| O2 wt% | Gas | T S/s | T 1/s | T S/T1 |
|---|---|---|---|---|
| >99.99 | O2 | 7.0 ± 0.1 | 1.06 ± 0.02 | 6.6 ± 0.1 |
| ∼20.95 | Air | 19.1 ± 0.6 | 1.46 ± 0.02 | 13.1 ± 0.6 |
| <0.01 | N2 | 45.6 ± 0.9 | 1.60 ± 0.08 | 28.5 ± 0.9 |
The singlet relaxation time constants plateau with an increasing gas bubbling time, as demonstrated in Fig. S1.† A plateau of the singlet relaxation time is reached at 180 s, and implies saturation of the gases in solution since no further extension/depletion of the singlet lifetime is observed, see the ESI† for details.
Henry's law empirically relates the partial pressure of a gas to the dissolved quantity in solution, for low partial pressures and gas concentrations.63 The molar concentration of gas dissolved in solution is given by:
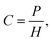 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O2 gas mixture, assuming complete saturation of the gas mixtures in solution after sample bubbling for 180 s. Small deviations in sample temperature, induced by the solution bubbling process, were ignored in the estimation of dissolved oxygen concentrations.
O2 gas mixture, assuming complete saturation of the gas mixtures in solution after sample bubbling for 180 s. Small deviations in sample temperature, induced by the solution bubbling process, were ignored in the estimation of dissolved oxygen concentrations.
Estimated singlet (TS−1) and longitudinal (T1−1) relaxation rate constants as a function of the solution oxygen concentration are presented in Fig. 4 (see Methods). TS−1 and T1−1 increase linearly as a function of the dissolved oxygen concentration. A linear relationship has been described previously for singlet and longitudinal relaxation resulting from paramagnetic transition metal ions in solution.48
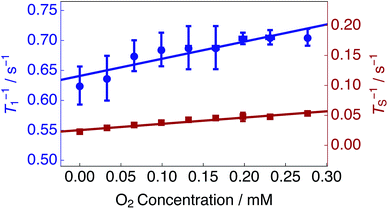 | ||
| Fig. 4 Singlet TS−1 (right hand axis) and longitudinal T1−1 (left hand axis) relaxation rate constants for 25 mM Ala–Gly–Gly dissolved in D2O solution acquired at 9.4 T (1H nuclear Larmor frequency = 400 MHz) and 298 K as a function of the O2 concentration in solution. Singlet lifetimes TS (red filled squares) were estimated by using the SLIC pulse sequence described in Fig. 2. Longitudinal lifetimes T1 (blue filled circles) were measured by using the inversion-recovery pulse sequence. Samples were prepared by saturating the D2O solution with known ratios of O2 and N2 gas, ranging from 0–20.95% O2 weight percentage (wt%), for 180 s prior to measurements of the singlet lifetime. The relaxation data were fitted with a straight line function including a non-zero intercept: Ti−1(C) = ri × C + Ti−1(0). Best fit values: singlet relaxation (red line): rS = 0.105 mM−1 s−1; TS−1(0) = 0.025 s−1; longitudinal relaxation (blue line): r1 = 0.287 mM−1 s−1; T1−1(0) = 0.641 s−1. The horizontal error bars are smaller than the data points. | ||
The experimental data were fit with relationships of the kind: Ti−1(C) = ri × C + Ti−1(0); where Ti−1(C) are the relaxation rate constants, ri are the experimental relaxivities, C is the concentration of oxygen in solution (estimated by using eqn (1)), and Ti−1(0) denotes the relaxation rate constants of an oxygen-free sample. The relaxivities for singlet rS and longitudinal r1 relaxation were determined from the slopes of a straight line fit to the experimental data (over the range of dissolved O2 concentrations shown in Fig. 4) to be: rS = 0.105 mM−1 s−1; r1 = 0.287 mM−1 s−1. The singlet relaxivity is a factor of ∼2.7 smaller than the relaxivity for longitudinal relaxation. These results indicate that singlet order is less sensitive than conventional magnetization to relaxation induced by paramagnetic oxygen dissolved in solution.
An oxygen concentration of ∼0 mM reveals the effects of additional contributions to longitudinal and singlet relaxation. The motional modulation of the in pair dipole–dipole coupling between the glycyl protons provides a dominant source of relaxation for longitudinal magnetization, but is absent for singlet order.52,64 For the case of a solution saturated with N2 gas, an impressive relaxation time ratio TS/T1 = 28.5 is observed, see Table 1.
4 Discussion
The ratio rS/r1 can be understood by employing a model in which the protons of the glycine residue experience a correlated fluctuating field generated by nearby paramagnetic oxygen species dissolved in solution.65–68 In the extreme-narrowing limit, relaxation rate expressions for TS−1 and T1−1 are:| TS−1 = 2γH2(B12 + B22−2κHHB1B2)τC, | (2) |
| T1−1 = γH2(B12 + B22)τC, | (3) |
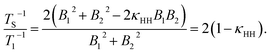 | (4) |
The assumption B1 = B2 has been included in the final step. Using eqn (4), and the ratio of rS/r1 = (2.7)−1, a correlation factor κHH = 0.82 is obtained, i.e. a strong correlation of the fluctuating fields at the nuclear sites. Similar values of κHH were found for the case of paramagnetic lanthanide salts dissolved in solution.48 The value of κHH implies that the two protons are somewhat close in space, relative to the proton–oxygen separations, and that there is likely to be a narrow subtended angle between the singlet nuclei and the paramagnetic oxygen species. Therefore, oxygen species must approach relatively closely to the spin-1/2 pair in order to significantly attenuate the singlet relaxation time. Further exploration of this behaviour is beyond the scope of this paper but estimates of the singlet relaxation rate induced by the presence of paramagnetic oxygen species dissolved in solution have previously been addressed in the literature,42,50 and could be further explored by deploying molecular dynamics simulations.47
Oxygen induced relaxation can be attenuated by quenching dioxygen, hydroperoxide and superoxide radical species dissolved in solution through chemical interaction with ascorbate forming diamagnetic complexes (Fig. 5, inset).69 Ascorbate has previously been used in LLS experiments to reduce the relaxation effects of paramagnetic agents,48 and to scavenge radicals in dissolution-dynamic nuclear polarization (dDNP) studies in the pursuit of minimizing polarization losses during low field sample transfer.70
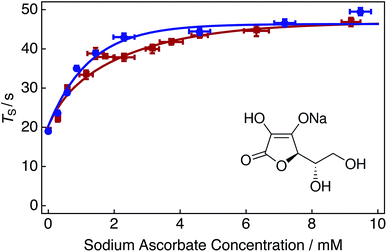 | ||
| Fig. 5 Singlet relaxation time constants TS of 25 mM Ala–Gly–Gly dissolved in D2O solution acquired at 9.4 T (1H nuclear Larmor frequency = 400 MHz) and 298 K as a function of the sodium ascorbate concentration in solution. Singlet lifetimes were estimated by using the SLIC pulse sequence described in Fig. 2. Samples were initially prepared by saturating the D2O solution with compressed air gas (∼20.95% O2 weight percentage, wt%) for 180 s. Sodium ascorbate was subsequently added step-wise to the solution. The delay between sample preparation and commencing singlet lifetime measurements was 15 minutes in each case. Red filled squares: no tap water added to solution; blue filled circles: 2 μL tap water added to solution. The fitted lines are intended to guide the eye. Inset: molecular structure of the oxygen radical quenching agent sodium ascorbate. | ||
D2O solutions were subjected to incremental additions of sodium ascorbate. After the addition of sodium ascorbate, samples were stored at 298 K for 15 minutes to allow the sample temperature to stabilize and for shifts in 1H resonance positions to settle. The experimental 1H NMR resonances of sodium ascorbate did not overlap with the relevant spectral region of Ala–Gly–Gly.
Fig. 5 shows singlet relaxation time constants TS as a function of the sodium ascorbate concentration in solution. The red curve demonstrates that singlet lifetimes increase with increasing sodium ascorbate concentration. A plateau is reached at a concentration of ∼10 mM, despite further addition of the chelating agent. This plateau is most likely due to the decreased availability of oxygen radicals in solution, leading to the decreased efficacy of the oxidation of sodium ascorbate (since encounters between sodium ascorbate and free oxygen radicals are of lower probability). The singlet lifetime recorded in the absence of sodium ascorbate (Fig. 5, leftmost data point) is given in Table 1 (compressed air). The singlet lifetime measured in the presence of ∼12 mM sodium ascorbate (Fig. 5, rightmost red data point) corresponds to a value of TS = 46.8 ± 1.1 s. The addition of sodium ascorbate clearly reduces the relaxation effects induced by dissolved radical oxygen species in solution. This value is in good agreement with that achieved by saturating the solution by bubbling with nitrogen gas (Fig. 3). This result is expected since both methods eliminate the source of paramagnetic oxygen induced relaxation. Bubbling solutions with N2 gas may be preferred to avoid sample contamination and overlapping spectral regions which may be problematic for 1H NMR measurements.
It is interesting to note that a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of sodium ascorbate to O2, i.e. ∼0.28 mM of sodium ascorbate, is insufficient as to quench the effects of oxygen induced relaxation in solution. In reality, a relatively large amount of sodium ascorbate (∼10 mM) is required to sufficiently suppress such effects. It is possible that the initial 15 minute waiting period is too short as to allow the reaction of oxygen and sodium ascorbate to fully complete. The kinetics of this reaction have not been investigated further.
1 ratio of sodium ascorbate to O2, i.e. ∼0.28 mM of sodium ascorbate, is insufficient as to quench the effects of oxygen induced relaxation in solution. In reality, a relatively large amount of sodium ascorbate (∼10 mM) is required to sufficiently suppress such effects. It is possible that the initial 15 minute waiting period is too short as to allow the reaction of oxygen and sodium ascorbate to fully complete. The kinetics of this reaction have not been investigated further.
Ascorbate can act as a bidentate ligand which has been shown to chelate to metal ions.71 Transition metal ions can catalyse the oxidation of ascorbate (quenching of radical oxygen) through the formation of intermediary metal ion–ascorbate–dioxygen complexes.71 This mechanism has been investigated for both iron and copper ions. It has been shown that ferric and cupric ions in solution result in the catalysis of ascorbate oxidation. Fe(III) and Cu(II) ions are usually found at low concentrations in regular tap water. Compositional data, published by Southern Water UK, the regional water supplier, states the iron and copper ion content of tap water to be 18.55 and 0.078 ppb, respectively.72
The blue curve in Fig. 5 shows singlet lifetimes for a range of sodium ascorbate concentrations in the case that a 2 μL aliquot of tap water was added to the D2O solution. Relaxation from paramagnetic iron and copper centers was assumed to be negligible. Following the addition of tap water, the maximum value of TS is reached at lower sodium ascorbate concentrations (∼5 mM). The reaction catalysis is demonstrated by the sharper initial increase of singlet lifetimes at reduced sodium ascorbate concentrations.
5 Conclusions
In Conclusion, the singlet lifetime of the proton pair in the glycine-terminal residue of the polypeptide Ala–Gly–Gly has been investigated as a function of the dissolved oxygen concentration in solution. Singlet relaxation rate constants were found to be linearly dependent on the quantity of oxygen in solution. The ratio of the relaxivities for singlet and longitudinal relaxation was found to be ∼(2.7)−1. Singlet and longitudinal relaxivities were described using a model of correlated fluctuating fields, with a correlation factor κHH = 0.82. It should also be noted that alternative mixtures of molecules and solvents will have unique correlation factors κHH dependent on the closest approach of paramagnetic oxygen to the target nuclei, the solubility of oxygen gas in solution, and the sample temperature. Nevertheless, the method presented here provides a relatively simple approach to establish known concentrations of oxygen in solution and for calibrating the extent of relaxation caused by dissolved oxygen, under suitable circumstances. The singlet lifetime was investigated in the presence of the radical scavenging salt sodium ascorbate. It was observed that relatively large concentrations of sodium ascorbate were required to quench relaxation effects from dissolved oxygen in solution. The presence of tap water was found to catalyse the oxidation of sodium ascorbate in solution.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Engineering and Physical Sciences Research Council (EPSRC) UK, grant codes EP/P009980/1, EP/N002482/1 and EP/L505067/1, Bruker Biospin UK and the Wolfson Foundation. The authors gratefully acknowledge Malcolm H. Levitt for support, guidance and encouragement, Giuseppe Pileio, Richard J. Whitby and Alexej Jerschow for enlightening discussions, Sami Jannin and Gabriele Stevanato for kindly reading the manuscript prior to submission, Hana Kouřilova, James Eills and Louis Cottey for experimental advice, and Ben Ellis for assistance with the graphical abstract.Notes and references
- M. Carravetta, O. G. Johannessen and M. H. Levitt, Phys. Rev. Lett., 2004, 92, 153003 CrossRef.
- M. Carravetta and M. H. Levitt, J. Am. Chem. Soc., 2004, 126, 6228–6229 CrossRef CAS.
- G. Pileio and M. H. Levitt, J. Magn. Reson., 2007, 187, 141–145 CrossRef CAS.
- A. K. Grant and E. Vinogradov, J. Magn. Reson., 2008, 193, 177–190 CrossRef CAS.
- G. Pileio, M. Carravetta, E. Hughes and M. H. Levitt, J. Am. Chem. Soc., 2008, 130, 12582–12583 CrossRef CAS.
- G. Pileio and M. H. Levitt, J. Chem. Phys., 2009, 130, 214501 CrossRef.
- W. S. Warren, E. Jenista, R. T. Branca and X. Chen, Science, 2009, 323, 1711–1714 CrossRef CAS.
- Y. Feng, R. M. Davis and W. S. Warren, Nat. Phys., 2012, 8, 831–837 Search PubMed.
- M. H. Levitt, Annu. Rev. Phys. Chem., 2012, 63, 89–105 CrossRef CAS.
- Y. Feng, T. Theis, X. Liang, Q. Wang, P. Zhou and W. S. Warren, J. Am. Chem. Soc., 2013, 135, 9632–9635 CrossRef CAS.
- Y. Zhang, P. C. Soon, A. Jerschow and J. W. Canary, Angew. Chem., Int. Ed., 2014, 53, 3396–3399 CrossRef CAS.
- K. Claytor, T. Theis, Y. Feng and W. S. Warren, J. Magn. Reson., 2014, 239, 81–86 CrossRef CAS.
- K. Claytor, T. Theis, Y. Feng, J. Yu, D. Gooden and W. S. Warren, J. Am. Chem. Soc., 2014, 136, 15118–15121 CrossRef CAS.
- Y. Zhang, K. Basu, J. W. Canary and A. Jerschow, Phys. Chem. Chem. Phys., 2015, 17, 24370–24375 RSC.
- G. Stevanato, S. Singha Roy, J. Hill-Cousins, I. Kuprov, L. J. Brown, R. C. D. Brown, G. Pileio and M. H. Levitt, Phys. Chem. Chem. Phys., 2015, 17, 5913–5922 RSC.
- Z. Zhou, K. Claytor, W. S. Warren and T. Theis, J. Magn. Reson., 2016, 263, 108–115 CrossRef CAS.
- S. Glöggler, S. J. Elliott, G. Stevanato, R. C. D. Brown and M. H. Levitt, RSC Adv., 2017, 7, 34574–34578 RSC.
- J. Bae, Z. Zhou, T. Theis, W. S. Warren and Q. Wang, Sci. Adv., 2018, 4, aar2978 CrossRef.
- K. L. Ivanov, T. Kress, M. Baudin, D. Guarin, D. Abergel, G. Bodenhausen and D. Kurzbach, J. Chem. Phys., 2018, 149, 054202 CrossRef.
- S. Mamone and S. Glöggler, Phys. Chem. Chem. Phys., 2018, 20, 22463–22467 RSC.
- S. J. Elliott, P. Kadeřávek, L. J. Brown, M. Sabba, S. Glöggler, D. J. O'Leary, R. C. D. Brown, F. Ferrage and M. H. Levitt, Mol. Phys., 2018, 117, 861–867 CrossRef.
- A. S. Kiryutin, M. S. Panov, A. V. Yurkovskaya, K. L. Ivanov and G. Bodenhausen, ChemPhysChem, 2019, 20, 766–772 CrossRef CAS.
- P. Saul, S. Mamone and S. Glöggler, Chem. Sci., 2019, 10, 413–417 RSC.
- K. F. Sheberstov, A. S. Kiryutin, C. Bengs, J. Hill-Cousins, L. J. Brown, R. C. D. Brown, G. Pileio, M. H. Levitt, A. V. Yurkovskaya and K. L. Ivanov, Phys. Chem. Chem. Phys., 2019, 21, 6087–6100 RSC.
- S. Glöggler, S. Yang, J. McCormick, S. Mamone and L.-S. Bouchard, Angew. Chem., Int. Ed., 2019, 58, 2879–2883 CrossRef.
- J.-N. Dumez, J. T. Hill-Cousins, R. C. D. Brown and G. Pileio, J. Magn. Reson., 2014, 246, 27–30 CrossRef CAS.
- G. Pileio, J.-N. Dumez, I.-A. Pop, J. T. Hill-Cousins and R. C. D. Brown, J. Magn. Reson., 2015, 252, 130–134 CrossRef CAS.
- G. Stevanato, J. T. Hill-Cousins, P. Håkansson, S. S. Roy, L. J. Brown, R. C. D. Brown, G. Pileio and M. H. Levitt, Angew. Chem., Int. Ed., 2015, 54, 3740–3743 CrossRef CAS.
- N. Salvi, R. Buratto, A. Bornet, S. Ulzega, I. Rentero Rebollo, A. Angelini, C. Heinis and G. Bodenhausen, J. Am. Chem. Soc., 2012, 134, 11076–11079 CrossRef CAS.
- R. Buratto, D. Mammoli, E. Chiarparin, G. Williams and G. Bodenhausen, Angew. Chem., Int. Ed., 2014, 53, 11376–11380 CrossRef CAS.
- R. Buratto, A. Bornet, J. Milani, D. Mammoli, B. Vuichoud, N. Salvi, M. Singh, A. Laguerre, S. Passemard, S. Gerber-Lemaire, S. Jannin and G. Bodenhausen, ChemMedChem, 2014, 9, 2509–2515 CrossRef CAS.
- T. Kress, A. Walrant, G. Bodenhausen and D. Kurzbach, J. Phys. Chem. Lett., 2019, 10, 1523–1529 CrossRef CAS.
- A. Bornet, X. Ji, D. Mammoli, B. Vuichoud, J. Milani, G. Bodenhausen and S. Jannin, Chem.–Eur. J., 2014, 20, 17113–17118 CrossRef CAS.
- A. S. Kiryutin, H. Zimmermann, A. V. Yurkovskaya, H.-M. Vieth and K. L. Ivanov, J. Magn. Reson., 2015, 261, 64–72 CrossRef CAS PubMed.
- J.-H. Ardenkjær-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158–10163 CrossRef.
- P. R. Vasos, A. Comment, R. Sarkar, P. Ahuja, S. Jannin, J.-P. Ansermet, J. A. Konter, P. Hautle, B. van den Brandt and G. Bodenhausen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18469–18473 CrossRef CAS.
- M. C. D. Tayler, I. Marco-Rius, M. I. Kettunen, K. M. Brindle, M. H. Levitt and G. Pileio, J. Am. Chem. Soc., 2012, 134, 7668–7671 CrossRef CAS PubMed.
- G. Pileio, S. Bowen, C. Laustsen, M. C. D. Tayler, J. T. Hill-Cousins, L. J. Brown, R. C. D. Brown, J.-H. Ardenkjaer-Larsen and M. H. Levitt, J. Am. Chem. Soc., 2013, 135, 5084–5088 CrossRef CAS.
- J.-N. Dumez, B. Vuichoud, D. Mammoli, A. Bornet, A. C. Pinon, G. Stevanato, B. Meier, G. Bodenhausen, S. Jannin and M. H. Levitt, J. Phys. Chem. Lett., 2017, 8, 3549–3555 CrossRef CAS.
- S. J. Elliott, B. Meier, B. Vuichoud, G. Stevanato, L. J. Brown, J. Alonso-Valdesueiro, L. Emsley, S. Jannin and M. H. Levitt, Phys. Chem. Chem. Phys., 2018, 20, 9755–9759 RSC.
- A. S. Kiryutin, B. A. Rodin, A. V. Yurkovskaya, K. L. Ivanov, D. Kurzbach, S. Jannin, D. Guarin, D. Abergel and G. Bodenhausen, Phys. Chem. Chem. Phys., 2019, 21, 13696–13705 RSC.
- G. Pileio, J. Chem. Phys., 2011, 134, 214505 CrossRef CAS.
- G. Pileio, J. T. Hill-Cousins, S. Mitchell, I. Kuprov, L. J. Brown, R. C. D. Brown and M. H. Levitt, J. Am. Chem. Soc., 2012, 134, 17494–17497 CrossRef CAS.
- G. Pileio, J. Chem. Phys., 2011, 135, 174502 CrossRef CAS.
- S. J. Elliott, C. Bengs, L. J. Brown, J. T. Hill-Cousins, D. J. O'Leary, G. Pileio and M. H. Levitt, J. Chem. Phys., 2019, 150, 064315 CrossRef CAS.
- B. Kharkov, X. Duan, E. S. Tovar, J. W. Canary and A. Jerschow, Phys. Chem. Chem. Phys., 2019, 21, 2595–2600 RSC.
- P. Håkansson, Phys. Chem. Chem. Phys., 2017, 19, 10237–10254 RSC.
- M. C. D. Tayler and M. H. Levitt, Phys. Chem. Chem. Phys., 2011, 13, 9128–9130 RSC.
- S. J. Elliott, L. J. Brown, J.-N. Dumez and M. H. Levitt, J. Magn. Reson., 2016, 272, 87–90 CrossRef CAS.
- Y. Zhang, X. Duan, P. C. Soon, V. Sychrovský, J. W. Canary and A. Jerschow, ChemPhysChem, 2016, 17, 2967–2971 CrossRef CAS PubMed.
- C. Bengs and M. H. Levitt, Magn. Reson. Chem., 2017, 56, 374–414 CrossRef.
- M. C. D. Tayler and M. H. Levitt, Phys. Chem. Chem. Phys., 2011, 13, 5556–5560 RSC.
- G. Pileio, M. Carravetta and M. H. Levitt, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17135–17139 CrossRef CAS.
- S. J. DeVience, R. L. Walsworth and M. S. Rosen, Phys. Rev. Lett., 2013, 111, 173002 CrossRef.
- T. Theis, Y. Feng, T. Wu and W. S. Warren, J. Chem. Phys., 2014, 140, 014201 CrossRef CAS.
- A. N. Pravdivtsev, A. S. Kiryutin, A. V. Yurkovskaya, H.-M. Vieth and K. L. Ivanov, J. Magn. Reson., 2016, 273, 56–64 CrossRef CAS.
- B. Kharkov, X. Duan, J. Canary and A. Jerschow, J. Magn. Reson., 2017, 284, 1–7 CrossRef CAS PubMed.
- B. A. Rodin, K. F. Sheberstov, A. S. Kiryutin, J. T. Hill-Cousins, L. J. Brown, R. C. D. Brown, B. Jamain, H. Zimmermann, R. Z. Sagdeev, A. V. Yurkovskaya and K. L. Ivanov, ArXiV, 2018, 1810.12697.
- S. J. Elliott and G. Stevanato, J. Magn. Reson., 2019, 301, 49–55 CrossRef CAS.
- D. Mammoli, B. Vuichoud, A. Bornet, J. Milani, J.-N. Dumez, S. Jannin and G. Bodenhausen, J. Phys. Chem. B, 2015, 119, 4048–4052 CrossRef CAS.
- S. J. Elliott, L. J. Brown, J.-N. Dumez and M. H. Levitt, Phys. Chem. Chem. Phys., 2016, 18, 17965–17972 RSC.
- M. H. Levitt, J. Magn. Reson., 2016, 262, 91–99 CrossRef CAS.
- R. Sander, Atmos. Chem. Phys., 2015, 15, 4399–4981 CrossRef CAS.
- M. C. D. Tayler, S. Marie, A. Ganesan and M. H. Levitt, J. Am. Chem. Soc., 2010, 132, 8225–8227 CrossRef CAS.
- A. Abragam, Principles of Nuclear Magnetism, Clarendon Press, Oxford, 1961 Search PubMed.
- R. Freeman, S. Wittekoek and R. R. Ernst, J. Chem. Phys., 1970, 52, 1529–1544 CrossRef CAS.
- M. Carravetta and M. H. Levitt, J. Chem. Phys., 2005, 122, 214505 CrossRef.
- J. Kowalewski and L. Mäler, Nuclear Spin Relaxation in Liquids: Theory, Experiments, and Applications, CRC Press, Boca Raton, 2006 Search PubMed.
- R. H. Bisby, C. G. Morgan, I. Hamblett and A. A. Gorman, J. Phys. Chem. A, 1999, 103, 7454–7459 CrossRef CAS.
- P. Miéville, P. Ahuja, R. Sarkar, S. Jannin, P. Vasos, S. Gerber-Lemaire, M. Mishkovsky, A. Comment, R. Gruetter, O. Ouari, P. Tordo and G. Bodenhausen, Angew. Chem., Int. Ed., 2010, 49, 6182–6185 CrossRef.
- M. Khan and A. Martell, J. Am. Chem. Soc., 1967, 89, 4176–4185 CrossRef CAS.
- Southern Water, H513 Rownhams 02 Water Supply Zone (18233), Southampton, Hampshire, UK, 2019 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra03748a |
| ‡ Centre de Résonance Magnétique Nucléaire à Très Hauts Champs – FRE 2034 Université de Lyon, CNRS, Université Claude Bernard Lyon 1, ENS de Lyon, 5 Rue de la Doua, 69100 Villeurbanne, Lyon, France. |
| This journal is © The Royal Society of Chemistry 2019 |