Surface protolytic property characterization of hydroxyapatite and titanium dioxide nanoparticles

Abstract

We provide characterization data of hydroxyapatite (nHAp) and titanium dioxide (nTiO₂) nanoparticles as potential materials for ion sorption, e.g. in targeted therapy, barrier materials for waste repositories or photovoltaics. The study is focused on the determination of the values of protonation and ion exchange constants and site densities (∑SOH, ∑X; [mol kg⁻¹]) of nTiO₂ and nHAp for further Ra kinetics and sorption experiments. These data are very important for further investigation of the materials, which can be used e.g. as drug delivery systems or in engineered barriers of deep geological repositories. The characterization was based on the evaluation of the dependence of titrating agent consumption on pH. Titration results were evaluated on the basis of several model combinations, however the combination of the Chemical Equilibrium Model (CEM) and Ion Exchange Model (IExM) fits best to the experimental titration curves. However, the differences between the two sorbents were relatively large. Due to stability in a broad pH range and available surface sites, nTiO₂ seems to have a wide application range. The applicability of nHAp is not so wide because of its dissolution under pH 5. Both sorbents are virtually able to sorb cationic species on deprotonated edge and layer sites with different capacities, which can be important for sorption and decontaminating applications.

---

Introduction

Both hydroxyapatite and titanium dioxide are known as low-toxicity compounds with high specific surface area.^1–3 These materials have a variety of applications in a wide range of areas like environmental science, photovoltaics and medicine, and applications exploiting their biocompatibility, sorption or photoelectric properties. Applications that exploit their sorption properties include water decontamination of different pollutants, such as metal ions^4–7 or organic compounds⁸ or the use of their nanoparticulate form as radionuclide carriers in nuclear medicine.^9–12 Doping these materials with metallic impurities also significantly influences their properties.^13–16 Understanding of the sorption mechanisms is thus extremely important for further investigations, particularly concerning the stability of the materials in biological systems.

One of the possible applications of these inorganic nanoparticles is a radionuclide-drug carrier system. They were chosen due to their radiation stability and size.¹⁷ Firstly, due to nanoparticle size and ability to resorb ions, recoil nuclei remain in the particle and no undesirable irradiation is therefore observed. Secondly, nanoparticles can be targeted to cancer by both passive and active mechanisms, due to the EPR effect or functionalization of the surface.¹⁸ Nanohydroxyapatite and nTiO₂ were chosen for this purpose because these materials are already widely used in medicine and cosmetics. They are stable, nontoxic, biocompatible, cheap, and easy to prepare.^19–22 Moreover, nanoparticles can be used for theranostic systems with bonded diagnostic nuclides such as ^99mTc, ⁶⁸Ga, ¹⁸F, etc. and therapeutic nuclides such as ²²³Ra, ²²⁵Ac, ²¹³Bi, ¹⁸⁶Re, ⁹⁰Y, etc.^23–28

Our aim was to determine nanomaterial properties including the parameters characterizing the protonation and ion-exchange processes taking place on the surface of nHAp and nTiO₂ for further ²²³Ra sorption studies, as a nanoparticle radionuclide carrier for nuclear medicine.^29–32 Due to modeling of the new material surface sorption processes, separate experiments should be performed in order to obtain credible input surface protolysis and site density data.

The study is mainly focused on modelling of the sorption mechanisms. Generally, there are two types of surface groups responsible for sorption: the edge sites on the edges of the surface structure, and the layer sites which appear due to isomorphic substitution of cations and lead to a permanent negative charge on the solid particle surface.^33,34 The presence of the charge depends on the crystallographic structure of a studied material, or, in some cases, on the conditions in a studied system (e.g. the surface of the material having only the edge sites can be contaminated with another material having the layer sites), and therefore the presence of both types of sites should be assumed.

The modeling of sorption processes requires surface protolysis and site density input data such as specific surface area, protonation and ion exchange constants, and the concentrations (densities) of edge sites and/or layer sites.

Protonation and sorption processes taking part on the edge sites can be described by several types of Surface Complexation Models (SCM) from which the following models are the most utilized: Constant Capacitance Model (CCM), Diffusion Double Layer Model (DLM), and non-electrostatistical Chemical Equilibrium Model (CEM).^33,34 The processes taking part on layer sites are always described by classical Ion Exchange Model (IExM). Since hydroxyapatite can substitute Ca²⁺ for other cations, the necessity to involve IExM into nHAp modeling seems to be obvious. According to the literature³⁵ the edge site density is approx. 3 mol kg⁻¹ for nHAp, and approx. 0.3 mol kg⁻¹ for nTiO₂, which points to its potentially very good sorption.

General material description was performed by FTIR spectroscopy, XRPD and TEM. Detailed surface description was carried out on the basis of titration experiments through material modeling which can be briefly described as follows: the reactions taking place on the surface of nHAp or nTiO₂ may be described by two equations. The first one is protonation reaction being in progress on edge sites (≡SOH), the second one describes the ion-exchange on layer sites (≡XH).

The balance equations of charge densities on edge sites (∑SOH) (1) and layer sites (∑X) (2) have to be taken into account in order to provide correct description of surface reactions:

ΣSOH = [SOH] + [SO⁻] + [SOH₂⁺] [mol kg⁻¹] (1)

ΣX = [XH] + [X⁻] = [XH] + [XNa] [mol kg⁻¹] (2)

It is important to notice that the edge sites of the nHAp are characterized as ≡POH functional groups,³⁶ while nTiO₂ edge sites are formed by ≡SOH groups.

Further description can be found in the ESI.† The description of the individual models and their application in detail were described by Filipská.³³

Experimental

Materials and methods

All chemicals were of analytical grade purchased from Merck and were used without further purification: tetrabutyl ortho-titanate (TBOT), 2-propanol (IPO), sodium hydroxide, phosphoric acid, boric acid, acetic acid, nitric acid, sodium nitrate, ammonium hydroxide solution (28%), calcium nitrate tetrahydrate, ammonium hydrogen phosphate. Demineralized water of 18 MΩ cm⁻¹ was obtained from Millipore, USA water purification system.

Sorbent preparation

nHAp. Bulk HAp was prepared by adding 1.2 M Ca(NO₃)₂ (24 mL) into 0.5 L of demineralized water. The pH of the mixture was set to 11 with ammonium hydroxide and maintained during the reaction, and 0.7 M (NH₄)₂HPO₄ (24 mL) was added dropwise under stirring. The mixture was left overnight under stirring, washed with DEMI water (3 × 20 mL) and dried. The resulting powder was fine-ground.

nTiO₂. The mixture of TBOT (1 mL, 2.8 mmol) in IPO (4 mL) was dropwise added to 100 mL of DEMI water in ultrasonic generator. The suspension was stirred for 30 minutes at the laboratory temperature. Prepared nanoparticles were washed with DEMI water (3 × 20 mL), once with IPO (10 mL) and then dried under vacuum. The resulting powder was fine-ground.

Characterization of the materials

The specific surface area was determined by selective sorption of nitrogen at the temperature of liquid nitrogen using a multi-point BET method. Confirmation of the composition of the materials was made with FTIR spectra recorded on Nicolet iS50 FTIR (ThermoScientific, USA) in middle infrared region 400–4000 cm⁻¹ with resolution 2 cm⁻¹ on a diamond crystal which were compared to relevant records in HR Inorganics I. – Minerals database.³⁷ Powder X-ray diffractograms using Rigaku MiniFlex 600 (Ni-filtered Cu-K_α1,2 radiation) equipped with NaI(Tl) scintillation detector were compared to the relevant records in the ICDD PDF-2 database (version 2013).³⁸

TEM analyses. The nanoparticles were dispersed in water, a small droplet (2 μL) of the suspension was dropped onto the standard TEM supporting copper grid covered with an electron transparent carbon film. The excess of the solution was removed after 1 min by touching the bottom of the grid by a thin strip of filter paper in order to avoid oversaturation and nanoprecipitation during the drying process. The specimens were then left to dry completely. After drying the samples were transferred to a TEM microscope (Tecnai G2 Spirit Twin 12; FEI Company, Czech Republic) and observed at accelerating voltage 120 kV. Morphology of the particles was observed with standard bright field imaging (TEM/BF), energy-dispersive analysis of X-rays (TEM/EDX) yielded the elemental composition, and selected area electron diffraction (TEM/SAED) was used to verify the crystalline structures. Electron diffraction patterns were transformed to 1D-diffractograms (by means of Process Diffraction³⁹) and compared with X-ray diffraction patterns (calculated with PowderCell⁴⁰) of the expected crystalline structures of nHAp and nTiO₂ (the structures were obtained from Crystallography Open Database⁴¹). An estimate of crystallite size from electron diffraction patterns and a calculation of particle size distribution and specific surface area in comparison with BET experiment is provided in ESI.†

Potentiometric titrations

Automatic titration was made on TIM845 Potentiometric Titrator (HACH, USA) equipped with Ag/AgCl electrode (HACH, USA).

The nHAp or nTiO₂ (150 mg) was dispersed in 50 mL of 0.1 M NaNO₃ to ensure stability of the ionic strength (suspension concentration was 3 g L⁻¹). Titration was performed at 23 ± 1 °C with 0.1 M NaOH for alkaline part of titration curve and 0.1 M HNO₃ for acidic one. During the titration with NaOH the sample and the titrant were bubbled with N₂ to eliminate atmospheric CO₂ absorption and dissolution.

In the case of nTiO₂, the studied pH range was between 2.5 and 10. In the case of nHAp, with regard to its possible dissolving in acidic medium, the lowest reached pH was approx. 5. The experiments were repeated three times for each line and solid phase. A blank experiment was performed with 50 mL of 0.1 M NaNO₃ without any solid phase added for the both acidic and alkaline part of the titration curve. Increment was set to 0.05 mL and stability conditions to 20 mpH min⁻¹. The pH was recorded after each addition of titrant as a function of its volume.

Results and discussion

Specific surface area, FTIR, XRPD

The specific surface areas via BET measurements were determined at 117 ± 8 m² g⁻¹ for nHAp and 330 ± 10 m² g⁻¹ for nTiO₂. FTIR spectra of the nHAp showed the characteristic vibration bands of hydroxyapatite: vibration bands at 600–473 cm⁻¹ and 1089–962 cm⁻¹ might be attributed to PO₄³⁻. Band at ∼1400 cm⁻¹ belongs to the characteristic vibration of the CO₃²⁻, that at 1630 cm⁻¹ corresponds to deformation vibration band of OH⁻ and that at 3500–3000 cm⁻¹ belongs to stretching mode of OH⁻. FTIR spectrum of nTiO₂ has the band at 3500–3000 cm⁻¹ that might be attributed to stretching mode of OH⁻ and at 1632 cm⁻¹ associated with deformation vibrations of OH⁻ bonds on the surface of TiO₂. Arms on the band at 1000–400 cm⁻¹ are assigned to Ti–O and Ti–O–Ti stretching modes.⁴² Both FTIR spectra were compared to database³⁷ records #15 and #216 for nHAp and nTiO₂ respectively; they fit properly.

Nanohydroxyapatite and nTiO₂ diffractograms showed that both samples are single phase. Experimental conditions for nHAp synthesis meet the requirements for hydroxyapatite formation. Titanium dioxide has the structure of anatase as proved by library data³⁸ comparison. Low intensity peaks of nTiO₂ can be interpreted either as nano-sized crystals or as amorphous phase formation. According to TEM/BF micrograph (Fig. 1B) the nanoparticle size is under 20 nm.

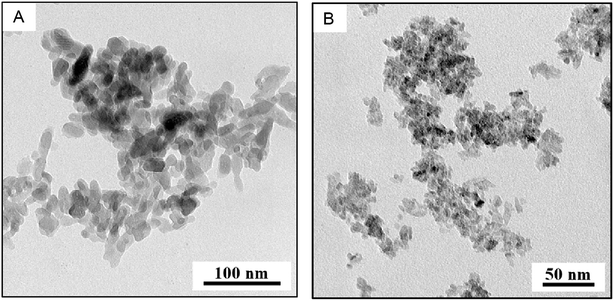Fig. 1 TEM analysis (A) TEM/BF micrograph showing the size and shape of nHAp, (B) TEM/BF micrograph showing the size and shape of nTiO₂.

Both FTIR and XRPD spectra could be found in the ESI (Fig. S1 and S2†).

TEM characterization of the nanoparticles

TEM characterization of nHAp and nTiO₂ is shown in Fig. 1 where TEM/BF micrographs demonstrated that both nanoparticles had quite narrow size distribution, nHAp (Fig. 1A) being larger than nTiO₂ (Fig. 1B). TEM/SAED diffractograms and their comparison with theoretically calculated XRD diffraction patterns confirmed the expected crystalline structures: hexagonal structure of nHAp (Crystallography Open Database⁴¹ COD #9001233) and tetragonal anatase structure of nTiO₂ (Crystallography Open Database⁴¹ COD #1526931). TEM/EDX spectra yielded the expected elemental composition and confirmed that both prepared nanoparticles were free from impurities (we note that C and Cu peaks come from the standard TEM supporting copper grids, which were covered with thin, electron transparent carbon film). TEM/SAED diffractograms and TEM/EDX spectra are shown in ESI (Fig. S3 and S4†).

TEM image analysis and calculation of specific surface area

Both TEM/BF micrographs and TEM/SAED diffraction patterns were employed in estimating the nanoparticle size. Image analysis of TEM/BF micrographs was based on direct measurement of >100 particles and yielded an average particle size (morphological descriptor: equivalent diameter), aspect ratios (morphological descriptor: elongation) and the particle size distributions (shown in Fig. 2); technical details concerning image analysis are given in the ESI.† An estimate of the nanoparticle sizes from TEM/SAED was based on Scherrer equation.⁴³ It is worth noting that Scherrer equation is applied mostly to X-ray diffraction data, but its application on SAED diffraction patterns is also possible, although it may not be so common.^43,44 The average particle sizes are summarized in Table 1.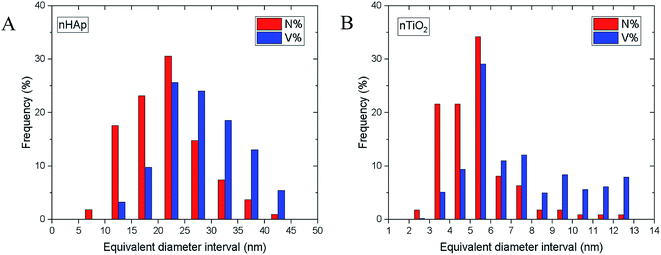

Fig. 2 Particle size distributions determined from image analysis of TEM/BF micrographs using program MDISTR^45–47 for (A) nHAp and (B) nTiO₂. The symbols N% and V% denote number and volume distributions, respectively.

Table 1 Morphological descriptors of the nanoparticles

Sample	Crystallite size^a [nm]	Equivalent diameter [nm]		Elongation [—]
		Average	StDev	Average	StDev
a Crystallite size was obtained from TEM/SAED diffractograms using Scherrer equation. Equivalent diameter and elongation were assessed from measurements of TEM/BF micrographs.
nHAp	5.18	21.7	6.9	1.70	0.49
nTiO2	2.44	5.3	1.7	1.50	0.41

---

The nHAp and nTiO₂ morphological descriptors (Table 1), particle size distributions (Fig. 2) and overall semi-quantitative characteristics of the observed nanoparticles (such as their roughness estimated from their shapes in higher magnification TEM/BF micrographs), were employed in the calculation of the specific surface area of the nanoparticles. The calculations, which are properly described in the ESI,† were performed by our program MDISTR.^45–47 The final calculated values were compared with the experimentally determined specific surface areas from BET experiments (Table 2). The agreement between theoretical calculations based on TEM data including all corrections and the experimental results from BET experiments was very good. In both samples, the SAED-based crystallite sizes resulted in overestimation of specific surface area in comparison with BET experiments (Table 2, compare results of Model 1 and BET experiments), which implied that SAED-based crystallite sizes were small, resulting in too high numbers of particles with too high specific surface area. Other models showed good agreement with BET experimental results. For more information see ESI.†

Table 2 Particle numbers and specific surface areas calculated by the MDISTR program

Model ID^a	nHAp		nTiO2
	N [—]	A [m^2 g^−1]	N [—]	A [m^2 g^−1]
a All calculations were performed by the MDISTR^45–47 program based on parameters from image analysis of TEM/BF micrographs and/or TEM/SAED diffraction patterns. N denotes number of particles and A denotes specific surface area of the nanoparticles. The models used for calculations were as follows: Model 1 = uniform spherical particles with average size determined from broadening of TEM/SAED diffractions (5.2 nm for nHAp, 2.4 nm for nTiO2); Model 2 = uniform spherical particles with average size determined from image analysis of TEM/BF micrographs (21.7 nm for nHAp, 5.3 nm for nTiO2); Model 3 = spherical particles with the size distribution determined from image analysis; Model 4 = the same as previous, but with additional corrections for elongation and flatness of the particles, which were measured or estimated from TEM micrographs; Model 5 = the same as previous, but with additional correction for surface roughness of the nanoparticles, which was estimated from TEM micrographs.
Model 1	4.35 × 10^18	367	3.11 × 10^19	581
Model 2	5.92 × 10^16	88	3.05 × 10^18	268
Model 3	4.49 × 10^16	73	2.25 × 10^18	218
Model 4	8.98 × 10^16	102	4.49 × 10^18	298
Model 5	8.98 × 10^16	107	4.49 × 10^18	342
BET experiment	—	117	—	330

---

Evaluation of the titration experiments

Experimentally obtained dependences are shown in Fig. 3. As mentioned above, due to nHAp dissolution the titration range was from 5 to 10. Strictly speaking, the dissolution of nHAp starts at aprox. pH = 7, but it is negligible if the titration is fast enough and pH = 5 is reached within a few minutes.

Fig. 3 Experimental dependences of added volume of titrant 0.1 M NaOH, for basic part and 0.1 M HNO₃ for acidic part of titration curves on pH and blank titration curve of 0.1 M NaNO₃.

The WSOS/DF value (weighted sum of squares of differences divided by the degrees of freedom) is taken as an appropriate criterion of goodness-of-fit and it should be in the interval 0.1 < WSOS/DS < 20, so the model used for the description of the given experimental dependence can be taken as acceptable. In addition, the physical meaning of individual parameter values has to be taken into account, as well. Evidently, the WSOS/DF criterion (Table 3) is completely fulfilled for nTiO₂, for nHAp it holds for CEM + IExM and DLM + IExM models, only. But, if we take into account the values in Tables 4 and 5, and if we allow for literature data ∑SOH and ∑POH mentioned above,³⁵ combination of CEM + IExM models describe experimental data in the most accurate way for both nHAp and nTiO₂.

Table 3 Evaluation of titration curves by six different models: the values of WSOS/DF characterizing the agreement between the experimental (22 ± 1 °C) and calculated data (N/A – evaluation was not performed)

Model	nHAp	nTiO2
	WSOS/DF	WSOS/DF
CEM	34.1	8.88
CEM + IExM	1.07	1.26
CCM	46.9	1.77
CCM + IExM	42.4	1.88
DLM	N/A	1.16
DLM + IExM	13.4	0.70

---

Table 4 The total nHAp concentration of edge sites (∑POH) and ion exchange groups (layer sites) (∑X), protonation (K₁, K₂), and ion exchange (K_Na⁺/H⁺) constants based on the titration curve evaluation

Model	∑POH [mol kg^−1]	∑X [mol kg^−1]	K1 [L mol^−1]	K2 [L mol^−1]	KNa^+/H^+ [—]
CEM + IExM	5.10 ± 1.20	0.15 ± 0.01	5.12 × 10^11 ±1.10 × 10^11	1.19 × 10^5 ± 2.73 × 10^4	3.01 × 10^6 ± 3.26 × 10^5
DLM + IExM	13.90 ± 4.35	0.20 ± 0.10	1.83 × 10^11 ± 6.84 × 10^10	1.80 × 10^7 ± 5.07 × 10^6	1.12 × 10^5 ± 3.34 × 10^5

---

Table 5 The total nTiO₂ concentration of edge sites (∑SOH) and ion exchange groups (layer sites) (∑X), protonation (K₁, K₂), and ion exchange (K_Na⁺/H⁺) constants based on evaluation of titration curves

Model	∑SOH [mol kg^−1]	∑X [mol kg^−1]	K1 [L mol^−1]	K2 [L mol^−1]	KNa^+/H^+ [—]
CEM + IExM	0.20 ± 0.01	0.67 ± 0.01	2.31 × 10^6 ± 1.93 × 10^4	1.84 × 10^4 ± 1.65 × 10^2	5.67 × 10^7 ± 2.01 × 10^6
DLM + IExM	1.42 ± 0.10	0.07 ± 0.01	3.26 × 10^7 ± 2.73 × 10^6	4.32 × 10^3 ± 2.61 × 10^2	6.96 × 10^4 ± 1.74 × 10^3

---

According to the chosen models, total concentrations of the edge sites and ion exchange groups, protonation and ion exchange constants (for Na⁺/H⁺ exchange) were calculated and their values were summarized in Table 4 for nHAp, and in Table 5 for nTiO₂. On comparing the parameter values in Tables 1–3 to each other and considering the literature data mentioned above,³⁵ the best model seems to be CEM + IExM for both materials.

The experimental and calculated titration curves are depicted as total surface charge density, Q [mol kg⁻¹],or (Q_cal)_i, on pH for nHAp and nTiO₂, respectively (Fig. 4A and 5A). The molar fractions of individual forms of sites (see the ESI†) can be found, again as the dependences on pH (Fig. 4B and 5B). In both cases, CEM + IExM model was used for experimental data evaluation.

Fig. 4 (A) Experimental data and calculated titration curve; (B) molar fractions of individual forms of surface sites for nHAp (CEM + IExM).

Fig. 5 (A) Experimental and calculated titration curve; (B) molar fractions of individual forms of surface sites for nTiO₂ (CEM + IExM).

Of course, there are great differences between nHAp and nTiO₂ not only in the density values of surface sites (∑SOH, ∑POH and ∑X), but above all in the values of protonation constants – what does it means, it is evident from the comparison of curves in Fig. 4B and 5B. Evidently, the pH value plays the basic role in the applicability of both materials to the surface sorption of anionic, cationic and molecular species (surface complexation). The applicability of nHAp is limited to pH interval from approx. 5 to 11, whereas in case of nTiO₂, it deals with pH from approx. 3 to 11. The both materials differ in the sorption property (ability) in respect of different species, such that on nHAp (Fig. 4B) can take place the sorption of cationic forms on PO⁻ and X⁻ or surface complexation can proceeds on PO⁻. As for nTiO₂ (Fig. 5B), cationic forms can be sorbed on SO⁻ and X⁻, and by analogy the surface complexation can proceed on SO⁻, in addition, the sorption of anionic species can be under way on SOH₂⁺. Evidently, in principle, both materials can be used as carrier of cation in question, i.e., ²²³Ra, namely, for example as ²²³Ra²⁺ or ²²³Ra(OH)⁺.

Conclusions

An investigation of nHAp and nTiO₂ preparation and surface sorption properties was performed in order to provide more detailed data for further studies considering ²²³Ra uptake on these sorbents. However, the differences between the two sorbents were relatively large, as follows from the values of parameters determined for nHAp (K₁ = 5.12 × 10¹ [L mol⁻¹]; K₂ = 1.19 × 10⁵ [L mol⁻¹]; ∑SOH = 5.10 [mol kg⁻¹]; K_ex = 3.01 × 10⁶ [—]; ∑X = 0.15 [mol kg⁻¹]), and for nTiO₂ (K₁ = 2.31 × 10⁶ [L mol⁻¹]; K₂ = 1.84 × 10⁴ [L mol⁻¹]; ∑SOH = 0.20 [mol kg⁻¹]; K_ex = 5.67 × 10⁷ [—]; ∑X = 0.67 [mol kg⁻¹]). Deep understanding of the surface properties of HAp and TiO₂ nanoparticles, as prospective carriers for targeted alpha-particle therapy by in vivo generators, is important.¹⁸ The results will allow us to predict and provide further evaluation of kinetics and sorption dependences of various ions and radionuclides, including ²²³Ra and its decay products which are present in the form of cations. Therefore, the studied nanoparticles, which are capable of both capture and resorption, due to their high capacity and suitable size, are a promising solution.

Based on our experiments and calculations it can be stated that applicability of nTiO₂ is high due to its stability in a broad pH range and available surface sites (∑SOH = 0.20 mol kg⁻¹; ∑X = 0.67 mol kg⁻¹). Evidently, cationic species sorption on nTiO₂ can proceed via ion-exchange on deprotonated edge sites (≡SO⁻) and on layer sites (≡X⁻) as well. Applicability of nHAp is not as wide as nTiO₂ because of its dissolution under pH 5. On the one hand, surface site density of nHAp is greater than that of nTiO₂ (∑POH = 5.10 mol kg⁻¹; ∑X = 0.15 mol kg⁻¹), which can be regarded as an advantage of nHAp. On the other hand, nHAp deprotonated edge sites (≡PO⁻) are virtually able to sorb only cationic species. Uptake of anionic and molecular species on edge sites of the two sorbents can also undergo surface complexation mechanism, but regarding the purposes of our study it was not taken into account.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Research at the Czech Technical University was supported by the grants of NV16-30544A (the Health Research Agency of the Czech Republic), CZ.02.1.01/0.0/0.0/15_003/0000464 (EU and the Ministry of Education, Youth and Sports of the Czech Republic), and SGS16/251/OHK4/3T/14 (Czech Technical University in Prague). Electron microscopy at the Institute of Macromolecular Chemistry was supported through grants 17-05007S (Czech Science Foundation) and POLYMAT LO1507 (Ministry of Education, Youth and Sports of the CR, program NPU I).

References

1. T. Jones and T. A. Egerton, Titanium Compounds, Inorganic, in Kirk-Othmer Encyclopedia of Chemical Technology, John Wiley & Sons, New York, 2000.
2. R. Z. LeGeros, A. Ito, A. Ishikawa, T. Sakae and J. P. LeGeros, in Advanced Biomaterials: Fundamentals, Processing, and Applications, The American Ceramic Society, Ohio, 2010, ch. 2, pp. 19–52.
3. S. A. Pappus, B. Ekka, S. Sahu, D. Sabat, D. Dash and M. Mishra, J. Nanopart. Res., 2017, 19(4), 136.
4. C. Bogatu, D. Perniu, C. Sau, O. Iorga, M. Cosnita and A. Duta, Ceram. Int., 2017, 43(11), 7963–7969.
5. A. Corami, S. Mignardi and V. Ferrini, J. Hazard. Mater., 2007, 146(1–2), 164–170.
6. S. Handley-Sidhu, T. K. Mullan, Q. Grail, M. Albadarneh, T. Ohnuki and L. E. Macaskie, Sci. Rep., 2016, 6(1), 23361.
7. L. Reddy, P. Venkata, B. Kavitha, P. Anil, K. Reddy and K. H. Kim, Environ. Res., 2017, 154, 296–303.
8. H. He, B. Wu and C. Yang, Int. J. Environ. Sci. Technol., 2018, 15 DOI:10.1007/s13762-018-2148-2.
9. E. Cędrowska, M. Pruszynski, A. Majkowska-Pilip, S. Męczyńska-Wielgosz, F. Bruchertseifer, A. Morgenstern and A. Bilewicz, J. Nanopart. Res., 2018, 20(3), 83.
10. D. Duan, H. Liu, Y. Xu, Y. Han, M. Xu, Z. Zhang and Z. Liu, ACS Appl. Mater. Interfaces, 2018, 10(6), 5278–5286.
11. A. Rajeswari, K. V. Vimalnath, H. D. Sarma, P. Shetty, S. K. Mohammed, J. Nuwad, S. Chakraborty and A. Dash, Appl. Radiat. Isot., 2017, 116, 85–91.
12. K. V. Vimalnath, S. Chakraborty, A. Rajeswari, H. D. Sarma, J. Nuwad, U. Pandey, K. Kamaleshwaran, A. Shinto and A. Dash, Nucl. Med. Biol., 2015, 42(5), 455–464.
13. X. Wu, W. Qin, S. Wang, Z. Jiang, Y. Guo and Z. Xie, Rare Met., 2006, 25(6), 169–172.
14. P. Mazierski, A. Mikolajczyk, B. Bajorowicz, A. Malankowska, A. Zaleska-Medynska and J. Nadolna, Appl. Catal., B, 2018, 233, 301–317.
15. S. Mondal, S. V. Dorozhkin and U. Pal, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2018, 10, e1504.
16. O. Kaygili, S. Keser, S. V. Dorozhkin, F. Yakuphanoglu, A. A. Al-Ghamdi, S. Kirbag, D. Sertkaya, T. Ates and N. Canan Gursoy, J. Inorg. Organomet. Polym., 2014, 24, 1001–1008.
17. J. Kozempel, M. Vlk, E. Malková, A. Bajzíková, J. Bárta, R. Santos-Oliveira and A. Malta Rossi, J. Radioanal. Nucl. Chem., 2015, 304, 443–447.
18. J. Kozempel, O. Mokhodoeva and M. Vlk, Molecules, 2018, 23(3), 581.
19. M. P. Ferraz, F. J. Monteiro and C. M. Manuel, J. Appl. Biomater. Funct. Mater., 2004, 2(2), 74–80.
20. S. Koutsopoulos, J. Biomed. Mater. Res., 2002, 62(4), 600–612.
21. M. Malekshahi Byranvand, A. Nemati Kharat, L. Fatholahi and Z. Malekshahi Beiranvand, J. Nanostruct., 2013, 3, 1–9.
22. S. Mital Gupta and M. Tripathi, Cent. Eur. J. Chem., 2012, 10(2), 279–294.
23. L. D. Esposti, A. Tampieri and M. Iafisco, in Nanotechnologies in Preventive and Regenerative Medicine, ed. V. Uskokovic, Elsevier, New York, 2017, ch. 6.3, pp. 465–486.
24. W. Zhou and J. Zheng, Adv. Mat. Res., 2012, 503/504, 688–691.
25. S. Chakraborty, K. V. Vimalnath, A. Rajeswari, H. D. Sarma, A. Shinto, E. R. Radhakrishnan and A. Dash, J. Radioanal. Nucl. Chem., 2017, 302(2), 875–881.
26. J. Xie, S. Lee and X. Chen, Adv. Drug Delivery Rev., 2010, 62(11), 1064–1079.
27. M. Sakmar, M. Vlk, P. Suchankova, E. Kukleva, J. Kozempel, M. Hruby and V. Lobaz, presented in part at 13^th international Symposium on the Synthesis and Application of Isotopically Labelled Compounds, Prague, June, 2018.
28. P. Micolova, E. Kukleva, P. Nykl, M. Sakmar, M. Vlk, L. Nespesna and J. Kozempel, presented in part at 22^nd International Symposium on Radiopharmaceutical Sciences, Dresden, May, 2017.
29. Xofigo – summary of product characteristics, http://www.ema.europa.eu/docs/en_GB/document_library/EPAR_-_Product_Information/human/002653/WC500156172.pdf, accessed January 2018.
30. S. Mirzadeh, Appl. Radiat. Isot., 1998, 49(4), 345–349.
31. E. Kukleva, J. Kozempel, M. Vlk, P. Micolova and D. Vopalka, J. Radioanal. Nucl. Chem., 2014, 304(1), 263–266.
32. O. Mokhodoeva, L. Guseva and N. Dogadkin, J. Radioanal. Nucl. Chem., 2014, 304(1), 449–453.
33. H. Filipská and K. Štamberg, Acta Polytech., 2005, 45(5), 11–18.
34. J. Lützenkirchen, Surface complexation modelling, Academic Press, Elsevier Ltd., London, 2006.
35. RES³T/Rossendorf Expert System for Surface and Sorption Thermodynamics, https://www.hzdr.de/db/res3t.login, accessed January 2018.
36. B. Sandrine, N. Ange, B. A. Didier, C. Eric and S. Patrick, J. Hazard. Mater., 2007, 139(3), 443–446.
37. HR Inorganics I. – Minerals database – FTIR, Thermo Scientific™ OMNIC™, USA.
38. ICDD PDF-2 database, Version 2013, ISDD, USA.
39. J. L. Lábár, Ultramicroscopy, 2005, 103, 237–249.
40. W. Kraus and G. Nolze, J. Appl. Crystallogr., 1996, 29, 301–303.
41. Crystallography Open Database—an open-access collection of crystal structures, http://www.crystallography.net/cod/search.html, accessed May 2018.
42. T. Ivanova and A. Harizanova, Solid State Ionics, 2001, 138, 227–232.
43. B. Ingham and M. F. Toney, Chapter 1: X-ray diffraction for characterizing metallic films, in Metallic Films for Electronic, Optical and Magnetic Application, ed. K. Barmak and K. Coffey, Elsevier, New York, 2014, pp. 3–38.
44. B. Fultz and J. Howe, Transmission electron microscopy and diffractometry of materials, Springer, Berlin, 3rd edn, 2008.
45. J. Gallo, M. Slouf and S. B. Goodman, J. Biomed. Mater. Res., Part B, 2010, 94B(1), 171–177.
46. M. Slouf, A. Ostafinska, M. Nevoralova and I. Fortelny, Polym. Test., 2015, 42, 8–16.
47. P. Fulín, D. Pokorný, M. Slouf, M. Lapčíková, E. Pavlova and E. Zolotarevová, Acta Chir. Orthop. Traumatol. Cech., 2011, 78(2), 131–137.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra03698a

---