Nature of intramolecular O–H⋯π interactions as elucidated by QTAIM dual functional analysis with QC calculations

Abstract

The intrinsic dynamic and static nature of intramolecular OH–*–π interactions is elucidated using a QTAIM dual functional analysis (QTAIM-DFA) after clarifying the structural features. Asterisks (*) are employed to emphasize the presence of bond critical points (BCPs) on the bond paths (BPs), which correspond to the interactions in question. Data from the fully optimized structures correspond to the static nature of the interactions. In our treatment, data from the perturbed structures, which are based around the fully optimized structure, are employed for the analysis in addition to those from the fully optimized structure, which represent the dynamic nature of the interaction. Seven intramolecular OH–*–C(π) interactions were detected in six-membered rings, with six BPs and BCPs for each, among the 72 conformers of the species examined here (1–15). The interactions are predicted to have a vdW or t-HB_nc (typical hydrogen bonds with no covalency) nature, which appeared in the pure closed shell region. They appear to be stronger than the corresponding intermolecular interactions. Nine BPs with BCPs were also detected for the intramolecular O–*–X interactions (X = C(π) and H(π), joined to C(π)) in the 5–7-membered rings. The E(2) values of the interactions, as obtained by NBO, are discussed in relation to the stabilities of the conformers and the BPs with BCPs.

---

Introduction

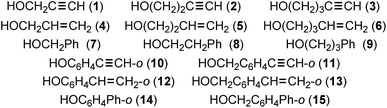
Hydrogen bonds (HBs) are of ongoing interest in all fields of chemical and biological sciences.^1–4 The conventional HBs in the shared proton interaction type (cv-HBs: B⋯H–X) are basic HBs. The B⋯H–X directions are controlled through the formation of HBs from X–H and B due to the contribution of the unsymmetric σ(3c–4e) (three centre-four electron interactions of the σ-type).^5–7 The energies involved in the formation of cv-HBs are typically 10–40 kJ mol⁻¹ for the neutral form.⁵ Another type of HB will form if π-orbitals are provided from ethyne, ethene, benzene and the derivatives to X–H. These X–H⋯π interactions, which are called π-HBs here, seem weaker than cv-HBs. The weaker proton-accepting ability of π-orbitals relative to the lone pair orbitals must primarily be responsible for the differences. We reported the behaviour of cv-HBs among the neutral and charged forms very recently by applying the QTAIM (quantum theory of atoms-in-molecules) approach.^4,8 The cv-HBs of the neutral form are predicted to have a vdW to CT-TBP (trigonal bipyramidal adduct formation through charge transfer) nature, while the cv-HBs of the charged form show a covalent bond nature (Cov).⁴ The natures of the XH⋯π interactions were also reported recently for the π-systems of benzene,^9,10 naphthalene,¹¹ anthracene¹² and/or coronene,¹³ where X = F, Cl, Br, I, HO, HS, HSe, MeO, H₂N, MeHN and/or Me₂N.

We also closely observed the intramolecular π-HBs since they play a very important role in the chemical and biological sciences.^14,15 What is the behaviour of the intramolecular π-HBs? What are the differences and similarities between the intramolecular and intermolecular π-HBs? How does steric hindrance affect the strength of the intermolecular π-HBs? It is challenging to clarify the nature of intramolecular π-HBs to understand the fundamental behaviour of π-HBs.^14,15 Chart 1 illustrates species 1–15, which were examined in this study.

Chart 1 Candidates 1–15, to examine the intramolecular HB interactions.

The bond critical point (BCP, *) is an important concept in the QTAIM approach that was introduced by Bader,^16,17 where the ρ(r) (charge density) reaches its minimum along the interatomic (bond) path while reaching its maximum on the interatomic surface separating the atomic basins. The ρ(r) at BCP is described by ρ_b(r_c), as are other QTAIM functions, such as the total electron energy densities H_b(r_c), potential energy densities V_b(r_c) and kinetic energy densities G_b(r_c) at BCPs. A chemical bond or interaction between atoms A and B is denoted by A–B, which corresponds to the bond path (BP) in QTAIM. We will use A–*–B for BP, in which the asterisk emphasizes the existence of a BCP in A–B.^16,17 Eqn (1), (2) and (2′) represent the relations between G_b(r_c), V_b(r_c), H_b(r_c) and ∇²ρ_b(r_c).

H_b(r_c) = G_b(r_c) + V_b(r_c) (1)

(ħ²/8m)∇²ρ_b(r_c) = H_b(r_c) – V_b(r_c)/2 (2)

(ħ²/8m)∇²ρ_b(r_c) = G_b(r_c) + V_b(r_c)/2 (2')

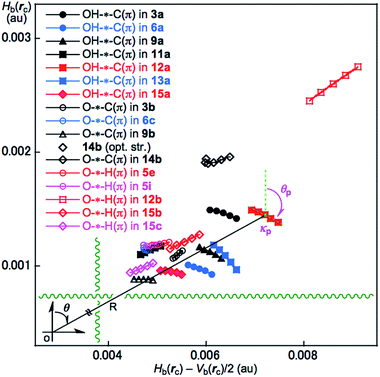
A QTAIM dual functional analysis (QTAIM-DFA) was recently formulated based on the QTAIM approach. H_b(r_c) is plotted versus H_b(r_c) – V_b(r_c)/2 (=(ħ²/8m)∇²ρ_b(r_c)) (cf.: eqn (2)) at BCPs in QTAIM-DFA. Data from the fully optimized structures are analysed using the polar coordinate (R, θ) representation, which corresponds to the static natures of the interactions.^18–21 In our treatment, data from the perturbed structures around the fully optimized ones are employed in addition to those from the fully optimized structures. Each interaction plot, which contains data from both the perturbed and fully optimized structures, includes a specific curve that provides important information about the interaction. This plot is expressed by (θ_p, κ_p), where θ_p corresponds to the tangent line of the plot and κ_p is the curvature. The dynamic nature of the interactions has been proposed based on (θ_p, κ_p).^{18 a–21} We call (R, θ) and (θ_p, κ_p) the QTAIM-DFA parameters, which are illustrated in Fig. 4, as exemplified by the intramolecular OH–*–C(π) interaction in 12a (C₁).

We very recently proposed a highly reliable method for generating the perturbed structures necessary for QTAIM-DFA.²² The method is called CIV, and it employs the coordinates derived from the compliance force constants C_ii, the diagonal elements in C_ij, for the internal vibrations. Eqn (3) defines C_ij as the partial second derivatives of the potential energy due to an external force, where i and j refer to internal coordinates, and the force constants f_i and f_j correspond to i and j, respectively. The dynamic nature of interactions based on perturbed structures with CIV is described as the “intrinsic dynamic nature of interactions,” since the coordinates are invariant relative to the choice of the coordinate system.

C_ij = ∂²E/∂f_i∂f_j (3)

QTAIM-DFA is applied to standard interactions, and rough criteria that distinguish the interaction in question from others are obtained. QTAIM-DFA has excellent potential for evaluating, classifying, characterizing and understanding weak to strong interactions according to a unified form.^18a–21 The QTAIM-DFA and the criteria are explained in the ESI using Schemes S1–S3, Fig. S1 and S2, Table S1 and eqn (S1)–(S7).† The basic concept of the QTAIM approach is also discussed.

When employing the perturbed structures generated with the CIV, we consider QTAIM-DFA to be well-suited for elucidating the nature of the intramolecular π-HB interactions in 1–15. Herein, we present the results of investigations on the intrinsic dynamic and static nature of the intramolecular π-HBs. BPs with BCPs corresponding to the intramolecular OH–*–π(C) interactions are detected in seven conformers, together with four intramolecular O–*–C(π) and five O–*–H(π) interactions among 72 conformers examined in 1–15, where H(π) indicates an H joined directly to a C(π). The nature of the intramolecular interactions is clarified for those detected by the BPs with BCPs. The intramolecular interactions are classified and characterized by employing the criteria as a reference. An NBO analysis²³ is applied to some selected conformers of 1–15. The nature of the intramolecular interactions will be discussed in relation to the results of the NBO analysis and the structural features.

Methodological details in calculations

The Gaussian 09 programs²⁴ were employed for the calculations. The calculations containing the NBO analysis²³ were performed with the 6-311++G(3df,3pd) basis set (BSS-A) at a second-order Møller–Plesset energy correlation (MP2) level (MP2/BSS-A).²⁵ The optimized structures were confirmed by the frequency analysis. The results of the frequency analysis were used to obtain the C_ii values and the coordinates corresponding to C_ii.^26–29 The B3LYP³⁰/BSS-A and M06-2X³¹/BSS-A methods were also applied to the limited cases for the examination of the effect from the DFT level. The optimizations were not corrected with the BSSE method.

Eqn (4) explains the method used to generate the perturbed structures with CIV. A k-th perturbed structure in question (S_iw) is generated by the addition of the coordinates (C_i) corresponding to C_ii to the standard orientation of a fully optimized structure (S_o) in the matrix representation. The coefficient g_kw in eqn (4) controls the structural difference between S_iw and S_o: g_kw is determined to satisfy eqn (5) for r, the interaction distance in the perturbed structure.³² The C_i values of five digits are used to predict the S_iw.

S_iw = S_o + g_iwC_i (4)

r = r_o + wa_o (w = (0), ±0.025 and ±0.05; a_o = 0.52918 Å) (5)

y = c_o + c₁x + c₂x² + c₃x³ (R_c²: square of the correlation coefficient) (6)

The QTAIM functions were calculated using the same method as the optimizations at the MP2 level, unless otherwise noted. The calculated values were analysed with the AIM2000³³ and AIMAll³⁴ programs. H_b(r_c) is plotted versus H_b(r_c) – V_b(r_c)/2 for the data from five points pertaining to w = 0, ±0.05 and ±0.1 in eqn (5) in QTAIM-DFA. Each plot is analysed using a regression curve of the cubic function, as shown in eqn (6), where (x, y) = (H_b(r_c) – V_b(r_c)/2, H_b(r_c)) (R_c² > 0.99999 in usual).³⁵

Results and discussion

Optimizations of species, 1–15

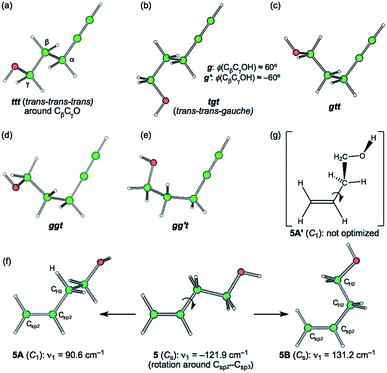
Species 1–15 were optimized with MP2/6-311++G(3df,3pd) (MP2/BSS-A). The most extended conformer was optimized for each of 1–15, first. The conformers were searched by the optimizations with the changing all torsional angles for each species. 72 conformers were optimized for 1–15. The conformers are explained first, as exemplified in 3. Fig. 1 illustrates the conformers of 3 with ϕ(C_βC_γOH) ≈ 180° (t), which are the ttt, tgt, gtt, ggt and gg′t conformers around C_β, C_γ and O. Three conformers around C_α in 3 are identical, as shown in Fig. 1. Therefore, the conformers will be distinguished by the conformations around C_β, C_γ and O. The gauche (g) and gauche′ (g′) notations are used for ϕ(C_βC_γOH) ≈ 60° and −60°, respectively, for example, in addition to the trans (t) notation for ϕ(C_βC_γOH) ≈ 180°. The g and g′ conformers around C_β (from the ttt conformer) are the same in this study. The optimizations were further performed with the torsional angles changing compared with those of the optimized structures, as mentioned above. Fourteen conformers were optimized for 3, although the systematic conformation analysis is not applied. The optimized conformer of the shortest OH⋯C(π) distance [r(H⋯C(π))] in 3 is called 3a. The optimized conformers will be called 3b, 3c, …, 3m and 3n, in the increasing order of the optimized OH⋯C(π) distances.

Fig. 1 Survey of the structural optimizations for 3 and 5, with MP2/BSS-A.

In the case of 5, the most extended structure of the C_s symmetry (5 (C_s)) has one imaginary frequency. The optimization converged a conformer of the C₁ symmetry (5A (C₁)) with the torsional angle of ϕ(C_sp2C_sp2C_H2H) ≈ 8.5° if started from the C₁ structure, close to 5 (C_s). However, the similar conformer with ϕ(C_sp2C_sp2C_H2H) ≈ 173.5° (5A′ (C₁)) was not optimized. Another type of conformer with C_s symmetry (5B (C_s)) was optimized, of which ϕ(C_sp2C_sp2C_H2C_H2) = 0. Fig. 1 contains the process from 5 (C_s) to 5A (C₁) and 5B (C_s) with 5A′ (C₁). The optimizations for 5 were performed by changing the torsional angles around the –CH₂OH group in 5A (C₁) and 5B (C_s). As a result, fifteen different conformers were optimized for 5. Conformers 5 (C_s), 5A (C₁) and 5B (C_s) correspond to 5n, 5m and 5o, respectively, among the 15 conformers (see Fig. S4 of the ESI†).

The optimizations of 1–15 other than 3 and 5 were performed in a similar way. There were greater efforts to search for the conformers with the shorter OH⋯C(π) distances than the ones with the longer distances, which would prevent the trivial optimizations of the conformers with no intramolecular OH⋯C(π) interactions. Finally, 72 conformers were optimized for 1–15. The optimized conformers in this study are denoted as xa, xb,… (x = 1–15), similar to 3. The selected structural parameters around the intramolecular OH⋯C(π) interactions in 1–15, r(O–H), r(H⋯C(π)), ∠OHC(π) and ∠HC(π)C(π), are collected in Table S2 of the ESI.† The optimized structures of 1–15 are not shown in the figures, but they can be found in the molecular graphs drawn on the optimized structures (see Fig. S3–S5 of the ESI† and Fig. 3).

The relative energies (ΔE) in 1–15 are calculated on the energy surface (ΔE_ES) and those with the corrections for the zero-point energies (ΔE_ZP). The energies of the conformers in 1–15, with the smallest r(H⋯C(π)) values among the optimized ones (called 1a–15a, respectively), were chosen as the standards. The ΔE values (ΔE_ES and ΔE_ZP) for 1–15 are also presented in Table S2 of the ESI.†

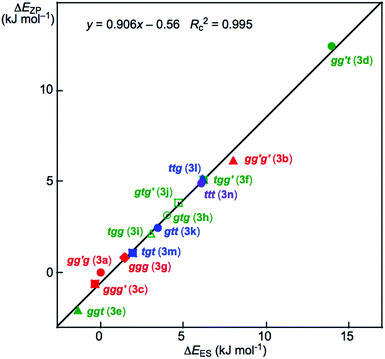
Fig. 2 shows the plot of ΔE_ZP versus ΔE_ES for the optimized 14 conformers in 3. The plot showed an excellent correlation (y = 0.906x – 0.56: R_c² = 0.995). The dependence of ΔE on the conformers in 3 seems well understood based on Fig. 2. The ΔE values for the conformers increase in the order shown in eqn (7) (less stable in the order), if ϕ(C_βC_γOH) are limited to 180° (t). The ttt conformer is predicted to be the second-most unstable one in the stability sequence shown in eqn (7).

ggt (3e) < tgt (3m) < gtt (3k) < ttt (3n) < gg′t (3d) (7)

Fig. 2 Plot of ΔE_ZP versus ΔE_ES for the conformers in 3, as optimized with MP2/BSS-A.

The prediction seems unusual at first glance since the conformers in 3 are expected to be less stable as the steric crowding increases if no mechanisms other than the steric one are operating to stabilize the conformer. The repulsive energy from the steric hindrance is expected to be the lowest in ttt (3n). However, ggt (3e), tgt (3m) and gtt (3k) are predicted to be more stable than ttt (3n), although gg′t (3d) is predicted to be most unstable relative to the others. The ΔE_ES values are calculated to be 14.0 and 8.0 kJ mol⁻¹ for gg′t (3d) and gg′g′ (3b), respectively, which are the most and second-most unstable conformers in 3. They seem to be the second and third-most sterically crowded ones in 3, respectively. The conformer 3a is expected to be the most sterically crowded one among those in 3, where the ΔE_ES value for gg′g (3a) is used as the standard (0.0 kJ mol⁻¹) for the conformers of 3. However, gg′g (3a) is close to the most stabilized conformer among those in 3. The intramolecular OH–*–C(π) interaction contributes to stabilizing gg′g (3a) by approximately 15 kJ mol⁻¹ in 3. Similar phenomena were observed among the optimized conformers in 1–15.

The ΔE_ZP values are similarly plotted versus the ΔE_ES for the 72 conformers. The plot is shown in Fig. S6 of the ESI.† The plot also gave a very good correlation (y = 0.897x – 0.20: R_c² = 0.990). As a result, ΔE_ES can be employed for the discussion of ΔE.

Before presenting a detailed discussion of the nature of the intramolecular OH–*–C(π) interactions, it is instructive to examine the molecular graphs with the contour plots.

Molecular graphs with contour plots for 1–15

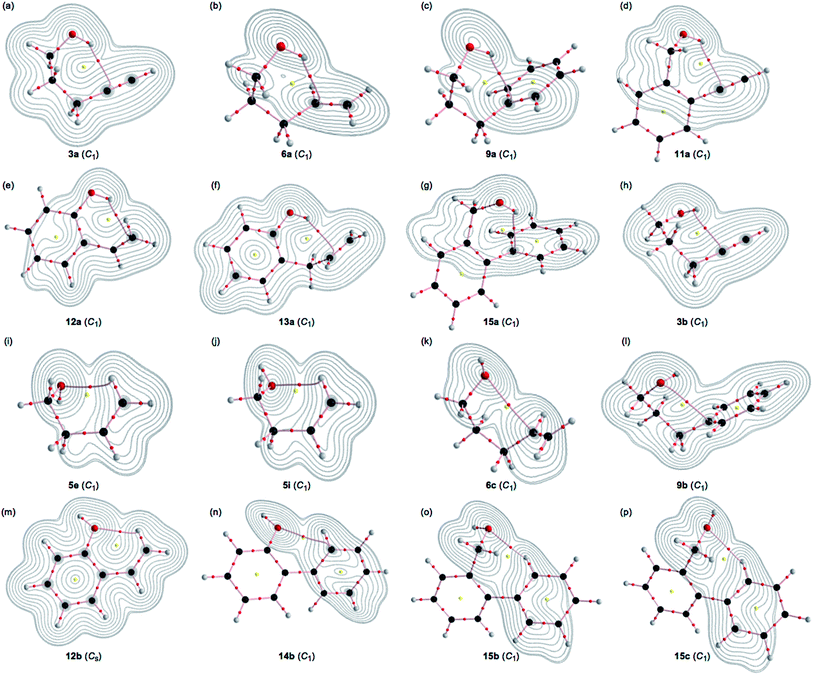
A BCP on a BP corresponding to the intramolecular OH–*–C(π) interaction was detected for 3a, 6a, 9a, 11a, 12a, 13a and 15a, whereas one corresponding to the intramolecular O–*–C(π) interaction was recorded for 3b, 6c, 9b and 14b, and that corresponding to the intramolecular O–*–H(π) interaction was for 5e, 5i, 12b, 15b and 15c, where the H(π) joined directly to the C(π). Fig. 3 illustrates the molecular graphs with the contour plots for the intramolecular OH–*–C(π), O–*–C(π) and O–*–H(π) interactions for the conformers discussed above. All the expected BCPs are clearly detected, and they contain the components for the intramolecular interactions. These BCPs seem to be appropriately located at the (three-dimensional) saddle points of ρ(r).

Fig. 3 Molecular graphs for the 16 conformers of 3a, 6a, 9a, 11a, 12a, 13a, 15a, 3b, 5e, 5i, 6c, 9b, 12b, 14b, 15b and 15c calculated with MP2/BSS-A (shown by (a)–(p), respectively, in the figure), where BPs with BCP corresponding to the intramolecular non-covalent interactions around the OH group are detected. The BCPs are denoted by red dots, RCPs (ring critical points) are indicated by yellow dots and BPs are indicated by pink lines. The carbon, hydrogen and oxygen atoms are shown in black, grey and red, respectively. Contour plots are drawn on the planes containing the intramolecular interaction for each. The contours (ea_o⁻³) are at 2^l (l = ±8, ±7 … and 0).

As shown in Fig. 3, each BP with BCP corresponding to the intramolecular OH–*–C(π) interaction appears in the six-membered ring of the –COH–*–CCC type. However, each BP with BCP corresponding to the intramolecular O–*–C(π) or O–*–H(π) interaction appears in the five, six, or seven-membered ring. A BCP on a BP corresponding to the intramolecular OH–*–C(π), O–*–C(π) or O–*–H(π) interaction is not detected for HOCC≡CH (1), HOCCC≡CH (2), HOCC=CH (4), HOCCC=CH (5) and HOCH₂Ph (7), HOCH₂CH₂Ph (8) and HOC₆H₄C=CH-o (10). The cyclic interaction seems not to satisfy the conditions for the appearance of BP with BCP in each of the above species. BPs with BCPs corresponding to both intramolecular OH–*–C(π) and O–*–C(π) interactions are detected in 6, while BPs with BCPs corresponding to the intramolecular OH–*–C(π) and O–*–H(π) interactions are detected in 12 and 15. However, only BP with BCP corresponding to the intramolecular OH–*–C(π) interaction appears in 13, whereas only BP with BCP corresponding to the intramolecular O–*–C(π) interaction appears in 14. The intramolecular OH–*–C(π) interactions, appearing in the six-membered rings, show clear contrast to the similar CH–*–C(π) interaction, expected to occur in the five-membered ring in the species similar to 5.³⁶

Molecular graphs are given in Fig. S3–S5 of the ESI† for the conformers in 1–15 without a BCP on a BP corresponding to the OH–*–C(π) or O–*–X interaction being recorded for each.

Survey of HB interactions in 1–15

The BPs corresponding to the intramolecular OH–*–C(π), O–*–C(π) and O–*–H(π) interactions shown in Fig. 3 appear somewhat curved, especially around the area close to the atoms at the ends of the BPs. To examine the linearity of the interactions further, the lengths of the BPs (r_BP) in question and the corresponding straight-line distances (R_SL) are calculated for those shown in Fig. 3. The values calculated with MP2/BSS-A are collected in Table S3 of the ESI,† together with the differences between them (Δr_BP = r_BP – R_SL). The magnitudes of Δr_BP are 0.01–0.30 Å for the BPs. Consequently, the intramolecular OH–*–C(π) interactions shown in Fig. 3 should be recognized as the curved ones, more or less. The curved nature of the intramolecular interactions would have originated from the twisted interaction due to the steric constraints in the optimized conformers. The r_BP values are plotted versus the R_SL, which is displayed in Fig. S7 of the ESI.† The Δr_BP values seem to increase in the order O–*–H(π) < O–*–C(π) < OH–*–C(π) in the average.

The QTAIM functions of ρ_b(r_c), H_b(r_c) – V_b(r_c)/2, H_b(r_c) and k_b(r_c) are calculated at the BCP on the BP corresponding to the intramolecular OH–*–C(π) interaction for 3a, 6a, 9a, 11a, 12a, 13a and 15a and at the factor corresponding to the intramolecular O–*–C(π) interaction for 3b, 6b, 9b and 14b, together with that corresponding to the intramolecular O–*–H(π) interaction for 5e, 5i, 12b, 15b and 15c. Table 1 shows the values, as evaluated with MP2/BSS-A. Fig. 4 shows the plots of H_b(r_c) versus H_b(r_c) – V_b(r_c)/2 for the data in Table 1 and those from the perturbed structures generated with CIV. The (R, θ) and (θ_p:CIV, κ_p:CIV) values were calculated by analysing the plots in Fig. 4 according to eqn (S1)–(S6) of the ESI.† The values are collected in Table 1, together with the C_ii values corresponding to CIV employed to generate the perturbed structures.

Table 1 QTAIM functions and QTAIM-DFA parameters for the intramolecular interactions around the O–H group, as elucidated with MP2/BSS-A and predicted using the predicted nature for the interactions^a,b

A–*–B(π), Compound	ρb(rc) (eao^−3)	c∇^2ρb(rc)^c (au)	Hb(rc) (au)	kb(rc)^d	R^e (au)	θ^f (°)	Cii^g (Å mdyn^−1)	θp:CIV^h (°)	κp:CIV^i (au^−1)	Predicted nature
a Data are collected for the conformers, where the intramolecular non-covalent interactions around the OH group are detected. Fig. 3 illustrates the molecular graphs with contour plots drawn on the optimized structures for the conformers shown in this table, while those other than the ones above are presented in Fig. S3–S5 of the ESI.b MP2/6-311+G(3df,3pd) for MP2/BSS-A.c ∇^2ρb(rc) = Hb(rc) – Vb(rc)/2, where c = ħ^2/8m.d kb(rc) = Vb(rc)/Gb(rc).e R = (x^2 + y^2)^1/2, where (x, y) = (Hb(rc) – Vb(rc)/2, Hb(rc)).f θ = 90° – tan^−1 (y/x).g Defined in eqn (3) in the text.h θp = 90° – tan^−1 (dy/dx).i κp = |d^2y/dx^2|/[1 + (dy/dx)^2]^3/2.j Data from w = ±0.0125, ±0.025 were employed for the evaluation.k Data from w = −0.0625, −0.050, −0.0375, −0.025, −0.0125 are employed for the evaluation.l H(π) bonded directly to C(π).m Calculated with M06-2X/BSS-A (r(H⋯C(π)) = 2.3277 Å versus 2.2797 Å (MP2)).n Calculated with B3LYP/BSS-A (r(H⋯C(π)) = 2.3782 Å versus 2.2797 Å (MP2)).
OH–*–C(π)
OH–*–^αC(π) in 3a	0.0161	0.0063	0.0015	−0.870	0.0065	77.0	7.81	97.7	335	p-CS/t-HBnc
OH–*–^αC(π) in 6a	0.0162	0.0059	0.0010	−0.909	0.0059	80.5	8.02	99.2	387	p-CS/t-HBnc
OH–*–^iC(π) in 9a	0.0155	0.0061	0.0011	−0.898	0.0062	79.5	7.46	101.8	288	p-CS/t-HBnc
OH–*–^αC(π) in 11a	0.0117	0.0048	0.0011	−0.867	0.0050	76.8	14.93	79.3	56.2	p-CS/vdW
OH–*–^βC(π) in 12a	0.0170	0.0072	0.0014	−0.888	0.0073	78.6	5.85	101.8	236	p-CS/t-HBnc
OH–*–^αC(π) in 13a	0.0178	0.0064	0.0011	−0.907	0.0065	80.3	7.58	115.9	420	p-CS/t-HBnc
OH–*–^iC(π) in 15a	0.0135	0.0053	0.0009	−0.901	0.0054	79.8	12.45	94.0	193	p-CS/t-HBnc
O–*–C(π)
O–*–^αC(π) in 3b^j	0.0125	0.0054	0.0011	−0.887	0.0055	78.5	7.31	49.7	5035	p-CS/vdW
O–*–^αC(π) in 6c	0.0098	0.0047	0.0011	−0.863	0.0049	76.4	7.48	107.2	7373	p-CS/t-HBnc
O–*–^iC(π) in 9b	0.0108	0.0047	0.0009	−0.897	0.0048	79.4	9.14	90.8	85.0	p-CS/t-HBnc
O–*–^oC(π) in 14b^k	0.0108	0.0060	0.0019	−0.807	0.0063	72.0	4.79	86.1	1631	p-CS/vdW
O–*–H(π)^l
O–*–^βH(π) in 5e	0.0107	0.0051	0.0012	−0.867	0.0052	76.8	12.74	86.3	266	p-CS/vdW
O–*–^βH(π) in 5i	0.0102	0.0049	0.0012	−0.862	0.0050	76.3	15.97	88.5	577	p-CS/vdW
O–*–^βH(π) in 12b	0.0164	0.0086	0.0026	−0.822	0.0090	73.2	4.43	73.4	19.8	p-CS/vdW
O–*–^oH(π) in 15b	0.0129	0.0056	0.0012	−0.877	0.0057	77.7	13.09	77.9	0.4	p-CS/vdW
O–*–^oH(π) in 15c	0.0112	0.0047	0.0010	−0.883	0.0048	78.2	16.49	79.9	24.3	p-CS/vdW
OH–*–C(π)
OH–*–^αC(π) in 3a^m	0.0147	0.0061	0.0018	−0.832	0.0063	73.9	7.95	82.7	185	p-CS/vdW
OH–*–^αC(π) in 3a^n	0.0132	0.0050	0.0016	−0.813	0.0053	72.5	9.68	81.0	199	p-CS/vdW

---

Fig. 4 Plots of H_b(r_c) versus H_b(r_c) – V_b(r_c)/2 for the intramolecular interactions around the OH group in 3a, 3b, 5e, 5i, 6a, 6c, 9a, 9b, 11a, 12a, 12b, 13a, 14b, 15a, 15b and 15c, as evaluated with MP2/BSS-A. The perturbed structures are generated with a CIV.

Nature of intramolecular OH–*–C(π), O–*–C(π) and O–*–H(π) interactions in the conformers of 1–15

The intramolecular OH–*–C(π), O–*–C(π) and O–*–H(π) interactions in the conformers of 1–15 given in Table 1 are classified and characterized based on the (θ, θ_p:CIV) values and evaluated with MP2/BSS-A. While θ classifies interactions, θ_p characterizes them. It is instructive to survey the criteria shown in Scheme S3 and Table S1 of the ESI† before engaging in detail discussion. The criteria indicate that 45° < θ < 180° (0 < H_b(r_c) – V_b(r_c)/2) for the CS interactions and 180° < θ < 206.6° (H_b(r_c) – V_b(r_c)/2 < 0) for the SS interactions.^18a,32 The CS interactions are sub-divided into 45°< θ < 90° (H_b(r_c) > 0) for the pure CS interactions (p-CS) and 90° < θ < 180° (H_b(r_c) < 0) for the regular CS interactions (r-CS). In the p-CS region of 45° < θ < 90°, the character of the interactions will be the vdW type for 45° < θ_p < 90° (45° < θ < 75°), whereas it will be the typical hydrogen bonds type with no covalency (t-HB_nc) for 90° < θ_p < 125° (75° < θ < 90°), where θ = 75° and θ_p = 125° are tentatively given for θ_p = 90° and θ = 90°, respectively. The CT interaction will appear in the r-CS region of 90° < θ < 180°. The t-HB interactions with the covalency (t-HB_wc) appear over the range 125° < θ_p < 150° (90° < θ < 115°), where (θ, θ_p) = (115°, 150°) are tentatively given as the borderline between the nature of t-HB_wc and CT-MC (molecular complex formation through CT). The borderline of the interactions between CT-MC and CT-TBP (TBP adduct formation through CT) types is defined by (θ, θ_p) = (150°, 180°), where θ = 150° is tentatively given as corresponding to θ_p = 180°. As a result, the (θ, θ_p) values of (75°, 90°), (90°, 125°), (115°, 150°), (150°, 180°) and (180°, 190°) correspond to the borderlines between the nature of interactions for vdW/t-HB_nc, t-HB_nc/t-HB_wc, t-HB_wc/CT-MC, CT-MC/CT-TBP and CT-TBP/Cov-w (weak covalent bonds), respectively. The parameters described in bold are superior to those tentatively given as parameters in the classification and/or characterization of interactions. The SS (180° < θ) and r-CS (90° < θ < 180°) interactions were not detected in each intramolecular HB interaction studied in this work. Therefore, R is not employed for the characterization in this work.

In the case of the intramolecular OH–*–C(π) interactions in Table 1, the (θ, θ_p:CIV) values are (77.0–80.5°, 94.0–115.9°) for all the intramolecular OH–*–C(π) interactions, except for 11a, of which (θ, θ_p:CIV) = (76.8°, 79.3°). Therefore, the intramolecular OH–*–C(π) interactions in 3a, 6a, 9a, 12a, 13a and 15a are predicted to have a t-HB_nc nature, as appeared in the p-CS region (p-CS/t-HB_nc), whereas the nature of the interaction in 11a has a p-CS/vdW nature. The intramolecular O–*–C(π) interactions show a similar trend relative to the intramolecular OH–*–C(π) interactions. The (θ, θ_p:CIV) values are (76.4–79.4°, 90.8–107.2°) for 6c and 9b, whereas the values are (72.0–78.5°, 49.7–86.1°) for 3b and 14b. Consequently, the nature of the intramolecular O–*–C(π) interactions in 6c and 9b is predicted to have a p-CS/t-HB_nc nature, while the predicted nature is p-CS/vdW for 3b and 14b. However, the (θ, θ_p:CIV) values are (73.2–78.2° and 73.4–88.5°) for the intramolecular O–*–H(π) interactions in 5e, 5i, 12b, 15b and 15c, which should have a p-CS/vdW nature. The strength of the three types of interactions is roughly predicted to be smaller in the order OH–*–C(π) > O–*–C(π) > O–*–H(π) (see Table 1).

The calculated θ_p:CIV values are usually larger than or close to the θ values for the usual interactions. However, the θ_p:CIV in 3b (49.7°) is predicted to be much smaller than θ (78.5°) for the O–*–C(π) interaction. The reason is unclear when using the data in Table 1. It would have originated from the substantially distorted nature of the O–*–C(π) interaction in 3b (Δr_BP = 0.295 Å). The BP for the intramolecular O–*–C(π) interaction in 3b seems to be very close to the O–H bond in 3b, which would also be a reason for this phenomena.

The effects from basis sets and levels on the optimized structures and the calculated natures of the interactions in question must be an important issue of QTAIM approach. The effects on the standard interactions, containing hydrogen bonds, are carefully examined, which will be discussed elsewhere.³⁷ The effects from the DFT level of M06-2X (M06-2X/BSS-A//M06-2X/BSS-A: M06-2X/BSS-A) and B3LYP (B3LYP/BSS-A//B3LYP/BSS-A: B3LYP/BSS-A) on the nature of OH–*–^αC(π) in 3a were examined, in this paper. Table 1 shows the results. The r(H⋯C(π) values were optimized as 2.3277 and 2.3782 Å at the M06-2X and B3LYP levels, respectively, which are 0.048 and 0.099 Å longer, relative to that optimized at the MP2 level (2.2797 Å). On the other hand, the (θ, θ_p:CIV) values of (73.9°, 82.7°) and (72.5°, 81.0°) were calculated for OH–*–^αC(π) in 3a at the M06-2X and B3LYP levels, respectively, irrespective of the calculated r(H⋯C(π) values, while the (77.0°, 97.7°) values were calculated at the PM2 level. As a result, the p-CS/vdW nature was predicted for OH–*–^αC(π) in 3a at the M06-2X and B3LYP levels, whereas the p-CS/t-HB_nc nature was at the MP2 level. The effects from M06-2X/BSS-A and B3LYP/BSS-A seem not small, relative to the case of MP2/BSS-A.

The strength of the intramolecular interactions is discussed in relation to those of the NBO analysis in the next section.

NBO analysis for intramolecular interactions

The stabilization energy E(2) is calculated by NBO analysis²⁴ for each donor NBO (i) and acceptor NBO (j) based on the second-order perturbation theory according to eqn (8). The q_i values in eqn (8) are the donor orbital occupancy, E_i and E_j are diagonal elements (orbital energies) and F(i,j) is the off-diagonal NBO Fock matrix element. The treatments will evaluate the CT terms of the intramolecular interactions.

E(2) = q_iF(i,j)²/(E_j – E_i) (8)

The NBO (version 3.0) was applied to the conformers, where BPs with BCPs corresponding to the intramolecular OH–*–C(π), O–*–C(π) and/or O–*–H(π) interactions were detected. The NBO (version 3.0) was also applied to the conformers for which the OH⋯C(π) distances are less than 2.9 Å. The E(2) values were successfully obtained under the threshold of 0.5 kcal mol⁻¹ (2.1 kJ mol⁻¹). Table 2 collects the results of the NBO analysis, as calculated with MP2/BSS-A. The CT terms of the π(C≡C/C=C) → σ*(H–O) type contribute to E(2) in 3a, 5a, 5b, 6a, 8a, 9a, 10a, 11a, 12a, 13a, 14a and 15a, together with the inverse σ(H–O) → π*(C≡C/C=C) type for 10a and 15b. The CT terms of the n_p(O) → π*(C≡C) type contribute to E(2) in 1a, 3b, 4a, 4c, 6a, 6b, 6c and 7a. However, the CT term of the n_p(O) → σ*(C–H) type was detected in 15c and that of the n_s(O) → π*(C–H) type was in 10b, while the term of the n_s(O) → σ*(C–H) type was in 12b and 15b.

Table 2 Results of the NBO analysis with NBO 3.0 for the intramolecular interactions around the OH group, as evaluated with MP2/BSS-A

Species	E(2)^a (kJ mol^−1)	E(j)–E(i)^b (au)	F(i,j)^c (au)	r(H⋯C(π)) (Å)
a Second order perturbation energy given by eqn (8).b The diagonal elements (orbital energies).c The off-diagonal NBO Fock matrix element.d 2.4027 Å for r(O⋯C(π)).e 2.9757 Å for r(O⋯C(π)).f 2.4170 Å for r(O⋯C(π)).g 2.4305 Å for r(O⋯C(π)).h 3.0039 Å for r(O⋯C(π)).i 3.0044 Å for r(O⋯C(π)).j 2.9581 Å for r(O⋯C(π)).k 3.0080 Å for r(O⋯C(π)).l 2.4484 Å for r(HO⋯H).m 2.74345 Å for r(O⋯C(π)).n 2.2155 Å for r(HO⋯H).o 2.3578 Å for r(HO⋯H).
CT term of the π(C≡C/C=C) → σ*(H–O) type
3a	10.0	1.14	0.047	2.2797
5a	4.8	1.09	0.032	2.4802
5b	3.7	1.10	0.028	2.6111
6a	13.8	1.11	0.054	2.3020
8a	2.7	1.02	0.025	2.5218
9a	7.2	1.05	0.042	2.3316
10a	4.5	1.52	0.036	2.2584
11a	2.1	1.13	0.021	2.4507
12a	11.6	1.08	0.049	2.4139
13a	20.1	1.09	0.065	2.2783
14a	8.9	1.00	0.045	2.3601
15a	4.4	1.05	0.032	2.3869
CT term of the σ(H–O) → π*(C≡C/C=C) type
10a	3.6	1.27	0.029	2.2584
15b	2.1	1.47	0.027	4.1125
CT term of the np(O) → π*(C≡C/C=C) type
1a	5.7	0.82	0.030	2.5155^d
3b	2.3	0.79	0.018	2.4272^e
4a	6.9	0.72	0.031	2.5383^f
4c	5.4	0.73	0.027	2.6315^g
6a	2.3	0.70	0.017	2.3020^h
6b	3.7	0.73	0.023	3.4771^i
6c	3.8	0.73	0.023	3.5116^j
7a	3.7	0.67	0.024	2.5311^k
CT term of the np(O) → σ*(C–H) type
15c	2.3	1.34	0.024	4.2452^l
CT term of the ns(O) → π*(C–H) type
10b	3.5	1.18	0.028	3.6982^m
CT term of the ns(O) → σ*(C–H) type
12b	3.3	1.59	0.032	3.8536^n
15b	19.3	7.82	0.170	4.1125^o

---

The E(2) values larger than 7.0 kJ mol⁻¹ were predicted for the CT terms of the π(C≡C/C=C) → σ*(H–O) interactions in 3a, 6a, 9a, 13a and 14a, for which the OH⋯C(π) distances are less than 2.36 Å. A BP with a BCP corresponding to the intramolecular OH–*–C(π) interaction was detected for each case, except for 14a. The E(2) values of less than 4.8 kJ mol⁻¹ were similarly predicted for 5a, 5b, 8a, 11a and 15a, among which the OH⋯C(π) distances were longer than 2.38 Å. In this case, the BP with the BCP was detected for 11a, 12a and 15a, whereas it was not detected for 5a, 5b, 8a and 10a. The E(2) value of 20.1 kJ mol⁻¹ was evaluated for the intramolecular OH–*–C(π) interaction in 13a, which is larger than those in 3a, 6a, 9a, 11a, 12a and 15a (2.1–13.8 kJ mol⁻¹). This must be the reason for the stronger intramolecular OH–*–C(π) interaction in 13a, relative to the cases in 3a, 6a, 9a, 11a, 12a and 15a evaluated with QTAIM-DFA. The large E(2) value of 20.1 kJ mol⁻¹ in 13a may come from the short OH⋯C(π) distance (2.28 Å), although the other advantageous structural parameters around the OH–*–C(π)-predicted CT interaction in 11a are not of the π(C≡C) → σ*(H–O) type but rather the inverse type of σ(H–O) → π*(C≡C). The E(2) value was evaluated to be 2.1 kJ mol⁻¹ for the intramolecular interaction of 11a.

Substantially large E(2) values are evaluated for the intramolecular OH⋯C(π) interaction by NBO, if a BP with a BCP corresponding to the intramolecular OH–*–C(π) interaction was detected for the conformer. In the case of 12b, a rather small E(2) value (3.3 kJ) was evaluated for the n_p(O) → σ*(H–C) interaction.

However, a much larger E(2) value of 19.3 kJ was predicted for the n_s(O) → σ*(C–H) interaction in 15b, which must be the reason for the predicted strong intramolecular O–*–H(π) interaction for 15b using QTAIM-DFA. The CT terms were not printed out for the intramolecular interactions in 5e and 5i, although the BPs with the BCPs of the O–*–^βH(π) type were detected. The results seem to be queries at first glance. They would be the results from the intramolecular vdW type interactions in 5e and 5i. The contributions of the CT terms must be (very) small for the vdW type interactions; therefore, the E(2) values should be evaluated to be (very) small, which would be buried in the threshold value of 2.1 kJ mol⁻¹ (0.5 kcal mol⁻¹).

The results of the NBO analysis are discussed in relation to the ΔE_ES values in the next section.

Intramolecular π(C≡C/C=C) → σ*(H–O) interactions as the factor to stabilize the conformers

Are the conformers effectively stabilized through the intramolecular CT interactions? The stability of the conformers are discussed in relation to the E(2) values calculated with the NBO, as exemplified by the energy differences between conformer a and b, ΔE_ES(xb/xa) [=ΔE_ES(xb) – ΔE_ES(xa)]. The x values were limited to 3, 6, 9, 11–13 and 15, where the BP with BCP of the OH–*–C(π) type were detected in xa. The OH⋯C(π) distance must be the shortest in xa by definition; therefore, the steric hindrance is expected to reach its maximum in xa, although the xa will contain the attractive factor based on the intramolecular OH⋯C(π) interaction. The intramolecular OH⋯C(π) distance in xb is the second shortest, by definition, and therefore the steric hindrance in xb would be somewhat released in most cases due to the change of ϕ(C_βC_γOH) from xa. As a result, the ΔE_ES(xb/xa) is expected to be a rough measure for the contribution from the intramolecular interaction in xa if the contribution from the intramolecular interaction is (almost) varnished in xb.

The nature of the interactions in question can be clarified based on the BPs with the BCPs, but the intramolecular interactions are carefully discussed based on BPs with BCPs. The theoretical treatment for the appearance and/or disappearance of BPs is very complex and very difficult.³⁸ Namely, the theoretical treatment for the intramolecular interactions in detail is beyond the scope of this work. Therefore, the ΔE_ES(xb/xa) values are discussed here, where the BPs with BCPs are detected for some of the conformers from 1–15, whereas some are not. The ΔE_ES(xb/xa) values are discussed in relation to the E(2) values for the intramolecular interactions evaluated with the NBO and the steric effect in the conformers.

Fig. 5 shows the plot of E(2) and ΔE_ES(xb/xa) for x = 3, 6, 9, 11–13 and 15 in red and blue, respectively. The ΔE_ES(xb/xa) values are evaluated over a range of 3.8 ≤ ΔE_ES ≤ 13.8 kJ mol⁻¹ for 3b/3a, 6b/6a, 9b/9a and 11b/11a to 13b/13a with ΔE_ES = −0.2 kJ mol⁻¹ for 15b/15a. However, the E(2) values are calculated at a range of 2.1 ≤ ΔE_ES ≤ 13.8 kJ mol⁻¹ for xa (x = 3, 6, 9, 11, 12 and 15) with 20.1 kJ mol⁻¹ for 13a, as shown in Fig. 5 and Table 2. The ΔE_ES values of 3b/3a (8.0 kJ mol⁻¹), 6b/6a (13.8 kJ mol⁻¹) and 9b/9a (10.0 kJ mol⁻¹) are close to the E(2) values of 3a (10.0 kJ mol⁻¹), 6a (13.8 kJ mol⁻¹) and 9a (7.2 kJ mol⁻¹). The results can be reasonably explained by assuming that the intramolecular π(C≡C/C=C) → σ*(H–O) interactions can effectively stabilize the conformers of the ethenyl and ethynyl derivatives of the aliphatic alcohols. In the case of the phenol and benzyl alcohol derivatives, the ΔE_ES values of 12b/12a (3.8 kJ mol⁻¹), 13b/13a (7.8 kJ mol⁻¹) and 15b/15a (−0.2 kJ mol⁻¹) are substantially smaller than the E(2) values of 12a (11.6 kJ mol⁻¹), 13a (20.1 kJ mol⁻¹) and 15a (4.4 kJ mol⁻¹), respectively. Other factors seem to waste the contributions from the attractive intramolecular π(C≡C/C=C) → σ*(H–O) interactions. A repulsive steric effect would greatly waste the attractive interactions in 12a and 13a. The intramolecular interactions operate more effectively to stabilize 12a and 13a relative to 12b and 13b, respectively, which would come from the steric hindrance in 12b and 13b larger than 12a and 13a, respectively. The ΔE_ES(15b/15a) value is predicted to be −0.2 kJ mol⁻¹. The intramolecular n_p(O) → σ*(C–H) interaction stabilizes 15b, very effectively, as shown by the NBO analysis (see, Table 2). In fact, the π(C≡C/C=C) → σ*(H–O) interaction acts to stabilize 15a (4.4 kJ mol⁻¹), but the σ(H–O) → π*(C≡C/C=C), n_p(O) → σ*(C–H) and n_s(O) → σ*(C–H) interactions also operate to stabilize 15b (2.1 kJ mol⁻¹), 15c (2.3 kJ mol⁻¹) and 15b (19.3 kJ mol⁻¹), respectively. The contributions from the intramolecular interactions to stabilize 15a and 15b must be the primary factor in the negative value of ΔE_ES(15b/15a), although the mechanism, similar to the case of 11b/11a and 11b/11a, must also be working.

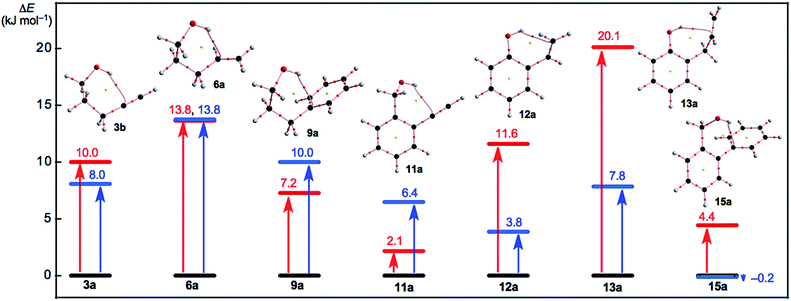Fig. 5 Plots of E(2) and ΔE_ES(xb/xa) for x = 3, 6, 9, 11–13 and 15 in red and blue, respectively. Molecular graphs for xa are shown, where BCP with BPs corresponding to the intramolecular OH–*–C(π), O–*–C(π), or O–*–H(π) interactions are given for each. Molecular graphs other than xa are drawn in Fig. S3–S5 of the ESI.†

The ΔE_ES(1b/1a: 6.6 kJ mol⁻¹) and ΔE_ES(5b/5a: 6.8 kJ mol⁻¹) values seem close to the ΔE_ES (3b/3a: 8.0 kJ mol⁻¹) and smaller than the ΔE_ES (6b/6a: 13.8 kJ mol⁻¹), for example. The intramolecular n_p(O) → π*(C≡C/C=C) and π(C≡C/C=C) → σ*(H–O) interactions operate to stabilize 1a (5.7 kJ mol⁻¹) and 5a (4.8 kJ mol⁻¹), respectively, while 3a (10.0 kJ mol⁻¹) and 6a (13.8 kJ mol⁻¹) are stabilized by the π(C≡C/C=C) → σ*(H–O) interaction. In this case, a BP with a BCP is detected for 3a and 6a, whereas a BP with a BCP is not detected in 1a and 5a. The conditions for the appearance of the BP with BCP would not be satisfied for the corresponding interaction in 1a and 5a.

Conclusions

Intramolecular cv-HBs are extremely important in the all fields of the chemical and biological sciences as are intramolecular π-HBs. The intrinsic dynamic and static nature of intramolecular π-HBs is elucidated here using QTAIM-DFA. The perturbed structures necessary for QTAIM-DFA are generated using coordinates derived from the compliance constants (CIV). Over 70 conformers were optimized for 1–15. BPs with BCPs corresponding to the intramolecular OH–*–C(π) interactions were detected in seven conformers that appeared in the six-membered rings of the –COH–*–CCC type. Those corresponding to the intramolecular O–*–C(π) interactions are also detected in four conformers together with those for the intramolecular O–*–H(π) interactions in five conformers. The intramolecular O–*–C(π) and O–*–H(π) interactions appeared in the 5–7-membered rings. The BPs are somewhat curved. The intramolecular OH–*–C(π) interactions are predicted to have a p-CS/vdW to p-CS/t-HB_nc nature. The strength of the intramolecular interactions appears to be generally weaker in the order OH–*–C(π) > O–*–C(π) > O–*–H(π) (see Table 1). The contributions from the intramolecular OH–*–C(π), O–*–C(π) and O–*–H(π) interactions towards stabilizing the conformers are also confirmed by the NBO analysis (see Table 2). The contributions of the intramolecular interactions used to stabilize the conformers are considered, even for the conformers with no appearance of BPs, which corresponds to the intramolecular interactions. The intramolecular interactions between the OH and C≡C/C=C groups, such as the OH–*–C(π), O–*–C(π), or O–*–H(π) types, may help to stabilize the conformers even if this interaction is not detected as a BP with BCP. The intramolecular OH–*–π interactions appear to be evaluated as somewhat stronger than the intermolecular interactions.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was partially supported by a Grant-in-Aid for Scientific Research (No. 17K05785) from the Ministry of Education, Culture, Sports, Science and Technology of Japan.

Notes and references

1. S. Scheiner, Hydrogen Bonding, A Theoretical Perspective, Oxford University Press, Oxford, U.K., 1997.
2. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology (IUCr Monographs on Crystallography), Oxford University Press, Oxford, 1999.
3. G. Gilli and P. Gilli, The Nature of the Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory (IUCr Monographs on Crystallography), Oxford University Press, Oxford, 2009.
4. S. Hayashi, K. Matsuiwa, M. Kitamoto and W. Nakanishi, J. Phys. Chem. A, 2013, 117, 1804–1816.
5. G. Buemi, Intramolecular Hydrogen Bonds. Methodologies and Strategies for Their Strength Evaluation, in Hydrogen Bonding – New Insights, Vol. 3, Challenges and Advances in Computational Chemistry and Physics, ed. S. J. Grabowski, Springer, New York, 2006, ch. 2.
6. Chemistry of Hypervalent Compounds, ed. K.-y. Akiba, Wiley-VCH, New York, 1999.
7. W. Nakanishi, Hypervalent Chalcogen Compounds, in Handbook of Chalcogen Chemistry: New Perspectives in Sulfur, Selenium and Tellurium, ed. F. A. Devillanova, Royal Society of Chemistry, Cambridge, 2006, ch. 10.3, pp. 644–668.
8. T. Nishide, S. Hayashi and W. Nakanishi, ChemistryOpen, 2018, 7, 565–575.
9. Y. Sugibayashi, S. Hayashi and W. Nakanishi, Phys. Chem. Chem. Phys., 2015, 17, 28879–28891.
10. Y. Sugibayashi, S. Hayashi and W. Nakanishi, Phys. Chem. Chem. Phys., 2016, 18, 9948–9960.
11. S. Hayashi, Y. Sugibayashi and W. Nakanishi, RSC Adv., 2016, 6, 49651–49660.
12. S. Hayashi, Y. Sugibayashi and W. Nakanishi, RSC Adv., 2017, 7, 31858–31865.
13. S. Hayashi, Y. Sugibayashi and W. Nakanishi, RSC Adv., 2018, 8, 16349–16361.
14. Hydrogen Bonding: New Insights (Challenges and Advances in Computational Chemistry and Physics), ed. S. J. Grabowski, Springer, The Netherlands, 2006, vol. 3.
15. K.-L. Han, and G.-J. Zhao, Hydrogen Bonding and Transfer in the Excited State, Wiley, Chichester, UK, 2010.
16. Atoms in Molecules. A Quantum Theory, ed. R. F. W. Bader, Oxford University Press, Oxford, UK, 1990.
17. C. F. Matta and R. J. Boyd, in An Introduction to the Quantum Theory of Atoms in Molecules In The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, ed. C. F. Matta and R. J. Boyd, Wiley-VCH, Weinheim, Germany, 2007, ch. 1.
18. (a) W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2009, 113, 10050–10057; (b) W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2008, 112, 13593–13599.
19. W. Nakanishi and S. Hayashi, Curr. Org. Chem., 2010, 14, 181–197.
20. W. Nakanishi and S. Hayashi, J. Phys. Chem. A, 2010, 114, 7423–7430.
21. W. Nakanishi, S. Hayashi, K. Matsuiwa and M. Kitamoto, Bull. Chem. Soc. Jpn., 2012, 85, 1293–1305.
22. W. Nakanishi and S. Hayashi, Int. J. Quantum Chem., 2018, 118, e25590.
23. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO 3.0 Program Manual, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, USA, 1990.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
25. (a) C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622; (b) J. Gauss, J. Chem. Phys., 1993, 99, 3629–3643; (c) J. Gauss, Ber. Bunsen-Ges. Phys. Chem., 1995, 99, 1001–1008.
26. The C_ii values and the coordinates corresponding to C_ii were calculated by using the Compliance 3.0.2 program released by Grunenberg and Brandhorst, http://www.oc.tu-bs.de/Grunenberg/compliance.html.
27. K. Brandhorst and J. Grunenberg, J. Chem. Phys., 2010, 132, 184101–184107.
28. K. Brandhorst and J. Grunenberg, Chem. Soc. Rev., 2008, 37, 1558–1567.
29. J. Grunenberg, Chem. Sci., 2015, 6, 4086–4088.
30. (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (c) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
31. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
32. The detailed method to generate the perturbed structures is explained in ref 18a. See also ref. 19–22.
33. F. Biegler-König, The AIM2000 program (Version 2.0) is employed to analyze and visualize atoms-in-molecules:, J. Comput. Chem., 2000, 21, 1040 , see also ref. 16.
34. T. A. Keith, AIMAll (version 17.11.14), TK Gristmill Software, Overland Park KS, USA, 2017, aim.tkgristmill.com.
35. W. Nakanishi and S. Hayashi, J. Phys. Chem. A, 2013, 117, 1795–1803.
36. M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873–13900.
37. S. Hayashi, T. Nishide, K. Ueda, K. Hayama and W. Nakanishi, ChemistrySelect DOI:10.1002/slct.201900998 , in press.
38. It is demonstrated that the detection of the BPs between two atoms in a molecule emerging from natural alignment of the gradient vector held of the one-electron density of a molecule is neither necessary nor a sufficient condition for the presence of a chemical bond between those atoms.³⁹ In this connection, it is pointed out that the terms line paths (LPs) and line critical points (LCPs) should be used in place of BPs and BCPs, respectively.^39b However, BPs and BCPs are used in this work..
39. (a) R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391–10396; (b) C. Foroutan-Nejad, S. Shahbazian and R. Marek, Chem.–Eur. J., 2012, 18, 4982–4993; (c) M. Garcıa-Revilla, E. Francisco, P. L. A. Popelier and A. M. Pendás, ChemPhysChem, 2013, 14, 1211–1218; (d) Z. A. Keyvani, S. Shahbazian and M. Zahedi, Chem.–Eur. J., 2016, 22, 5003–5009.

---

Footnote

† Electronic supplementary information (ESI) available: QTAIM-DFA approach, computational data, and the fully optimized structures given by Cartesian coordinates, together with total energies of species 1–15. See DOI: 10.1039/c9ra01788g

---