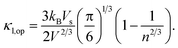DOI:
10.1039/C8RA10471A
(Paper)
RSC Adv., 2019,
9, 3847-3855
Effects of Ga substitution on electronic and thermoelectric properties of gapless semiconductor V3Al
Received
21st December 2018
, Accepted 14th January 2019
First published on 29th January 2019
Abstract
Thermoelectric properties of the antiferromagnetic (AF) gapless semiconductor (GS) V3Al were optimized by substituting Al with the isoelectric element Ga in the D03 structure. Structural and mechanical stability, electronic structure and transport properties of V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) compounds have been studied based on first-principles calculations with the combination of the semi-classical Boltzmann theory and deformation potential theory. All the compounds are structurally and mechanically stable gapless semiconductors. The Ga substitution for Al leads to an appreciably decreased thermal conductivity and an undesirable decrease in power factor, but contributes more to the decreased thermal conductivity. Consequently, the figure of merit (zT) is effectively improved in V3Al0.75Ga0.25 and V3Ga compounds with respect to V3Al.
1 Introduction
High efficiency thermoelectric (TE) materials are significant components for power generation devices that can convert waste heat into electricity. The conversion efficiency of TE materials is generally characterized by the dimensionless figure of merit defined as zT = S2σT/κ,1,2 where S, σ, T, and κ are the Seebeck coefficient, the electrical conductivity, the absolute temperature, and the total thermal conductivity respectively. The total thermal conductivity (κ) is composed of two parts, κ = κe + κl, where κe (κl) is the carrier (lattice) thermal conductivity. The thermally-driven electrical performance of TE materials is measured by the power factor (PF = S2σ). To improve zT, one has to enhance PF and/or weaken κ. The main challenge is how to make an improvement in the value of zT owing to the interdependency of the transport parameters (S, σ, and κe). The electronic thermal conductivity (κe) is positively related to the electrical conductivity (σ) by the Wiedemann–Franz law and a counteracted relationship between S and σ is often observed. Therefore, the optimization of zT is a great and challenging task for obtaining highly effective TE materials.
Among promising thermoelectric materials, half-Heusler alloys have been mostly studied due to their large power factor, mechanical properties and thermal stability.3 The semiconducting half-Heusler alloys have shown to exhibit large Seebeck coefficients (∼300 μV K−1) at room temperature and moderate electrical conductivities (∼1000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Ω−1 cm−1),4–7 which are attributed to their narrow bands associated to high effective masses. Nevertheless, their relatively high thermal conductivities lead to their low thermoelectric efficiencies. In order to decrease the lattice thermal conductivity which is the predominant contribution to the thermal conductivity,8 some efforts have been made by synthesizing compounds with complicated structures by nanostructuring, forming nanocomposites, and isoelectronic alloying,3 which enhances the phonon scattering by point defects due to mass differences (mass fluctuations) and size differences (strain field impurities) between the impurity atoms and the host atoms. Typically, a zT ∼ 1 can be achieved for the nanostructured p-type Nb0.6Ti0.4FeNiSb0.95Sn0.05 composition near 973 K with a cost-effective mass-production nanocomposite approach.9 The thermal conductivity (κ) of a TiNiSn0.95Sb0.05 sample synthesized by ball milling and shock compaction can drop from 10.6 to 3.7 W m−1 K−1 by reducing the grain size diameter of the sample from ∼10 to 1 μm.10 The isoelectronic substitution of Zr for Hf in HfNiSn-based alloys remarkably reduced the lattice thermal conductivity and a zT ∼ 1.0 was achieved at 1000 K for Hf0.6Zr0.4NiSn0.98Sb0.02 (ref. 11) and an even higher zT ∼ 1.2 for Hf0.6Zr0.4NiSn0.995Sb0.005.12 Record-high zT values have been obtained for n-type Ti0.5Zr0.25Hf0.025NiSn0.998Sb0.002 (zT ∼ 1.5 at 700 K,13 zT ∼ 1.2 at 830 K (ref. 14)) and for p-type FeNb0.86Hf0.14Sb (zT ∼ 1.5 at 1200 K (ref. 15)) and FeTi0.2Nb0.8Sb (zT ∼ 1.1 at 1100 K (ref. 16)). In addition, semiconducting full-Heuslers with 24 valence electrons are other remarkable candidates for moderate temperature thermoelectric modules. Although only low zT values of 0.1–0.2 were achieved17–19 in the full-Heusler alloys due to lower density of states close to the Fermi level compared to half-Heusler alloys, a significant edge of improvement exists if the thermal conductivity is reduced and PF is further increased via manipulation of the electronic properties. Hole-type doping by Mn substitution at the Fe site and electron-type doping by Sb substitution at the Sn site have been explored in Fe2TiSn samples prepared by arc melting plus spark plasma sintering or annealing. The remarkable PF ∼ 0.4 mW m−1 K−2 in Fe2−xMnxTiSn (x = 0.0185)20 and PF ∼ 1.3 mW m−1 K−2 in FeTiSn1−xSbx (x = 0.1)21 at room temperature indicated a more than double increase in PF at room temperature in the doped samples compared to that of the undoped one, which has been attributed to a strong resonant level induced by doped atoms near the Fermi level. Hole and isoelectronic doped Fe2VAl by Ta substitution both at the Al19,22,23 and at the V site23,24 have been demonstrated to exhibit power factors in the range of 5–9 mW m−1 K−2 above room temperature.
000 Ω−1 cm−1),4–7 which are attributed to their narrow bands associated to high effective masses. Nevertheless, their relatively high thermal conductivities lead to their low thermoelectric efficiencies. In order to decrease the lattice thermal conductivity which is the predominant contribution to the thermal conductivity,8 some efforts have been made by synthesizing compounds with complicated structures by nanostructuring, forming nanocomposites, and isoelectronic alloying,3 which enhances the phonon scattering by point defects due to mass differences (mass fluctuations) and size differences (strain field impurities) between the impurity atoms and the host atoms. Typically, a zT ∼ 1 can be achieved for the nanostructured p-type Nb0.6Ti0.4FeNiSb0.95Sn0.05 composition near 973 K with a cost-effective mass-production nanocomposite approach.9 The thermal conductivity (κ) of a TiNiSn0.95Sb0.05 sample synthesized by ball milling and shock compaction can drop from 10.6 to 3.7 W m−1 K−1 by reducing the grain size diameter of the sample from ∼10 to 1 μm.10 The isoelectronic substitution of Zr for Hf in HfNiSn-based alloys remarkably reduced the lattice thermal conductivity and a zT ∼ 1.0 was achieved at 1000 K for Hf0.6Zr0.4NiSn0.98Sb0.02 (ref. 11) and an even higher zT ∼ 1.2 for Hf0.6Zr0.4NiSn0.995Sb0.005.12 Record-high zT values have been obtained for n-type Ti0.5Zr0.25Hf0.025NiSn0.998Sb0.002 (zT ∼ 1.5 at 700 K,13 zT ∼ 1.2 at 830 K (ref. 14)) and for p-type FeNb0.86Hf0.14Sb (zT ∼ 1.5 at 1200 K (ref. 15)) and FeTi0.2Nb0.8Sb (zT ∼ 1.1 at 1100 K (ref. 16)). In addition, semiconducting full-Heuslers with 24 valence electrons are other remarkable candidates for moderate temperature thermoelectric modules. Although only low zT values of 0.1–0.2 were achieved17–19 in the full-Heusler alloys due to lower density of states close to the Fermi level compared to half-Heusler alloys, a significant edge of improvement exists if the thermal conductivity is reduced and PF is further increased via manipulation of the electronic properties. Hole-type doping by Mn substitution at the Fe site and electron-type doping by Sb substitution at the Sn site have been explored in Fe2TiSn samples prepared by arc melting plus spark plasma sintering or annealing. The remarkable PF ∼ 0.4 mW m−1 K−2 in Fe2−xMnxTiSn (x = 0.0185)20 and PF ∼ 1.3 mW m−1 K−2 in FeTiSn1−xSbx (x = 0.1)21 at room temperature indicated a more than double increase in PF at room temperature in the doped samples compared to that of the undoped one, which has been attributed to a strong resonant level induced by doped atoms near the Fermi level. Hole and isoelectronic doped Fe2VAl by Ta substitution both at the Al19,22,23 and at the V site23,24 have been demonstrated to exhibit power factors in the range of 5–9 mW m−1 K−2 above room temperature.
The ternary Heusler phases often display defects including vacancy, antisite and swap defects, specifically, there is a natural tendency toward off-stoichiometry, predictable from thermodynamic theory, which may affect and even destroy the semiconductivity and transport properties,25 as observed experimentally in half-Heusler ZrNiSn26 and full-Heusler Fe2TiSn.21,27 In contrast to the ternary Heuslers, the binary Heusler alloys have slight disorder compared to the ternary ones because there is only one type of transition metal. In particular, V3Al has been recently predicted theoretically28 and then confirmed experimentally29 to be an antiferromagnetic (AF) gapless semiconductor (GS) with a stable cubic D03 structure. The thermoelectric behavior of D03-V3Al has been studied and a zT ∼ 0.32 and a PF ∼ 800 mW m−1 K−2 were expected for p-type AF-D03-V3Al at a temperature of 500 K.30 Although the thermoelectric performance and efficiency of V3Al are largely enhanced compared to the full-Heusler alloys, it cannot compete with the efficiency of conventional power generators or refrigerators mainly due to its high thermal conductivities. To further explore this enhanced performance, we have made some attempts to reduce the thermal conductivity by substituting Al with the isoelectronic element, Ga, in a V3Al alloy. For this purpose, the electronic and thermoelectric properties of V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) have been systematically studied. In addition, the mechanical stability and robustness of the doped V3Al compounds were asserted by calculating elastic constants (Cij) and moduli (bulk modulus B, shear modulus G, and Young’s modulus E). The thermoelectric properties of V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) were predicted by applying the semi-classical Boltzmann transport theory.
2 Computational method and process
The D03-type Ga doped V3Al-based compounds V3Al1−xGax have face-centered cubic structures and have the space group of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.28,29,31,32 In the Wyckoff coordination, Al atoms are located at the 4a (0,0,0) site, whereas the position of the V atoms is complicated. There are 12 V atoms in the unit cell of the V3Al compound, 8 of which occupy the 4b (0.5,0.5,0.5) and the other 4 V atoms are at 4c (0.25,0.25,0.25) and 4d (0.75,0.75,0.75) (labeled V1 and V2). The doping concentrations of x = 0.25, 0.5, 0.75 and 1 in the V3Al1−xGax compounds mean that 1, 2, 3 or 4 Al atoms are substituted by Ga atoms in the V3Al unit cell. All properties of V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) were calculated from first-principles within the framework of the projector augmented wave (PAW) method33 as conducted using the package VASP.34–36 The generalized gradient approximation (GGA) and the Perdew–Burke–Ernzerhof (PBE)37 were adopted for the exchange–correlation energy of electrons. For all the structures, the plane wave cut-off energy and a Monkhorst–Pack k-mesh sample in the whole Brillouin zone were 560 eV and 15 × 15 × 15 respectively, which are the same as those used in our previous work for V3Al.30 For V, Al, and Ga, 3d34s2, 3s23p1, and 4s24p1 states are considered as the valence states. The atom position is fully relaxed until the magnitude of the energy change and the force acting on each atom are smaller than 10−5 eV and 0.01 eV Å−1. As shown in the previous work,30 V3Al is more stable in the AF phase, and therefore all the calculations were conducted for AF D03 Ga-doped V3Al.
m.28,29,31,32 In the Wyckoff coordination, Al atoms are located at the 4a (0,0,0) site, whereas the position of the V atoms is complicated. There are 12 V atoms in the unit cell of the V3Al compound, 8 of which occupy the 4b (0.5,0.5,0.5) and the other 4 V atoms are at 4c (0.25,0.25,0.25) and 4d (0.75,0.75,0.75) (labeled V1 and V2). The doping concentrations of x = 0.25, 0.5, 0.75 and 1 in the V3Al1−xGax compounds mean that 1, 2, 3 or 4 Al atoms are substituted by Ga atoms in the V3Al unit cell. All properties of V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) were calculated from first-principles within the framework of the projector augmented wave (PAW) method33 as conducted using the package VASP.34–36 The generalized gradient approximation (GGA) and the Perdew–Burke–Ernzerhof (PBE)37 were adopted for the exchange–correlation energy of electrons. For all the structures, the plane wave cut-off energy and a Monkhorst–Pack k-mesh sample in the whole Brillouin zone were 560 eV and 15 × 15 × 15 respectively, which are the same as those used in our previous work for V3Al.30 For V, Al, and Ga, 3d34s2, 3s23p1, and 4s24p1 states are considered as the valence states. The atom position is fully relaxed until the magnitude of the energy change and the force acting on each atom are smaller than 10−5 eV and 0.01 eV Å−1. As shown in the previous work,30 V3Al is more stable in the AF phase, and therefore all the calculations were conducted for AF D03 Ga-doped V3Al.
To examine the mechanical stability of V3Al1−xGax, we need to evaluate the elastic constants, which can be obtained by the stress–strain method. For a cubic crystal, there are only three independent components, namely, C11, C12, and C44. Among them, C11 represents the elasticity in length, while C12 and C44 characterize the elasticity in shape. These elastic constants can be determined by computing the stress generated by applying a small strain to an optimized unit cell. More details of the calculations can be found in the literature.38–40 The bulk modulus (B), shear modulus (G), and Young’s modulus (E) can be expressed according to the elastic constants by the Voigt–Reuss–Hill (VRH) approximation.41 Thus, the mechanical stability of V3Al1−xGax can be judged by the following conditions:42,43
| | |
C11 + 2C12 > 0, C44 > 0, C11 − C12 > 0.
| (1) |
Electronic transport coefficients are predicted by using the semi-classical Boltzmann theory within the accurate band structures. In this approach, the electrical conductivity (σ) and electronic thermal conductivity (κe) are dependent on the relaxation time (τ). To calculate thermoelectric properties, we have to first calculate the relaxation time which is usually very complicated since it depends on phonon scattering, carrier scattering, and defect scattering mechanisms. Unlike some of the previous theoretical works where σ and κe were calculated based on a constant relaxation time44,45 or an experimental non-constant relaxation time,46,47 we determine relaxation time by using the combination of deformation potential (DP) theory and effective mass approximation which produces a reliable evaluation of electronic transport coefficients for FeNbSb-based half-Heusler thermoelectric materials compared with experimental data.48 As the lattice constant is much smaller in comparison with the wavelength of thermally activated carriers, the electron-acoustic phonon coupling is the dominant mechanism.49 The scheme is fortunately simplified. Accordingly, the relaxation time for a three-dimensional system can be calculated by the following formula:50
| |
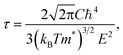 | (2) |
where
ℏ is the Planck constant,
kB is the Boltzmann constant, and
T is the absolute temperature.
C is the elastic constant which can be expressed as
| |
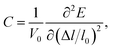 | (3) |
where
V0 and
l0 are the equilibrium volume and lattice constant of the unit cell. Δ
l =
l −
l0 is the lattice strain and
E is the corresponding total energy of the system. When calculating the effective mass (
m*) of electrons and holes, we have considered the band degeneracy.
51 In formula
(2), the deformation potential constant (
E) representing the conduction (valence) band edge shift per unit strain is given by
| |
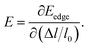 | (4) |
To calculate the lattice thermal conductivity (κl), we use the associated semi-empirical model52,53 from ground-state DFT calculations. In this approach, κl is modeled as simple descriptors including acoustic (κl,ac) and optical phonon modes (κl,op).54 The predominant contribution stems from the acoustic phonon mode (κl,ac). Based on a simplified Debye–Callaway approach, the κl,ac can be approximated to be
| |
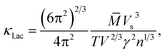 | (5) |
in which
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif)
and
V are the average mass and volume per atom respectively.
n is the number of total atoms in the primitive cell. The value of the Grüneisen constant (
γ) at different temperatures can be obtained from the crystal structure data by applying the quasi-harmonic Debye model.
55,56 Vs is the velocity of sound and is approximately equal to
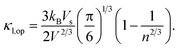
, where
B is the bulk modulus and
d is the density. The optical phonon mode is in the form of
| |
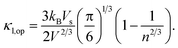 | (6) |
All of these required parameters can be obtained from ground-state calculations.
3 Results and discussion
3.1 Formation energy and structural stability
We firstly assessed the structural stability of the V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) compounds based on the calculated formation energy. The formation energy of these doped compounds is in the form of| | |
Ef = EV3Al1−xGax + xEAl − (EV3Al + xEGa),
| (7) |
where EV3Al1−xGax and EV3Al stand for the total energies of the doped compounds and the ideal V3Al per unit cell, EAl and EGa are the chemical potentials of Al and Ga atoms respectively, and x is the number of doped atoms. The calculated formation energies of all of the compounds are summarized in Table 1. Obviously, all the obtained values are negative, which indicates the thermodynamic stability of these doped compounds. The geometry structures of the V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) alloys in antiferromagnetic phase were then fully optimized based on energy minimization calculations. The configurations of the lowest energy were considered for further calculations. In Fig. 1, we present the total energy of V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) as a function of the strained lattice parameter with respect to the equilibrium parameter Δl/l0 ranging from −0.05 to 0.05. By fitting these calculated data to the third-order Birch–Murnaghan equation of state (EOS),57,58 the optimal lattice parameters for all the compounds were obtained and are shown in Fig. 1 and collected in Table 1. It is shown that the lattice constant decreases as the doping concentration increases from 0 to 1 in V3Al1−xGax, exhibiting good linear dependence and obeying Vegard’s law.59 The obtained equilibrium lattice constants for V3Al and V3Ga are consistent with other theoretical and experimental results,28,29 which indicates the reliability of the computational method used in this study. Unfortunately, we are not aware of available data to compare with our results for other doped compounds. In Table 1, we also present the anti-aligned atom-resolved magnetic moments (AMM). The AMM of V3 increases with an increase in the doping concentration whereas there is a decreasing trend for V2 due to the incorporation of Ga atoms in V3Al.
Table 1 The calculated formation energies (Ef) (in eV), lattice constants (a) with available results (in Å), and atom-resolved magnetic moments (AMM) (in μB) for V3Al1−xGax (x = 0, 0.25, 0.5, 0.75 and 1)
| |
x |
| 0 |
0.25 |
0.5 |
0.75 |
1 |
| Experimental results in ref. 29. Theoretical results in ref. 28. |
| Ef |
|
−0.049 |
−0.090 |
−0.124 |
−0.151 |
| a |
6.072 (6.092a, 6.06b) |
6.064 |
6.056 |
6.048 |
6.042 (6.03b) |
| AMM (V1) |
−1.527 |
−1.509 |
−1.482 |
−1.460 |
−1.446 |
| AMM (V2) |
1.527 |
1.509 |
1.482 |
1.460 |
1.446 |
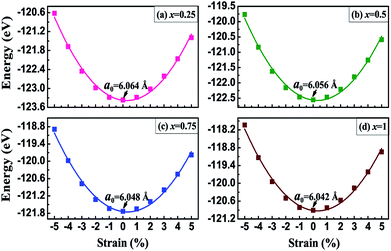 |
| | Fig. 1 The total energy as a function of the uniaxial strain Δl/l0 with Δl = l − l0 for V3Al1−xGax alloys where (a) x = 0.25, (b) x = 0.5, (c) x = 0.75, and (d) x = 1. | |
3.2 Mechanical stability and elastic properties
The three independent elastic constants (C11, C12, and C44) for V3Al1−xGax (x = 0, 0.25, 0.5, 0.75 and 1) are presented as a function of the doping concentration in Fig. 2 and Table 2. The considered compounds satisfy the mechanical stability criteria (1) and hence are mechanically stable. As is seen in Fig. 2, C12 increases monotonically with the doping concentration, to which C11 shows opposite variation. Meanwhile, C44 is kept almost unvaried with the concentration of Ga. The obtained bulk modulus (B), shear modulus (G), and Young’s modulus (E) are also shown in Fig. 2. It is obvious that the value of B shows an increasing trend as the doping concentration increases from 0 (V3Al) to 1 (V3Ga), indicating that it is more and more difficult to compress the listed compounds. The largest shear modulus (G) for V3Al among all of the compounds means that V3Al can withstand the largest shear strain. As is well known, the Young’s modulus (E), defined as the ratio of stress and strain, is used to predict the stiffness of a material. The descending E value of these compounds manifests that their stiffness becomes weaker with an increasing x. The ratio between the bulk modulus and the shear modulus (B/G) is used to provide a measure of ductility or brittleness of a material. When B/G is larger than 1.75, the material is ductile, otherwise it is a brittle material. Our calculated B/G values for the five alloys are all above 1.75, indicating that they are prone to be ductile.
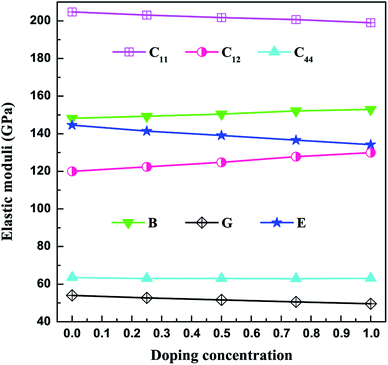 |
| | Fig. 2 Elastic constants and moduli as a function of the doping concentration. | |
Table 2 Calculated elastic constants (Cij) and moduli (B, G, and E) (all in GPa), and Grüneisen constants (γ) for V3Al1−xGax (x = 0, 0.25, 0.5, 0.75 and 1)
| x |
C11 |
C12 |
C44 |
B |
G |
B/G |
E |
γ |
| 0 |
204.801 |
119.963 |
63.568 |
148.242 |
54.053 |
2.743 |
144.587 |
0.337 |
| 0.25 |
203.056 |
122.354 |
62.968 |
149.255 |
52.679 |
2.833 |
141.400 |
0.342 |
| 0.5 |
201.735 |
124.807 |
62.956 |
150.450 |
51.668 |
2.912 |
139.082 |
0.346 |
| 0.75 |
200.722 |
127.786 |
62.930 |
152.098 |
20.559 |
3.008 |
136.548 |
0.350 |
| 1 |
198.977 |
129.906 |
63.103 |
152.930 |
49.545 |
3.087 |
134.149 |
0.354 |
3.3 Electronic properties
Within the crystal structures at their equilibrium lattice constants, we further calculated the band structures and density of states (DOS) for the V3Al1−xGax (x = 0, 0.25, 0.5, 0.75 and 1) compounds. Fig. 3 shows the band structures and DOS for x = 0 (V3Al) and x = 1 (V3Ga). It can be seen from the left panel that the conduction band edge is very close to the valence band edge, forming narrow bandgaps of 0.08 eV (x = 0) and 0.06 eV (x = 1). The obtained bandgap values are both less than 0.1 eV, and therefore V3Al and V3Ga are antiferromagnetic gapless semiconductors.29 The experimental verification29 of such antiferromagnetic gapless semiconducting behavior of V3Al confirms the reliability of our calculations. In the right column of Fig. 3, the minimum of the conduction band is mainly derived from the d–d hybridization between different V atoms and the maximum of the valence band is mostly contributed by the 3d states of V atoms that possess positive magnetic moment. We then plotted the band structures and density of states for the doped systems (x = 0.25, 0.5 and 0.75) in Fig. 4. The change of the valence band maximum (VBM) and the conduction band minimum (CBM) with Ga substitution creates a small direct bandgap of 0.04 eV for all of these doped systems, which is smaller than those of V3Al and V3Ga. Such a small bandgap implies that all of the doped systems exist as gapless semiconductors. It can be seen from the DOS for these three doped systems that the states higher than the minimum of the conduction band are ascribed to the 3d orbital of the V atoms with a negative magnetic moment whereas the 3d state hybridization between the other two V atoms forms most of that lower than the maximum of the valence bands. In addition, the energy band near the VBM and CBM of the doped systems that is flatter than that of V3Al suggests enhanced effective masses for all of the doped systems compared to V3Al.
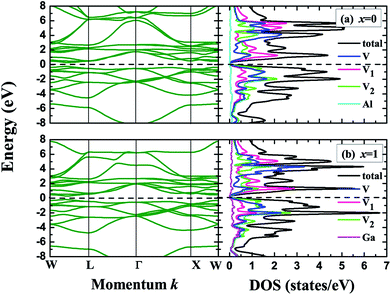 |
| | Fig. 3 Band structures (left), total and atom-projected density of states (right) for (a) x = 0 (V3Al) and (b) x = 1 (V3Ga). The dashed lines denote the Fermi levels. | |
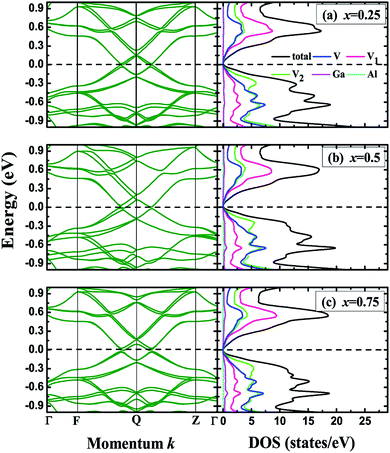 |
| | Fig. 4 Band structures (left), total and atom-projected density of states (right) for (a) x = 0.25, (b) x = 0.5 and (c) x = 0.75. The dashed lines denote the Fermi levels. | |
3.4 Thermoelectric properties
With the help of deformation potential theory, the obtained carrier relaxation times (τ) of V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) for electrons and holes are summarized in Table 3, together with the elastic constants (C), deformation potential constants (E), and effective masses (m*). The values of effective mass for electrons are smaller than those for holes in all of the systems, which is mainly derived from the sharper energy band around the CBM as shown in Fig. 3 and 4. The varying effective mass as the doping concentration (x) increases from 0 to 1 in V3Al1−xGax is due to the significant influence on band structures made by substituting Ga for Al. Typically, τ = 493 fs for n-type V3Al, and is almost 5 times as high as that for n-type V3Al0.25Ga0.75, and τ for p-type V3Al is 273 fs, which is about 2.7 times higher than that for p-type V3Al0.25Ga0.75. The low relaxation time in these Ga-containing materials results from the spatially localized nature of the transition metal 3d orbital.60 The experimental Néel temperature for D03 V3Al is 600 K.29 A detailed study on the thermoelectric properties when the temperature ranges from 300 to 600 K was carried out in this section. However, theoretical computation showed that the Néel temperature for D03 V3Al is as high as 988 K due to the large antiferromagnetic exchange interactions.31 As a result, the thermoelectric properties at 900 K are also given for comparison.
Table 3 The calculated elastic constants (C), deformation potential constants (E), effective masses (m*), and obtained relaxation times (τ) at room temperature
| x |
Carrier type |
C |
E (eV) |
m* (me) |
τ (fs) |
| 0.25 |
Electron |
1.459 |
27.595 |
0.071 |
355.602 |
| Hole |
1.459 |
28.420 |
0.082 |
268.294 |
| 0.5 |
Electron |
1.471 |
27.241 |
0.129 |
150.160 |
| Hole |
1.471 |
27.683 |
0.132 |
139.793 |
| 0.75 |
Electron |
1.483 |
26.575 |
0.166 |
108.191 |
| Hole |
1.483 |
26.967 |
0.172 |
100.298 |
| 1 |
Electron |
1.498 |
26.560 |
0.153 |
123.751 |
| Hole |
1.498 |
26.455 |
0.171 |
106.129 |
Fig. 5 shows the carrier concentration (n) dependence of the Seebeck coefficient (S) and the power factor (PF) at the temperatures of 300, 450, 600, and 900 K for the V3Al1−xGax (x = 0, 0.25, 0.5, 0.75 and 1) compounds. The absolute value of S can reach a peak at a particular concentration for both p-type and n-type systems with an increasing n. The peak height becomes low and shifts slightly towards the higher carrier concentration with the enhancement of the temperature. It is obvious to find that the peak of the Seebeck coefficient at 300 K becomes higher with increasing Ga content in V3Al1−xGax. In addition, the highest absolute values of the Seebeck coefficient are obtained with x = 1 for both p-type and n-type systems. The peak values are 128.51 (x = 0) and 166.04 μV K−1 (x = 1) for p-type systems, and −112.57 (x = 0) and −151.33 μV K−1 (x = 1) for n-type systems. This indicates that the D03 V3Ga compound may have more favorable thermoelectric performance than V3Al. It is clear that the calculated power factor first increases to a maximum and then is reduced with a further increase in the carrier concentration and it is expected that PF reaches the second maximum at high n for all of the n-type systems at room temperature. The peak location gets smaller and shifts to the high carrier concentration range with increasing temperature. As the doping concentration increases from 0 to 0.75, the increased effective mass leads to a higher Seebeck coefficient but contributes more to decreased carrier mobility. Therefore, the values of PF for the doped systems distinctly decrease with increasing effective mass. When m* is decreased in V3Ga (x = 1), the optimal power factor increases. The thermal conductivities (κ) and figures of merit (zT) as a function of the carrier concentration (n) at the temperatures of 300, 450, 600, and 900 K for the V3Al1−xGax (x = 0, 0.25, 0.5, 0.75 and 1) compounds are shown in Fig. 6. The κ values of the p-type systems are smaller than those of the n-type ones, which indicates that the thermoelectric performances of the n-type systems could be less favorable than those of the p-type ones. Fortunately, the increasing Ga content causes rapidly decreased total thermal conductivity over the measured temperatures due to the significant decrease in the lattice thermal conductivity. As a result, Ga doping of V3Al1−xGax is an effective way to reduce the κ of V3Al. By inserting calculated thermoelectric transport parameters into zT = S2σT/κ, we can evaluate the thermoelectric performances of all of these compounds. The p-type systems exhibit larger zT values than the n-type ones at 300, 450, and 600 K, and it is completely different when the temperature is 900 K, at which the largest zT value is obtained for the n-type system. This indicates that good thermoelectric properties for all of the five compounds can be realized in p-type systems at 300, 450, and 600 K. At the relatively high temperature of 900 K, n-type compounds can be used as promising thermoelectric materials. When the temperature is varied from 300 to 900 K, the maximal value of zT firstly increases and then decreases. The optimal zT values were 0.319 (x = 0), 0.298 (x = 0.25), 0.276 (x = 0.5), 0.264 (x = 0.75), and 0.298 (x = 1) for p-type systems at 600 K and they were 0.297 (x = 0), 0.290 (x = 0.25), 0.267 (x = 0.5), 0.262 (x = 0.75), and 0.280 (x = 1) respectively for n-type systems. As discussed above, the changed band structure induced by Ga substitution leads to greatly decreased thermal conductivity although there is an undesirable decrease in power factor. So, an enhanced zT could be anticipated in the Ga doping of V3Al1−xGax. It should be pointed out that zT peaks at room temperature are significantly enhanced in some of the Ga doping systems. The highest obtained zT values were 0.268 (x = 0.25) and 0.275 (x = 1) for p-type systems, and 0.244 (x = 0.25) and 0.243 (x = 1) for n-type ones. Otherwise, the maximal zT for pure V3Al is 0.259 (p-type) and 0.242 (n-type). Thus, in spite of having smaller power factors than pure V3Al, V3Al0.75Ga0.25 and V3Ga have higher zT values because of the larger S and lower κ. As a result, the thermoelectric performance of V3Al can be effectively improved by Ga doping. In Fig. 7, we present the figure of merit (zT) as a function of the temperature (T) for both the n-type and p-type V3Al1−xGax (x = 0, 0.25, 0.5, 0.75 and 1) compounds. Four optimal doping concentrations were chosen based on the maximum zT at 300, 450, 600, and 900 K. From the variation of the figure of merit with temperature, the values of T at which zT achieves the maxima are higher with increasing carrier concentration and lies in the range of 500 to 700 K. As such, p-type systems exhibit favorable TE performance even at low temperatures.
 |
| | Fig. 5 The Seebeck coefficient (S) ((a–e) are for n-type systems and (f–j) are for p-type systems) and the power factor (PF) ((k–o) are for n-type systems and (p–t) are for p-type systems) for V3Al1−xGax (x = 0, 0.25, 0.5, 0.75 and 1) as a function of the carrier concentration at temperatures of 300, 450, 600, and 900 K. Solid and dashed lines refer to results for n-type and p-type systems, respectively. | |
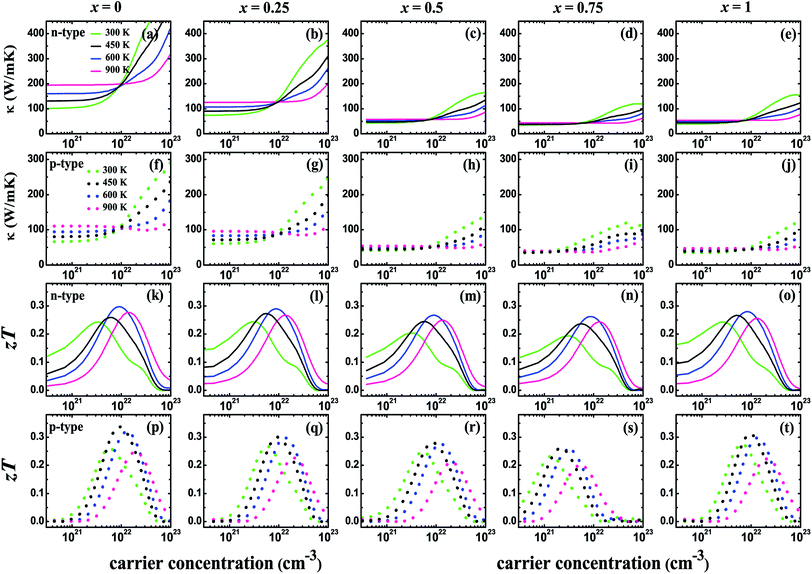 |
| | Fig. 6 The thermal conductivity (κ) ((a–e) are for n-type systems and (f–j) are for p-type systems) and figure of merit (zT) ((k–o) are for n-type systems and (p–t) are for p-type systems) for V3Al1−xGax (x = 0, 0.25, 0.5, 0.75 and 1) as a function of the carrier concentration at temperatures of 300, 450, 600, and 900 K. Solid and dashed lines refer to results for n-type and p-type systems, respectively. | |
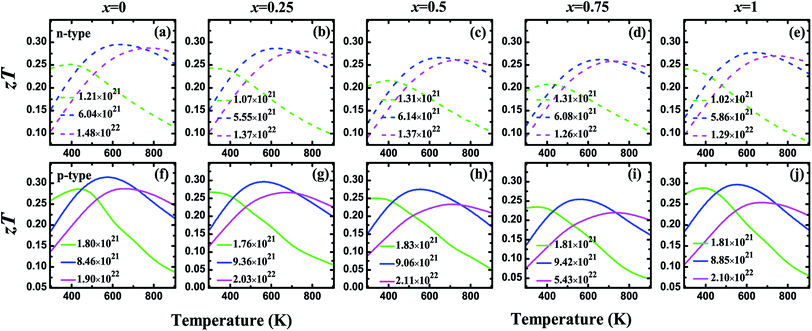 |
| | Fig. 7 The figure of merit (zT) as a function of temperature for n-type (a–e) and p-type (f–j) V3Al1−xGax (x = 0, 0.25, 0.5, 0.75 and 1) at four different optimal carrier concentrations. Solid and dashed lines refer to results for n-type and p-type systems, respectively. | |
4 Conclusions
In this work, structural and mechanical stability, electronic structure and transport properties of V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) compounds have been investigated and compared with those of V3Al based on density functional theory combined with semi-classical Boltzmann theory. All of the studied systems were thermodynamically and mechanically stable. These compounds show narrow energy gaps of 0.04 eV (x = 0.25, 0.5 and 0.75) and 0.06 eV (x = 1) and exist as antiferromagnetic gapless semiconductors. Ga substitution in pure V3Al makes the energy band near the CBM and VBM a little flatter, which results in an enhanced effective mass and a decreased power factor, but contributes more to decreased thermal conductivity. Thus, the maximal zT is enhanced from 0.242 (n-type) and 0.259 (p-type) to 0.244 (x = 0.25) and 0.243 (x = 1) for n-type systems and 0.268 (x = 0.25) and 0.275 (x = 1) for p-type systems at room temperature.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 11875226 and 11874306, the Natural Science Foundation of Chongqing under Grant No. CSTC-2017jcyjBX0035, and the Postgraduates’ Research and Innovation Project of Chongqing No. CYB17077.
Notes and references
- G. D. Mahan and J. O. Sofo, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 7436–7439 CrossRef CAS.
- F. J. DiSalvo, Science, 1999, 285, 703–706 CrossRef CAS.
- S. Chen and Z. F. Ren, Mater. Today, 2013, 16, 387–395 CrossRef CAS.
- M. Schwall and B. Balke, Appl. Phys. Lett., 2011, 98, 042106 CrossRef.
- C. Uher, J. Yang, S. Hu, D. T. Morelli and G. P. Meisner, Phys. Rev. B, 2009, 59, 8615–8621 CrossRef.
- W. Xie, Q. Jin and X. Tang, J. Appl. Phys., 2008, 103, 043711 CrossRef.
- M. Zhou, L. D. Chen, C. D. Feng, D. L. Wang and J. F. Li, J. Appl. Phys., 2007, 101, 113714 CrossRef.
- C. Uher, J. Yang, S. Hu, D. T. Morelli and G. P. Meisner, Phys. Rev. B, 1999, 59, 8615–8621 CrossRef CAS.
- G. Joshi, R. He, M. Engber, G. Samsonidze, T. Pantha, E. Dahal, K. Dahal, J. Yang, Y. C. Lan, B. Kozinsky and Z. F. Ren, Energy Environ. Sci., 2014, 7, 4070–4076 RSC.
- S. Bhattacharya, T. M. Tritt, Y. Xia, V. Ponnambalam, S. J. Poon and N. Thadhani, Appl. Phys. Lett., 2002, 81, 43–45 CrossRef CAS.
- C. Yu, T. J. Zhu, R. Z. Shi, Y. Zhang, X. B. Zhao and J. He, Acta Mater., 2009, 57, 2757–2764 CrossRef CAS.
- L. Chen, S. Gao, X. Zeng, A. M. Dehkordi, T. M. Tritt and S. J. Poon, Appl. Phys. Lett., 2015, 107, 041902 CrossRef.
- S. Sakurada and N. Shutoh, Appl. Phys. Lett., 2005, 86, 082105 CrossRef.
- M. Schwall and B. Balke, Phys. Chem. Chem. Phys., 2013, 15, 1868 RSC.
- C. G. Fu, S. Q. Bai, Y. T. Liu, Y. S. Tang, L. D. Chen, X. B. Zhao and T. J. Zhu, Nat. Commun., 2015, 6, 8144 CrossRef PubMed.
- C. Fu, T. Zhu, Y. Liu, H. Xiea and X. Zhao, Energy Environ. Sci., 2015, 8, 216 RSC.
- Y. Nishino, S. Deguchi and U. Mizutani, Phys. Rev. B, 2006, 74, 115115 CrossRef.
- M. Mikami, Y. Kinemuchi, K. Ozaki, Y. Terazawa and T. Takeuchi, J. Appl. Phys., 2012, 111, 093710 CrossRef.
- K. Renard, A. Mori, Y. Yamada, S. Tanaka, H. Miyazaki and Y. Nishino, J. Appl. Phys., 2014, 115, 033707 CrossRef.
- T. Zou, T. Jia, W. Xie, Y. Zhang, M. Widenmeyer, X. Xia and A. Weidenkaff, Phys. Chem. Chem. Phys., 2017, 19, 18273–18278 RSC.
- I. Pallecchi, M. Pani, F. Ricci, S. Lemal, D. I. Bilc, P. Ghosez, C. Bernini, N. Ardoino, G. Lamura and D. Marre, Phys. Rev. Mater., 2018, 2, 075403 CrossRef.
- M. Vasundhara, V. Srinivas and V. V. Rao, Phys. Rev. B, 2008, 77, 224415 CrossRef.
- H. Miyazaki, S. Tanaka, N. Ide, K. Soda and Y. Nishino, Mater. Res. Express, 2014, 1, 015901 CrossRef.
- H. Miyazaki, M. Inukai and Y. Nishino, J. Appl. Phys., 2016, 120, 125106 CrossRef.
- X. M. Li, L. Tao, Z. F. Chen, H. Fang, X. S. Li, X. R. Wang, J. B. Xu and H. W. Zhu, Appl. Phys. Rev., 2017, 4, 021306 Search PubMed.
- P. Qiu, J. Yang, X. Huang, X. Chen and L. Chen, Appl. Phys. Lett., 2010, 96, 152105 CrossRef.
- M. L. C. Buffon, G. Laurita, L. Lamontagne, E. E. Levin, S. Mooraj, D. L. Lloyd, N. White, T. M. Pollock and R. Seshadri, J. Phys.: Condens. Matter, 2017, 29, 405702 CrossRef PubMed.
- G. Y. Gao and K. L. Yao, Appl. Phys. Lett., 2013, 103, 232409 CrossRef.
- M. E. Jamer, B. A. Assaf, G. E. Sterbinsky, D. Arena, L. H. Lewis, A. A. Saul, G. Radtke and D. Heiman, Phys. Rev. B, 2015, 91, 094409 CrossRef.
- X. R. Chen, Y. H. Huang and H. Chen, RSC Adv., 2017, 7, 44647–44654 RSC.
- I. Galanakis, S. Tirpanci, K. Ozdogan and E. Sasioglu, Phys. Rev. B, 2016, 94, 064401 CrossRef.
- Y. L. Han, Z. B. Chen, M. Q. Kuang, Z. H. Liu, X. J. Wang and X. T. Wang, Results Phys., 2019, 12, 435–446 CrossRef.
- P. E. Blochl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B, 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- X. R. Chen, M. M. Zhong, Y. Feng, Y. Zhou, H. K. Yuan and H. Chen, Phys. Status Solidi B, 2015, 252, 2830–2839 CrossRef CAS.
- Y. Li, H. K. Yuan, J. H. Xia, G. L. Zhang, M. M. Zhong, A. L. Kuang, G. Z. Wang, X. R. Zheng and H. Chen, Eur. Phys. J.: Appl. Phys., 2015, 70, 31001 CrossRef.
- E. Haque and M. A. Hossain, Results Phys., 2018, 10, 458–465 CrossRef.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–355 CrossRef.
- G. V. Sinko and N. A. Smirnov, J. Phys.: Condens. Matter, 2002, 14, 6989–7005 CrossRef CAS.
- S. Yip, J. Li, M. J. Tang and J. G. Wang, J. Mater. Sci. Eng. A, 2001, 317, 236–240 CrossRef.
- A. N. Gandi and U. Schwingenschlogl, Chem. Mater., 2014, 26, 6628–6637 CrossRef CAS.
- V. K. Gudelli, V. Kanchana, G. Vaitheeswaran, D. J. Singh, A. Svane, N. E. Christensen and S. D. Mahanti, Phys. Rev. B, 2015, 92, 045206 CrossRef.
- S. Q. Hao, F. Y. Shi, V. P. Dravid, M. G. Kanatzidis and C. Wolverton, Chem. Mater., 2016, 28, 3218–3226 CrossRef CAS.
- K. P. Ong, D. J. Singh and P. Wu, Phys. Rev. B, 2011, 83, 115110 CrossRef.
- A. J. Hong, L. Li, R. He, J. J. Gong, Z. B. Yan, K. F. Wang, J. M. Liu and Z. F. Ren, Sci. Rep., 2016, 6, 22778 CrossRef CAS PubMed.
- Y. Q. Cai, G. Zhang and Y. W. Zhang, J. Am. Chem. Soc., 2014, 136, 6269–6275 CrossRef CAS PubMed.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72–80 CrossRef CAS.
- M. A. Green, J. Appl. Phys., 1990, 67, 2944–2954 CrossRef CAS.
- J. Yan, P. Gorai, B. Ortiz, S. Miller, S. A. Barnett, T. Mason, V. Stevanovic and E. S. Toberer, Energy Environ. Sci., 2015, 8, 983–994 RSC.
- J. Callaway, Phys. Rev., 1959, 113, 1046–1051 CrossRef CAS.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843–15852 RSC.
- E. Francisco, J. M. Recio, M. A. Blanco, A. M. Pendas and A. Costales, J. Phys. Chem. A, 1998, 102, 1595–1601 CrossRef CAS.
- A. Zevalkink, D. M. Smiadak, J. L. Blackburn, A. J. Ferguson, M. L. Chabinyc, O. Delaire, J. Wang, K. Kovnir, J. Martin, L. T. Schelhas, T. D. Sparks, S. D. Kang, M. T. Dylla, G. J. Snyder, B. R. Ortiz and E. S. Toberer, Appl. Phys. Rev., 2018, 5, 021303 Search PubMed.
- F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247 CrossRef CAS.
- F. Birch, Phys. Rev., 1947, 71, 809–824 CrossRef CAS.
- L. Vegard, Proc. Natl. Acad. Sci. U. S. A., 1921, 5, 17–26 CAS.
- J. Yang, P. Qiu, R. Liu, L. Xi, S. Zheng, W. Zhang, L. Chen, D. J. Singh and J. H. Yang, Phys. Rev. B, 2011, 84, 235205 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Hong Chen
and
Hong Chen *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Ω−1 cm−1),4–7 which are attributed to their narrow bands associated to high effective masses. Nevertheless, their relatively high thermal conductivities lead to their low thermoelectric efficiencies. In order to decrease the lattice thermal conductivity which is the predominant contribution to the thermal conductivity,8 some efforts have been made by synthesizing compounds with complicated structures by nanostructuring, forming nanocomposites, and isoelectronic alloying,3 which enhances the phonon scattering by point defects due to mass differences (mass fluctuations) and size differences (strain field impurities) between the impurity atoms and the host atoms. Typically, a zT ∼ 1 can be achieved for the nanostructured p-type Nb0.6Ti0.4FeNiSb0.95Sn0.05 composition near 973 K with a cost-effective mass-production nanocomposite approach.9 The thermal conductivity (κ) of a TiNiSn0.95Sb0.05 sample synthesized by ball milling and shock compaction can drop from 10.6 to 3.7 W m−1 K−1 by reducing the grain size diameter of the sample from ∼10 to 1 μm.10 The isoelectronic substitution of Zr for Hf in HfNiSn-based alloys remarkably reduced the lattice thermal conductivity and a zT ∼ 1.0 was achieved at 1000 K for Hf0.6Zr0.4NiSn0.98Sb0.02 (ref. 11) and an even higher zT ∼ 1.2 for Hf0.6Zr0.4NiSn0.995Sb0.005.12 Record-high zT values have been obtained for n-type Ti0.5Zr0.25Hf0.025NiSn0.998Sb0.002 (zT ∼ 1.5 at 700 K,13 zT ∼ 1.2 at 830 K (ref. 14)) and for p-type FeNb0.86Hf0.14Sb (zT ∼ 1.5 at 1200 K (ref. 15)) and FeTi0.2Nb0.8Sb (zT ∼ 1.1 at 1100 K (ref. 16)). In addition, semiconducting full-Heuslers with 24 valence electrons are other remarkable candidates for moderate temperature thermoelectric modules. Although only low zT values of 0.1–0.2 were achieved17–19 in the full-Heusler alloys due to lower density of states close to the Fermi level compared to half-Heusler alloys, a significant edge of improvement exists if the thermal conductivity is reduced and PF is further increased via manipulation of the electronic properties. Hole-type doping by Mn substitution at the Fe site and electron-type doping by Sb substitution at the Sn site have been explored in Fe2TiSn samples prepared by arc melting plus spark plasma sintering or annealing. The remarkable PF ∼ 0.4 mW m−1 K−2 in Fe2−xMnxTiSn (x = 0.0185)20 and PF ∼ 1.3 mW m−1 K−2 in FeTiSn1−xSbx (x = 0.1)21 at room temperature indicated a more than double increase in PF at room temperature in the doped samples compared to that of the undoped one, which has been attributed to a strong resonant level induced by doped atoms near the Fermi level. Hole and isoelectronic doped Fe2VAl by Ta substitution both at the Al19,22,23 and at the V site23,24 have been demonstrated to exhibit power factors in the range of 5–9 mW m−1 K−2 above room temperature.
000 Ω−1 cm−1),4–7 which are attributed to their narrow bands associated to high effective masses. Nevertheless, their relatively high thermal conductivities lead to their low thermoelectric efficiencies. In order to decrease the lattice thermal conductivity which is the predominant contribution to the thermal conductivity,8 some efforts have been made by synthesizing compounds with complicated structures by nanostructuring, forming nanocomposites, and isoelectronic alloying,3 which enhances the phonon scattering by point defects due to mass differences (mass fluctuations) and size differences (strain field impurities) between the impurity atoms and the host atoms. Typically, a zT ∼ 1 can be achieved for the nanostructured p-type Nb0.6Ti0.4FeNiSb0.95Sn0.05 composition near 973 K with a cost-effective mass-production nanocomposite approach.9 The thermal conductivity (κ) of a TiNiSn0.95Sb0.05 sample synthesized by ball milling and shock compaction can drop from 10.6 to 3.7 W m−1 K−1 by reducing the grain size diameter of the sample from ∼10 to 1 μm.10 The isoelectronic substitution of Zr for Hf in HfNiSn-based alloys remarkably reduced the lattice thermal conductivity and a zT ∼ 1.0 was achieved at 1000 K for Hf0.6Zr0.4NiSn0.98Sb0.02 (ref. 11) and an even higher zT ∼ 1.2 for Hf0.6Zr0.4NiSn0.995Sb0.005.12 Record-high zT values have been obtained for n-type Ti0.5Zr0.25Hf0.025NiSn0.998Sb0.002 (zT ∼ 1.5 at 700 K,13 zT ∼ 1.2 at 830 K (ref. 14)) and for p-type FeNb0.86Hf0.14Sb (zT ∼ 1.5 at 1200 K (ref. 15)) and FeTi0.2Nb0.8Sb (zT ∼ 1.1 at 1100 K (ref. 16)). In addition, semiconducting full-Heuslers with 24 valence electrons are other remarkable candidates for moderate temperature thermoelectric modules. Although only low zT values of 0.1–0.2 were achieved17–19 in the full-Heusler alloys due to lower density of states close to the Fermi level compared to half-Heusler alloys, a significant edge of improvement exists if the thermal conductivity is reduced and PF is further increased via manipulation of the electronic properties. Hole-type doping by Mn substitution at the Fe site and electron-type doping by Sb substitution at the Sn site have been explored in Fe2TiSn samples prepared by arc melting plus spark plasma sintering or annealing. The remarkable PF ∼ 0.4 mW m−1 K−2 in Fe2−xMnxTiSn (x = 0.0185)20 and PF ∼ 1.3 mW m−1 K−2 in FeTiSn1−xSbx (x = 0.1)21 at room temperature indicated a more than double increase in PF at room temperature in the doped samples compared to that of the undoped one, which has been attributed to a strong resonant level induced by doped atoms near the Fermi level. Hole and isoelectronic doped Fe2VAl by Ta substitution both at the Al19,22,23 and at the V site23,24 have been demonstrated to exhibit power factors in the range of 5–9 mW m−1 K−2 above room temperature.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.28,29,31,32 In the Wyckoff coordination, Al atoms are located at the 4a (0,0,0) site, whereas the position of the V atoms is complicated. There are 12 V atoms in the unit cell of the V3Al compound, 8 of which occupy the 4b (0.5,0.5,0.5) and the other 4 V atoms are at 4c (0.25,0.25,0.25) and 4d (0.75,0.75,0.75) (labeled V1 and V2). The doping concentrations of x = 0.25, 0.5, 0.75 and 1 in the V3Al1−xGax compounds mean that 1, 2, 3 or 4 Al atoms are substituted by Ga atoms in the V3Al unit cell. All properties of V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) were calculated from first-principles within the framework of the projector augmented wave (PAW) method33 as conducted using the package VASP.34–36 The generalized gradient approximation (GGA) and the Perdew–Burke–Ernzerhof (PBE)37 were adopted for the exchange–correlation energy of electrons. For all the structures, the plane wave cut-off energy and a Monkhorst–Pack k-mesh sample in the whole Brillouin zone were 560 eV and 15 × 15 × 15 respectively, which are the same as those used in our previous work for V3Al.30 For V, Al, and Ga, 3d34s2, 3s23p1, and 4s24p1 states are considered as the valence states. The atom position is fully relaxed until the magnitude of the energy change and the force acting on each atom are smaller than 10−5 eV and 0.01 eV Å−1. As shown in the previous work,30 V3Al is more stable in the AF phase, and therefore all the calculations were conducted for AF D03 Ga-doped V3Al.
m.28,29,31,32 In the Wyckoff coordination, Al atoms are located at the 4a (0,0,0) site, whereas the position of the V atoms is complicated. There are 12 V atoms in the unit cell of the V3Al compound, 8 of which occupy the 4b (0.5,0.5,0.5) and the other 4 V atoms are at 4c (0.25,0.25,0.25) and 4d (0.75,0.75,0.75) (labeled V1 and V2). The doping concentrations of x = 0.25, 0.5, 0.75 and 1 in the V3Al1−xGax compounds mean that 1, 2, 3 or 4 Al atoms are substituted by Ga atoms in the V3Al unit cell. All properties of V3Al1−xGax (x = 0.25, 0.5, 0.75 and 1) were calculated from first-principles within the framework of the projector augmented wave (PAW) method33 as conducted using the package VASP.34–36 The generalized gradient approximation (GGA) and the Perdew–Burke–Ernzerhof (PBE)37 were adopted for the exchange–correlation energy of electrons. For all the structures, the plane wave cut-off energy and a Monkhorst–Pack k-mesh sample in the whole Brillouin zone were 560 eV and 15 × 15 × 15 respectively, which are the same as those used in our previous work for V3Al.30 For V, Al, and Ga, 3d34s2, 3s23p1, and 4s24p1 states are considered as the valence states. The atom position is fully relaxed until the magnitude of the energy change and the force acting on each atom are smaller than 10−5 eV and 0.01 eV Å−1. As shown in the previous work,30 V3Al is more stable in the AF phase, and therefore all the calculations were conducted for AF D03 Ga-doped V3Al.
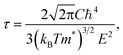
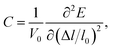
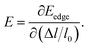
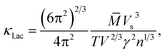
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) and V are the average mass and volume per atom respectively. n is the number of total atoms in the primitive cell. The value of the Grüneisen constant (γ) at different temperatures can be obtained from the crystal structure data by applying the quasi-harmonic Debye model.55,56 Vs is the velocity of sound and is approximately equal to
and V are the average mass and volume per atom respectively. n is the number of total atoms in the primitive cell. The value of the Grüneisen constant (γ) at different temperatures can be obtained from the crystal structure data by applying the quasi-harmonic Debye model.55,56 Vs is the velocity of sound and is approximately equal to 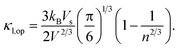 , where B is the bulk modulus and d is the density. The optical phonon mode is in the form of
, where B is the bulk modulus and d is the density. The optical phonon mode is in the form of