Open Access Article
Open Access ArticleChemical space exploration guided by deep neural networks†
Dmitry S. Karlov *a,
Sergey Sosnin
*a,
Sergey Sosnin ad,
Igor V. Tetko
ad,
Igor V. Tetko bc and
Maxim V. Fedorov
bc and
Maxim V. Fedorov ad
ad
aSkolkovo Institute of Science and Technology, Skolkovo Innovation Center, Moscow 143026, Russia. E-mail: d.karlov@skoltech.ru
bHelmholtz Zentrum München – Research Center for Environmental Health (GmbH), Institute of Structural Biology, Ingolstädter Landstraße 1, D-85764 Neuherberg, Germany
cBIGCHEM GmbH, Ingolstädter Landstraße 1, G. 60w, D-85764 Neuherberg, Germany
dSyntelly LLC, 42 Bolshoy Boulevard, Skolkovo Innovation Center, Moscow, 143026, Russia
First published on 11th February 2019
Abstract
A parametric t-SNE approach based on deep feed-forward neural networks was applied to the chemical space visualization problem. It is able to retain more information than certain dimensionality reduction techniques used for this purpose (principal component analysis (PCA), multidimensional scaling (MDS)). The applicability of this method to some chemical space navigation tasks (activity cliffs and activity landscapes identification) is discussed. We created a simple web tool to illustrate our work (http://space.syntelly.com).
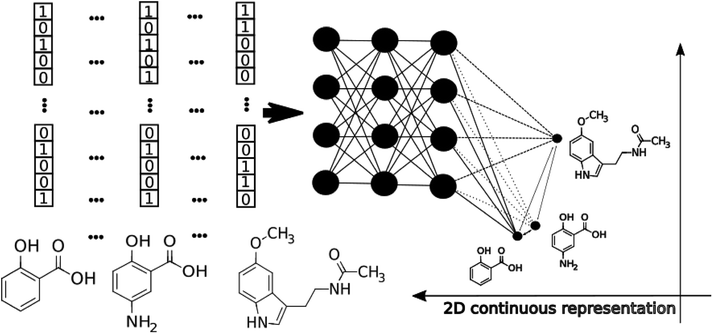
Chemical space is usually considered as the union of all feasible chemical compounds. While the number of such compounds is extremely high, it is estimated to be 1060 possible structures,1 only a small fraction of it can be processed and analyzed at the same time. Visual representation of the chemical space is growing in popularity as a technique used by medicinal chemists to have the better understanding of chemical data.2 Technically, it is an information-losing projection from multi-dimensional molecular space (commonly described by molecular descriptors, so-called descriptor space) into two- or three-dimensional space, in which humans can operate easily. The majority of chemical space visualization methods use two discrete procedures: (i) calculation of molecular descriptors (ii) performing a projection from descriptor space into a 2D plane or 3D volume by one of several known techniques.3 There is the option to combine different descriptors with different dimensionality reduction algorithms, however, sometimes authors of a visualization method propose a suitable combination of molecular descriptors and algorithms for better performance, e.g. GTM4 (developed by C. Bishop) may be successfully combined with ISIDA descriptors.5
The type and the length of the descriptor vector influences the details of the chemical representation, and the choice of the feature set is driven by the expected depth of description. Molecular quantum number (MQN)6 is an example of a simple molecular descriptor set consisting of atomic and bond counts and some other topological descriptors. Despite the fact that the size of the descriptor set is relatively short (42 descriptors), this method performed very well in the identification of the novel nAChR allosteric modulators.7 Alternatively one can use a fingerprint description of the molecular structure, which is a bit string where each bit indicates the existence of predefined substructure (MACCS Structural Keys; Symyx Software: San Ramon, CA, 2002.) or the certain atom types in the predefined atomic environment (ECFP fingerprints).8
A number of dimensionality reduction techniques were utilized for the processing of molecular databases and here we will briefly review the most important of them, commenting on their relative strengths and drawbacks.
The algorithm of Principal Component Analysis (PCA) performs an iterative search of directions with the highest variation in a multidimensional data space. Usually the first two components are easily interpretable and explain 60–80% of the whole variation in the data.2 PCA-based mapping is fast, deterministic, and new compounds may be easily mapped using the PC of an existing data set, but this method omits non-linear feature interactions9 and some map regions become overloaded with data.10 The method of Self-Organizing Maps (SOM)11,12 usually treats non-linearities in a better way, mapping the feature space to the low dimensional visualizable space. The Generative Topographic Mapping4 approach represents a probabilistic alternative to SOM.13 This approach was applied to large data set collections identifying desirable chemical space regions for drug design14 and was successfully used for large-scale SAR exploration.15 It is worth mentioning non-coordinate based approaches developed by the group of Jürgen Bajorath, which transform multidimensional chemical space to a graph with nodes representing chemical compounds, and edges connecting compounds within a specified similarity cut-off.16 The other approach, so-called Scaffold Trees, treat the chemical space as a tree where leaves represents individual chemical compounds and the intermediate nodes represents scaffolds and subscaffolds.17
A number of useful tools combining a variety of visualization approaches were created in the recent years. Stardrop (Optibrium Ltd., Cambridge, UK) and DataWarrior (http://openmolecules.org) combine a variety of visualization approaches with chemoinformatic data analysis. The CheS-Mapper18 tool, which is used for the visualization of chemical data sets in 3D space, provides both a number of chemical descriptors and several projection algorithms i.e. PCA, t-SNE, and also gives users the possibility to combine them.
The application of modern deep learning techniques began to be very popular and useful for QSAR/QSPR,19–21 developing novel approaches for molecular docking22,23 and force field development.24,25 Here we describe an application of deep feed-forward neural networks as a t-SNE mapper to the bioactivity data taken from a Database of Useful Decoys (DUDe)26 and the Trace Amine Associated Receptor (TAAR1) ligands visualization task. The workflow consists of three main stages. First, we trained a set of the mapper functions varying the perplexity level in the loss function with the overfitting controlled by the external test set (Fig. 1). Second, since the dimensionality reduction techniques lead to information loss, we trained a set of classifiers on the mapped 2D data and compared the resulting accuracy. Third, we provide the visualization and analysis of the TAAR1 data set taken from Pubchem.
1 Materials and methods
1.1 Data sets
1.2 Parametric t-SNE
Today's Big Data in chemistry requires new approaches to the processing and visualizing of data.30 The t-SNE approach, proposed by L. van der Maaten, has gained tremendous popularity in data visualization, however, it has two notable drawbacks: (i) it can not be applied to new data (in other words when a new portion of data is obtained the whole data set must be reevaluated again) (ii) the computational complexity of the distance calculation is quadratic which requires the usage of approximations (i.e. Barnes–Hut approach) for the analysis of large databases. In practice, even with the Barnes–Hut approximation, applying t-SNE to more than 105 compounds on modern computers is computationally unfeasible. To combat these problems we focused our attention on the parametric t-SNE algorithm that was proposed by the same author.31 In parametric t-SNE, a function which performs a mapping from the high-dimensional descriptor space to a low-dimensional space (2D or 3D) f: X → Y is a normal feed-forward neural network with trainable weights. It should be noted that in the original paper the authors used Restricted Boltzmann Machines as their mapping function because they provide a good speed of computation, however, nowadays feed-forward neural networks trained on GPUs can be feasibly used as an alternative. At the first stage of the algorithm a distance matrix should be computed using a task-relevant distance metric. Then each row of the distance matrix is transformed into the probability distribution:
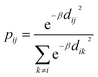 | (1) |
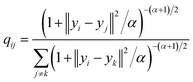 | (2) |
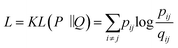 | (3) |
We tried two different distance metrics: Euclidean and Jaccard distances. Due to the fingerprints' sparsity the common approach of cosine distance is inconvenient for this task and in our experiments Euclidean distance tended to overestimate similarity among small molecules. Because of the possibility of performing the training process in batch mode it is not necessary to compute the distance matrix for the whole data set, which reduced computational time and memory consumption and allows the processing of very large data sets.
1.3 Machine learning methods
To compare the quality of mapping numerically, we built classification models with different machine learning methods on the base of 2D projections obtained by different methods. We used the implementations of these methods from scikit-learn.36 Below we present a brief description of each method that was used in our experiments.Support vector machines: is a machine learning method which is based on the construction of optimal separation hyperplanes in high-dimensional space.37 This method is widely used in chemoinformatics.
Random forest: is a method based on construction of a consensus model (a forest) of decision trees. Proposed by Breiman38 the method further gained popularity in chemoinformatics due to the efficiency and small number of tunable parameters.
XGBoost: is a variant gradient boosting schemes where each new tree (or other simple predictor) is trained to correct the residuals of previous trained predictors.39 After proper hyperparameter optimization this approach can achieve excellent results.
K-nearest neighbors: is method which yields a prediction as a weighted sum of data from the k closest data points in some descriptor space with certain metrics. This method is successfully used for small data sets.40
1.4 Dimensionality reduction methods
Principal component analysis: is an orthogonal linear transformation which transforms the data into a new coordinate system where the first direction of the greatest variance become the new coordinate axis.41 This iterative approach allows the creation of new orthogonal basis sets and gives 2–3 components which usually explain the majority of data variance.Multidimensional scaling: seeks the low-dimensional representation of high-dimensional data where distances in both representations are maximally close to each other.42
1.5 Validation protocols
To control overfitting during training our mapper ANN we used 10% of the data as test set. Stratified five-fold cross-validation was carried out to prevent overfitting and to compare the performance of the classification methods trained on the mapped data. For our multiclass classification models we calculated the accuracy of classification among all classes.2 Results and discussions
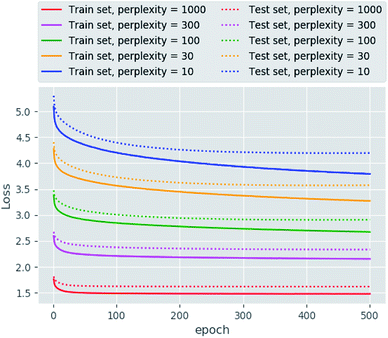
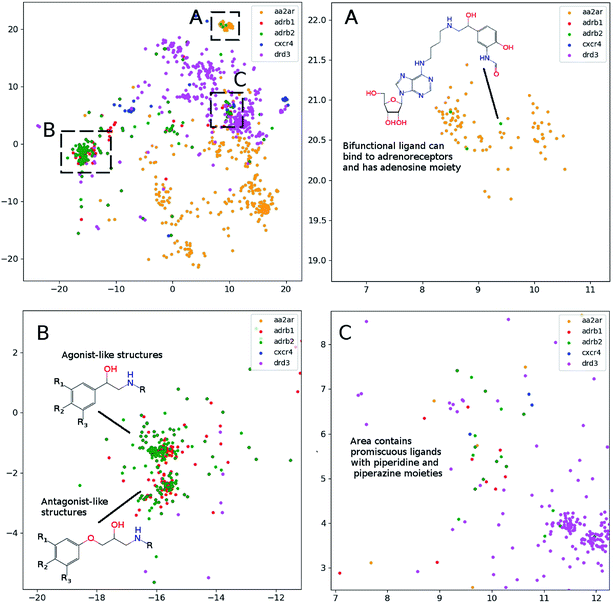
The main goal of good scientific visualization is to generate insight helpful in choosing the next step in the research. This is especially important for SAR exploration due to the fact that even small modifications of a scaffold may require additional synthetic efforts and one may want to correctly prioritize further modifications to explore interesting regions of the chemical space.43 Let us clarify which regions of the chemical space are interesting. First, we should mention the areas of chemical space where the activity changes only slightly upon gradual structural changes which may be considered as activity plateaus and are useful for ADME tuning in the course of lead optimization. Second, the regions where small structural changes lead to gradual changes in activity are called activity cliffs and associated with large SAR information content. The straightforward visualization and identification of such regions requires similarity preservation while mapping from high-dimensional descriptor space. Thus, the usage of the t-SNE objective perfectly meets this requirement. The learning curves are shown in Fig. 2. The lowest and the highest loss values were obtained for perplexity values equal to 1000 and 10, respectively, as one may expect. Interestingly, the same trend was found for the loss decay during training: perplexity values of 1000 leads to a larger decrease in loss in comparison to perplexity values of 10. Also we tried to optimize the α value in the loss formulation which lead to significant loss decay as compared to the fixed α = 1.0. Unfortunately, this parameter tended to zero during optimization on the ChEMBL data set. The decrease in this parameter means that the span of the map will increase allowing the map to occupy more area.In order to assess visualization performance we used data sets collected from DUDe28 which has been successfully used for assessment of molecular docking performance. Two subsets containing GPCR and nuclear receptors' ligands and having relatively high similarity inside each group were selected for analysis. It should be noted that GPCR and nuclear receptors' data sets are highly balanced in terms of class composition and contain information about 1480 and 2995 chemical compounds, respectively. Fig. 3 demonstrates the results of the neural network mapping for the GPCR ligand subset. The subgraph in the upper-left corner shows the overall view of the 2D representation. It should be noted that GPCR ligands used for analysis turned out to be highly separable and the overlap between classes is observed for highly similar receptors: β1 and β2 adrenergic receptors. Unfortunately, DUDe does not contain any information about the promiscuity of the active compounds but the cluster overlap may indicate such properties. Fig. 3(B) demonstrates the separation of the two clusters of β adrenergic receptors ligands: agonists and antagonists. Fig. 3(A) demonstrates the existence of the of the β2 adrenergic ligand (green) in adenosine A2 ligand cluster. Interestingly, all these ligands contain an adenosine moiety which explains the mapping results. Area C (Fig. 3(C)) shows the mixture of promiscuous ligands based on piperazine and piperidine scaffolds which can be found in different GPCR ligands (opioid, dopamine, serotonin receptors, etc.)
All dimensionality reduction techniques are often performed to get rid of noise in data but at the same time some information loss should be expected. Thus, we carried out the estimation of classification accuracy for two DUDe subsets containing GPCR and nuclear receptor ligands using widely known machine learning methods. The dimensionality of the data sets was reduced with PCA, MDS (Jaccard dissimilarity was used to construct the distance matrix) and pTSNE trained as discussed above. The results of the performance estimation are shown in Table 1. First, it should be noted that the best achieved accuracy differs between the used data sets probably due to the fact that the GPCR subset contains fewer classes. For all constructed models the best accuracy was achieved for the initial descriptors (ECFP6 fingerprints) as was expected, and the pTSNE dimensionality reduction technique significantly outperformed the other ones. The search for the optimal parameter set resulted in highly converged accuracies for methods on untransformed fingerprints. For example, the difference in accuracy is observed only in the third decimal place when applying kNN, SVM and XGBoost on the GPCR data set, implying near-optimal models prior to mapping. The parameter sets yielding the highest accuracies were relatively similar for different dimensionality reduction techniques and appeared to be quite different for the both data sets. For example, the number of neighbours to achieve the highest accuracy for kNN was 24 for the GPCR and 9 for NR data sets. Interestingly, the SVM method demonstrated good performance for the initial fingerprints and the results of PCA, while the application of non-linear dimensionality reduction techniques (pTSNE and MDS) yielded relatively worse performance. The XGBoost hyperparameter optimization resulted in a relatively similar set with variation only in the L2 regularization term, while the tree depth and the learning rate practically did not differ. It was found that the best value of the perplexity parameter is data set specific: 30 resulted in highest accuracy for the GPCR set after pTSNE dimensionality reduction while 100 was the best for nuclear receptor ligands. These results are consistent with the fact that a perplexity value of 30 is a good starting point for visualization and usually recommended.
| Descriptor set | ML method | Accuracy | |
|---|---|---|---|
| GPCR ligands | NR ligands | ||
| ECFP6 descriptors | kNN | 0.829 | 0.526 |
| SVM | 0.821 | 0.549 | |
| XGBoost | 0.821 | 0.540 | |
| Random forest | 0.788 | 0.537 | |
| pTSNE mapping (2D space) | kNN | 0.763 | 0.383 |
| SVM | 0.704 | 0.336 | |
| XGBoost | 0.764 | 0.394 | |
| Random forest | 0.745 | 0.360 | |
| PCA mapping (2 components) | kNN | 0.739 | 0.296 |
| SVM | 0.735 | 0.345 | |
| XGBoost | 0.743 | 0.360 | |
| Random forest | 0.735 | 0.349 | |
| MDS mapping (2D space) | kNN | 0.725 | 0.326 |
| SVM | 0.543 | 0.250 | |
| XGBoost | 0.712 | 0.333 | |
| Random forest | 0.707 | 0.328 | |
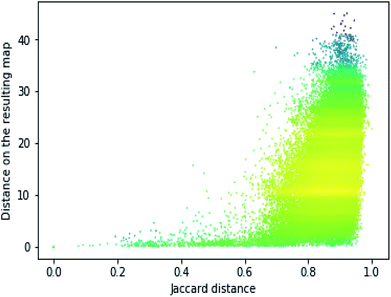
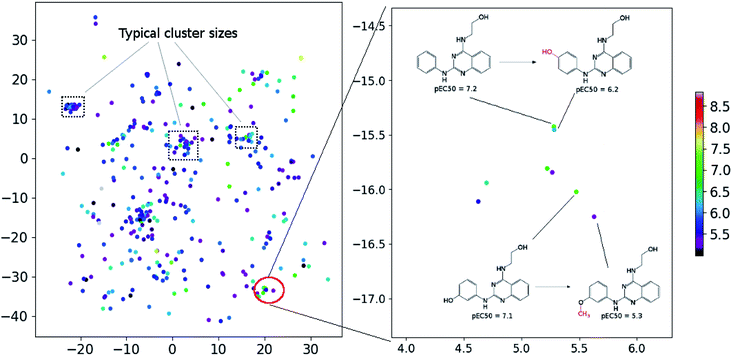
In order to assess the performance of the trained neural network to analyze the activity landscapes we used the TAAR1 receptor agonists' database collected from ChEMBL with measured activity in pEC50 and containing information about 376 chemical compounds. Let us compare the distance distribution in this data set in the original space and in the 2D mapped space (Fig. 4). First, the distribution practically does not depend on the perplexity level. Second, similar compounds (Jaccard distances within 0.1–0.5) are very close together and dissimilar compounds (Jaccard distances more than 0.6) can be at any distance on the map. We estimated the uncertainty of the mapping performing the forward pass of the network using weights obtained during the last 100 epochs of training and found that in average the point position remained within 0.5 for both axes. As one can notice from Fig. 5 (left) the typical cluster size lies within 2.0–3.0 and the compounds' distributions within the clusters remain relatively stable upon small perturbations in network weights near the local minimum. This is why one can easily analyze the activity landscapes. Unfortunately, the mapping does not guarantee that “very–very” similar compounds will be closer together than just “very” similar compounds as one can notice from Fig. 5 (right).
3 Conclusions
Understanding the internal relations in the chemical database is a key feature for the exploration of the chemical space to develop new substances with predefined properties. Visualization of the target chemical space by mapping from multidimensional descriptor space into space convenient to perceive is still a challenging task for chemoinformatics and computational medicinal chemistry. Unfortunately, Stochastic Neighbour Embedding (SNE) and its modification t-SNE which preserves the points' positions in the target space to be t-distributed are not widely used for chemoinformatics tasks possibly due to a number of problems: the high dimensionality of the initial descriptor space which is necessary to correctly describe chemical structure, computational cost, and non-deterministic results due to the stochastic nature of mapping are the most important ones. All these disadvantages can be solved using a parametric t-SNE approach which yields a neural-network-based function to map new portions of data. The speed of computation is comparable with other fast and widely used methods (PCA, MDS, etc.) and preserves more information compared with the mentioned methods. We hope that this approach will aid in the interpretation of structurally-conditioned biological properties of chemical compounds.Conflicts of interest
IVT is CEO of BIGCHEM GmbH, which licenses the OCHEM (http://ochem.eu) software. The other authors declared that they have no actual or potential conflicts of interests.Acknowledgements
This work has been carried out using computing resources of the federal collective usage center Complex for Simulation and Data Processing for Mega-science Facilities at NRC “Kurchatov Institute”, http://ckp.nrcki.ru. The authors are thankful to Michael Withnall for fruitful discussions. This study has been partially supported by ERA-CVD (http://era-cvd.eu) project “Cardio-Oncology”, BMBF 01KL1710.References
- C. M. Dobson, Nature, 2004, 432, 824–828 CrossRef CAS PubMed.
- D. I. Osolodkin, E. V. Radchenko, A. A. Orlov, A. E. Voronkov, V. A. Palyulin and N. S. Zefirov, Expert Opin. Drug Discovery, 2015, 10, 959–973 CrossRef PubMed.
- C. O. S. Sorzano, J. Vargas and A. P. Montano, arXiv:1403.2877 [cs, q-bio, stat], 2014.
- C. M. Bishop, M. Svensén and C. K. I. Williams, Neural Computation, 1998, 10, 215–234 CrossRef.
- I. I. Baskin, V. P. Solov’ev, A. A. Bagatur’yants and A. Varnek, J. Comput.-Aided Mol. Des., 2017, 31, 701–714 CrossRef CAS PubMed.
- J.-L. Reymond, R. van Deursen, L. C. Blum and L. Ruddigkeit, MedChemComm, 2010, 1, 30 RSC.
- J. J. Bürgi, M. Awale, S. D. Boss, T. Schaer, F. Marger, J. M. Viveros-Paredes, S. Bertrand, J. Gertsch, D. Bertrand and J.-L. Reymond, ACS Chem. Neurosci., 2014, 5, 346–359 CrossRef PubMed.
- R. C. Glem, A. Bender, C. H. Arnby, L. Carlsson, S. Boyer and J. Smith, IDrugs, 2006, 9, 199–204 Search PubMed.
- V. S. Rose, I. F. Croall and H. J. H. Macfie, Quant. Struct.-Act. Relat., 1991, 10, 6–15 CrossRef CAS.
- L. C. Blum, R. van Deursen and J.-L. Reymond, J. Comput.-Aided Mol. Des., 2011, 25, 637–647 CrossRef CAS PubMed.
- T. Kohonen, Biol. Cybern., 1982, 43, 59–69 CrossRef.
- M. Awale and J.-L. Reymond, J. Cheminf., 2016, 8, 25 Search PubMed.
- N. Kireeva, I. I. Baskin, H. A. Gaspar, D. Horvath, G. Marcou and A. Varnek, Mol. Inf., 2012, 31, 301–312 CrossRef CAS PubMed.
- H. A. Gaspar, I. I. Baskin, G. Marcou, D. Horvath and A. Varnek, J. Chem. Inf. Model., 2015, 55, 84–94 CrossRef CAS PubMed.
- S. Kayastha, R. Kunimoto, D. Horvath, A. Varnek and J. Bajorath, J. Comput.-Aided Mol. Des., 2017, 31, 961–977 CrossRef CAS PubMed.
- A. de la Vega de León and J. Bajorath, Future Med. Chem., 2016, 8, 1769–1778 CrossRef PubMed.
- A. Schuffenhauer, P. Ertl, S. Roggo, S. Wetzel, M. A. Koch and H. Waldmann, J. Chem. Inf. Model., 2007, 47, 47–58 CrossRef CAS PubMed.
- M. Gütlein, A. Karwath and S. Kramer, J. Cheminf., 2012, 4, 7 Search PubMed.
- I. Wallach, M. Dzamba and A. Heifets, arXiv:1510.02855 [cs, q-bio, stat], 2015.
- S. Sosnin, M. Misin, D. S. Palmer and M. V. Fedorov, J. Phys.: Condens. Matter, 2018, 30, 32LT03 CrossRef PubMed.
- Y. Xu, J. Pei and L. Lai, J. Chem. Inf. Model., 2017, 57, 2672–2685 CrossRef CAS PubMed.
- M. Ragoza, J. Hochuli, E. Idrobo, J. Sunseri and D. R. Koes, J. Chem. Inf. Model., 2017, 57, 942–957 CrossRef CAS PubMed.
- J. Hochuli, A. Helbling, T. Skaist, M. Ragoza and D. R. Koes, J. Mol. Graphics, 2018, 84, 96–108 CrossRef CAS PubMed.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 13890 CrossRef PubMed.
- K. Yao, J. E. Herr, D. W. Toth, R. Mckintyre and J. Parkhill, Chem. Sci., 2018, 9, 2261–2269 RSC.
- M. M. Mysinger, M. Carchia, J. J. Irwin and B. K. Shoichet, J. Med. Chem., 2012, 55, 6582–6594 CrossRef CAS PubMed.
- A. Gaulton, A. Hersey, M. Nowotka, A. P. Bento, J. Chambers, D. Mendez, P. Mutowo, F. Atkinson, L. J. Bellis, E. Cibrián-Uhalte, M. Davies, N. Dedman, A. Karlsson, M. P. Magariños, J. P. Overington, G. Papadatos, I. Smit and A. R. Leach, Nucleic Acids Res., 2017, 45, D945–D954 CrossRef CAS PubMed.
- M. M. Mysinger, M. Carchia, J. J. Irwin and B. K. Shoichet, J. Med. Chem., 2012, 55, 6582–6594 CrossRef CAS PubMed.
- S. Kim, P. A. Thiessen, E. E. Bolton, J. Chen, G. Fu, A. Gindulyte, L. Han, J. He, S. He, B. A. Shoemaker, J. Wang, B. Yu, J. Zhang and S. H. Bryant, Nucleic Acids Res., 2016, 44, D1202–D1213 CrossRef CAS PubMed.
- M. Withnall, H. Chen and I. V. Tetko, ChemMedChem, 2018, 13, 599–606 CrossRef CAS PubMed.
- L. van der Maaten, Proceedings of the Twelfth International Conference on Artificial Intelligence and Statistics, Hilton Clearwater Beach Resort, Clearwater Beach, Florida USA, 2009, pp. 384–391 Search PubMed.
- L. van der Maaten and G. Hinton, J. Mach. Learn. Res, 2008, 9, 2579–2605 Search PubMed.
- S. Kullback and R. A. Leibler, Ann. Math. Stat., 1951, 22, 79–86 CrossRef.
- S. Ioffe and C. Szegedy, arXiv:1502.03167 [cs], 2015.
- K. He, X. Zhang, S. Ren and J. Sun, arXiv:1502.01852 [cs], 2015.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res, 2011, 12, 2825–2830 Search PubMed.
- C. Cortes and V. Vapnik, Machine Learning, 1995, 20, 273–297 Search PubMed.
- L. Breiman, Machine Learning, 2001, 45, 5–32 CrossRef.
- T. Chen and C. Guestrin, arXiv: 1603.02754 [cs], 2016.
- S. B. Gunturi, K. Archana, A. Khandelwal and R. Narayanan, QSAR Comb. Sci., 2008, 27, 1305–1317 CrossRef CAS.
- C. Bishop, Pattern Recognition and Machine Learning, Springer, 2006 Search PubMed.
- J. B. Kruskal, Psychometrika, 1964, 29, 115–129 CrossRef.
- M. Vogt, Expert Opin. Drug Discovery, 2018, 13, 605–615 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra10182e |
| This journal is © The Royal Society of Chemistry 2019 |