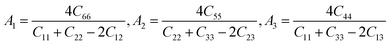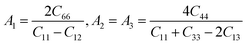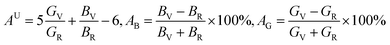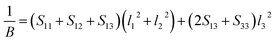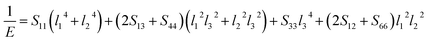DOI:
10.1039/C8RA08711C
(Paper)
RSC Adv., 2019,
9, 5302-5312
First-principles calculations of mechanical and thermodynamic properties of tetragonal Be12Ti
Received
21st October 2018
, Accepted 4th February 2019
First published on 12th February 2019
Abstract
The elastic and thermodynamic properties of tetragonal Be12Ti under high temperature and pressure are investigated by first-principles calculations based on pseudopotential plane-wave density functional theory (DFT) within the generalized gradient approximation (GGA) and quasi-harmonic approximation (QHA). The calculated lattice parameters and bulk modulus are in good agreement with the available experimental data. The calculated elastic constants of Be12Ti increase monotonously with increasing pressure, and the elastic stability criterion and the phonon dispersion calculation show that the Be12Ti crystal satisfies the mechanical and dynamic stability under applied pressure (0–100 GPa). The related mechanical properties such as bulk modulus (B), shear modulus (G), Young's modulus (E), and Poisson's ratio (ν) are also studied for polycrystalline of Be12Ti; the calculated B/G value shows that Be12Ti behaves in a brittle manner, and higher pressure can significantly improve the brittleness of Be12Ti. The elastic anisotropy is demonstrated by the elastic anisotropy factors. The direction-dependent Young's modulus and bulk modulus of Be12Ti are dealt with in detail under pressure from 0 GPa to 100 GPa. The pressure and temperature dependencies of the relative volume, the bulk modulus, the elastic constants, the heat capacity and the thermal expansion coefficient, as well as the entropy are obtained and discussed using the quasi-harmonic approximation in the ranges of temperature 0–1600 K and pressure 0–100 GPa.
1. Introduction
It is well known that titanium beryllide Be12Ti is an alternative to metallic beryllium as a material for neutron multipliers in blanket designs of fusion reactors.1–3 In particular, Be12Ti alloy has a higher melting point and better compatibility with structural materials, better oxidation resistance and resistance to a swelling under neutron irradiation compared with metallic beryllium in the fusion blanket design of a DEMO reactor.4–7 As we know, in the DEMO reactor, as functional materials, Be12Ti alloys will be used at high temperature and high pressure as well as in a high neutron flux environment where the blanket has a temperature up to 1123 K, a neutron damage dose of an order of 50 dpa and helium accumulation of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 appm.8,9 At high temperature, the Be12Ti alloy has thermal stress problems, which will produce microcracks and effect the application and lifetime of the Be12Ti material, even affecting the performance parameters of fusion reactors. However, thermal stresses are related to the elastic anisotropy and thermodynamic properties of the materials at corresponding temperatures. In addition, pressure is an important role in the mechanical and elastic properties of the materials,10,11 it can be produced phase transitions and changes of physical and chemical properties in the materials.12,13 From early literature, more research has focused on experimental aspects for Be12Ti, especially for the fabrication and tritium release under normal conditions.14–17 Although there are a few theoretical calculations for Be–Ti alloys, they mainly focus on hexagonal Be12Ti alloy,18,19 as for the tetragonal Be12Ti, its elastic and thermodynamic properties under high temperature and pressure are missing. Hence, it is necessary to obtain the elastic anisotropy and thermodynamic properties of tetragonal Be12Ti alloy at high temperature and high pressure. The first-principles density functional theory method (DFT) is a useful tool for predicting the physical properties of the solid materials, particularly elastic and thermodynamic properties, and it has been widely applied in various materials.20–27
000 appm.8,9 At high temperature, the Be12Ti alloy has thermal stress problems, which will produce microcracks and effect the application and lifetime of the Be12Ti material, even affecting the performance parameters of fusion reactors. However, thermal stresses are related to the elastic anisotropy and thermodynamic properties of the materials at corresponding temperatures. In addition, pressure is an important role in the mechanical and elastic properties of the materials,10,11 it can be produced phase transitions and changes of physical and chemical properties in the materials.12,13 From early literature, more research has focused on experimental aspects for Be12Ti, especially for the fabrication and tritium release under normal conditions.14–17 Although there are a few theoretical calculations for Be–Ti alloys, they mainly focus on hexagonal Be12Ti alloy,18,19 as for the tetragonal Be12Ti, its elastic and thermodynamic properties under high temperature and pressure are missing. Hence, it is necessary to obtain the elastic anisotropy and thermodynamic properties of tetragonal Be12Ti alloy at high temperature and high pressure. The first-principles density functional theory method (DFT) is a useful tool for predicting the physical properties of the solid materials, particularly elastic and thermodynamic properties, and it has been widely applied in various materials.20–27
In this present work, the effects of temperature and pressure on the structure, elasticity and thermodynamic properties of tetragonal Be12Ti alloys are studied by using the first-principles method and quasi-harmonic approximation (QHA). The calculated results are expected to provide valuable estimation for the experimental and theoretical research of Be12Ti intermetallic compound. The rest paper is organized as follows: in Section 2, we have given the theoretical method and the computation details. Some results and discussions are described in Section 3. Finally, the summary of our main results and conclusions is summarized in Section 4.
2. Computational methods and details
In present work, all calculations are performed by first-principles based on VASP software package,28 which is based on density functional theory (DFT). We describe the interaction between core ions and valence electrons using PAW pseudopotentials29,30 and the exchange-correlation function are treated by the generalized gradient approximation (GGA) within Perdew–Burke–Ernzerhof (PBE). The plane wave cut-off energy was taken as 550 eV. Pseudo atomic calculations of Be12Ti are performed for Be 2s2 and Ti 3s23p63d24 s2. For the Brillouin-zone sampling, we use the 8 × 8 × 14 Monkhorst–Pack mesh for k-space integration, where the self-consistent convergence of the total energy is set to 1.0 × 10−6 eV per atom, the maximum ionic force on the atom is below 0.0001 eV Å−1. These all parameters including k-point convergence test have been carefully tested.
In order to obtain the equilibrium volume and bulk modulus of, the E–V results obtained from the first calculation will be fitted by the following Birch–Murnaghan EOS:31
| |
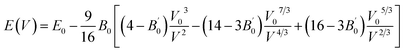 | (1) |
where
E0 is the equilibrium energy at
P = 0, the
B0 is the bulk modulus,
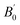
is the pressure derivative on bulk modulus. As for elastic properties, here we have used stress–strain approach based on the Hooke's law to calculate the elasticity, in which the elastic stiffness tensor [
Cij] can be expressed as
32where {
δij} and {
εij} are stress and strain tensors respectively. For tetragonal Be
12Ti crystal, there are six independent components (
C11,
C12,
C13,
C33,
C44 and
C66). Based on above
Cij values, other elastic parameters for example bulk modulus
B and shear modulus
G and Young's modulus
E can be obtained by Voigt–Reuss–Hill approximation from elastic constants in
ref. 33 and 34.
3. Results and discussion
3.1. Crystal structure and stability
The crystal structure of Be12Ti in this study belongs to the tetragonal with space group I4/mmm,35 in its unit cell, the Be atoms occupy Wyckoff position 8f (0.25, 0.25, 0.25), 8i (0.35, 0, 0), 8j (0.28, 0.5, 0) and Ti atoms occupy 2a (0, 0, 0), respectively (see Fig. 1). In order to determine the equilibrium structure of Be12Ti, we first carried out the structural optimization calculation under different pressure (pressure range of 0–100 GPa), obtained the corresponding energy E and volume V. Then, fitted above the E and V to the Birch–Murnaghan equation of state (EOS)29 to get the bulk modulus (B0) and its pressure derivative 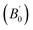 at 0 K and 0 GPa. Fitted energy E – volume V relations of Be12Ti are shown in Fig. 2, and the fitting results of the bulk B0 and its derivative
at 0 K and 0 GPa. Fitted energy E – volume V relations of Be12Ti are shown in Fig. 2, and the fitting results of the bulk B0 and its derivative 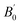 and equilibrium lattice constants are given in Table 1. It can be seen from Table 1 that the calculated lattice constants (a and c) and bulk modulus (B0) are very close to the previous experimental data35,36 even the experimental values were obtained in the 273 K environment, while pressure derivative
and equilibrium lattice constants are given in Table 1. It can be seen from Table 1 that the calculated lattice constants (a and c) and bulk modulus (B0) are very close to the previous experimental data35,36 even the experimental values were obtained in the 273 K environment, while pressure derivative 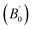 has not yet been compared with the experimental data. Nevertheless, this work is a significant attempt to predict the characteristics of tetragonal Be12Ti alloys. It can provide reference data for further research on the properties of Be12Ti alloy.
has not yet been compared with the experimental data. Nevertheless, this work is a significant attempt to predict the characteristics of tetragonal Be12Ti alloys. It can provide reference data for further research on the properties of Be12Ti alloy.
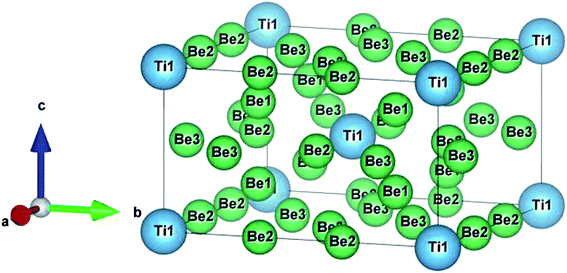 |
| | Fig. 1 Crystal structure of the tetragonal Be12Ti. | |
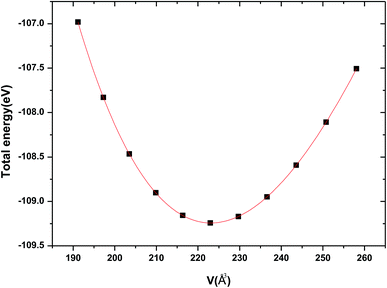 |
| | Fig. 2 The calculated total energy E varies unit cell volume V for tetragonal Be12Ti. | |
Table 1 Calculated equilibrium lattice constants a and c (Å), equilibrium volume V0 (Å3), bulk modules B0 (GPa) and its pressure derivative 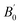 (GPa) of Be12Ti at zero pressure
(GPa) of Be12Ti at zero pressure
| Phase |
|
a (Å) |
c (Å) |
V0 (Å3) |
B0 (GPa) |
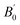
(GPa) |
| Ref. 35. Ref. 36. |
| Be12Ti |
This calc. |
7.25 |
4.17 |
223.097 |
121.0 |
3.46 |
| Experimental (T = 273 K). |
7.35a |
4.19a |
226.354 |
117b |
— |
Usually, the pressure can deform the material and even cause the phase transition of the material. But for different materials, the effect of pressure on the structure parameters is different. For tetragonal Be12Ti, there are differences in lattice constants and volume changes (a/a0, c/c0, V/V0) under external pressure. Fig. 3 shows the variation of a/a0, c/c0, and V/V0 with pressure in the range of 0 to 100 GPa, where a0, c0 and V0 denote the equilibrium structural parameters and cell volume at T = 0 K and P = 0 GPa, respectively. It can be seen that with increasing pressure, the equilibrium ratios a/a0, c/c0 and V/V0 decrease smoothly, but V/V0 decrease quickly than c/c0 and a/a0, and c/c0 decreases slightly faster than a/a0, indicating that the compression along the a-axis is slightly smaller than that along the c-axis. This suggests that the lattice constant c is more sensitive to external pressure than a. Nevertheless, change value of the a/c is not large and it remains almost constant in the range of pressure from 0 to 100 GPa.
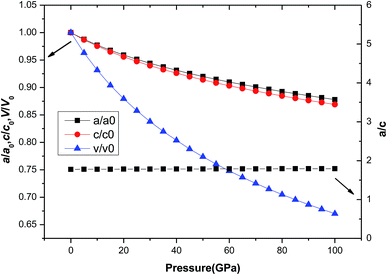 |
| | Fig. 3 The dependence of normalized lattice constants a/a0, c/c0, and cell volume V/V0 on pressure for tetragonal Be12Ti. | |
3.2. Elastic properties
The elastic property is important parameter which is related to many physical properties of the solid materials, including specific heat, Debye temperature, thermal expansion, Grüneisen parameter and melting point. Some mechanical properties and dynamical behaviors of the materials can be obtained by its elastic constants. For tetragonal Be12Ti, there are six independent elastic constants C11, C12, C13, C33, C44 and C66. In the Fig. 4(a) and (b), we presented the elastic constants and its increasing rate with pressure of Be12Ti under various pressures. From Fig. 4(a), we can see that all elastic constants increase with applied pressure up to 100 GPa for Be12Ti. The increasing rate of each elastic constant with pressure is derived from the slope of the corresponding linear fitted curve, as shown in Fig. 4(b). Among them, the variation of C11 is the most sensitive at 4.62, while C13 has the least increasing rate at 0.67. According to calculated elastic constants and mentioned formulas in ref. 34, we have calculated the mechanical properties of Be12Ti under various pressure, such as bulk modulus B, shear modulus G, Young's modulus E, and Poisson's ration ν, which are listed with other theoretical data in Table 2. It is obvious from Table 2 that the Voigt–Reuss–Hill approximations bulk modulus BH (114.27 GPa) at 0 GPa is very close to the value B0 (121.0 GPa) obtained with above Birch–Murnaghan EOS31 and experimental data.36 It indicates that our calculations are reliable and calculation method is correct. On the other hand, the bulk modulus B and shear modulus G can represent the resistance to volume change and shape change, respectively. The Young's modulus is related to the stiffness of materials. From Table 2, we also found that the bulk modulus B and shear modulus G and Young's modulus E increase with growing pressures till 40 GPa, indicating that the increase of resistance ability to volume and shape, and the stiffness of Be12Ti is getting harder and harder, and the Be12Ti becomes more and more difficult to compress as pressure increases. At the same time the value of B is greater than G, implies the principal parameter limiting the stability of tetragonal Be12Ti is the shear modulus.37
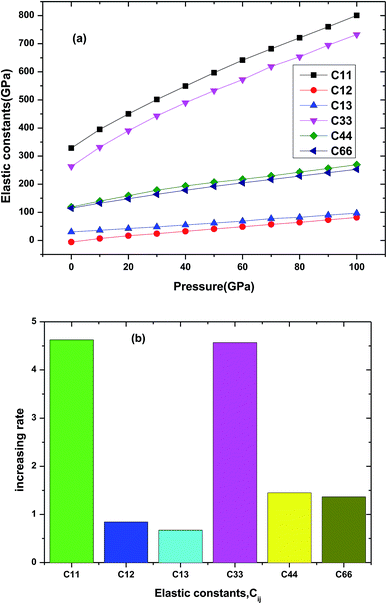 |
| | Fig. 4 The dependencies of elastic constants (a) and increasing rate (b) for each elastic constant for Be12Ti. | |
Table 2 The calculated elastic constants Cij (GPa), bulk modulus B (GPa), shear modulus G (GPa), Young's modulus E (GPa), Zener anisotropy factor A and Poisson's ratio ν of Be12Ti at different pressure
| P |
BV |
GV |
BR |
GR |
BH |
GH |
E |
B/G |
ν |
| Ref. 36. Present work-fitted by BMEOS. |
| 0 |
114.40 |
128.14 |
114.13 |
125.61 |
114.27 |
126.87 |
277.80 |
0.90 |
0.09 |
| 117.00a |
| 121.0b |
| 10 |
142.07 |
151.86 |
141.80 |
149.02 |
141.93 |
150.44 |
333.50 |
0.94 |
0.11 |
| 20 |
165.75 |
172.42 |
165.51 |
169.30 |
165.63 |
170.86 |
381.43 |
0.97 |
0.12 |
| 30 |
187.36 |
192.43 |
187.15 |
189.09 |
187.25 |
190.76 |
427.21 |
0.98 |
0.12 |
| 40 |
208.09 |
209.57 |
207.86 |
205.95 |
207.97 |
207.76 |
467.57 |
1.00 |
0.13 |
| 50 |
228.34 |
225.41 |
228.06 |
221.37 |
228.20 |
223.39 |
505.29 |
1.02 |
0.13 |
| 60 |
247.49 |
239.05 |
247.15 |
234.49 |
247.32 |
236.77 |
538.47 |
1.04 |
0.14 |
| 70 |
267.28 |
253.14 |
267.04 |
248.28 |
267.16 |
250.71 |
572.92 |
1.07 |
0.14 |
| 80 |
283.56 |
267.42 |
283.25 |
262.45 |
283.41 |
264.94 |
605.98 |
1.07 |
0.14 |
| 90 |
302.27 |
281.59 |
301.99 |
276.49 |
302.13 |
279.04 |
640.08 |
1.08 |
0.15 |
| 100 |
320.45 |
295.48 |
320.12 |
290.17 |
320.29 |
292.83 |
673.29 |
1.09 |
0.15 |
For a tetragonal crystal, the traditional mechanical stability conditions under isotropic pressure are given by the following equations:38
| |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 11 > 0, 11 > 0, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 33 > 0, 33 > 0, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 44 > 0, 44 > 0, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 66 > 0, 66 > 0, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 11 − 11 − ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 12 > 0, ( 12 > 0, (![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 33 + 33 + ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 11 − 2 11 − 2![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 13) > 0, (2 13) > 0, (2![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 11 + 2 11 + 2![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 12 + 12 + ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 33 + 4 33 + 4![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 13) > 0 13) > 0
| (3) |
where
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) αα
αα =
Cαα −
P (
a = 1, 3, 4, 6),
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 12
12 =
C12 +
P,
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 13
13 =
C13 +
P. It is evident that from calculated results the elastic constants of Be
12Ti satisfy all of these conditions above at pressure up to 100 GPa, which indicates that tetragonal structure Be
12Ti under applies pressure is elastic stable. In order to determine the dynamic stability under the pressure considered, we also calculate the phonon dispersion based on linear response (DFPT) for the 2 × 2 × 2 supercell with 104 atoms at 0, 20, 40, 60 GPa and 100 GP in
Fig. 5 where no imaginary frequencies in the whole Brillouin zone of Be
12Ti and do not show any anomaly for all the phonon modes, confirming that Be
12Ti with tetragonal structure is at least stable dynamically up to 100 GPa. Meanwhile, we found that the acoustic and optical modes become more compact and frequency range increase as the pressure increasing, when the pressure reaches 100 GPa, the phonon spectrum intervals between acoustic and optical modes have disappeared.
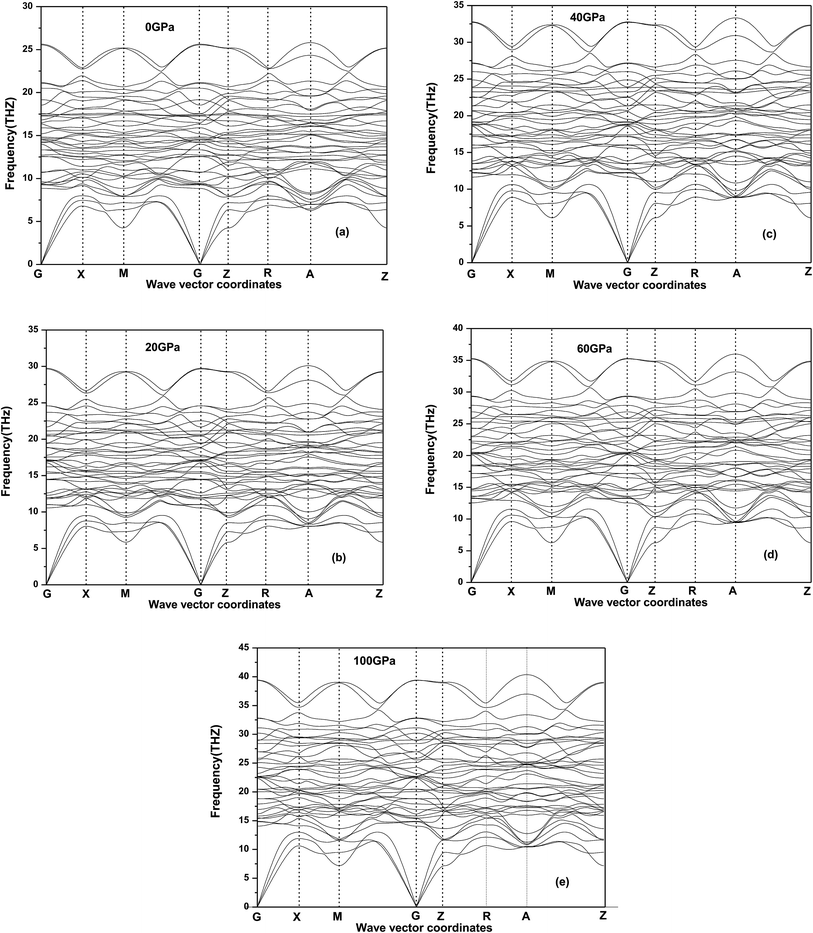 |
| | Fig. 5 Phonon dispersion curves for tetragonal Be12Ti at 0 GPa (a), 20 GPa (b), 40 GPa (c), 60 GPa (d) and 100 GPa (e). | |
Poisson's ratio ν can be used to estimate the ductility and brittleness of the materials. As for Be12Ti, its Poisson's ratio value has been listed in Table 2, we can see that from Table 2 all Poisson's ratio values are less than 1/3 under applied pressure, which means that the Be12Ti is brittle in nature.39 Meanwhile, according to the Pugh's criterion,41 the ratio of the bulk modulus to the shear modules B/G can be used to predict the whether a material will behave in a brittle or ductile manner. A high B/G ratio is associated with ductility, whereas a low value corresponds to a brittle material, the critical value between them is around 1.75.40 If B/G is less than 1.75, then brittle behavior is predicted; otherwise, the material behaves in a ductile manner. In this study, calculated B/G values for tetragonal Be12Ti as a function of pressure are shown in Table 2 and Fig. 6. It is noted that the value of B/G is 0.90 at 0 K and 0 GPa, showing that tetragonal Be12Ti has a brittle nature under these conditions. When applied pressure increases from 0 GPa to 100 GPa, B/G monotonously increases from 0.90 to 1.09, which is always remaining smaller than 1.75. This trend is markedly different from ref. 17. This indicates that Be12Ti will also behave in a brittle manner at pressure up to 100 GPa, but it has a tendency towards the development of ductility, indicating that the external pressure can improve the brittleness of tetragonal Be12Ti alloys.
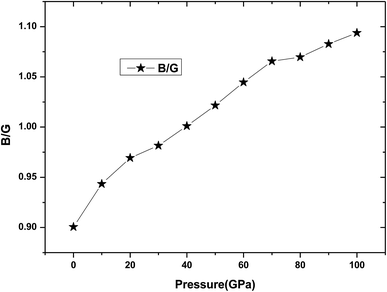 |
| | Fig. 6 The dependencies of B/G ratio on pressure for Be12Ti. | |
3.3. Elastic anisotropy
Anisotropic behavior has an important implication in engineering science as well as crystal physics since it is highly related with the possibility to induce microcracks in materials. By means of elastic anisotropy, we can know more information about the material. Such as phase transformation, precipitation, dislocation dynamics, and microcracks formation i.e.41 Usually, the elastic anisotropy can be represented by three elastic factors, which are shear anisotropic factors (A1, A2 and A3) of different crystallographic planes and universal anisotropic index (AU) and the percentage of anisotropy in compression and shear (AB and AG). In this work, we have calculated above three type anisotropy of tetragonal Be12Ti under applied pressure and listed in Table 3, the detail calculation equations as follows42,43| |
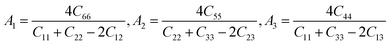 | (4) |
Table 3 The shear anisotropy factors (A1, A2), universal elastic anisotropy index (AU) and the percentage of anisotropy (AB and AG) of Be12Ti under various pressure
| Pressure (GPa) |
A1 |
A2 |
AU |
AB |
AG |
| 0 |
6.844 × 10−1 |
8.955 × 10−1 |
1.031 × 10−1 |
1.146 × 10−3 |
9.979 × 10−3 |
| 10 |
6.825 × 10−1 |
8.539 × 10−1 |
9.741 × 10−2 |
9.800 × 10−4 |
9.454 × 10−3 |
| 20 |
6.834 × 10−1 |
8.409 × 10−1 |
9.348 × 10−2 |
7.320 × 10−4 |
9.117 × 10−3 |
| 30 |
6.860 × 10−1 |
8.406 × 10−1 |
8.953 × 10−2 |
5.580 × 10−4 |
8.764 × 10−3 |
| 40 |
6.900 × 10−1 |
8.334 × 10−1 |
8.907 × 10−2 |
5.500 × 10−4 |
8.720 × 10−3 |
| 50 |
6.902 × 10−1 |
8.231 × 10−1 |
9.242 × 10−2 |
6.080 × 10−4 |
9.038 × 10−3 |
| 60 |
6.907 × 10−1 |
8.067 × 10−1 |
9.877 × 10−2 |
6.960 × 10−4 |
9.643 × 10−3 |
| 70 |
6.942 × 10−1 |
7.998 × 10−1 |
9.859 × 10−2 |
4.460 × 10−4 |
9.675 × 10−3 |
| 80 |
6.978 × 10−1 |
8.027 × 10−1 |
9.580 × 10−2 |
5.420 × 10−4 |
9.383 × 10−3 |
| 90 |
7.014 × 10−1 |
8.038 × 10−1 |
9.313 × 10−2 |
4.640 × 10−4 |
9.136 × 10−3 |
| 100 |
7.035 × 10−1 |
8.030 × 10−1 |
9.258 × 10−2 |
5.030 × 10−4 |
9.074 × 10−3 |
For a tetragonal structure,
| |
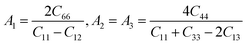 | (5) |
| |
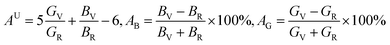 | (6) |
where the
A1,
A2,
A3 are shear anisotropic factor for the (001) and (010) and (100) shear planes, respectively. The
BV,
BR,
GV, and
GR stand for the Voigt and Reuss approximation for bulk modulus (
B) and shear modulus (
G), respectively. For isotropic structural materials, the factors
A1,
A2 and
A3 should be equated to one, the value of the
AU is also zero, while any deviations from one or zero means the degree of elastic anisotropy of the crystal. The maximum value of
AB and
AG is 100% and the minimum is zero, the zero value means isotropy, while 100% represent maximum anisotropy. From
Table 3, one can see clearly that
A1 and
A2 are smaller than one, when the applied pressure increases, the
A1 and
A2 only have slightly changed than that value at zero pressure. For
AU, it is seen that Be
12Ti have the small degree of universal elastic anisotropic behavior, which means Be
12Ti is slightly anisotropic, and that characteristics are enhanced gradually with the increasing pressure. As for percentage of anisotropy
AB and
AG, it is found that as the pressure increases, the anisotropy of
AB almost keep constant, whereas the shear modulus anisotropy
AG increases gently indicating that tetragonal Be
12Ti is more anisotropy in shear than in compressibility. Meanwhile, the calculated value of
AG is larger that
AB under different pressure, also implying that the shear modulus shows stronger directional dependence than bulk modulus.
Actually, the anisotropy of material also can be revealed by three dimensional curved surfaces of Young's and Bulk modulus on crystallographic directions. For a tetragonal structure Be12Ti, the direction dependent of Young's modulus (E) and Bulk modulus (B) is defined as follows:
| |
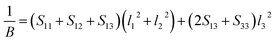 | (7) |
| |
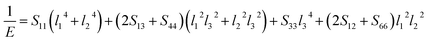 | (8) |
where
Sij are the elastic compliance constants, and
l1,
l2 and
l3 are the directional cosines to the
X,
Y and
Z axes under spherical coordinates, respectively.
44 The three-dimensional surface of the Young's and Bulk modulus for Be
12Ti with tetragonal structure at 0 GPa and 40 GPa is shown in
Fig. 7 and
8, respectively. From
Fig. 7 and
8, we can see that the distances between the origin of coordinate and the 3D surface are not same in any direction, and the Young's and Bulk modulus have small changes under high pressure, implies that as increasing of pressure from 0 GPa to 40 GPa, the elastic anisotropy of Be
12Ti becomes not more obvious. In addition, we have presented the two-dimensional projections of Young's modulus and bulk modulus on different crystallography planes at 0 GPa and 40 GPa in
Fig. 7 and
8, which are consistent with the above conclusions in three-dimensional space.
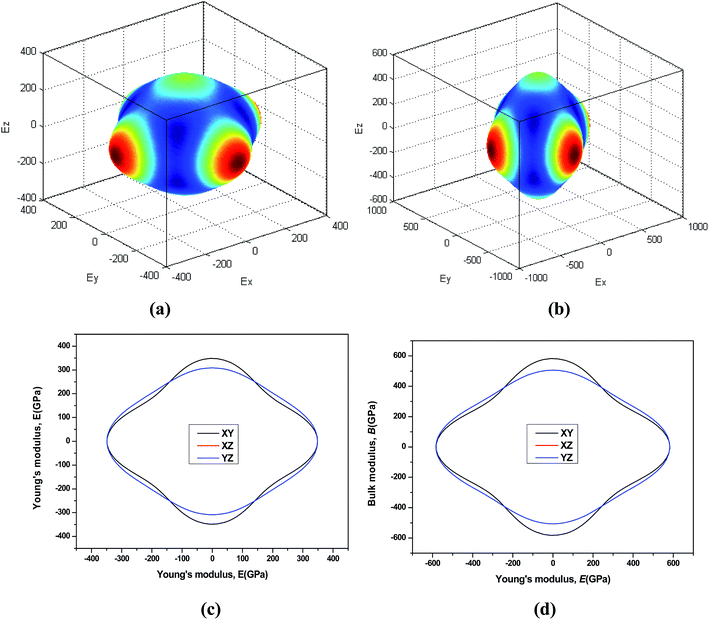 |
| | Fig. 7 Directional dependence of the Young's modulus for Be12Ti under 0 GPa (a) and 40 GPa (b). The corresponding projections in different planes (XY plane, and XZ plane, and YZ plane) of Young's modulus are also shown in (c) and (d). | |
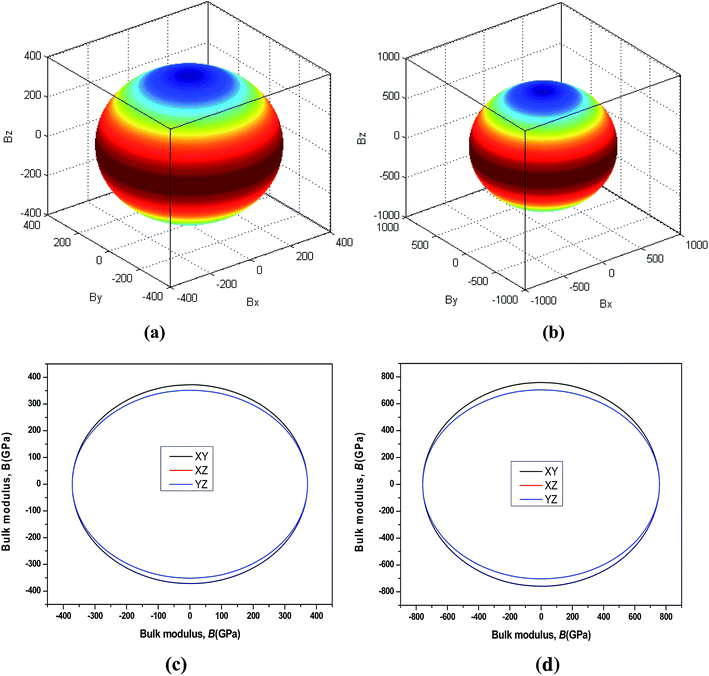 |
| | Fig. 8 Directional dependence of the Bulk modulus for Be12Ti under 0 GPa (a) and 40 GPa (b). The corresponding projections in different crystal planes (XY plane, and XZ plane, and YZ plane) of Bulk modulus are also shown in (c) and (d). | |
3.4. Thermodynamic properties
We have used the quasi-harmonic approximation (QHA) to investigate the thermodynamic properties of tetragonal Be12Ti in the temperature range 0–1600 K and pressure range 0–100 GPa, which has been successfully applied to several materials,45–47 the detail calculation method are presented in ref. 46 and are not described here. To obtain the equilibrium volume and bulk modulus of Be12Ti at different temperature, we have calculated the Helmholtz free energy F(V, T) dependence of the volume V, the equilibrium volume and the bulk modulus are obtained by above the formula (1) Birch–Murnaghan EOS. They are shown in Fig. 9 and 10, respectively. From Fig. 9, we can see that the free energy value decreases gradually and its change range in the same temperature interval (such as 200 K) enhances as increase of temperature. If we connected the minimum values of free energy using one line we can obviously find that the equilibrium volume of Be12Ti expands with the increasing of temperature. Also, clearly, the bulk modulus decreases with the increase of temperature from 0 K to 1600 K, and when the temperature is near 270 K, the calculated result of bulk modulus are close to the experimental data.
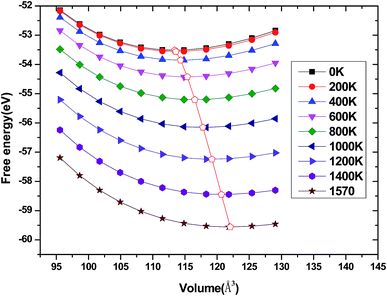 |
| | Fig. 9 Dependence of the Helmholtz free energy F(V, T) on crystal volume at various temperatures and the locus of the minimum of the free energy for Be12Ti. | |
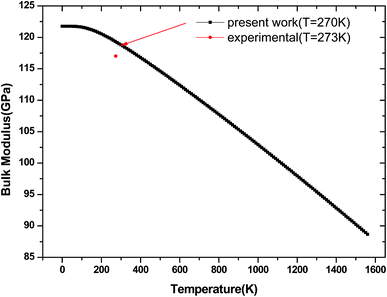 |
| | Fig. 10 Temperature dependence of the bulk modulus for Be12Ti. | |
The investigation on the heat capacity of crystal is an old topic of the condensed matter physics,48 because as one variation of the thermal properties, the heat capacity of a substance not only provides essential insight into its vibrational properties but is also mandatory for many applications. According to the laws of thermodynamics, there are two kinds of heat capacities in a material, namely heat capacity at constant volume Cv and heat capacity at constant pressure CP, the Cv and CP can be calculated from ref. 46. Fig. 11 shows the variation of Cv and CP with temperature at 0 GPa. One can easily see that Cv and CP increases with the increase of temperature, and when temperature lower that 300 K, they are almost equal, while the temperature is higher than 300 K, Cp is always larger than Cv, but the discrepancy between them becomes significant as the temperature enhances. Meanwhile, the constant volume Cv at various pressure is calculated and displayed in Fig. 12. It is obvious that the Cv at different pressure has a similar trend if compared with the Cv at 0 GPa. That is while T < 400 K Cv increases rapidly with temperature at a given pressure and decreases with increasing pressure at a given temperature. Namely, the variation of Cv is dependent on both temperature and pressure at low temperature. At the same time at sufficiently low temperatures (T < 400 K), Cv is approximately proportional to T3.49 However, the anharmonic effect on Cv is suppressed at higher temperature, the heat capacity Cv approaches to a constant Dulong–Petit limit 3nNAKB (≈324.53 J mol−1 K−1),33 where n = 13 is number of atoms for Be12Ti unit cell, NA is the Avogadro number and KB is the Boltzmann's constant. At intermediate temperatures, the temperature dependence of Cv is governed by the details of vibrations of the atoms. It indicates that the atomic interaction occurs at low temperature in Be12Ti alloys. The effects of temperature on heat capacity are more significant than that of the pressure for Be12Ti, and the Cv is more sensitive to the temperature than that of the pressure. Here, we also plotted the change of entropy with temperature at various pressure in Fig. 13 for Be12Ti. It can be seen that the entropy increase quickly as increasing temperature and decreases with increasing of pressure. It's consistent with common sense, because the entropy of a crystal is generated by lattice vibrations and electronic excitation, and as the temperature goes up, the lattice vibrations of the crystal increases and the electrons are more likely to be excited.
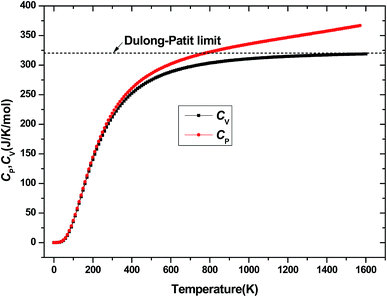 |
| | Fig. 11 Heat capacity of constant volume Cv and constant pressure CP as a function of temperature at 0 GPa. | |
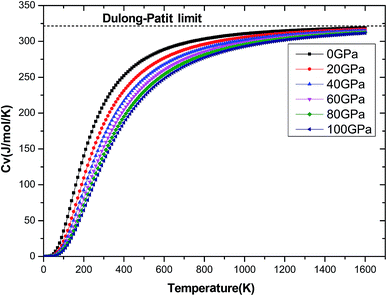 |
| | Fig. 12 Dependencies of the constant volume heat capacity Cv on temperatures at high pressure. | |
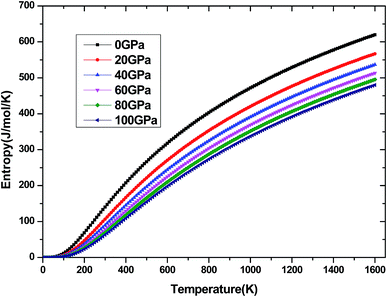 |
| | Fig. 13 Dependence of the entropy S on temperature at high pressure. | |
The dependence of the thermal expansion α with temperature T and pressure P is illustrated in Fig. 14. It is similar to the heat capacity, when the temperature T is below 400 K, α rises sharply with temperature, the propensity of increment becomes gently and gradually approaches to a liner increase at high temperature. For comparison, the experimental values of thermal expansion for tetragonal Be12Ti from ref. 50 are also presented in Fig. 14. The comparison demonstrates that our calculated results are in excellent agreement with the experimental data in the temperature range 300–800 K. This further indicates that the above calculation method and model for tetragonal Be12Ti are reliable and effective. Unfortunately, the experimental data are only in the range of 300–800 K, and more experimental values under high temperature are expected to be compared in the future.
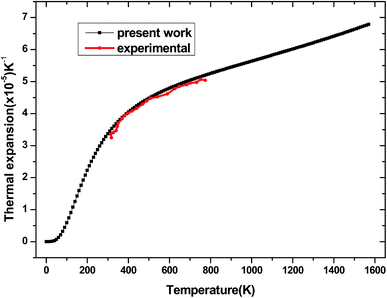 |
| | Fig. 14 The thermal expansion α of tetragonal Be12Ti as a function of temperature. | |
4. Conclusions
In this work, the structure, elastic anisotropy and thermodynamic properties of tetragonal Be12Ti at different temperature and pressure are investigated using the pseudo-potential plane-wave method in combination with the quasi-harmonic approximation. The calculated equilibrium structure parameters and bulk modulus are good agreement with the available experimental data and other theoretical results. The calculated elastic constants Cij and interrelated quantities G, E, ν show that Be12Ti alloy possesses brittle nature at ambient conditions and Be12Ti exhibits no pronounced elastic anisotropy by the 3D surface of Young's modulus. The higher the temperature, cell compression for Be12Ti at a given pressure is more difficult. Phonon dispersions has been carried out, shows that the Be12Ti crystal is dynamic stability up to 100 GPa. Under the QHA method, the thermodynamic properties of Be12Ti are obtained successfully. The pressure and temperature dependence of heat capacity and thermal expansion are also predicted in the pressure ranges of 0–100 GPa and temperature range of 0–1600 K. Heat capacity Cv of different pressure is found to increase with temperature and close to the Dulong–Petit limit at high temperatures. Furthermore, thermal expansion α enhances with temperature but the variety tendency get slower at high temperature, and they are in excellent agreement with experimental data.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The author would like to thanks Dr C. Cao and Dr Z. H. Yuan and J. M. Yan for his useful discussions about anisotropy elasticity. This project was supported by the National Magnetic Confinement Fusion Science Program of China under No. 2015GB109005.
References
- V. Chakin, M. Klimekov, R. Rolli, P. Kurinskiy, A. Moeslang and C. Dorn, J. Nucl. Mater., 2011, 417, 769 CrossRef CAS.
- K. Wada, K. Munakata, J. H. Kim, K. Yonehara, D. Wakai and M. Nakamichi, J. Nucl. Mater., 2013, 442, 5494 CrossRef.
- T. Otsuka, T. Tanabe and K. Tokunaga, J. Nucl. Mater., 2013, 438, S1048–S1051 CrossRef CAS.
- Y. K. Vohra and P. T. Spencer, Phys. Rev. Lett., 2001, 86, 3068 CrossRef CAS PubMed.
- B. T. Wang, W. D. Li and P. Zhang, J. Nucl. Mater., 2012, 420, 501 CrossRef CAS.
- M. Grosse, G. Kuehne, M. Steinbrueck, E. Lehmann, J. Stuckert and P. Vontobel, J. Phys.: Condens. Matter, 2008, 20, 104263 CrossRef.
- C. Li, C.-L. Feng and H. Y. Oderji, et al., Review of LIBS application in nuclear fusion technology, Front. Phys., 2016, 11(6), 114214 CrossRef.
- W. Liu, B. Li, L. Wang, J. Zhang and Y. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 144107 CrossRef.
- M. T. Perez-Prado and A. P. Zhilyaev, Phys. Rev. Lett., 2009, 102, 175504 CrossRef CAS PubMed.
- S. H. Zhang, Y. Zhu, X. Y. Zhang, S. L. Zhang, Q. Li and R. P. Liu, Comput. Mater. Sci., 2010, 50, 179 CrossRef CAS.
- S. H. Zhang, X. Y. Zhang, Y. Zhu, S. L. Zhang, Q. Li and R. P. Liu, Comput. Mater. Sci., 2012, 61, 42 CrossRef CAS.
- O. Rapp, J. Less-Common Met., 1970, 21, 27 CrossRef CAS.
- J. Z. Liu, A. van de Walle, G. Ghosh and M. Asta, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 144109 CrossRef.
- H. Kawamura, H. Takahashi, N. Yoshida, Y. Mishima and K. Ishida, J. Nucl. Mater., 2004, 329, 112 CrossRef.
- V. Chakin, M. Klimenkov, R. Rolli and P. Kurinskiy, J. Nucl. Mater., 2011, 417, 769 CrossRef CAS.
- M. Uchida, E. Ishitsuka and H. Kawamura, J. Nucl. Mater., 2002, 307, 653 CrossRef.
- P. Kurinskiy, A. Moeslang, V. chakin, M. Klimenkov, R. Rolli, S. Van Til and A. A. Goraieb, Fusion Eng. Des., 2013, 88, 2198 CrossRef CAS.
- S. M. Peng, J. Nucl. Mater., 2015, 464, 230 CrossRef CAS.
- X. K. Liu, W. Zhou, X. Liu and S. M. Peng, RSC Adv., 2015, 5, 59648 RSC.
- X. L. Yuan, D. Q. Wei, X. R. Chen, Q. M. Zhang and Z. Z. Gong, J. Alloys Compd., 2011, 509, 769 CrossRef CAS.
- M. Mbarki and A. Rebey, J. Alloys Compd., 2012, 530, 36 CrossRef CAS.
- Z. W. Yang, D. M. Shi, B. Wen and R. Melnik, J. Alloys Compd., 2012, 524, 53 CrossRef CAS.
- G. Yao, Y. D. Liu, W. B. Zhang, X. Y. An and Y. Chen, J. Alloys Compd., 2013, 5081, 109 CrossRef.
- G. Sai Gautam and K. C. Hari Kumar, J. Alloys Compd., 2014, 587, 380 CrossRef CAS.
- R. R. Hao, X. Y. Zhang and J. Q. Qin, RSC Adv., 2015, 5, 77399 RSC.
- B. B. Zheng, M. G. Zhang and H. G. Luo, AIP Adv., 2015, 5, 037123 CrossRef.
- Y. Wang, C.-M. Hao and H.-M. Huang, et al., Elastic, dynamical, and electronic properties of LiHg and Li3Hg: first-principles study, Front. Phys., 2018, 13(2), 137102 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- F. Birch, J. Geophys. Res., B, 1978, 83, 1257 CrossRef CAS.
- S. I. Shang and G. Sheng, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 052102–052105 CrossRef.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- K. Liu, B. Dong, X. L. Zhou, S. M. Wang, Y. S. Zhao and J. Chang, J. Alloys Compd., 2015, 632, 830 CrossRef CAS.
- A. Zalkin, E. Sands, R. G. Bedford and O. H. Krikorian, Acta Crystallogr., 1961, 14, 63 CrossRef CAS.
- R. L. Fleischer and R. J. Zabala, Metall. Trans. A, 1989, 20, 1279 CrossRef.
- J. P. Poirier, Introduction to the Physics of the Earth's Interior, Cambridge University Press, Oxford, 2000, vol. 39 Search PubMed.
- C. V. Sinko and N. A. Smirnow, J. Phys.: Condens. Matter, 2002, 14, 6989 CrossRef.
- W. C. Hu, Y. Liu, D. J. Li, X. Q. Zeng and C. S. Xu, Comput. Mater. Sci., 2014, 83, 27 CrossRef CAS.
- S. F. Pugh, Philos. Mag., 1954, 45, 823 CAS.
- R. R. Hao, X. Y. Zhang, J. Q. Qin, J. L. Ning, S. H. Zhang, Z. Niu, M. Z. Ma and R. P. Liu, RSC Adv., 2015, 5, 77399 RSC.
- X. Ji, Y. Yu, J. Y. Ji, J. P. Long, J. P. Chen and D. J. Liu, J. Alloys Compd., 2015, 623, 304 CrossRef CAS.
- S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504 CrossRef PubMed.
- J. F. Nye, Physical Properties of Crystals, Clarendon Press, Oxford, 1985 Search PubMed.
- Y. Lu, D. F. Li, B. T. Wang, R. W. Li and P. Zhang, J. Nucl. Mater., 2011, 408, 136 CrossRef CAS.
- R. Wang, S. F. Wang and X. Z. Wu, Intermetallics, 2013, 43, 65 CrossRef CAS.
- X. L. Wen, Y. X. Liang, P. P. Bai, B. W. Luo, T. Fang, L. Yue, T. An, W. Y. Song and S. Q. Zheng, Physica B Condens. Matter., 2017, 525, 119 CrossRef CAS.
- T. Belaroussi, T. Benmessabih, F. Hamdache and B. Amrani, Physica B Condens. Matter., 2008, 403, 2649 CrossRef CAS.
- J. P. Poirier, Introduction to the Physics of the Earth's Interior, Cambridge University Press, Oxford. 2000, vol. 39 Search PubMed.
- M. L. Jackson, P. A. Burr and R. W. Grimes, Acta Crystallogr., Sect. A: Found. Adv., 2016, B72, 277–280 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Qijie Fenga,
Bin Tanga,
Jian Zhenga,
Zhou Zhengb,
Wei Zhoua,
Jiting Tiana and
Jing Wangc
*a,
Qijie Fenga,
Bin Tanga,
Jian Zhenga,
Zhou Zhengb,
Wei Zhoua,
Jiting Tiana and
Jing Wangc
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 appm.8,9 At high temperature, the Be12Ti alloy has thermal stress problems, which will produce microcracks and effect the application and lifetime of the Be12Ti material, even affecting the performance parameters of fusion reactors. However, thermal stresses are related to the elastic anisotropy and thermodynamic properties of the materials at corresponding temperatures. In addition, pressure is an important role in the mechanical and elastic properties of the materials,10,11 it can be produced phase transitions and changes of physical and chemical properties in the materials.12,13 From early literature, more research has focused on experimental aspects for Be12Ti, especially for the fabrication and tritium release under normal conditions.14–17 Although there are a few theoretical calculations for Be–Ti alloys, they mainly focus on hexagonal Be12Ti alloy,18,19 as for the tetragonal Be12Ti, its elastic and thermodynamic properties under high temperature and pressure are missing. Hence, it is necessary to obtain the elastic anisotropy and thermodynamic properties of tetragonal Be12Ti alloy at high temperature and high pressure. The first-principles density functional theory method (DFT) is a useful tool for predicting the physical properties of the solid materials, particularly elastic and thermodynamic properties, and it has been widely applied in various materials.20–27
000 appm.8,9 At high temperature, the Be12Ti alloy has thermal stress problems, which will produce microcracks and effect the application and lifetime of the Be12Ti material, even affecting the performance parameters of fusion reactors. However, thermal stresses are related to the elastic anisotropy and thermodynamic properties of the materials at corresponding temperatures. In addition, pressure is an important role in the mechanical and elastic properties of the materials,10,11 it can be produced phase transitions and changes of physical and chemical properties in the materials.12,13 From early literature, more research has focused on experimental aspects for Be12Ti, especially for the fabrication and tritium release under normal conditions.14–17 Although there are a few theoretical calculations for Be–Ti alloys, they mainly focus on hexagonal Be12Ti alloy,18,19 as for the tetragonal Be12Ti, its elastic and thermodynamic properties under high temperature and pressure are missing. Hence, it is necessary to obtain the elastic anisotropy and thermodynamic properties of tetragonal Be12Ti alloy at high temperature and high pressure. The first-principles density functional theory method (DFT) is a useful tool for predicting the physical properties of the solid materials, particularly elastic and thermodynamic properties, and it has been widely applied in various materials.20–27
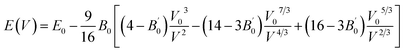
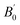 is the pressure derivative on bulk modulus. As for elastic properties, here we have used stress–strain approach based on the Hooke's law to calculate the elasticity, in which the elastic stiffness tensor [Cij] can be expressed as32
is the pressure derivative on bulk modulus. As for elastic properties, here we have used stress–strain approach based on the Hooke's law to calculate the elasticity, in which the elastic stiffness tensor [Cij] can be expressed as32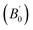 at 0 K and 0 GPa. Fitted energy E – volume V relations of Be12Ti are shown in Fig. 2, and the fitting results of the bulk B0 and its derivative
at 0 K and 0 GPa. Fitted energy E – volume V relations of Be12Ti are shown in Fig. 2, and the fitting results of the bulk B0 and its derivative 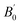 and equilibrium lattice constants are given in Table 1. It can be seen from Table 1 that the calculated lattice constants (a and c) and bulk modulus (B0) are very close to the previous experimental data35,36 even the experimental values were obtained in the 273 K environment, while pressure derivative
and equilibrium lattice constants are given in Table 1. It can be seen from Table 1 that the calculated lattice constants (a and c) and bulk modulus (B0) are very close to the previous experimental data35,36 even the experimental values were obtained in the 273 K environment, while pressure derivative 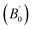 has not yet been compared with the experimental data. Nevertheless, this work is a significant attempt to predict the characteristics of tetragonal Be12Ti alloys. It can provide reference data for further research on the properties of Be12Ti alloy.
has not yet been compared with the experimental data. Nevertheless, this work is a significant attempt to predict the characteristics of tetragonal Be12Ti alloys. It can provide reference data for further research on the properties of Be12Ti alloy.
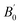 (GPa) of Be12Ti at zero pressure
(GPa) of Be12Ti at zero pressure


![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 11 > 0,
11 > 0, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 33 > 0,
33 > 0, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 44 > 0,
44 > 0, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 66 > 0,
66 > 0, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 11 −
11 − ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 12 > 0, (
12 > 0, (![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 33 +
33 + ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 11 − 2
11 − 2![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 13) > 0, (2
13) > 0, (2![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 11 + 2
11 + 2![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 12 +
12 + ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 33 + 4
33 + 4![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 13) > 0
13) > 0
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) αα = Cαα − P (a = 1, 3, 4, 6),
αα = Cαα − P (a = 1, 3, 4, 6), ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 12 = C12 + P,
12 = C12 + P, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) 13 = C13 + P. It is evident that from calculated results the elastic constants of Be12Ti satisfy all of these conditions above at pressure up to 100 GPa, which indicates that tetragonal structure Be12Ti under applies pressure is elastic stable. In order to determine the dynamic stability under the pressure considered, we also calculate the phonon dispersion based on linear response (DFPT) for the 2 × 2 × 2 supercell with 104 atoms at 0, 20, 40, 60 GPa and 100 GP in Fig. 5 where no imaginary frequencies in the whole Brillouin zone of Be12Ti and do not show any anomaly for all the phonon modes, confirming that Be12Ti with tetragonal structure is at least stable dynamically up to 100 GPa. Meanwhile, we found that the acoustic and optical modes become more compact and frequency range increase as the pressure increasing, when the pressure reaches 100 GPa, the phonon spectrum intervals between acoustic and optical modes have disappeared.
13 = C13 + P. It is evident that from calculated results the elastic constants of Be12Ti satisfy all of these conditions above at pressure up to 100 GPa, which indicates that tetragonal structure Be12Ti under applies pressure is elastic stable. In order to determine the dynamic stability under the pressure considered, we also calculate the phonon dispersion based on linear response (DFPT) for the 2 × 2 × 2 supercell with 104 atoms at 0, 20, 40, 60 GPa and 100 GP in Fig. 5 where no imaginary frequencies in the whole Brillouin zone of Be12Ti and do not show any anomaly for all the phonon modes, confirming that Be12Ti with tetragonal structure is at least stable dynamically up to 100 GPa. Meanwhile, we found that the acoustic and optical modes become more compact and frequency range increase as the pressure increasing, when the pressure reaches 100 GPa, the phonon spectrum intervals between acoustic and optical modes have disappeared.