Supramolecular forces and their interplay in stabilizing complexes of organic anions: tuning binding selectivity in water†
Matteo
Savastano
 ac,
Carla
Bazzicalupi
ac,
Carla
Bazzicalupi
 a,
Celeste
García-Gallarín
a,
Celeste
García-Gallarín
 b,
Maria Dolores
López de la Torre
b,
Maria Dolores
López de la Torre
 b,
Antonio
Bianchi
b,
Antonio
Bianchi
 *a and
Manuel
Melguizo
*a and
Manuel
Melguizo
 *b
*b
aDepartment of Chemistry “Ugo Schiff”, University of Florence, Via della Lastruccia 3, 50019 Sesto Fiorentino, Italy. E-mail: antonio.bianchi@unifi.it
bDepartment of Inorganic and Organic Chemistry, University of Jaén, 23071 Jaén, Spain. E-mail: mmelgui@ujaen.es
cCSGI, University of Florence, Via della Lastruccia 3, 50019 Sesto Fiorentino, Italy
First published on 20th November 2018
Abstract
How do different supramolecular forces contribute to the stabilization of complexes of organic anions in water? Oftentimes, when debating such a theme, we refer to broad concepts like positive or negative cooperative effects; the focus of the present work is rather on their interplay, i.e. on the way different kinds of stabilizing interactions (salt bridges, H-bonds, anion–π interactions, π–π stacking, solvent effects, etc.) dialogue among themselves. What happens if we tune the strengths of salt bridges by altering the basicity of the anion? What if we change the geometry of the charged group? How does shifting towards more hydrophilic or hydrophobic anions impact the stability of complexes in water? What happens in the solid state? Will aromatic anions go for a π–π stacking or an anion–π interaction mode and do they all behave in the same manner? Does the host/guest size make any difference? What if we play with regiochemistry: will one of the isomers be selectively recognized? Here we present a case study featuring the tetrazine-based ligands L1 and L2 and a series of selected organic anions; potentiometric, NMR, and XRD data and in silico simulations are employed to render such a complex picture.
Introduction
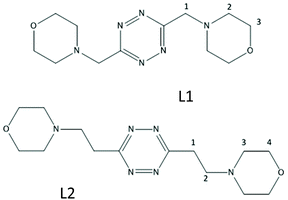
Anion coordination in solution revolves around a combination of supramolecular forces, selected among a shortlist by incorporating the required structural features within the receptor; although individually weak, such interactions can collectively furnish enough stabilization to afford polyfunctional ligands capable of strong and selective anion binding.1,2We should, however, keep in mind two facts. First, supramolecular forces are not equally represented in the panorama of anion receptors, hydrogen bonds easily taking the lion's share, being among the most stabilizing and directional of intermolecular forces and widely recognized for that, while other forces, including anion–π interactions3 and halogen bonds,4 are still struggling for the endorsement by part of the scientific community. In the second instance, we have to be aware that classifying is an inborn means of rationalization of the human mind: when we say, for example, that a receptor is hydrogen bond-based, what we mean is that its anion complexes are stabilized by an interplay of supramolecular forces, among which hydrogen bonding plays a major role. This goes beyond semantics, as the importance of such interplay, an exquisitely supramolecular topic, is receiving an across-the-board growing recognition from researchers working in the most diverse fields of chemistry, spanning from structural biology, with implications for both living beings5 and new synthetic analogues of biomolecules,6 up to materials chemistry7 and crystal engineering.8
We have recently shown that protonated forms of the tetrazine-based receptors L1 and L2 (Fig. 1), decorated with morpholine pendants of variable lengths, bind polyatomic inorganic anions of several different geometries both in aqueous solution and in the solid state.9 In the case of L2, the binding of spherical halide anions,10 of some linear polyhalogen derivatives11 as well as of pseudohalogen anions of the same geometry,12 has also been reported. Crystal structures substantiated an interplay of supramolecular forces, mainly involving strong anion–π interactions, salt bridges and CH⋯anion contacts, while the solution studies highlighted the crucial role of solvent effects in promoting the association phenomenon.
The present paper tackles the bigger picture, i.e. the interplay of different supramolecular forces in anion binding in aqueous solution, by inspecting the interactions of ligands with a new list of anionic species that were selected with the explicit intention to play with the following parameters: (i) the basicity of the anion; (ii) solvation/capability to establish π–π stacking interactions; (iii) the stereochemistry of the interacting groups; and (iv) the host–guest mutual size.
The inorganic anions investigated so far, with the obvious exception of F− (and the fringe one of SCN−), are all conjugate bases of strong acids. Since the strength of salt bridges and hydrogen bonds in general depends on the relative basicity of the interacting partners, peaking when their ΔpKa approaches 0,13 no discrimination was possible on this basis in previous cases. The basicity of L1 (pKa1 = 4.45(3), Table S1†) suggested an acetate (pKa = 4.51(1), Table S1†) as a suitable candidate, together with its essentially non-basic sulfonate analogue, methanesulfonate.
The acetate ion incidentally appears in the Hofmeister series as one of the most hydrated monovalent organic anions. With manifest solvent effects already observed in our preliminary study,9 and bearing in mind that delocalized aromatic anions are less solvated, we also studied the aromatic analogues benzoate and benzenesulfonate. This offers not only the possibility to tune the strength of solvent effects, but also adds to the mix the possibility of π–π stacking interactions, partially moving the complexation phenomenon towards the solvent-driven association of organic molecules in polar solvents. This is expected to be a particularly prominent effect for our ligands, as s-tetrazine in water has been documented to be not just poorly solvated, but hosted in a clathrate-like water molecule cage without relevant solvent–solute hydrogen bonding.14
In this framework, phthalate and isophthalate provided the chance of checking the effect of a second anionic group and the influence of the mutual disposition of the divergent binding sites on the anion.
Finally, the effect of the host–guest size was evaluated varying the length of the aliphatic spacer in the ligand, affecting also the flexibility and preorganization,15 to properly prosecute the evaluation carried out in previous studies.
The core of the current paper revolves around the study of anion complex formation in aqueous solution, investigated mainly through potentiometric titrations. The use of XRD crystal structures of the complexes to identify and assess the role of the key supramolecular interactions in the solid state, consolidated in our previous papers, was once again a precious tool allowing us to draw parallels with the solution studies. However, due to the coexistence of a large number of complex species (differing both for the protonation state and stoichiometry), 1H NMR experiments and the extensive use of in silico simulations have been exploited to bridge the gap between XRD data and potentiometric measurements, allowing for a proper evaluation of the interplay of the different supramolecular forces in aqueous solution.
Results and discussion
Crystal structures
Among all the possible substrates, only hydrogen phthalate, hydrogen isophthalate and benzenesulfonate afforded single crystals of anion complexes of sufficient quality for XRD analysis. Although each of the solved structures is described in detail below, it is interesting to take a synoptic view of them, noticing how all of the expected supramolecular interactions are indeed found in the solid state, but their relevance and overall interplay are different in each case: such a synopsis is presented in Table 1. As evidenced in Table 1, all sorts of situations are encountered: from an essentially cooperative behaviour between salt bridge formation and π-forces (HPhtalate−) to the predominance of charge–charge interactions (C6H5SO3− (b)), passing from intermediate cases where salt bridges and π interactions, either anion–π (C6H5SO3− (a)) or π–π stacking (HIsophthalate−), establish an active dialogue among themselves. An in-depth analysis of the solved crystal structures is provided in the dedicated sections below.| Interaction type | Anionic guest in the crystal structure | |||
|---|---|---|---|---|
| HPht− | HIPht− | C6H5SO3− (a)a | C6H5SO3− (b)a | |
| a Two non-symmetry related anions (a and b) are found in the crystal structure. Refer to Fig. 4 and the dedicated discussion section. b Salt bridge was labelled “direct” if it involved the same ligand molecule with which the anion formed π–π or anion–π contacts (if any). c Salt bridge was labelled “bridging” if it involved a ligand molecule different from the one with which the anion formed π–π or anion–π contacts. | ||||
| Anion–π | + | − | + | − |
| π-Stacking | − | + | − | − |
| Direct salt bridge N–H+⋯Ob | + | − | − | + |
| Bridging salt bridge N–H+⋯Oc | − | + | + | − |
| C–H⋯O contacts | + | − | + | + |
Crystal structure of (H2L2)(HPhthalate)2·2H2O
In the phthalate salt, the ligand assumes a chair-type conformation with the morpholine pendant arms placed in the trans position with respect to the tetrazine ring (Fig. 2).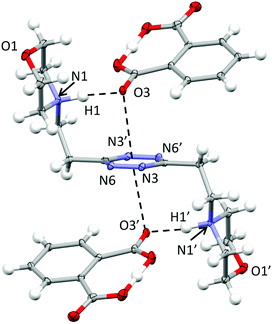 | ||
| Fig. 2 ORTEP drawing of the (H2L)(HPhthalate)2 complex in the (H2L2)(HPhthalate)2·2H2O crystal structure. Selected contacts are shown. | ||
The chair-type conformation was previously observed by the XRD analysis of the complexes formed by the ligand with several anions, such as chloride, bromide, nitrate, thiocyanate, perchlorate and hexafluorophosphate anions.9,10,12 In all these structures, as well as in the present one, the ligand is centrosymmetric and interacts with two symmetry-related anions via NH+⋯X salt bridges and additional anion–π interactions. Actually, the monoprotonated phthalate is almost completely flat, the acidic hydrogen being shared between two oxygens from the two –CO2 groups. One –CO2 oxygen is in contact at the same time with the protonated morpholine nitrogen (N1⋯O3 distance: 2.740(2) Å; N1H1⋯O3 distance: 1.72(3) Å) and with the tetrazine ring, the geometric parameters defining the anion–π interactions being as follows: O3⋯ring–centroid distance = 3.01 Å and O3⋯ring–plane distance = 2.97 Å, offset with respect to the normal to the plane = 0.49 Å. The external oxygen from the other –CO2 group is in contact with the aliphatic hydrogen atoms of the morpholine from a symmetry-related ligand and contributes to the overall crystal packing stabilization. Interestingly, no mutual π–π stacking interactions involve the ligand or the phthalate aromatic ring, while additional contributions to the overall stability are provided by the disordered solvent water molecules.
Crystal structure of (H2L2)(HIsophthalate)2
Different from the phthalate crystal structure, in the isophthalate salt, the ligand assumes a centrosymmetric planar conformation (Fig. 3). Both sides of the tetrazine ring are in contact via offset π-stacking with an isophthalate protonated anion. The anions and the tetrazine rings are almost coplanar and placed at 3.19 Å from one another, while the ring centroids are offset by 1.36 Å (Fig. 3). Moreover, each anion accepts a salt bridge from the protonated morpholine nitrogen of a symmetry-related ligand molecule (N3⋯O4 distance: 2.666(2) Å and N3H1′⋯O4 distance: 1.729(2) Å) and forms head-to-tail O–H⋯O hydrogen-bonds with the adjacent anions in the crystal lattice (O3⋯O5′: 2.530(2) Å; O3–H2⋯O5′: 1.55(5) Å), forming an infinite zig-zag chain (Fig. 3b).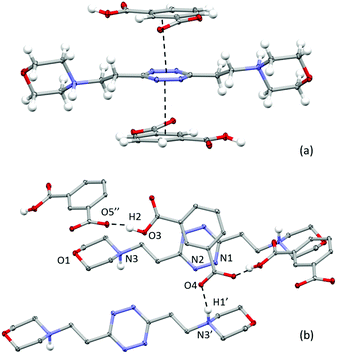 | ||
| Fig. 3 ORTEP drawing of the (H2L2)(HIsophthalate)2 crystal structure. (a) Lateral view of the complex; (b) details of the crystal packing. Selected contacts are shown. | ||
Interestingly, on the basis of the intermolecular potentials evaluated by the Uni force field implemented in Mercury,16,17 the most stabilizing interactions in the crystal packing are the π–π stacking ones (about 54 kJ mol−1), while a lesser extent of stabilization is due to the ligand/anion couples linked by the NH+⋯O salt bridges between morpholine nitrogen and the anion (about 30 kJ mol−1) and, to an even lesser extent, to the head-to-tail H-bonded anions in the anions’ zigzag chain (about 25 kJ mol−1). Following these data, it could be hypothesized that the π-stacking could be an important stabilizing contribution even in solution.
Crystal structure of H2L2(C6H5SO3)2·H2O
As shown in Fig. 4, in this case, the ligand assumes a planar conformation. Two symmetry-non-equivalent benzenesulfonate anions are present in this structure. Both form a salt bridge with the protonated nitrogen atom of the ligand; however only one exhibits a marked interaction with the tetrazine ring, bringing one of the sulfonate oxygen atoms at 3.440 Å from the ring centroid, the interaction being particularly strong with one of the tetrazine nitrogen atoms (O23⋯N2: 3.066 Å and O–N-centroid angle: 93.98°) (Fig. 4). It is to be underlined that, as shown in Fig. 4, these two interactions, the salt bridge and the ring contact, are exerted by the same benzenesulfonate ion with two distinct, symmetry-related, ligand molecules. The other two oxygen atoms of the sulfonate group are found giving rise to either, as said above, a bridge–bond interaction with a distinct, symmetry-related ligand molecule (N5′⋯O21 2.700(3) Å, N5′H5′⋯O21 1.739(2) Å) or multiple CH⋯O contacts.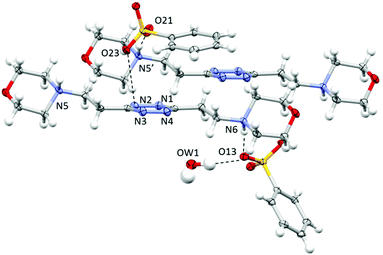 | ||
| Fig. 4 ORTEP drawing and details of the crystal packing of the H2L2(C6H5SO3)2·H2O crystal structure. Selected contacts are shown. | ||
The second anion, required to guarantee the electroneutrality of the system, but probably too bulky to be accommodated in proximity to the tetrazine ring, is found mainly interacting through hydrogen bonds with the co-crystallized water molecule (O13⋯OW1: 2.892(3) Å; OW1–H1⋯O13: 167(4)°) and a salt bridge with the protonated nitrogen atom of the morpholine moiety (N6⋯O13: 2.733(3) Å; N6H6⋯O13: 1.773(2) Å). Several CH⋯anion contacts are also recognizable.
As evidenced in Fig. 4, the π–π stacking interaction offers a modest contribution to the overall stability of the structure, the two closest carbon atoms of the benzene ring being in the 3.5–3.8 Å range from the tetrazine. The relative positions of the two rings, probably imposed by their sizes, by the non-planarity of the sulfonate group, by the geometric constraints of the hydrogen bond network and by the preference of the tetrazine for the anionic head rather than for the aromatic portion of the anion, produce a 13.01° angle between the ring planes, limiting their superimposition. The argument is much more valid for the second benzenesulfonate anion, with an angle in-between the ring planes of 53.34°, which does not give rise to contacts with the tetrazine ring.
Anion binding in solution
As in the case of their inorganic counterparts, the investigated series of organic anions does give rise to detectable interactions with our receptors in water. The stability constants of the anion complexes, obtained through potentiometric titrations performed in 0.10 M NMe4Cl at 298.1 ± 0.1 K, are reported in Table 2 for L1 and Table 3 for L2. 1H NMR experiments were also performed at selected pH values, chosen to be mostly representative of a single complex species in solution: shifting of both anion and ligand signals, demonstrating complex formation, was observed. Complexation induced shift (CIS) values are reported in Tables 4 and 5 for L1 and L2, respectively. In one case ([H2L1(C6H5SO3)]+), it was possible to confirm the stability constant obtained from potentiometric measurements by using NMR data (see the Experimental section and Table 2).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K) for L1 anion complex formation determined at 298.1 ± 0.1 K in 0.1 M NMe4Cl aqueous solution. Figures in parentheses are standard deviations of the last significant figure
K) for L1 anion complex formation determined at 298.1 ± 0.1 K in 0.1 M NMe4Cl aqueous solution. Figures in parentheses are standard deviations of the last significant figure
| Equilibrium | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
|---|---|
| a Determined by 1H NMR titration. | |
| HL1+ + CH3SO3− = [HL1(CH3SO3)] | 2.21(9) |
| H2L12+ + CH3SO3− = [H2L1(CH3SO3)]+ | 1.6(2) |
| HL1+ + C6H5SO3− = [HL1(C6H5SO3)] | 2.49(5) |
| H2L12+ + C6H5SO3− = [H2L1(C6H5SO3)]+ | 2.48(5) |
| 2.8(9)a | |
| L1 + CH3COO− = [L1(CH3COO)]− | 2.71(8) |
| L1 + CH3COOH = [L1(CH3COOH)] | 3.27(5) |
| HL1+ + CH3COOH = [HL1(CH3COOH)]+ | 3.09(3) |
| L1 + C6H5COO− = [L1(C6H5COO)]− | 3.02(1) |
| HL1+ + C6H5COO− = [HL1(C6H5COO)] | 3.16(3) |
| H2L12+ + C6H5COO− = [H2L1(C6H5COO)]+ | 2.95(4) |
| L1 + Pht2− = [L1(Pht)]2− | 2.88(2) |
| L1 + HPht− = [L1(HPht)]− | 2.87(3) |
| HL1+ + HPht− = [HL1(HPht)] | 2.56(3) |
| H2L12+ + HPht− = [H2L1(HPht)]+ | 2.60(3) |
| HL1+ + IPht2− = [HL1(IPht)]− | 3.40(5) |
| HL1+ + HIPht− = [HL1(HIPht)] | 2.73(8) |
| H2L12+ + HIPht− = [H2L1(HIPht)]+ | 3.45(5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K) for L2 anion complex formation determined at 298.1 ± 0.1 K in 0.1 M NMe4Cl aqueous solution. Figures in parentheses are standard deviations of the last significant figure
K) for L2 anion complex formation determined at 298.1 ± 0.1 K in 0.1 M NMe4Cl aqueous solution. Figures in parentheses are standard deviations of the last significant figure
| Equilibrium | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
|---|---|
| HL2+ + CH3SO3− = [HL2(CH3SO3)] | 1.41(8) |
| H2L22+ + CH3SO3− = [H2L2(CH3SO3)]+ | 1.8(3) |
| HL2+ + C6H5SO3− = [HL2(C6H5SO3)] | 1.44(6) |
| H2L22+ + C6H5SO3− = [H2L2(C6H5SO3)]+ | 1.84(2) |
| HL2+ + CH3COO− = [HL2(CH3COO)] | 2.33(9) |
| H2L22+ + CH3COO− = [H2L2(CH3COO)]+ | 2.0(1) |
| H2L22+ + CH3COOH = [H2L2(CH3COOH)]2+ | 2.67(6) |
| [H2L2(CH3COOH)]2+ + CH3COO− = [H2L2(CH3COOH)(CH3COO)]+ | 2.74(6) |
| L2 + C6H5COO− = [L2(C6H5COO)]− | 1.82(9) |
| HL2+ + C6H5COO− = [HL2(C6H5COO)] | 2.18(5) |
| H2L22+ + C6H5COO− = [H2L2(C6H5COO)]+ | 2.62(3) |
| [H2L2(C6H5COO)]+ + C6H5COO− = [H2L2(C6H5COO)2] | 2.69(7) |
| HL2+ + Pht2− = [HL2(Pht)]− | 2.27(2) |
| H2L22+ + Pht2− = [H2L2(Pht)] | 2.6(3) |
| H2L22+ + HPht− = [H2L2(HPht)]+ | 2.0(7) |
| H2L22+ + H2Pht = [H2L2(H2Pht)]2+ | 1.9(1) |
| [H2L2(Pht)] + Pht2− = [H2L2(Pht)2]2− | 2.16(9) |
| [H2L2(Pht)] + HPht− = [H2L2(HPht)(Pht)]− | 1.64(3) |
| [H2L2(HPht)]+ + H2Pht = [H2L2(H2Pht)(HPht)]+ | 2.97(7) |
| [H2L2(H2Pht)]2+ + H2Pht = [H2L2(H2Pht)2]2+ | 2.42(3) |
| L2 + IPht2− = [L2(IPht)]2− | 1.75(6) |
| HL2+ + IPht2− = [HL2(IPht)]− | 1.79(6) |
| H2L22+ + IPht2− = [H2L2(IPht)] | 2.37(1) |
| Substrate | CISa ligandb | CISa anionc | pH | Reference species |
|---|---|---|---|---|
| a δ (ppm)/% formation of complex species. b Referring to 1, 3 and 2 groups as designated in Fig. 1. c Referring to ortho, para and meta positions, respectively, for aromatic substrates. | ||||
| Acetate | −0.02 | −0.46 | 3.5 | [HA-HL1] |
| −0.01 | ||||
| −0.02 | ||||
| Methanesulfonate | −0.97 | −0.89 | 4.0 | [A-HL1] |
| −0.57 | ||||
| −1.02 | ||||
| Benzoate | 0.04 | −0.22 | 8.0 | [A-L1] |
| 0.05 | −0.28 | |||
| 0.06 | −0.22 | |||
| Benzenesulfonate | −5.77 | −3.63 | 3.0 | [A-H2L1] |
| −2.08 | −3.92 | |||
| −4.86 | −3.86 | |||
| Substrate | CISa ligandb | CISa anionc | pH | Reference species |
|---|---|---|---|---|
| a δ (ppm)/% formation of complex species. b Referring to 4, 2, 3 and 1 groups as designated in Fig. 1. c Referring to ortho, para and meta positions, respectively, for aromatic substrates. | ||||
| Acetate | 1.10 | −0.09 | 3.0 | [HA-H2L2] |
| 1.10 | ||||
| 1.09 | ||||
| 1.10 | ||||
| Methanesulfonate | 1.71 | −0.21 | 3.0 | [A-H2L2] |
| 1.72 | ||||
| 1.71 | ||||
| 1.72 | ||||
| Benzoate | 1.03 | −0.06 | 4.5 | [A-H2L2] |
| 0.93 | −0.04 | |||
| 0.93 | −0.04 | |||
| 1.22 | ||||
| Benzenesulfonate | −0.11 | −0.04 | 3.0 | [A-H2L2] |
| −0.62 | −0.05 | |||
| −0.17 | −0.03 | |||
| −0.04 | ||||
Equilibrium constants for the formation of anion complexes in solution were obtained through a computer-aided analysis of potentiometric titration curves. The HYPERQUAD18 analysis software furnishes stability constants of complexes according to the general equilibria jAn− + kL + mH+ = (AjLkHm)(m−jn)+. Such equilibria are indicative of complex stoichiometry but do not provide any insight into the location of the m protons within each complex species. Such an ambiguity is not due to the data treatment, but is inherent to the potentiometric experiment; the glass electrode probes only the point by point free H+ concentration in solution, so that, as long as the same m number of protons are present in a given complex species, their localization cannot affect the shape of the titration curve. Other studies showed that the formation of anion complexes tends not to modify the protonation pattern of ligands, although a modest general shift of NMR signals, corresponding to the increase of the ligand basicity brought about by anion complexation, has been observed.19 Accordingly, the location of protons in the complexes was assumed to be generally regulated by the basicity of the interacting species and the relevant stability constants were calculated following this rule. In those cases where matching of protonation constants between the ligand and the anion required a closer inspection, in silico simulations were employed; Tables 2 and 3 list the stability constants of complexes compiled through the double-criteria of basicity of the isolated components and the higher computational stability of the displayed complexes over their possible tautomers. However, the possible coexistence in solution of scarce amounts of complex tautomers alongside the most stable form (presented in Tables 2 and 3) cannot be completely ruled-out.
Since we want to deal with the interplay of different supramolecular forces in solution, whose net sum is mirrored by stability constants of complexes, it is important to abstract from the individual data looking for general trends. Conditional stability constants are one of the abstraction tools at our disposal. They can be calculated as a function of pH in the form Kcond = ∑[Hi+jLA]/(∑[HiL] × ∑[HjA]), where i and j are the number of acidic protons on the ligand and on the anion, respectively, allowing a direct comparison of the affinity of each ligand for the different anions eluding the problems connected with the different speciation of the systems.20 As anticipated from the beginning, two main stability trends are expected: salt bridge strength is expected to increase with the basicity of the anion (carboxylates > sulfonates), while stacking forces and solvent effects are anticipated to be more prominent for hydrophobic substrates (aromatic > aliphatic); overall, for the monocharged anion series, this should result in the order of stability: benzoate > acetate > benzenesulfonate > methanesulfonate. Examining Fig. 5, such a trend is indeed found for both ligands above pH 4.5 and is maintained over all the pH range by sulfonate anions. The difference between sulfonate and carboxylate complexes is marked, following the expected order, and the preferential affinity for the acetate or benzoate is strongly pH dependent, the latter being invariably favoured in more alkaline media, suggesting a π–π stacking/hydrophobic effect driven association. Below pH 4.5, acetate complexes become more stable because anion protonation only disables the benzoate for coordination.
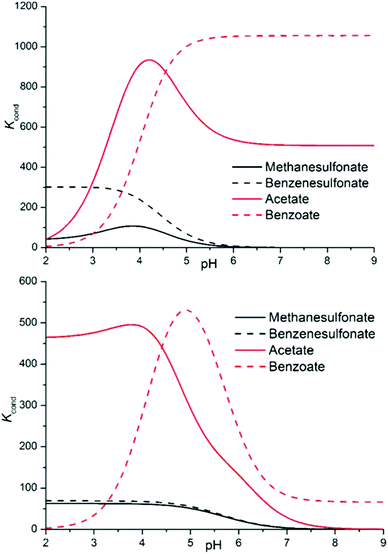 | ||
| Fig. 5 Conditional stability constants for complexes L1 (top) and L2 (bottom) with a series of monovalent anions. | ||
Such coincidence between theory and experimental data, although intriguing, can be severely misleading. Accordingly, we will prosecute our search for general trends and re-evaluate selectivity remarks in light of the whole discussion. The following material is divided into 7 focal points, as follows: (i) correlation between the stability of complexes and charge separation between hosts and guests; (ii) comparison between carboxylates and sulfonates; (iii) distinction between aromatic and aliphatic guests; (iv) differences in the stabilities of complexes between the two ligands; (v) stoichiometries of the formed adducts; (vi) the re-evaluation of selectivity features; and (vii) the effect of the regiochemistry of dicarboxylate anions.
In relation to the complexes involving protonated ligands, a manifest poor correlation between the stability of the complexes and substrate–receptor charge separation is observed (point i). In particular, for a given anion, increasing the ligand charge does not result at all in the stability gain expected for the formation of a single salt bridge in water (5 ± 1 kJ mol−1).21,22
This finding is perfectly in line with the evidence from our previous studies, indicating the anion–π interactions, rather than salt bridges, as the main force in play, along with strongly exoentropic solvent effects, in promoting the association of anions with L1 and L2.9
Since this was demonstrated for simple inorganic species, the reinforcement of this notion is not surprising for the less hydrated, and potentially stronger interacting (due to the possibility of π–π stacking), organic anions. Here, the direct involvement of the tetrazine in anion binding is also suggested by NMR data, as upfield shifts of 1H signals are observed, to different extents, for all the anions (Tables 4 and 5, Fig. S1†). If in many cases the formation of strong salt bridges may be invoked as an explanation, it is noteworthy that shielding is nevertheless observed in simply hydrogen bonded systems, lacking proper +/− charge separation between the partners (e.g. HL1+-HAcetate, Table 4, H2L22+-HAcetate, Table 5), or lacking hydrogen bonds at all (e.g. L1-benzoate−, Table 4). If the explanation of the CIS is to be found, at least partially, in aromatic ring currents, then the anion must be located right above the tetrazine ring, as expected for π–π or anion–π interaction modes; the CIS observed for the L1-benzoate− complex (Table 4) is a good case in point here.
Focusing now on complexes involving neutral ligands, they are steadily observed only for carboxylate anions (point ii). Contrary to what we could expect, the extra stability provided by the matching of basicity among receptor and substrate protonable sites does not translate into a straightforward extra contribution to complex stability (Tables 2 and 3). The main reason for this lack of correlation, which becomes evident in the simulated most stable conformations of the complexes (e.g.Fig. 6 and 7), is to be ascribed to the different geometries of the anions.
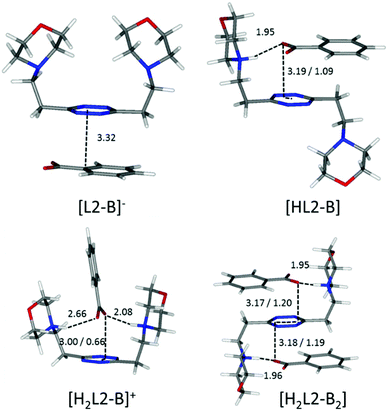 | ||
| Fig. 6 Calculated solution conformations of L2 complexes with benzoate (B−) in solution. Distances in Å. Parameters for anion–π contacts given as plane/offset values. | ||
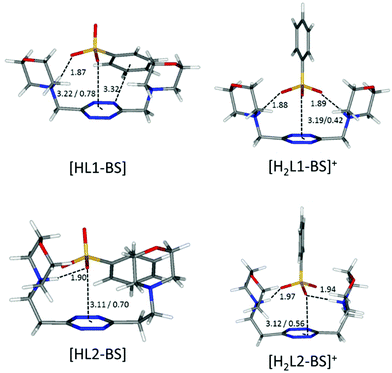 | ||
| Fig. 7 Calculated solution conformations of L1 (top) and L2 (bottom) complexes with benzenesulfonate (BS−) in solution. Distances in Å. Parameters for anion–π contacts given as plane/offset values. | ||
Flat carboxylates are invariably preferred because of their ability to sit on the tetrazine and stick to it, causing extensive desolvation of both host and guest surfaces, while giving rise to salt bridges at the same time, whenever possible (Fig. 6 and 8). Things are a little more complicated for the three-dimensional sulfonates, which have to choose between salt bridges and anion–π interactions or π–π stacking interactions. In the case of neutral ligands, that would mean managing to accommodate their bulkier polar groups without getting too close to the electronegative morpholine atoms: as a matter of fact, such complexes are not experimentally observed.
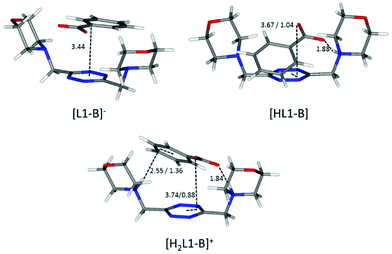 | ||
| Fig. 8 Calculated solution conformations of L1 complexes with benzoate (B−) in solution. Distances in Å. Parameters for anion–π contacts given as plane/offset values. | ||
Maintaining the focus on complexes of neutral, non-protonated, ligands, we can also see that they are systematically encountered only for aromatic guests (point iii), aliphatic ones being solely represented by the L1-acetate complex. The spontaneous association of non-polar solutes in water is commonplace, and it is well-known to be driven by the hydrophobic effect. The studied aliphatic anions are both missing any contribution from the stacking interaction and are far less hydrophobic than their aromatic counterparts, resulting in non-detectable, at least by means of our potentiometric method, association equilibria. Interestingly, there is good coincidence between the in silico simulation of the benzoate complex of the neutral, non-protonated, L1 (Fig. 8) and 1H NMR data (Table 4), the upfield shift of the anion signals being ascribable to the tetrazine ring current. This reinforces the notion that the direct interaction of the π clouds is indeed a factor in play for our complexes. The same can be concluded comparing the stability of L1 complexes with monovalent aliphatic and aromatic anions, the latter being found more stable whenever the speciation of the systems allows for a direct comparison. A similar conclusion cannot be drawn at once for potentiometric data of L2, which, different from L1, does not maintain a similar conformation in all of its complexes; its increased flexibility accounts for the more shifting nature of the data, which are less prone to direct comparison (cf.Fig. 5 and its relative discussion in point vi for an inclusive analysis based on conditional stability constants).
The scarce or total lack of additivity between π–π stacking interactions and other supramolecular forces for sulfonate anions is manifest in the comparison between the stability of L1 and L2 complexes with methane- and benzene-sulfonate severally (L1: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 2.21 vs. log
K = 2.21 vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 2.49 for monoprotonated complexes, log
K = 2.49 for monoprotonated complexes, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 1.6 vs. log
K = 1.6 vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 2.48 for diprotonated complexes, respectively; L2: log
K = 2.48 for diprotonated complexes, respectively; L2: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 1.41 vs log
K = 1.41 vs log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 1.41 for monoprotonated complexes, log
K = 1.41 for monoprotonated complexes, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 1.8 vs. log
K = 1.8 vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 1.84 for diprotonated complexes, respectively; Tables 2 and 3). The insensitivity of stability constants to the aromatic or aliphatic nature of the guests, log
K = 1.84 for diprotonated complexes, respectively; Tables 2 and 3). The insensitivity of stability constants to the aromatic or aliphatic nature of the guests, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values found close for L1 and equal within the experimental error in the case of L2 complexes of analogous anions, demonstrates the scarce contribution of stacking forces for these tetrahedral anions. It is worth mentioning that the experimental results mirror perfectly the in silico studies, which, as shown in Fig. 7, demonstrate the marginal involvement of contacts between host and guest aromatic rings in complex stabilization, especially in the case of L2 adducts.
K values found close for L1 and equal within the experimental error in the case of L2 complexes of analogous anions, demonstrates the scarce contribution of stacking forces for these tetrahedral anions. It is worth mentioning that the experimental results mirror perfectly the in silico studies, which, as shown in Fig. 7, demonstrate the marginal involvement of contacts between host and guest aromatic rings in complex stabilization, especially in the case of L2 adducts.
Centring the discussion on the ability of ligands L1 and L2 to form anion complexes, contrary to our previous data for inorganic anions,9 here, L1 complexes are generally more stable than L2 ones (point iv). Fig. S2† allows for a direct comparison between the two ligands, showing how the L1 species are invariably more abundant in a simulated competition setting.
A possible explanation of this trend reversal is provided by the most stable conformations calculated for these complexes in solution. In the case of the benzoate, for instance, analogous [L(C6H5COO)]−, [HL(C6H5COO)] and [H2L(C6H5COO)]+ (L = L1, L2) species are formed. As shown in Fig. 8, L1 is invariably found to be U-shaped, with all the binding sites converging towards the anion (Fig. 8), while this is not always the case for L2 (Fig. 6). Furthermore, the shorter methylenic spacer allows for a steady and significant contribution of the anion arenic portion to the interaction, which is found scarce in all the minimum energy conformations of L2 complexes.
These same observations are also found to be true for another series of analogous complexes, that of benzenesulfonate. As one can see in Fig. 7, the more curled-up structure of L1 invariably results in an increased involvement of the benzenic ring in the host–guest interactions.
Accordingly, the higher overall stability observed for L1 complexes appears congruent with what should be expected due to its more rigid structure (higher preorganization/reduced loss of conformational degrees of freedom upon complexation), better convergence of binding sites and higher charge density when fully protonated, compared to its superior homologue L2.
The main difference justifying the opposite stability trend observed for inorganic anions (L2 > L1)9 lies in the geometry and charge distribution of the guest. Trigonal, tetrahedral and octahedral anions offer the more flexible L2 the possibility to wrap around them more easily than the flat aromatic anions of the new series (cf. the case of the benzoate, Fig. 6), offering several electron-rich binding sites amenable for accepting salt bridges or interacting with the tetrazine ring. In contrast, L1, whose inability to fold led to the replacement of salt bridges with CH⋯anion contacts in the case of inorganic anions,9 now manages to maintain in contact host and guest aromatic portions, while giving rise to salt bridges with the anionic groups protruding from the benzenic ring. This, reinforced by the magnified importance of solvation effects, the hydrophobicity of the anions being greatly increased in comparison with the inorganic ones, explains the discrepancy in the relative stability of the complexes among the two series of studied anions.
Coming to the subject of stoichiometry, L2 demonstrates a marked tendency to form 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ligand
2 ligand![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anion complexes, which is totally absent in the case of L1 (point v). As one can observe, for example in Fig. 6, monoprotonated complexes are found in the signature chair conformation, stabilized by the concomitant establishment of both salt bridge and anion–π interactions. This interaction mode leaves out the other face of the tetrazine ring and the additional morpholine group for the interaction with a second anion, resembling the centrosymmetric arrangement observed in the crystal structures of inorganic anion complexes (NO3−, ClO4−, PF6−, Cl−, Br− and SCN−)9,10,12 and in the phthalate complex (Fig. 2). Such a conformation is not amenable in solution for the less flexible L1, which, in fact, sticks to the 1
anion complexes, which is totally absent in the case of L1 (point v). As one can observe, for example in Fig. 6, monoprotonated complexes are found in the signature chair conformation, stabilized by the concomitant establishment of both salt bridge and anion–π interactions. This interaction mode leaves out the other face of the tetrazine ring and the additional morpholine group for the interaction with a second anion, resembling the centrosymmetric arrangement observed in the crystal structures of inorganic anion complexes (NO3−, ClO4−, PF6−, Cl−, Br− and SCN−)9,10,12 and in the phthalate complex (Fig. 2). Such a conformation is not amenable in solution for the less flexible L1, which, in fact, sticks to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry.
1 stoichiometry.
Interestingly, only carboxylate anions (acetate, benzoate, phthalate, and isophthalate) do give rise to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes with L2. This correlates well with the discussion on the influence of the anion geometry. Carboxylate groups lay coplanar to their benzenic ring, allowing the charged groups to form salt bridges while the aromatic moieties can freely engage in parallel displaced π–π stacking interactions, which ultimately lead to the chair conformation observed for the ligand in L2 complexes (Fig. 6). This is not the case for sulfonate anions; the trigonal shape of the charged –SO3− group forces the system to choose: if a linear strong salt bridge is formed, imperfect matching in the π–π stacking interaction is not avoidable; else, if the stacking interaction is preferred, the contribution of charge–charge interaction is greatly sacrificed. According to our simulations, when the ligands are diprotonated, they wrap around the anion as portrayed in Fig. 7, two salt bridges taking the upper hand over π–π stacking. A point worth mentioning here, reinforcing the notion and showing good agreement between experimental and in silico data, is the fact that diprotonated complexes of benzenesulfonate are found to be equally or marginally more stable than their monoprotonated counterparts for both ligands (log
2 complexes with L2. This correlates well with the discussion on the influence of the anion geometry. Carboxylate groups lay coplanar to their benzenic ring, allowing the charged groups to form salt bridges while the aromatic moieties can freely engage in parallel displaced π–π stacking interactions, which ultimately lead to the chair conformation observed for the ligand in L2 complexes (Fig. 6). This is not the case for sulfonate anions; the trigonal shape of the charged –SO3− group forces the system to choose: if a linear strong salt bridge is formed, imperfect matching in the π–π stacking interaction is not avoidable; else, if the stacking interaction is preferred, the contribution of charge–charge interaction is greatly sacrificed. According to our simulations, when the ligands are diprotonated, they wrap around the anion as portrayed in Fig. 7, two salt bridges taking the upper hand over π–π stacking. A point worth mentioning here, reinforcing the notion and showing good agreement between experimental and in silico data, is the fact that diprotonated complexes of benzenesulfonate are found to be equally or marginally more stable than their monoprotonated counterparts for both ligands (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values: 2.49 vs. 2.48 for L1 and 1.84 vs. 1.44 for L2, Tables 2 and 3). This mirrors what was observed in the predicted minimum energy conformations (Fig. 7), where the second protonation brings not only stronger enthalpic contributions but also entropic losses due to the exposure of the hydrophobic part of the anion to the solvent. The preference of the tetrazine for the polar group rather than the aromatic portion of the anion, as found in the simulations (Fig. 7), is also supported, at least in the case of L2, by the arrangement found in the crystals of H2L2(C6H5SO3)2·H2O (Fig. 4). The U folding assumed in solution by both diprotonated ligands when forming benzenesulfonate complexes (Fig. 7) leaves no possibility of other stoichiometries in solution but 1
K values: 2.49 vs. 2.48 for L1 and 1.84 vs. 1.44 for L2, Tables 2 and 3). This mirrors what was observed in the predicted minimum energy conformations (Fig. 7), where the second protonation brings not only stronger enthalpic contributions but also entropic losses due to the exposure of the hydrophobic part of the anion to the solvent. The preference of the tetrazine for the polar group rather than the aromatic portion of the anion, as found in the simulations (Fig. 7), is also supported, at least in the case of L2, by the arrangement found in the crystals of H2L2(C6H5SO3)2·H2O (Fig. 4). The U folding assumed in solution by both diprotonated ligands when forming benzenesulfonate complexes (Fig. 7) leaves no possibility of other stoichiometries in solution but 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, even for the flexible L2.
1, even for the flexible L2.
A borderline, and thus interesting, case is offered by an acetate, which surely maintains the geometrical features of the other carboxylate anions, yet lacks entirely the aromatic portion, partially invalidating some of the above arguments. In fact, without the stabilizing contribution of π–π stacking, the ligand in the [H2L2(Acetate)]+ complex is predicted to be in a folded conformation by our simulations (Fig. 9), closely resembling the situation encountered for sulfonate anions. Different from them, however, the acetate is a base, although of modest strength, and thus it can undergo protonation; in the calculated conformation of [H2L2(HAcetate)]2+, the ligand opens up once more in the familiar chair conformation (Fig. 9), again resulting in the possibility of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry, which is indeed empirically encountered (Table 3).
2 stoichiometry, which is indeed empirically encountered (Table 3).
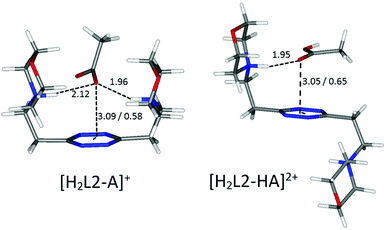 | ||
| Fig. 9 Calculated solution conformations of selected L2-acetate (A−) complexes in solution. Distances in Å. Parameters for anion–π contacts given as plane/offset values. | ||
Overall, the tendency of L2 to form 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ligand
2 ligand![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anion complexes is due to its increased flexibility compared to L1, but it is subject to the geometry of the anions and their basicity. This ultimately leads to discrimination of the tetrahedral and essentially non-basic sulfonates from their carboxylate counterparts.
anion complexes is due to its increased flexibility compared to L1, but it is subject to the geometry of the anions and their basicity. This ultimately leads to discrimination of the tetrahedral and essentially non-basic sulfonates from their carboxylate counterparts.
Finally, building on the previous discussion (points i–v), we may now re-evaluate properly the selectivity features disclosed by the analysis of conditional stability constants shown in Fig. 5 (point vi). Indeed, as commented above, the theoretical order of stability expected on the basis of the salt bridge strength and solvation/π-stacking contribution to the overall host–guest interaction is experimentally encountered for the series of monocharged anions; yet, in light of the close inspection carried out above, we are forced to conclude that other factors subtend to the observed stability trend. If we admit, as demonstrated in point i, that we have a poor charge–charge control of the association phenomena, then the salt bridge strength may not be invoked to justify the stability gap observed between carboxylate and sulfonate anion complexes. In contrast, we may argue that looking at the salt bridge contribution only, in the complexes of diprotonated ligands, sulfonate anions might even be more stabilized than carboxylate ones; even if in the latter case the intrinsic strength of the salt bridge is higher, carboxylates never form more than 1 salt bridge each in our simulations (Fig. 6, 8 and 9), while sulfonates can easily form 2 (Fig. 7). The reason for this difference lies in the geometry of the anion, the geometry which was also found to be responsible for the different stoichiometries of the formed adducts (point v) (affecting selectivity in the case of L2) and for the overall higher tendency of carboxylates to establish π-stacking interactions (point ii). Geometry's regulating function on the cooperativity of the different supramolecular forces is also manifest in the different selectivities observed for aliphatic over aromatic substrates (point iii). In the case of carboxylate anions, where cooperativity is favoured, we can clearly see that the aromatic benzoate is highly preferred over the aliphatic acetate starting from alkaline media (where the association resembles that of aromatic molecules due to solvent effects and π–π stacking interactions) until the different speciation of the systems allows so. In contrast, since the tetrahedral shape of sulfonates does not allow stacking interactions (L2, Fig. 7) or allows them poorly (L1, Fig. 7), selectivity is indeed found to be scarcely affected (L1), if at all (L2), by the aromatic or aliphatic nature of the substrate.
The overall lesson is that amenability for selected interactions of the single binding sites of a substrate is of no use without an arrangement which favours the cooperativity of different supramolecular forces. In the present case, the success of carboxylate guests over sulfonate ones is due to the topology of their binding sites, rather than the net strength of the formed salt bridges.
Finally, the regiochemistry of dicarboxylate anions is taken into account (point vii). Despite leading to the very same conclusions, it is instructive to undertake the analysis from a double viewpoint. If we look at the solution data (Tables 2 and 3) from the ligands’ perspective, L1 and L2 present different selectivities for the substrates: L1 forms more stable complexes with an isophthalate than with a phthalate, while the contrary is true for L2. Conditional stability constant comparisons (Fig. S3†) reveal that isophthalate binding is preferential in the 2.0–5.0 pH range for L1, while L2 privileges the phthalate over its isomer in the 2.0–7.0 pH range. In both cases, the selective recognition of one or the other regioisomer is possible under different conditions.
Instead, if we examine the data in terms of the affinity of the same anion for the two different receptors, L1 and L2, we find that both phthalate and isophthalate bind preferentially to L1, rather than L2, over a large pH range (see dedicated selectivity diagrams in Fig. S2† and/or compare values of conditional stability constants in Fig. S3†).
In summary, L1 forms more stable complexes than L2 with both anions, which should not surprise according to the general discussion in point iv, yet, when the two substrates compete for the same ligand, L1 recognizes preferentially the isophthalate over the phthalate, while L2 behaves in contrast, preferring the phthalate to its isomer.
A guiding light for rationalizing the data is provided by the in silico simulation of the monoprotonated L2 complexes with both anions (Fig. 10) and their comparison with the solved crystal structures of complexes featuring these anions (Fig. 2 and 3). The isophthalate has an inner tendency to simultaneously interact with both ligand arms, thus reducing the availability of binding sites for a second guest, and to involve its aromatic nucleus in the interaction. It should be noted that such an involvement of the stacking interaction in anion binding was also the main feature observed in the solved (H2L2)(HIsophthalate)2 crystal structure (Fig. 3), both visually and according to intermolecular potentials (see the crystal structure of (H2L)(HIsophthalate)2).
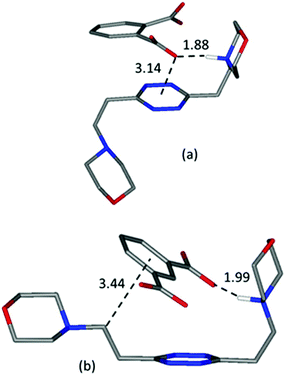 | ||
| Fig. 10 Calculated most stable conformations in solution of HL2+ complexes with phthalate (a) and (b) isophthalate dianions, respectively. | ||
The phthalate, in contrast, due to the more gathered arrangement of its anionic sites, interacts with the tetrazine ring and just one morpholinic pendant (Fig. 10). The L2 ligand assumes an overall chair-like conformation, stabilized by a short hydrogen bond contact (H⋯O 1.88 Å) and by an anion–π interaction involving the same oxygen atom (O⋯ring-centroid distance = 3.14 Å, X⋯ring-plane distance = 2.99 Å, offset with respect to the normal to plane = 0.94 Å) allowing, as in the case of the benzoate (Fig. 6), the interaction of a second anion with the residual vacant binding sites of the ligand. Here, the resemblance with the (H2L)(HPhthalate)2 crystal structure (Fig. 2) is even more striking, strongly supporting a chair arrangement of the ligand which allows for the facile formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ligand
2 ligand![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anion complexes in solution. The formation of such complexes necessarily favours phthalate over isophthalate binding by mass action in the case of L2, resulting in the observed selectivity.
anion complexes in solution. The formation of such complexes necessarily favours phthalate over isophthalate binding by mass action in the case of L2, resulting in the observed selectivity.
On the other hand, the more gathered structure of L1, already shown to account for the across-the-board higher stability of its complexes (point iv) and also to prevent complex stoichiometries different from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (point v), matches the tendency of the isophthalate anion to interact simultaneously with the two ligands’ arms: the 1,3 disposition of the anion binding sites matching far better the para arrangement of the morpholine pendants around the 1,2,4,5 tetrazine core.
1 (point v), matches the tendency of the isophthalate anion to interact simultaneously with the two ligands’ arms: the 1,3 disposition of the anion binding sites matching far better the para arrangement of the morpholine pendants around the 1,2,4,5 tetrazine core.
It should be mentioned that regiochemistry per se may not account for the detected differences: more subtle factors, better described with the broader concept of stereoelectronic effects, are in play. Geometry itself, beyond the ortho or meta disposition of the anionic sites, is not trivial either. Stereoelectronic reasons allow better planarity for the isophthalate dianion than for the phthalate, torn between maximizing electron delocalization on the ring and minimizing charge–charge repulsion between carboxylate groups (Fig. 10). The situation is not static either, the protonation of the phthalate implying its complete flattening due to the formation of a strong intramolecular hydrogen bond, as observed in the solid state for the case of the complexes with the monoprotonated anions (Fig. 2). As a consequence, not only does the mutual disposition of the divergent binding sites of the two substrates differ beyond the ortho or meta orientation, pointing in or out of the benzene plane, but it is also subject, at least the phthalate, to noticeable modification due to the protonation state. Solvation effects due to proximal or distal charged sites may also play an active role for these dianions. The basicity of the two regioisomers is also greatly affected; due to the formation of the aforementioned intramolecular hydrogen bonds, it is much easier to protonate once the phthalate than the isophthalate, and, conversely, it is easier to protonate twice the isophthalate than the phthalate (see Table S1†). Interestingly enough, in this game of stereoelectronic effects and basicity constants, the phthalate ends up possessing a persistent monoanionic form right where the diprotonated form of L2, H2L22+, starts reaching its maximum (pH 4.0), thus inevitably promoting the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes and favouring selectivity. The isophthalate instead is left with basicity constants which match almost perfectly those of L1 (pKa1 = 4.32 vs. pKa1 = 4.45 and pKa2 = 3.28 vs. pKa2 = 3.45, respectively; see Table S1†): hence, the matching of pKas might be actually one of the features contributing to the selectivity observed for the L1–isophthalate system.
2 complexes and favouring selectivity. The isophthalate instead is left with basicity constants which match almost perfectly those of L1 (pKa1 = 4.32 vs. pKa1 = 4.45 and pKa2 = 3.28 vs. pKa2 = 3.45, respectively; see Table S1†): hence, the matching of pKas might be actually one of the features contributing to the selectivity observed for the L1–isophthalate system.
Conclusions
The focus of this work is on the interplay of different supramolecular forces in stabilizing organic anion complexes both in solution and in the solid state. The studied substrates have been selected to possess different but related stereoelectronic properties, allowing the rationalization of a broad sample case of possible interactions. The study has been intentionally undertaken in water, despite it being one of the most challenging solvents for anion binding studies, to demonstrate how the interplay of different weak forces is able to stabilize anion complexes even in aqueous media, provided that certain criteria of host–guest electronic and structural complementarity are met.The observed interactions include three main kinds of forces, salt bridge/hydrogen bonds, anion–π interactions and π–π stacking, together with other contributions to complex stability such as the hydrophobic effect or size/shape complementarity with the two homologous ligands L1 and L2. For the series of monoanionic species, both L1 and L2 complexes show a stability trend which follows the order: benzoate ≥ acetate > benzenesulfonate > methanesulfonate, i.e. carboxylate > sulfonate and aromatic > aliphatic.
Salt bridge strength, which was anticipated to be higher for carboxylate than for sulfonate anions due to the better matching of pKas of the ligands and anions, could be invoked to justify the data. However, the geometry of the anions was found to be a controlling factor, so that sulfonates could be even more stabilized by salt-bridges than carboxylates in some cases, due to the fact that, owing to the shape of the charged group, they are able to form 2 salt bridges instead of only 1.
Anion–π interactions are also found to play an important role in these complexes, being preferred over π–π forces in most cases. Their importance for carboxylate anions manifests itself in the stabilization of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ligand
2 ligand![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anion complexes, which are ubiquitous with L2.
anion complexes, which are ubiquitous with L2.
Stacking interactions were found to contribute to the overall stability of complexes, but their participation is intermittent. Stacking is found to be the key force promoting the association of aromatic carboxylates to neutral non-protonated ligands, yet it contributes almost nothing to the overall stabilization of sulfonate complexes.
The same is true also for the hydrophobic effect: it is found to occur in every case for flat carboxylate substrates, while it does not in the case of sulfonates.
Geometrical features of the anions and size/shape effects of the ligands appear to be the most important factors in orchestrating the interplay of the different supramolecular forces. Indeed, L1, with a more gathered converging disposition of binding sites and a rigid structure, forms complexes of higher stability than L2, while the higher flexibility of L2 favours the formation of complexes with different stoichiometries. Overall, the size/shape of the ligands determine the selectivity for the studied anions, including the intriguing one observed for the phthalate regioisomers: L1 preferentially binds to the isophthalate, while L2 to the phthalate. Although geometry appears once more as a key feature, the provided explanation of the experimental data could not overlook global stereoelectronic considerations, exceeding a simplistic view of isomerism.
Experimental
Materials
L1 and L2 (3,6-bis(morpholin-4-ylmethyl)-1,2,4,5-tetrazine and 3,6-bis(morpholin-4-ylethyl)-1,2,4,5-tetrazine, respectively) were synthesized as previously described.9 Pink crystals of H2L2(C6H5SO3)2·H2O were obtained upon evaporation at room temperature of an aqueous solution of L2 (0.01 M) at pH 4.0 containing an excess of benzenesulfonate. For the phthalate and isophthalate complexes, an ethanolic solution of the corresponding dicarboxylic acids was prepared separately and added dropwise to an ethanolic solution of the ligand without further pH adjustment. Slow evaporation at room temperature led to pink crystals of (H2L)(HPhthalate)2 and (H2L)(HIsophthalate)2, respectively.Potentiometric measurements
Potentiometric (pH-metric) titrations employed for the determination of equilibrium constants were carried out in 0.1 M NMe4Cl degassed aqueous solutions at 298.1 ± 0.1 K by using previously described equipment and procedures.23 The determined ionic product of water was pKw = 13.83(1) (298.1 ± 0.1 K, 0.1 M NMe4Cl). High purity commercial reagents were purchased and employed for the potentiometric measurements without further purification. The computer program HYPERQUAD18 was used to calculate the equilibrium constants from potentiometric data derived from at least three independent titration experiments. The protonation constants of ligands were previously determined,9 while the anion protonation constants were re-determined under our experimental conditions: these data are available in the ESI (Table S1†). For complexation studies, the ligand concentration was either 5 × 10−4 M (L1) or 1 × 10−3 M (L2), while the anion concentrations ranged from 2 to 5 equivalents for each anion. Only in the case of benzenesulfonate, measurements were extended up to 10 equivalents of the anion. The studied pH range was 3.0–9.0. Different equilibrium models for the complex systems were generated by eliminating and introducing different complex species. Only those models for which the HYPERQUAD program furnished a variance of the residuals σ2 ≤ 9 were considered acceptable. Such a condition was unambiguously met by a single model for each system.1H NMR
Stock solutions of ligands and anions at the desired pH value were prepared in D2O and mixed to obtain the desired anion![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ligand ratio; further pH adjustment was performed after mixing whenever needed. pH adjustments were performed by the addition of DCl or NaOD solutions; pD and pH were correlated according to the pH = pD − 0.4 equivalence. Spectra were recorded on a Bruker Avance III 400 MHz spectrometer. The equilibrium constant for the formation of the [H2L1(C6H5SO3)]+ complex was determined by treatment with the program HypNMR24 of NMR titration data (Fig. S4†) obtained upon the addition of increasing amounts of C6H5SO3− solution (0.01 M, D2O) to a solution of H2L12+ (5 × 10−4 M, D2O) at pD 3.0.
ligand ratio; further pH adjustment was performed after mixing whenever needed. pH adjustments were performed by the addition of DCl or NaOD solutions; pD and pH were correlated according to the pH = pD − 0.4 equivalence. Spectra were recorded on a Bruker Avance III 400 MHz spectrometer. The equilibrium constant for the formation of the [H2L1(C6H5SO3)]+ complex was determined by treatment with the program HypNMR24 of NMR titration data (Fig. S4†) obtained upon the addition of increasing amounts of C6H5SO3− solution (0.01 M, D2O) to a solution of H2L12+ (5 × 10−4 M, D2O) at pD 3.0.
X-ray structure analyses
Pink crystals of (H2L2)(HPhthalate)2·2H2O (a), (H2L2)(HIsophthalate)2 (b) and H2L2(C6H5SO3)2·H2O (c) were used for X-ray diffraction analysis. A summary of the crystallographic data is reported in Table S2.† The integrated intensities were corrected for Lorentz and polarization effects and an empirical absorption correction was applied.25 The structures were solved by direct methods (SIR92).26 Refinements were performed by means of full-matrix least-squares using SHELXL Version 2014/7.27 All the non-hydrogen atoms were anisotropically refined. All hydrogen atoms were introduced in the calculated position and their coordinates were refined according to the linked atoms, with the exception of those belonging to the water molecules in (a) which were not found in the Fourier difference map and the ammonium hydrogen in (a), the carboxylic hydrogen atoms in (a) and (b) and the water hydrogen atoms in (c) which were instead localized and freely refined with isotropic treatment. CCDC 1835198–1835200† contain the supplementary crystallographic data for this paper.Molecular modelling calculations
Molecular modelling investigations were carried out on the following complexes (charges are omitted for clarity) in order to take into account possible different protons’ distributions, as suggested by potentiometric results:Acetate: L1/S, L1/HS, L2/HS, HL1/S, HL2/S, HL1/HS, HL2/HS, H2L1/S, H2L2/S, H2L2/HS, HL2/HS/HS, H2L2/HS/S
Benzoate: L1/S, L2/S, L1/HS, L2/HS, HL1/S, HL2/S, HL1/HS, HL2/HS, H2L1/S, H2L2/S, H2L2/S/S, HL2/HS/S
Benzenesulfonate: HL1/S, HL2/S, H2L1/S, H2L2/S
Phthalate and isophthalate: HL2/S
Calculations were performed by means of the empirical force field method AMBER3 as implemented in the Hyperchem 7.51 package,28 using an implicit simulation of an aqueous environment (ε = 4r) and atomic charges evaluated at the semiempirical level of theory (PM3).29 The potential energy surfaces of all the systems were explored by means of simulated annealing (T = 600 K, equilibration time = 10 ps, run time = 10 ps and cooling time = 10 ps, time step = 1.0 fs). For each studied system, 80 conformations were sampled.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Italian MIUR (project 2015MP34H3) and from the Spanish MINECO (project MAT2014-60104-C2-2-R) is gratefully acknowledged.References
-
Anion Coordination Chemistry, ed. K. Bowman-James, A. Bianchi and E. García-España, Wiley-VHC, New York, 2012 Search PubMed
.
-
J. L. Sessler, P. A. Gale; and W. S. Cho, Anion Receptor Chemistry, Monographs in Supramolecular Chemistry, RSC Publishing, Cambridge, U.K., 2006 Search PubMed
.
-
(a) D.-X. Wang and M.-X. Wang, J. Am. Chem. Soc., 2013, 135, 892–897 CrossRef CAS
; (b) P. Arranz-Mascarós, C. Bazzicalupi, A. Bianchi, C. Giorgi, M. L. Godino-Salido, M. D. Gutiérrez-Valero, R. Lopez-Garzón and M. Savastano, J. Am. Chem. Soc., 2013, 135(1), 102–105 CrossRef
; (c) B. L. Schottel, H. T. Chifotides and K. R. Dunbar, Chem. Soc. Rev., 2008, 37, 68–83 RSC
.
-
(a) V. Stilinović, G. Horvat, T. Hrenar, V. Nemec and D. Cinčić, Chem. – Eur. J., 2017, 23, 5244 CrossRef
; (b) S. J. Grabowski, Chem. – Eur. J., 2013, 19, 14600–14611 CrossRef CAS
; (c) G. R. Desitaju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713 Search PubMed
.
-
(a) X. Lucas, A. Bauzá, A. Frontera and D. Quiñonero, Chem. Sci., 2016, 7, 1038–1050 RSC
; (b) Y. P. Yurenko, J. Novotný and R. Marek, Chem. – Eur. J., 2017, 23, 5573–5584 CrossRef CAS
.
-
(a) R. V. Nair, S. Kheria, S. Rayavarapu, A. S. Kotmale, B. Jagadeesh, R. G. Gonnade, V. G. Puranik, P. R. Rajamohanan and G. J. Sanjayan, J. Am. Chem. Soc., 2013, 135(31), 11477–11480 CrossRef CAS
; (b) G. N. M. Reddy, A. Marsh, J. T. Davis, S. Masiero and S. P. Brown, Cryst. Growth Des., 2015, 15(12), 5945–5954 CrossRef CAS
.
-
(a) Y.-L. Wang, A. Laaksonen and M. D. Fayer, J. Phys. Chem. B, 2017, 121(29), 7173–7179 CrossRef CAS
; (b) M. Lübtow, I. Helmers, V. Stepanenko, R. Q. Albuquerque, T. B. Marder and G. Fernández, Chem. – Eur. J., 2017, 23, 6198–6205 CrossRef
.
-
(a) M. A. Uddin, T. H. Lee, S. Xu, S. Y. Park, T. Kim, S. Song, T. L. Nguyen, S. Ko, S. Hwang, J. Y. Kim and H. Y. Woo, Chem. Mater., 2015, 27(17), 5997–6007 CrossRef CAS
; (b) M. Müller, M. Albrecht, V. Gossen, T. Peters, A. Hoffmann, G. Raabe, A. Valkonen and K. Rissanen, Chem. – Eur. J., 2010, 16, 12446–12453 CrossRef
; (c) M. Savastano, C. Bazzicalupi, P. Mariani and A. Bianchi, Molecules, 2018, 23(3), 572 CrossRef
.
- M. Savastano, C. Bazzicalupi, C. Giorgi, C. García-Gallarín, M. D. López de la Torre, F. Pichierri, A. Bianchi and M. Melguizo, Inorg. Chem., 2016, 55(16), 8013–8024 CrossRef CAS
.
- M. Savastano, C. Bazzicalupi, C. García-Gallarín, C. Giorgi, M. D. López de la Torre, F. Pichierri, A. Bianchi and M. Melguizo, Dalton Trans., 2018, 47, 3329–3338 RSC
.
- M. Savastano, C. Bazzicalupi, C. García, C. Gellini, M. D. López de la Torre, P. Mariani, F. Pichierri, A. Bianchi and M. Melguizo, Dalton Trans., 2017, 46, 4518–4529 RSC
.
- M. Savastano, C. García, M. D. López de la Torre, F. Pichierri, C. Bazzicalupi, A. Bianchi and M. Melguizo, Inorg. Chim. Acta, 2018, 470, 133–138 CrossRef CAS
.
-
(a) S. Shan, S. Loh and D. Herschlag, Science, 1996, 272, 97–101 CrossRef CAS
; (b) G. Gilli and P. Gilli, The Nature of Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory, Oxford University Press, New York, 2009 CrossRef
.
- M. Odelius, B. Kirchner and J. Hutter, J. Phys. Chem., 2004, 108(11), 2044–2052 CrossRef CAS
.
- L. K. S. von Krbek, A. J. Achazi, S. Schoder, M. Gaedke, T. Biberger, B. Paulus and C. A. Schalley, Chem. – Eur. J., 2017, 23, 2877 CrossRef CAS
.
- A. Gavezzotti, Acc. Chem. Res., 1994, 27(10), 309–314 CrossRef CAS
.
- A. Gavezzotti and G. Filippini, J. Phys. Chem., 1994, 98(18), 4831–4837 CrossRef CAS
.
- P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739–1753 CrossRef CAS
.
-
(a) A. Bianchi, M. Micheloni and P. Paoletti, Inorg. Chim. Acta, 1988, 151, 269–272 CrossRef CAS
; (b) A. Andrés, J. Aragó, A. Bencini, A. Bianchi, A. Domenech, V. Fusi, E. García-España, P. Paoletti and J. A. Ramírez, Inorg. Chem., 1993, 32, 3418–3424 CrossRef
; (c) C. Bazzicalupi, A. Bencini, A. Bianchi, M. Cecchi, B. Escuder, V. Fusi, E. García-España, C. Giorgi, S. V. Luis, G. Maccagni, V. Marcelino, P. Paoletti and B. Valtancoli, J. Am. Chem. Soc., 1999, 121, 6807–6815 CrossRef CAS
.
- C. Bazzicalupi, A. Bianchi, C. Giorgi, M. P. Clares and E. Garcia-España, Coord. Chem. Rev., 2011, 256, 13–27 CrossRef
.
- H.-J. Schneider, Chem. Soc. Rev., 1994, 22, 227–234 RSC
.
- H.-J. Schneider, Angew. Chem., Int. Ed., 2009, 48, 3924–3977 CrossRef CAS
.
- C. Bazzicalupi, A. Bianchi, T. Biver, C. Giorgi, S. Santarelli and M. Savastano, Inorg. Chem., 2014, 53, 12215–12224 CrossRef CAS
.
- C. Frassineti, L. Alderighi, P. Gans, A. Sabatini, A. Vacca and S. Ghelli, Anal. Bioanal. Chem., 2003, 376, 1041–1052 CrossRef CAS
.
-
CrysAlisPro, Agilent Technologies, Version 1.171.37.35g (release 09-12-2014 CrysAlis171 .NET), Agilent Technologies, Oxfordshire, England Search PubMed
.
- A. Altomare, G. Cascarano, C. Giacovazzo, A. Guagliardi, M. C. Burla, G. Polidori and M. Camalli, J. Appl. Crystallogr., 1994, 27, 435–436 Search PubMed
.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed
.
-
Hyperchem, Release 7.51 for Windows MM System, Hypercube, Inc., Gainesville, FL, USA, 2002 Search PubMed
.
-
(a) J. J. P. Stewart, J. Comput. Chem., 1989, 10, 209–220 CrossRef CAS
; (b) J. J. P. Stewart, J. Comput. Chem., 1989, 10, 221–264 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1835198–1835200. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8qo01152d |
| This journal is © the Partner Organisations 2019 |