Characterization and high piezoelectric performance of Pb(Fe1/2Nb1/2)O3–Pb(In1/2Nb1/2)O3–PbTiO3 ternary ceramics
Abstract
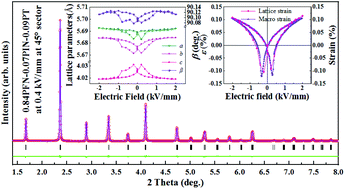
A (0.93 − x)Pb(Fe1/2Nb1/2)O3–0.07Pb(In1/2Nb1/2)O3–xPbTiO3 (0.06 ≤ x ≤ 0.11) ternary system was synthesized using a B-site precursor solid-state reaction method. The maximum piezoelectric coefficient d33 = 673 pC N−1 was achieved at the morphotropic phase boundary (MPB) composition x = 0.09 and its Curie temperature was 141 °C. In situ high energy synchrotron X-ray diffraction (SXRD) results demonstrate that tetragonal and monoclinic phases coexist at the MPB composition. It is interesting to observe that the stable single monoclinic phase induced by the electric field exhibits the characteristics of flexible lattice parameters in response to the electric field. The large piezoelectric response of PFN–PIN–PT is found to be mainly ascribed to the intrinsic lattice strain.
- This article is part of the themed collection: 2019 Inorganic Chemistry Frontiers HOT articles


 Please wait while we load your content...
Please wait while we load your content...