Intrinsic zero thermal expansion in cube cyanurate K6Cd3(C3N3O3)4†
Abstract
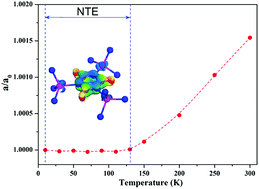
Zero thermal expansion (ZTE) materials are rare, but have intriguing properties which can be used in precise optical devices to prevent thermal fluctuation. Here, a new cube ZTE compound K6Cd3(C3N3O3)4, composed of conjugated [C3N3] rigid six-membered-rings and [CdN4] tetrahedra, has been reported for the first time. Its thermal expansion coefficient is as small as 0.06 MK−1, which is one-order of magnitude lower than that of the commercially available Invar alloy. In addition, the ZTE mechanism was elucidated using first-principles calculations.
- This article is part of the themed collection: 2019 Inorganic Chemistry Frontiers HOT articles


 Please wait while we load your content...
Please wait while we load your content...