Interrogation of fractional crystallization behavior of a newly exploited chiral resolution method for racemic 1-(pyridin-2-yl)ethylamine via DFT-D3 calculations of cohesive energy

Abstract

A novel chiral resolution method for racemic 1-(pyridin-2-yl)ethylamine (PEA) was developed in this study. Sequential conversion of 1-(pyridin-2-yl)ethylamine to 1-(pyridin-2-yl)-N-((4R)-1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethylamine (PIC) and to dichloro{(E)-1-(pyridin-2-yl)-N-(1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethylamine}zinc (PIC-Zn) allowed for the spontaneous separation of dichloro{(1R,E)-1-(pyridin-2-yl)-N-(1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethylamine}zinc (RE-PIC-Zn) and dichloro{(1S,E)-1-(pyridin-2-yl)-N-(1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethylamine}zinc (SE-PIC-Zn) by fractional crystallization. The overall yields of both (S)- and (R)-PEA were 24.8% with estimated ee values of 98 and 99%, respectively. The preferred formation of diastereopure crystals over that of diastereomeric mixture crystals was interrogated by comparing the cohesive energies (E_coh) of the respective crystals, as obtained via DFT calculations under periodic boundary conditions with a plane wave basis set based on the experimentally determined X-ray crystallographic structure. The E_coh values of diastereopure SE-PIC-Zn and RE-PIC-Zn were −45.8 and −44.4 kcal mol⁻¹, respectively. The E_coh values of the diastereomeric mixture crystal (RE-PIC-Zn·SE-PIC-Zn·2CHCl₃) and its virtual counterpart lacking CHCl₃ (RE-PIC-Zn·SE-PIC-Zn) were −56.0 and −37.2 kcal mol⁻¹, respectively. These data provided the background underlying the spontaneous segregation of the diastereopure crystals where the energy preference for forming diastereopure crystals over their corresponding diastereomeric mixture crystals is ca. 8 kcal mol⁻¹.

---

1. Introduction

Typically, only one enantiomer of a chiral drug is physiologically active toward the biological target because biomacromolecules are constructed using L-amino acids as building blocks.¹ This necessitates chiral resolution in the pharmaceutical industry first and across many fields of chemistry.^2,3 Since the demonstration of the first chiral resolution by Louis Pasteur,⁴ the development of production processes to generate or isolate pure enantiomers has been remarkable.^1–3,5–21 The numerous methods for producing pure enantiomers can be divided into two main approaches: (A) the chiral approach that aims for the selective synthesis of a single enantiomer and (B) the racemic approach that provides separation methods for chiral mixtures.¹ The latter has attracted significant attention recently due to the progress in crystallization-based separation techniques.

The propensity to form conglomerates of pure enantiomers rather than racemic crystals would be desirable for industrial scale enantioseparation, a process known as preferential crystallization.^22–28 However, the probability of this type of behavior occurring is only 5–10%,⁵ hampering the wide application of this approach as a major enantioseparation method. The fractional crystallization of diastereomers that specifically implies spontaneous segregation into enantiopure diastereomers rather than forming diastereomeric mixtures is more complex compared to preferential crystallization of a conglomerate system. This may be a good alternative for outnumbering racemates provided that chemical conversion of those racemates into their corresponding diastereomers is easily accessible.^29–31 Development of a novel protocol enabling fractional crystallization is thus indispensable.

Our group has extensively investigated asymmetric catalysis with a variety of metal complexes using newly synthesized chiral ligands.^32–36 During the search for a chiral ligand, we encountered optically active 1-substituted-1-(pyridyl)methylamines. They are naturally occurring bioactive compounds that include tobacco alkaloids (i.e. nicotine, nornicotine, and anatabine)^37–41 and histamine H1-receptor agonists.^42–44 However, their potential as building blocks for the chiral ligand pool has attracted more of our attention. In this study, we focus on the chiral resolution of 1-(pyridin-2-yl)ethylamine, hereafter referred to as PEA, first reported in 1973 by Smith et al.⁴⁵ by way of a classical approach using (+)-tartaric acid and only the (S)-form was obtained with an ∼9.5% overall yield. The enantiomeric excess (ee) of (S)-PEA was later confirmed to be 99% based on HPLC analysis of the (S)-PEA/(+)-tartaric acid salt.⁴⁶ In 1977, Westley et al. separated (R)-PEA in a higher yield (37%) with much lower ee (78%) using lasalocid as a chiral derivatizing agent (CDA).⁴⁷ In 1997, Gotor et al. separated both (R)- and (S)-PEA in 50% conversion with a moderately high ee (90 and 91% for (R)- and (S)-PEA, respectively) via enzyme catalyzed enantioselective aminolysis.⁴⁸ This approach was later improved by McEachern et al., achieving a 52% yield with 75% ee for (R)-PEA and 41% yield with 99% ee for the corresponding (S)-enantiomer.⁴⁹ On the other hand, enzyme catalyzed asymmetric synthesis from racemic 1-pyridylethylalcohol afforded enantiopure (R)- and (S)-PEA in >96% yield with ∼99% ee.⁵⁰

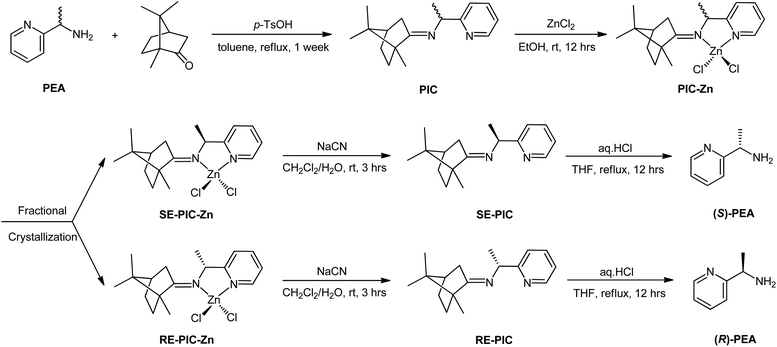
The primary objective of this study was to develop a novel experimental protocol for the chiral resolution of PEAvia fractional crystallization. A classical approach was used for racemic PEA: treatment with CDA and subsequent separation. However, the interaction motif between the racemate and CDA was not a simple electrostatic interaction but formation of a strong N=C imino bond via condensation between the primary amine of PEA and the ketone group of (+)-camphor. Moreover, secondary metal coordination of the generated Schiff base ligand to a ZnCl₂ moiety was devised to ensure solidification. The fractional crystallization conditions of spontaneous segregation into diastereopure (S,R,R)- and (R,R,R)-diastereomers were serendipitously obtained with ca. 60% overall yield and >98% diastereomeric excess (de). Details of the separation procedures are provided later in this manuscript.

Another objective was to elucidate the background of the fractional crystallization behavior of the generated diastereomeric systems quantitatively. We adopted the benchmark calculation protocol for non-covalent interactions in solids via DFT calculations under periodic boundary conditions (PBCs) with dispersion corrections (PBE-D3).⁵¹ This was made possible by the successful growth of three different molecular crystals, diastereopure (SRR)- and (RRR)-diastereomers and their mixture (SRR/RRR). We computed the cohesive energies of the respective crystal systems, representing the experimental sublimation energies.⁵² The calculated cohesive energies between the diastereopure and the diastereomeric mixture differed significantly (7.4–11.4 kcal mol⁻¹), exceeding the chemical accuracy target (∼1 kcal mol⁻¹) and explaining the fractional crystallization behavior, even considering the errors in the calculation. In addition to the cohesive energies, we computed the crystallization energies of both diastereopure (SRR)- and (RRR)-diastereomers, obtaining the zero-point energy exclusive electronic energy difference between solid and solution states to explain the preferred formation of the (S,R,R)-diastereomer over that of its (R,R,R)-counterpart. These results provide useful insights into the fractional crystallization behavior by providing quantitative measures as a benchmark for the future design of crystallization-based chiral resolution methods.

2. Experimental

2.1. Materials

All manipulations were carried out under air unless otherwise noted. Reagent grade toluene, dichloromethane, chloroform, methanol, and absolute ethanol were purchased from Aldrich and used without further purification. THF was purchased from Aldrich and was dried over Na/benzophenone ketyl and subsequently distilled from these reagents under nitrogen prior to use. Zinc chloride, sodium cyanide, and p-toluenesulfonic acid were purchased from Aldrich and were used without further purification.

2.2. Instrumentation

Elemental analysis (C, H, and N) of the synthesized metal complexes was performed using an elemental analyzer (EA 1108; Carlo-Erba, Milan, Italy). The NMR spectra were recorded using a Bruker Avance III 500 NMR spectrometer. Chemical shifts of the ¹H NMR spectra are relative to residual protons in the deuterated solvent (CDCl₃, δ = 7.24). All coupling constants are reported in Hz. The chemical shifts of the ¹³C NMR spectra were measured relative to CDCl₃ (77.00 ppm). Infrared (IR) spectra were recorded using a Bruker Alpha FT-IR spectrometer and the data are reported in reciprocal centimeters (cm⁻¹). Circular dichroism (CD) spectra were recorded on a Jasco 715 spectropolarimeter.

2.3. X-ray crystallographic analysis

Single crystals were mounted in a thin-walled glass capillary on an Enraf-Nonius CAD-4 diffractometer at 25 °C using graphite-monochromated Mo Kα radiation (λ = 0.71073 Å). Unit cell parameters were determined by least-squares analysis of 25 reflections. The intensity data were collected in the ω/2θ scan mode and three standard reflections were monitored every 1 h during data collection. The data were corrected for Lorentz-polarization effects and decay and empirical absorption corrections with ψ-scans were applied. The structure was solved using the Patterson method and refined by full-matrix least squares techniques on F² using the SHELXS and SHELXL programs of SHELX-97 package.^53,54 The absolute structures were confirmed by anomalous dispersion effects with Friedel pairs which were not merged. All non-hydrogen atoms were refined anisotropically except for the disordered atoms. All hydrogen atoms were refined and positioned geometrically using the riding model with fixed isotropic thermal factors. The crystallographic data and the result of refinements are summarized in Table 1. The CCDC reference numbers are 1914650–1914652.†

Table 1 Crystal data and structure refinements of SE-PIC-Zn, RE-PIC-Zn, and 0.5SE-PIC-Zn·0.5RE-PIC-Zn·CHCl₃

	SE-PIC-Zn	RE-PIC-Zn	0.5RE-PIC-Zn·0.5SE-PIC-Zn·CHCl3
Empirical formula	C17H24Cl2N2Zn	C17H24Cl2N2Zn	C34H48Cl4Zn2N4·2CHCl3
Formula weight	392.65	392.65	1024.04
Temperature (K)	293(2)	293(2)	293(2)
Crystal system	Orthorhombic	Orthorhombic	Monoclinic
Space group	P212121	P212121	P21
Unit cell dimensions
a (Å)	9.7176(8)	11.1816(9)	12.7939(15)
b (Å)	10.6577(6)	12.7406(12)	13.5872(10)
c (Å)	18.0389(12)	13.2577(13)	13.4322(9)
α (°)	90	90	90
β (°)	90	90	93.677(8)
γ (°)	90	90	90
Volume (Å^3)	1868.2(2),	1888.7(3)	2330.2(4)
Z	4	4	2
Density (calculated) (Mg m^−3)	1.396	1.381	1.46
Absorption coefficient (mm^−1)	1.598	1.581	1.633
F(000)	816	816	1048
Theta range for data collection (°)	2.22 to 25.47	2.22 to 25.47	1.52 to 25.48
Index ranges	−11 ≤ h ≤ −11	−13 ≤ h ≤ −13	−15 ≤ h ≤ 15
	−12 ≤ k ≤ −12	−15 ≤ k ≤ −15	−16 ≤ k ≤ 16
	−21 ≤ l ≤ −21	−16 ≤ l ≤ −16	−16 ≤ l ≤ 16
Reflections collected	4120	4053	9552
Independent reflections	3460 [R(int) = 0.0139]	3496 [R(int) = 0.0174]	8664 [R(int) = 0.0550]
Reflections observed (>2sigma)	2739	3176	6739
Data/restraints/parameters	3460/0/203	3496/0/194	8664/1/474
Goodness-of-fit on F^2	1.036	1.175	1.139
Refinement method	Full-matrix least-squares on F^2	Full-matrix least-squares on F^2	Full-matrix least-squares on F^2
Final R indices [I > 2sigma(I)]	R 1 = 0.0262	R 1 = 0.0347	R 1 = 0.0497
	wR2 = 0.0648	wR2 = 0.1163	wR2 = 0.1640
R indices (all data)	R 1 = 0.0452	R 1 = 0.0421	R 1 = 0.0713
	wR2 = 0.0682	wR2 = 0.1292	wR2 = 0.1951
Absolute structure parameter	−0.016(14)	0.04(2)	−0.018(19)
Largest diff. peak and hole (e Å^−3)	0.262 and −0.236	0.402 and −0.410	0.971 and −0.608

---

2.4. Syntheses

1-(Pyridin-2-yl)-N-((4R)-1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethanamine (PIC). A 250 mL round-bottom flask fitted with a Dean–Stark trap connected to an efficient condenser was charged with PEA (7 g, 0.057 mol), (+)-camphor (8.7 g, 0.057 mol), and p-toluenesulfonic acid (4.7 g, 0.024 mol). Reagent grade toluene (100 mL) was added to the flask and the reaction mixture was refluxed for two weeks. After the solution was cooled, 40 mL of H₂O was added to the mixture and stirred for 1 h at 25 °C. The mixture was moved to a separatory funnel and the organic layer was washed with H₂O (2 × 50 mL), dried over anhydrous MgSO₄, filtered, and evaporated. A yellow sticky oil was recovered; isolated yield = 13.9 g, 0.054 mol (94.7%). ¹H NMR (CDCl₃, 500 MHz, 298 K): 8.49–8.51 (m, 1H, pyridyl-CH), 7.61–7.65 (m, 1H, pyridyl-CH), 7.52–7.54 (m, 1H, pyridyl-CH), 7.09–7.12 (m, 1H, pyridyl-CH), 4.55–4.61 (m, 1H, pyridyl-CH–CH₃), 2.30–2.48 (m, 1H, camphor-CH of PIC-diastereomer), 1.85–1.96 (m, 2H, camphor-CH₂), 1.63–1.84 (m, 2H, camphor-CH₂), 1.44–1.46 (m, 3H, N–C–CH₃), 1.09–1.43(m, 2H, camphor-CH₂), 1.04, 1.05 (s, s, 3H, camphor-CH₃), 0.92, 0.93 (s, s, 3H, camphor-CH₃), 0.64, 0.81 (s, s, 3H, camphor-CH₃). ¹³C NMR (CDCl₃, 125 MHz, 298 K): δ = 180.18–180.46 (1C, N=C), 164.37 (1C, pyridyl-C), 147.52–147.60 (1C, pyridyl-C), 135.46 (1C, pyridyl-C), 120.44–120.47 (1C, pyridyl-C), 119.68 (1C, pyridyl-C), 60.76–61.02 (1C, N–C), 52.63–52.70 (1C, camphor-C), 45.90 (1C, camphor-C), 42.89 (1C, camphor-C), 34.39–34.53 (1C, camphor-C), 31.11 (1C, camphor-C), 26.42–26.52 (1C, camphor-C), 21.90 (1C, N–C–CH₃), 18.51 (1C, camphor-CH₃), 18.01 (1C, camphor-CH₃), 10.65–10.49 (1C, camphor-CH₃). IR (liquid neat; cm⁻¹): 3062(w), 2956(w), 2871(w), 1683(w), 1588(w), 1569(w), 1471(w), 1431(w), 1387(w), 1079(w), 748(w).

Dichloro{(E)-1-(pyridin-2-yl)-N-(1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethanamine}zinc (PIC-Zn). A mixture of PIC (13.9 g, 0.054 mol) and an equimolar amount of zinc chloride (7.4 g, 0.054 mol) in absolute ethanol (99%, 150 mL) was allowed to stir for 12 hours at ambient temperature. White precipitates were collected on a glass frit and dried in an oven; isolated yield = 20 g, 0.051 mol (94.4%). Anal. calcd for C₁₇H₂₄Cl₂N₂Zn (%): C, 51.99; H, 6.16; N, 7.13. Found: C, 51.97; H, 6.18; N, 7.12. ¹H NMR (CDCl₃, 500 MHz, 298 K): δ = 8.66–8.74 (m, 1H, pyridyl-CH), 7.96–8.00 (m, 1H, pyridyl-CH), 7.50–7.52 (m, 1H, pyridyl-CH), 7.42–7.43 (d, J = 7.9 Hz, 1H, pyridyl-CH), 4.90–5.04 (m, 1H, pyridyl-CH–CH₃ of PIC diastereomer), 2.72–2.84 (m, 1H, camphor-CH of PIC-diastereomer), 2.21–2.28(m, 2H, camphor-CH₂), 1.81–2.00 (m, 2H, camphor-CH₂), 1.58–1.72 (m, 1H, camphor-CH_aCH_b), 1.58–1.60 (m, 3H, N–C–CH₃), 1.56, 1.59 (s, s, 3H, camphor-CH₃), 1.25–1.32 (m, 1H, camphor-CH_aCH_b) 0.99, 1.00 (s, s, 3H, camphor-CH₃), 0.81, 0.87 (s, s, 3H, camphor-CH₃ of PIC-diastereomer). ¹³C NMR (CDCl₃, 125 MHz, 298 K): δ = 194.73–195.53 (1C, N=C), 158.48–158.58 (1C, pyridyl-C), 147.04–146.59 (1C, pyridyl-C), 139.79 (1C, pyridyl-C), 123.61 (1C, pyridyl-C), 121.48–121.60 (1C, pyridyl-C), 60.00–60.71 (1C, N–C), 55.63 (1C, camphor-C), 46.77–48.95 (1C, camphor-C), 42.07–42.55 (1C, camphor-C), 36.74–37.59 (1C, camphor-C), 29.82–31.12 (1C, camphor-C), 25.89–25.92 (1C, camphor-C), 23.08–23.73 (1C, N–C–CH₃), 18.75–18.80 (1C, camphor-CH₃), 17.85–18.02 (1C, camphor-CH₃), 11.21–11.99 (1C, camphor-CH₃). IR (solid neat; cm⁻¹): 2963 (w), 1653 (w), 1608 (w), 1573 (w), 1483 (w), 1443 (w), 1373 (w), 1285 (w), 1261 (w), 1105 (w), 784 (w).

Dichloro{(1S,E)-1-(pyridin-2-yl)-N-(1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethanamine}zinc (SE-PIC-Zn). A 500 mL round bottom flask connected to a condenser was filled with PIC-Zn (20.0 g, mol) and 90% methanol (90% methanol + 10% water, v/v, exactly 400 mL). The amount and water/methanol ratio were very important as the amount was insufficient to fully dissolve the whole solids. The solution was allowed to stir until it was refluxed and subsequently filtered in hot over a glass frit. A certain amount of white solids remained on the frit. The hot filtrate was cooled slowly to 25 °C and white aggregates formed as fine powders during cooling, which were collected by filtration. The white solids remaining on the glass filter during the first stage were placed into a round bottom flask with a reduced amount of 90% methanol (exactly 100 mL). The same procedures were repeated. The combined white powders were identified as SE-PIC-Zn; isolated yield = 6 g, 15.3 mmol (30.0%). Anal. calcd for C₁₇H₂₄Cl₂N₂Zn (%): C, 51.99; H, 6.16; N, 7.13. Found: C, 51.98; H, 6.19; N, 7.11. [α]²⁸_D = +54° (c 1, CHCl₃). ¹H NMR (CDCl₃, 500 MHz, 298 K): δ = 8.65–8.67 (m, 1H, pyridyl-CH), 7.96–7.99 (m, 1H, pyridyl-CH), 7.50–7.53 (m, 1H, pyridyl-CH), 7.43 (d, J = 8.2 Hz, 1H, pyridyl-CH), 5.04 (q, J = 6.8 Hz, 1H, pyridyl-CH–CH₃ of PIC-RRS), 2.79–2.84 (m, 1H, camphor-CH of PIC-RRS), 2.12–2.27 (m, 2H, camphor-CH₂), 1.81–1.95 (m, 2H, camphor-CH₂), 1.66–1.72 (m, 1H, camphor-CH_aCH_b), 1.60 (d, J = 5.0 Hz, 3H, N–C–CH₃), 1.59 (s, 3H, camphor-CH₃), 1.25–1.30 (m, 1H, camphor-CH_aCH_b), 1.00 (s, 3H, camphor-CH₃), 0.87 (s, 3H, camphor-CH₃ of PIC-RRS). ¹³C NMR (CDCl₃, 125 MHz, 298 K): δ = 196.49 (1C, N=C), 159.44 (1C, pyridyl-C), 147.69 (1C, pyridyl-C), 140.73 (1C, pyridyl-C), 124.61 (1C, pyridyl-C), 122.49 (1C, pyridyl-C), 61.72 (1C, N–C), 56.65 (1C, camphor-C), 49.97 (1C, camphor-C), 43.08 (1C, camphor-C), 38.56 (1C, camphor-C), 30.81 (1C, camphor-C), 26.91 (1C, camphor-C), 24.07 (1C, N–C-CH₃), 19.76 (1C, camphor-CH₃), 19.03 (1C, camphor-CH₃), 12.22 (1C, camphor-CH₃). IR (solid neat; cm⁻¹): 2967 (w), 1656 (w), 1608 (w), 1574 (w), 1485 (w), 1372 (w), 1287 (w), 1166 (w), 1053 (w), 783 (w). CD (CH₃CN solution; nm): 235(−).

Dichloro{(1R,E)-1-(pyridin-2-yl)-N-(1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethanamine}zinc (RE-PIC-Zn). The separately combined filtrate (575 mL) in the above procedure, containing a larger amount of RE-PIC-Zn (∼25.4 mmol) and a small amount of SE-PIC-Zn (∼10.2 mmol), was reduced to 500 mL and stored at room temperature. White crystalline solids were collected on a glass frit, washed with hot methanol and were assigned as RE-PIC-Zn; isolated yield = 6 g, 15.3 mmol (30.0%). Anal. calcd for C₁₇H₂₄Cl₂N₂Zn (%): C, 51.99; H, 6.16; N, 7.13. Found: C, 51.97; H, 6.19; N, 7.14. [α]²⁹_D = +160° (c 1, CHCl₃). ¹H NMR (CDCl₃, 500 MHz, 298 K): δ = 8.73–8.75 (m, 1H, pyridyl-CH), 7.96–7.99 (m, 1H, pyridyl-CH), 7.51–7.54 (m, 1H, pyridyl-CH), 7.41 (d, J = 7.9 Hz 1H, pyridyl-CH), 4.90 (q, J = 6.9 Hz, 1H, pyridyl-CH–CH₃), 2.72–2.77 (m, 1H, camphor-CH), 2.15–2.27 (m, 2H, camphor-CH₂), 1.85–1.99 (m, 2H, camphor-CH₂), 1.58–1.62 (m, 1H, camphor-CH_aCH_b), 1.60 (d, J = 5.0 Hz, 3H, N–C–CH₃), 1.56 (s, 3H, camphor-CH₃), 1.27–1.32 (m, 1H, camphor-CH_aCH_b), 1.00 (s, 3H, camphor-CH₃), 0.81 (s, 3H, camphor-CH₃). ¹³C NMR (CDCl₃, 125 MHz, 298 K): δ = 195.74 (1C, N=C), 159.61 (1C, pyridyl-C), 147.97 (1C, pyridyl-C), 140.86 (1C, pyridyl-C), 124.52 (1C, pyridyl-C), 122.54 (1C, pyridyl-C), 60.99 (1C, N–C), 57.35 (1C, camphor-C), 47.76 (1C, camphor-C), 43.55 (1C, camphor-C), 37.77 (1C, camphor-C), 32.13 (1C, camphor-C), 26.91 (1C, camphor-C), 24.73 (1C, N–C–CH₃), 19.81 (1C, camphor-CH₃), 18.85 (1C, camphor-CH₃), 12.99 (1C, camphor-CH₃). IR (solid neat; cm⁻¹): 2958 (w), 1659(w), 1608 (w), 1574(w), 1485(w), 1444(w), 1374(w), 1288(w), 1160(w), 1104(w), 784(w). CD (CH₃CN solution; nm): 236(+).

RE-PIC . A 100 mL round-bottom flask was filled with RE-PIC-Zn (6.0 g, 15.3 mmol) and dichloromethane (50 mL). After stirring for 10 min, an aqueous solution of NaCN (4.5 g, 9.18 mmol in 10 mL of distilled water) was slowly added. The mixture was stirred for 3 h at ambient temperature and subsequently poured into a separatory funnel and water (10 mL) was added. The product was extracted with dichloromethane (3 × 50 mL). The combined organic layer was washed with water (3 × 20 mL) and dried over CaCl₂. After removing the solvent using a rotary evaporator, the product was obtained as a yellow sticky oil; isolated yield = 3.8 g, 14.8 mmol (96.7%). [α]²⁷_D = +142° (c 1, CHCl₃). ¹H NMR (CDCl₃, 500 MHz, 298 K): δ = 8.49–8.51 (m, 1H, pyridyl-CH), 7.63–7.65 (m, 1H, pyridyl-CH), 7.54 (d, J = 7.9 Hz 1H, pyridyl-CH), 7.09–7.12 (m, 1H, pyridyl-CH), 4.58 (q, J = 6.7 Hz, 1H, pyridyl-CH–CH₃), 2.31–2.35 (m, 1H, camphor-CH), 1.91–1.97 (m, 2H, camphor-CH₂), 1.84–1.88 (m, 1H, camphor-CH_aCH_b), 1.68–1.74 (m, 1H, camphor-CH_aCH_b), 1.47 (d, J = 5.0 Hz, 3H, N–C–CH₃), 1.39–1.44 (m, 1H, camphor-CH_cCH_d), 1.22–1.27 (m, 1H, camphor-CH_cCH_d), 1.05 (s, 3H, camphor-CH₃), 0.93 (s, 3H, camphor-CH₃), 0.65 (s, 3H, camphor-CH₃). ¹³C NMR (CDCl₃, 125 MHz, 298 K): δ = 181.46 (1C, N=C), 165.37 (1C, pyridyl-C), 148.52 (1C, pyridyl-C), 136.47 (1C, pyridyl-C), 121.44 (1C, pyridyl-C), 120.69 (1C, pyridyl-C), 61.77 (1C, N–C), 53.71 (1C, camphor-C), 46.90 (1C, camphor-C), 43.91 (1C, camphor-C), 35.54 (1C, camphor-C), 32.12 (1C, camphor-C), 27.53 (1C, camphor-C), 23.01 (1C, N–C–CH₃), 19.53 (1C, camphor-CH₃), 19.04 (1C, camphor-CH₃), 11.49 (1C, camphor-CH₃). IR (liquid neat; cm⁻¹): 3051 (w), 2955 (w), 2872 (w), 1683 (w), 1588 (w), 1470 (w), 1431 (w), 1388(w), 1047 (w), 764 (w), 748(w). CD (CH₃CN solution; nm): 221(−), 238(+), 277(+).

SE-PIC . A similar procedure to that of RE-PIC was applied. SE-PIC was obtained as a yellow sticky oil; isolated yield = 3.8 g, 14.8 mmol (96.7%). [α]²⁸_D = +84° (c 1, CHCl₃). ¹H NMR (CDCl₃, 500 MHz, 298 K): δ = 8.51–8.52 (m, 1H, pyridyl-CH), 7.63–7.66 (m, 1H, pyridyl-CH), 7.55 (d, J = 7.9 Hz, 1H, pyridyl-CH), 7.11–7.13 (m, 1H, pyridyl-CH), 4.60 (q, J = 6.7 Hz, 1H, pyridyl-CH-CH₃), 2.44–2.49 (m, 1H, camphor-CH), 1.85–1.95 (m, 2H, camphor-CH₂), 1.79–1.85 (m, 1H, camphor-CH_aCH_b), 1.64–1.69 (m, 1H, camphor-CH_aCH_b), 1.46 (d, J = 5.0 Hz, 3H, N–C–CH₃), 1.29–1.34(m, 1H, camphor-CH_cCH_d), 1.10–1.15 (m, 1H, camphor-CH_cCH_d), 1.06 (s, 3H, camphor-CH₃), 0.95 (s, 3H, camphor-CH₃), 0.82 (s, 3H, camphor-CH₃). ¹³C NMR (CDCl₃, 125 MHz, 298 K): δ = 180.15 (1C, N=C), 164.34 (1C, pyridyl-C), 147.59 (1C, pyridyl-C), 135.45 (1C, pyridyl-C), 120.46 (1C, pyridyl-C), 119.82 (1C, pyridyl-C), 61.01 (1C, N–C), 52.62 (1C, camphor-C), 45.97 (1C, camphor-C), 42.89 (1C, camphor-C), 34.37 (1C, camphor-C), 31.17 (1C, camphor-C), 26.42 (1C, camphor-C), 21.89 (1C, N–C–CH₃), 18.51 (1C, camphor-CH₃), 18.01 (1C, camphor-CH₃), 10.65 (1C, camphor-CH₃). IR (liquid neat; cm⁻¹): 3064 (w), 2957(w), 2871(w), 1682 (w), 1588(w), 1568(w), 1471(w), 1431(w), 1387(w), 1120(w), 748(w). CD (CH₃CN solution; nm): 223(+), 240(−), 275(−).

(R)-PEA . A 100 mL round-bottom flask was charged with RE-PIC (3.8 g, 14.8 mmol), THF (40 mL), and aqueous HCl (4 M, 5.5 mL, 22.0 mmol). The mixture was refluxed for 12 h and moved to a separatory funnel. The yellow aqueous layer was collected in a 100 mL round bottom flask and 50 mL of dichloromethane was added. Solid NaOH (1.3 g, 32.5 mmol) was slowly added to the solution with stirring. After stirring for another 30 min, the product was extracted with dichloromethane (3 × 50 mL). The combined organic layer was washed with water (3 × 20 mL) and dried over CaCl₂. After removing the solvent using a rotary evaporator, the product was obtained as a yellow sticky oil; isolated yield = 1.7 g, 13.8 mmol (93.2%). [α]²⁶_D = +21° (c 1, CHCl₃). ¹H NMR (CDCl₃, 500 MHz, 298 K): δ = 8.54–8.55 (m, 1H, pyridyl-CH), 7.62–7.66 (m, 1H, pyridyl-CH), 7.29–7.31 (m, 1H, pyridyl-CH), 7.13–7.16 (m, 1H, pyridyl-CH), 4.15 (q, J = 6.7 Hz, 1H, pyridyl-CH–CH₃), 1.81 (br s, 2H, NH), 1.43 (d, J = 6.7 Hz, 3H, pyridyl-CH–CH₃). CD (CH₃CN solution; nm): 243(+), 269(−).

(S)-PEA . A similar procedure to that of SE-PIC was applied. (S)-PEA was obtained as yellow oil: isolated yield = 1.7 g, 13.8 mmol (93.2%). [α]²⁶_D = −21° (c 1, CHCl₃). ¹H NMR (CDCl₃, 500 MHz, 298 K): δ = 8.53–8.54 (m, 1H, pyridyl-CH), 7.61–7.65 (m, 1H, pyridyl-CH), 7.28–7.30 (m, 1H, pyridyl-CH), 7.12–7.15 (m, 1H, pyridyl-CH), 4.14 (q, J = 6.7 Hz, 1H, pyridyl-CH–CH₃), 1.86 (br s, 2H, NH), 1.42 (d, J = 6.7 Hz, 3H, pyridyl-CH–CH₃). CD (CH₃CN solution; nm): 243(−), 269(+).

2.5. Computational details

The DFT calculations of the isolated molecules were performed using the Gaussian 16 program package (A.03 version).⁵⁵ Geometry optimizations of the organic molecules (PIC) were performed using the PBE1PBE hybrid functional,^56–58 while those of the metal complexes (PIC-Zn) were performed using the GGA functional with dispersion corrections (PBE-D3)^58,59 for consistency with the PBC calculations which used the plane wave basis set. All calculations were performed with the Karlsruhe basis sets developed by Ahlrichs et al. (def2TZVP).^60,61 For Zn, relativistic ECPs for the inner 10 electrons were represented by Stuttgart RSC 1997 (SDD).^62–64 Geometry optimizations of all model compounds were performed both in the gas phase and in solvents. The solvent was modeled as a dielectric continuum using a self-consistent reaction field (SCRF)^65–67 approach by a conductor-like polarizable continuum model (CPCM)^68,69 in toluene (PIC) and methanol (PIC-Zn) as implemented in Gaussian 16.

Vibrational frequency calculations were performed under the same solvent environment with the optimized geometries. The obtained information was used to calculate the free energy of the given molecule. Solvation energies were calculated using the thermodynamic parameters obtained from the optimized structures computed in the gas phase and dielectric continuum. Rotational barriers through N=C double bonds in the PIC molecules that connect the 1,7,7-trimethylbicyclo[2.2.1]heptyl and 1-(pyridin-2-yl)ethylamine groups were estimated from the potential surface scan by varying the dihedral angle.

DFT calculations of the molecular crystals were performed using the VASP program (v5.4)⁷⁰ with the PAW potentials.^71,72 A plane wave basis set with a cutoff of 600 eV was used for the calculations. All calculations employed a 2 × 2 × 2 k-point mesh after confirming that finer k-point grids gave virtually the same result. The break condition for the electronic SCF loop was set to 10⁻⁴ eV, while that for the ionic relaxation was set to 10⁻³ eV. The PBE exchange–correlation functional with dispersion corrections (PBE-D3)^58,59 was used, as implemented in VASP.⁷³ The optimization process began from the atomic coordinates and lattice parameters of the experimentally determined X-ray structures. Both the atomic coordinates and lattice parameters were optimized to reach energy minima. The energy of the gas-phase molecule (E_gas) was approximated by putting a single molecule in an enlarged unit cell (25 × 20 × 20 Å) to eliminate interactions between neighboring molecules for comparison with the results obtained from Gaussian 16. Based on the work by Moellmann and Grimme, the cohesive energy was calculated using the following relation:⁵¹

E_coh = E_solid/N − E_gas

where N is the number of molecules per unit cell (4 for the SE-PIC-Zn and RE-PIC-Zn crystals) and all energies are electronic energies. The crystallization energy (E_cryst) was computed as follows:

E_cryst = E_solid/N − E_sol

This relation specifically describes the dissolution energy with the opposite sign calculated using the zero-point exclusive electronic energy. It should be noted that E_solid was obtained by PBC calculations with a plane wave basis set implemented in the VASP program, while E_sol was obtained via CPCM calculations with a Gaussian basis set (def2TZVP) implemented in the Gaussian 16 program. For the Gaussian calculations, the same PBE-D3 was used.

For calculations of the SE-PIC-Zn·RE-PIC-Zn·CHCl₃ mixed crystal, E_coh was computed by

E_coh = [E_solid − {2E_gas (SE-PIC-Zn) + 2E_gas (RE-PIC-Zn) + 4E_gas (CHCl₃)}]/4

since there are two molecules of SE-PIC-Zn and RE-PIC-Zn, respectively, and four molecules of CHCl₃ in the unit cell.

The optimization of the virtual crystal SE-PIC-Zn·RE-PIC-Zn began from the experimentally determined atomic coordinates and lattice parameters after removing the 4 CHCl₃ molecules. E_coh was computed by

E_coh = [E_solid − {2E_gas (SE-PIC-Zn) + 2E_gas (RE-PIC-Zn)}]/4.

3. Results and discussion

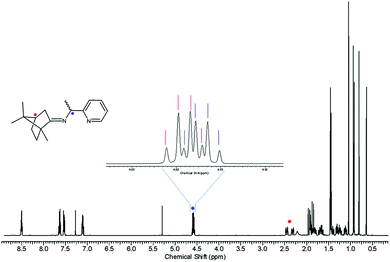
Inspired by the work of Pedro et al.,^74,75 racemic PEA was converted into separable diastereomers, 1-(pyridin-2-yl)-N-(1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethylamine (PIC), by condensation with (1R)-(+)-camphor. In contrast to Pedro et al., p-toluenesulfonic acid was used as a catalyst, affording a high yield (94.7%). While four different diastereomers are anticipated to be formed, as illustrated in Scheme 1, the ¹H NMR results indicated that only two isomers were present in the product mixture (Fig. 1). Two sets of multiplets, each indicative of the methine proton in the camphor group, distinctively resided at δ 2.33 and δ 2.47 in a 1 : 1 intensity ratio. The multiplet in the δ 4.55–4.61 region was composed of two overlapping quartets, each characteristic of the methine proton at the carbon near the imino group. This product mixture was hardly separable via column chromatography, which required further investigation.

Scheme 1 Possible structures of the 4 diastereomeric isomers of PIC. (a) (1S,E)-1-(pyridin-2-yl)-N-(1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethylamine (SE-PIC), (b) (1R,E)-1-(pyridin-2-yl)-N-(1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethylamine (RE-PIC), (c) (1S,Z)-1-(pyridin-2-yl)-N-((4R)-1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethylamine (SZ-PIC), and (d) (1R,Z)-1-(pyridin-2-yl)-N-((4R)-1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethylamine (RZ-PIC).

Fig. 1 ¹H NMR spectrum of PIC.

Recently, we reported the facile separation of the diastereo-chiral N,N′-diamine ligand via fractional crystallization and demetallation of the corresponding Zn(II) complex.⁷⁶ Metallation of the diastereomeric mixture, containing (2R,3R)-N²,N³-bis((R)-1-phenylethyl)butane-2,3-diamine (RR) and (2S,3S)-N²,N³-bis((R)-1-phenylethyl)butane-2,3-diamine (SS), with ZnCl₂ yielded the corresponding Zn(II) complexes, among which only RR was selectively separated by fractional crystallization. Considering this precedent, we attached the ZnCl₂ moiety to the PIC mixture anticipating that the propensity for fractional crystallization could be generated by metal complexation. The reaction proceeded very smoothly and stirring the mixture of PIC and an equimolar amount of ZnCl₂ in ethanol at ambient temperature afforded the desired product (PIC-Zn) in 94.4% yield. The Zn metallated diastereomeric mixture complexes were segregated by fractional crystallization under optimized conditions. MeOH was most effective as a crystallizing solvent. The detailed separation procedure described in the Experimental section is summarized in Scheme 2 and graphically illustrated in Fig. 2.

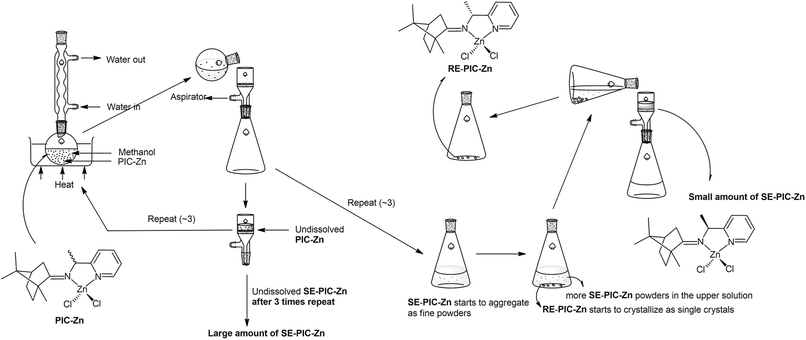Fig. 2 Schematic illustration of separation flow of the diastereomeric mixture PIC-Znvia fractional crystallization. See the Experimental section for details.

Scheme 2 Separation scheme of PEA.

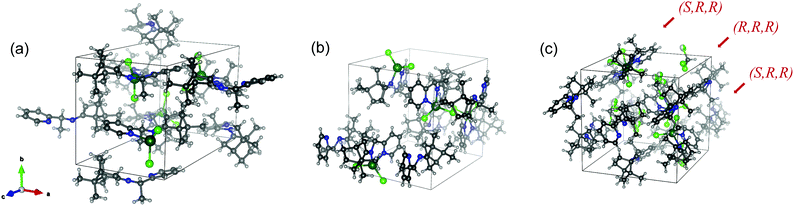
Single crystals of RE-PIC-Zn suitable for X-ray crystallographic analysis were obtained via slow evaporation of a hot MeOH solution containing the compounds of interest to 25 °C. However, SE-PIC-Zn could not be grown in the same solvent system due to its low solubility and was separately grown via layering of n-hexane in CH₂Cl₂ solution. Crystal data, details regarding the data collection, and refinement parameters are listed in Table 1. The ORTEP drawings of the complexes are shown in Fig. 3 with atomic labelling for nonhydrogen atoms. Selected bond distances and angles are listed in Table 2. The crystal structure of the white precipitates formed during the cooling process of the hot filtrate was revealed as dichloro{(1S,E)-1-(pyridin-2-yl)-N-(1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethylamine}zinc (SE-PIC-Zn). The other compound was dichloro{(1R,E)-1-(pyridin-2-yl)-N-(1,7,7-trimethylbicyclo[2.2.1]heptan-2-ylidene)ethylamine}zinc (RE-PIC-Zn). Because the added (+)-camphor moiety was in the (R,R) configuration, the overall configurations of SE-PIC-Zn and RE-PIC-Zn were (S,R,R) and (R,R,R), respectively. It should be noted that both structures have the (E)-configuration for the imino N=C double bond. As noted earlier, only two diastereomers instead of the possible four were confirmed by X-ray crystallography.

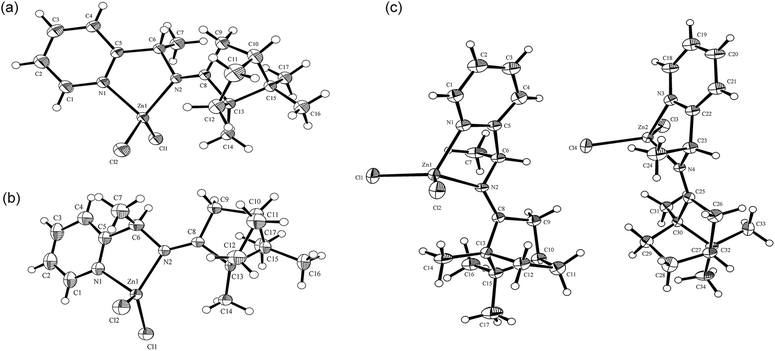Fig. 3 ORTEP drawings of (a) SE-PIC-Zn and (b) RE-PIC-Zn and (c) SE-PIC-Zn and RE-PIC-Zn from 0.5RE-PIC-Zn·0.5SE-PIC-Zn·CHCl₃. CHCl₃ molecules are not shown.

Table 2 Selected bond lengths (Å) and angles (°) of SE-PIC-Zn, RE-PIC-Zn, and 0.5RE-PIC-Zn·0.5SE-PIC-Zn·CHCl₃

Crystal system	SE-PIC-Zn	RE-PIC-Zn	0.5RE-PIC-Zn·0.5SE-PIC-Zn·CHCl3
Configuration	(S,R,R)	(R,R,R)	(S,R,R)	(R,R,R)^a
a Numbering scheme for the RRR form in the 0.5RE-PIC-Zn·0.5SE-PIC-Zn·CHCl3 crystal system in Table 2 follows that of the RRS form with the corresponding bond lengths and angles instead of using that of the ORTEP diagram in Fig. 3.
Zn(1)–N(1)	2.056	2.052	2.059	2.060
Zn(1)–N(2)	2.063	2.076	2.056	2.090
Zn(1)–Cl(1)	2.217	2.207	2.207	2.210
Zn(1)–Cl(2)	2.208	2.216	2.211	2.210
N(1)–C(5)	1.344	1.325	1.346	1.320
N(1)–C(1)	1.338	1.341	1.335	1.344
N(2)–C(8)	1.265	1.264	1.303	1.260
N(2)–C(6)	1.485	1.478	1.449	1.482
C(5)–C(6)	1.500	1.511	1.533	1.512
C(6)–C(7)	1.549	1.545	1.533	1.536
N(1)–Zn(1)–N(2)	82.2	81.9	81.9	82.5
N(1)–Zn(1)–Cl(1)	107.8	102.7	113.1	105.3
N(2)–Zn(1)–Cl(1)	115.2	126.8	113.8	125.1
N(1)–Zn(1)–Cl(2)	108.6	115.8	105.5	113.7
N(2)–Zn(1)–Cl(2)	117.3	107.7	118.5	108.8
Cl(1)–Zn(1)–Cl(2)	118.6	116.6	117.8	116.4
C(5)–N(1)–Zn(1)	113.6	113.9	113.3	114.0
C(1)–N(1)–Zn(1)	126.8	126.4	126.9	127.2
C(8)–N(2)–C(6)	117.9	118.1	116.3	119.1
C(8)–N(2)–Zn(1)	130.8	133.1	132.8	133.5
C(6)–N(2)–Zn(1)	110.3	108.2	110.9	106.9
N(1)–C(5)–C(6)	118.0	117.0	116.7	116.2
N(2)–C(6)–C(5)	111.0	110.5	109.9	112.0
N(2)–C(6)–C(7)	107.8	109.3	110.0	107.9
C(5)–C(6)–C(7)	109.8	108.8	109.1	110.2

---

The dominant formation of the (E)-conformation in the condensation step deserves additional consideration. We performed DFT calculations for the four diastereomeric geometries of the PIC molecule. The relative free energies of the four diastereomers in the gas phase at 298.15 K were 0.14, 0.00, 6.22, and 6.42 kcal mol⁻¹ for SE-, RE-, SZ-, and RZ-PIC, respectively. The values calculated in the dielectric continuum of toluene were −0.03, 0.00, 6.62, and 6.45, respectively, which are similar to those obtained in the gas phase. Both results clearly indicate that the PIC molecule prefers the E-conformation for the imino N=C double bond by ca. 6 kcal mol⁻¹. This energy difference is significant and corresponds to a ca. 25 000-fold excess of the E-conformation over the Z-counterpart. The estimated rotational barrier between the E- and Z-conformations is ∼24 kcal mol⁻¹, indicating that the condensation reaction for two weeks at the boiling temperature of toluene should be sufficient to shift the equilibrium toward the E-conformation whether the chiral center is S or R.

The overall geometries of both SE-PIC-Zn and RE-PIC-Zn were determined to be an ordinary distorted tetrahedron composed of a ZnL₂Cl₂-type skeleton with larger Cl(1)–Zn–Cl(2) angles (118.6° and 116.6° for SE-PIC-Zn and RE-PIC-Zn, respectively) and smaller N(1)–Zn–N(2) angles (82.2° and 81.9°, respectively). The lengths of the corresponding bonds between the two structures were very similar with a maximum difference of 0.024 Å for the C1–C2 bond. However, notable differences in the bond angles were found for the angles containing a Zn metal center. For example, the N(2)–Zn–Cl(1) angle of SE-PIC-Zn was 115.2° while that of RE-PIC-Zn was 126.8°, a difference of 11.6°.

The crystal system and space group of the two structures are both orthorhombic and non-centrosymmetric P2₁2₁2₁, respectively, as the most abundant form for the enantiopure chiral molecular crystals. The unit cell dimensions, a, b, and c, differed dramatically: 9.7176, 10.6577, and 18.0389 Å for SE-PIC-Zn and 11.1816, 12.7406, and 13.2577 Å for RE-PIC-Zn, respectively (Fig. 4). The overall shape of the unit cell of RE-PIC-Zn is close to cubic while that of SE-PIC-Zn is elongated tetragonal. Both unit cells contain four molecules of the corresponding diastereomers. The overall cell volumes were similar to each other: 1868.2 and 1888.7 ų for SE-PIC-Zn and RE-PIC-Zn, respectively, leading to similar densities (1.396 and 1.381 g cm⁻³).

Fig. 4 Unit cells of (a) SE-PIC-Zn, (b) RE-PIC-Zn, and (c) 0.5RE-PIC-Zn·0.5Se-PIC-Zn·CHCl₃.

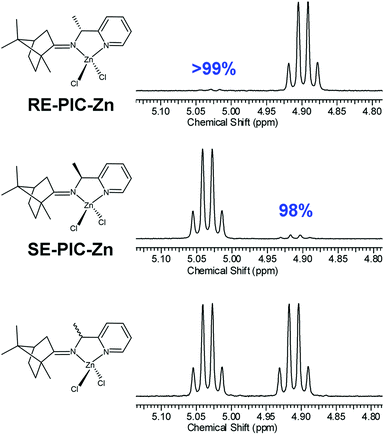
The diastereomeric excess of the separated diastereomers was determined by ¹H NMR. The methine region (C6) of the ¹H NMR spectra is shown in Fig. 5, showing 98 and 99% of diastereomeric excess for SE-PIC-Zn and RE-PIC-Zn, respectively, indicating that fractional crystallization segregated two diastereomers almost completely.

Fig. 5 Methine region ¹H NMR spectra of diastereopure RE-PIC-Zn (top), SE-PIC-Zn (middle) and the diastereomeric mixture PIC-Zn (bottom). The detailed conformation of N=C double bonds of both complexes was determined by X-ray crystallography.

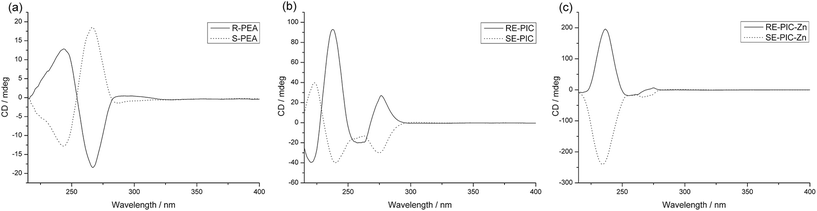
The CDA removal processes were straightforward and smooth. The ZnCl₂ moiety in the RE-PIC-Zn (or SE-PIC-Zn) was easily removed by treatment with aqueous NaCN in dichloromethane solution at ambient temperature, affording a virtually quantitative yield (96.7%). The separated RE-PIC and SE-PIC were analyzed by ¹H NMR, ¹³C NMR, and IR spectroscopic methods. The ¹H NMR spectra of the demetallated species are shown in Fig. 6. The camphor group in the RE-PIC (or SE-PIC) was removed by hydrolysis: THF solution of RE-PIC (or SE-PIC) in the presence of aqueous HCl was refluxed for 12 h, affording an ∼93% yield of the desired product. The overall yields of the obtained pure (S)- and (R)-PEA were both 24.2%. The circular dichroism (CD) spectra of the separated diastereomers, RE-PIC/SE-PIC and RE-PIC-Zn/SE-PIC-Zn, as well as enantiomers, R-PEA/S-PEA, were measured in acetonitrile (Fig. 7). The CD spectra of the enantiomeric couple were found to be mirror images of each other. R-PEA exhibited positive and negative Cotton effects at 243 and 269 nm, respectively. For RE-PIC/SE-PIC diastereomers, CD spectra were not mirror images of each other, although the regions of the Cotton effect were similar to each other. RE-PIC exhibited a positive Cotton effect at 238 nm and negative ones at 221 and 277 nm. SE-PIC showed a positive Cotton effect at 223 and 275 nm and a negative one at 240 nm. Interestingly, only the intensity of the negative Cotton effect observed in SE-PIC was a factor of two smaller than that of the positive Cotton effect of RE-PIC. In the case of RE-PIC-Zn/SE-PIC-Zn diastereomers, CD spectra were fortuitously mirror images of each other. The positive/negative Cotton effects of RE-PIC-Zn/SE-PIC-Zn were observed at 234/235 nm, respectively. The intensity of the positive Cotton effect in RE-PIC-Zn was a bit smaller than that of the negative Cotton effect in SE-PIC-Zn.

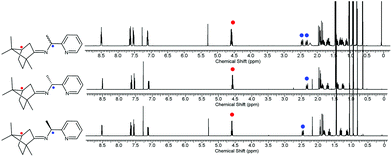Fig. 6 ¹H NMR spectra of the diastereomeric mixture of PIC (top), diastereopure RE-PIC (middle), and SE-PIC (bottom).

Fig. 7 Observed CD spectra of (a) R-PEA (solid) and S-PEA (dotted) (c = 1.0 mM), (b) RE-PIC (solid) and SE-PIC (dotted) (c = 2.0 mM), and (c) RE-PIC-Zn (solid) and SE-PIC-Zn (dotted) (c = 2.0 mM) in CH₃CN.

During the fractional crystallization tests, we obtained single crystals that contained both SE-PIC-Zn and RE-PIC-Zn in the same unit cell by layering n-hexane over the CHCl₃ solution of the SE-PIC-Zn and RE-PIC-Zn mixture. The crystal data, details of the data collection, and refinement parameters for the diastereomeric mixture crystal are listed in Table 1, and the ORTEP drawings of the complexes are shown in Fig. 3 with the atomic labeling for nonhydrogen atoms. Selected bond distances and angles are listed in Table 2. The structural parameters and characteristic features found for the SE-PIC-Zn·RE-PIC-Zn·2CHCl₃ crystal are similar to those of the corresponding diastereopure crystals. Interestingly, if not very unusually, equal numbers of additional solvent molecules were observed in the unit cell. The total number of molecules in the unit cells was 8: 2 SE-PIC-Zn, 2 RE-PIC-Zn, and 4 CHCl₃. The unit cell dimensions increased due to the crowding and were 12.79, 13.59, 13.43 Å for a, b, and c, respectively, forming a nearly cubical cell shape. The cell volume was 2330.2 Å, which is ca. 25% larger than that of the diastereopure crystal.

The experimentally determined 3-dimensional structures of both diastereopure and diastereomeric mixture crystals allowed for the subsequent DFT calculations to elucidate the underlying background of the observed fractional crystallization behavior. Specifically, we attempted to provide an explanation for the generation of diastereopure crystals in a MeOH solution of a diastereomeric mixture and a diastereomeric mixture crystal in the corresponding CHCl₃ solution. The calculation was performed to obtain accurate energies of the molecular crystals and further details regarding the calculation criteria are now discussed. For calculations of molecular crystals, it is important to describe the long-range London dispersion interactions. Recent progress in DFT has overcome its intrinsic lack of dispersion interactions (e.g., DFT-D3 by Grimme^59,77–79 and DFT + vdW by Tkatchenko^80–82) which include the pairwise interaction. An improvement by considering the many body dispersions (MBDs) that mainly correct for the overestimation of lattice energies by pairwise interactions was later made.^83–86 According to Grimme et al. who tested the calculation protocols with a 23 benchmark test set, the mean absolute error of the MBD approach was larger than that of the pairwise approach when the PBE functional was used.⁵¹ Therefore, we did not consider the MBD effect. For selecting an exchange–correlation functional, it is largely accepted that a hybrid functional exhibits better performance compared to a GGA. Grimme's report indicates that the performance difference between the hybrid PBE0 and GGA PBE functionals is a maximum of only 0.5 kcal mol⁻¹.⁵¹ Our test results for molecular crystals showed that a longer computational time of nearly an order of magnitude was required when the PBE0 functional was used compared to that of PBE. Thus, DFT-D3 with the PBE exchange–correlation functional was used to obtain the cohesive energies (E_coh) of the molecular crystals to evaluate their relative lattice energies. For consistency, we also used the PBE functional for the Gaussian calculations.

The calculated lattice parameters of the four crystal systems are summarized in Table 3. The calculated crystal structures of SE-PIC-Zn, RE-PIC-Zn, and RE-PIC-Zn·SE-PIC-Zn·2CHCl₃ were well reproduced by optimization. The calculated cell dimensions were slightly smaller than experimentally determined dimensions, indicating that the dispersion interaction was slightly overestimated.

Table 3 Compared unit cell parameters

	SE-PIC-Zn			RE-PIC-Zn			0.5RE-PIC-Zn·0.5SE-PIC-Zn·CHCl3			0.5RE-PIC-Zn·0.5SE-PIC-Zn
	Calc.	Error (%)	Exp.	Calc.	Error (%)	Exp.	Calc.	Error (%)	Exp.	Calc.
a (Å)	9.65	0.7	9.72	10.97	1.9	11.18	12.56	1.9	12.79	12.33
b (Å)	10.39	2.5	10.66	12.50	1.9	12.74	13.44	1.1	13.59	13.23
c (Å)	17.80	1.3	18.04	13.17	0.7	13.26	13.45	0.1	13.43	13.29
α (°)	90.00	0	90.00	90.00	0	90.00	90.00	0	90.00	90.00
β (°)	90.00	0	90.00	90.00	0	90.00	93.83	0.2	93.68	94.82
γ (°)	90.00	0	90.00	90.00	0	90.00	90.00	.0	90.00	90.00
V (Å^3)	1786.0	4.4	1868.2	1805.4	4.4	1888.7	2262.3	2.9	2330.2	2159.4

---

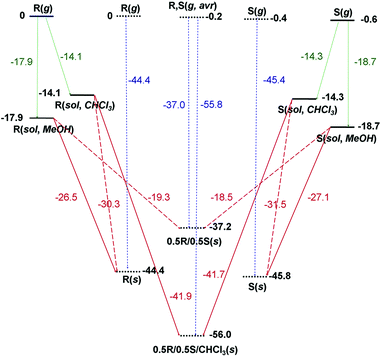
The calculated E_coh values were −45.8 and −44.4 kcal mol⁻¹ for SE-PIC-Zn and RE-PIC-Zn, respectively (Fig. 8), representing largely similar values with that of SE-PIC-Zn being only slightly lower by 1.4 kcal mol⁻¹. However, the E_coh of RE-PIC-Zn·SE-PIC-Zn·2CHCl₃ was −56.0 kcal mol⁻¹, which was approximately 10 kcal mol⁻¹ more negative compared to that of the diastereopure crystals. This cohesive energy is actually for the 0.5SE-PIC-Zn/0.5RE-PIC-Zn/CHCl₃ molecular composition, which is somewhat different from those of the pure SE-PIC-Zn and RE-PIC-Zn in which contribution from CHCl₃ is absent. The additional CHCl₃ molecules likely acts as an adhesive, increasing the overall lattice energy. This result explains the favored formation of the diastereomeric mixture in the presence of CHCl₃.

Fig. 8 Calculated energy profile of the gas phase (g), solution phase (sol) with a designated solvent, and solid phase (s) of RE-PIC (R) and SE-PIC (S). Stationary states are represented as thick solid lines (isolated molecules) or thick dotted lines (molecular crystals). Numbers in bold type beside the state lines are zero-point exclusive electronic energies of states. Numbers in normal type beside the arrows are energy differences between two states, which represent solvation energies (green), crystallization energies (the opposites of dissolution energies, dark red), and cohesive energies (blue).

On the other hand, the E_coh value for the crystal composed only of two diastereomers was computed from the crystal structure obtained by optimization after removing four CHCl₃ molecules manually. The cell angles of the optimized SE-PIC-Zn·RE-PIC-Zn crystal were well preserved and the monoclinic system was maintained. The lattice parameters were slightly reduced after the removal of the CHCl₃ molecules and the cell volume was reduced by 4.6%. The E_coh value was −37.2 kcal mol⁻¹, which is 7.2 and 8.6 kcal mol⁻¹ more positive than those of SE-PIC-Zn and RE-PIC-Zn, respectively. This is very interesting in two respects; although the energy of the SE-PIC-Zn·RE-PIC-Zn crystal system was obtained from the local minimum around the RE-PIC-Zn·SE-PIC-Zn·2CHCl₃ structure, which is most likely a metastable diastereomeric mixture state, the degree of destabilization of E_coh relative to those of pure SE-PIC-Zn and RE-PIC-Zn was similar to that of the stabilization of E_coh originating from RE-PIC-Zn·SE-PIC-Zn·2CHCl₃. In addition, the amount of destabilization energy was well beyond the coveted “chemical accuracy” target (1 kcal mol⁻¹) and likely much larger than the error range derived from the misleading calculation protocol, if any, based on the previously published reports.⁵¹ Therefore, it is not unreasonable to speculate that the formation of diastereopure crystals, either SE-PIC-Zn or RE-PIC-Zn, is favorable compared to that of the diastereomeric mixture crystal by ca. 8 kcal mol⁻¹.

We also considered the fractional crystallization behavior in terms of crystallization energy point of view. In this manuscript, the crystallization energy specifically implies the electronic energy difference between the solid state and the solution state. As shown in Fig. 8, the MeOH solution of both SE-PIC-Zn and RE-PIC-Zn, which are similar in energy, tends to form the diastereopure crystal rather than the mixed one as explained above. They cannot form the RE-PIC-Zn·SE-PIC-Zn·2CHCl₃ crystal due to the absence of CHCl₃ molecules in spite of ∼11 kcal mol⁻¹ preference. The CHCl₃ solution of SE-PIC-Zn and RE-PIC-Zn, however, prefers to form the mixed crystal containing the CHCl₃ molecules within the crystal rather than forming the diastereopure crystal. They do not form RE-PIC-Zn·SE-PIC-Zn because of its 18.8 kcal mol⁻¹ higher energy.

Collet suggested that the preponderance of racemic crystals over conglomerates originates from the entropic free energy penalty of ca. 0.5 kcal mol⁻¹ in conglomerates for demixing in the solid state.^87,88 This level of energy difference was experimentally proved with metastable conglomerates and stable racemic crystals of 2-chloromandelic acid.⁸⁹ Our results clearly indicated that the energy difference between diastereopure and diastereomeric mixture crystals is far beyond such a level and explains why the conversion into diastereomers from the racemate facilitates the enantioseparation. It is worth noting the energy difference between the two diastereomers, SE-PIC-Zn and RE-PIC-Zn, at this point. Both E_coh and E_cryst of SE-PIC-Zn are commonly larger in magnitude than those of RE-PIC-Zn by 1.4 and 0.6 kcal mol⁻¹, respectively. Although this level of energy difference between SE-PIC-Zn and RE-PIC-Zn is small relative to that between diastereopure and mixture crystals revealed in this study, it is comparable to that enough to segregate conglomerates and racemic crystals or that between polymorphs. The fact that the formation of the SE-PIC-Zn crystal precedes that of the RE-PIC-Zn one can be partly explained by this result.

4. Conclusion

In summary, we have developed a new enantioseparation method for PEA that consists of (i) combining (+)-camphor as a CDA by a condensation reaction, (ii) ZnCl₂ coordination, (iii) separation of diastereomers by the solubility difference of diastereomers and fractional crystallization, (iv) demetallation, and (v) detaching the CDA by hydrolysis. The overall yields of both (S)-PEA and (R)-PEA were 24.8% with estimated ee of 98 and 99%, respectively. We have obtained the E_coh of diastereopure crystals of both SE-PIC-Zn (−45.8 kcal mol⁻¹) and RE-PIC-Zn (−44.4 kcal mol⁻¹) as well as diastereomeric mixture crystals of RE-PIC-Zn·SE-PIC-Zn·2CHCl₃ (−56.0 kcal mol⁻¹) and RE-PIC-Zn·SE-PIC-Zn (−37.2 kcal mol⁻¹) through DFT calculations under periodic boundary conditions with a plane wave basis set, which were based on the experimentally determined X-ray crystallographic data. We also obtained the E_cryst values through DFT calculations of the isolated molecule with a standard Gaussian basis set, which were −27.1 and −26.5 kcal mol⁻¹ for SE-PIC-Zn and RE-PIC-Zn, respectively. These data provided the underlying background of spontaneous segregation of diastereopure crystals as well as preferred formation of the SE-PIC-Zn crystal over the RE-PIC-Zn one. This work suggested that the energy preference for forming diastereopure crystals over their corresponding mixture ones is ca. 8 kcal mol⁻¹, which is far beyond the level of that discriminating conglomerates and racemic crystals (∼0.5 kcal mol⁻¹). Our result gives a benchmark reference for future crystallization-based chiral resolution research.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF-2017R1D1A3B03030670) and the National Research Foundation of Korea (NRF) grant funded by the Korea Government (2015R1D1A1A01058566 and 2018R1D1A1B07049976). This work was supported by the Korea Institute of Science and Technology Information with supercomputing resources including technical support (KSC-2016-C2-0049 and KSC-2017-C2-0040).

References

1. H. Lorenz and A. Seidel-Morgenstern, Angew. Chem., Int. Ed., 2014, 53, 1218–1250.
2. P. Cintas, Angew. Chem., Int. Ed., 2002, 41, 1139–1145.
3. A. M. Rouhi, Chem. Eng. News, 2003, 81, 56–61.
4. L. Pasteur, C. R. Acad. Sci., 1848, 26, 535–539.
5. A. Collet, M. J. Brienne and J. Jacques, Chem. Rev., 1980, 80, 215–230.
6. W. H. Porter, Pure Appl. Chem., 1991, 63, 1119–1122.
7. R. A. Sheldon, Chirotechnology, 1993, Mercel Dekker, N.Y..
8. A. Collet, Angew. Chem., Int. Ed., 1998, 37, 3239–3241.
9. R. Vespalec and P. Boček, Chem. Rev., 2000, 100, 3715–3753.
10. N. M. Maier, P. Franco and W. Lindner, J. Chromatogr. A, 2001, 906, 3–33.
11. C. A. M. Afonso and J. G. Crespo, Angew. Chem., Int. Ed., 2004, 43, 5293–5295.
12. N. G. Anderson, Org. Process Res. Dev., 2005, 9, 800–813.
13. T. Matsuura and H. Koshima, J. Photochem. Photobiol., C, 2005, 6, 7–24.
14. T. J. Ward, Anal. Chem., 2006, 78, 3947–3956.
15. B. Chankvetadze, J. Chromatogr. A, 2007, 1168, 45–70.
16. Z. Wang, J. Ouyang and W. R. G. Baeyens, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2008, 862, 1–14.
17. I. Ilisz, R. Berkecz and A. Péter, J. Pharm. Biomed. Anal., 2008, 47, 1–15.
18. F. Faigl, E. Fogassy, M. Nógrádi, E. Pálovics and J. Schindler, Tetrahedron: Asymmetry, 2008, 19, 519–536.
19. R. E. Morris and X. Bu, Nat. Chem., 2010, 2, 353–361.
20. M. Lämmerhofer, J. Chromatogr. A, 2010, 1217, 814–856.
21. D. P. Glavin, J. E. Elsila, A. S. Burton, M. P. Callahan, J. P. Dworkin, R. W. Hilts and C. D. K. Herd, Meteorit. Planet. Sci., 2012, 47, 1347–1364.
22. D. Zbaida, M. Lahav, K. Drauz, G. Knaup and M. Kottenhahn, Tetrahedron, 2000, 56, 6645–6649.
23. M. P. Elsner, D.-F. Menéndez, E. A. Muslera and A. Seidel-Morgenstern, Chirality, 2005, 17, S183–S195.
24. G. Coquerel, Top. Curr. Chem., 2007, 269, 1–51.
25. H. Lorenz, A. Perlberg, D. Sapoundjiev, M. P. Elsner and A. Seidel-Morgenstern, Chem. Eng. Process., 2006, 45, 863–873.
26. H. Lorenz, D. Polenske and A. Seidel-Morgenstern, Chirality, 2006, 18, 828–840.
27. N. Wermester, E. Aubin, M. Pauchet, S. Coste and G. Coquerel, Tetrahedron: Asymmetry, 2007, 18, 821–831.
28. M. P. Elsner, G. Ziomek and A. Seldel-Morgenstern, AIChE J., 2009, 55, 640–649.
29. D. G. Allen, G. M. McLaughlin, G. B. Robertson, W. L. Steffen, G. Salem and S. B. Wild, Inorg. Chem., 1982, 21, 1007–1014.
30. H. Lorenz, P. Sheehan and A. Seidel-Morgenstern, J. Chromatogr. A, 2001, 908, 201–214.
31. L. Mimassi, C. Guyard-Duhayon, M. N. Rager and H. Amouri, Inorg. Chem., 2004, 43, 6644–6649.
32. M. S. Kang, J. Cho, S. Nayab and J. H. Jeong, Polyhedron, 2019, 158, 135–143.
33. J. Cho, M. K. Chun, S. Nayab and J. H. Jeong, Transition Met. Chem., 2019, 44, 175–185.
34. S. Park, J. Lee, J. H. Jeong, H. Lee and S. Nayab, Polyhedron, 2018, 151, 82–89.
35. J. H. Ham, J. Cho, S. Nayab and J. H. Jeong, Inorg. Chim. Acta, 2018, 480, 33–41.
36. K. S. Kwon, S. Nayab and J. H. Jeong, Polyhedron, 2017, 130, 23–29.
37. G. Chelucci, S. Baldino, S. Chessa, G. A. Pinna and F. Soccolini, Tetrahedron: Asymmetry, 2006, 17, 3163–3169.
38. N. D. P. Cosford, L. Bleicher, A. Herbaut, J. S. McCallum, J.-M. Vernier, J. H. Dawson, J. P. Whitten, P. Adams, L. Chavez-Noriega, L. D. Correa, J. H. Crona, L. S. Mahaffy, F. Menzaghi, T. S. Rao, R. Reid, A. I. Sacaan, E. Santori, K. A. Stauderman, K. Whelan, G. K. Lloyd and I. A. McDonald, J. Med. Chem., 1996, 39, 3235–3237.
39. J.-L. Galzi and J.-P. Changeux, Neuropharmacology, 1995, 34, 563–582.
40. G. K. Lloyd and M. Williams, J. Pharmacol. Exp. Ther., 2000, 292, 461–467.
41. F. F. Wagner and D. L. Comins, Org. Lett., 2006, 8, 3549–3552.
42. T. Tachibana, W. Ueoka, Md. S. I. Khan, R. Makino and M. A. Cline, Domest. Anim. Endocrinol., 2019, 66, 57–63.
43. E. Tamaddonfard, A. Erfanparast, H. Ghasemi, F. Henareh-Chareh, M. Hadidi, N. Mirzakhani, S. Seyedin, M. Taati, R. Salighedar, S. Salimi and F. Safaei, Eur. J. Pharmacol., 2016, 791, 696–702.
44. Y. T. Qin, S. H. Ma, Q. X. Zhuang, Y. H. Qiu, B. Li, Y. P. Peng and J. J. Wang, Neurosci. Lett., 2011, 502, 133–137.
45. H. E. Smith, L. J. Schaad, R. B. Banks, C. J. Wiant and C. F. Jordan, J. Am. Chem. Soc., 1973, 95, 811–818.
46. J. W. Canary, Y. Wang, R. Roy Jr., L. Que Jr. and H. Miyake, Inorg. Synth., 1998, 32, 70–75.
47. J. W. Westley, R. H. Evans Jr. and J. F. Blount, J. Am. Chem. Soc., 1977, 99, 6057–6061.
48. L. E. Iglesias, V. M. Sánchez, F. Rebolledo and V. Gotor, Tetrahedron: Asymmetry, 1997, 8, 2675–2677.
49. K. A. Skupinska, E. J. McEachern, I. R. Baird, R. T. Skerlj and G. J. Bridger, J. Org. Chem., 2003, 68, 3546–3551.
50. L. Martínez-Montero, V. Gotor, V. Gotor-Fernández and I. Lavandera, Green Chem., 2017, 19, 474–480.
51. J. Moellmann and S. Grimme, J. Phys. Chem. C, 2014, 118, 7615–7621.
52. A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Phys., 2012, 137, 054103.
53. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
54. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
55. M. J. e. a. Frisch, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016.
56. C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664–675.
57. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
58. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
59. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
60. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
61. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
62. P. Fuentealba, H. Stoll, L. von Szentpaly, P. Schwerdtfeger and H. Preuss, J. Phys. B: At., Mol. Opt. Phys., 1983, 16, L323–L328.
63. U. Wedig, M. Dolg, H. Stoll and H. Preuss, Energy-Adjusted Pseudopotentials for Transition-Metal Elements, Springer, Dordrecht, 1986.
64. D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141.
65. S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.
66. S. Miertuš and J. Tomasi, Chem. Phys., 1982, 65, 239–245.
67. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
68. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
69. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
70. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
71. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
72. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
73. J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Angyán, J. Chem. Phys., 2006, 124, 154709.
74. G. Blay, E. Climent, I. Fernández, V. Hernández-Olmos and J. R. Pedro, Tetrahedron: Asymmetry, 2006, 17, 2046–2049.
75. G. Blay, E. Climent, I. Fernández, V. Hernández-Olmos and J. R. Pedro, Tetrahedron: Asymmetry, 2007, 18, 1603–1612.
76. S. Nayab and J. H. Jeong, Inorg. Chem. Commun., 2016, 65, 35–38.
77. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
78. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
79. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
80. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
81. L. Kronik and A. Tkatchenko, Acc. Chem. Res., 2014, 47, 3208–3216.
82. K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. De Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Grånäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iuşan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küçükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G. M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. Van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G. X. Zhang and S. Cottenier, Science, 2016, 351, aad3000.
83. B. M. Axilrod and E. Teller, J. Chem. Phys., 1943, 11, 299–300.
84. O. Anatole von Lilienfeld and A. Tkatchenko, J. Chem. Phys., 2010, 132, 234109.
85. A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Phys., 2013, 138, 054103.
86. T. Risthaus and S. Grimme, J. Chem. Theory Comput., 2013, 9, 1580–1591.
87. A. Collet, The homochiral versus heterochiral packing dilemma, in Chiral Molecules Problems and Wonders of Chiral Molecules, ed. M. Simonyi, Akad. Kiado, Budapest, Hung., 1990, pp. 91–109.
88. R. J. Davey, G. Sadiq, C. C. Seaton, R. G. Pritchard, G. Coquerel and C. Rougeot, CrystEngComm, 2014, 16, 4377–4381.
89. H. Lorenz, J. von Langermann, G. Sadiq, C. C. Seaon, R. J. Davey and A. Seidel-Morgenstern, Cryst. Growth Des., 2011, 11, 1549–1556.

---

Footnote

† Electronic supplementary information (ESI) available: ¹H NMR spectra, ¹³C NMR spectra, IR spectra, DFT calculation results. CCDC 1914650–1914652. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9qi00523d

---