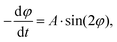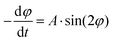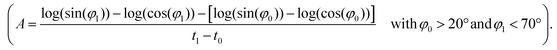Open Access Article
Open Access ArticlePredicting the orientation of magnetic microgel rods for soft anisotropic biomimetic hydrogels†
Jonas C.
Rose
 a,
Maaike
Fölster
a,
Lukas
Kivilip
b,
Jose L.
Gerardo-Nava
a,
Maaike
Fölster
a,
Lukas
Kivilip
b,
Jose L.
Gerardo-Nava
 a,
Esther E.
Jaekel
a,
David B.
Gehlen
a,
Esther E.
Jaekel
a,
David B.
Gehlen
 a,
Wilko
Rohlfs
*b and
Laura
De Laporte
a,
Wilko
Rohlfs
*b and
Laura
De Laporte
 *ac
*ac
aDWI – Leibniz-Institute for Interactive Materials, Aachen, Germany. E-mail: delaporte@dwi.rwth-aachen.de
bRWTH Aachen University, Institute of Heat and Mass Transfer, Aachen, Germany. E-mail: rohlfs@wsa.rwth-aachen.de
cRWTH Aachen University, Institute for Technical and Macromolecular Chemistry, Aachen, Germany
First published on 18th October 2019
Abstract
Living multicellular organisms comprise a high degree of soft anisotropic tissues but the development of controlled artificial assembly processes to mimic them remains challenging. Therefore, injectable, polymeric, magneto-responsive microgel rods are fabricated to orient within a low magnetic field. The incorporated superparamagnetic nanoparticles induce local dipole moments, resulting in a total magnetic torque that endows microgels with different structural, mechanical, and biochemical properties. In this report, a predictive macroscopic model based on an ellipsoidal element dispersed in a Newtonian fluid is adjusted using experimental data, which enables the prediction of the orientation rate and the required magnetic field strength for various microgel design parameters and fluid viscosities. The ordered microgels are fixed by crosslinking of a surrounding hydrogel, and can be employed for a wide variety of applications where anisotropic composite hydrogels play a crucial role; for instance as adaptive materials or in biomedical applications, wherein the model predictions can reduce animal experiments.
Introduction
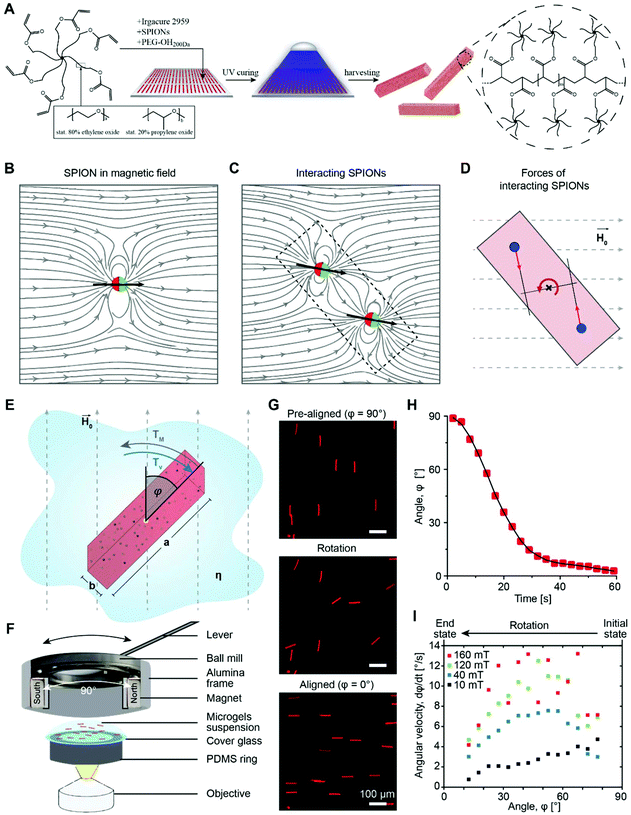
Nature's way of forming complex tissues with hierarchical architectures involves combinations of molecules to construct biocomposites with specific mechanical, biochemical, and structural properties.1 Assembled soft, nanometer-scale filamentous structures form the macroscopic extracellular matrix (ECM), surrounding the cells inside the tissues and providing a specific cell niche. These constructs are typically anisotropic with dynamic properties as they are constantly remodeled by cells. Synthetic fabrication of biomimetic matrices with comparable complexity is, however, still a great challenge. While hard tissues are composed of biomineral crystals and structural proteins (mainly collagen), soft tissues comprise a wavy, fibrous network of different proteins and proteoglycans.2 Distinct heterogeneous patterns guide cellular growth and junctions, while influencing the cytoskeletal architecture.3 To reproduce soft tissues, hydrogels are designed with synthetic and biological molecules (e.g. poly(ethylene glycol) (PEG) and hyaluronic acid4) and aim at mimicking the strain-stiffening behavior of the ECM (e.g. polyisocyanopeptides or fibrin5) or introducing viscoelasticity with an adjustable time-scale to achieve stress relaxation (e.g. PEG-linkers conjugated to alginate6 and hydrazone7). To artificially reinforce soft hydrogels and locally alter the mechanical and topographic signals to the cells, nanometer- to micrometer-sized colloids, microgels, or fibers are mixed with the precursor solution before gelation.8 By magnetically aligning anisometric elements, material anisotropy is achieved inside a hydrogel (Anisogel) to locally guide the cells in a unidirectional manner (see Fig. 1A and Fig. S1†).9 Superparamagnetic iron oxide nanoparticles (SPIONs) are incorporated into rod-shaped microgels to render them magnetic, as they can induce an ultrahigh magnetic response,10 do not undergo magnetic hysteresis, and are unmagnetized in the absence of a magnetic field.11 Co-delivery of the microgels with an in situ crosslinkable biocompatible hydrogel allows for the fixation of the assembly after injection and magnetic ordering. These types of magnetically responsive biomaterials can be manipulated over centimeter length scales using low field magnetic strengths in a non-invasive and biorthogonal manner. The artificial assembly process provides a simple alternative for the more complex and sophisticated natural assembly and disassembly mechanisms on nano, micro, and macro length scales, which bypass the thermodynamic equilibrium by metastable states and a supply of energy.12 The injectable Anisogel with rod-shaped polyethylene glycol (PEG) microgels has been previously demonstrated to align cells and nerves with a minimal amount of guiding elements (1–2 vol%).13 The ECM produced by the cells is also oriented and can form a recreated native anisotropic structure that can replace the synthetic matrix over the course of degradation.9b RGD modification of the microgels further improves the orientation of the cells but significantly reduces fibronectin production. Interestingly, the mechano-sensitive protein yes-associated protein (YAP) shuttles to the nucleus due to the mechanical anisotropy of the Anisogel. In vitro experiments of cultured dorsal root ganglion explants revealed regenerated, aligned and functional nerves with spontaneous activity and electrical signals propagating along the anisotropy axis of the material.9aIn the present study, the magnetic orientation of soft, water swollen microgel rods is studied as they have recently been demonstrated to be an important building block in biomedical research.13,14 To render the polymeric microgels magneto-responsive, a small volume fraction of SPIONs (∼5 × 10−3 vol%) is incorporated and distributed inside the nano-porous microgel matrix by mixing them in the polymer precursor solution before crosslinking using an in mold-polymerization technique.13 SPIONs are not covalently bound to the polymer but do not leak out as they are physically entrapped inside the network. This has been demonstrated in a previous study by elemental analysis.13 The rod-shaped microgels are produced with variable lengths ranging from 12.5 to 200 μm and diameters ranging from 2.5 to 10 μm, which are large enough to make microgel movement primarily dependent on the magnetic field and not on Brownian motion.15
The effect of different microgel design parameters (dimension, aspect ratio, stiffness, and SPION concentration) and the influence of the viscosity of the surrounding fluid and the magnetic field strength on the microgel orientation rate are investigated. In order to establish a prediction method for the microgel orientation rate or the minimal magnetic field required to form the Anisogel, experimental observations are compared with a physical model. A better understanding of the physics behind the microgel orientation mechanism is essential to control the final assembly of the microgel rods inside the biocomposite. Finally, the injection and orientation of the Anisogel inside a clinically relevant tissue model is verified.
Results and discussion
Microgel orientation theory
A theoretical and experimental model comparable to the Anisogel system with regard to physics has been reported by Erb et al.10 In their study, solid micro-rods are homogenously coated over the rod shell with SPIONs resulting in isotropic magnetic properties. Force contributions from magnetic torque, thermal fluctuations (Brownian motion), and gravity are compared depending on the magnetic field strength below 10 mT and particle geometry. For explaining and illustrating the magnetic orientation of the microgel rods, a novel microscopic model approach is developed and utilized.The embedded SPIONs inside the microgels function as single domain magnetic particles of spherical shape with radius R and magnetize in the presence of an external field. With their dipole moment 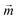 (Fig. 1B, eqn (1)), the SPIONs create a local field around themselves (Hlocal), which is a superposition of the magnetic field induced by the dipole,
(Fig. 1B, eqn (1)), the SPIONs create a local field around themselves (Hlocal), which is a superposition of the magnetic field induced by the dipole, 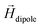 , and other surrounding dipoles, and the external magnetic field. The dipole moment
, and other surrounding dipoles, and the external magnetic field. The dipole moment 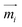 of the SPION depends on the volumetric magnetization
of the SPION depends on the volumetric magnetization 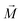 of the SPION material and the SPION volume.
of the SPION material and the SPION volume.
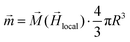 | (1) |
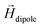 decays cubically
decays cubically 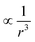 with r being the distance from the dipole (SE1, ESI†) and contributes to the local magnetic field (Hlocal) formed by the neighboring dipoles, as the SPIONs are closely distributed throughout the microgels (Fig. 1C).
with r being the distance from the dipole (SE1, ESI†) and contributes to the local magnetic field (Hlocal) formed by the neighboring dipoles, as the SPIONs are closely distributed throughout the microgels (Fig. 1C).
Due to the SPION interaction, the resulting superposed magnetic field, created by the external field and the SPIONs, requires an iterative solution method. The magnetic field is sequentially used to calculate the force to which each dipole is subjected, resulting in a total magnetic torque acting on the microgel induced by all SPIONs, where 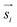 is the distance from the SPION to the center of rotation (Fig. 1D, eqn (2))
is the distance from the SPION to the center of rotation (Fig. 1D, eqn (2))
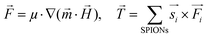 | (2) |
An illustration of this SPION interaction (Fig. S2†) reveals that SPIONs in the center of the microgel contribute less to the total torque than those at the edges due to a stronger asymmetry of the magnetic field. Hence, longer aspect ratio geometries result in a higher magnetic driving force.
Experimental microgel orientation
A microscopic setup allows the recording of the microgel orientation (Fig. 1E and F) in order to experimentally determine the microgel rotation kinetics in a magnetic field. Separate analyses are performed for altering the parameters: the magnetic field strength and direction, viscosity of the surrounding fluid, microgel dimensions and aspect ratio, and SPION-content. An external magnetic field is induced by attaching two static rare earth magnets, which oppose each other, to the inner ring of a ball mill. The orientation of the magnetic field is modified by rotating the magnets without affecting the sample position. To vary the field strength, either the distance between the two magnets or the magnet material is changed. A reproducible initial position is achieved by pre-aligning the microgels in the magnetic field. With a 90° turn of the magnetic field, the rotation and recording are started (Fig. 1G). Importantly, the analyzed microgel dispersions are below the critical volume fractions, at which the packing entropy contributes to the orientation.16Exemplary experimental results of the orientation process are shown in Fig. 1H for microgels with a size of 10 × 10 × 50 μm3 and a very small volume fraction of SPIONs (∼5 × 10−3 vol%). Differences in microgel orientation for varying magnetic fields are detected, and the angle-dependent orientation rate is obtained by clustering the time derivative data into 5° intervals (Fig. 1I). In the case of a sufficiently high magnetic field, the magnetization of the SPIONs is saturated and the orientation rate follows a sinusoidal function with a maximum at 45°. For lower magnetic fields (<40 mT) the maximum is reduced and for even smaller fields (<20 mT), the maximum shifts towards higher angles, which corresponds to a high angular velocity at the beginning of the orientation and a decaying velocity as the long microgel axis approximates the direction of the field lines.
Macroscopic model
To predict the orientation rate of microgels with a large number of SPIONs, the calculation of the magnetic torque using the microscopic SPION interaction model is not time-efficient. Therefore, a macroscopic approach is employed that accounts for the main physical mechanisms and the applied external parameters. In this study, a previously published model concerning the rotation of homogeneous ellipsoids (long axis a and short axis b) in a magnetic field is adopted.17 The model is based on balancing the magnetic torque, TM, and the viscous torque, Tν, and is thus applicable to the microgels studied here, as they are sufficiently small to neglect inertia (low Reynolds number) but sufficiently large such that Brownian motion is of minor importance. In this case, the sum of the two torques vanishes, i.e. TM + Tν = 0, which allows for an expression for the angular velocity Ω (eqn (3)):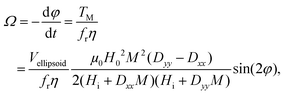 | (3) |
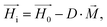 | (4) |
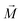 throughout the ellipsoid does not change, leading to a homogeneous internal field
throughout the ellipsoid does not change, leading to a homogeneous internal field 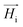 for a constant angle.
for a constant angle.
On the other hand, magnetization curves of ferromagnetic materials characteristically have an initial linear region, followed by a non-linear magnetization, and finally undergo saturation wherein a further increase in the magnetic field does not elevate the magnetization anymore. In the study reported by Erb et al., only low magnetic fields are applied,18 which does not take into account the non-linear magnetization effects of ferromagnetic materials. In contrast, when magnetic fields above 10 mT are applied, non-linear SPION magnetization with saturation needs to be taken into consideration.17 In the case of rod-shaped microgels, consisting mostly of water and SPIONs in the polymeric portion of the microgel, the magnetization is unknown. The very small SPION concentration (<0.005 vol%) in the microgel suggests a volume-averaged microgel magnetization that is at least an order of magnitude below the applied magnetic field. In this case, deviations between the internal and external magnetic fields could be neglected (eqn (4), Hi ≈ H0), leading to a sinusoidal function of the angular velocity in eqn (3). However, the experimental data in Fig. 2H show a strong asymmetry with a shift to the right (initial part of the orientation) at low magnetic field intensities. This demonstrates the large influence of demagnetization at the tested magnetic field strengths and indicates a non-homogeneous magnetic field within the microgel. One potential reason may be the interaction between the SPIONs, which is not accounted for in a volume-averaged magnetization value. Note that models for demagnetizing factors of complicated particle mixtures have been reported based on effective medium theory19 but they do not predict the strong increase of demagnetization as experimentally observed here, necessitating the consideration of non-linear terms and nanoscale effects.20 To adapt eqn (4) to the higher influence of demagnetization, the model parameter Cdemag is introduced (eqn (5)):
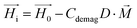 | (5) |
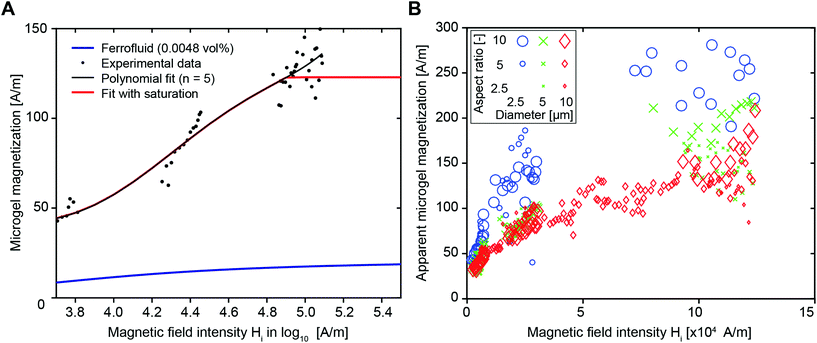
For the predictive model of this present study, the microgel magnetization was first approximated by the magnetization curve of the diluted ferrofluid, provided by the manufacturer (Ferrotec, Fig. S3,† blue line), which yielded a significant underestimation of the rotation velocity. This can either result from an overestimation of the viscous torque or an underestimation of the magnetic torque. The hydrodynamic torque is likely smaller for swollen polymeric microgels compared to solid particles due to slip at their surface21 and the potential pressure-induced fluid transport through the microgels. Microgels have an open structure and contain >80% water, in contrast to solid particles, which are the core elements of the model. On the other hand, the microgel magnetization may be higher due to inhomogeneous SPION distributions. To systematically assess the differences between the experiment and predictions, an apparent microgel magnetization is introduced, which is the hypothetical magnetization of the microgel, necessary to rotate the microgel with the experimentally observed rotation velocity. We choose to use an apparent magnetization, although we also believe that the rotational torque has an impact due to the non-rigid and open structure of the microgels.
The apparent microgel magnetization is calculated by an iterative estimation using eqn (3) and (4) with a fixed model parameter Cdemag and the experimentally obtained angular velocities. The latter are retrieved from the microgel orientation, for which 5° intervals, ranging from an orientation angle of 10° to 80°, are used. This procedure is applied to a dataset (microgel dimensions of 10 × 10 × 50 μm3, 400 μg mL−1 SPIONs, and magnetic field strengths of 10, 40, 120 mT) yielding the relation between the internal magnetic field and apparent microgel magnetization shown in Fig. 2A (dotted black values). Note that data from 160 mT are not used due to a significant volatility of the rotation speed, which is a result of the quick rotation compared to the acquisition frequency (1 Hz). Due to a good fit with the experimental data, Cdemag of 500 is initially chosen (Fig. S5† for Cdemag = 200 and 800). A fifth-degree polynomial (similar to Shine and Armstrong17a) is fitted to the data points to obtain an estimate of the magnetization curve, depicted by the red line in Fig. 2A. Here, a saturation behavior above H = 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 A m−1 is taken into account, as the increase in the external magnetic field from 80 to 160 mT does not further increase the angular velocity (Fig. 1I and Fig. S6†).
000 A m−1 is taken into account, as the increase in the external magnetic field from 80 to 160 mT does not further increase the angular velocity (Fig. 1I and Fig. S6†).
The microgel size remains constant throughout the evaluation process as shown in Fig. 2A and Fig. 2B shows the estimated apparent microgel magnetization for differently sized microgels, keeping Cdemag constant at 500. According to theory, magnetization is a specific quantity (material property), which does not depend on volume or geometry.22 Based on the experimental analysis of the microgels, an equal scaling with volume of the magnetic and viscous torque does not hold (Fig. 2B). A strong dependency of the apparent microgel magnetization on the microgel diameter (illustrated by marker color) with an increasing magnetization for decreasing the microgel diameter is identified. For the larger diameter of 10 μm, the aspect ratio (illustrated by marker size) has a minor influence. For small microgels (diameter 2.5 μm and AR = 10, large blue circles), the apparent microgel magnetization reaches up to values around 250 A m−1 in the saturation region, while higher volume microgels (diameter 10 μm and AR = 10, large red diamonds) exhibit a saturation of approximately 150 A m−1.
As discussed above, the estimated magnetization is higher than the theoretical magnetization (blue line) and significantly depends on the diameter of the microgel. Note, for a constant diameter (e.g. 10 μm, red diamonds), the apparent microgel magnetization follows a typical magnetization curve with a saturation behavior at higher magnetic field intensities. However, a severe increase of the apparent magnetization is required in the case of lower diameter microgels.
The increase of the apparent microgel magnetization with decreasing microgel volume translates to an increased overestimation of the viscous torque or an increased underestimation of the magnetic torque. The differences in the surface-to-volume ratio of the cavities in the PRINT mold during the crosslinking process may cause variations in the SPION-distribution and magnetic interaction between the SPIONs and polymeric network of the microgels.23 In addition, the inhomogeneous SPION distribution inside the microgels demonstrates the tendency of the SPIONS to segregate at the microgel surface (Fig. S4†). As smaller microgels have a larger surface-to-volume ratio, a larger percentage of SPIONs may be located at the surface of these microgels, which may generate a higher magnetic momentum because of a larger distance to the axis of rotation. This has been demonstrated for surface coated ellipse-shaped solid particles that are more magnetically responsive than isotropically distributed SPION ellipsoids (Erb et al.10). In addition, a previous report demonstrated that a PEG coating on SPIONs reduces their magnetization.24 As the SPIONs (EMG 700, FerroTec) have a proprietary anionic coating, they may interact with the polymer network, which will in total be reduced for smaller microgel volumes and thus less SPIONs for constant SPION concentration.
As mentioned above, besides magnetic effects, changes in friction may be responsible for the increased rotation rate, which could be more pronounced for smaller microgels.
More details on the calculation of the apparent microgel magnetization and subsequent angular velocity, as well as a more in-depth explanation on the physics of microgel orientation, can be found in the ESI.†
In the final optimization step, using the optimization method fminsearch in Matlab,25 the coefficients of the polynomial function, as well as Cdemag, are tuned in order to best fit the experimental data yielding the following formula (eqn (6)):
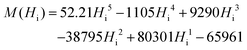 | (6) |
Comparison of the experimental and modeling results
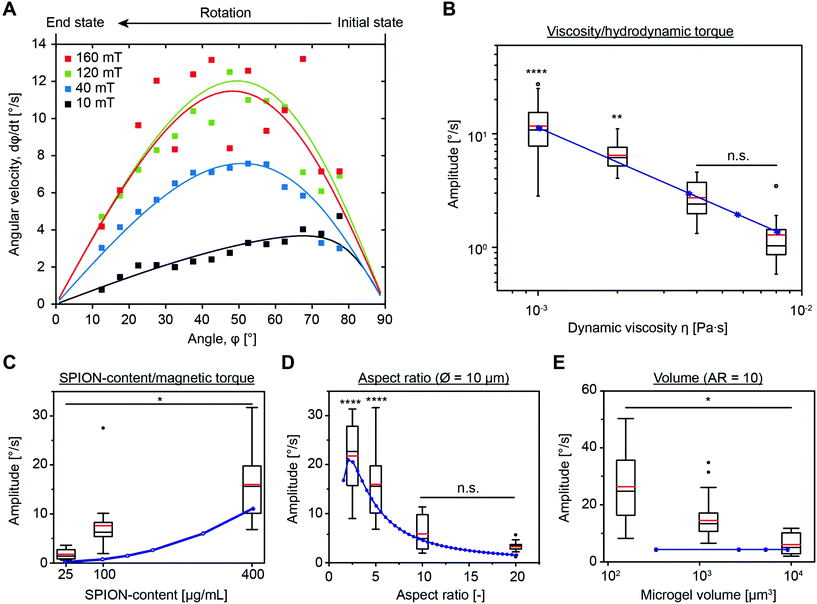
Using the experimental setup explained above, a large data set, including variations in the microgel size and aspect ratio, magnetic field intensity, SPION concentration, and viscosity of the bulk liquid, is obtained in the present study. As the standard, microgels with 20 wt/vol% polymer, a size of 10 × 10 × 50 μm, and a SPION content of 400 μg mL−1 in water are chosen. First, a systematic variation of the magnetic field intensity reveals the saturation of the angular rotation speed above approximately 80 mT (Fig. 3A and Fig. S6†). The saturation behavior is attributed to the fact that all magnetic moments inside the SPIONs are oriented, impeding a further increase of the material magnetization. The mean amplitude in the saturated regime is around 12° s−1. It is noteworthy that the recorded microgel orientation motions are associated with experimental variations, which is probably caused by an inhomogeneous SPION distribution inside the microgels (Fig. S4†). SPIONs may aggregate during the microgel fabrication process or during the gelation of the microgel prepolymer, which follows a phase separation process during crosslinking, resulting in polymer rich and poor regions.13 During washing and purification, the SPIONs remain in the reactive polymer-rich phase surrounding the microscopic pores and do not leak out.A comparison between the model predictions and experimental results of the angular velocity for different angles is shown in Fig. 3A. Tuning the microgel magnetization curve and the demagnetization constant as described before is suitable to predict the rotation dynamics for the specific microgel diameter. The macroscopic model and the experimental orientation measurements reveal the sinusoidal curves for magnetic fields ≥40 mT. For low magnetic fields (10 mT), the influence of the demagnetization tensor increases, shifting the maximum rotation speed to higher angles. Because the effect of demagnetization decreases with increasing the external magnetic field, experimental results with sufficiently high magnetic fields are used to examine the effect of different experimental and microgel parameters (Fig. S7†). This allows for an estimation of the amplitude (A) from the experimental data by the integration of
The effect of the dynamic viscosity of the surrounding liquid, and thus the viscous torque Tν on the microgel alignment, is investigated by dispersing the microgels in fluids with various viscosities ranging from 1 × 10−3 to 8 × 10−3 Pa s (Fig. 3B). As confirmed by the good fit between the experimental data and model predictions, the rotation speed decreases according to the theoretical predictions with increasing viscosity. Predictability of the microgel orientation in different fluids is of particular importance for the desired application as the microgels are dispersed in prepolymeric solutions with variable viscosities to fix their assembly in vivo after crosslinking to enable the removal of the magnetic field.
Varying the SPION concentration is another suitable way to modify the rotation rate of the microgel. This parameter affects the apparent microgel magnetization and as such the magnetic torque TM. As high SPION concentrations in the microgel prepolymer solution tend to aggregate, a maximal SPION-loading of 400 μg mL−1 is used and compared to lower SPION amounts of 25 and 100 μg mL−1. Experimental results in the area of magnetic saturation (160 mT) reveal a four-fold increase in the rotation rate by increasing the SPION content from 25 to 100 μg mL−1. A further increase from 100 and 400 μg mL−1 only leads to a doubling in amplitude (Fig. 3C). These experimental findings disagree with the model, as eqn (3) shows a quadratic increase in the rotation rate with increasing SPION content (Hi ≫ DiiM and Hi ≈ H0 for saturated magnetization, thus dφ/dt ∼ M2). This may be caused by an increase in the SPION aggregation in the case of 400 μg mL−1 in comparison to 100 μg mL−1, which is also reflected in Fig. S8,† where the apparent magnetization for both 100 and 400 μg mL−1 SPIONs is very similar at the high magnetic field intensity used for this experiment. Interestingly, this observation contradicts a previous report, demonstrating that SPION aggregation should not affect magnetization.26 Alternatively, an increased effect of SPION interaction with the surrounding polymer network or other yet unknown effects may be a cause for the overestimation of the magnetic torque when comparing experimental results and model predictions.
Owing to the complex and up to now unknown relationship between the SPION concentration and apparent microgel magnetization, an individual magnetization curve is required for each SPION concentration (Fig. S8†). Because of the constant microgel dimensions, it is not expected that the viscous torque changes with the SPION concentration.
The influence of the microgel size and aspect ratio is addressed by changing the aspect ratio (length/width) from 2.5 to 20 for a constant diameter of 10 μm and the microgel diameter from 2.5 to 5 up to 10 μm for an aspect ratio of 10 (Fig. S9†). In particular, the aspect ratio has a strong impact on the orientation rate17b because the viscous torque increases more strongly than the magnetic torque for increasing ratio. The experimental data in Fig. 3D show that the amplitude approximately halves by doubling the aspect ratio. These observations are in good agreement with the model predictions confirming that utilizing Perry's friction factors for a solid ellipsoidal shape is a good approximation for the shape-dependency of the friction in the case of the microgels. This does not imply a correct estimation of the absolute friction, which can be altered by slip effects and the permeability of the swollen microgel. The model further suggests a decrease in the amplitude by a reduction of the aspect ratio from 2.5 to 1, which is reasonable, as the formation of a magnetic easy axis is inhibited by a diagonal alignment as the only option for square-like elements.27
According to theory, the volume of the microgel should not influence the rotation rate for the constant aspect ratio (eqn (6)) as both the magnetic and viscous torque scale in the same manner. In strong contrast, experimental data reveal a reduction in the orientation rate with increasing microgel volume (here equal to 10 d3) (Fig. 3E). This is not surprising as we previously calculated a varying apparent microgel magnetization depending on the microgel volume with smaller diameters leading to higher apparent magnetization and thus faster rotation. In addition, as the microgels are softer than solid particles, simultaneous deformations may have an effect.
Finally, as soft microgels allow for strong deformations,28 including bending, the effect of microgel stiffness is studied (Ebending ∼ EYoung). This is particularly relevant for the high aspect ratio microgels, as the bending force scales down with the squared length (Fc ∼ A·κ), where A is the boundary condition and κ the bending rigidity.29 The stiffness is altered by varying the polymer content, which is directly related to the crosslinking densities and thus the elastic moduli.13,30 For a magnetic field of 40 mT, no significant differences in the orientation rate are observed for microgels prepared with a polymer concentration ranging from 11–40 wt/vol% (Fig. S10†). In the case of 160 mT, only 11 wt/vol% soft microgels oriented slightly slower than the stiffer microgels. This may be due to a reduction in the efficiency of SPION-entrapment due to the lower crosslinking density in comparison with 20 wt/vol% polymer microgels, which entrap ∼100% of the SPIONs.13 Additionally, the increased swelling and reduced persistence length of the microgels can influence the magnetic response. Nevertheless, for polymer contents equal to and higher than 15 wt/vol% polymer content, the magnetic response is not affected, indicating no or negligible effects of microgel deformation during magnetic orientation.
In vivo applicability
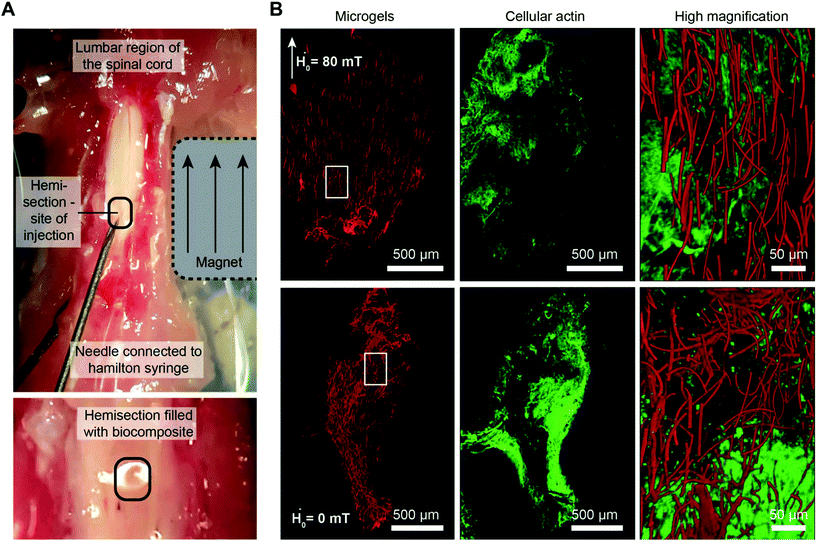
To test whether the hybrid material, containing magneto-responsive microgels, can be injected inside an animal injury model in the presence of an external magnetic field and lead to oriented structures, the spine from mice is extracted and a hemisection is performed to prepare a cavity. Microgels of 2.5 × 2.5 × 50 μm3 are co-injected with a surrounding natural pre-polymer solution (fibrinogen with a dynamic viscosity ≤15 Pa s, Fig. S11†) that crosslinks enzymatically at the injury site.31 As it is important to adjust the gelation time of the surrounding gel to the required time for microgel orientation, the model helps to estimate this time. The data reveal that microgels of 2.5 × 2.5 × 50 μm3 have an orientation time (t1° to 89°) of 9.2 s in water, at a saturated magnetic field (∼80 mT). Taking the increased dynamic viscosity of the surrounding precursor solution (fibrinogen 4 mg mL−1 ∼ 15 Pa s, Fig. S11†) into account, a maximal orientation time of approximately 130 s is expected. After including a mixing and injection time of 10 s, a gelation time of approximately 140 s is aimed for, which is achieved by applying a thrombin concentration of 0.125 U mL−1 and 4 U mL−1 Factor XIII (Fig. S12†). A longer gelation time might further improve the alignment; however, in vivo, rapid gelation is essential to prevent dilution of the material by body fluids and dispersion of the microgels from the injection site.32Initial tests in a hemisection cavity using a tubular structure as an artificial ‘spinal cord’ demonstrate complete microgel alignment (Fig. S13†). Therefore, the hybrid hydrogel is sequentially injected into a rectangular-shaped hemisection cavity in the lumbar region of a mouse spinal cord, which is a common model to study spinal cord regeneration.33 After injection, a static magnet is placed adjacent to the spinal cord resulting in magnetic field lines parallel to the tissue. As the rod-shaped microgels orient, the surrounding fibrin gel crosslinks to stabilize the oriented microgels inside the cavity (Fig. 4A). In the absence of a magnetic field, the microgels are randomly oriented (Fig. 4B). Deep confocal imaging reveals the precise microgel assembly over z-ranges ≥100 μm (Movies S1 and S2†).
These initial studies substantiate the applicability of the material for in vivo purposes. By applying a static magnet close to the spinal cord immediately after injecting a small Anisogel volume with a Hamilton syringe, this novel material concept is readily transferrable to animal studies. The predictive model described here is a helpful tool when designing the material parameters to optimize microgel orientation with regard to the gelation time of the surrounding gel. However, the experiments show an up-to-date only partially predictable behavior, emphasizing the importance of these carefully conducted experiments for understanding the physics of microgel orientation as a fundamental step towards predictive modeling.
Conclusions
In conclusion, it is crucial to have insight into the orientation rate of rod-shaped microgels, as the ordered microgels need to be fixed in a surrounding matrix to fabricate defined anisotropic matrices for tissue regeneration. By predicting the orientation time for specific microgel parameters, the gelation kinetics of a prepolymer solution with a particular viscosity can be adapted. To establish the model, an initial calibration of the apparent microgel magnetization is performed using experimental results in water for one standard microgel type (10 × 10 × 50 μm3) and SPION concentration (400 μg mL−1). Afterwards, model predictions are compared to the experimental data by investigating the effect of the applied external magnetic field, viscosity of the surrounding fluid, magnetic loading, microgel aspect ratio, and microgel volume. While the predictions for most parameters closely fit the experimental data, the SPION content and microgel volume do not follow the model physics. Only by calibrating the model to each specific microgel diameter and SPION content, the orientation times could be predicted correctly. In summary, the approximation of the apparent microgel magnetization enables the use of the model for the material system presented and allows for directed fabrication of a variety of microgel-in-hydrogel biocomposites to regenerate complex anisotropic tissues. Moreover, through the predictions of the macroscopic model, the material performance inside tissues could be better controlled by adjusting the design parameters, thereby reducing the need for animal experiments.Experimental section
Fabrication of rod-shaped magneto-responsive microgels
Microgels are prepared as described previously.13 In brief, a prepolymer of 3 kDa, six-armed, star-shaped poly(ethylene oxide-stat-propylene oxide)-acrylate (sPEG-A) is mixed with 1 mol% 2-hydroxy-4′-(2-hydroxy-ethoxy)-2-methylpropiophenone (Irgacure 2959, BASF), related to total acrylate groups, 0.05 wt% methacryloxyethyl thiocarbamoyl rhodamine B (Polysciences), and DMSO to obtain a 100 wt/vol% sPEG-A solution. After stirring for 4 h, 200 Da PEG (Sigma-Aldrich) with an appropriate amount of SPIONs (EMG 700, Ferrotec) is added as a diluent to prepare precursor solutions with variable wt/vol% reactive polymer, which is ultrasonicated as previously described.13 This solution is cast on an inverse polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning) wafer replicate with a sacrificial polyethylene terephthalate (PET) (Goodfellow GmbH) sheet. By removing the PET sheet, the PDMS mold surface is cleared from the polymer solution and only the cavities remain filled, allowing single microgel fabrication after UV-curing for 60 min in a nitrogen atmosphere. The microgels are released from the mold by a sticky water-soluble polyvinylpyrrolidone layer (PVP, 50 wt/vol%, 360 kDa, Sigma-Aldrich). In the case of ultrasoft microgels with 11 wt/vol% polymer, the star-PEG-acrylate is first mixed in a 25 vol% to 75 vol% ratio with PEG-diacrylate (Sigma-Aldrich).Purification and preparation of microgel dispersions
Microgels are released from PVP by the addition of water and collected in 2 mL LoBind tubes (Sigma-Aldrich), followed by centrifugation at 4500g for 10 min. The microgels are purified by sequential removal of supernatants and resuspension in water, which is repeated three times. Afterward, the microgels are counted using a Neubauer counting chamber and the concentration is adjusted to 0.02 to 0.1 vol%, depending on the microgel size ranging from 156.25 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μm3, respectively. To increase the viscosity of the surrounding fluid, glycerin is added depending on the desired dynamic viscosity and the temperature is kept constant at 20 °C during analysis.
000 μm3, respectively. To increase the viscosity of the surrounding fluid, glycerin is added depending on the desired dynamic viscosity and the temperature is kept constant at 20 °C during analysis.
Fibrin rheology and gelation
To measure the dynamic viscosity, a Discovery Hybrid Rheometer (TA Instruments HR-3 Rheometer PHR3) is used with a heating plate and a conical geometry with a 20 mm diameter (2° inclination). All measurements are performed with 74 μL sample volume and a truncation gap of 51 μm. The gelation rate of fibrin is studied by mixing the fibrinogen-media mixture with the enzyme solution consisting of thrombin, factor XIII, HEPES buffer, and calcium chloride (5 mmol L−1), and subsequent testing of the solution fluidity by pipetting every 10 s. When the solution cannot be pipetted anymore, it is considered a gel.Confocal microscopy imaging
Confocal microscopy imaging is conducted with a Leica SP8 confocal microscope equipped with a 10× objective (spinal cord model, Fig. 4B) or 93× objective (single microgels; Fig. S9†), a white light laser (λ = 550 nm for rhodamine-coupled microgels) or a diode pumped solid state laser of 561 nm and a helium–neon laser of 633 nm, and a HyD detector (gating of 0–6 ns; 560–640 nm for rhodamine-coupled microgels).Microgel orientation studies
A 20 μL microgel suspension is placed on an 8 mm round cover glass on top of a PDMS ring which rests on a glass cover slide on the microscope stage. Rotatable magnets are placed on top. The set-up consists of 2 squared magnets (1 × 1 cm with different thicknesses ranging from 1 mm to 1 cm), which are separated by an aluminum frame. The obtained magnetic field is determined via a tesla-meter. The frame is mounted on the inner ring of a ball bearing, allowing rotation. The outer ring of the ball mill is glued to a circular aluminum frame serving as a stand. After pre-aligning the microgels for ≈60 s, the magnetic field is rotated by 90°.Spinal cord injection and staining
C57BL/6J mice are deeply anesthetized with isoflurane gas and decapitated. Afterward, the dorsal skin is removed and the spine dissected from the body and fixed by needles on a PDMS coated Petri dish. Connective and muscle tissues are cleared from the lumbar spine and the bone removed via laminectomy to expose the spinal cord. Subsequently, the dura mater is cut and removed from the spinal cord tissue, followed by cutting of a rectangular-shaped hemisection using a scalpel. A 1 cm3 square-shaped rare earth magnet (Magnet-shop.net) is placed next to the spinal cord in order to create a magnetic field of ≥80 mT in the direction of the spinal cord tissue. A 100 μL Hamilton syringe is filled with 10 μL of the microgel–fibrinogen solution containing 4 mg mL−1 fibrinogen and the microgels (0.3 vol% for 2.5 × 2.5 × 50 μm3 microgels) as well as the freshly added enzyme mixture (thrombin and factor XIII; volume of 34 μL) and cell culture media (DMEM, Lonza). The total volume is injected and allowed to crosslink for ∼5 min. After this, the tissue is fixed with 4% paraformaldehyde for 24 h and stained for 6 h with 1 μmol L−1 SiR-actin (Spirochrome AG), followed by washing for 1 h with PBS (Lonza).All procedures for harvesting tissue from experimental animals were authorized by the local ethics committee from the University Hospital RWTH Aachen and in accordance with the guidelines and recommendations from the European Commission (European Directive of 2010/63/EU).
Data acquisition
The orientation is recorded in phase contrast using a Zeiss AxioObserver Z1 with a rate of 1 image per s for 120–300 s, depending on the required orientation time. The orientation of single microgels is determined using ImageJ. A spherical region of interest containing one only microgel at a time is drawn and the orientation is determined using the plugin OrientationJ and the “dominant direction” function. The determined direction is visually compared to the acquired images to control the accuracy of measurements.Data evaluation and post-processing
The determined dominant orientations at the respective time points are exported from ImageJ and applied for the subsequent analysis. The change in angle per second (orientation rate) can be calculated and related to either time (Fig. 1H) or the respective orientation state (Fig. 1I). For magnetic field strengths equal to and above 40 mT, the angular velocity for each microgel is plotted as a function of the angle, resulting in a sine–like function, of which the amplitude is calculated by integrating the simplified oscillatory function between the two experimental data points at ≥20° and ≤70° and the time required to orient between these angles.Amplitudes are depicted as boxplots showing the mean value as a red line, the median as a black line, the box as the middle 50% of the data, and the whiskers are 1.5·IQR.
Statistics
Statistics are performed with OriginPro 2016G. For comparison of significance ANOVA is performed with a post-hoc Bonferroni comparison (*p < 0.05, **p < 0.01, ***p < 0.001, and ****p < 0.0001). Data are represented as box plots, including the median, mean value, upper and lower quartiles, and outliers. Experiments are conducted using a Design of Experiment34 if applicable; however, due to the high experimental fluctuations, boundary conditions (e.g., highest and lowest magnetic fields, etc.) are also chosen to allow for experimental feasibility.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr G. Brook for supplying the mouse tissue and are grateful to Dr K. Rahimi, S. Moli, N. Jansen, C. May, and S. Mallmann for experimental assistance. We acknowledge funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (ANISOGEL, grant agreement no 63785), the Deutsche Forschungsgemeinschaft (DFG) within the SFB 985 “Functional Microgels and Microgel Systems”, and the European Commission (EUSMI, 731019). This work was performed in part at the Center for Chemical Polymer Technology CPT, which was supported by the EU and the federal state of North Rhine-Westphalia (grant EFRE 30 00 883 02).References
- (a) U. G. K. Wegst, H. Bai, E. Saiz, A. P. Tomsia and R. O. Ritchie, Bioinspired structural materials, Nat. Mater., 2015, 14(1), 23–36 CrossRef CAS PubMed; (b) J. C. Rose and L. De Laporte, Hierarchical Design of Tissue Regenerative Constructs, Adv. Healthcare Mater., 2018, 7, 1701067 CrossRef CAS PubMed.
- C. Frantz, K. M. Stewart and V. M. Weaver, The extracellular matrix at a glance, J. Cell Sci., 2010, 123(24), 4195–4200 CrossRef CAS.
- (a) S. L. K. Bowers, I. Banerjee and T. A. Baudino, The extracellular matrix: At the center of it all, J. Mol. Cell. Cardiol., 2010, 48(3), 474–482 CrossRef CAS; (b) Q. Z. Tseng, E. Duchemin-Pelletier, A. Deshiere, M. Balland, H. Guillou, O. Filhol and M. Thery, Spatial organization of the extracellular matrix regulates cell-cell junction positioning, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(5), 1506–1511 CrossRef CAS PubMed.
- A. T. Hillel, S. Unterman, Z. Nahas, B. Reid, J. M. Coburn, J. Axelman, J. J. Chae, Q. Y. Guo, R. Trow, A. Thomas, Z. P. Hou, S. Lichtsteiner, D. Sutton, C. Matheson, P. Walker, N. David, S. Mori, J. M. Taube and J. H. Elisseeff, Photoactivated Composite Biomaterial for Soft Tissue Restoration in Rodents and in Humans, Sci. Transl. Med., 2011, 3(93), 12 Search PubMed.
- M. Jaspers, S. L. Vaessen, P. van Schayik, D. Voerman, A. E. Rowan and P. H. J. Kouwer, Nonlinear mechanics of hybrid polymer networks that mimic the complex mechanical environment of cells, Nat. Commun., 2017, 8, 15478 CrossRef.
- O. Chaudhuri, L. Gu, D. Klumpers, M. Darnell, S. A. Bencherif, J. C. Weaver, N. Huebsch, H. P. Lee, E. Lippens, G. N. Duda and D. J. Mooney, Hydrogels with tunable stress relaxation regulate stem cell fate and activity, Nat. Mater., 2016, 15(3), 326–334 CrossRef CAS.
- M. A. Azagarsamy, I. A. Marozas, S. Spaans and K. S. Anseth, Photoregulated Hydrazone-Based Hydrogel Formation for Biochemically Patterning 3D Cellular Microenvironments, ACS Macro Lett., 2016, 5(1), 19–23 CrossRef CAS.
- A. Sydney Gladman, E. A. Matsumoto, R. G. Nuzzo, L. Mahadevan and J. A. Lewis, Biomimetic 4D printing, Nat. Mater., 2016, 15(4), 413–418 CrossRef CAS.
- (a) A. Omidinia-Anarkoli, S. Boesveld, U. Tuvshindorj, J. C. Rose, T. Haraszti and L. De Laporte, An Injectable Hybrid Hydrogel with Oriented Short Fibers Induces Unidirectional Growth of Functional Nerve Cells, Small, 2017, 13(36), 8 CrossRef; (b) J. C. Rose, D. B. Gehlen, T. Haraszti, J. Koehler, C. J. Licht and L. De Laporte, Biofunctionalized aligned microgels provide 3D cell guidance to mimic complex tissue matrices, Biomaterials, 2018, 163, 128–141 CrossRef CAS.
- R. M. Erb, R. Libanori, N. Rothfuchs and A. R. Studart, Composites Reinforced in Three Dimensions by Using Low Magnetic Fields, Science, 2012, 335(6065), 199–204 CrossRef CAS PubMed.
- M. S. Wang, L. He and Y. D. Yin, Magnetic field guided colloidal assembly, Mater. Today, 2013, 16(4), 110–116 CrossRef CAS.
- (a) B. A. Grzybowski, C. E. Wilmer, J. Kim, K. P. Browne and K. J. M. Bishop, Self-assembly: from crystals to cells, Soft Matter, 2009, 5(6), 1110–1128 RSC; (b) G. M. Whitesides, Bioinspiration: something for everyone, Interface Focus, 2015, 5(4), 10 CrossRef; (c) A. R. Studart, Biologically inspired dynamic material systems, Angew. Chem., Int. Ed., 2015, 54(11), 3400–3416 CrossRef CAS; (d) A. M. Rosales and K. S. Anseth, The design of reversible hydrogels to capture extracellular matrix dynamics, Nat. Rev. Mater., 2016, 1(2), 15 Search PubMed; (e) Y. Lu, A. A. Aimetti, R. Langer and Z. Gu, Bioresponsive materials, Nat. Rev. Mater., 2017, 2(1), 17 Search PubMed.
- J. C. Rose, M. Camara-Torres, K. Rahimi, J. Koehler, M. Moeller and L. De Laporte, Nerve Cells Decide to Orient inside an Injectable Hydrogel with Minimal Structural Guidance, Nano Lett., 2017, 17(6), 3782–3791 CrossRef CAS.
- S. Tasoglu, E. Diller, S. Guven, M. Sitti and U. Demirci, Untethered micro-robotic coding of three-dimensional material composition, Nat. Commun., 2014, 5, 3124–3124 CrossRef CAS.
- D. D. Jia, J. Hamilton, L. M. Zaman and A. Goonewardene, The time, size, viscosity, and temperature dependence of the Brownian motion of polystyrene microspheres, Am. J. Phys., 2007, 75(2), 111–115 CrossRef CAS.
- (a) M. J. Solomon and P. T. Spicer, Microstructural regimes of colloidal rod suspensions, gels, and glasses, Soft Matter, 2010, 6(7), 1391–1400 RSC; (b) L. Onsager, The Effects of Shape on the Interaction of Colloidal Particles, Ann. N. Y. Acad. Sci., 1949, 51(4), 627–659 CrossRef CAS.
- (a) A. D. Shine and R. C. Armstrong, The rotation of a suspended axisymmetric ellipsoid in a magnetic field, Rheol. Acta, 1987, 26(2), 152–161 CrossRef CAS; (b) A. D. Shine and R. C. Armstrong, Experimental studies of suspended ferromagnetic fibers in a magnetic-field, Rheol. Acta, 1987, 26(2), 162–171 CrossRef CAS.
- R. M. Erb, R. Libanori, N. Rothfuchs and A. R. Studart, Composites Reinforced in Three Dimensions by Using Low Magnetic Fields, Science, 2012, 335(6065), 199–204 CrossRef CAS PubMed.
- (a) R. Skomski, G. C. Hadjipanayis and D. J. Sellmyer, Effective demagnetizing factors of complicated particle mixtures, IEEE Trans. Magn., 2007, 43(6), 2956–2958 CAS; (b) M. Anhalt, B. Weidenfeller and J. L. Mattei, Inner demagnetization factor in polymer-bonded soft magnetic composites, J. Magn. Magn. Mater., 2008, 320(20), E844–E848 CrossRef CAS; (c) A. A. Likhachev and K. Ullakko, Magnetic-field-controlled twin boundaries motion and giant magneto-mechanical effects in Ni-Mn-Ga shape memory alloy, Phys. Lett. A, 2000, 275(1–2), 142–151 CrossRef CAS.
- R. Skomski, J. Y. Li, J. Zhou and D. J. Sellmyer, Multiscale phenomena in Bruggeman composites, in Materials for Space Applications, ed. M. Chipara, D. L. Edwards, R. S. Benson and S. Phillips, Materials Research Society, Warrendale, 2005, vol. 851, pp. 27–38 Search PubMed.
- (a) T. Shoaib, J. Heintz, J. A. Lopez-Berganza, R. Muro-Barrios, S. A. Egner and R. M. Espinosa-Marzal, Stick-Slip Friction Reveals Hydrogel Lubrication Mechanisms, Langmuir, 2018, 34(3), 756–765 CrossRef CAS; (b) S. Aktas, D. M. Kalyon, B. M. Marín-Santibáñez and J. Pérez-González, Shear viscosity and wall slip behavior of a viscoplastic hydrogel, J. Rheol., 2014, 58(2), 513–535 CrossRef CAS.
- D. J. Griffiths, Introduction to electrodynamics, Pearson, Boston, MA, 2006, vol. 4 Search PubMed.
- C. Pfeiffer, C. Rehbock, D. Hühn, C. Carrillo-Carrion, D. J. de Aberasturi, V. Merk, S. Barcikowski and W. J. Parak, Interaction of colloidal nanoparticles with their local environment: the (ionic) nanoenvironment around nanoparticles is different from bulk and determines the physico-chemical properties of the nanoparticles, J. R. Soc., Interface, 2014, 11(96), 20130931 CrossRef.
- B. Thapa, D. Diaz-Diestra, J. Beltran-Huarac, B. R. Weiner and G. Morell, Enhanced MRI T (2) Relaxivity in Contrast-Probed Anchor-Free PEGylated Iron Oxide Nanoparticles, Nanoscale Res. Lett., 2017, 12(1), 312–312 CrossRef.
- J. C. Lagarias, J. A. Reeds, M. H. Wright and P. E. Wright, Convergence properties of the Nelder-Mead simplex method in low dimensions, SIAM J. Optim., 1998, 9(1), 112–147 CrossRef.
- M. Wu, D. Zhang, Y. Zeng, L. Wu, X. Liu and J. Liu, Nanocluster of superparamagnetic iron oxide nanoparticles coated with poly (dopamine) for magnetic field-targeting, highly sensitive MRI and photothermal cancer therapy, Nanotechnology, 2015, 26(11), 115102 CrossRef.
- (a) M. Susano, M. P. Proenca, S. Moraes, C. T. Sousa and J. P. Araujo, Tuning the magnetic properties of multisegmented Ni/Cu electrodeposited nanowires with controllable Ni lengths, Nanotechnology, 2016, 27(33), 335301 CrossRef CAS; (b) A. M. Leshansky, K. I. Morozov and B. Y. Rubinstein, Shape-controlled anisotropy of superparamagnetic micro-/nanohelices, Nanoscale, 2016, 8(29), 14127–14138 RSC.
- (a) A. C. Brown, S. E. Stabenfeldt, B. Ahn, R. T. Hannan, K. S. Dhada, E. S. Herman, V. Stefanelli, N. Guzzetta, A. Alexeev, W. A. Lam, L. A. Lyon and T. H. Barker, Ultrasoft microgels displaying emergent platelet-like behaviours, Nat. Mater., 2014, 13, 1108 CrossRef CAS PubMed; (b) T. J. Merkel, S. W. Jones, K. P. Herlihy, F. R. Kersey, A. R. Shields, M. Napier, J. C. Luft, H. Wu, W. C. Zamboni, A. Z. Wang, J. E. Bear and J. M. DeSimone, Using mechanobiological mimicry of red blood cells to extend circulation times of hydrogel microparticles, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(2), 586–591 CrossRef CAS PubMed.
- C. P. Brangwynne, F. C. MacKintosh, S. Kumar, N. A. Geisse, J. Talbot, L. Mahadevan, K. K. Parker, D. E. Ingber and D. A. Weitz, Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement, J. Cell Biol., 2006, 173(5), 733–741 CrossRef CAS PubMed.
- M. B. Browning, T. Wilems, M. Hahn and E. Cosgriff-Hernandez, Compositional control of poly(ethylene glycol) hydrogel modulus independent of mesh size, J. Biomed. Mater. Res., Part A, 2011, 98(2), 268–273 CrossRef CAS.
- K. Lederer and J. Schurz, High shear rate viscosity measurements with dilute solutions of bovine fibrinogen, Biopolymers, 1972, 11(9), 1989–1993 CrossRef CAS PubMed.
- J. J. Martin, B. E. Fiore and R. M. Erb, Designing bioinspired composite reinforcement architectures via 3D magnetic printing, Nat. Commun., 2015, 6, 8641 CrossRef PubMed.
- D.-H. Lee and J. K. Lee, Animal models of axon regeneration after spinal cord injury, Neurosci. Bull., 2013, 29(4), 436–444 CrossRef PubMed.
- W. Kleppmann, Versuchsplanung - Produkte und Prozesse optimieren, Carl Hanser Verlag München Wien, Germany, 2016, vol. 9 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional explanation, Movies S1 and S2, and Fig. S1 to S13. See DOI: 10.1039/c9py01008d |
| This journal is © The Royal Society of Chemistry 2020 |