Spectral shifts of BODIPY derivatives: a simple continuous model

Abstract

The BODIPY dyes are a versatile family of chromophores that have found use in fluorescence based bioimaging and other applications. The BODIPY core can be substituted in a vast number of ways, but the photophysical changes, such as shifts in absorption spectra, are not always immediately obvious from the molecular structure. We introduce a simple model that let you vary the electron withdrawing or electron donating character of each substituent continuously to get an overview of the landscape of possible spectral shifts. The features of substituted BODIPY cores are compared to the corresponding linear system, giving a new perspective on BODIPY photophysics. Using the model, we are able to rationalize the trend seen in a family of BODIPY, with chalcogen-containing substituents, as being due to a change in electronegativity.

---

1 Introduction

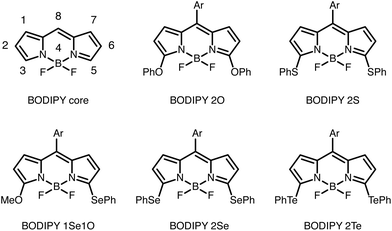
Since the introduction of the first difluoro-boraindacene (BODIPY) in 1968, the BODIPY core has been substituted with a large range of functional groups in order to tune its photophysical properties.^1–6 As a result, BODIPY fluorophores have found numerous applications in fluorescence based bio-imaging.⁷ Besides imaging and tracking of labeled compounds, the BODIPY fluorophores have also found applications as sensor probes, e.g. for monitoring of pH, ion concentrations, viscosity, and temperature.^8–13

Fluorophores in the red and NIR region of the spectrum are usually more favorable than their shorter wavelength counterparts, because they can minimize unwanted auto-fluoresence from biological material and increase penetration depth in tissue.¹⁴ Therefore, understanding how substituents and their position shift the absorption and emission spectra is important for tailoring new BODIPY fluorophores for specific applications. Many groups have explored the properties of substituted BODIPY species, often with symmetric substitutions.^1,15–20

Fron et al. studied the effect of substituting different chalcogen containing groups (O, S, Se, Te), which acted as electron donating groups (EDGs), due to the lone pair on the chalcogen, on sites 3 and 5 (a symmetric site pattern) of the BODIPY core, see Fig. 1.¹⁵ They found that a red-shift occurred as they moved down the chalcogen group of the periodic table if the same EDGs are added to both sites. This could be due to both the electron donating nature of the substituents or an extension of the π-system. Fron et al. suggested that the red-shift was due to the electronegativity of the chalcogen atom.¹⁵ Others have seen similar trends in other chalcogen substituted fluorophores.^21–23

Fig. 1 Molecular structures of the BODIPY core, with the atom numbering, along with the chalcogen substituted BODIPY derivatives studied by Fron et al. Ph corresponds to a phenyl group, Me is a methyl group, while Ar is a meso-aryl (methyl-phenyl) group.

In the case where sites 3 and 5 had an asymmetric substitution pattern with chalcogens, the absorption band was positioned between the bands of the corresponding molecules with symmetric substitution patterns. The absorption maxima of BODIPY 1Se1O was between that of BODIPY 2O and BODIPY 2Se.¹⁵ Rohand et al. saw a similar trend when the π-system was extended symmetrically and asymmetrically at sites 3 and 5.¹⁶

To explain these observations and trends, we construct a simple model describing the BODIPY π-system, where the frontier orbitals reside, at the Hückel theory/tight binding level. The impact of a substituent is represented by a single parameter shifting the on-site energy of the carbon atom in the BODIPY core according to the electron-donating or -withdrawing nature of the substituent. With this model we can explore the consequences of arbitrary substitution of a BODIPY core. We provide a range of results revealing some general trends and possible strategies for extreme red-shifts. Additionally, a detailed comparison of the spectral shifts of substituted BODIPY cores to the corresponding linear systems gives us a new perspective on BODIPY photophysics.

Using our model we are able to rationalize the trends of spectral shifts of the chalcogen substituted BODIPY cores reported by Fron et al.¹⁵ Also, the behavior of a series of halogen substituted BODIPY cores can be understood.¹⁹ We discuss the inherent limitations of the model, emphasizing that it can provide a quick overview of the effects of substitutions, but that it will not replace high-level calculations of spectral shifts for specific dyes.

2 Methods

2.1 Hückel model

We represent the electronic structure of BODIPY by a Hückel (or tight-binding) Hamiltonian. The frontier orbitals of a dye like BODIPY reside almost exclusively on the conjugated π-system, thus we make the basic assumption that it will suffice to treat only the π-system. The Hamiltonian contains α and β parameters, representing the Coulomb integral of each orbital and the resonance integrals between directly bonded atoms respectively.^24,25 For the BODIPY core 11 orbitals are involved, one p_z-orbital for each carbon atom and a lone pair for each of the two nitrogen atoms. The α and β parameters can vary across the elements, thus the Hamiltonian, (which can be seen in the ESI†) contains four parameters: site energies for carbon and nitrogen, α_C, α_N and coupling parameters for C–C or C–N bonds, β_CC, β_CN. Finally, the Hamiltonian is diagonalized and the HOMO–LUMO gap is used as an approximate excitation energy.

Substitutions to the core are modeled by changing the α parameter of the addition site. If a substituent is added to site n the parameter is changed as:

α_n = α_C + S_n.

If the substituent is an EDG, the substitution parameter is positive, S_n > 0, and conversely, if the substituent is an EWG, the parameter is negative, S_n < 0. We note that this simple model cannot treat substituents which extend the conjugated system of the BODIPY core.

2.2 Hückel parameters

We rely on literature values for the Hückel parameters. Purcell and Singer have parametrized the variation across elements in terms of reference parameters α₀ and β₀.²⁶ They define:

α_N = α₀ + h_N·β₀α_C = α₀ + h_C·β₀

β_CN = k_CN·β₀β_CC = k_CC·β₀

and we use their parameters h_N = 0.24, h_C = 0.07, k_CN = 1, k_CC = 1. The α₀ parameter sets the zero point of the energy scale and can arbitrarily be set to zero, α₀ = 0 eV. The value for the β₀ = −2.7 eV parameter is taken from Garner et al.²⁷ Our final parameters take the values α_N = −0.648, α_C = −0.189, and β_CN = β_CC = β₀ = −2.7 eV. All substitution parameters and spectral shifts will be reported in electron volts, but we have suppressed the unit in the notation.

With the chosen parameters, the excitation energy of the BODIPY core equals 2.55 eV or approximately 486 nm. This compares to experimental absorption wavelengths of 499–505 nm.^28,29 We could, of course, have reparametrized our model to reproduce this range, but we would have no guarantee that the excitation energies of substituted species would be equally accurate. Hückel theory does not provide high quality quantitative predictions.

In the simulations presented below, the substitution parameters S_n cover the range from −3 to 3 (eV). This roughly covers the experimentally accessible range. More quantitative comments on this are made below, when we study a specific family of substituted BODIPY dyes.

Throughout, we plot or report the peak shift defined as the excitation energy of the BODIPY core minus the excitation energy of the species in question (ΔE):

Peak shift = 2.55 eV − ΔE.

With this sign convention, red-shifted absorption correspond to positive peak shifts, and blue-shifted absorption correspond to negative peak shifts.

2.3 DFT calculations

All electronic structure calculations presented in this article where performed with the Gaussian09 software. DFT geometry optimizations of the ground state of the BODIPY derivatives were done using the CAM-B3LYP/6-311G(d) level of theory.^30–34 The same level of theory was used for the TD-DFT calculations, these can be seen in the ESI.† The functional CAM-B3LYP is a popular choice for TD-DFT, as it includes a long-range correction.³⁰ It has previously been used to investigate BODIPY dyes and other fluorophores.^21,35–37

3 Results and discussion

3.1 Symmetric substitution

Many groups have studied symmetrically substituted BODIPY dyes, and we focus on these in this section.^1,15–20 Results for asymmetric substitutions are presented in the ESI.†

Fig. 2 compares peak shifts of symmetrically substituted BODIPY cores with the corresponding linear systems. In part A of the figure, the familiar behavior, known from color structure relationship theory, for an odd numbered linear chain of π-orbitals is shown.^38,39 Substitutions on the unstarred sites (3,5 or 1,7 or 8) show similar behavior. EDGs induce blue-shifts and EWGs induce red-shifts. Substitution on the starred atoms (2,6) show the opposite trend.

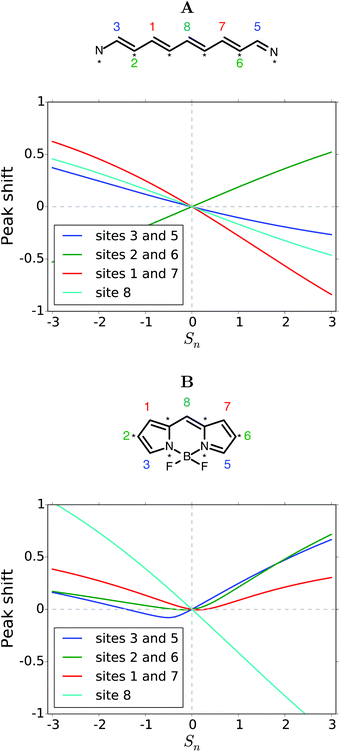Fig. 2 (A) Peak shift induced by symmetric substitution of the linear molecule corresponding to the BODIPY core. (B) Peak shift induced by symmetric substitution of the BODIPY core.

When the π-system is fused onto itself with two five-membered rings as in BODIPY, the trends are markedly different, as can be seen in Fig. 2B. Substitution on site 8 does induce the same shift as for the linear system. However, the susceptibility (slope) is twice as large. All other symmetric substitutions now seem to red-shift absorption. Substitution on sites 3 and 5 does dip slightly into the blue-shifted region, but only for an interval of S_n parameters between −1.5 and 0. Strong red-shifts are obtained by EWGs on atom 8 or EDGs elsewhere. A discussion of the shift in the underlying frontier orbital energies is provided in the ESI.†

When more than one substituent will be fused onto the core, we could envision varying their electron donating or electron withdrawing character independently. Fig. 3 explores the possibilities in this case. In each panel, the substitution parameter S_n for the site(s) indicated is varied along one axis. The peak shift is indicated by an intuitive color coding.

Fig. 3 Calculated peak shifts. Negative values correspond to a blue-shift. Positive values to a red-shift. Linear molecule with two substituents on atoms: (A) 3 and 5, (B) 2 and 6, (C) 1 and 7. BODIPY with two substituents on atoms: (D) 3 and 5, (E) 2 and 6, (F) 1 and 7. BODIPY with three substituents, one on atom 8 and two on atoms: (G) 3 and 5, (H) 2 and 6, (I) 1 and 7.

The linear system is treated in panels A–C. The corresponding curves of Fig. 2A are found along the diagonals of the panels. The sign of the peak shift alternates across the panels as the substitutions are on unstarred (3,5 or 1,7) or starred (2,6) atoms. Off the diagonal there is a slight curvature, showing that the effects of the substituents are not merely additive. In panels A, C (and the blue part of panel B), the red-shift is slightly weaker, or the blue-shift stronger, than if the effects were additive. This effect is reversed in the red-shifted part of panel B. We note that the magnitude of the peak shift is larger when the substituents are closer to the center of the chain. The panels D–F showing BODIPY substitutions are qualitatively different. In panels D and E the combined peak shift is highly non-additive. The red-shift is largely set by the strongest EDG. In panel F we get the counterintuitive suggestion that the strongest red-shift is obtained when an EDG is combined with an EWG. A general disclaimer may be relevant here. The model is based on molecular orbital theory, thus we cannot expect charge transfer excited states, relevant for strong push–pull systems, to be described very well, if at all. Blue-shifts are barely possible in panels D–F. Only a small blob near the center of panel D. These panels predict that substitution of EDG's on to sites 2 and 6 will lead to the largest red-shift.

Panels G–I explore symmetric trisubstitutions. They are qualitatively similar and largely symmetrical around a vertical axis close to the center. Substituents on sites 3,5 or 2,6 or 1,7 will red-shift the absorption. It does not matter much whether the substituents are EDG or EWG. The red-shift is strongest in combination with an EWG on atom 8. Blue-shift only occurs with an EDG on atom 8.

Asymmetric substitution patterns are explored in the ESI.†

3.2 Maximum peak shifts

Lu et al. have studied several BODIPY derivatives, reviewing experimental and TD-DFT calculation data, and found that the largest red-shift was achieved at sites 3 and 5.⁴⁰ According to our model, Fig. 3D–F, site 2 and 6 are able to give the largest red-shifts. However, the difference between 3,5 and 2,6 is small.

In order to sample the full range of possible shifts, we tested all possible substitution patterns with up to 7 substituents on the BODIPY core, see ESI.† A highly EWG on atom 8 leads to a large red-shift. Yet, an even larger red-shift is obtained by also substituting strong EDGs on atoms 1 and 2. A strongly EDG on atom 8 gave rise to a large blue-shift. Slightly larger blue-shifts were observed when multiple EWGs were added, while the EDG on atom 8 remained.

The full exploration of possible shifts also revealed a key shortcoming of our model. Fig. 4 shows the excitation energies of the maximally red- and blue-shifted substituted BODIPYs as a function of the number of substituents. It is based on data provided in the ESI.†

Fig. 4 Excitation energies of the maximally red- and blue-shifted substituted BODIPYs as a function of the number of substituents.

With three substituents the excitation energy drops to zero for the most red-shifted species! We do not expect BODIPY dyes to turn metallic. It seems reasonable that the most red-shifted excitation energies will plateau, but our model can not provide a credible estimate of a converged excitation energy.

Similarly, the excitation energy of the maximally blue-shifted species also plateaus. Considering the red-shift plateau, a similar element may be in play here suggesting that we cannot have much confidence in the excitation energies beyond a few substituents.

3.3 Chalcogen substituted BODIPY dyes

We have used the model to investigate the BODIPYs studied by Fron et al. Other than the compounds seen in Fig. 1, Fron et al. also studied BODIPY 2Cl where chlorine was placed on site 3 and 5.

3.3.1 DFT geometry. The BODIPY fluorophores studied by Fron et al. had several groups that could contribute to the π-system – the meso-aryl (methyl-phenyl) group on site 8 and the phenyl groups of the chalcogen substituents on sites 3 and 5. We determined the extent of the π-system using the DFT optimized structures. These showed that the meso-aryl group and the chalcogen substituents were all out of plane with the BODIPY core and did not contribute to the π-system, see Fig. 5. The chalcogen atoms may have contributed to the π-system to some extent. However, we have assumed that they did not. In all derivatives the core was almost planar, giving optimal overlap of the pz and lone-pair orbitals, see the ESI† for all structures. This meant that the Hückel matrix for the BODIPY core used above was sufficient to study the chalcogen substituted BODIPY derivatives.

Fig. 5 Optimized structure of BODIPY 2O. Calculations performed at the DFT/CAM-B3LYP/6-311G(d) level of theory.

3.3.2 Symmetric substitution. Using the model described in Section 2 we have looked at the BODIPY derivatives studied by Fron et al. The meso-aryl group on atom 8 is slightly electron donating. Yet, for simplicity we assume S^aryl₈ = 0.

To model the symmetric BODIPY derivatives we found the S_3/5 value of each substituent by fitting the excitation energies to the experimental results in THF.¹⁵ Due to the lone-pair on the chalcogen binding atoms the chalcogen groups are EDGs. From probing the model we knew that the S_3/5 values became larger as the excitation energy was red-shifted. The S_3/5 values along with the experimental and modeled excitation energies are seen in Table 1 and the modeled spectrum can be seen in Fig. 6.

Fig. 6 Absorption spectra calculated from the Hückel model. Only the symmetric derivatives are shown here: (blue) no substituents, (green) BODIPY 2O, (red) BODIPY 2S, (light blue) BODIPY 2Se, and (purple) BODIPY 2Te. Gaussian functions are added to emulate spectra.

Table 1 Peak shift and excitation energies, ΔE, (experimentally in THF). Along with S_3/5 values of the substituents and electronegativity (EN) of the binding atoms^15,41,42

Derivative	Peak shift (eV)	ΔE (eV)	S 3/5	EN
BODIPY 2O	0.15	2.40	0.59	3.44
BODIPY 2S	0.40	2.15	1.67	2.58
BODIPY 2Se	0.43	2.12	1.82	2.55
BODIPY 2Te	0.55	2.00	2.38	2.10
BODIPY 2Cl	0.12	2.43	0.50	3.16

---

3.3.3 Asymmetric substitution pattern. We also modeled one BODIPY derivative (BODIPY 1Se1O) with an oxygen and a selenium containing substituent on sites 3 and 5 (an asymmetric substitution pattern). We used the S_3/5 values found above for BODIPY 2O and BODIPY 2Se. The excitation energy from the model was close to the excitation energy of the experiment, see Table 2. As seen in experiments the excitation energy of an asymmetric BODIPY dye (BODIPY 1Se1O) was between the excitation energy of the two symmetric BODIPY dyes.¹⁵ This shows that the model can be used to approximately predict excitation energies of dyes using the fitted S^m_n values from experimental data for the substituted groups on specific sites.

Table 2 Excitation energies, ΔE, of BODIPY 1Se1O from experiment in THF and calculated with the Hückel model

BODIPY 1SE1O	Experiment	Model
Peak shift (eV)		0.33
ΔE (eV)	2.27	2.22
S ^m n		0.59 and 1.82

---

This substitution pattern is seen in panel D of Fig. 3. Where BODIPY 2O and BODIPY 2Se are on the diagonal and BODIPY 1Se1O is positioned of diagonal, see Fig. 7. Panel E of Fig. 3 shows the same trend, but panel F does not. If the same S^m_n(0.59 and 1.82) values were used on sites 1 and 7 the excitation energy of the asymmetric BODIPY would be lower (have a higher peak shift) than both the corresponding symmetric BODIPYs.

Fig. 7 Symmetric and asymmetric substitution on site 3 and 5. (Yellow dot) BODIPY 2O, (blue dot) BODIPY 2Se, and (green dot) BODIPY 1Se2O.

3.4 Other substituents on sites 3 and 5

Rohand et al. studied BODIPY derivatives with a meso-aryl group on site 8 and EDG's on site 3 and 5 and analyzed them in methanol, see structures in ESI.† The EDG's had oxygen, nitrogen, sulfur, and carbon as binding atoms. We found S_3/5 values for each substituent, see Table 3. The oxygen containing group (OMe) had a S^OMe_3/5value of 0.48, close to the S^OPh_3/5 value of 0.59 found for BODIPY 2O. The sulfur containing group (S–C-1ester) had an ester instead of a phenyl ring and the S^S_3/5value, of 1.45, was only slightly lower than the S^SPh_3/5value of 1.67 found for BODIPY 2S. Rohand et al. also studied two nitrogen containing substituents. We found a S^N_3/5 value of 1.58 for piperidine and a S^NHPH_3/5 value of 1.85 for NHPh which are also similar. The variations to the S_3/5 values between similar substituent occur because we are capturing all their differences in one parameter. However, the binding atom can still give a good indication of the S_3/5 value.

Table 3 Peak shift and transtion energies, ΔE, experimental and calculated with the Hückel method. Along with S_3/5 and S₈ values of the substituents, and electronegativities (EN) of the binding atoms. The structures of all compounds studied can be found in ESI^17–19,41

Site 3 and 5					Site 8
Substituent	Peak shift (eV)	ΔE^a (eV)	S 3/5	EN	Substituent	Peak shift (eV)	ΔE^b (eV)	S 8	EN
a Experimentally in methanol. b Experimentally in THF.
OMe	0.12	2.43	0.48	3.44	Cl	0.08	2.47	−0.21	3.16
S–C-1ester	0.35	2.20	1.45	2.58	Br	0.09	2.46	−0.22	2.96
Piperidine	0.38	2.17	1.58	3.04	I	0.10	2.45	−0.26	2.66
NHPh	0.44	2.11	1.85	3.04	OMe	−0.25	2.80	0.61	3.44
					OPh	−0.17	2.72	0.41	3.44
					SPh	0.06	2.49	−0.15	2.58
					NHPh	−0.45	3.00	1.09	3.04

---

Looking at Fig. 3D it is clear that for a symmetric substitution on sites 3 and 5 there are two possible S_3/5 parameters which give the same positive peak shift (red-shift). One S_3/5 is positive and the other is negative, corresponding to EDG's and EWG's. In most cases we know if a substituent is an EDG or an EWG but the Halogens are a borderline case. Halogens are EWG with regards to the inductive effect and EDG with regards to the resonance effect. Removing or adding energy to the on-site energies, in the Hückel matrix, corresponds to the inductive effect. However, due to the parameters being fitted to experimental values we also include the resonance effect. For Cl on site 3 and 5 (studied by Fron et al.) we have chosen the positive S^Cl_3/5 value of 0.50, letting the resonance effect dominate, rather than the negative value of −2.59. If S^Cl_3/5 = −2.59 had been chosen, we would be implying that Cl is a highly EWG, which it is not.

3.5 Other substituents on site 8

A different type of variation on the BODIPY core – not on site 3 and 5 – is to add different groups to site 8, and leave the other sites with just hydrogen. Boens et al. substitued with halogens (Cl, Br, and I) and studied the absorption in several solvents. Between the solvents the S₈ value varied with up to 0.1. Both Boens et al. and Leen et al. studied these BODIPY derivatives in THF with similar results. We found S₈ values of −0.21, −0.22, and −0.26 for Cl, Br, and I respectively, see Table 3.

Using the data from Fron et al. we found S^Cl_3/5 = 0.50. So on sites 3/5 (with the ignored meso-aryl group on 8) the resonance effect dominates where as on site 8 the inductive effect is dominant.^18,19

Boens et al. also added chalcogen and pnictogen substituents to site 8 and studied the absorption in several solvents. In THF, the oxygen containing group OMe had a S^OMe₈ value of 0.61, see Table 3. While the substituent OPh has a S^OPh₈ value of 0.41 on site 8. The sulfur containing group SPh has a S^SPh₈ value of −0.15. So, according to the model, the SPh group acts as a slightly EWG on site 8 but as an EDG on sites 3 and 5 (in methanol with the ignored meso-aryl group on 8).¹⁸ The nitrogen containing group (NHPh) has a S^NHPh₈ value of 1.09 which is lower than the S^NHPh_3/5 value of 1.85. Generally we saw that the binding atom could give an indication of what an appropriate S^m_nmay be for a substituent. However, this was not always the case. In some cases, adding the same substituent to different sites gave very different S^m_nvalues. We also saw that the solvent does not seem to play a major role.

3.6 Electronegativity

Fron et al. speculated that the red-shift of the excitation energy as we moved down the chalcogen group could be related to the electronegativity (EN) of the binding atom, see Table 1. We tested this theory for the chalcogen, halogen, and pnictogen substituents found in Tables 1 and 3, see Fig. 8.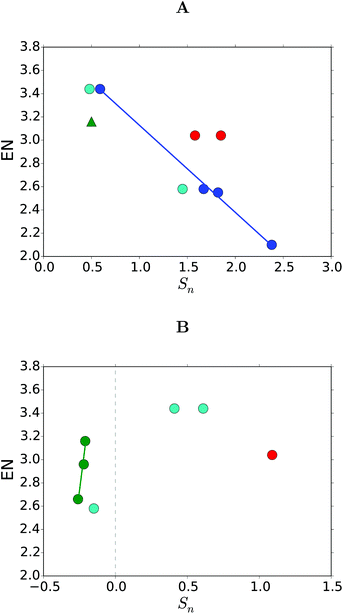

Fig. 8 Correlations between the S_n values and the electronegativity (EN) with substitutions on (A) site 3 and 5, and (B) site 8. The substituents are (green) the halogens in THF, (blue) chalcogens from Fron et al.,¹⁵ (light blue) chalcogens in THF or methanol^17–19 (red) nitrogen in THF or methanol, and (green triangle) Cl in THF.⁴¹

We found a linear correlation between the ENs and the S_n values within a group (the chalcogens and the halogens), but only when looking at the same substitution site (8 for halogens and 3/5 for chalcogens). The linear correlation was not present when we looked between the sites or groups of the periodic table.

4 Conclusion

By creating a simple Hückel model, where only the on-site energies of the BODIPY core were varied, we were able to test all the possible site and substitution patterns. We found very different trends when comparing the symmetric substitutions on the BODIPY core to the symmetric substitutions on the corresponding linear molecule. In the linear molecule substitutions to site 3/5 behaved in a similar manner to substitutions on site 1/7 and substitution to site 2/6 behaved quite differently, as expected from color structure relationship theory. However, when the molecule is closed (by nitrogen and boron) into BODIPY it is substitutions on site 3/5 and 2/6 which act in a similar way.

By studying all possible substitutions, we found that the more groups we substitute on to the core the larger we were able to get the red-shift. An EWG on site 8 gave a large red-shift in most cases. However, if two substituents were added the largest red-shift occurred with EDGs on sites 1 and 2.

We succeeded in modeling the absorption spectra of 3, 5 chalcogen substituted BODIPY dyes. The binding atom of the substituent can give an indication of the on site energy. Within a group in the periodic table, we saw a good correlation between the EN of the binding atoms of the substituents and the on site energies on specific substitution sites.

The model can easily be set up for other chromophores by changing the Hamiltonian of the core so it represents a new π-system.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Sten Rettrup for helpful discussion. Thorsten Hansen is grateful for financial support from the Lundbeck Foundation.

References

1. A. Loudet and K. Burgess, Dyes and their derivatives: Syntheses and spectroscopic properties, Chem. Rev., 2007, 107, 4891–4932.
2. G. Ulrich, R. Ziessel and A. Harriman, The chemistry of fluorescent BODIPY dyes: versatility unsurpassed, Angew. Chem., Int. Ed., 2008, 47(7), 1184–1201.
3. A. Treibs and F.-H. Kreuzer, Difluorboryl-komplexe von di-und tripyrrylmethenen, Justus Liebigs Ann. Chem., 1968, 718(1), 208–223.
4. N. Boens, B. Verbelen and W. Dehaen, Postfunctionalization of the BODIPY core: synthesis and spectroscopy, Eur. J. Org. Chem., 2015,(30), 6577–6595.
5. V. Leen, D. Miscoria, S. Yin, A. Filarowski, J. M. Ngongo, M. Van der Auweraer, N. Boens and W. Dehaen, 1, 7-disubstituted boron dipyrromethene (BODIPY) dyes: synthesis and spectroscopic properties, J. Org. Chem., 2011, 76(20), 8168–8176.
6. M. Bacalum, L. Wang, S. Boodts, P. Yuan, V. Leen, N. Smisdom, E. Fron, G. Knippenberg, S. Fabre, P. Trouillas, D. Beljonne, N. Dehaen, W. Boens and M. Ameloot, A blue-light-emitting BODIPY probe for lipid membranes, Langmuir, 2016, 32(14), 3495–3505.
7. T. Kowada, H. Maeda and K. Kikuchi, BODIPY-based probes for the fluorescence imaging of biomolecules in living cells, Chem. Soc. Rev., 2015, 44(14), 4953–4972.
8. M. Baruah, W. Qin, N. Basaric, W. M. De Borggraeve and N. Boens, BODIPY-based hydroxyaryl derivatives as fluorescent pH probes, J. Org. Chem., 2005, 70(10), 4152–4157.
9. L. E. Shimolina, M. A. Izquierdo, I. López-Duarte, J. A. Bull, M. V. Shirmanova, L. G. Klapshina, E. V. Zagaynova and M. K. Kuimova, Imaging tumor microscopic viscosity in vivo using molecular rotors, Sci. Rep., 2017, 7, 41097.
10. A. Vyšniauskas, I. López-Duarte, N. Duchemin, T.-T. Vu, Y. Wu, E. M. Budynina, E. P. Volkova, Y. A. Cabrera, D. E. Ramírez-Ornelas and M. K. Kuimova, Exploring viscosity, polarity and temperature sensitivity of BODIPY-based molecular rotors, Phys. Chem. Chem. Phys., 2017, 19(37), 25252–25259.
11. B. J. Müller, S. M. Borisov and I. Klimant, Red-to NIR-emitting, BODIPY-based, k+-selective fluoroionophores and sensing materials, Adv. Funct. Mater., 2016, 26(42), 7697–7707.
12. S. Radunz, H. R. Tschiche, D. Moldenhauer and U. Resch-Genger, Broad range on/off pH sensors based on pKa tunable fluorescent BODIPY, Sens. Actuators, B, 2017, 251, 490–494.
13. N. Boens, V. Leen and W. Dehaen, Fluorescent indicators based on BODIPY, Chem. Soc. Rev., 2012, 41(3), 1130–1172.
14. Y. Ni and J. Wu, Far-red and near infrared BODIPY dyes: synthesis and applications for fluorescent pH probes and bio-imaging, Org. Biomol. Chem., 2014, 12(23), 3774–3791.
15. E. Fron, E. Coutino-Gonzalez, L. Pandey, M. Sliwa, M. Van der Auweraer, F. C. De Schryver, J. Thomas, Z. Dong, V. Leen and M. Smet, et al., Synthesis and photophysical characterization of chalcogen substituted BODIPY dyes, New J. Chem., 2009, 33(7), 1490–1496.
16. T. Rohand, W. Qin, N. Boens and W. Dehaen, Palladium-catalyzed coupling reactions for the functionalization of BODIPY dyes with fluorescence spanning the visible spectrum, Eur. J. Org. Chem., 2006,(20), 4658–4663.
17. T. Rohand, M. Baruah, W. Qin, N. Boens and W. Dehaen, Functionalisation of fluorescent BODIPY dyes by nucleophilic substitution, Chem. Commun., 2006,(3), 266–268.
18. N. Boens, L. Wang, V. Leen, P. Yuan, B. Verbelen, W. Dehaen, M. Van der Auweraer, W. D. De Borggraeve, L. Van Meervelt, J. Jacobs, D. Beljonne, C. Tonnelé, R. Lazzaroni, M. J. Ruedas- Rama, A. Orte, L. Crovetto, E. M. Talavera and J. M. Alvarez-Pez, 8-halo BODIPYs and their 8-(c, n, o, s) substituted analogues: Solvent dependent UV–vis spectroscopy, variable temperature NMR, crystal structure determination, and quantum chemical calculations, J. Phys. Chem. A, 2014, 118(9), 1576–1594.
19. V. Leen, P. Yuan, L. Wang, N. Boens and W. Dehaen, Synthesis of meso-halogenated BODIPYs and access to meso-substituted analogues, Org. Lett., 2012, 14(24), 6150–6153.
20. A. Burghart, H. Kim, M. B. Welch, L. H. Thoresen, J. Reibenspies, K. Burgess, F. Bergström and L. B.-Å. Johansson, 3, 5-diaryl-4, 4-difluoro-4-bora-3a, 4a-diaza-s-indacene (BODIPY) dyes: synthesis, spectroscopic, electrochemical, and structural properties, J. Org. Chem., 1999, 64(21), 7813–7819.
21. A. Bourouina, M. Rekhis and M. Trari, DFT/TD-DFT study of ruthenium bipyridyl-based dyes with a chalcogen donor (x = s, se, te), for application as dye-sensitized solar cells, Polyhedron, 2017, 127, 217–224.
22. M. R. Detty, P. B. Merkel and S. K. Powers, Tellurapyrylium dyes as photochemotherapeutic agents. Surprising tellurium atom effects for the generation of rates of reaction with singlet oxygen, J. Am. Chem. Soc., 1988, 110(17), 5920–5922.
23. S. K. Powers, D. L. Walstad, J. T. Brown, M. Detty and P. J. Watkins, Photosensitization of human glioma cells by chalcogenapyrylium dyes, J. Neurooncol., 1989, 7(2), 179–188.
24. E. Hückel, Zur quantentheorie der doppelbindung und ihres stereochemischen verhaltens, Z. Elektochem. Angew. P., 1930, 36(9), 641–645.
25. E. Hückel, Quantentheoretische beiträge zum benzolproblem, Z. Phys., 1931, 70(3–4), 204–286.
26. W. P. Purcell and J. A. Singer, A brief review and table of semiempirical parameters used in the Hueckel molecular orbital method, J. Chem. Eng. Data, 1967, 12(2), 235–246.
27. M. H. Garner, G. C. Solomon and M. Strange, Tuning conductance in aromatic molecules: Constructive and counteractive substituent effects, J. Phys. Chem. C, 2016, 120(17), 9097–9103.
28. I. J. Arroyo, R. Hu, G. Merino, B. Z. Tang and E. Pena-Cabrera, The smallest and one of the brightest. Efficient preparation and optical description of the parent borondipyrromethene system, J. Org. Chem., 2009, 74(15), 5719–5722.
29. A. Schmitt, B. Hinkeldey, M. Wild and G. Jung, Synthesis of the core compound of the BODIPY dye class: 4,4′-difluoro-4- bora-(3a, 4a)-diaza-s-indacene, J. Fluoresc., 2009, 19(4), 755–758.
30. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the coulomb-attenuating method (cam-B3LYP), Chem. Phys. Lett., 2004, 393(1), 51–57.
31. W. J. Hehre, R. Ditchfield and J. A. Pople, Self-consistent molecular orbital methods. xii. further extensions of Gaussian-type basis sets for use in molecular orbital studies of organic molecules, J. Chem. Phys., 1972, 56(5), 2257–2261.
32. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, Self-consistent molecular orbital methods. xxiii. a polarization-type basis set for second row elements, J. Chem. Phys., 1982, 77(7), 3654–3665.
33. M. J. Frisch, J. A. Pople and J. S. Binkley, Self-consistent molecular orbital methods 25. supplementary functions for Gaussian basis sets, J. Chem. Phys., 1984, 80(7), 3265–3269.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Ivengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pompelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zarkazewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
35. M. R. Momeni and A. Brown, Why do TD-DFT excitation energies of BODIPY/aza-BODIPY families largely deviate from experiment? answers from electron correlated and multireference methods, J. Chem. Theory Comput., 2015, 11(6), 2619–2632.
36. R. Misra, Tuning of second-order nonlinear optical response properties of aryl-substituted boron-dipyrromethene dyes: Unidirectional charge transfer coupled with structural tailoring, J. Phys. Chem. C, 2017, 121(10), 5731–5739.
37. M. M. Alam, R. Misra and K. Ruud, Interplay of twist angle and solvents with two-photon optical channel interference in aryl-substituted BODIPY dyes, Phys. Chem. Chem. Phys., 2017, 19(43), 29461–29471.
38. J. Griffiths, Colour and Constitution of Organic Molecules, Academic Press, 1976.
39. M. Rosenberg, K. R. Rostgaard, Z. Liao, A. Ø. Madsen, K. L. Martinez, T. Vosch and B. W. Laursen, Design, synthesis, and time-gated cell imaging of carbon-bridged triangulenium dyes with long fluorescence lifetime and red emission, Chem. Sci., 2018, 9(12), 3122–3130.
40. H. Lu, J. Mack, Y. Yang and Z. Shen, Structural modification strategies for the rational design of red/NIR region BODIPYs, Chem. Soc. Rev., 2014, 43(13), 4778–4823.
41. A. L. Allred, Electronegativity values from thermochemical data, J. Inorg. Nucl. Chem., 1961, 17(3–4), 215–221.
42. L. C. Allen, Electronegativity is the average one-electron energy of the valence-shell electrons in ground-state free atoms, J. Am. Chem. Soc., 1989, 111(25), 9003–9014.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8pp00430g

---