Nanocellulose/graphene oxide layered membranes: elucidating their behaviour during filtration of water and metal ions in real time

Abstract

The deposition of a thin layer of graphene oxide onto cellulose nanofibril membranes, to form CNF–GO layered-composite membranes, dramatically enhances their wet-mechanical stability, water flux and capacity to adsorb water pollutants (P. Liu, C. Zhu and A. P. Mathew, J. Hazard. Mater., 2019, 371, 484–493). In this work, we studied in real time the behavior of these layered membranes during filtration of water and metal ion solutions by means of in situ SAXS and reactive molecular dynamics (ReaxFF) computational simulations. SAXS confirms that the GO layers limit the swelling and structural deformations of CNFs during filtration of aqueous solutions. Moreover, during filtration of metal ion solutions, the connection of the CNF–GO network becomes highly complex mass-fractal like, with an increment in the correlation length. In addition, after ion adsorption, the SAXS data revealed apparent formation of nanoparticles during the drying stage and particle size increase as a function of time during drying. The molecular dynamics simulations, on the other hand, provide a deep insight into the assembly of both components, as well as elucidating the motion of the metal ions that potentially lead to the formation of metal clusters during adsorption, confirming the synergistic behavior of GO and CNFs for water purification applications.

---

Introduction

Driven by the severe current environmental issues, there is nowadays an urgent impetus towards the development of fast and inexpensive solutions for water purification. Over the past decade, extensive research has demonstrated the prominent potential of nanocellulose (NC) as a building block to develop porous membranes,^1–5 owing to the ease of pore-size tunability,⁶ as well as the reactive surface of NC membranes that allows the introduction of functional groups for ion adsorption.³ Nevertheless, although the use of nanocellulose-based materials for water purification is indeed very promising, there are several challenges that need to be addressed, for instance, to improve the adsorption-capacity for filtration of complex water-streams, reduction of biofouling formation, and enhancement of the mechanical robustness of membranes in the wet-state, considering that the structural integrity of NC-based materials is significantly compromised by water-induced swelling.³ A common strategy to improve the performance of membranes is via formulation of composite materials that yield higher efficiency than native NC in removing hazardous species and enhanced mechanical robustness.

Graphene oxide (GO), prepared by chemical exfoliation of graphite, has been recently demonstrated to be a promising nanomaterial for adsorption applications due to its highly reactive surface arising from the abundant hydroxyl and carboxyl functional groups, as well as its large surface area, and super hydrophobic π–π interaction.^7,8 Moreover, GO also exhibits excellent mechanical properties, amphiphilic behavior⁹ and good antifouling properties.¹⁰ The hybridization of NC with GO has been previously studied, proving great synergistic interaction between GO and cellulose nanofibrils (CNFs), presumably due to good interfacial contact between both components, suggesting that the flexible 1D-structure of CNFs allows establishing efficient bonding with the 2D-GO-nanosheets.¹¹ The potential of cellulose/graphene oxide-based composite films has been readily explored for different applications, for instance in rechargeable zinc-air batteries,¹² forward osmosis¹³ and ion permeation.¹⁴ Moreover, in our previously published work,¹⁵ we have observed that the incorporation of a layer of GO sheets onto CNF membranes via sequential water filtration (to form layered-composite CNF–GO membranes) improves the performance of the cellulosic membranes in several aspects; for instance, their mechanical properties dramatically improves under dry, wet (4-fold higher strength than pristine CNF membranes) and re-dried conditions. Furthermore, although the pore-size in the dry-state of the composite CNF–GO membranes is smaller than that of the reference CNF membrane, the incorporation of GO increases significantly the water flux (5-fold higher), presumably through the creation of water transport nano-channels in a random manner at which GO nanosheets accommodate within the cellulose matrix. In addition, the composite membranes exhibit >90% rejection of dyes, both negatively and positively charged. However, there is still a lack of fundamental understanding on the in operando structural evolution of CNF–GO composite membranes. In this work we investigate in real time the behavior of CNF–GO layered-composite membranes during filtration of water and heavy metal ion solutions by utilizing X-ray as a probe as well as computational simulations to concertedly describe the various effects on the micro-, nano- and atomic-scales. While in situ small angle X-ray scattering (SAXS) provides valuable insights into the structure development from dry to swollen states during filtration and ion-adsorption, reactive molecular dynamics (RMD) simulations realistically predict the adsorption of metal ions under various environmental conditions.

Experimental section

Materials

Cellulose nanofibrils (CNFs, 1.8 wt%) employed for the preparation of the membranes were acquired from Borregard, Norway, as the commercial product Exilva. Graphene oxide suspension (GO, 4 mg mL⁻¹ in water), copper nitrate (Cu[NO₃]₂) and silver nitrate (AgNO₃) were purchased from Sigma-Aldrich and used as received.

Membrane preparation

The CNF–GO layered-composite membrane was prepared following our previously reported procedure¹⁵via sequential vacuum filtration of the CNF suspension (0.48 g CNF, 0.8 g L⁻¹) followed by the GO suspension (4.8 mg GO in 600 mL of distilled water) in a filtration setup, resulting in membranes (GO : CNF mass ratio of 1 : 100) with a thickness of 19.3 ± 4.0 μm (determined by SEM), where the GO layer corresponds only to 110 nm of the membrane thickness. The average pore size of the composite membrane is 7 nm calculated using the Barrett–Joyner–Halenda (BJH) method. A reference membrane comprising only CNFs was prepared in a similar manner (excluding the deposition of GO), exhibiting a BJH pore size of 9.8 nm.

Characterization

The morphology of the membranes was studied with a fast scan atomic force microscope (AFM, Bruker, Nanoscope controller, Santa Barbara, California, USA). In all cases, the height sensor and the peak force error images were recorded using a probe (Model: ScanAsyst-air, Bruker) under peak force tapping mode. The collected data were processed with NanoScope Analysis 1.5 (Bruker) software. The cross-section of the membranes was investigated using a field emission scanning electron microscope (SEM, JSM-7401F, Japan) after sputter coating (JEOL, JFC-1200) with gold for 30 seconds operating at 1 or 2 kV. The pore size of the membranes in the dry-state was determined from nitrogen adsorption–desorption measurements at 77 °K using the BJH method. The measurements were carried out in a Micromeritics ASAP 2020 instrument and the samples were degassed at 110 °C for 24 h under dry N₂ conditions prior to measurement.

In situ SAXS measurements

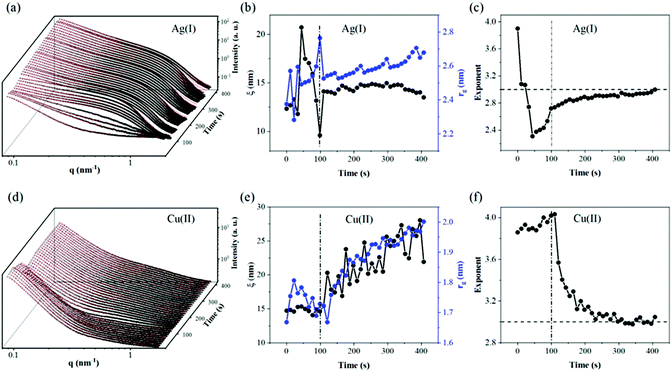
To in situ examine the evolution of structures of CNFs and CNF–GO membranes during filtration of water and metal ion solutions (AgNO₃ and Cu(NO₃)₂ at 10 mg L⁻¹ in water), synchrotron radiation-based SAXS experiments were performed. The experiments were carried out at the P03 “MiNaXS” beamline with an incident photon energy of 13 keV and a sample-to-detector distance of 1.5 m. The scattered photons were detected using a 2-dimensional Pilatus 300 K detector. The beam damage was carefully checked by evaluating the intensity change at a single illuminated area under consecutive X-ray exposures. A set-up similar to the one used in our previous work has also been utilized here for the vacuum filtration of water and metal salt solutions.¹⁶ The data were collected separately from three different states: (i) dry membranes before filtration, (ii) during filtration of water, Ag(I) and Cu(II) solutions at 100 mg L⁻¹ and (iii) during drying of the wet membranes.

To describe the SAXS data [scattering intensity vs. magnitude of scattering vector (q)] of in situ filtration, we use a two-stage model by combining the correlation model and Gaussian function. The first term on the left depicts the network built by the CNF in correlation length ξ with n as the Porod exponent, describing the network connection; the second term is a generalized Guinier form assigned to entangled regions in the radius of gyration, r_g, on a smaller scale.

The scattering intensity of polydisperse-sized nanoparticles without strong interference, i.e. structure factor ∼1, can be depicted by

I(q) = scale·∑f(r) × F(q, r) + background (2)

where the form factor [F(q)] of a sphere with a given radius r is written as eqn (3) while the size distribution f(r) accounting for the polydispersity of the system described by a Lognormal distribution is given in eqn (4):with Norm numerically estimated as the integrated area of f(r) between r_min = 0 nm and r_max = 50 nm, the region of which is sufficiently large to cover the particle size distribution. r_Med is the median value of the size distribution and σ is the width of the distribution.

The nanoparticle growth kinetics was modeled by

The first term on the right is the Kolmogorov-Johnson-Mehl-Avrami (KJMA) model which is well fit for some cases of nanoparticle growth, and the second term is attributed to Ostwald ripening. In the equation, n is known as the Avrami exponent, r_∞ is a scaling factor, t is the time, t_g is a rate parameter, w is the arbitrary time width parameter chosen as 2 min (ref. 17), t_OR is the Ostwald ripening “turn-on” time, and k_OR is the Ostwald ripening rate.

Computational simulations

All MD simulations were carried out by means of the Amsterdam Density Functional (ADF)/ReaxFF implementation^18,19 [ReaxFF 2017, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com (2017)]. The main force field parameters were taken from the force field used in a previous study²⁰ and the parameters for silver, extracted from ref. 21, were extended to describe the interaction with the nitrogen atom (considering the NO₂ and NO₃ groups only). A small training set of structures (20 in all) was prepared by optimizing the built geometries at the QM level with the B3LYP functional and the DZVP basis set following previous studies reporting similar systems with silver ion interactions.^22,23 The parameters of the NO₃ group were taken from ref. 24. The force field used is available upon request to the authors.

The systems were energy minimized at T = 100 K in the NVT ensemble and then heated to 300 K. Equilibration was carried out for about 300 ps. Then, the production dynamics were performed in the NVT ensemble for about 350 ps and the system structures were collected every 0.1 ps. Temperature was controlled through a Berendsen thermostat²⁵ with a relaxation constant of 0.1 ps and the time step was set to 0.25 fs.

The analysis of the production trajectories was focused on the position of the metal ions in relation to the support, atom–atom radial distribution functions (RDFs), spatial distribution functions (SDFs), connections of the metals to the oxygen atoms of the support, and hydrogen bonds. Visual inspection of the trajectories was essential to disclose metal clustering and the adsorption locations in terms of chelation and trapping. Solvation effects were also checked to reveal the role played by water and counterions.

Results and discussion

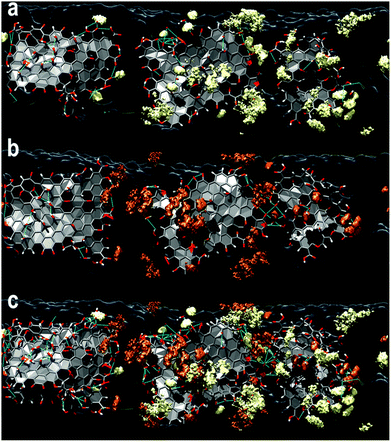
The outstanding adsorption properties of GO have been demonstrated to be suitable for the removal of several types of heavy metal ions, for instance, Cd(II),²⁶ Co(II),²⁶ Eu(II)²⁷ and U(VI),²⁸ where the efficient adsorption capacity arises from its hydrophilic properties and the presence of oxygen containing functional groups that can efficiently bind the metal ions by sharing an electron pair.²⁹ In the current work we have prepared layered CNF–GO composite membranes, in which a dense ultrathin layer of GO was deposited on top of a relatively thick and porous CNF network by vacuum filtration (Fig. 1a). The resultant structure of the membranes is displayed in Fig. 1b–e. The membrane architecture is a fundamental parameter in a fine design, as it has been demonstrated in a number of papers that the response of sorbents is markedly influenced by the arrangement of the species, which could be assembled through relatively strong or weak intermolecular interactions.^30,31 As a consequence, an appropriate scheme should be defined by a synergistic association of selected species, which would result in efficient low-cost filters^32,33. Indeed, layered-anisotropic membranes made of cellulose nanofibrils and graphene oxide sheets were flexible (see the inset image) and appeared to be more efficient than the corresponding isotropic structures in trapping metal ions and dyes from aqueous media.^15,20

Fig. 1 (a) Schematic illustration of the preparation of the CNF–GO layered membranes. (b) Cross-sectional SEM image of the CNF–GO membrane. (c) Computational model of the structure of a CNF–GO layered membrane. (d and e) Surface topography of a CNF membrane before (d) and after (e) deposition of GO, measured by atomic force microscopy; a folded CNF–GO membrane is shown in the inset.

The computational models of the CNF–GO layered membranes, displayed in Fig. 1c, show that GO sheets are stably adsorbed on the CNF supports through a dense network of intermolecular hydrogen bonds involving the hydroxyl groups of the two species that determined, together with self-interactions, their relative orientation on the interface. The dynamic nature of these types of interactions is responsible for the moderate mobility of the sheets and their relocation, which is driven by the morphology of the fibril facet and by the presence of the other GO units nearby. Closer inspection of the sampled configurations reveals that a greater stability of the layer is acquired when the oxygen–hydroxyl and hydroxyl–hydroxyl intermolecular hydrogen bonds are reinforced by the participation of the carboxyl groups of GO. Indeed, the presence of carboxyl groups confers a negatively charged character to the supports that, as such, are prone to attract metal cations. This was confirmed by checking the molecular electrostatic potential generated by the polarizable charges assigned to the atoms of the final structures through the electronegativity equalization method (EEM) on the solvent accessible surface of the substrate models.

In situ SAXS measurements

To get a deeper understanding of the structure evolution of the layered membranes during filtration of water and salt solutions, synchrotron radiation-based SAXS measurements of the membranes before and after deposition of the GO phase were performed. For the measurements, a custom vacuum filtration cell was utilized, as has been described in our previous reports.¹⁶ In Fig. 2, ex situ SAXS data of the CNF (a) and CNF–GO (b) membranes in the as-prepared (black), wet (red) and re-dried (blue) states are shown. In the dry state, both CNF–GO (black dots) and pure CNF (black circles) membranes show similar scattering patterns. By using eqn (1) to extract some fitting parameters (Table S1†), we found that the correlation lengths ξ of membranes are in the 10 to 20 nm range and the r_g of entangled regions on a smaller scale is around 2 nm.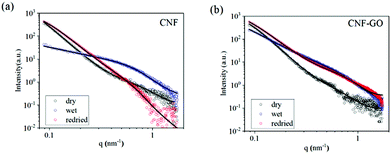

Fig. 2 Ex situ SAXS characterization of a pure CNF membrane (a) and CNF–GO membranes (b) in dry (black), wet (blue) and re-dried (red) states. The solid lines are fitting results by eqn (1).

The contribution of GO to the scattering is not obvious because GO is a dense ad-layer on top of CNFs with a broad domain size distribution, which might contribute to forward scattering shielded behind the direct beam-stop when the X-ray beam is perpendicular to the membrane surface. Thus, the fitting results mainly reflect the dried CNF network structure in the two types of membranes.

Membrane interaction with water. When both membranes are immersed in water, a clear intensity increase in the high q region is observed, indicating a dramatic change on a small scale. By comparing the r_g obtained from the Guinier term in eqn (1), we found a slight increase compared to the as-prepared dry states, as water swells the entangled region. The higher I_G also suggests that more such entangle regions could be observed. This is in line with the change in the low q region: first the Porod exponent α changes from around 4 to lower numbers, namely, 2.4 for CNF–GO and 1.5 for CNFs. A Porod exponent α of approximately 4 usually indicates that a large structure with a smooth surface exists. If α is between three and four, such a structure has a rough surface morphology with a surface fractal dimension d_s = 6 − α; when 2 < α < 3, such a structure has a mass fractal structure with a fractal morphology d_m = α; when 1 < α < 2, the structure can be depicted as a branched structure with a 1D backbone. In the wet state, water infiltrates the large structure with a smooth surface and swells it by enlarging the correlation length. This makes the connection more complicated than in a densely packed case. The lower exponent of the CNF membrane suggests that the fibrillary networks are more dissociated than those of the CNF–GO membrane, despite the slightly larger ξ obtained for CNF–GO via fitting, which only provides an average value of the correlation length. This behavior indicates that the GO ad-layer protects the CNF network in the CNF–GO composite membrane against the water flow during filtration. After re-drying the membranes, both CNFs and CNF–GO recover their structure only up to a certain extent, indicating some irreversible structural changes. For example, in the low q region, the Porod exponent becomes larger, again approaching 4, suggesting that the fibril network contracts to denser structures with smaller correlation lengths. However, at high q, where the small entangled regions dominate the contribution, CNF–GO and CNF membranes show different trends. In the CNF membrane, the fitted r_g increases further with a strong intensity reduction, suggesting that the entangled regions become larger as the fibril network becomes densely packed, while in the CNF–GO membrane, the fitted r_g becomes smaller with only a slight decrease of intensity, which can be directly observed from the scattering profiles (overlapping of the red and blue curves – Fig. 2(b)). This suggests that when the GO adlayer is present, the cellulosic entangled structures on a smaller scale did not collapse or merge into large structures during re-drying but just self-contracted. In sum, during wetting and re-drying, the GO ad-layer protects the cellulose fibrillary network against dramatic structural variations. Overall, SAXS results show that the presence of GO prevents the swelling as well as loss of the integral structure of the CNF, on its interaction with water compared to that observed in the pure CNF membrane. This may be related to the reduction of the intake or the absorption of water and might also contribute to increased water flow while restricting the passage of metal ions.

Membrane interaction with metal ion solutions. After verifying the protective action of the GO ad-layer on the CNF network, we proceeded to evaluate the filtration performance of the CNF–GO membrane with salt solution. In Fig. 3(a and d), the profile of the evolution of the SAXS spectrum of the CNF–GO membrane from the dry to stable wet state in Ag(I) and Cu(II) solutions is depicted. The fitting curves (red lines) calculated by eqn (1) can reproduce the experimental data (black circles) to a good extent, even though the scattering profiles show different features in two solutions. The evolutions of the correlation length ξ and r_g as a function of time in Ag(I) and Cu(II) solutions are plotted in Fig. 3(b) and (e), respectively. In both cases, the infiltration starts to enter a stable phase after 100 s as marked by a dash-dot line in (b–f). Despite the rather different absolute values of the fitting parameters, which might be related to a batch variation such as different r_g values, and different instant filtration conditions, e.g. fitting parameter fluctuation before 100 s in (b), the general trends of ξ and r_g are quite consistent: both parameters increase in the stable infiltration phase compared to the dry membrane. The instability in the beginning of the filtration is also reflected in the Porod exponent, which depicts the complexity of the morphology of the network at a distance comparable to correlation distance (ξ). As noted earlier, the Porod exponent is close to 4 for both membranes in the dry state, indicating a largely aggregated and rather smooth surface. In the case of Ag(I), this value quickly reduces to 2.4 upon the filtration, suggesting that water rushes into the membrane and breaks the aggregates into highly entangled networks, while on the other hand, in the case of Cu(II), the water seems to wet the aggregated surface to further smoothen it, with the Porod exponent even closer to 4. One of the reasons leading to the instability could be pressure stock generated when the vacuum pump started, which could lead to unpredictable pressure-differences and subsequently different solution flow rates, which may modify the morphology of the membrane differently. As the pumping process continues, the solution flow rate becomes more stable. It is also reflected in Fig. 3c and f that the Porod exponent quickly approaches 3 in the stable infiltration phase, suggesting that the connection of the CNF–GO network becomes highly complex mass-fractal like. These structural changes under continuous directional salt solution flow show similar features to the pure water swelling structure, changing the morphology from a densely packed fractal surface to a mass-fractal network with increased ξ and r_g. The metal ion adsorption during the process as well as during the re-drying stage may also contribute to such changes (as suggested by simulation results in the following section).

Fig. 3 In situ SAXS (black circles) and fitting result (red line) of CNF–GO membranes in Ag(I) solution filtration (a) and Cu(II) solution filtration (d). The evolution of the correlation distance and radius of gyration extracted from fitting parameters for Ag(I) (b) and Cu(II) (e); the corresponding exponent is plotted in (c) for Ag(I) and in (f) for Cu(II).

After filtration of metal salt solutions, the re-drying of the membranes was also followed in situ by SAXS, by stopping the flow of the metal salt solution, followed by vacuum-drying the membranes within the filtration cell (see Fig. 4).

Fig. 4 In situ SAXS during drying of CNF–GO membranes after silver (a) and copper solution (b) infiltration. Black circles are intensity differences by subtracting the first scattering profile from the subsequent ones. The fitting results are plotted as red lines. The arrow marks the progress as a function of time. (c) Growth kinetics of the nanoparticles: the left axis is the median size of nanoparticles (black) and the right axis is the width of lognormal size distribution (blue); filled spheres are the variations in median size while squares represent the variations in the width of the size distribution.

To show clearly the increased intensities during drying, the intensity difference is plotted in Fig. 4a and b by subtracting the first scattering profile as a background from the subsequent ones. The observed intensity variation suggests the formation of nanoparticles which gradually grow as a function of drying time. The size and distribution of the so-formed nanoparticles were fitted by combining eqn (3)–(5) with a spherical form factor and lognormal size distribution, and plotted as a red curve (Fig. 4). The evolution of the form factor of nanoparticles and no indication of a strong structure factor are in line with other studies on nanoparticle growth kinetics by SAXS.^34,35 Considering that the CNF–GO membrane contributes more to a scattering intensity variation in the low q region than in the high q region, the information of the nanoparticle size and distribution was fitted to the data when q was greater than 0.15 nm⁻¹ as marked by the dashed vertical lines.

The nanoparticles show a two-stage growth mode. Fitting the median radius with eqn (5) it was found that for both Cu²⁺ and Ag⁺, the r_∞, n (Avrami exponent) and Ostwald ripening set-on time t_OR were very close to each other (see Table S2†). For copper, the nanoparticles displayed larger Avrami and Ostwald ripening rates than for Ag, suggesting a faster growth process for copper (fitting parameters in the ESI†). Nevertheless, how are these nanoparticles formed? As far as our knowledge goes neither neat-CNFs nor GO exhibits the capacity to form metal oxide NPs without adding further reducing agents or under hydrothermal conditions. However, can they form such nanoparticles when they act synergistically together? Or is it just due to “post-crystallization” of the respective metal salt solutions upon drying as suggested by Sun et al.,³⁶ for graphene-oxide films. Although we do not explore the nature of such nanoparticles in this work, we consider that it's a prominent focus for future research effort to elucidate this behavior and the functionality of such nanoparticles.

Computational simulations

The contribution from GO in terms of adsorption of water pollutants has been further probed by studying the behavior of Ag⁺ and Cu²⁺ ions in relation to the CNF–GO support by means of reactive molecular dynamics simulations (ReaxFF approach), following our previous work.²⁰

The examination of the plots shown in Fig. 5a suggests the adsorption of the cations on CNF–GO surfaces, which is confirmed by the sharp peaks at short distances in the radial distribution functions (RDFs) between the metal and the oxygen atoms of the composite supports (Fig. 5c and d). Even though at the beginning of the simulations all metal ions were relatively far from the interface, at the end of the sampling they were found in various locations on top of the surface connected mainly to the carboxyl groups of the edge regions of the GO sheets (first blue peaks in the RDFs –Fig. 5a) or entrapped by the concerted action of the different oxygen species (Fig. 5c and d). They were stably adsorbed on the support and could be organized into small clusters of various sizes and shapes depending on their relative locations.

Fig. 5 (a) Normalized RDFs of the adsorption of Cu²⁺ and Ag⁺ on CNF–GO. Atom–Atom Y is the metal ion and X is the selected oxygen species. RDFs are between the metal ions and the oxygens of CNF (O(CNF)) and GO (O(GO)). Ag–Ag and Cu–Cu RDFs are also shown. (b) Average number of metal ions found around each metal ion (within 7 Å) during the simulation. The total number of metal ions is 32 in each case. (c) Ag+ ions are represented with light grey spheres and NO³⁻ ions are rendered with ball and stick models (blue nitrogen atoms). (d) Adsorption of Cu²⁺ ions on CNF–GO (layer model). Final structure extracted from the production simulations. Cu²⁺ ions are represented with orange spheres and NO³⁻ ions are rendered with ball and stick models (blue nitrogen atoms). Various binding modes of the metal ions to the support are displayed. Cu²⁺ and Ag⁺ are connected to the carboxyl groups of GO and to other oxygen atoms of the sheets. Multiple types of interactions are visible and the closeness of Cu²⁺ is highlighted with cyan lines. CNFs are rendered through red (oxygen) and white (hydrogen) surface patches (carbon – light grey), and GO is displayed through dark grey stick models with filled aromatic rings. A few water molecules surrounding these selected portions of the configuration have been included and displayed as lines to give an idea of the complexity of the whole environment. Silver clusters are visible in the left hand side images.

RDF plots shows that the closest and strongest connections are between metal ions and O(GO) with peaks at about 1.9 and 2.3 Å for Cu(II) and Ag(I), respectively. These data are in perfect agreement with previous studies where copper ion coordination^21,37 at approximately 1.94 Å identified the first shell and an equatorial position of the oxygen, and silver nitrate^38,39 Ag–O separations explored a slightly wider range (2.31–2.45 Å) depending on the method used to characterize them. As far as the coordination number corresponding to these peaks is concerned, it is around 1.6 for both species, suggesting that the ions could be connected most probably to two oxygen of GO. Instead, the interaction with CNFs seems to be hindered by the presence of the GO layer and only the Cu²⁺ ions seem capable of reaching the cellulose chains. Ion self-interactions are confirmed by the trend of both metal–metal RDFs where it can be seen that the copper clusters could be more packed (closer distance around 2.8 Å) than silver ones (the first neighbors are found at around 3.5 Å), which display a broader peak.

Examination of the average number of metal ions around each metal ion (in a range of 7 Å) during the simulations (Fig. 5b) indicates that the copper clusters contain a greater number of atoms (8 at most) than those made of silver, where the maximum number is 6 and the interatomic distances are longer. A few clusters of the two species and their adsorption modes on the supports are shown in Fig. 5c and d.

Further confirmation of the experimental evidence of the stability of the two types of metal ions on the surface comes from the inspection of the permanence profiles on the interface and their level of penetration in the composite matrices (2D and 3D density plots, Fig. 6) derived from the simulations. These data were collected considering the occupation of specific positions (x and y coordinates) on the interface and perpendicular to it (z coordinate) in each model (Fig. 6 – right hand side). It is apparent that the general trend of the copper ions is to be more strongly connected to the interface (confirmed by the highly populated sites visible in Fig. 6) and to go more deeply into the substrate, reaching sometimes the CNF cavities, than silver. This is visible in Fig. 6b where two sharp peaks at shorter CNF–Cu separations are present and a more compact organization of the ions closer to the sheet is observed, which is in line with the Cu–O(CNF) trend in the RDF plot displayed in Fig. 5a. On the other hand, in the case of silver the distribution of the z distance is shifted to longer separations and only a peak in the CNF region is present. The different adsorption behavior of the silver ions is also confirmed by the lower peaks in Fig. 6b. These data have been complemented with three dimensional iso-surface (spatial distribution functions – SDFs) analyses to identify the most populated regions of the metal ions in the two cases. The results are displayed in Fig. 7. The comparison confirms a greater mobility of the Ag⁺ ions due to their more superficial location (more areas of the surface are explored) but a similar binding mode to the membrane with the propensity to migrate towards the carboxyl moieties of the GO sheets, suggesting the higher adsorption capacity in the presence of GO sheets in the layered-composite membrane.

Fig. 6 Left-hand-side: population density of the metal ions on the support (X–Y co-ordinate). The XY plane represents the interface where the dimensions are those of the simulation box. Right-hand-side: population density of the metal ions on the support (Z-coordinate). The z positions of the supports are evidenced with the colored regions and their distributions are the black and red histograms visible in the two plots. (a) Copper ions and (b) silver ions.

Fig. 7 Spatial distribution functions of the Ag⁺ (white regions) and Cu²⁺ (orange regions) ions on an average structure of the CNF–GO model. GO is rendered through stick models with filled aromatic rings. CNFs are represented with a black solvent accessible surface. (a) Adsorption of Ag⁺, (b) adsorption of Cu²⁺, and (c) superposition of the two models.

Conclusions

In this work, the behavior of CNF–GO layered-composite membranes was studied in real time by means of synchrotron SAXS together with reactive molecular dynamics (ReaxFF) simulations. The structural evolution of the membranes was followed by in situ SAXS during filtration of water and metal (Ag⁺ and Cu²⁺) ion solutions and the subsequent drying process. The results demonstrate that the incorporation of a GO layer prevents the expansion of the CNF network during water filtration, presumably resulting in the enhanced wet-mechanical properties previously observed. The GO ad-layer also seems to protect the cellulosic network against dramatic structural variations during re-drying, avoiding dramatic collapse or aggregation as compared to a pristine CNF membrane. Furthermore, the in situ SAXS studies during filtration of metal ion solutions confirmed that membrane swelling induces a very complicate re-structuring of the CNF–GO network that reached a fractal dimension close to 3, masking the effect due to adsorption of metal ions. In addition, during drying of the pre-wet membranes after metal ion adsorption, an evident intensity increase in the low q region of the scattering profiles suggests the formation of nanoparticles which gradually grow as a function of drying-time. The molecular dynamics simulations elucidated that the GO sheets are stably adsorbed on the CNF support through a dense network of intermolecular hydrogen bonds, together with self-interactions, while the carboxyl groups of GO stabilize the ad-layer of GO on CNFs, reinforcing the oxygen–hydroxyl and hydroxyl–hydroxyl intermolecular bonds among the phases. Moreover, the simulations also supported and confirmed all the observed experimental data and explained at the atomic level the motion of the metal ions, their specific location in the CNF–GO layered configuration, the dynamic behavior during adsorption and formation of metal nanoclusters.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the Swedish research council (VR, grant No: 2017–04254) and the MULTIMAT project (H2020-MSCA-ITN-2014, Grant No. 676045) for research funding. The authors also thank DESY, Hamburg, Germany, for the beamtime I-20170358 and beamline scientist Dr Wiebke Ohm for her support during the experiments. S. M. acknowledges the CINECA award, under the ISCRA initiative, for providing high-performance computing resources and support. S. M. is also grateful to the SCM group for suggestions and support (ADF/ReaxFF program).

References

1. K. Tan, S. Heo, M. Foo, I. M. Chew and C. Yoo, Sci. Total Environ., 2019, 650, 1309–1326.
2. N. Lavoine and L. Bergström, J. Mater. Chem. A, 2017, 5, 16105–16117.
3. H. Voisin, L. Bergström, P. Liu and A. Mathew, Nanomaterials, 2017, 7, 57.
4. J. N. Putro, A. Kurniawan, S. Ismadji and Y.-H. Ju, Environ. Nanotechnol. Monit. Manag., 2017, 8, 134–149.
5. M. Delgado-Aguilar, I. González, A. María Jiménez, Q. Tarrés, G. Quintana and P. Mutjé, Cellul. Chem. Technol., 2016, 50, 369–375.
6. Z. Karim, S. Claudpierre, M. Grahn, K. Oksman and A. P. Mathew, J. Membr. Sci., 2016, 514, 418–428.
7. D. Chen, H. Feng and J. Li, Chem. Rev., 2012, 112, 6027–6053.
8. W. Peng, H. Li, Y. Liu and S. Song, J. Mol. Liq., 2017, 230, 496–504.
9. A. J. Paulista Neto and E. E. Fileti, Phys. Chem. Chem. Phys., 2018, 20, 9507–9515.
10. J. Alam, A. K. Shukla, M. Alhoshan, L. Arockiasamy Dass, M. R. Muthumareeswaran, A. Khan and F. A. Ahmed Ali, Adv. Polym. Technol., 2018, 37, 2597–2608.
11. Y. Li, H. Zhu, S. Zhu, J. Wan, Z. Liu, O. Vaaland, S. Lacey, Z. Fang, H. Dai, T. Li and L. Hu, NPG Asia Mater., 2015, 7, e150.
12. J. Zhang, J. Fu, X. Song, G. Jiang, H. Zarrin, P. Xu, K. Li, A. Yu and Z. Chen, Adv. Energy Mater., 2016, 6, 1–8.
13. X. Wang, X. Wang, P. Xiao, J. Li, E. Tian, Y. Zhao and Y. Ren, Colloids Surf., A, 2016, 508, 327–335.
14. Q. Fang, X. Zhou, W. Deng, Z. Zheng and Z. Liu, Sci. Rep., 2016, 6, 1–11.
15. P. Liu, C. Zhu and A. P. Mathew, J. Hazard. Mater., 2019, 484–493.
16. L. Valencia, S. Kumar, B. Jalvo, A. Mautner, G. Salazar-Alvarez and A. P. Mathew, J. Mater. Chem. A, 2018, 6, 16361–16370.
17. S. P. Shields, V. N. Richards and W. E. Buhro, Chem. Mater., 2010, 22, 3212–3225.
18. A. C. T. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409.
19. K. Chenoweth, A. C. T. Van Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 1040–1053.
20. C. Zhu, S. Monti and A. P. Mathew, ACS Nano, 2018, 12, 7028–7038.
21. A. Lloyd, D. Cornil, A. C. T. van Duin, D. van Duin, R. Smith, S. D. Kenny, J. Cornil and D. Beljonne, Surf. Sci., 2016, 645, 67–73.
22. H. El Aribi, T. Shoeib, Y. Ling, C. F. Rodriquez, A. C. Hopkinson and K. W. M. Siu, J. Phys. Chem. A, 2002, 106, 2908–2914.
23. H. El Aribi, C. F. Rodriquez, T. Shoeib, Y. Ling, A. C. Hopkinson and K. W. M. Siu, J. Phys. Chem. A, 2002, 106, 8798–8805.
24. M. F. Russo, D. Bedrov, S. Singhai and A. C. T. van Duin, J. Phys. Chem. A, 2013, 117, 9216–9223.
25. H. J. C. Berendsen, J. P. M. Postma, W. F. Van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
26. G. Zhao, J. Li, X. Ren, C. Chen and X. Wang, Environ. Sci. Technol., 2011, 45, 10454–10462.
27. A. Y. Romanchuk, A. S. Slesarev, S. N. Kalmykov, D. V. Kosynkin and J. M. Tour, Phys. Chem. Chem. Phys., 2013, 15, 2321–2327.
28. G. Zhao, T. Wen, X. Yang, S. Yang, J. Liao, J. Hu, D. Shao and X. Wang, Dalton Trans., 2012, 41, 6182–6188.
29. R. Sitko, E. Turek, B. Zawisza, E. Malicka, E. Talik, J. Heimann, A. Gagor, B. Feist and R. Wrzalik, Dalton Trans., 2013, 42, 5682–5689.
30. I. Cerkez, H. B. Kocer, S. D. Worley, R. M. Broughton and T. S. Huang, Langmuir, 2011, 27, 4091–4097.
31. Y. Fu, S. Bai, S. Cui, D. Qiu, Z. Wang and X. Zhang, Macromolecules, 2002, 35, 9451–9458.
32. D. W. O'Connell, C. Birkinshaw and T. F. O'Dwyer, Bioresour. Technol., 2008, 99, 6709–6724.
33. H. Deng, L. Yang, G. Tao and J. Dai, J. Hazard. Mater., 2009, 166, 1514–1521.
34. H. Koerner, R. I. MacCuspie, K. Park and R. A. Vaia, Chem. Mater., 2012, 24, 981–995.
35. X. Chen, J. Schröder, S. Hauschild, S. Rosenfeldt, M. Dulle and S. Förster, Langmuir, 2015, 31, 11678–11691.
36. P. Sun, M. Zhu, K. Wang, M. Zhong, J. Wei, D. Wu, Z. Xu and H. Zhu, ACS Nano, 2013, 7, 428–437.
37. I. Persson, P. Persson, M. Sandström and A.-S. Ullström, J. Chem. Soc., Dalton Trans., 2002, 1256.
38. A. Laaksonen and H. Kovacs, Can. J. Chem., 1994, 72, 2278–2285.
39. I. Persson and K. B. Nilsson, Inorg. Chem., 2006, 45, 7428–7434.

---

Footnotes

† Electronic supplementary information (ESI) available: Fitting parameters for SAXS analysis and details regarding the model building for the computational simulations. See DOI: 10.1039/c9nr07116d

‡ Equal contribution from all authors.

---