Open Access Article
Open Access ArticleComplex oscillatory decrease with size in diffusivity of {100}-epitaxially supported 3D fcc metal nanoclusters†
King C.
Lai
 * and
James W.
Evans
* and
James W.
Evans
 *
*
Division of Chemical & Biological Sciences, Ames Laboratory, USDOE and Department of Physics & Astronomy, Iowa State University, Ames IA 50011, USA. E-mail: kclai@iastate.edu; evans@ameslab.gov
First published on 10th September 2019
Abstract
Diffusion and coalescence of supported 3D metal nanoclusters (NCs) leads to Smoluchowski Ripening (SR), a key pathway for catalyst degradation. Variation of the NC diffusion coefficient, DN, with size N (in atoms) controls SR kinetics. Traditionally, a form DN ∼ N−β was assumed consistent with mean-field analysis. However, KMC simulation of a stochastic model for diffusion of {100}-epitaxially supported fcc NCs mediated by surface diffusion reveals instead a complex oscillatory decrease of DN with N. Barriers for surface diffusion of metal atoms across and between facets, along step edges, etc., in this model are selected to accurately capture behavior for fcc metals. (This contrasts standard bond-breaking prescriptions which fail dramatically.) For strong adhesion, equilibrated NCs are truncated pyramids (TP). Local minima of DN sometimes but not always correspond to sizes, NTP, where these have a closed-shell structure. Local maxima generally correspond to N ≈ NTP + 3 for N = O(102). For weak adhesion, equilibrated NCs are truncated octahedra (TO), and local minima of DN occur for sizes close or equal to those of just a subset of closed-shell structures. Analytic characterization of energetics along the NC diffusion pathway (which involves dissolving and reforming outer layers of facets) provides fundamental insight into the behavior of DN, including the strong variation with N of the effective NC diffusion barrier.
1. Introduction
Smoluchowski Ripening (SR) involving diffusion and coalescence of supported 3D metal nanoclusters (NCs), also known as Particle Migration & Coalescence (PMC), is of central importance as a pathway for catalyst degradation.1–5 Classic studies have analyzed SR kinetics which is controlled by the size-dependence of NC diffusivity.1,2 Consequently, there has been sustained interest in the variation of the NC diffusion coefficient, DN, with size N (in atoms).2,6 The traditional perception was that DN decreases monotonically with N. This behavior is consistent with a mean-field analysis for NC diffusion mediated by uncorrelated hopping of individual atoms across the surface of the NC with single characteristic rate, h. In this scenario, each hop of a surface atom shifts the NC center of mass (CM) by δRCM ∼ a/N, where ‘a’ is the surface lattice constant. The dimensionless NC surface area, A, scales like A ∼ N2/3, and the total rate of surface atom hopping like H ∼ hA. It is convenient to set h = ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Es/(kBT)], and D° = a2ν. Here, ν is an attempt frequency, Es is the assumed single surface hopping barrier, kB is the Boltzmann constant, and T is the surface temperature. Then, the mean-field treatment predicts that
exp[−Es/(kBT)], and D° = a2ν. Here, ν is an attempt frequency, Es is the assumed single surface hopping barrier, kB is the Boltzmann constant, and T is the surface temperature. Then, the mean-field treatment predicts that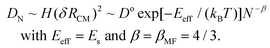 | (1) |
Our focus is on diffusion of epitaxially supported 3D NCs where diffusivity is generally lower than for non-epitaxially supported 3D NCs.6 Detailed analysis of the epitaxially supported case is limited. One Kinetic Monte Carlo (KMC) simulation study for 3D epitaxial NCs,7 and another for the analogous 2D case,8 found an oscillatory variation of DN with N, and suggested that minima correspond to sizes with closed-shell structures. However, subsequent analysis revealed a much more complex scenario for the 2D case,9,10 and no detailed analysis exists in 3D. Thus, our goal here is to characterize and provide fundamental insight into the “fine structure” in the variation of DN with N for 3D epitaxial NCs.
Specifically, we develop a stochastic lattice-gas model for diffusion of {100}-epitaxially supported metallic fcc NCs mediated by diffusive transport of metal atoms across the surface of the NC. We emphasize that for realistic modeling, not just NC thermodynamics, but also the multiple barriers for surface diffusion across facets, along step edges and around kinks or corners, between layers or facets, etc., must be chosen to realistically capture behavior for fcc metals.5,11 KMC simulation of such stochastic modeling allows direct access to the relevant time scale for surface diffusion, and precise characterization of the variation of DN with size N and other key control parameters such as temperature, T. However, for deeper insight into the observed complex behavior, we also identify NC diffusion pathways (which involve dissolving and reforming outer layers of facets). We provide an analytic assessment of the associated variation of atomistic-level NC energetics along such minimum energy pathways, as well as a corresponding coarse-grained continuum analysis.
This article is organized as follows. The stochastic model is described in the next section, as well as procedure for reliable extraction of NC diffusion coefficient, DN. Then, we present detailed KMC results for DNversus N for the case of strong NC adhesion to the substrate, as well as a complementary analytic characterization. Next, we more briefly analyze NC diffusion behavior for the case of weak NC adhesion. Finally, we provide additional Discussion including assessment of related systems, and brief Conclusions.
2. Modeling and methods
2.1. Model formulation
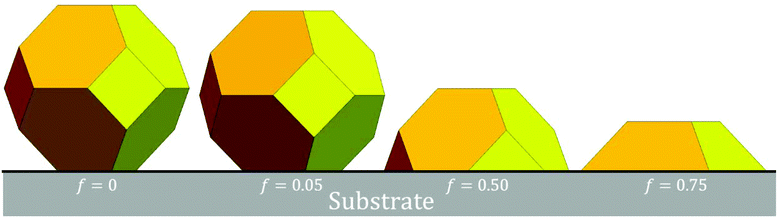
The following provides a description our realistic stochastic lattice-gas model for diffusion of {100}-epitaxially supported metallic fcc NCs. NC diffusion is mediated by diffusive transport of individual metal atoms across the surface of the NC. This surface diffusion is described by hopping of under-coordinated atoms to available nearest-neighbor (NN) fcc sites still connected to the cluster. Thus, we exclude atom detachment particularly from the contact line at the base of the NC, thereby preserving NC size.With regard to NC thermodynamics, interactions within the fcc metal NC cluster are described by an effective NN attraction of strength ϕ > 0. This prescription was shown in recent DFT analysis to effectively capture NC surface energetics for many fcc metals.12 In fact, the value of ϕ extracted from this DFT analysis reasonably recovers surface energies, but is much weaker than that extracted from bulk energetics as one sixth of the cohesive energy, Ec (e.g., ϕ = 0.225 eV versus Ec/6 = 0.49 eV for Ag).11 In fact, the bulk cohesive energy is not incorporated as a parameter into our model. This is not unreasonable since NC diffusion is controlled by surface rather than bulk thermodynamics and kinetics. Each atom in the bottom {100} NC layer is regarded as supported by 4 atoms in the top {100} substrate layer. Adhesion is described by a NN attraction of strength ϕs = fϕ between NC and substrate atoms. Thus, f measures the strength of adhesion, and f = 1 corresponds to homoepitaxy. We focus on the regime of strong adhesion choosing f = 0.75 (where supported NCs resemble truncated pyramids), but for contrast more briefly consider weak adhesion where f ≤ 0.05 (where the supported NCs resemble unsupported Wulff shapes).
The total NC energy, EN < 0, is obtained as the sum of the total interaction energy within the NC, and the total adhesion energy. Ground state NC configurations have the minimum EN. Equilibrated NCs exist in excited states with finite probability as determined by a Boltzmann factor based on EN. In the large-size continuum limit, fluctuations around a well-defined equilibrium shape vanish. For negligible adhesion (f ≈ 0), this equilibrium NC shape corresponds to the Wulff shape of an unsupported NC. For our model, the Wulff shape corresponds to a regular truncated octahedron (TO) where all edges have equal length.13 Equilibrium shapes of {100}-epitaxially supported NCs with significant adhesion are determined from the Winterbottom construction which truncates a portion of the unsupported Wulff cluster adjacent to a {100} facet.13 Specifically, in the continuum regime, when measured from the center of the unsupported Wulff cluster, the distance to the top {100} facet, h100, and to the substrate, hsub, are related by h100/γ100 = hsub/(γ100 − βad). Here, γ100 = 2ϕa−2 denotes the surface energy of {100} facets, and βad = 4ϕsa−2 denotes the adhesion energy. It follows that hsub/h100 = 1 − 2f. Negative values mean that the location of the substrate for the supported NC is above the center of the unsupported NC. See Fig. 1. In our atomistic model, equilibrium shapes mimic continuum shapes. See below.
Diffusion of supported NCs is sensitively dependent on the prescription of the kinetics of adatom surface diffusion. In stochastic lattice-gas modeling, often a simple IVA bond-breaking prescription is applied to determine the activation barriers for hopping in diverse local surface environments.14,15 However, these (and alternative Metropolis type prescriptions) fail dramatically to describe key features of surface diffusion barriers on fcc metal surfaces, e.g., the relative magnitude of terrace diffusion on different facets, of terrace versus step edge diffusion, and of intra- versus inter-layer diffusion.11 Consequently, we apply a refined BEP formalism with sufficient flexibility to capture all key diffusion barriers, as described in the next subsection.5,11
For specificity, our model parameters are chosen to correspond to Ag. Supported 3D Ag NCs have been studied on graphite,16 and on various oxide surfaces17,18 including Al2O3,19,20 TiO2,21,22 and MgO.23 Theoretical analysis indicates that Ag NC on MgO(001) exhibits cube-on-cube {100} epitaxy at least for N = 40 to 2800, rather than {111} epitaxy or a decahedral structure.24 Thus, Ag/MgO(001) falls within the class of systems described by our model.
2.2. Prescription of surface diffusion kinetics for fcc metal NCs
Realistic prescription of the surface diffusion kinetics is more challenging than that of NC thermodynamics.5,11 Rates for hopping of surface atoms to NN sites have an Arrhenius form, h = ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Eact/(kBT)], where the activation barrier, Eact, depends sensitively on the local environment (for which there are many possibilities). Again T denotes the surface temperature, and ν is a vibrational attempt frequency. (Typically, one finds that ν ≈ 1012.5 s−1 for fcc metal systems, although the value of this prefactor will not affect the results presented here.) Below Ei (Ef) denote the energies associated with an atom in the initial (final) state before (after) a NN hop. A conventional IVA bond-breaking form, Eact = E0 − Ei is typically chosen, but this fails dramatically describe fcc metal surfaces.5,11 Thus, we instead choose a generalized symmetric BEP form11Eact = Cα + ½ (Ef − Ei) with distinct Cα for different classes α of hops, e.g., α = TD {terrace diffusion + attachment/detachment at steps} and ED {step edge diffusion}, and with separate subclasses for {111} and {100} facets, and also for intra- and interlayer diffusion. Each class includes the reverse process for every forward process (e.g., detachment as the reverse of attachment to step edges) in order to satisfy detailed-balance.
exp[−Eact/(kBT)], where the activation barrier, Eact, depends sensitively on the local environment (for which there are many possibilities). Again T denotes the surface temperature, and ν is a vibrational attempt frequency. (Typically, one finds that ν ≈ 1012.5 s−1 for fcc metal systems, although the value of this prefactor will not affect the results presented here.) Below Ei (Ef) denote the energies associated with an atom in the initial (final) state before (after) a NN hop. A conventional IVA bond-breaking form, Eact = E0 − Ei is typically chosen, but this fails dramatically describe fcc metal surfaces.5,11 Thus, we instead choose a generalized symmetric BEP form11Eact = Cα + ½ (Ef − Ei) with distinct Cα for different classes α of hops, e.g., α = TD {terrace diffusion + attachment/detachment at steps} and ED {step edge diffusion}, and with separate subclasses for {111} and {100} facets, and also for intra- and interlayer diffusion. Each class includes the reverse process for every forward process (e.g., detachment as the reverse of attachment to step edges) in order to satisfy detailed-balance.
The Cα are selected to recover precise value for terrace, edge, and interlayer diffusion for the metal of interest. See the ESI sec. 1.† For Ag, we select CTD100 = 0.425 eV, CTD111 = 0.10 eV, CED111B = 0.30 eV, and CED111A = CED100 = 0.275 eV for intralayer diffusion.11 Here, A and B indicate close-packed {100}- and {111}-microfaceted steps on {111} facets, respectively. The local geometry of the former is the same as for close-packed steps on {100} facets. For interlayer diffusion for Ag, our Cα also incorporate an additional Ehrlich-Schwoebel barrier for downward interlayer diffusion of δES = 0.1 eV for close-packed (but not kinked) steps on {100} facets, and for A (but not B) steps on {111} facets. We use the same Cα for hopping between the lowest and next highest layer of the NC. For atoms at the periphery of the lowest layer hopping around the contact line of the NC: (i) the same Cα are used for strong adhesion; and (ii) Cα are selected by neglecting substrate atoms for weak adhesion. We also allow atoms to hop to second NN sites in order to round corners of the contact line base the NC.
As indicated above, our model dynamics allows diffusion of metal atoms across the NC surface, but not detachment of atoms from the NC at its base (which would be followed by diffusion across the substrate, and possible reattachment to the NC). The rationale is as follows. The effective barrier for NC surface diffusion (detachment) is determined by the sum of: (i) the energy change upon moving an atom at a kink site on the NC to a facet on the NC (to the substrate); and (ii) the terrace diffusion barrier across the facet (across the substrate). The effective barrier is significantly higher for detachment justifying our neglect of this process. See the ESI sec. 2† for further discussion.
2.3. KMC simulation of NC diffusion
KMC simulation, which implements the various hopping processes with probabilities proportional to their physical rates, allows tracking of the evolution of the configuration of the NC as it diffuses across the surface. From such simulations, one can extract the lateral position, rCM(t), of the NC center of mass (CM) at time t. Then, δrCM(δt) = rCM(t + δt) − rCM(t) gives the CM displacement in a time interval δt. One defines a time-dependent diffusion coefficient for the NC of N atoms as DN(δt) = <δrCM(δt)·δrCM(δt)>/(4δt). Generally, DN(δt) decreases from a “high” value for short δt to a plateau value as δt → ∞, which corresponds to the true diffusion coefficient, DN = limδt→∞DN(δt). The decrease in DN(δt) corresponds to subtle “back-correlations” in the walk of the cluster CM.10 Simulations readily yield extensive statistics and thus precise values for DN(δt) for small δt, but not so readily for δt = δtp sufficiently large that DN(δtp) has reached its plateau value. See ESI sec. 3.† Thus, it is necessary to run simulations for an extended total time of 200 δtp in order to precise determination NC diffusivity.Fig. 2 shows KMC simulation results for a typical diffusion trajectory for the CM of an NC of size N = 50 atoms for the case of strong adhesion with f = 0.75 at 900 K. During diffusion, the NC can be regarded as remaining in equilibrium state. However, as noted above, the NC in this state does not just correspond to a fixed ground state NC configuration, but rather samples excited states. In the ESI sec. 4,† we show snapshots which illustrate the NC evolving through a sequence of configurations during diffusion, and we also provide a movie of NC diffusion. Further discussion of key configurations accessed during diffusion is provided in sec.3 and 4. For the system under consideration here, our analysis will reveal a complex dependence of DN on size N. It will prove instructive to consider an effective activation barrier, Eeff > 0, for NC diffusion where DN ∼ exp[−Eeff/(kBT)] for fixed N at various T. In contrast to the MF treatment, Eeff = Eeff(N) will depend strongly on N, and this dependence will in fact induce the complex variation of DN with N.
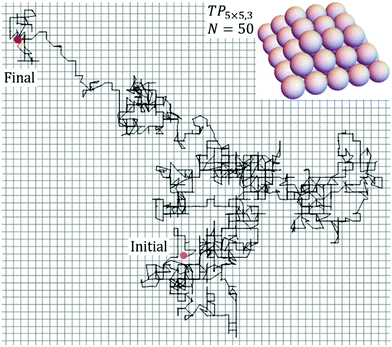 | ||
| Fig. 2 Diffusion trajectory from KMC simulation for a closed-shell Ag TP with size N = 50 for the case of strong adhesion with f = 0.75 at 900 K. | ||
3. Results for strong adhesion f = 0.75
3.1. Ground-state NC shapes with strong adhesion with f = 0.75
The adhesion energy per atom in the lowest NC layer is 4fϕ given the four supporting substrate atoms, which equals 3ϕ for f = 0.75. Thus, conveniently, the total NC energy EN is an integer multiple of ϕ. The continuum Winterbottom NC shape is a truncated square pyramid (TP) where the length of the edges of the top square {100} facet equals that of the edges between {111} side facets. See Fig. 1. For the atomistic model, ground state structures tend to mimic the continuum shape. Particularly stable ground state structures correspond to a subset of closed-shell k-layer TP with bases of m × n atoms, denoted by TPm×n,k. For these TPm×n,k structures, the total number of atoms, N = Nm×n,k, is given by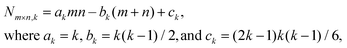 | (2) |
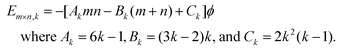 | (3) |
Ground state TPm×n,k structures have m = n square or m = n + 1 near-square bases, and also k ≤ min(n,m) − 1 so that the top layer is 2 × 2 or larger. Corresponding, ground states sizes in bold font are:
N m×n,1 = 4, 6, 9, 12 (degen.), (but not 16,…) for m × n = 2 × 2, 3 × 2, 3 × 3, 4 × 3, (but not 4 × 4,…);
N m×n,2 = 13, 18, 25, 32, 41, (but not 50,…) for m × n = 3 × 3, 4 × 3, 4 × 4, 5 × 4, 5 × 5, (but not 6 × 5,…);
N m×n,3 = 29, 38, 50, 62, 77, 92, 110, 128, 149 (degen.), (but not 170,…) for m × n = 4 × 4,…, (but not 9 × 8,…);
N m×n,4 = 54, 68, 86, 104, 126, 148, 174,… for m × n = 5 × 5,…,8 × 8,…
N m×n,5 = 135, 160,… (but not 90, or 110) for m × n = 7 × 7, 8 × 7,… (but not 6 × 6, or 7 × 6)
etc.
for single- double-, triple-, quadruple, quintuple-layer NCs, etc. The particular stability of these sizes is quantified below. Sizes are also indicated which are not ground states, and N = 12 & 149 are degenerate with higher-layer structures.
3.2. KMC results for DNversus N
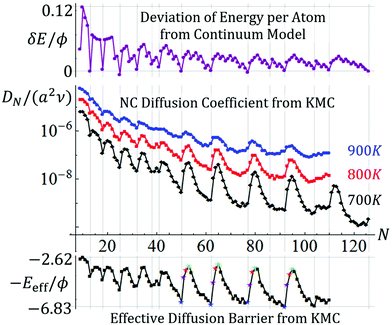
Analysis of the type of simulation data for the trajectories of {100}-epitaxially supported 3D Ag NCs for strong adhesion with f = 0.75 shown in Fig. 2 produces the results shown in Fig. 3 (middle frame) for the variation of DN with N up to N ∼ 190. Behavior for larger sizes is reported in the ESI sec. 5,† and is briefly discussed in sec. 3.5. A complex oscillatory variation is most evident at the lowest temperature shown, T = 700 K. These features are diminished by entropic effects at higher T, as shown for T = 800 K and 900 K. The vertical lines mark the sizes for the non-degenerate closed-shell ground state TPs listed above with sizes denoted N = NTP. Often, but not always, these correspond to local minima in DN. Often, local maxima in DN correspond to N = NTP + 2 or NTP + 3 in the size range shown. Closed-shell TPs are expected to be relatively stable. Indeed, a measure, δE = δEN, of the deviation from the continuum form of the energy per atom, also shown in Fig. 3 (top), correlates with the variation of DN (i.e., relatively high average coordination per atom implies relatively low diffusivity). From the variation of DN with T for fixed N, we can extract from KMC data an effective barrier, Eeff(N), for NC diffusion for each N as is also shown in Fig. 3 (bottom). It is instructive to compare Eeff for different classes of NCs where N = NTP + n for small n: Eeff(NTP + n) ≈ 1.5, 1.1, 0.85, 0.75 eV decreases as n increases from n = 0, 1, 2, and 3, respectively, as is most clearly evident for NTP = 50, 62, 77, and 92.Finally, we note that while many previous studies of NC diffusion have focused on simple size scaling, DN ∼ N−β, such a routine analysis is not applicable here given the complex oscillatory behavior. However, one could consider the partial scaling of DN with N, e.g., restricting N to local maxima (max) of DN. Based on the three maxima at N = 65, 80, and 95 in Fig. 3, one obtains βmax ≈ 3.1, 2.6, and 2.1 at 700 K, 800 K, and 900 K, respectively, which are higher than but shifting towards βMF = 1.33 for increasing T.
3.3. Mechanism & energetics for NC diffusion
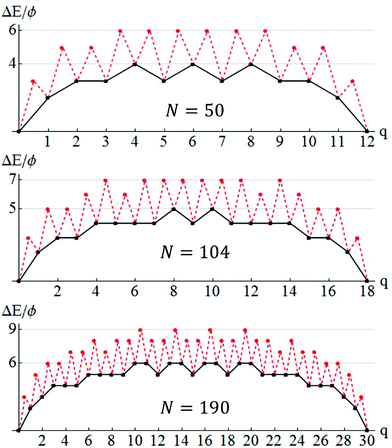
To elucidate the behavior of DN, we first describe the mechanistic pathway leading to long-range NC diffusion for the case where NC ground states are closed-shell TPs. The pathway involves dissolution of an outer layer of the NC on a single facet, transfer of those atoms to another side of the NC, and formation of a new complete outer layer on that side. Specifically, for a square n × n base, the outer layer is transferred to the opposite side. For a rectangular n × (n + 1) base, the outer layer on a short side is transferred to one of the other three sides. Atom transfer between facets generally occurs across edges between adjacent side {111} facets, rather than across the top {100} facet or around the base of the NP. The latter are kinetically inhibited by high diffusion barriers in our model (a feature which dominates the thermodynamic preference for adatoms to reside on {100} versus {111} facets). Complete transfer of an outer layer recovers the initial closed-shell ground-state structure, but with shifted CM, thereby leading to long-range NC diffusion.The above process can be quantified analytically by tracking the energy change, ΔE(q), as a function of the number, q, of atoms transferred between different sides of the NC for the minimum energy path (MEP). The MEP has the smallest ΔE(max) = maxq ΔE(q). By symmetry, ΔE(q) = ΔE(qtot − q), where qtot = k(2n − k + 1)/2 is the total number of atoms in the facet supplying atoms with base with of n atoms and height of k layers. Examples are provided in Fig. 4 (black curves) for TP5×5,3 (NTP = 50), TP7×6,4 (NTP = 104), and TP8×8,5 (NTP = 190) with ΔE(max) = 4ϕ, 5ϕ, and 6ϕ, respectively. ΔE(max) gives a measure of the difficulty of mass transfer, and thus of NC diffusion (but it does not account for the details of surface diffusion kinetics or entropic effects).
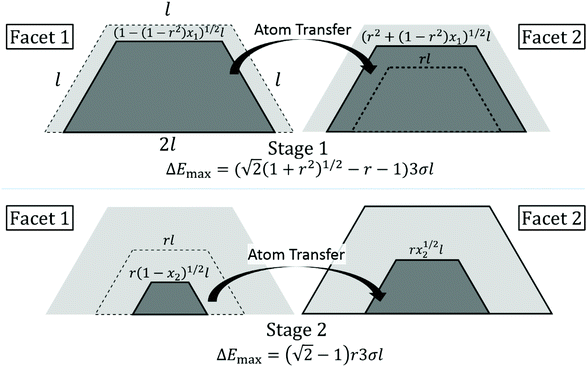
Analysis is more complex for non-closed or open-shell TPs which one generally can regard as a closed-shell TP with an additional incomplete layer on one facet. Consider the following two-stage diffusion pathway. In the first stage, atoms are transferred to complete an incomplete 2D layer on a facet labeled 2 from a complete facet labeled 1 on the opposite side. In the second stage, the incomplete layer now existing on facet 1 is transferred to facet 2. Then, the original NC structure is recovered, but with shifted CM. ΔE(q) versus q has a different form in each stage, but vanishes at the end of each stage. See below. Other cases involve shifting the incomplete layer to an adjacent (rather than the opposite) side facet. Even more complicated scenarios can occur in some cases where the ground state NC structure is k-layer, but the diffusion path with the lowest ΔE(max) goes through a (k − 1)-layer NC configurations. One example is for N = 66 where the ground state is a 4-layer structure, but the optimum diffusion pathway goes through 3-layer structures. See ESI sec. 6.†
Fig. 5 provides comprehensive analytic results for ΔE(max) versus N up to N = 110 for both open- and closed-shell TPs. ΔE(max) for closed-shell TPs correspond to local maxima, and the ΔE(max) variation with N correlates reasonably with that of DN. Fig. 5 also indicates a slow increase in ΔE(max) with N, somewhat obscured by the strong oscillatory behavior. This feature will be elucidated below. ΔE(max) just characterizes the thermodynamics rather than the kinetics of the NC diffusion process.
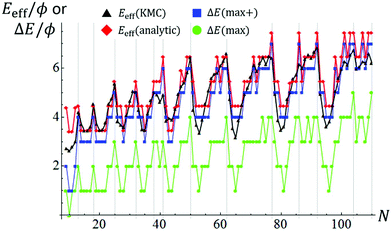 | ||
| Fig. 5 Variation of ΔE(max), ΔE(max+), Eeff(analytic), and Eeff(KMC) with N. Vertical lines indicate sizes for closed-shell ground state TPs. | ||
To assess kinetics, we note that ΔE(q) just describe energies relative to the ground state after each transfer of an adatom between facets and incorporation into a growing 2D layer. Thus, naturally the system energy is higher mid-atom transfer, and thus the actual energy barrier which the system must surmount for NC diffusion is higher. For large NCs, the increased barrier will reflect energy difference of 3ϕ between an isolated atom in transit at a 3fh site on a {111} facet and that atom incorporated into a kink site at the periphery of an incomplete layer. However, for smaller NCs, this energy difference is often 2ϕ. Fig. 4 also shows the energy profile along the MEP incorporating energies mid-atom transfer as a dashed red line, and Fig. 5 also shows the corresponding boosted ΔE(max+) versus N. Finally, the actual effective barrier for Eeff for the above process must add a diffusion barrier which is typically but not always equal to that for terrace diffusion on {111} facets of 0.1 eV for Ag. This analytic estimate of Eeff(analytic) versus N is also shown in Fig. 5. Again we caution that this analysis does not account for entropic effects. The analytic treatment is successful in capturing the key features of our KMC estimate, Eeff(KMC) (reproduced from Fig. 2).
3.4. Continuum analysis of energetics
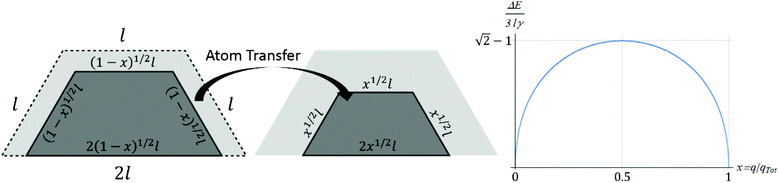
Fig. 5 indicates a slow increase in ΔE(max) with N, somewhat obscured by the strong oscillatory behavior. To elucidate this trend, and the variation of ΔE(q) with q, it is instructive to perform a continuum analyses for behavior in the large NC size regime. For a closed-shell (CS) TP, Fig. 6 shows schematically the process of transferring atoms from an initially complete outer layer on one facet to another facet. One issue is the shape of 2D island constituting the incomplete layer. This island is bounded by close-packed step edges on the sides and top as shown in Fig. 6, and these have the same step energy σ = ϕ/a. For our model with f = 0.75, the higher coordination of atoms on the bottom step at the contact line with substrate atoms dominates the weaker binding strength to those atoms resulting in a vanishing effective step energy. See ESI sec. 7.† With these step energies, minimization of total 2D island step energy for fixed island area reveals that the minimum energy shape has equal length step edges on the sides and top, and double that length on the bottom. Thus, the equilibrium 2D island shape is identical to the overall side facet shape of the TP. Given this island shape, it is straightforward to determine the change in system energy,| ΔE(x)|CS = 3σl[(1 − x)1/2 + x1/2 − 1] with x = q/qtot, | (4) |
| ΔE(max)|CS = (√2 − 1)3σl ≈ 1.24σl ∼ N1/3, | (5) |
Next, we more briefly present a continuum treatment for open-shell (OS) TPs. As discussed above, the mechanism for mass transfer leading to NC diffusion has two stages. First, atoms are transferred from a complete facet 1 to grow an initially incomplete layer on facet 2 (which becomes complete). Second, the incomplete layer remaining on facet 1 is transferred to facet 2. Fig. 7 shows the case where the dimensions of the initial incomplete layer are smaller by a factor of r than those of the complete facet. Here, x1 (x2) denotes the fraction of atoms transferred in the first (second) stage. Evaluating the energy change as a function of the amount of material transferred (see ESI sec. 8†), one finds that ΔE(max1)|OS = [√2(1 + r2)1/2 − r − 1]3σl in the first stage, and ΔE(max2)|OS = 3(√2 − 1)rσl in the second. The effective barrier ΔE(max)|OS = maxj ΔE(maxj)|OS for the open-shell TP is below ΔE(max)|CS for a closed-shell TP for all 0 < r < 1, consistent with the lower ΔE(max) for open-shell TPs shown in Fig. 5. The smallest value of ΔE(max)|OS = 3(√2 − 1)σl/(2√2) ≈ 0.439σl occurs for r = 1/(2√2) ≈ 0.354.
3.5. Local minima and maxima of DN
As noted in sec. 1, a general expectation in previous studies7,8 both for 2D and 3D epitaxially supported NCs is that NCs with closed-shell ground state correspond to local minima in diffusivity. However, this expectation is not realized in 2D,9,10 and needs critical assessment in 3D. The above analysis of energetics 3D {100}-epitaxially supported Ag NCs shows that generally closed-shell ground state TPs correspond to local maxima in ΔE(max) and related quantities, at least for smaller N. This feature is compatible with local minima in DN occurring for these sizes N = NTP. Nonetheless, our precise KMC results for DN in Fig. 2 reveal that local minima in DN can occur for sizes other than N = NTP. Specifically, these sizes include N = NTP − 1 and NTP − 3 (at least for larger NTP). To explain this behavior, note that for NTP = 104, 110 or 126, Eeff(analytic) actually has the same local maximum value for N = NTP and NTP − 1. Also, if Ω0 denotes the ground state degeneracy, then one has Ω0 = 1 for N = NTP with a square base versus Ω0 = 8 for N = NTP − 1. Finally, let ΩTS denote the degeneracy in the transition state at q ≈ qtot/2 where half a complete layer has been transferred from one side of the NC to another. Then, based upon the heuristic estimate25DN ∼ (ΩTS/Ω0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Eeff(analytic)/(kBT)], exp[−Eeff(analytic)/(kBT)], | (6) |
As noted above, local maxima in DN tend to occur for N = NTP + 3 for larger sizes with N = O(102). Consistently, Eeff displays a local minima for these sizes corresponding to local minimum in ΔE(max) for NTP + 3 or NTP + 4. For these sizes, the ground state corresponds to a small 2D cluster of 1, 2, 3,… atoms on a facet of a closed-shell TP. The presence of this small 2D cluster naturally facilitates initial transfer of atoms from another complete side of the NC, thereby reducing ΔE(q), ΔE(max), and related quantities.
Finally, we briefly comment of behavior of DN for larger sizes, which is reported in the ESI sec. 5.† The basic features observed in the smaller size range up to N ≈ 190 are preserved, i.e., complex oscillatory decay of DNversus N. However, it should be noted that local minima in DN do not occur for all sizes with closed-shell ground states, but only at or near a subset of these. A similar feature is manifested for the case of weak adhesion described in sec. 4. An effective criterion to assess the subset of closed-shell sizes corresponding to local minima in DN is again provided by (the occurrence of local minima in) the readily calculated quantity δE. See ESI sec. 5.†
4. Results for weak adhesion f ≤ 0.05
4.1. Ground-state NC shapes with weak adhesion where f ≈ 0
The Winterbottom shapes for smaller sizes N = O(102) when f ≈ 0 will roughly correspond to that of unsupported Wulff clusters. For certain sizes, these correspond to closed-shell Truncated Octahedra (TO) bounded by {111} and {100} facets. Let n111 (n100) denote the number of atoms on edges between adjacent {111} facet pairs (adjacent {111} and {100} facets). Then, the symmetric regular TO where n111 = n100 = n with “magic” sizes26| NTO(n) = 16n3 − 33n2 + 24n − 6 = 38, 201, 586,… for n = 2, 3, 4,… | (7) |
| NTO+(n) = 16n3 − 63n2 + 84n − 38 = 79, 314, 807,… for n = 3, 4, 5,… | (8) |
A recent analysis revealed 49 additional sizes of various asymmetric closed-shell TO (including TO+) between each consecutive pair of magic regular TO sizes, which are also relatively stable compared to non-closed-shell structures.28 For each of these sizes between NTO = 38 and 201, there is a corresponding size between NTO = 201 and 586, etc., so structures repeat quasi-periodically. For example, the closed-shell structure for N = 244 corresponds to that for N = 52; the N = 314 TO+ corresponds to the N = 79 TO+.
Excitation of a closed-shell structure by moving a corner atom to a {111} ({100}) facet increases the energy by Eex = 3ϕ (2ϕ). Given the restricted number, M, of adsorption sites on facets for the NC sizes considered here, it follows that exp[−Eex/(kBT)]M ≪ 1 so the ground state structure predominates for 700 K.
4.2. KMC results for DNversus N
Next, we describe briefly analysis of diffusion of supported NCs with weak adhesion corresponding to f ≤ 0.05. Fig. 8 (middle frame) shows the variation of DN with N for {100}-epitaxially supported 3D Ag NCs at T = 700 K for weak adhesion with f = 0.05 (and with f = 0 where the NC is constrained to be attached to the substrate). A complex oscillatory variation is evident. The vertical lines mark the sizes for the symmetric TO and TO+ listed in sec. 3, as well as all other less symmetric ground state closed-shell TO. Sizes associated with (or sometimes close to) symmetric regular TO and to TO+ correspond to strong local minima in DN, and sizes close to a restricted subset of the other closed-shell ground state TO correspond to less prominent local minima. For sizes associated with these minima, the closed-shell TOs are relatively stable. A measure, δEN, of the relative energy per atom, also shown in Fig. 8 (top), correlates reasonably with the variation of DN with N.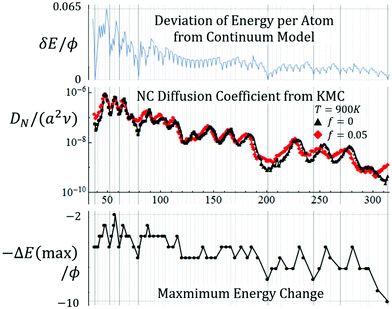 | ||
| Fig. 8 Top: δE = [EN − EN(cont)]/N where28EN(cont)/ϕ = −1.59 + 0.061N1/3 + 7.554N2/3 − 6N recovers EN for regular TO with N = 38, 201, 586, and 1289. Middle: KMC results for DNversus N for an Ag TO at 700 K for f = 0.05 (black) and f = 0 (red). Bottom: Analytic results for −ΔE(max)/ϕ, where the negative sign is included so that peaks and valleys correspond to those of DN. Note: vertical lines correspond to sizes for closed-shell structures, with those for TO, TO+, and other particularly stable structures, indicated as thicker lines. | ||
4.3. Mechanism & energetics for NC diffusion and continuum analysis
To elucidate the behavior of DN, we first discuss the mechanistic pathway for long-range NC diffusion where ground states are closed-shell regular TOs. One pathway involves dissolution of the outer layer of two vertical {100} facets (on the left and center in Fig. 1) and two {111} facets (on the left in Fig. 1), transfer of those atoms around the NC surface, and formation of a new complete outer layer on the other two vertical {100} facets and on the two {111} facets on the opposite side from those donating atoms. (There are four other {111} facets which remain largely unchanged.) Clearly, this process is more complex than that described for diffusion of closed-shell TP with f = 0.75. Nonetheless, analytical quantification is still possible tracking the energy change, ΔE(q), as a function of the number, q, of atoms transferred along the MEP. By symmetry for regular TO, ΔE(q) = ΔE(qtot − q), where qtot is the total number of atoms transferred. The maximum value, ΔE(max), of ΔE(q), again gives a measure of the difficulty of the process (not accounting for the details of surface diffusion kinetics or entropic effects).The additional challenge here compared to the analysis for TP with f = 0.75 is the variety of possibilities for transferring atoms which must be considered to determine the MEP and ΔE(max). The general principle, as for f = 0.75, is to select atoms to transfer which break the minimum number of bonds and to arrange them on the receiving facet to create the maximum number of bonds. As an example, for NTO = 38, one removes atoms from a {111} then a {100} then a {111} and finally a {100} facet, and builds up layers in the reverse sequence (first on a {100} facet, etc.) to obtain ΔE(max) = 5ϕ. See ESI sec. 10† for further discussion and detailed analysis for NTO = 201.
For the less symmetric closed-shell TO, {100} facets generally have multiple different sizes and shapes. In this case, a separate analysis of ΔE(q) is performed for each possible type of supporting facet. The minimum ΔE(max) from these different possibilities is selected. Results from extensive analysis of ΔE(max) for regular and less symmetric closed-shell ground state TO are reported in Fig. 8 (lower frame).
We do not present a detailed continuum analysis here. However, from the formalism presented for f = 0.75, it is clear that irrespective of the detailed pathway for atom transfer, one has that ΔE(max) ∝ ϕl/a ∼ N1/3. This slow increase in ΔE(max) with N is reflected in Fig. 8 (bottom), again somewhat hidden by oscillatory structure.
4.4. Local maxima and minima of DN
Regular TO for N = 38, 201, etc. and TO+ for N = 79, 314, etc., are well recognized as being particularly stable, so it is not surprising that DN has prominent local minima reflecting these sizes. However, the prominent oscillatory structure of DN is not determined by TO and TO+ alone, but by augmenting these with a subset of less symmetric closed-shell ground state TO. These less symmetric closed-shell TO still have enhanced stability measured by prominent local minima in δE, and prominent local maxima in ΔE(max), relative to nearby closed-shell TO. Examples include N = 52 and 244 which correspond to “elongated” TO, and N = 61 and 269 which have a slab-like structure with 3-fold symmetry. See ESI sec. 11.† The variation in DN repeats quasi-periodically matching the repeat of closed-shell ground states described above between each pair of magic sizes. Thus, prominent minima at N = 38, 52, 61, and 79 are repeated at N = 201, 244, 269, and 314, respectively. Prominent local maxima in DN often correspond to inhibited stability as measured by δE, and somewhat more prominent local minima in ΔE(max). These also repeat quasi-periodically.5. Discussion
Complex oscillatory decay of diffusivity, DN, with N is evident in the above analyses for both strong and weak adhesion. In fact, this behavior applies more generally. We have also considered moderate adhesion with f = 0.5 where the continuum Winterbottom shape of supported NC corresponds to half of a Wulff cluster. See Fig. 1. Closed-shell ground state structures for f = 0.5 in the atomistic model up to N = O(102) sometimes correspond to TP, and sometimes to TP with lower corner atoms removed. KMC reveals oscillatory decay of DN. Local minima do not always correspond to closed-shell ground states. Here, we find that ΔE(max) and Eeff exhibit “flat” local maxima corresponding several consecutive N (rather than maxima just occurring just at isolated sizes with close-shell ground states), explaining why open-shell structures can have the lowest DN. On the other hand, local minima in ΔE(max) and Eeff often occur for a single N, or consecutive pair of N, and correspond to local maxima in DN. See ESI sec. 12.† In addition, we assess behavior for smaller f = 0.17 corresponding to the relatively weak adhesion of Ag NCs on MgO(001).18 In this case, the oscillatory decay of DN with N is similar to that found for f ≤ 0.05. See ESI sec. 13.†The observed oscillatory decay of DN with N appears in marked contrast to the traditional picture of algebraic scaling DN ∼ D°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Eeff/(kBT)]N−β, where mean-field analysis gives that Eeff is size-independent, and βMF = 4/3. In fact, our analysis shows that the effective barrier for diffusion has a strong oscillatory size dependence, with an overall increase with N like Eeff ∼ N1/3. This corresponds to faster than algebraic asymptotic decay of DN for large N. Analogous observations have been made for NC reshaping.14,29 Despite this feature, we have shown that for strong adhesion, f = 0.75, an effective β can be reasonably extracted from selected peaks of DN (for a fixed range of sizes). Reported results show this βeff decreasing from 3.1 at 700 K to 2.1 at 900 K. Furthermore, oscillations in DN disappear for sufficiently high T, and classic mean-field scaling βeff → 4/3 of DN is recovered. This behavior can be understood given that the structure of supported NCs become less facetted and more irregular with a randomly rough surface as T increases. In this regime, surface hopping becomes uncorrelated as assumed in the mean-field analysis. This type of recovery of mean-field behavior for increasing T is a general phenomenon applying for any adhesion strength.
exp[−Eeff/(kBT)]N−β, where mean-field analysis gives that Eeff is size-independent, and βMF = 4/3. In fact, our analysis shows that the effective barrier for diffusion has a strong oscillatory size dependence, with an overall increase with N like Eeff ∼ N1/3. This corresponds to faster than algebraic asymptotic decay of DN for large N. Analogous observations have been made for NC reshaping.14,29 Despite this feature, we have shown that for strong adhesion, f = 0.75, an effective β can be reasonably extracted from selected peaks of DN (for a fixed range of sizes). Reported results show this βeff decreasing from 3.1 at 700 K to 2.1 at 900 K. Furthermore, oscillations in DN disappear for sufficiently high T, and classic mean-field scaling βeff → 4/3 of DN is recovered. This behavior can be understood given that the structure of supported NCs become less facetted and more irregular with a randomly rough surface as T increases. In this regime, surface hopping becomes uncorrelated as assumed in the mean-field analysis. This type of recovery of mean-field behavior for increasing T is a general phenomenon applying for any adhesion strength.
As an aside, for diffusion of 2D epitaxial NCs, mean-field scaling is recovered asymptotically as N → ∞ for any T (not just as T → ∞). This fundamental difference arises from the feature that 2D NCs, in contrast to 3D NCs, are not facetted in the large-N continuum regime.
One could consider {111}- rather than {100}-epitaxially supported 3D fcc metal NC. Now, each atom in the lowest layer is regarded as supported by three atoms in the substrate, again with an effective NN substrate-NC atom attraction of ϕs = fϕ. Then, the distance to the top {111} facet, h111, and to the substrate, hsub, are related by hsub/h111 = 1 − 2f. By analogy with f = 0.75 for the {100}-supported case, the Winterbottom shape for f = 2/3 is a truncated hexagonal pyramid where the edge length for the top hexagonal {111} facet matches that of the edges between the six alternating {100} and {111} side facets. For f ≈ 0, the equilibrium shape is a Wulff TO, now supported on a {111} facet. Behavior of diffusivity in these cases is analogous to that for {100}-supported NCs with complex oscillatory decay in DNversus N, and where again detailed insight comes from an atomistic-level analysis of energetics along the MEP or from a continuum analysis.
Finally, some additional comments are appropriate on T-dependence of DN, and in particular on the disappearance of oscillations for high T. Oscillatory structure relies on the distinction between closed-shell and other NC structures. For sufficiently low T, NCs with closed-shell ground states will most likely be found in those configurations as discussed above accounting for excited-state Boltzmann factors and configurational degeneracy. However, for high T, the NC will most likely be in a non-closed-shell excited state. This type of entropic effect diminishes distinction between open- and closed-shells, and thus degrades the oscillatory fine structure of DNversus N.
6. Conclusions
Our KMC simulation analysis of the diffusion of epitaxial supported 3D NCs reveals a ubiquitous oscillatory decay of DNversus N. This behavior is in marked contrast to the traditional picture of algebraic decay, DN ∼ N−β. While KMC simulation precisely quantifies DN, it does not necessarily offer fundamental insight into the origin of behavior. However, such insight is provided by our identification of the mechanistic pathway for NC diffusion, i.e., facet dissolution and reformation, together with a comprehensive analytical characterization of the energetics along the minimum energy pathway (MEP) for this process. A coarse-grained continuum analysis of MEP energetics provides additional insight, particularly regarding the increase in the effective barrier for NC diffusion with size.For diffusion of either supported 2D or 3D epitaxial NCs exhibiting oscillatory decay, it is natural to anticipate that local minima correspond to sizes with closed-shell NC ground state structures with sizes N = NCS.7,8 Our analysis does reveal some correlation between local minima in DN and closed-shell structures. However, for strong adhesion, we find local minima for sizes N = NCS − 1 and NCS − 3 and explain this feature as due to higher ground state degeneracy for these sizes relative to closed-shell NCs. For moderate and weak adhesion, local minima only correlate strongly with a subset of closed-shell structures. Thus, a comprehensive and fundamental understanding of the fine structure of DNversus N necessarily requires the type of analytic characterization of energetics along MEP for diffusion provided here.
Finally, we remark that our results for DNversus N can provide input to analysis of SR kinetics of distributions of supported NCs. We have noted the importance of this process for catalyst degradation. However, it might also be noted that under reaction conditions, adsorption of reactants on the NC surface can alter both NC surface thermodynamics and diffusion kinetics, and thus NC diffusivity. Nonetheless, the current study of NC diffusion in a vacuum environment is a valuable precursor to understanding of such behavior in more complex environments.
Conflicts of interest
There are no conflicts of interest.Acknowledgements
We thank Alex Travesset for discussions on TO, TO+ and related structures for unsupported NCs. This work was supported by the U.S. Department of Energy (USDOE), Office of Science, Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences through the Ames Laboratory Chemical Physics program. The work was performed at Ames Laboratory which is operated for the USDOE by Iowa State University (ISU) under Contract No. DE-AC02-07CH11358.Notes and references
- E. Ruckenstein and B. Pulvermacher, Kinetics of Crystallite Sintering during Heat Treatment of Supported Metal Catalysts, AIChE J., 1973, 19, 356–364 CrossRef CAS.
- P. Wynblatt and N. A. Gjostein, Supported Metal Crystallites, Prog. Solid State Chem., 1975, 9, 21–58 CrossRef CAS.
- T. W. Hansen, A. T. DeLaRiva, S. R. Challa and A. K. Datye, Sintering of Catalytic Nanoparticles: Particle Migration or Ostwald Ripening?, Acc. Chem. Res., 2013, 46, 1720–1730 CrossRef CAS PubMed.
- Y. Dai, P. Lu, Z. Cao, C. T. Campbell and Y. Xia, The Physical Chemistry and Materials Science behind Sinter-resistant Catalysts, Chem. Soc. Rev., 2018, 47, 4314–4331 RSC.
- K. C. Lai, Y. Han, P. Spurgeon, W. Huang, P. A. Thiel, D.-J. Liu and J. W. Evans, Reshaping, Intermixing, and Coarsening for Metallic Nanocrystals: Non-equilibrium Statistical Mechanical and Coarse-grained Modeling, Chem. Rev., 2019, 119, 6670–6768 CrossRef CAS PubMed.
- P. Jensen, Growth of Nanostructures by Cluster Deposition: Experiments and Simple Models, Rev. Mod. Phys., 1999, 71, 1695–1735 CrossRef CAS.
- L. Li, P. N. Plessow, M. Rieger, S. Sauer, R. S. Sánchez-Carrera, A. Schaefer and F. Abild-Pedersen, Modeling the Migration of Platinum Nanoparticles on Surfaces using a Kinetic Monte Carlo Approach, J. Phys. Chem. C, 2017, 121, 4261–4269 CrossRef CAS.
- J. Heinonen, I. Koponen, J. Merikoski and T. Ala-Nissila, Island Diffusion on Metal fcc (100) Surfaces, Phys. Rev. Lett., 1999, 82, 2733–2736 CrossRef CAS.
- K. C. Lai, J. W. Evans and D.-J. Liu, Communication: Diverse Nanoscale Cluster Dynamics: Diffusion of 2D Epitaxial Clusters, J. Chem. Phys., 2017, 147, 201101 CrossRef PubMed.
- K. C. Lai, D.-J. Liu and J. W. Evans, Diffusion of 2D Epitaxial Clusters on Metal(100) Surfaces: Facile versus Nucleation-mediated Behavior and their Merging for Larger Sizes, Phys. Rev. B, 2017, 96, 235406 CrossRef.
- K. C. Lai and J. W. Evans, Reshaping and Sintering of 3D fcc metal Nanoclusters: Stochastic Atomistic Modeling with a Realistic Surface Diffusion Kinetics, Phys. Rev. Mater., 2019, 3, 026001 CrossRef CAS.
- L. T. Roling, L. Li and F. Abild-Pedersen, Configurational Energies of Nanoparticles Based on Metal−Metal Coordination, J. Phys. Chem. C, 2017, 121, 23002–23010 CrossRef CAS.
- C. R. Henry, Morphology of Supported Nanoparticles, Prog. Surf. Sci., 2005, 80, 92–116 CrossRef CAS.
- N. Combe, P. Jensen and A. Pimpinelli, Changing Shapes in the Nanoworld, Phys. Rev. Lett., 2000, 85, 110–113 CrossRef CAS PubMed.
- T. H. Lim, D. McCarthy, S. C. Hendy, K. J. Stevens, S. A. Brown and R. D. Tilley, Real-Time TEM and Kinetic Monte Carlo Studies of the Coalescence of Decahedral Gold Nanoparticles, ACS Nano, 2009, 3, 3809–3813 CrossRef CAS PubMed.
- I. M. Goldby, L. Kuipers, B. Issendorff and R. E. Palmer, Diffusion and Aggregation of Size-selected Silver Clusters on a Graphite Surface, Appl. Phys. Lett., 1996, 69, 2819–2821 CrossRef CAS.
- M. Chen and D. W. Goodman, Oxide-supported Metal Clusters, in Chemical Physics of Solid Surfaces, Elsevier, Amsterdam, 2007, ch. 5, vol. 12 Search PubMed.
- S. L. Hemmingson and C. T. Campbell, Trends in Adhesion Energies of Metal Nanoparticles on Oxide Surfaces: Understanding Support Effects in Catalysis and Nanotechnology, ACS Nano, 2017, 11, 1196–1203 CrossRef CAS PubMed.
- N. Nilius, N. Ernst and H.-J. Freund, Photon Emission Spectroscopy of Individual Oxide-Supported Silver Clusters in a Scanning Tunneling Microscope, Phys. Rev. Lett., 2000, 84, 3994–3997 CrossRef CAS PubMed.
- W. Benten, N. Nilius, N. Ernst and H. J. Freund, Photon Emission Spectroscopy of Single Oxide-Supported Ag-Au Alloy Clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045403 CrossRef.
- D. A. Chen, M. C. Bartelt, S. M. Seutter and K. F. McCarty, Small, Uniform, and Thermally Stable Silver Particles on TiO2(110)-(1×1), Surf. Sci., 2000, 464, L708–L714 CrossRef CAS.
- K. Luo, T. P. St. Clair, X. Lai and D. W. Goodman, Silver Growth on TiO2(110) (1×1) and (1×2), J. Phys. Chem. B, 2000, 104, 143050–143057 Search PubMed.
- J. H. Larsen, J. T. Ranney, D. E. Starr, J. E. Musgrove and C. T. Campbell, Adsorption Energetics of Ag on MgO(100), Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 195410 CrossRef.
- R. Ferrando, G. Rossi, A. C. Levi, Z. Kuntová, F. Nita, A. Jelea, C. Mottet, G. Barcaro, A. Fortunelli and J. Goniakowski, Structures of Metal Nanoparticles Adsorbed on MgO(001). I. Ag and Au, J. Chem. Phys., 2009, 130, 174702 CrossRef PubMed.
- New Trends in Kramer's Reaction Rate Theory, ed. P. Talkner and P. Hanggi, Kluwer, Dordrecht, 1995 Search PubMed.
- D. Wales, Energy Landscapes, Cambridge University Press, Cambridge, 2003 Search PubMed.
- R. L. Whetten, J. T. Khoury, M. M. Alvarez, S. Murthy, I. Vezmar, Z. L. Wang, P. W. Stephens, C. L. Cleveland, W. D. Luedtke and U. Landman, Nanocrystal Gold Molecules, Adv. Mater., 1996, 8, 428–433 CrossRef CAS.
- K. C. Lai, X. Zha, J. W. Evans and A. Travesset, Structure of Polydisperse fcc Nanocrystals: Implications for Crystal Fractionalization, J. Phys. Chem. C, 2019, 123, 9528–9537 CrossRef CAS.
- W. W. Mullins and G. S. Rohrer, Nucleation Barrier for Volume-Conserving Shape Changes of Faceted Crystals, J. Am. Ceram. Soc., 2000, 83, 214–216 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr05845a |
| This journal is © The Royal Society of Chemistry 2019 |