Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Heat generation by branched Au/Pd nanocrystals: influence of morphology and composition†
Marta
Quintanilla
 ab,
Christian
Kuttner
ab,
Christian
Kuttner
 a,
Joshua D.
Smith
c,
Andreas
Seifert
a,
Joshua D.
Smith
c,
Andreas
Seifert
 de,
Sara E.
Skrabalak
de,
Sara E.
Skrabalak
 *c and
Luis M.
Liz-Marzán
*c and
Luis M.
Liz-Marzán
 *ae
*ae
aCIC biomaGUNE and CIBER-BBN, Paseo Miramón 182, 20014 Donostia-San Sebastián, Spain. E-mail: llizmarzan@cicbiomagune.es
bMaterials Physics Department, Facultad de Ciencias, Universidad Autónoma de Madrid, 28049 Madrid, Spain
cDepartment of Chemistry, Indiana University, Bloomington, Indiana 47405, USA. E-mail: sskrabal@indiana.edu
dCIC nanoGUNE, Avda. Tolosa 76, 20018 Donostia-San Sebastián, Spain
eIkerbasque, Basque Foundation of Science, 48013 Bilbao, Spain
First published on 4th October 2019
Abstract
Bimetallic gold–palladium particles were originally proposed as catalysts with tunable reaction rates. Following the development of synthesis routes that offer better control on the morphology and composition of the particles, novel optical sensing functionalities were more recently proposed. Since temperature is a fundamental parameter that interplays with every other proposed application, we studied the light-to-heat conversion ability of Au/Pd bimetallic nanoparticles with a regular octapodal shape. Both compositional (Au-to-Pd ratio) and structural (diagonal tip-to-tip distance and tip width) characteristics were screened and found to be essential control parameters to promote light absorption and efficient conversion into heat. Electromagnetic simulations reveal that the Pd content, and specifically its distribution inside the branched particle geometry, has a profound impact on the optical properties and is an essential criterion for efficient heating. Notably, the optical and photothermal responses are shown to remain stable throughout extended illumination, with no noticeable structural changes to the branched nanocrystals due to heat generation.
Introduction
The microscopic characteristics of a material, such as lattice parameters or the presence of defects, are fundamentally connected to its physicochemical properties. In the case of palladium, when a thin layer is epitaxially grown on top of a different metal, the spacing of its first-neighbour atoms is modified, triggering changes in the position and overlap of the materials’ d-orbitals and, thus, the electronic properties of the surface. Given that palladium is often used as a catalyst, this ability to change the electronic structure of surfaces opens up a path to create materials with tuned reaction rates, using either macroscale1 or nanoscale structures.2–5 Nanocatalysts have gained particular attention as they open the possibility of triggering reactions in remote locations. This is the case, for instance, for tumour tissues, where they can be used to initiate pathological effects. Indeed, a range of techniques based on localized catalysis have been proposed as possible intratumoral therapies, including chemodynamic therapy, gas therapy or tumour-starving therapy, to cite some.6The interest on the synthesis of colloidal bimetallic structures is further supported by the added functionalities that nanometre sizes bring. Specifically, gold-rich nanocrystals may also present plasmonic resonances that can be exploited for optical applications, such as sensors based on refractive index modifications or on surface-enhanced Raman spectroscopy.7,8 Just as the catalytic activity of the colloids depends on their size and shape (i.e., facet expression), the plasmonic properties of colloids are also linked to these parameters. In fact, their resonance wavelengths are closely linked to such structural parameters and can be tuned within the visible and the near-infrared range.9 Also, the character of the plasmonic mode, i.e., to what extent it is due to scattering or absorption, depends on particle geometry and composition, and so do the possible functionalities of the resulting material. Particularly, while elastic scattering (Sca) can affect the density of phonon or photon states of surrounding molecules, eventually leading to the enhancement of their luminescent or Raman signals,10,11 absorption (Abs) is linked to the particles heating characteristics.12–14 As a consequence, synthetic routes that allow tuning the size and shape of bimetallic structures, LSPR position, and Abs/Sca ratio, gain relevance.15
Theoretical studies have demonstrated that in a nanoparticle only the fraction of material close to the surface efficiently contributes to heating, whereas the inner fraction hardly does. Accordingly, the most advantageous geometries for heating are those with flat features, small size or long and sharp structures. Besides, smaller structures also present weaker scattering.16 In the case of gold nanoparticles, branched geometries have been particularly exploited for sensing and photothermal applications, given the fact that their many thin branches are optimal both for electromagnetic field enhancement, often applied to SERS,17 and light-to-heat conversion.18 However, stellated structures often suffer from reshaping, i.e., migration of weakly bonded atoms from the tips of the branches (high convex curvature) to the branches base (concave curvature). Accordingly, the geometry of the particles evolves to higher sphericity, and thus to lower Gibbs energy.19 Such a reshaping can be critical for applications based on plasmonic properties, as not only the strength of the plasmon mode, but also the main resonance wavelength will be affected.20,21
Related geometries have also been studied in the case of branched gold–palladium structures, showing lower SERS enhancement ratios than pure gold, but substantially increased thermal stability.22 Indeed, reshaping of branched gold–palladium particles with Oh symmetry, also known as octopods, is only observed above ≈450 °C in vacuum, while analogous all-gold octopods start reshaping already at 200 °C under the same environment. Reshaping, though, depends on the environment, as the thermal threshold shifts to lower temperatures in air.22 As a consequence, Au/Pd nanoparticles may become interesting candidates for applications that require performing in harsh atmospheres, at high temperatures, or during long times. Specifically, the modification of local temperature is key in photocatalytic applications, as temperature is intimately linked to the rate of chemical reactions.
Motivated by these findings, and under the idea that nanomaterials with catalytic and heating properties may lead to local control of chemical reactions,23 we investigate the light-to-heat conversion abilities of stellated gold–palladium structures dispersed in aqueous media. Although a variety of structures could have been selected for this study, the thermal stability, high symmetry, and single-crystallinity (i.e., without grain boundaries or planar defects that serve as sites for phonon scattering) of these particles render them good candidates for a study that combines experiment and simulation, allowing a clear correlation of observations. Accordingly, we aim at understanding the effects of shape and composition (Pd content and its distribution) on the heat generation of the prepared nanoparticles, so nanoscale control of optical heating can be achieved. Our results find the nanocrystals to be stable photothermal heaters, with heating efficiencies between ≈40% and ≈60%, this value being largely related to their size and palladium content.
Experimental
Materials and synthetic approach
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm/12
000 rpm/12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g) for 15 min, removed from supernatant and diluted to a volume of 3 mL with water for subsequent use.
000g) for 15 min, removed from supernatant and diluted to a volume of 3 mL with water for subsequent use.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm/12
000 rpm/12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g) for 15 min, removed from supernatant and dispersed in 1 mL of water. A summary of specific reagent volumes per sample is provided in Table S1† and correspond with those in Table 1.
000g) for 15 min, removed from supernatant and dispersed in 1 mL of water. A summary of specific reagent volumes per sample is provided in Table S1† and correspond with those in Table 1.
| Sample | X (nm) | Y (nm) | Q (nm) | Volume (× 105 nm3) | Pd (%) | LSPR max. (nm) | Abs/Ext at 808 nm | η (%) |
|---|---|---|---|---|---|---|---|---|
| A | 144 ± 11 | 26 ± 5 | 62 ± 6 | 11 ± 3 | 9.0 ± 0.6 | 820 | 0.52 ± 0.03 | 38 ± 2 |
| B | 132 ± 10 | 9 ± 3 | 52 ± 5 | 6 ± 2 | 13.3 ± 0.4 | 950 | 0.67 ± 0.04 | 60 ± 2 |
| C | 144 ± 8 | 12 ± 5 | 67 ± 8 | 12 ± 3 | 8.7 ± 0.5 | 790 | — | 39 ± 1 |
| D | 132 ± 7 | 10 ± 3 | 55 ± 5 | 7 ± 2 | 8.3 ± 0.7 | 808 | 0.61 ± 0.03 | 44 ± 1 |
| E | 128 ± 8 | 28 ± 5 | 51 ± 6 | 7 ± 2 | 12.8 ± 0.5 | 860 | 0.63 ± 0.02 | 48 ± 2 |
Structural and optical characterization
Samples for scanning electron microscopy (SEM) were prepared by drop-casting a dispersed particle solution onto a Si wafer. After the solvent evaporated, the Si wafers were rinsed at an angle in a stream of methanol several times to remove excess surfactant. Images were obtained with a FEI Quanta FEG 600 field-emission environmental SEM operating at 30 kV with a spot size of 3 nm. The SEM was interfaced to an Oxford Inca detector for energy-dispersive X-ray spectroscopy (EDS); 3–5 full-coverage regions (>1 μm3) were analysed per sample. Samples for analysis by scanning transmission electron microscopy (STEM) were prepared by washing a carbon-coated copper grid with chloroform to remove Formvar and then drop-casting a dilute nanoparticle dispersion onto the grid. STEM images were obtained with a JEOL JEM 3200FS transmission electron microscope at 300 kV, equipped with a camera Gatan 4kx4k Ultrascan 4000. EDX spectra were measured with an Oxford INCA dispersive X-ray system interfaced to the microscope, operating at 300 kV. Extinction spectra were acquired with a photodiode-array spectrophotometer Agilent 8453 UV-Visible (Agilent Technologies Deutschland GmbH). The absorption and scattering transmittance spectra were determined using a home-made diffuse reflectance setup, see ESI for details (section ESI.2, Fig. S4†).Heating efficiency
Heating efficiency was determined following the technique described by Roper et al.,26 based on optical and transient temperature measurements. In our experiments, 1 mL of octopods dispersion was evenly illuminated with a laser (fiber-coupled laser diode, Lumics LU0808T040) at 808 nm. The laser beam was collimated and expanded with lenses to form a spot that covers the whole sample (1 cm in diameter). In every case, the laser power illuminating the sample was 750 mW. Heating and cooling curves were then recorded with a thermal camera (FLIR A35) that monitors the surface of the solution from above. Thermal curves were recorded for several (between three and five) sample concentrations, varying the optical density at the laser wavelength. As heating efficiency remains constant regardless of the concentration (for low enough concentrations), the final value is an average of the different measurements. A sample containing only water was measured to provide a background that excludes any heating contributions related to the medium. Further details regarding the measuring protocol and data analysis can be found in the ESI (section ESI.3†).Electromagnetic simulations
Numerical simulations were performed using the commercial software FDTD Solutions (v.8.20.1731) from Lumerical Solutions, Inc. The dielectric functions were fitted to tabulated experimental data by Johnson and Christy for Au and by Palik for Pd (RMS errors <0.9).27,28 The effective dielectric functions of Au/Pd alloys were approximated by an effective medium based on a Maxwell–Garnett homogenization (EMA, 5–20% Pd, section ESI.5†). The background index was set to 1.33 to mimic water. Total-field scattered-field (TFSF) plane-wave sources, ranging from 400 to 1200 nm, were used to separate the computation region into two distinct regions – one containing the total field (i.e., the sum of the incident field and the scattered field), and another that contains only the scattered field. Mesh values were set to 2 nm for the empty space and 1 nm for the particle space. All simulations reached a convergence of 10−7 before reaching 300 fs simulation time.Results and discussion
Structural and optical characterization
Au/Pd nanocrystals studied here were prepared by seed-mediated co-reduction of Au and Pd salts in the presence of octahedral Au seeds. This process produces stellated structures with eight tips symmetrically distributed (Oh symmetry) and proceeding along 〈111〉 directions, as shown in the SEM images and the scheme of Fig. 1. The excellent size homogeneity of the particles leads to the ordered packing that can be seen in the images. On account of the synthetic method, the final octopods consist of an inner octahedral gold core from the seed and a branched outer layer of Au/Pd alloy that is enriched with Pd at the tips.15 In previous works, this alloy composition has been confirmed by powder XRD as well as electron diffraction patterns,29 Fourier transforms of atomic resolution lattice images, and atomic spacing measurements of the branches.7 Also, STEM-EDS elemental maps and line-scans revealed that the tips and edges are enriched with Pd compared to the alloyed branches and Au interior from the seeds, which has been confirmed here (Fig. S1†).7,30 | ||
| Fig. 1 Octopod morphologies: (a–e) SEM images of Au/Pd nanocrystals (samples A–E, labelled in order) of different dimensions and Au/Pd compositions (see Table 1). Scale bars in insets: 100 nm. (f) Schematic depiction of an octopod with indicated main structural parameters: face diagonal tip-to-tip length X, tip width Y, and branch base width Q. | ||
The dimensions of the octopods (tip length and morphology) and their composition (Pd content) can be tuned during the synthesis process.8,15 For instance, the Au-to-Pd ratio can be tuned by the ratio of metal precursors in the overgrowth step. Also, the face diagonal size or tip-to-tip distance (X in Fig. 1f) of the particles can be controlled in a range between approx. 60 and 200 nm by changing the precursor-to-seed ratio. However, high ratios (larger amounts of precursors per volume of seeds) lead to dull and flattened tips (Y in Fig. 1f). Accordingly, to fine-tune the sharpness of the tips Y, the CTAB used in the overgrowth step can be replaced with a mixture of CTAC and NaBr of varying amounts.15
Following these principles, octopods with defined structural features (parameters X and Y) can be prepared. In this work, to study the effect of the geometry of the particles on their light-to-heat conversion, we prepared a set of five samples with different characteristics (see Fig. 1 and Table 1). Particularly, we prepared samples with two tip-to-tip lengths (≈130 or ≈144 nm) and two tip widths (≈10 or ≈27 nm). A complete description of the tip morphology should also include the width of their base Q, which is roughly the same (≈58 ± 7 nm) within the set of samples investigated. In addition, to understand the effect of the presence of Pd, we prepared samples with two different Pd contents (≈8.7% and ≈13%). For details, see Table 1. For further clarity, visual representations are provided in Fig. S2.†
Octopods can feature a variety of intense plasmon modes, depending on their morphology and composition, as shown in previous works.8 Accordingly, the main dipolar-like LSPR at low energy can be tuned throughout the visible and near-infrared ranges by varying these parameters. We chose to perform light-to-heat conversion experiments at a fixed wavelength of 808 nm, which falls within the near-infrared transparency region of water and minimizes heat transfer to the solvent. Besides, as it matches also a transparency window of haemoglobin,31,32 it is a technologically relevant wavelength for optical sensors that can be used in aqueous environments, as well as for biomedical applications including in vivo or in vitro catalysis,33,34 and photodynamic therapy.35 Since the study requires octopods with the plasmon mode close to 808 nm, the range in which size and composition parameters can be varied is limited. To clarify this aspect, a discussion on the impact of the structural parameters X, Y, and Q on the LSPR position and intensity performed through FDTD simulations can be found in the ESI (section ESI.6†).
Fig. 2 shows the extinction spectra of the five samples under study, which were synthesized to overlap with the illumination wavelength as well as possible. The aim to unravel the relationship between composition, geometry and heating efficiency of the nanoparticles imposes restrictions on the number of variables that can be changed between samples. As a result, some particles (in particular sample B) present a certain mismatch between LSPR and laser wavelength. In the following sections we will consider this mismatch as an additional parameter for discussion.
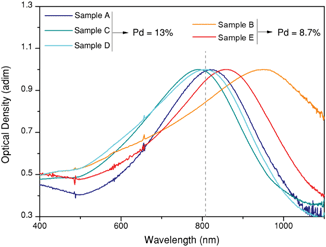 | ||
| Fig. 2 Optical properties of octopods dispersed in water. Normalized UV/Vis/NIR extinction spectra showing intense plasmon bands close to the excitation wavelength (808 nm, grey dashed line). | ||
At the plasmon resonance wavelength, the interaction of the particles with light is strong, and it can occur through either light scattering or light absorption. As mentioned above, the ability to transform light into heat is directly linked to light absorption. To what extent light is scattered or absorbed by the particles, largely depends on their size, geometry and composition.16,36 For this reason, different heating capabilities can be expected depending on the structural characteristics of the octopods. How these parameters influence heat generation in bimetallic structures, including Pd content and its distribution, is an open question, though.
Thermal stability and heating efficiency
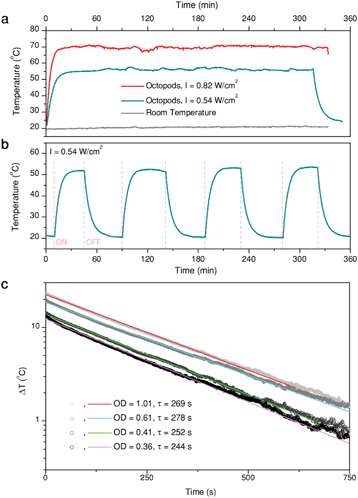
As previously mentioned, Au/Pd particles present a high thermal stability, though the threshold temperature at which reshaping becomes evident depends on the environment.22 In this work, octopods were dispersed in aqueous solution and thus temperature was limited by water evaporation. To test their thermal stability under these conditions, we monitored the temperature of a dispersion of octopods (1 mL, optical density of 0.51 at the laser wavelength) evenly illuminated at its whole surface with a laser of 808 nm wavelength. Temperature was monitored from the upper surface of the solution using a thermal camera. Examples of the heating curves obtained are shown in Fig. 3a and b, where the illumination intensity was limited to avoid evaporation of the solvent (condensation on the cuvette walls was already observed at 80 °C) and changes of sample concentration during the experiments.Fig. 3a presents representative heating curves of sample B solution, illuminated at two different laser intensities. First, the profile confirms generation of heat when illuminated at 808 nm. The medium temperature keeps rising within a timeframe of about 10 min until thermal equilibrium is reached, with heat dissipation to the environment compensating the thermal energy provided by the particles upon illumination. Consequently, the maximum temperature depends on both the laser intensity and the environment, which does not change during the experiments (grey trace). Illumination over 5 h was applied to test the stability of the particles and the constancy of heat generation. The maximum temperature remains stable over the whole illumination time, apart from slight fluctuations due to the automatic electrical recalibration of the thermal imaging camera every few minutes (in our case ≈20 min), during the continuous sensor reading. This consistency indicates that the particles are thermally stable under the given conditions. As a further proof, extinction spectra of the sample solutions were measured before and after the experiments, to verify that the LSPR remained unaltered (Fig. S3c†). Additionally, no structural changes are evident from SEM characterization of the samples after heating (Fig. S3a and b†). Because the optical and structural properties did not show any noticeable changes, we confirm that the particles display a high thermal stability. The reproducibility of the heating (and cooling) curves was also tested (Fig. 3b) over four consecutive cycles, in which heating was triggered or stopped by switching the laser on and off.
Having tested the stability of the particles under the selected heating conditions, we studied the extent of light-to-heat conversion for different particle morphologies and compositions. For this purpose, we used the heating efficiency as a reference parameter, which enabled a fair comparison. Heating efficiency is the percentage of light that is transformed into heat, the maximum total energy being the total amount of intercepted photons, i.e. combined scattering and absorption contributions. Thus, assuming no additional ways to release energy into the environment (e.g. luminescence or chemical reactions), the heating efficiency is directly related to the ratio between extinction (the total spectral losses) and absorption, i.e. the losses that are transformed into heat. Based on thermal equilibrium equations, Roper et al.26 developed an expression for the heating efficiency η, which depends solely on thermal and optical parameters:
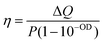 | (1) |
The measured heating efficiency values are given in Table 1, together with the standard deviations, obtained from measuring several samples, as shown in Fig. 3c. The prepared particles feature heating efficiencies between 38% and 60%, showing that variability exists, as a function of composition and/or structure. To place these values in the context of currently existing optical heaters, we can compare them with the heating capacities of the best photothermal nanoparticles reported so far, which lie between 40% and 100%. Gold nanostars, for instance, typically exhibit efficiencies between 40% and 100% at 808 nm, depending on the morphology of their branches and tips;37 gold nanorods can exhibit efficiencies between 50% and 95% at their longitudinal LSPRs, depending on their aspect ratio;37,38 and gold nanospheres can vary between 65% and 80% at 532 nm, depending on their diameter.39 Accordingly, the heating efficiency of the octopods investigated here are within the range of the best photothermal probes proposed, though in the lower range, which appears to be a good starting point for bimetallic nanoparticles, especially given their increased thermal stability compared to gold-only structures. These results further indicate that for most optical applications, the photothermal ability of the nanoparticles should be considered as it may interfere with their performance as sensors or photocatalysts.
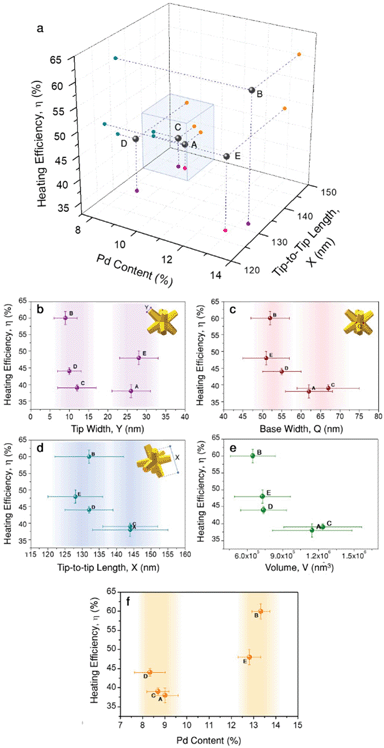
Just as observed for all these groups of gold nanoparticles, heat generation from bimetallic nanocrystals should be affected by several aspects related to their geometry and composition. Aiming to shed light on the parameters having a larger effect on heating efficiency, we plotted all the obtained results in a 3D correlation plot (Fig. 4a), and seeking for further details, heating efficiency was also plotted vs. tip-width (Fig. 4b), tip-base (Fig. 4c) tip-to-tip length (Fig. 4d), nanoparticle volume (Fig. 4e) and Pd content (Fig. 4f).
The high heating efficiency of gold nanostars was attributed to the presence of several thin and sharp tips.13,16 Based on this observation, tip-width seems to be a logical starting point. Fig. 4b shows two groups of particles: one with sharper tips of Y ≈ 10 nm, and another with blunt tips of Y ≈ 27 nm, i.e., almost three times larger tip diameters. According to the obtained results, both groups contain particles with low heating efficiencies (38% and 39%, samples A and C, respectively), as well as particles with high heating efficiencies (60% and 48%, samples B and E, respectively). Considering the variability obtained within both groups, it can be hardly said that tip-width is strongly affecting heating efficiency. Of course, this does not mean that its effect is negligible, but it does not appear as the dominant aspect at this point.
Another parameter related to tip morphology is the tip base, Q, i.e. the branch base width. Its variability within the samples is smaller, but they could still be roughly grouped in two sets: Q ≈ 53 nm and Q ≈ 64 nm. Plotting heating efficiency vs. tip-base (Fig. 4c) suggests that smaller Q, i.e. thinner and slender branches (samples B, D, E) tend to account for higher heating efficiencies. This observation seems reasonable as heating is typically favoured by geometries in which most material is close to the surface, as the bulk contributes less.16 Also, the base width correlation shows high similarity to the tip-to-tip length, X, at least within the prepared particles. This suggests that the particles fall into the same groups, with the smaller particles (X ≈ 130 nm) offering higher heating efficiencies above 40%, while the larger ones (X ≈ 144 nm) fall below 40% (Fig. 4d). This relationship is consistent within the indicated groups of particles, even though the tip-to-tip difference between both groups varies only by about 10%. Moreover, this agrees well with the general expectation that particles of larger sizes scatter more intensely, and thus their heating efficiency ought to be lower. Such a dependence becomes clearer if the heating efficiency is plotted versus the nanoparticle volume, V, which depends on every geometrical variable considered, X, Q, and Y, as given by eqn (S3).40 Hence, it provides a more complete description. The obtained values (Table 1 and Fig. 4e) support that smaller particles have a higher heating efficiency as they scatter less, in agreement with Mie theory.39 Putting together all the different observations so far, we can conclude that smaller octopods heat more due to their volume, but also due to thinner, slender branches, both for sharp and dull tips.
Within the group of smaller particles and thinner tips, the variability in heating efficiency is found to be larger, with values ranging between 44% and up to 60% in a rather narrow volume range. Consequently, we propose that a parameter different to diagonal tip-to-tip distance or base-width should affect heat generation. Fig. 4f displays the correlation of heating efficiency versus Pd content, in which the clear separation of points shows that samples with a higher Pd content (≈13%) heat more efficiently (η > 45%) than those containing less Pd (≈8.7%, η < 45%). This analysis adds bimetallic composition to the list of parameters strongly affecting heating efficiency.
We now compare two pairs of samples with equivalent size and Pd content: A and C (X ≈ 144 nm, ≈8.7% Pd); and B and E (X ≈ 132 nm, ≈13% Pd). While samples A and C only slightly differ in heating efficiency (38% vs. 39%), the difference between samples B and E is significant (60% vs. 48%). In both cases, one of the samples has sharper tips than the other. Particularly, sample B, the most efficient heater within this study, belongs to the morphological group of particles with sharp tips. Considering all these observations, we can now sketch out an experimental hypothesis: within the ranges studied here, both morphology and composition play leading roles. In general, smaller nanoparticles with larger amounts of Pd are favoured in terms of efficient heat generation, whereas larger particles with lower Pd content release less heat (blue cube in Fig. 4a). The sharpness of the tips may gain relevance in the case of smaller nanocrystals, accounting for modifications of the photothermal efficiency of ≈10%.
The relationship between particle size and morphology is consistent with observations made for gold nanoparticles, as described above (small size and long sharp tips favour heating efficiency).16 However, to understand the reasoning behind the beneficial effect of Pd for the conversion of light into heat is not intuitively clear. Aiming to clarify the physical basis of this effect, and to test our hypothesis, we carried out electromagnetic simulations and additional optical measurements.
Influence of Pd content and distribution on optical properties
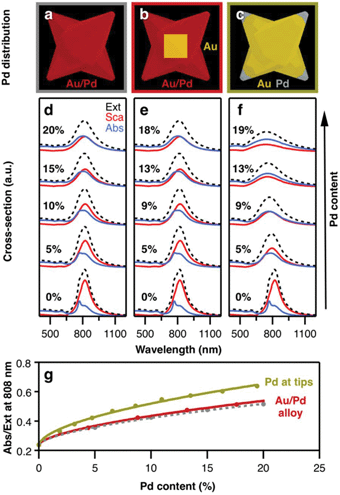
To investigate the influence of palladium on heating capacity, we performed FDTD numerical modelling in which the composition of the bimetallic nanocrystals was varied. For this purpose, we first designed a simple model that builds on a homogenous and uniform distribution of Pd throughout the whole particle volume (Fig. 5a). The dielectric properties of Au/Pd alloys were obtained using an effective-medium approximation (EMA) based on the Maxwell–Garnett theory for volume fractions between 5% and 20% (see ESI, section ESI.5, Fig. S6†). This approximation considers the specific dielectric functions of the components to describe small inclusions of Pd inside a host matrix of Au as an optically homogenous (effective) medium. Compared to pure gold, Au/Pd alloys exhibit higher (ordinary) refractive indices, and consequently higher imaginary parts of permittivity. The influence of the latter can be visualized by considering a simple forced damped oscillator, where the real part describes the phase lag between driving force and response frequency, and the imaginary part embodies the damping factor and thus, the loss of energy. Consequently, by increasing the Pd content, the plasmon resonance (total extinction cross-section) becomes attenuated and broadened, as exemplified by a model octopod of X = 145 nm, Y = 10 nm, and Q = 50 nm (Fig. 5d, black dashed line). Besides plasmon damping, the presence of Pd also significantly reduces the scattering contributions. The same effect has been reported for dark-field studies of Pd-coated gold nanorods.41 In contrast, the absorption cross-section shows the opposite behaviour and increases with Pd content, following an equivalent behaviour as the one reported in Ag/Pt nanocubes.42Next, we consider the presence of the octahedral gold core to make the simulation model more realistic (Fig. 5b). By introducing a volume of pure Au in the centre of the particle, the effective Pd content in the branched exterior is slightly increased (by approx. 10% for the given particle dimensions). Consequently, slightly lower Pd content is necessary to yield the same optical properties as in the first case (Fig. 5e). Apart from that, the gold core has no further influence on the optical properties which seems reasonable as localized surface plasmon resonances are essentially dictated by dielectric/metal interfaces, i.e. the external particle boundaries. For this reason, we consider in the next case that palladium is only present at the octopod tips, with the remaining particle consisting of gold (Fig. 5c). In direct comparison to the other models, the plasmon damping and broadening is more pronounced at similar Pd contents (Fig. 5f). Although the modes are broader, the absorption cross-sections are of similar intensity at the resonance position and the scattering losses are further reduced. Moreover, a 9% Pd content is already sufficient to balance absorption and scattering, whereas 18–20% Pd was required for the alloy models. This higher sensitivity of the optical properties for Pd located at the tips can be seen in the different changes of the absorption-to-extinction ratio (Abs/Ext) for variation of the Pd content (Fig. 5g). Here, the Abs/Ext ratio serves as a suitable quality factor, since absorption is associated with heating gain and extinction serves as a normalization parameter that also accounts for scattering losses in the light-to-heat conversion process. Accordingly, the maximum value Abs/Ext may take is 1, when no scattering losses are present. For the real system, the Pd distribution is complex. It should be noted that, electron tomography and EDS studies have revealed that the branches of the octopods are a gradient alloy, with significant accumulation of Pd at the tips.7,30
Correlation between optical properties and heating efficiency
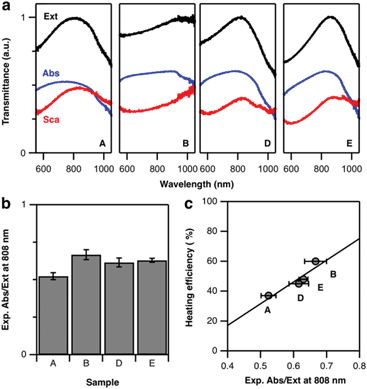
According to the above theoretical predictions, samples with higher Pd content present lower extinction cross-sections. Because this damping affects scattering more than absorption, heating efficiency improves. To verify this assumption, we performed diffuse reflectance (DR) spectroscopy using an integrating sphere. While standard transmission spectroscopy only quantifies the total extinction of light, DR measurements distinguish between absorption and scattering-related contributions. A specific set of experiments was thus performed with the sample being placed in an integrating sphere (see ESI, section ESI.2†).43 This way, additional diffuse losses by scattering could be detected and evaluated. As a result, we obtained the transmittance of the octopod samples indicating significant differences in their spectral properties (Fig. 6a). While their extinction signatures, the sum of absorption and scattering, are in line with the results obtained from transmission vis/NIR spectroscopy (Fig. 2), the ratio of their diffuse contribution allows us to assess their suitability for heating by 808 nm illumination (Fig. 6b). Sample B shows not only the most favourable Abs/Ext ratio but also the most pronounced heating efficiency at 808 nm. Following this trend, the decrease in heating capacity of samples E, D, and A is nicely correlated to their diffuse optical properties (Fig. 6c). Correlation between Abs/Ext and heating efficiency is expected, as the absorbed photons provide the energy available to heat up the sample. To have a complete picture, when connecting absorbance and heating, we should not forget about additional routes of energy dissipation. In particular, absorbed energy can also be released in a non-thermal way, starting with formation of hot electrons that may provide energy to chemical reactions on the surface, contributing to catalysis. This relaxation route typically presents a low probability, although the bimetallic character of the octopods can eventually play an important role on this aspect.44,45 Still, the thermal pathway is the main relaxation route, and thus diffuse reflectance indirectly allows for a comparison of the heating abilities of the nanoparticles.It is worth discussing some additional important aspects that Fig. 6a (as well as the simulations in Fig. 5d–f) reveals: absorption and scattering curves show a spectral mismatch, i.e. their maxima are not at the same wavelength. Then, when both contributions are added to form the extinction spectrum, a single maximum is obtained, which we are considering as the main LSPR. This maximum, though, separates a range of lower wavelengths where absorption dominates, from a range of higher wavelengths with dominant scattering. In the context of heat generation, this indicates that illuminating at wavelengths below the LSPR maximum is favourable for heating. Going back to Fig. 2, this would mean that the excitation wavelength selection favours sample B over the others, which explains the large difference observed in heating efficiency. To test the impact of such a LSPR-excitation mismatch, we used FDTD simulations to calculate the Abs/Ext ratio at 808 nm for octopods of different morphologies, varying X, Y, and Q (see Fig. S8†). Varying these geometrical parameters implies that the LSPR appears at different wavelengths, so this simulation considers both, resonant and off-resonance illuminations. When the LSPR is close to 808 nm, the theoretical predictions fully support the experimental hypothesis enunciated above that a smaller tip-to-tip distance, X, branch base width, Q, as well as smaller tip width, Y, are favourable for light-to-heat conversion. However, it seems also clear that when heating is required, those morphological properties should be combined with slightly blue-shifted illumination to match the absorption maximum.
Conclusions
Bimetallic gold–palladium nanoparticles with octopod shape were shown to display efficient photothermal effects and high thermal stability. Based on octopods with LSPRs close to 808 nm, we determined heating efficiencies between 40% and 60%. The highest efficiencies were observed for smaller octopods, with sharper tips, slender branches, and higher Pd content. By shifting any of these features, the efficiency was found to decrease by at least 10%. This shows how heating efficiency can be tuned to different needs. Indeed, for some geometries/compositions the local temperature released by the particles to their surroundings should be taken into account to understand their behaviour as sensors, as it may interfere with their sensing ability. Regarding catalysis, thermal modifications can be optically triggered, thus affecting reaction rates.Our results demonstrate that the presence of Pd increases the absorption/extinction ratio. The distribution of Pd within the nanoparticles has a stronger effect when it is located at the tips, rather than inside the branches or the core. Consequently, the ratio between absorption and extinction, and the related suitability for different applications strongly depends on the amount and location of Pd. Finally, since absorption and scattering spectra present maxima at different wavelengths, heating was found to be favoured when the particles are illuminated at a wavelength slightly blue-shifted to the extinction maximum.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. E. S. and J. D. S. acknowledge support from the U.S. National Science Foundation award number CHE-1602476 and CHE-1904499. S. E. S. and her stay at CIC biomaGUNE was supported by a fellowship from the Fulbright U.S. Scholar Program. L. M. L.-M. acknowledges financial support from the Spanish Ministerio de Economía, Industria y Competitividad (Grant MAT2017-86659-R) and the European Research Council (ERC AdG No. 787510, 4DbioSERS). C. K. acknowledges financial support from the European Commission under the Marie Skłodowska-Curie program (H2020-MSCA-799393, NANOBIOME). This work was performed under the María de Maeztu Units of Excellence Program from the Spanish State Research Agency – Grant No. MDM-2017-0720.References
- L. A. Kibler, A. M. El-Aziz, R. Hoyer and D. M. Kolb, Angew. Chem., Int. Ed., 2005, 44, 2080 CrossRef CAS PubMed.
- K. Deplanche, M. L. Merroun, M. Casadesus, D. T. Tran, I. P. Mikheenko, J. A. Bennett, J. Zhu, I. P. Jones, G. A. Attard, J. Wood, S. Selenska-Pobell and L. E. Macaskie, J. R. Soc., Interface, 2012, 9, 1705 CrossRef CAS PubMed.
- D. Chen, J. Li, P. Cui, H. Liu and J. Yang, J. Mater. Chem. A, 2016, 4, 3813 RSC.
- P. Venkatesan and J. Santhanalakshmi, Nanosci. Nanotechnol., 2011, 1, 43 CrossRef.
- G. J. Hutchings and C. J. Kiely, Acc. Chem. Res., 2013, 46, 1759 CrossRef CAS PubMed.
- H. Lin, Y. Chen and J. Shi, Chem. Soc. Rev., 2018, 47, 1938 RSC.
- E. Ringe, C. J. DeSantis, S. M. Collins, M. Duchamp, R. E. Dunin-Borkowski, S. E. Skrabalak and P. A. Midgley, Sci. Rep., 2015, 5, 17431 CrossRef CAS PubMed.
- C. J. DeSantis and S. E. Skrabalak, Langmuir, 2012, 28, 9055 CrossRef CAS PubMed.
- A. F. Smith, R. G. Weiner and S. E. Skrabalak, J. Phys. Chem. C, 2016, 120, 20563 CrossRef CAS.
- S. Fischer, F. Hallermann, T. Eichelkraut, G. von Plessen, K. W. Krämer, D. Biner, H. Steinkemper, M. Hermle and J. C. Goldschmidt, Opt. Express, 2012, 20, 271 CrossRef CAS PubMed.
- Surface Enhanced Raman Spectroscopy: Analytical, Biophysical and Life Science Applications, ed. S. Schlücker, Wiley-VCH, Weinheim, Germany, 2010 Search PubMed.
- G. Baffou, R. Quidant and F. J. García de Abajo, ACS Nano, 2010, 4, 709 CrossRef CAS PubMed.
- G. Baffou and R. Quidant, Laser Photonics Rev., 2013, 7, 171 CrossRef CAS.
- M. B. Cortie, X. Xu, H. Chowdhury, H. Zareie and G. Smith, in Smart Structures, Devices, and Systems II, ed. S. F. Al-Sarawi, SPIE, Sydney (Australia), 2005, vol. 5649, p. 565 Search PubMed.
- C. J. DeSantis, A. C. Sue, M. M. Bower and S. E. Skrabalak, ACS Nano, 2012, 6, 2617 CrossRef CAS PubMed.
- G. Baffou, R. Quidant and C. Girard, Appl. Phys. Lett., 2009, 94, 153109 CrossRef.
- D. Jimenez de Aberasturi, A. B. Serrano-Montes, J. Langer, M. Henriksen-Lacey, W. J. Parak and L. M. Liz-Marzán, Chem. Mater., 2016, 28, 6779 CrossRef CAS.
- T. Vo-Dinh, Y. Liu, B. M. Crawford, H.-N. Wang, H. Yuan, J. K. Register and C. G. Khoury, J. Immunol. Sci., 2018, 2, 1 CrossRef.
- H. Vanrompay, E. Bladt, W. Albrecht, A. Béché, M. Zakhozheva, A. Sánchez-Iglesias, L. M. Liz-Marzán and S. Bals, Nanoscale, 2018, 10, 22792 RSC.
- L. Rodríguez-Lorenzo, J. M. Romo-Herrera, J. Pérez-Juste, R. A. Alvarez-Puebla and L. M. Liz-Marzán, J. Mater. Chem., 2011, 21, 11544 RSC.
- A. B. Taylor, A. M. Siddiquee and J. W. M. Chon, ACS Nano, 2014, 8, 12071 CrossRef CAS PubMed.
- W. Albrecht, E. Bladt, H. Vanrompay, J. D. Smith, S. E. Skrabalak and S. Bals, ACS Nano, 2019, 13, 6522 CrossRef CAS PubMed.
- F. Wang, C. Li, H. Chen, R. Jiang, L.-D. Sun, Q. Li, J. Wang, J. C. Yu and C.-H. Yan, J. Am. Chem. Soc., 2013, 135, 5588 CrossRef CAS PubMed.
- C.-C. Chang, H.-L. Wu, C.-H. Kuo and M. H. Huang, Chem. Mater., 2008, 20, 7570 CrossRef CAS.
- R. G. Weiner, C. J. DeSantis, M. B. T. Cardoso and S. E. Skrabalak, ACS Nano, 2014, 8, 8625 CrossRef CAS PubMed.
- D. K. Roper, W. Ahn and M. Hoepfner, J. Phys. Chem. C, 2007, 111, 3636 CrossRef CAS PubMed.
- Handbook of Optical Constants of Solids, ed. E. D. Palik, Academic Press, San Diego (CA), USA, 1991 Search PubMed.
- P. Johnson and R. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370 CrossRef CAS.
- C. J. DeSantis, A. A. Peverly, D. G. Peters and S. E. Skrabalak, Nano Lett., 2011, 11, 2164 CrossRef CAS PubMed.
- A. F. Smith, R. G. Weiner, M. M. Bower, B. Dragnea and S. E. Skrabalak, J. Phys. Chem. C, 2015, 119, 22114 CrossRef CAS.
- A. M. Smith, M. C. Mancini and S. Nie, Nat. Nanotechnol., 2009, 4, 710 CrossRef CAS PubMed.
- E. Hemmer, P. Acosta-Mora, J. Mendez-Ramos and S. Fischer, J. Mater. Chem. B, 2017, 5, 4365 RSC.
- M. A. Miller, B. Askevold, H. Mikula, R. H. Kohler, D. Pirovich and R. Weissleder, Nat. Commun., 2017, 8, 15906 CrossRef CAS PubMed.
- R. M. Yusop, A. Unciti-Broceta, E. M. V. Johansson, R. M. Sánchez-Martín and M. Bradley, Nat. Chem., 2011, 3, 239 CrossRef CAS PubMed.
- N. Neubauer, J. Palomaeki, P. Karisola, H. Alenius and G. Kasper, Nanotoxicology, 2015, 9, 1059 CrossRef PubMed.
- J. Stehr, C. Hrelescu, R. A. Sperling, G. Raschke, M. Wunderlich, A. Nichtl, D. Heindl, K. Kürzinger, W. J. Parak, T. A. Klar and J. Feldmann, Nano Lett., 2008, 8, 619 CrossRef CAS PubMed.
- L. M. Maestro, P. Haro-Gonzalez, A. Sanchez-Iglesias, L. M. Liz-Marzan, J. García Solé and D. Jaque, Langmuir, 2014, 30, 1650 CrossRef CAS PubMed.
- J. R. Cole, N. A. Mirin, M. W. Knight, G. P. Goodrich and N. J. Halas, J. Phys. Chem. C, 2009, 113, 12090 CrossRef CAS.
- K. Jiang, D. A. Smith and A. Pinchuk, J. Phys. Chem. C, 2013, 117, 27073 CrossRef CAS.
- C. J. DeSantis, A. C. Sue, A. Radmilovic, H. Liu, Y. B. Losovyj and S. E. Skrabalak, Nano Lett., 2014, 14, 4145 CrossRef CAS PubMed.
- S. Y. Lee and J. W. Ha, Phys. Chem. Chem. Phys., 2016, 18, 32682 RSC.
- U. Aslam, S. Chavez and S. Linic, Nat. Nanotechnol., 2017, 12, 1000 CrossRef CAS PubMed.
- R. P. M. Höller, M. Dulle, S. Thomä, M. Mayer, A. M. Steiner, S. Förster, A. Fery, C. Kuttner and M. Chanana, ACS Nano, 2016, 10, 5740 CrossRef PubMed.
- K. Sytwu, M. Vadai and J. A. Dionne, Adv. Phys.: X, 2019, 4, 1619480 Search PubMed.
- S. Chavez, U. Aslam and S. Linic, ACS Energy Lett., 2018, 3, 1590 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details on synthesis, experimental methods, and simulations. See DOI: 10.1039/c9nr05679c |
| This journal is © The Royal Society of Chemistry 2019 |