Control of highly anisotropic electrical conductance of tellurene by strain-engineering†
Abstract
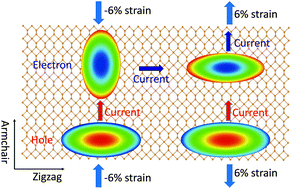
Tailoring the electronic anisotropy of two-dimensional (2D) semiconductors with strain-engineering is critical in nanoelectronics. Recently, 2D tellurene has been predicted theoretically and fabricated experimentally. It has potential applications in nanoelectronics, in particular, β-phase tellurene (β-Te) shows a desirable direct band gap (1.47 eV), high carrier mobility (2.58 × 103 cm2 V−1 s−1) and high stability under ambient conditions. In this work, we demonstrated, with first-principles density functional theory calculations, that the highly anisotropic electron mobility and electrical conductance of β-Te can be controlled by strain-engineering. The direction of electrical conductance of β-Te can be changed from the armchair to the zigzag direction at the strain between −1% and 0%. Meanwhile, we found that the bandgap of β-Te under strain experiences an indirect-direct transition with a conduction band minimum (CBM) shift from the X to Γ point. The significant dispersion of the bottom of the conduction bands along the Γ–Y direction switches to the X–Γ direction under uniaxial or biaxial strain which makes the rotation of the effective masses tensor. The qualitative rotation of the spatial anisotropic electron effective masses tensor by 90° also rotates the direction of the electrical conduction as the carrier mobility is inversely dependent on the effective masses. On the another hand, we also found that the deformation potential constant also plays an important role in the rotation of electrical conductance anisotropy. While anisotropic conductance of hole is impregnable under strain. In order to verify that β-Te can sustain large strain, we studied its stability and mechanical properties and found that β-Te shows superior mechanical flexibility with a small Young's modulus (27.46 GPa (armchair)–61.99 GPa (zigzag)) and large anisotropic strain-stress (12.89 N m−1 at the strain of 38% along armchair direction and 25.72 N m−1 at the strain of 26% along zigzag direction). The high anisotropic carrier mobility and superior mechanical flexibility of β-Te make it a promising candidate for flexible nanoelectronics.
- This article is part of the themed collection: Nanoscale 10th Anniversary Special Issue


 Please wait while we load your content...
Please wait while we load your content...