Open Access Article
Open Access ArticleSelective ion sieving through arrays of sub-nanometer nanopores in chemically tunable 2D carbon membranes†
Pauline M. G.
van Deursen
a,
Zian
Tang
b,
Andreas
Winter
b,
Michael J.
Mohn
c,
Ute
Kaiser
c,
Andrey A.
Turchanin
bd and
Grégory F.
Schneider
 *a
*a
aLeiden University, Leiden Institute of Chemistry, Einsteinweg 55, 2333 CC Leiden, Leiden, The Netherlands. E-mail: g.f.schneider@chem.leidenuniv.nl
bFriedrich Schiller University Jena, Institute of Physical Chemistry, Lessingstraße 10, 07743, Jena, Germany
cUlm University, Central Facility of Electron Microscopy, Albert Einstein Allee 11, D-89081 Ulm, Germany
dCenter for Energy and Environmental Chemistry Jena (CEEC Jena), Philosophenweg 7a, 07743 Jena, Germany
First published on 11th October 2019
Abstract
Two-dimensional (2D) membranes featuring arrays of sub-nanometer pores have applications in purification, solvent separation and water desalination. Compared to channels in bulk membranes, 2D nanopores have lower resistance to transmembrane transport, leading to faster passage of ions. However, the formation of nanopores in 2D membranes requires expensive post-treatment using plasma or ion bombardment. Here, we study bottom-up synthesized porous carbon nanomembranes (CNMs) of biphenyl thiol (BPT) precursors. Sub-nanometer pores arise intrinsically during the BPT-CNM synthesis with a density of 2 ± 1 pore per 100 nm2. We employ BPT-CNM based pore arrays as efficient ion sieving channels, and demonstrate selectivity of the membrane towards ion transport when exposed to a range of concentration gradients of KCl, CsCl and MgCl2. The selectivity of the membrane towards K+ over Cl− ions is found be 16.6 mV at a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 concentration ratio, which amounts to ∼30% efficiency relative to the Nernst potential for complete ion rejection. The pore arrays in the BPT-CNM show similar transport and selectivity properties to graphene and carbon nanotubes, whilst the fabrication method via self-assembly offers a facile means to control the chemical and physical properties of the membrane, such as surface charge, chemical nature and pore density. CNMs synthesized from self-assembled monolayers open the way towards the rational design of 2D membranes for selective ion sieving.
1 concentration ratio, which amounts to ∼30% efficiency relative to the Nernst potential for complete ion rejection. The pore arrays in the BPT-CNM show similar transport and selectivity properties to graphene and carbon nanotubes, whilst the fabrication method via self-assembly offers a facile means to control the chemical and physical properties of the membrane, such as surface charge, chemical nature and pore density. CNMs synthesized from self-assembled monolayers open the way towards the rational design of 2D membranes for selective ion sieving.
Introduction
In ultrafiltration, solvent separation, desalination and reverse osmosis, 2D materials represent an ultimately thin barrier for passing solutes and are therefore prospected to compete with conventional membranes in energy efficiency.1–6 The unique filtration properties of nanopores can best be exploited when pore dimensions are brought down to the size of single molecules and ions, so that the pores reject the passage of ions and molecules based on size exclusion and electrostatic repulsion. However, the reproducible formation of sub-nanometer pores in 2D membranes with high pore density remains a challenge.7,8 Porous 2D membranes are commonly fabricated via top-down methods: starting with a continuous 2D layer, followed by the formation of pores by ion bombardment, electron bombardment or reactive plasma exposure.9 As evident from a recent review focusing on top-down approaches to fabricate porous 2D membranes, pore densities of 1–10 pores per 100 nm2 were the highest obtained.10 To achieve these densities, as well as effective control over the pore sizes, the post-modification of a pristine 2D membrane requires highly advanced facilities for controlled electron or ion exposure.A more versatile route is the bottom-up synthesis of porous 2D membranes from precursor molecules.11,12 A straightforward advantage of the bottom-up approach is its scalability without the need for post-modification steps, high-end lithographic facilities or cleanrooms. In bottom-up fabrication, pore formation is intrinsic to the membrane synthesis, arising from stacking defects during molecular self-assembly. Another advantage lies in the wide variety of precursor molecules that can be incorporated in the membrane. The choice of precursor molecule gives control over pore size and density, as well as over the chemical composition of the membrane – for instance to tune the hydrophobicity of the membrane or to induce specific interactions between the membrane and solute ions or molecules. In particular, carbon nanomembranes (CNMs), formed via self-assembly of aromatic thiol-precursor molecules, have been shown to display pore densities in the range required for applications such as desalination by reverse osmosis and as separation membranes.13–15 Beside the pore density, which determines through-put, a key factor in the efficiency of filtration is the pore size distribution in a 2D membrane, with smaller pores yielding higher selectivity in trans-membrane transport. Previous studies have revealed that the pore size in CNMs is determined by the size and structure of the precursor molecules. Precursors of decreasing molecular size yield membranes with decreasing pore diameter, as well as a thinner membrane. In the current work, we use the precursor molecule 1,1′-biphenyl-4-thiol (BPT): one of the smallest precursor that still forms a stable CNM, with a near-2D thickness of ∼0.9 nm and strong enough to be suspended over micrometers.
The BPT-CNM is therefore an ideal candidate for ion filtration applications. However, the porosity of the BPT-CNM has not been characterized to date, due to the difficulty of imaging sub-nanometer features in 2D membranes.16 Whereas nanopores of sub-nanometer sizes have been resolved in crystalline graphene layers produced via pyrolysis of CNMs, the disordered nature of the CNMs complicates the visualization of sub-nanometer pores. The smallest CNM in which porosity has been resolved was made from [1′′,4′,1′,1]-terphenyl-4-thiol (TPT) precursors, for which pore dimensions of 0.7 ± 0.1 nm have recently been reported.13
Here, we determine the pore density in the BPT-CNM for the first time, using a combination of high-resolution transmission electron microscopy (HR-TEM) imaging and ionic conductance measurements. In an earlier study, TEM has been used to resolve BPT-CNM membrane based pores of several nanometers in diameter, which were induced by ion beam exposure, and did not reveal any pores with smaller sizes.32 On the other hand, we show here that pores are in fact present in the pristine BPT-CNM, as evident from transmembrane ion conductivity through the BPT-CNM membrane. The number and size of pores in a well-defined area of the membrane are determined using the ion flow through the membrane. In this way, the porosity of each membrane sample can be determined in operando. Next, we demonstrate the use of the BPT-CNM as ion-sieving membranes. In saline solution, one ion type is preferentially transmitted through the sub-nanometer pores in the BPT-CNM while counter-ions are rejected. This ion selectivity is essential to applications in desalination, energy generation and energy storage. Ion selectivity in transport through the membrane pores is based on electrostatic repulsion by charges present on the membrane surface, as shown by a range of studies probing charge-selective ion transport through nanoporous 2D membranes.17–19 In the BPT-CNM, charged groups include residual sulfide groups.20 Moreover, ion selectivity in 2D nanoporous membranes has been observed even in chemically neutral membranes, including graphene and molybdenum sulfide. It has therefore been suggested that in aqueous environment, adsorbed oxygen species add a negative surface charge to 2D membranes irrespective of the chemical composition of the membrane.21
Results and discussion
To estimate the pore density in the BPT-CNM, we expressed the measured ionic conductance in terms of the length and diameter of the membrane-based pores, according to a model developed for the description of conductance through nanopores in SiN membranes,22 assuming continuous charge flow: | (1) |
Herein, d and l describe the average diameter and length of a single pore through which the conductance G is measured. The bulk electrolyte conductivity σe, with the units Siemens per meter (S m−1), is determined by the ionic strength of the solution. We adjusted this model to describe not the conductance of a single pore, but of an array of pores in a suspended CNM, defining the number of sub-nanometer pores in the exposed membrane area in terms of the recorded conductance (Gmeas) of the carbon nanomembrane:
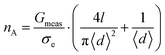 | (2) |
Here, nA is the number of pores in the suspended membrane area A and 〈d〉 the average pore diameter.
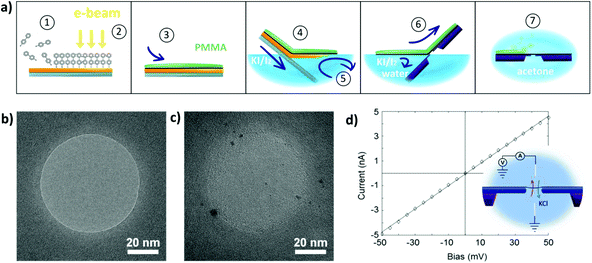
In order to expose a well-defined BPT-CNM area, the CNM was deposited on a SiN chip featuring an aperture that was sculpted in the SiN membrane using the focused beam of an electron microscope. The diameter of the nano-aperture ranged between 20 and 80 nm. Fig. 1a depicts the deposition method: the CNM was synthesized by self-assembly of precursor molecules on a gold film on a mica support (Fig. 1a, step 1). Subsequent cross-linking by electron irradiation (step 2) resulted in a covalent 2D network.16 The membrane was then transferred onto the SiN aperture-chip using PMMA-assisted transfer, as presented in Fig. 1a and in detail in the Experimental section. Fig. 1b shows a SiN aperture prior to membrane deposition imaged by TEM after sculpting the aperture. The aperture chip was imaged again after deposition of the CNM, using aberration-corrected high-resolution (HR) TEM. Fig. 1c shows one membrane imaged by HR-TEM, revealing an integral membrane with no visible pores. From the integrity of the membrane in the electron images, we can assume that the size of the pores in BPT-CNM does not exceed 1 nm. This is a rather conservative estimate, given the instrumental resolution that can be attained in principle by aberration-corrected HR-TEM at the 80 kV operating voltage is 0.18 nm. However, we take into account several factors limiting the resolution attained in TEM imaging: firstly, a high defocus was required to gain sufficient contrast from the amorphous BPT-CNM membrane, which reduced the resolution. Secondly, the applicable electron dose for imaging is limited because the BPT-CNM was observed to deteriorate significantly at too high electron doses, with holes forming during imaging at dose rates >105 e− nm−2 s−1.
To collect information about the pores in the BPT-CNM, trans-membrane ionic conductance measurements were performed. The ionic conductance through the CNM exposed by the SiN aperture was determined from current–voltage curves recorded in the flow cell, such as shown in the inset of Fig. 1d. The conductance of the membrane can in principle be simply determined using Ohm's law. However, for ion transport through 2D nanopores, deviations from ohmic behavior have been reported in literature23–25 and observed in our measurements, too. Two types of non-linear IV-characteristics occurred: rectification and activation. Rectification is a difference in conductance in the positive voltage range respective to the negative voltage range. Activation is the superlinear increase of conductance with increasing voltage across the pore. Both effects have been shown to be related to dehydration phenomena in the confinement of 2D nanochannels. In this work, our sole interest lies with the conductance of the pore towards hydrated ions. Therefore, the conductance was determined applying Ohm's law in the region close to zero bias, where the conductance of hydrated ions is most closely approximated.
The ionic conductance through eleven CNM-coated SiN apertures was measured, both before and after CNM deposition. The data are presented in Fig. 2a. Typically, deposition of the membrane (blue) led to a 30% drop in the measured conductance relative to the bare SiN aperture (red). The conductance of the CNM samples with different free-standing areas falls faithfully on the same line, reflecting the homogeneity of the membrane. The linearity of the conductance versus membrane area furthermore confirms that the conductance stems from the ionic current passing through the membrane, without significant contributions from leak currents.
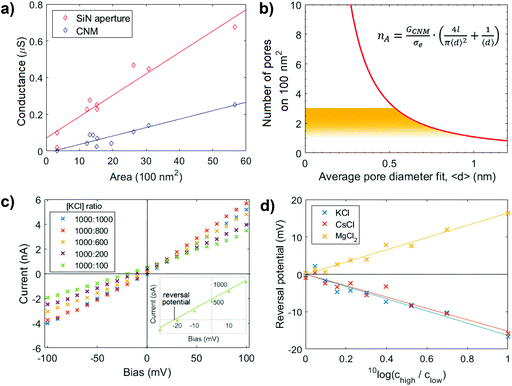 | ||
| Fig. 2 Ion transport measurements. (a) Ionic conductance through BPT-CNM with varying free-standing membrane area exposed on both sides to 1 M KCl solution. The solid line represents the linear regression through the data points. (b) Geometric model relating the average pore diameter to the number of pores in a 100 nm2 area (eqn (2)). The yellow region indicating the physically relevant solutions to the equation, from which the pore density is predicted to lie between 1 and 2.7 pores per 100 nm2. (c) Ionic current–voltage (IV) curves measured in the presence of an electrolyte concentration gradient over a 50 nm diameter CNM membrane. The inset shows a close-up of one of the measurements, highlighting the reversal potential at which the osmotic potential due to the concentration gradient is compensated. (d) The reversal potential over the membrane in (c) at concentration ratios ranging between 1 and 10, with the higher concentration kept constant at 1000 mM. The reversal potential is of equal magnitude and opposite sign to the membrane potential. | ||
The membrane conductance in 1 M KCl was used to make a quantitative statement about the porosity of the BPT-CNM. From the linear regression of the conductance value in Fig. 2a (blue data points), the average membrane conductance (GCNM) per area was found to be 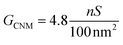 . Based on this value, we estimated the porosity of the BPT-CNM according to eqn (2). Note that the contribution to the resistance from the SiN aperture is not negligible and was accounted for by subtracting the bare aperture conductance (red) from the CNM conductance (blue) – see ESI S1.†
. Based on this value, we estimated the porosity of the BPT-CNM according to eqn (2). Note that the contribution to the resistance from the SiN aperture is not negligible and was accounted for by subtracting the bare aperture conductance (red) from the CNM conductance (blue) – see ESI S1.†
Eqn (2) contains two unknown parameters: n, the number of pores contributing to ion transport and 〈d〉, the average diameter of the pores. The solution, thus, is a set of possible combinations of n and 〈d〉, shown in Fig. 2b. To find the actual values for both n and 〈d〉, we considered first, a lower limit to the size of the pores contributing to the ionic current, which is given by the radius of the smallest charge carrier. Of the main charge carriers in KCl electrolyte, K+ is the smallest, with a hydrated diameter of 0.56 nm.26 As ions are expected to be excluded by pores smaller than the hydrated ion diameter, K+ sets the lower limit to the pore diameter at dmin = 0.56 nm. The upper limit to the pore diameter was defined considering that the membrane imaged by HR-TEM appears free of pores larger than 1 nm.
We concluded that the diameter of the pores contributing to the ionic current falls in the range of 0.56 < 〈d〉 < 1 nm (indicated by the yellow region in Fig. 2b). It follows that the pore density of the BPT-CNM lies between 1 and 2.7 pores per 100 nm2. The exposed membrane area ranged from 20 to 80 nm diameter, so that between 10 and 200 pores partook as conductive channels.
Next, the membrane potential across the BPT-CNM was determined following Nernst-Plank membrane theory.27 The membrane potential is the potential difference between the two sides of the membrane in the presence of an electrolyte concentration gradient. In the presence of such a concentration gradient, diffusion drives ions to the lower concentration side of the membrane. If both cations and anions pass through the membrane at equal rates, no potential would arise. However, in the case of an ion selective membrane, preferential transport of one ion type over the counter-ion results in a net ionic current. The membrane potential is the voltage associated with this current.
Current–voltage characteristics measured in the presence of varying concentration ratios are shown in Fig. 2c. The inset shows the IV-curve measured at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 concentration ratio in close-up around the origin. To find the membrane potential, we determined the voltage measured at zero current (i.e., the intersection with the x-axis of the linear fit through the data points). This is the potential at which the selective ionic current was exactly compensated, called the reversal potential. The reversal potential is of equal magnitude (although of opposite sign) to the membrane potential. To obtain a reliable value of the reversal potential, the concentration ratio was varied and the linear regression gave an accurate value of the reversal potential. Fig. 2d shows the reversal potential as a function of the concentration ratio. At a concentration ratio of 1
10 concentration ratio in close-up around the origin. To find the membrane potential, we determined the voltage measured at zero current (i.e., the intersection with the x-axis of the linear fit through the data points). This is the potential at which the selective ionic current was exactly compensated, called the reversal potential. The reversal potential is of equal magnitude (although of opposite sign) to the membrane potential. To obtain a reliable value of the reversal potential, the concentration ratio was varied and the linear regression gave an accurate value of the reversal potential. Fig. 2d shows the reversal potential as a function of the concentration ratio. At a concentration ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 in KCl, the reversal potential was found to be −16.6 mV. The membrane potential, thus, is +16.6 mV.
10 in KCl, the reversal potential was found to be −16.6 mV. The membrane potential, thus, is +16.6 mV.
The efficiency of ion rejection in the BPT-CNM can be quantified by comparing the measured membrane potential to the Nernst membrane potential. The Nernst membrane potential is the theoretical potential that would arise from a membrane that allows only the passage of one ion type and completely rejects counter ions. The Nernst potential at a concentration ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 is 52 mV (the calculation of the Nernst potential is presented in Table S2†). The BPT-CNM membrane potential is thus 32% of the Nernst potential.
10 is 52 mV (the calculation of the Nernst potential is presented in Table S2†). The BPT-CNM membrane potential is thus 32% of the Nernst potential.
For the BPT-CNM, a higher value than 32% of the theoretical Nernst potential may have been expected, since ion selectivity should be very efficient in pores that approach the size of hydrated ions – as is the case in the BPT-CNM. This discrepancy can be understood considering that the Nernst-Planck membrane theory was developed for conventional, 3D ion selective membranes. In 3D porous membranes, ion selectivity arises due to a bulk membrane phase that is distinct from the adjacent electrolyte phases. In 2D membranes, on the other hand, a bulk membrane phase is ill-defined because of the near-zero length of pore channels. The use of 2D membrane thus allows easier ion transport because of the minimal barrier separating the bulk electrolyte phases on either side of the membrane, resulting in a membrane potential of only 32% of the expected membrane potential for 3D membranes. From these results it is clear that the description of ion selective transport in 2D membranes requires an extension of Nernst-Planck theory to accurately describe measured membrane potentials.
The positive membrane voltage reveals the selectivity towards cations in KCl electrolyte. Conversely, repeated measurement of the membrane potential in MgCl2 and CsCl solutions revealed the dependence of selectivity to the valency of the electrolyte salt used, as the membrane potential changes sign in the case of divalent MgCl2 (Fig. 2d). This observation may be attributed to charge inversion, a phenomenon in which divalent cations overcompensate the negative charge on a surface, effectively changing the sign of the surface charge.28 An alternative explanation is that the electrostatic charges causing selectivity are screened more efficiently in a divalent salt solution – that has a three times higher ionic strength than a monovalent salt solution of the same concentration. When charges on the pore edge are efficiently screened, the factor determining selective transport is the ion mobility. The Cl− ion, with a higher diffusion coefficient than the Mg2+ ion,29 becomes the main charge carrier in MgCl2 electrolyte. This results in an opposite membrane potential to KCl and CsCl, where the cations were the main charge carriers. The selectivity of the membrane is thus responsive to the electrolyte composition and valency.
More insight in the specific interactions between membrane and electrolyte can be obtained by changing the chemical composition of the membrane. As the chemical synthesis of the CNM allows control over the membrane chemistry, such as the addition of specific charged groups, this kind of membranes hold the prospect of increasing our understanding into the nature of membrane–electrolyte interactions, and result in new selective transport phenomena.
To conclude, the bottom-up synthesized carbon nanomembranes provide a scalable and reproducible approach to obtain high density sub-nanometer pores in a 2D membrane. Integrating the BPT-CNM in an ionic conductance measurement flow-cell, we showed that the pores in the BPT-CNM act as effective ion sieving channels. We were able to determine the density of ion channels in operando, allowing the individual characterization of the porosity in each membrane sample and finding a highly uniform and reproducible pore density. The density of pores contributing to ion transport in the BPT-CNM was 1–2.7 pores per 100 nm2, comparable with the high-end top-down approaches where pores are induced in post-modification steps involving ion or electron bombardment. The significant deviation of the membrane potential from the Nernst potential, as well as membrane charge inversion in the presence of MgCl2, are typical to transport through 2D membranes. The BPT-CNM membrane is thus a suitable platform to study the mechanisms underlying ion transport through 2D sub-nanometer pores, more easily obtained than for instance in carbon nanotubes or graphene nanopores produced by lithography. In addition, the possibility of tuning – chemically – the composition of the membrane holds the prospect of rational design of membranes with desired surface properties and chemical functionality.
Experimental
SiN aperture sculpting
SiN windows of 50 × 50 μm2, supported on SiO2 chips, were purchased from Norcada. The SiN/SiO2 chips were cleaned in piranha solution before insertion in the electron microscope (Tecnai T20 operating at 200 keV; Thermo Fischer Scientific, previously FEI). Nano-apertures were sculpted in the SiN window using the focused electron beam.30 After sculpting, the SiN/SiO2 chips were stored in a sonicated mixture of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 EtOH
50 EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (absolute ethanol, >98%, Sigma Aldrich; Milli-Q) for protection against vibrations as well as prevention of clogging the nano-aperture by contaminations, until the moment BPT-CNM deposition.
H2O (absolute ethanol, >98%, Sigma Aldrich; Milli-Q) for protection against vibrations as well as prevention of clogging the nano-aperture by contaminations, until the moment BPT-CNM deposition.
BPT-CNM fabrication
A gold/mica substrate (Georg Albert PVD-Coatings) was cleaned for 1 minute in oxygen plasma (Zepto 115320, Diener). The gold/mica substrate was then immersed in a ∼0.1 mM solution of 1,1′-biphenyl-4-thiol (BPT, Sigma Aldrich) in degassed DMF (Sigma Aldrich, 99.9%) for 72 h under dark conditions, during which a self-assembled BPT monolayer formed on the gold surface. After the self-assembly, the substrate was taken out and immediately washed three times with DMF followed by three times washing with ethanol (Sigma Aldrich, 99.8%) to remove possible residual BPT molecules that may have adsorbed on top of the monolayer. The samples were then dried under nitrogen flow (5.0, Linde) and transferred to a high vacuum chamber (1 × 10−8 mbar) for electron exposure. An electron beam at 100 eV and 50 mC cm−2 electron dose induced molecular cross-linking of the BPT-SAM molecules on the gold surfaces to form a stable membrane. The quality of the formed BPT-SAMs and BPT-CNMs were monitored using X-ray photoelectron spectroscopy (XPS, Fig. S3 and S4†). XPS was carried out on an ultra-high vacuum Multiprobe UHV system (base pressure 1 × 10−10 mbar) from Scienta Omicron, using a monochromatic X-ray source (Al Kα) and an electron analyzer (Argus) with a spectral resolution of 0.6 eV.Transfer of the CNMs onto SiN/SiO2 chips
The transfer procedure was conducted as described elsewhere.31 A PMMA layer (100 nm, 50 kDa, All-Resist, AR-P 671.04) was spin coated onto the CNM on gold/mica and hardened for 10 min at 90 °C. Subsequently, a thicker layer of PMMA (200 nm, 950 kDa, All-Resist, AR-P 679.04) was spin coated on top of the first one and hardened for 10 min at 90 °C. The PMMA-CNM-Au sandwich was cleaved from the mica substrate by repeatedly and gradually dipping the sample into water. An etching solution (I2/KI/H2O, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 by mass) was used to dissolve the gold layer at room temperature. Molecular I2 which adheres to the bottom side of the CNM was removed by floating the CNM-PMMA layer on NaS2O3 (0.1 wt%) solution for 5 min. The CNM-PMMA layer was washed 6 times with ultrapure water before transfer to the target substrate, followed by baking at 90 °C for 1 h. The PMMA layer was removed by dipping the sample into acetone (Sigma Aldrich, 99.9%). To clean the free-standing areas from PMMA impurities, and to avoid rupture of the free-standing CNMs caused by the drying of acetone, acetone was exchanges with liquid CO2 in a critical point dryer (Autosamdri 815, Tousimis) and the CO2 was removed by forming a super critical fluid.
10 by mass) was used to dissolve the gold layer at room temperature. Molecular I2 which adheres to the bottom side of the CNM was removed by floating the CNM-PMMA layer on NaS2O3 (0.1 wt%) solution for 5 min. The CNM-PMMA layer was washed 6 times with ultrapure water before transfer to the target substrate, followed by baking at 90 °C for 1 h. The PMMA layer was removed by dipping the sample into acetone (Sigma Aldrich, 99.9%). To clean the free-standing areas from PMMA impurities, and to avoid rupture of the free-standing CNMs caused by the drying of acetone, acetone was exchanges with liquid CO2 in a critical point dryer (Autosamdri 815, Tousimis) and the CO2 was removed by forming a super critical fluid.
HR-TEM imaging
Aberration-corrected high-resolution TEM (AC-HRTEM) on the BPT-CNM after deposition on the Si3N3 aperture was performed using an FEI Titan 80–300 microscope with third-order aberration correction by a hexapole image corrector. The TEM acceleration voltage was set to 80 kV in order to minimize electron beam-induced damage. The AC-HRTEM images of BPT-CNMs were recorded using a Gatan Ultrascan 1000XP CCD camera with frame sizes of 2048 × 2048 pixels, at electron dose rates of the order of 106 e− nm−2 s−1.Ionic conductance measurements
Current–voltage traces were recorded in a custom fabricated flow cell designed to clamp the SiN/SiO2 chip between two electrolyte reservoirs of approximately 150 μL. After insertion of the chip into the flow-cell, both reservoirs were flushed with a sonicated mixture of ethanol in ultrapure water (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50) to prevent air bubbles from sticking to the membrane surface. Subsequently, ultrapure water (Milli-Q) was flushed three times, followed by two times flushing electrolyte solution. When the electrolyte was changed during measurements of reversal potential, the reservoir was flushed twice with the new concentration electrolyte.
50) to prevent air bubbles from sticking to the membrane surface. Subsequently, ultrapure water (Milli-Q) was flushed three times, followed by two times flushing electrolyte solution. When the electrolyte was changed during measurements of reversal potential, the reservoir was flushed twice with the new concentration electrolyte.
For the preparation of fresh Ag/AgCl electrodes, silver wire (Alfa Aesar, 99.999% percent purity) was cut to pieces ∼2 cm pieces. The tip of the cut piece was immersed in bleach for at least 30 minutes. After formation of a AgCl layer, the electrode tip was rinsed with ultrapure water and used the same day. The flow cell was placed in a Faraday cage and the two compartments of the flow cell were connected to an Axopatch 200B Patch Clamp setup, through freshly prepared Ag/AgCl electrodes. Current–voltage traces were recorded and analyzed using pCLAMP software.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
GFS and PMGD acknowledge the funding received from the Netherlands Organization for Scientific Research (NWO) under the VIDI program (723.013.007) and from the European Research Council under the European Union's Seventh Framework Program (FP/2007-2013/ERC Grant Agreement no. 335879 project acronym Biographene). ZT, AW, AAT, MM and UK acknowledge the Deutsche Forsuchungsgemeinschaft (DFG) for the funding received through the CataLight program (SFB/TRR 234) under projects B07, Z02 (ZT, AW, AAT), and C04 (UK). M. J. M. and U. K. acknowledge funding from the European Union's Horizon 2020 research and innovation program under grant agreement No. 785219. In addition, ZT, AW and AAT acknowledge the DFG Research Infrastructure Grant (INST 275/257-1 FUGG). Furthermore the authors would like to thank Mandakranta Ghosh and Jeffery A. Wood (University of Twente, Faculty of Science and Technology, Department of Soft matter, Fluidics and Interfaces) for the discussions on the results presented in this work.References
- D. Cohen-Tanugi, L. Lin and C. Grossman, Multilayer nanoporous graphene membranes for water desalination, Nano Lett., 2016, 16, 1027–1033 CrossRef CAS PubMed.
- E. N. Wang and R. Karnik, Graphene cleans up water, Nat. Nanotechnol., 2012, 7, 552–554 CrossRef CAS PubMed.
- P. Sun, K. Wang and H. Zhu, Recent developments in graphene-based membranes: structure, mass-transport mechanism and potential applications, Adv. Mater., 2016, 28, 2287–2310 CrossRef CAS PubMed.
- J. Park, P. Bazlewski and G. Fanchini, Porous graphene-based membranes for water purifi cation from metal ions at low differential pressures, Nanoscale, 2016, 8, 9563–9571 RSC.
- D. G. Haywood, A. Saha-shah, L. A. Baker and S. C. Jacobson, Fundamental studies of nano fluidics: nanopores, nanochannels, and nanopipets, Anal. Chem., 2014, 87, 172–187 CrossRef PubMed.
- L. Cao, et al., On the Origin of Ion Selectivity in Ultrathin Nanopores: Insights for Membrane-Scale Osmotic Energy Conversion, Adv. Funct. Mater., 2018, 28, 1–8 Search PubMed.
- G. Liu, W. Jin and N. Xu, Two-dimensional-material membranes: a new family of high-performance separation membranes, Angew. Chem., Int. Ed., 2016, 55, 13384–13397 CrossRef CAS PubMed.
- L. Madauß, et al., Fabrication of nanoporous graphene/polymer composite membranes, Nanoscale, 2017, 10487–10493 RSC.
- G. Liu, W. Jin and N. Xu, Graphene-based membranes, Chem. Soc. Rev., 2015, 44, 5016–5030 RSC.
- L. Wang, M. S. H. Boutilier, P. R. Kidambi, D. Jang and N. G. Hadjiconstantinou, Fundamental transport mechanisms, fabrication and potential applications of nanoporous atomically thin membranes, Nat. Nanotechnol., 2017, 12, 509–522 CrossRef CAS PubMed.
- P. Angelova, et al., A universal scheme to convert aromatic molecular monolayers into functional carbon nanomembranes, ACS Nano, 2013, 7, 6489–6497 CrossRef CAS PubMed.
- A. Turchanin and A. Gölzhäuser, Carbon Nanomembranes, Adv. Mater., 2016, 28, 6075–6103 CrossRef CAS PubMed.
- Y. Yang, et al., Rapid water permeation through carbon nanomembranes with sub-nanometer channels, ACS Nano, 2018, 12, 4695–4701 CrossRef CAS PubMed.
- A. Beyer, et al., Imaging of carbon nanomembranes with helium ion microscopy, Beilstein J. Nanotechnol., 2015, 6, 1712–1720 CrossRef CAS PubMed.
- C. Sun, B. Wen and B. Bai, Recent advances in nanoporous graphene membrane for gas separation and water purification, Sci. Bull., 2015, 60, 1807–1823 CrossRef CAS.
- A. Turchanin, et al., One nanometer thin carbon nanosheets with tunable conductance and stiffness, Adv. Mater., 2009, 21, 1233–1237 CrossRef CAS.
- S. P. Koenig, L. Wang, J. Pellegrino and J. S. Bunch, Selective molecular sieving through porous graphene, Nat. Nanotechnol., 2012, 7, 728–732 CrossRef CAS PubMed.
- S. Sarkar and A. K. Sengupta, The donnan membrane principle: opportunities for sustainable engineered processes and materials, Environ. Sci. Technol., 2010, 44, 1161–1166 CrossRef CAS PubMed.
- M. Ghosh, K. F. A. Jorissen, A. Wood and R. G. H. Lammertink, Ion Transport through Perforated Graphene, J. Phys. Chem. Lett., 2018, 9, 6339–6344 CrossRef CAS PubMed.
- Z. Zheng, et al., Hybrid van der Waals heterostructures of zero-dimensional and two-dimensional materials, Nanoscale, 2015, 7, 13393–13397 RSC.
- M. I. Walker, et al., Extrinsic cation selectivity of 2D membranes, ACS Nano, 2017, 11, 1340–1346 CrossRef CAS PubMed.
- S. W. Kowalczyk, A. Y. Grosberg, Y. Rabin and C. Dekker, Modeling the conductance and DNA blockade of solid-state nanopores, Nanotechnology, 2011, 22, 315101 CrossRef PubMed.
- T. Jain, et al., Heterogeneous sub-continuum ionic transport in statistically isolated graphene nanopores, Nat. Nanotechnol., 2015, 10, 1–6 CrossRef PubMed.
- J. Feng, et al., Observation of ionic Coulomb blockade in nanopores, Nat. Mater., 2016, 15, 850–855 CrossRef CAS PubMed.
- E. R. Cruz-Chu, A. Aksimentiev and K. S, Ionic current rectification through silica nanopores, J. Phys. Chem. C, 2010, 113, 1850 CrossRef PubMed.
- Y. Marcus, Ionic Radii in Aqueous Solutions, Chem. Rev., 1988, 88, 1475–1498 CrossRef CAS.
- T. Sata, Ion exchange membranes: preparation, characterization, modification and application, Royal Society of Chemistry, Cambridge, 2007, pp. 13–16 Search PubMed.
- Y. He, D. Gillespie, D. Boda, I. Vlassiouk, R. S. Eisenberg and A. Z. S. Siwy, Tuning transport properties of nanofluidic devices with local charge inversion, J. Am. Chem. Soc., 2009, 131, 5194–5202 CrossRef CAS PubMed.
- L. Yuan-Hui and S. Gregory, Diffusion of ions in sea water and in deep-sea sediments, Geochim. Cosmochim. Acta, 1974, 38, 703–714 CrossRef.
- A. J. Storm, J. H. Chen, X. S. Ling, H. W. Zandbergen and C. Dekker, Fabrication of solid-state nanopores with single-nanometre precision, Nat. Mater., 2003, 2, 537 CrossRef CAS PubMed.
- A. Winter, et al., Lateral heterostructures of two-dimensional materials by electron-beam induced stitching, Carbon, 2018, 128, 106–116 CrossRef CAS.
- R. A. Wilhelm, et al., Threshold and efficiency for perforation of 1 nm thick carbon nanomembranes with slow highly charged ions, 2D Mater., 2015, 2, 35009 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr05537a |
| This journal is © The Royal Society of Chemistry 2019 |