Exploring antiaromaticity in single-molecule junctions formed from biphenylene derivatives

Abstract

We report the synthesis of a series of oligophenylene-ethynylene (OPE) derivatives with biphenylene core units, designed to assess the effects of biphenylene antiaromaticity on charge transport in molecular junctions. Analogues with naphthalene, anthracene, fluorene and biphenyl cores are studied for comparison. The molecules are terminated with pyridyl or methylthio units. Single-molecule conductance data were obtained using the mechanically controllable break junction (MCBJ) technique. It is found that when electrons pass from one electrode to the other via a phenylene ring, the electrical conductance is almost independent of the nature of the pendant π-systems attached to the phenylene ring and is rather insensitive to antiaromaticity. When electrons pass through the cyclobutadiene core of the biphenylene unit, transport is sensitive to the presence of the relatively weak single bonds connecting the two phenylene rings of biphenylene, which arise from partial antiaromaticity within the cyclobutadiene core. This leads to a negligible difference in the molecular conductance compared to the fluorene or biphenyl analogues which have standard single bonds. This ability to tune the conductance of molecular cores has no analogue in junctions formed from artificial quantum dots and reflects the quantum nature of electron transport in molecular junctions, even at room temperature.

---

Introduction

A major goal of molecular electronics is to achieve chemical control over charge transport at the single-molecule level,^1–10 so that molecules could serve as active components in nanoscale electronic circuitry and thereby overcome some of the obstacles, which are limiting further miniaturization in the semiconductor industry.^11,12 Mechanically controlled break junction (MCBJ)¹³ and scanning tunnelling microscopy-break junction (STM-BJ) techniques¹⁴ are well-established experimental methods for measuring charge transport through single molecules wired into nanoscale metal–molecule–metal assemblies. It is clear from combined experimental and theoretical studies that charge transport through a molecular junction is a property of the whole system, and is highly dependent on the structural and electronic properties of the molecular backbone, the terminal anchor groups, and the metal electrodes.

Important molecular parameters are the length, the conformation, the alignment of the molecular orbitals relative to the Fermi level of the metal leads, and the binding geometry at the molecule–metal contacts. Molecules with an oligo(phenyleneethynylene) (OPE) backbone and various anchor groups have been widely studied as single-molecule bridges between two metal electrodes. Para-Linked OPE-3 systems (3 refers to the number of phenylene rings in the backbone) are benchmark molecules in this context.^15–24 OPEs are synthetically versatile and their conjugative and functional properties have been systematically tuned across many parameters.^25–27 The alkyne bonds in para-linked OPEs serve two main purposes: (i) they ensure a length-persistent rigid-rod structure with no possibility of geometrical isomerization (unlike oligophenylenevinylenes) (OPVs) and (ii) they space the phenyl rings apart, which enables the rings to rotate freely and achieve coplanarity, thereby maximizing the frontier orbital overlap along the molecule. The OPE-type framework is therefore an ideal test-bed for probing the effects on single-molecule conductance of incorporating Hückel aromatic, non-aromatic or antiaromatic core units into a molecular backbone.

The role of aromatic and heteroaromatic rings in molecules wired into metal–single-molecule–metal assemblies has been well explored and in some cases the low-bias conductance is shown to be sensitive to the extent of aromaticity. Independent theoretical studies by Solomon and coworkers,^28,29 and experimental STM-BJ studies by Venkataraman et al.³⁰ concluded that increased aromaticity at the core of a molecular wire decreases the conductance of the molecular junction. For example, the experimental conductance of a series of molecules with amine anchors clearly followed the sequence 2,5-disubstituted-thiophene < -furan < -cyclopentadiene.³⁰ In contrast, a study on a comparable series of 2,5-disubstituted-furan, -pyrrole, -thiophene and -cyclopentadiene derivatives with pyridyl anchors found no statistically significant dependence of the conductance on the aromaticity of the core.³¹ For molecules with tricyclic cores, it has been shown that increasing aromaticity at the core decreases the conductance for the para-linked molecules (dibenzothiophene < carbazole < dibenzofuran < fluorene) with pyridyl anchors,³² in agreement with Venkatarman et al.³⁰ However, the sequence is different for the isomers where the tricyclic core is meta-linked into the backbone (dibenzothiophene ≈ dibenzofuran < carbazole ≈ fluorene).³²

It is therefore of particular interest to explore the effect of incorporating 4n π-electron antiaromatic rings into the backbone of molecules that are wired into junctions. There are very few reported measurements on molecules of this type as they are usually demanding to synthesize and they are often unstable under ambient conditions. However, there are recent experimental precedents that antiaromaticity can be harnessed to enhance the conductance of single-molecule junctions. Yin et al. reported a single-molecule switch with a 9,9′–biindeno[2,1–b]thiophenylidene core that becomes antiaromatic with 6–4–6π-electrons upon electrochemical oxidation: a concomitant increase in conductance (on–off ratio of ca. 70) was observed.³³ Fujii et al. reported that the conductance of an antiaromatic 16π-electron norcorrole-based nickel complex is more than one order of magnitude higher than that of its aromatic 18π-electron nickel-porphyrin based analogue.³⁴

These two recent studies^33,34 concern structurally rather complex molecules for which there are few appropriate model systems. Further work on new families of molecules is therefore timely in order to achieve a better understanding of the relationship between aromaticity, antiaromaticity and conductance in molecular junctions. For this study we focus on OPE derivatives with a biphenylene core unit. Biphenylene is a classic example of a stable molecule containing a 4-π-electron ring.³⁵ The extent of resonance stabilization, electron delocalization and aromaticity of the peripheral benzene rings, and the related antiaromaticity of the central 4-π cyclobutadiene ring of biphenylene has been widely debated.^36–40 The experimental and theoretical evidence shows that there is antiaromaticity in the central ring, but this antiaromaticity is partly alleviated by a degree of bond fixation in the benzene rings analogous to Kekulé-type structures. We are aware of only one report of biphenylene derivatives in a molecular junction. Biphenylene was 2,7-disubstituted with amine and cyclic thioether anchoring groups, and no significant increase in conductance was found in STM experiments, compared with the fluorene analogues.⁴⁰ It is noteworthy that neutral biphenylene is isoelectronic with the highly-conductive 6–4–6 π-electron cation referred to above.³³

We now report the synthesis, single-molecule conductance measurements and theoretical studies of eight OPE-based compounds shown in Fig. 1, with particular focus on the new biphenylene derivatives 1–4. Key molecular design features are as follows: (i) all the molecules have terminal pyridyl^22,41 or methylthio^22,42 anchor groups at both ends. These anchors are known to bind efficiently to gold^22,41,42 and they have good chemical stability during the synthetic steps. They were chosen in preference to thiol anchors, because the thiol group would require additional protection/deprotection steps during the synthesis/assembly onto gold.⁴³ (ii) The biphenylene cores are incorporated into the backbone with two different connectivities (1,4- or 2,7-difunctionalized).

Fig. 1 (a) The structures of molecules 1–8 studied in this work. (b) Schematics of the MCBJ technique and the single-molecule junction of molecule 1.

The 1,4–disubstitution (molecules 1 and 3) allows for a conduction pathway between the leads through a typical OPE-3 framework, with the cyclobutadiene ring as a pendant feature. On the other hand, the 2,7-disubstitution (molecules 2 and 4) dictates that the conduction pathway is through the entire biphenylene core. (iii) Molecules 5–8 are studied as model OPE analogues. At the outset the main question we sought to address was: Can biphenylene antiaromaticity lead to a measurable effect on charge transport in this series of molecules?

Experimental section

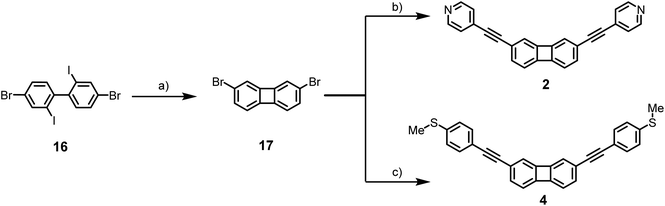
The details of the synthesis and characterization of 1–8 are given in the ESI.† The general multi-step synthetic route to the 1,4-disubstituted biphenylene derivatives 1 and 3 is shown in Scheme 1, starting from the commercially-available reagent 9, and proceeding via the known precursor 10.⁴⁴ The key intermediate 13 was obtained efficiently and underwent palladium-catalyzed two-fold Sonogashira reaction with 4-ethynylpyridine or 1-ethynyl-4-(methylsulfanyl)benzene to give the desired products 1 and 3 in 75–87% yields, respectively.

Scheme 1 Reagents and conditions: (a) H₂SO₄, I₂, 140 °C, 36 h, 85%; (b) 2-bromo-phenylboronic acid, Pd(PPh₃)₄, aq. Na₂CO₃ (1 M), DME, 90 °C, 16 h, 74%; (c) n-BuLi, THF, −78 °C, 1 h, then ZnCl₂, THF, −50 °C, 0.5 h, then CuCl₂, −78 °C to rt, 16 h, 59%; (d) lithium diisopropylamide, TMSCl, THF, −78 °C, 15 h, 90%; (e) t-BuLi, THF/Et₂O (1 : 1 v/v), −78 °C, 1 h, 85%; (f) ICl, DCM, 0 °C to rt, 1 h, 95%; (g) 4-ethynylpyridine, Pd(dba)₂, CuI, PPh₃, DIPEA, THF, 35 °C, 4 h, 75%; (h) 1-ethynyl-4-(methylsulfanyl)-benzene, PdCl₂(PPh₃)₂, CuI, PPh₃, DIPEA, THF, 35 °C, 2 h, 87%.

The route to the 2,7-difunctionalized biphenylene derivatives 2 and 4 starting from the readily-available commercial reagent 9 is shown in Scheme 2. Compound 16 was synthesized by a literature route in three steps from commercial 2,5-dibromonitrobenzene.⁴⁵ Model compounds 4–8 were synthesized by analogous methods from the dihalogenated core units (see ESI†).

Scheme 2 Reagents and conditions: (a) n-BuLi, THF, −78 °C, 1 h, then ZnCl₂, THF, −50 °C, 0.5 h, then CuCl₂, −78 °C to rt, 16 h, 61%; (b) 4-ethynylpyridine, PdCl₂(PhCN)₂, CuI, P(t-Bu)₃, DIPEA, 1,4-dioxane, 85 °C, 16 h, 70%; (c) 1-ethynyl-4-(methylsulfanyl)-benzene, PdCl₂(MeCN)₂, CuI, P(t-Bu)₃, DIPEA, 1,4-dioxane, 85 °C, 16 h, 49%.

The mechanically controllable break junction (MCBJ) technique was used to characterize the single-molecule conductance of compounds 1–8, as shown in Fig. 1b. The experiments were carried out under ambient conditions by employing a homebuilt I–V converter with a sampling rate of 10 kHz.⁴⁶ During the measurements, the breaking/connecting process of a notched gold wire was performed under the control of a combination of a stepping motor and a piezo stack. In this way, single-molecule junctions were formed by the repeatedly breaking/connecting of gold point contacts in solution (tetrahydrofuran : 1,3,5-trimethylbenzene = 1 : 4 v/v) with molecules at 0.1–0.4 mM concentration. Meanwhile the evolution of conductance characteristics was recorded at a fixed bias voltage of 100 mV, and then more than 1000 curves were used for further statistical analysis. More details are reported in our previous paper.⁴⁷

Results and discussion

Typical conductance traces for compounds 1–4 and 5–8 are displayed in Fig. 2a and b. These were recorded during the breaking process of the MCBJ measurements. The step-like plateau at 1 G₀ (conductance quantum, G₀ = 2e²/h) indicates the formation of a gold atomic point contact.⁴⁸ After rupture of the gold atomic point contact, followed by a sharp drop in conductance to 10⁻³G₀, well-defined conductance plateaus were obtained for 1–8, which are attributed to the formation of single-molecule junctions. In particular, two conductance plateaus were observed for molecule 7 and the low conductance plateaus appeared in accordance with high conductance plateaus. Upon further stretching, single-molecule junctions were broken and the conductance decreased to the noise level (10^−8.0G₀, details are in Fig. S2 in ESI†). To determine the most probable conductance values quantitatively, 1D conductance histograms were constructed for 1–4 (Fig. 2c) and 5–8 (Fig. 2d). The conductance of pyridyl-terminated 1,4-disubstituted biphenylene 1 (10^−4.6±0.41G₀) agrees well with that of 1,4-bis(4-pyridylethynyl)benzene in our previous work (10^−4.5G₀),¹⁸ indicating that the pendant antiaromatic side group in 1 has no observable effect on charge transport. When the electron pathway passes directly through the antiaromatic core unit, the conductance of the 2,7-disubstituted biphenylene derivative 2 is 32 times lower than that of 1, which agrees with its fluorene analogue in a previous report.³² Molecule 3 with SMe anchoring groups shows a slightly higher conductance value (10^−4.4±0.52G₀) than that of its pyridyl analogue 1 and agrees well with 1,4-bis(p-methylthiophenylethynyl)benzene in a previous report.²¹ Surprisingly, the conductance of molecule 4 terminated with SMe increases to 10^−4.9±0.82G₀ which is significantly higher than that its pyridyl analogue 2 (10^−6.1±0.90G₀). A similar trend is also found in a previous report on linear OPE-3 derivatives by van der Zant et al. and the higher conductance of SMe-terminated molecular junctions is attributed to better energy alignment between the molecular frontier orbital and the Fermi level than that of pyridyl-terminated junctions.²¹ Additionally, we tentatively propose that the conductance of 2 is anomalously low because of different (weaker) binding of the pyridyl anchors to the electrodes in such a bent configuration. As a consequence of this higher conductance of 4, the conductance of 4 is only approximately 3 times lower than that of 3. The lower conductance of 2 and 4, compared with 1 and 3, respectively, is consistent with the increased length of the central π-electron transmission pathway in 2 and 4.

Fig. 2 Typical conductance traces for compounds 1–4 (a) and 5–8 (b), respectively. One-dimensional (1D) conductance histograms for compounds 1–4 (c) and 5–8 (d) and the count numbers are scaled for better comparison. The conductance bin size is 0.01 log(G/G₀). Two-dimensional (2D) conductance-distance clouds and the relative stretching distance histograms of compounds 1 (e) and 5 (f). The bin size for the relative displacement distributions is 0.007 nm, and 1100 bins were used for the whole conductance range from 10¹G₀ to 10⁻¹⁰G₀. Error bars were determined from standard deviation in the Gaussian fitting.

Moreover for molecules 2 and 4, (with 2,7-connectivity) the single bond length of the cyclobutadiene core is longer than the single bonds within the phenylene rings (see Fig. S4 in the ESI†). Consequently, the electronic coupling in the former is weaker than in the latter. Therefore, transport is sensitive to the presence of the relatively weak single bonds connecting the two phenylene rings. This decreases the transmission within the gap and hence decreases the electrical conductance (see Fig. S6 in the ESI†).

To determine the effect on charge transport of a pendant cyclobutadiene unit on the OPE-3 system, molecules 5 and 7 comprising a similar core structure to 3 were investigated (Fig. 2d for 5 and 7). No significant difference in conductance values was observed among molecules 3, 5 and 7, which is evidence that the pendant cyclobutadiene of 3 has essentially no effect on charge transport. The low conductance state with broader peak width of 7 is attributed to either: (i) π-stacked dimer junctions through intermolecular interactions^20,49–51 or (ii) the same single-molecule junction with different contact geometries.⁵² Molecules 6 and 8 which are analogues of the 2,7-disubstituted biphenylene 4, without the antiaromatic core, were also synthesized and studied, as shown in Fig. 2d. Biphenyl derivative 6 shows slightly lower conductance than that of 8, because of the larger torsion angle between the two phenyl rings of 6, compared to the planar fluorene unit of 8.^31,53–55 Furthermore, the conductance of antiaromatic molecule 4 is comparable with that of 6 and 8, and no enhancement in charge transport due to the biphenylene unit in 4 is observed. This agrees with a previous comparison of conductance through a biphenylene and a fluorene core reported by Venkataraman et al.⁴⁰

To reveal the evolution of the stretching process, 2D conductance-distance clouds were constructed by normalizing more than 1000 typical conductance traces to a relative zero point at 10^−0.3G₀ and plotted as intensity graphs⁵⁴ as shown in Fig. 2e, f and S3.† The features at 1 G₀ correspond to the construction of atomic gold–gold contacts just before the breaking process. The distinct high-density clouds between 10^−4.0 and 10^−6.0G₀ are ascribed to the formation of single-molecule junctions. The relative stretching distance Δz histograms were constructed from 10^−0.3G₀ to the end of the conductance peaks in the 1D conductance histograms, which is one order of magnitude lower than the most probable conductance value. The most probable absolute stretching distance z* is obtained by adding the snap-back distance z_corr = 0.5 nm to the most probable relative stretching distance Δz*: z* = Δz* + z_corr.⁴¹ These values are in good agreement with the molecular length and the results are summarized in Table 1.

Table 1 Single-molecule conductance and lengths from MCBJ measurements

Compounds	Calculated conductance/log(G/G0)^a	Measured conductance/log(G/G0)^a	Measured length z^*/nm
a Most probable conductance values and the error bars are based on the standard deviation in the Gaussian fitting of the 1D conductance histograms.
1	−4.05	−4.6 ± 0.41	1.35 ± 0.17
2	−4.90	−6.1 ± 0.90	1.91 ± 0.23
3	−3.47	−4.4 ± 0.52	1.87 ± 0.22
4	−3.65	−4.9 ± 0.82	1.96 ± 0.32
5	−3.35	−4.2 ± 0.46	1.50 ± 0.23
6	−3.60	−4.8 ± 0.50	1.90 ± 0.27
7	−3.40	−4.1 ± 0.49	1.49 ± 0.17
		−5.9 ± 0.77	1.90 ± 0.29
8	−3.75	−4.7 ± 0.44	2.34 ± 0.29

---

In order to model charge transport across these molecular junctions, we used scattering theory combined with density functional theory (DFT). The optimal geometry and ground state Hamiltonian were obtained using the SIESTA⁵⁶ implementation of DFT and the transmission coefficients T(E) of electrons with energy E passing from one electrode to another through the molecules shown in Fig. S9† were calculated using the Gollum quantum transport code.⁵⁷ Details of the computational methods are reported in the ESI.†

Fig. 3 shows the calculated T(E) of compounds 1–8, from which their electrical conductances are given by G/G₀ ≈ T(E_F).Since the Fermi energy of the electrodes E_F relative to the frontier orbital energies is not usually predicted accurately by DFT, electrical conductances are plotted as functions of E_F relative to the DFT-predicted value E^DFT_F. The highlighted area shows the Fermi energy at which the calculated conductances are in qualitative agreement with the experimental findings. In this region of E_F, Fig. 3b and c show that molecules 3, 5 and 7, and molecules 4, 6 and 8, respectively, have similar conductances. Furthermore, Fig. 3a shows that the conductance of 3 is slightly higher than that of 4, in agreement with experiment, while the ratio of conductances of the pyridyl-terminated molecules 1 and 2 is significantly higher than that of the SMe-terminated molecules 3 and 4. Interestingly, this difference in the conductance ratios of 1 : 2 compared with 3 : 4 would not be predicted by a simple tight binding model, in which all bonds are assigned the same hopping integral, because the cyclobutadiene unit enforces different bond lengths within the cores of these molecules. This aspect is discussed in detail in the ESI.†

Fig. 3 DFT results of the transmission coefficients for (a) compounds 1–4, (b) 3, 5 and 7 and (c) 4, 6 and 8. The highlighted area shows the Fermi energy at which the calculated conductances are in qualitative agreement with the experimental findings. The relaxed structures are shown in Fig. S9 in the ESI.†

Conclusions

To conclude, we have synthesized and investigated the electrical conductance of six molecules with SMe anchor groups and two with pyridyl anchor groups. Comparison between 3, 5 (experimentally) and 3, 5, 7, (theoretically) shows that for the 1,4-connectivity in which electrons pass from one electrode to the other via a phenylene ring (i.e. for molecules 1, 3, 5 and 7) the electrical conductance is almost independent of the nature of the pendant groups attached to the phenylene ring and antiaromaticity has only a small effect. This behaviour is also consistent with a simple Hückel model of transport through these molecules, presented in Fig. S8 of the ESI.† For molecule 4 with 2,7-connectivity where electrons pass through the cyclobutadiene core, transport is influenced of the relatively weak single bonds connecting the two phenylene rings. In consequence, a negligible difference is observed experimentally and theoretically in the molecular conductance compared to the fluorene or biphenyl analogues 6 and 8 which have standard single bonds. Therefore, although the single bonds in the central cyclobutadiene ring of 4 are a consequence of partial antiaromaticity, we conclude that the presence of single bonds is the crucial feature, rather than antiaromaticity itself.

For the future, it would be of interest to examine variants of these molecules with alternative connectivities, since both of the biphenylene cores considered here have odd–even connectivities (1,4- for 1 and 3, or 2,7- for 2 and 4). Fig. S6† shows a numbering system for the pz orbitals and transmission curves of the biphenylene core with a variety of connectivities. The calculations reveal that molecules with even–even (such as 2,8) or odd–odd (such as 1,7) connectivities exhibit a strong destructive interference feature within the HOMO–LUMO gap, independent of the degree of antiaromaticity of the cyclobutadiene core. However, these alternative connectivities of substituents onto the biphenylene core pose significant synthetic chemistry challenges. This ability to tune the conductance of molecular cores has no analogue in junctions formed from artificial quantum dots and reflects the quantum nature of electron transport in molecular junctions, even at room temperature.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by the EC H2020 FET Open project 767187 “QuIET” and the EU project Bac-To-Fuel. M. R. B. thanks EPSRC grant EP/K0394/23/1 for funding equipment used in this work. C. J. L. acknowledges EPSRC support from grant EP/P027156/1, EP/N03337X/1 and EP/N017188/1. W. H. thanks National Key R&D Program of China (2017YFA0204902) and the Natural Science Foundation of China (No 21722305, 21673195). S. S. acknowledges the Leverhulme Trust (Leverhulme Early Career Fellowship no. ECF-2018-375) for funding. G. O. thanks the Danish Council for Independent Research, Technology and Production Sciences for funding (grant FTP, 8027-00005B).

Notes and references

1. N. Weibel, S. Grunder and M. Mayor, Org. Biomol. Chem., 2007, 5, 2343–2353.
2. T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002.
3. E. Leary, A. La Rosa, M. T. Gonzalez, G. Rubio-Bollinger, N. Agraıt and N. Martın, Chem. Soc. Rev., 2015, 44, 920–942.
4. M. Ratner, Nat. Nanotechnol., 2013, 8, 378–381.
5. J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific Publishing Co. Pte. Ltd., Singapore, 2010.
6. Single-Molecule Electronics: An Introduction to Synthesis, Measurements and Theory, ed. M. Kiguchi, Springer, Singapore, 2016.
7. K. Moth-Poulsen and T. Bjørnholm, Nat. Nanotechnol., 2009, 4, 551–556.
8. E. Lörtscher, Nat. Nanotechnol., 2013, 8, 381–384.
9. D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440.
10. C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888.
11. W. M. Mitchell, Nature, 2016, 530, 145–147.
12. H. N. Khan, D. A. Hounshell and E. R. H. Fuchs, Nat. Electron., 2018, 1, 14–21.
13. M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252–254.
14. B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223.
15. J. M. Tour, A. M. Rawlett, M. Kozaki, Y. Yao, R. C. Jagessar, S. M. Dirk, D. W. Price, M. A. Reed, C.-W. Zhou and J. Chen, et al. , Chem. – Eur. J., 2001, 7, 5118–5134.
16. R. Huber, M. T. Gonzalez, S. Wu, M. Langer, S. Grunder, V. Horhoiu, M. Mayor, M. R. Bryce, C. Wang and R. Jitchati, et al. , J. Am. Chem. Soc., 2008, 130, 1080–1084.
17. V. Kaliginedi, P. Marino-Garcia, H. Valkenier, W. Hong, V. M. Garcia-Suarez, P. Buiter, J. L. H. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 5262–5275.
18. X. Zhao, C. Huang, M. Gulcur, A. S. Batsanov, M. Baghernejad, W. Hong, M. R. Bryce and T. Wandlowski, Chem. Mater., 2013, 25, 4340–4347.
19. M. T. González, X. Zhao, D. Z. Manrique, D. Miguel, E. Leary, M. Gulcur, A. S. Batsanov, G. Rubio-Bollinger, C. J. Lambert and M. R. Bryce, et al. , J. Phys. Chem. C, 2014, 118, 21655–21662.
20. S. Wu, M. T. Gonzalez, R. Huber, S. Grunder, M. Mayor, C. Schoenenberger and M. Calame, Nat. Nanotechnol., 2008, 3, 569–574.
21. R. Frisenda, S. Tarkuc, E. Galan, M. L. Perrin, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Beilstein J. Nanotechnol., 2015, 6, 1558–1567.
22. R. Frisenda, S. Davide and H. S. J. van der Zant, Acc. Chem. Res., 2018, 51, 1359–1367.
23. Z. Wei, T. Hansen, M. Santella, X. Wang, C. R. Parker, X. Jiang, T. Li, M. Glyvradal, K. Jennum and E. Glibstrup, et al. , Adv. Funct. Mater., 2015, 11, 1700–1708.
24. C. R. Parker, E. Leary, R. Frisenda, Z. Wei, K. S. Jennum, E. Glibstrup, P. B. Abrahamsen, M. Santella, M. A. Christensen and E. A. Della Pia, et al. , J. Am. Chem. Soc., 2014, 136, 16497–16507.
25. N. M. Jenny, M. Mayor and T. R. Eaton, Eur. J. Org. Chem., 2011, 4965–4983.
26. U. H. F. Bunz, Chem. Rev., 2000, 100, 1605–1644.
27. X. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z. Y. Xiao, W. Hong, C. J. Lambert and S. X. Liu, Angew. Chem., Int. Ed., 2017, 56, 173–176.
28. M. H. Garner, G. C. Solomon and M. Strange, J. Phys. Chem. C, 2016, 120, 9097–9103.
29. A. Borges and G. C. Solomon, J. Phys. Chem. C, 2017, 121, 8272–8279.
30. W. Chen, H. Li, J. R. Widawsky, C. Appayee, L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2014, 136, 918–920.
31. Y. Yang, M. Gantenbein, A. Alqorashi, J. Wei, S. Sangtarash, D. Hu, H. Sadeghi, R. Zhang, J. Pi and L. Chen, et al. , J. Phys. Chem. C, 2018, 122, 14965–14970.
32. M. Gantenbein, L. Wang, A. A. Al-Jobory, A. K. Ismael, C. J. Lambert, W. Hong and M. R. Bryce, Sci. Rep., 2017, 7, 1794.
33. X. Yin, Y. Zang, L. Zhu, J. Z. Low, Z.-F. Liu, J. Cui, J. B. Neaton, L. Venkataraman and L. M. Campos, Sci. Adv., 2017, 3, eaao2615.
34. S. Fujii, S. Marques-Gonzalez, J.-Y. Shin, H. Shinokubo, T. Masuda, T. Nishino, N. P. Arasu, H. Vazquez and M. Kiguchi, Nat. Commun., 2017, 8, 15984.
35. W. C. Lothrop, J. Am. Chem. Soc., 1941, 63, 1187–1191.
36. R. H. Mitchell and V. S. Iyer, J. Am. Chem. Soc., 1996, 118, 2903–2906.
37. I. Fishtik, J. Phys. Org. Chem., 2011, 24, 263–266.
38. S. M. Bachrach, J. Phys. Chem. A, 2008, 112, 7750–7754.
39. R. Breslow and S. T. Schneebeli, Tetrahedron, 2011, 67, 10171–10178.
40. S. Schneebeli, M. Kamenetska, F. Foss, H. Vazquez, R. Skouta, M. Hybertsen, L. Venkataraman and R. Breslow, Org. Lett., 2010, 12, 4114–4117.
41. W. Hong, D. Z. Manrique, P. Moreno-Garcia, M. Gulcur, A. Mischchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 2292–2305.
42. E. J. Dell, B. Capozzi, J. Xia, L. Venkataraman and L. M. Campos, Nat. Chem., 2015, 7, 209–214.
43. H. Valkenier, E. H. Huisman, H. P. van Hal, D. M. de Leeuw, R. C. Chiechi and J. C. Hummelen, J. Am. Chem. Soc., 2011, 133, 4930–4939.
44. D. Lehnherr, J. M. Alzola, E. B. Lobkovsky and W. R. Dichtel, Chem. – Eur. J., 2015, 21, 18122–18127.
45. C. W. Keyworth, K. L. Chan, J. G. Labram, T. D. Anthopoulos, S. E. Watkins, M. McKiernan, A. J. P. White, A. B. Holmes and C. K. Williams, J. Mater. Chem., 2011, 21, 11800–11814.
46. G. Meszaros, C. Li, I. Pobelov and T. Wandlowski, Nanotechnology, 2007, 18, 424004.
47. W. Hong, H. Valkenier, G. Meszaros, D. Z. Manrique, A. Mishchenko, A. Putz, P. M. Garcia, C. J. Lambert, J. C. Hummelen and T. Wandlowski, Beilstein J. Nanotechnol., 2011, 2, 699–713.
48. N. Agrait, A. Y. Yeyati and J. M. van Ruitenbeek, Phys. Rep., 2003, 377, 81–279.
49. S. Martin, I. Grace, M. R. Bryce, C. Wang, R. Jitchati, A. S. Batsanov, S. J. Higgins, C. J. Lambert and R. J. Nichols, J. Am. Chem. Soc., 2010, 132, 9157–9164.
50. R. Frisenda, V. Jansen, F. C. Grozema, H. S. J. van der Zant and N. Renaud, Nat. Chem., 2016, 8, 1099–1104.
51. A. Magyarkuti, O. Adak, A. Halbritter and L. Venkataraman, Nanoscale, 2018, 10, 3362–3368.
52. P. Moreno-García, M. Gulcur, D. Z. Manrique, T. Pope, W. Hong, V. Kaliginedi, C. Huang, A. S. Batsanov, M. R. Bryce, C. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2013, 135, 12228–122240.
53. A. Mishchenko, D. Vonlanthen, V. Meded, M. Burkle, C. Li, I. V. Pobelov, A. Bagrets, J. K. Viljas, F. Pauly, F. Evers, M. Mayor and T. Wandlowski, Nano Lett., 2010, 10, 156–163.
54. A. Mishchenko, L. A. Zotti, D. Vonlanthen, M. Burkle, F. Pauly, J. C. Cuevas, M. Mayor and T. Wandlowski, J. Am. Chem. Soc., 2011, 133, 184–187.
55. W. Haiss, C. Wang, R. Jitchati, I. Grace, S. Martin, A. S. Batsanov, S. J. Higgins, M. R. Bryce, C. J. Lambert, P. S. Jensen and R. J. Nichols, J. Phys.: Condens. Matter, 2008, 20, 374119.
56. J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779.
57. J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey and K. Gillemot, et al. , New J. Phys., 2014, 16, 093029.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthesis and characterization of compounds 1–8; methods and results for the single-molecule conductance measurements of compounds 1–8; computational methods for calculating the transmission coefficients. See DOI: 10.1039/c9nr05375a

‡ M. G., X. L. and S. S. contributed equally to this work.

§ M. R. B. coordinated the writing of the manuscript with contributions from all authors. All authors have given approval to the final version of the manuscript.

---