Carbon fragments as highly active metal-free catalysts for the oxygen reduction reaction: a mechanistic study

Abstract

In metal-free carbon-fullerene-based or defective graphene-based electrocatalysts, pentagon rings are known to play a key role in boosting catalytic activities for the oxygen reduction reaction (ORR). However, the fundamental chemical mechanism underlying the remarkable catalytic effect of the pentagon rings towards the ORR is still not fully understood. Herein, we perform a comprehensive computational study of the catalytic activities of various carbon fullerenes and fullerene fragment species, all containing pentagon rings, by using the density functional theory (DFT) and computational hydrogen electrode (CHE) methods. We find that more active sites on carbon are associated with more neighbouring pentagon rings and stronger adsorption of the key intermediates of O*, OH* and OOH* for the ORR. Importantly, two C₆₀-based fragments, namely, C₆₀-frag1 and C₆₀-frag2l, show a very high activity towards the ORR, as both yield overpotentials as low as 0.389 and 0.407 V, and entail suitable adsorption free energy of OH* and OOH* species. These desirable chemical properties of fullerene fragments can be attributed to the high-energy HOMO orbitals, induced by the low-symmetry fullerene-fragment structures. Both the number of neighbouring pentagon rings and the degree of overall symmetry of the fragment appear to be the two important factors that can be adjusted for the design of optimal metal-free carbon electrocatalysts towards high ORR activities.

---

Introduction

The oxygen reduction reaction (ORR) is a key and rate-limiting process in many applications associated with renewable energy conversion, for example, rechargeable metal–air batteries and proton-exchange membrane fuel cells. The state-of-the-art ORR catalysts include precious-group metal (PGM) platinum (Pt) and Pt-based catalysts, while their large-scale commercial applications are still hindered by the high cost and scarcity and by Pt's sensitivity to deactivation in the presence of CO. Intense studies have been devoted to improve the efficiency of utilization of platinum^1,2 or to search for alternative more cost-effective Non-precious-group-metal (N-PGM) based electrocatalysts. For example, carbon or metal oxide material supported nanoparticles or single atom electrocatalysts can significantly reduce the dosage of precious Pt while maintaining a good ORR activity.^1,2 One particular class of Pt replacement electrocatalysts, many belong to the N-PGM catalysts,³ are atomically dispersed M–N–C catalysts^4–6 which show a comparable ORR performance as Pt.

Another class of promising and alternative electrocatalysts for the ORR is the metal-free heteroatom-doped carbon materials (carbon nanotubes,⁷ graphene,^8–10 graphite^11,12 and mesoporous carbon^13–15). This class of catalysts has been extensively investigated since Dai et al.⁷ first discovered that nitrogen-doped carbon nanotubes (N-C) can exhibit a high electrocatalytic activity, long-term operation stability, and high tolerance to crossover effect in alkaline fuel cells. Heteroatom-doping can effectively tune the carbon materials’ local electronic properties and induce charge/spin redistribution on the sp²-conjugated carbon matrix, thereby promoting the ORR on the doped C electrode.^7,16,17 Moreover, co-doping of N and another heteroatom such as B, S, and P can further modulate the catalysts’ electronic properties and polarization,^18–20 thereby enhancing the overall catalytic activity.

Recently, it was demonstrated that bare carbon materials containing appropriate defects²¹ or a large number of edge sites^18,22 can also exhibit outstanding ORR activity. Indeed, a perfect graphene sheet is known as a poor ORR catalyst, whereas a defective graphene catalyst exhibits a much higher ORR performance.^23,24 For example, Yao et al.²³ indicated that a defective graphene catalyst for a Zn–air battery presents very stable charge and discharge voltages, high current and power density, all comparable to those of Pt. Dai et al.²² predicated that dopant-free and edge-rich graphene is a highly efficient ORR catalyst. Intrinsic pentagon carbon rings can also play a critical role in enhancing the carbon materials’ ORR activity.^25,26 This is because pentagons and other defects or edges can markedly strengthen the adsorption of O species, compared with the graphene basal plane, leading to desirable intermediate chemisorption. Note that 0-dimensional carbon fullerenes also contain intrinsic pentagon rings.²⁷

Although previous work indicated that pentagon rings can effectively enhance the carbon materials’ ORR activity,²⁵ and carbon nanocatalysts with adjacent pentagon and hexagon rings yield the lowest overpotential for the ORR,^24,26,28 a detailed chemical mechanism on how pentagon rings affect the ORR's activity is still not fully understood. Is the most active site solely dependent on the number of neighbouring pentagon rings? Would the carbon site with adjacent pentagon and hexagon rings show good ORR activities? In this study, we address these questions by performing a systematic investigation on the ORR activities of various carbon fullerene species, including C₆₀,²⁹ C₃₆,³⁰ C₂₄,³¹ and C₂₀,³² as well as fullerene-based carbon fragments with H saturated edges. Interestingly, we find that fullerene fragments contain both intrinsic pentagon rings and numerous edge sites entail an outstanding ORR performance comparable to that of Pt.

Results and discussion

Results of the catalytic activities of small- and mid-sized fullerenes

Fullerenes are 0-dimensional carbon materials. Here, four kinds of small- and mid-sized fullerenes (C₂₀, C₂₄, C₃₆ and C₆₀), all containing pentagon carbon rings, are considered as possible metal-free electrocatalysts for the ORR. The structures of C₆₀,²⁹ C₃₆,³⁰ C₂₄,³¹ and C₂₀ ³² are taken from the literature. Fig. 1 shows the geometrical structures of C₂₀, C₂₄, C₃₆ and C₆₀. It can be seen that C₂₀ possesses pentagon rings only, while C₂₄, C₃₆ and C₆₀ possess both pentagon and hexagon rings. For C₂₀, each C atom has three adjacent pentagon rings. We denote the active site in C₂₀ as the “C₂₀-3p” site. Meanwhile, for C₆₀, each C atom has two adjacent hexagon and one adjacent pentagon rings. We denote the active site as the “C₆₀-1p2h” site. For either C₆₀ or C₂₀, all the C atoms have the same neighbouring polygons and thus all are the same active sites. For C₂₄, two types of active sites can be seen: one (denoted as C₂₄-2p1h site) has two adjacent pentagon and one adjacent hexagon rings, and another (denoted as C₂₄-3p) has three adjacent pentagon rings. For C₃₆, there are three types of active sites: one (denoted as C₃₆-1p2h site) has one adjacent pentagon and two adjacent hexagon rings. The other two sites have two adjacent pentagon and one adjacent hexagon rings, denoted as “C₃₆-2p1h-1” and “C₃₆-2p1h-2” sites.

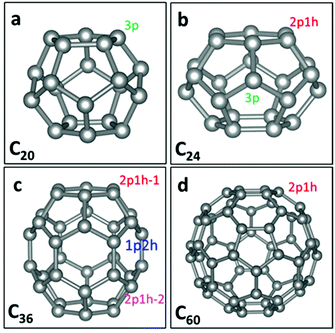Fig. 1 Graphs of C₂₀, C₂₄, C₃₆, and C₆₀ fullerene structures. The grey balls represent carbon atoms. 3p, 2p1h and 1p2h denote different active sites on four types of fullerenes.

Next, we examine the adsorption properties of the key intermediates (O*, OH*, and OOH*) at various sites of C₂₀, C₂₄, C₃₆, and C₆₀ fullerenes. Table 1 presents the computed Gibbs adsorption free energies (ΔG(O*), ΔG(OH*), and ΔG(OOH*)) of O*, OH* and OOH* species at all distinctly different sites. In ESI Fig. S1,† the lowest-energy adsorption structures are displayed, where it can be seen that the O atom favors being adsorbed on the bridge site between two adjacent C atoms by forming two O–C bonds, but OH* and OOH* species are more likely to be adsorbed on the top site of a C atom by forming one O–C bond. As shown in ESI Fig. S1d† and Table 1, O* adsorbed on the bridge sites of C₂₄-3p and C₂₄-2p1h on C₂₄ exhibits the same Gibbs adsorption free energy. Similarly, the C₃₆-2p1h-2 site entails the same ΔG(O*) as C₃₆-1p2h as both sites are bridge sites. For OH*, its adsorption free energies follow the trend ΔG(OH*)_C60-1p2h > ΔG(OH*)_C36-1p2h > ΔG(OH*)_C36-2p1h-1 > ΔG(OH*)_C36-2p1h-2 > ΔG(OH*)_C24-2p1h > ΔG(OH*)_C24-3p > ΔG(OH*)_C20-3p. So the C₆₀-1p2h site is the weakest adsorption site whereas the C₂₀-3p site is the strongest site for OH*. It seems that the site with more adjacent pentagon rings exhibits a stronger adsorption of OH* species.

Table 1 ΔG(O*), ΔG(OH*), and ΔG(OOH*) are Gibbs adsorption free energy values (unit: eV) of the key O species (O*, OH* and OOH*) adsorbed on different active sites of C₂₀, C₂₄, C₃₆, and C₆₀. ΔG₁, ΔG₂, ΔG₃, and ΔG₄ are reaction free energy values in each ORR step at U = 0 V (unit: eV). U_over is the calculated ORR theoretical overpotential (unit: V)

Sites	ΔG(O*)	ΔG(OH*)	ΔG(OOH*)	ΔG1	ΔG2	ΔG3	ΔG4	U over
C20-3p	0.111	−0.687	2.566	−2.354	−2.455	−0.798	0.687	1.917
C24-3p	0.068	−0.532	2.770	−2.150	−2.703	−0.600	0.532	1.762
C24-2p1h	0.068	−0.251	3.022	−1.898	−2.954	−0.319	0.251	1.481
C36-2p1h-1	1.481	0.342	3.608	−1.312	−2.128	−1.139	−0.342	0.888
C36-2p1h-2	1.594	−0.240	3.039	−1.881	−1.445	−1.834	0.240	1.470
C36-1p2h	1.594	1.090	4.354	−0.566	−2.760	−0.504	−1.090	0.726
C60-1p2h	1.836	1.367	4.627	−0.293	−2.790	−0.470	−1.367	0.937

---

For the site with the same number of adjacent pentagon and hexagon rings, the adsorption strength depends on the size of fullerenes: the larger the size of the fullerene, the weaker the adsorption of the OH* species. Note that O* and OOH* species also follow this generic trend for their adsorption.

Based on the adsorption of key O species on fullerenes, the ORR activities are evaluated (see Table 1). All of the four fullerenes are not good ORR catalysts since the overpotentials of various active sites on four fullerenes are all higher than 0.7 V, as shown in Table 1. On the sites with more than two adjacent pentagon rings of C₂₀, C₂₄, and C₃₆, the step involving the last electron transfer and OH* reduction to water is the rate-limiting step, and the corresponding ORR activities are very poor due to very strong OH* adsorption (i.e., ΔG(OH*) is much smaller than 1.23 eV). In addition, on the sites with only one adjacent pentagon ring of C₃₆ or C₆₀, the third electron transfer step to form OH* or the first electron transfer step to form OOH* is the rate limiting step, respectively, and the ORR activities are still not high due to very strong O* adsorption (i.e., ΔG(O*) is much smaller than 2.46 eV) and very weak OH* and OOH* adsorption.

Results of the catalytic activities of C₆₀ fragments

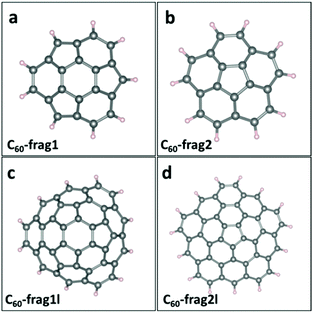
Since perfect small- and mid-sized fullerenes exhibit poor ORR activities, edge modulation is introduced as a promising strategy to tune the catalytic activities of fullerene-based materials. Here, we divide C₆₀ fullerene into smaller fragments and passivate the edge with H atoms. Fig. 2a–d presents the structures of four distinct C₆₀-based fragments, namely, C₆₀-frag1, C₆₀-frag2, C₆₀-frag1l and C₆₀-frag2l, respectively. C₆₀-frag1 is composed of one central hexagon ring, and three peripheral pentagon and three peripheral hexagon rings. C₆₀-frag2 is composed of one central pentagon ring and five peripheral hexagon rings. Compared with C₆₀-frag1 and C₆₀-frag2, C₆₀-frag1l and C₆₀-frag21 exhibit one more layer of hexagon rings surrounding the central C₆₀-frag1 and C₆₀-frag2, respectively. The thermal stabilities of the four fragments are examined by computing the formation energy of the four fragments with respect to gaseous hydrogen molecules and C₆₀ fullerene. As shown in ESI Table S1,† the formation energies are all negative, indicating that the formation reactions of C₆₀-frag1 and C₆₀-frag2, C₆₀-frag1l and C₆₀-frag21 from C₆₀ would all be exothermic.

Fig. 2 Four C₆₀-based fragment structures with H passivation at the edges. a, b, c, and d display C₆₀-frag1, C₆₀-frag2, C₆₀-frag1l and C₆₀-frag2l structures, respectively. The grey spheres represent C atoms and the pink spheres represent H atoms.

Next, adsorption of the key ORR intermediates of O species, O*, OH* and OOH*, on the four C₆₀ fragments is evaluated. For all the four fragments, the most favorable active sites are those C atoms associated with the central hexagonal or pentagon ring. ESI Table S2† presents the computed Gibbs adsorption free energies of the intermediate species on the most favorable adsorption sites, while ESI Fig. S2† displays the corresponding adsorption structures. Again, the O atoms favor to be adsorbed on the bridge site between the active C atom and one adjacent C atom, forming two C–O bonds. The ΔG(O*) associated with C₆₀-frag1, C₆₀-frag2, C₆₀-frag1l and C₆₀-frag2l fragments are 2.625, 2.505, 2.276 and 2.309 eV, respectively, all notably greater than 1.836 eV on a perfect C₆₀. This result indicates that the adsorption of O* on C₆₀ fragments is much weaker than that on C₆₀, which can facilitate the ORR on fragments since the adsorption of O* on C₆₀ fragments is not too strong. The adsorption free energies of OH* and OOH* species differ appreciably on different fragments. As shown in ESI Table S2,† ΔG(OH*) on C₆₀-frag1, C₆₀-frag2, C₆₀-frag1l and C₆₀-frag2l fragments are 0.850, 1.826, 1.439, and 0.848 eV respectively. So the adsorption of OH* on C₆₀-frag1 and C₆₀-frag2l is much stronger than that on C₆₀-frag1l and C₆₀-frag2; even these four fragments exhibit similar active sites but different edges. The adsorption free energy of OOH on four fragments exhibits a similar trend, i.e., ΔG(OOH*)_C60-frag1 < ΔG(OOH*)_C60-frag2l < ΔG(OOH*)_C60-frag1l < ΔG(OOH*)_C60-frag2. Thus, both OH* and OOH* species are adsorbed more strongly on C₆₀-frag1 and C₆₀-frag2l than on C₆₀-frag2 and C₆₀-frag1l, as well as than on C₆₀. It is understood that OH* and OOH* show the same adsorption trend on different fragments, since there is a widely accepted scaling relationship between OH* and OOH* on their adsorption free energies.³³ On adsorption structures, both OH* and OOH* are adsorbed on the active sites of fragments, forming one O–C bond as on fullerenes. Bader charge analysis (see ESI Table S3†) suggests that all the adsorbed O*/OH*/OOH* species gain electrons during the adsorption, while the active C atoms lose electrons.

Note that the four-electron reaction pathways are commonly associated with metal-free carbon catalysts. Here, we focus on the four-electron reaction pathways. Fig. 3 shows the obtained four-electron ORR free-energy diagram at U⁰ = 0 V for the four model fragments, based on the CHE model. ESI Table S2† gives the corresponding ORR free-energy changes in the four-electron transfer steps. Both ESI Fig. 3 and Table S2† show that the rate-limiting steps for the ORR are the first step of electron transfer and O₂ reduction to OOH*: O₂* + H₂O(l) + e⁻ → OOH* + OH⁻. Except for the first step for C₆₀-frag2, all other 15 steps for the four fragments are exothermic with ΔG < 0. Notably, C₆₀-frag1 yields the lowest overpotential of 0.389 V, suggesting that the C₆₀-frag1 is the most active ORR catalyst among the four fragments. Meanwhile, the overpotential of C₆₀-frag2l (0.407 V) is only slightly higher than that of C₆₀-frag1, consistent with the previous results.^26,28 Both C₆₀-frag1's and C₆₀-frag2l's ORR activities are comparable to those of Pt catalysts, as the onset potential of Pt catalysts is about 0.8 V. So, the overpotential of Pt catalysts would be about 0.43 V.^34–37 In contrast, the computed overpotentials of C₆₀-frag1l and C₆₀-frag2 are 0.986 and 1.377 V, respectively, much higher than those of C₆₀-frag1 and C₆₀-frag2l, indicating that both C₆₀-frag1l and C₆₀-frag2 are poor ORR catalysts. Overall, the weakened O* adsorption and enhanced OH*, OOH* species adsorption both boost the ORR catalytic performance of C₆₀-frag1 and C₆₀-frag2l, thereby rendering both as highly active ORR catalysts.

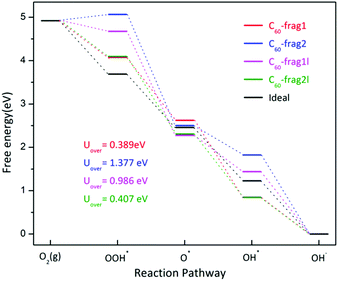Fig. 3 Four-electron ORR free-energy diagram on C₆₀-frag1, C₆₀-frag2, C₆₀-frag1l and C₆₀-frag2l fragments. U_over is the corresponding ORR overpotential.

Discussions

From the aforementioned calculation results, we can see that similar active sites of C atoms with one adjacent pentagon and two adjacent hexagon rings can exhibit markedly different ORR activities. To gain insights into this puzzling behaviour, we focus on the effect of the edges of fullerene fragments on their overall ORR activities. The active sites of C₆₀-frag1 and C₆₀-frag1l are all associated with the central hexagon ring, and possess the same first-nearest-neighbours. Moreover, C₆₀-frag2 and C₆₀-frag2l have similar active sites, but show very different activities. The apparent differences in ORR activities on similar active sites are likely due to the different adsorption behaviours of the key O species, especially OH* and OOH* species. So our attention is placed on understanding the edge dependent adsorption behaviour of OH* and OOH* species.

The OH* and OOH* species are adsorbed on the C₆₀ fragments by forming one O–C bond. As mentioned above, the adsorption free energies follow the trend ΔG_OH*/OOH* (C₆₀-frag1) < ΔG_OH*/OOH* (C₆₀-frag2l) < ΔG_OH*/OOH* (C₆₀-frag1l) < ΔG_OH*/OOH* (C₆₀-frag2), indicating that C₆₀-frag1 and C₆₀-frag2l exhibit much stronger adsorption towards the OH*/OOH* species. To understand this trend, we performed Bader charge analysis. ESI Table S3† shows the charge variation during the adsorption and Fig. 4 shows the calculated HOMO and LUMO energy levels. Clearly, C₆₀-frag1 and C₆₀-frag2l exhibit a much higher HOMO level than C₆₀-frag2 and C₆₀-frag1l, suggesting that C₆₀-frag1 and C₆₀-frag2l are more likely to lose electrons compared to C₆₀-frag2 and C₆₀-frag1l. This frontier orbital behaviour explains why C₆₀-frag1 and C₆₀-frag2l fragments can adsorb OH*/OOH* species much more strongly. In general, OH*/OOH* species tend to gain electrons during the adsorption while the fragments lose electrons. The higher HOMO level of the fragments can lead to the stronger adsorption of OH*/OOH* species.

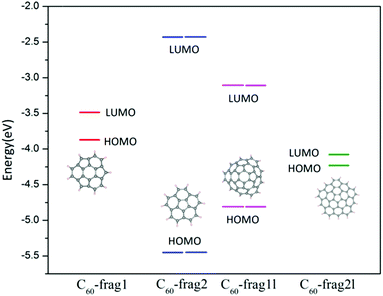Fig. 4 Frontier orbital energy level diagram of C₆₀-frag1, C₆₀-frag2, C₆₀-frag1l and C₆₀-frag2l fragments.

Moreover, we note that the geometry structures of C₆₀-frag1, C₆₀-frag2, C₆₀-frag1l and C₆₀-frag2l exhibit C_s, C_5v, C_3v and C₁ symmetry, respectively. As shown in Fig. 4, C₆₀-frag2 and C₆₀-frag1l exhibit relatively lower HOMO levels. So it seems that the trend in HOMO levels and the trend in the degree of the overall point-group may be correlated, since the lowered symmetry results in higher HOMO levels, thereby facilitating the adsorption. Indeed, we notice that among the four fragments, C₆₀-frag2 possesses the highest symmetry C_5v and the lowest HOMO level, and the latter leads to the weakest adsorption of OH* and OOH* species. Compared with C₆₀-frag2 and C₆₀-frag1l, C₆₀-frag1 and C₆₀-frag2l exhibit a lower symmetry and higher HOMO levels, thereby leading to a stronger adsorption of OH*/OOH* species. So even though C₆₀-frag1 and C₆₀-frag1l possess similar active sites, they have different edges and point-group symmetry. The same reasoning is applicable to C₆₀-frag2 and C₆₀-frag2l. In sum, the rings at the edges dictate the point-group symmetry of C₆₀-frag1 and C₆₀-frag2l fragments and the HOMO level, thereby affecting the strength of adsorption of OH*/OOH* species and the ORR activities.

To further confirm the correlation between the overall structural symmetry and the ORR activities, we modulate the structure of C₆₀-frag2 by substituting half of the passivation hydrogen atoms by fluorine atoms (denoted as C₆₀frag2-HF); or by changing one peripheral hexagon ring to one heptagon ring (denoted as C₆₀frag2-hep). Both modifications lower the overall symmetry of C₆₀-frag2 to C₁, one is due to change of the passivation atom and another is due to change of the carbon framework. ESI Fig. S3† presents the structures, and ESI Table S4† gives the corresponding adsorption free energies of the key O species and the reaction free energy for each electron transfer step in the ORR. For the most active site on C₆₀frag2-HF, the OH*/OOH* adsorption free energy (ΔG(OH*) = 1.786 eV, ΔG(OOH*) = 5.040 eV) decreases slightly and the ORR activity (U_over = 1.350 V) improves a little, compared with C₆₀-frag2 ((ΔG(OH*) = 1.826 eV, ΔG(OOH*) = 5.067 eV, U_over = 1.377 V). For C₆₀frag2-hep, the OH*/OOH* adsorption free energies increase more substantially while the ORR activity exhibits marked improvement at the most favorable active sites, i.e., the two central C atoms in the heptagon ring. ΔG_OH* and ΔG_OOH* are reduced to 0.955 and 4.212 eV, respectively, while the overpotential is only 0.522 V, much lower than that on C₆₀-frag2 (1.377 V). These additional results confirm that by lowering the point-group symmetry, especially through changing the carbon framework, the ORR activities can be significantly improved.

In addition to the central active sites, we investigated the ORR activities on other sites of the four fragments and various sites on three other fragments (C₆₀frag2l, C₂₄frag1, and C₃₆frag1). ESI Fig. S4† displays all the active sites on the seven fragments and ESI Table S5† presents all the adsorption free energies, reaction free energies and overpotentials of various active sites. Generally, fullerene-based fragments exhibit better ORR activities than the corresponding full fullerenes. ESI Fig. S5† shows a plot of overpotentials versus ΔG(OH*). It is noted that ΔG(OH*) between 0.8 and 0.9 eV exhibits the lowest overpotential of about 0.4 V. As discussed, the central active sites of C₆₀-frag1 and C₆₀-frag2l (C₆₀frag1C3 and C₆₀frag2lC3) yield overpotentials as low as 0.389 and 0.407 V, respectively. Moreover, C₆₀-frag1C2, C₆₀-frag1C4, and C₆₀-frag1l2C1 also exhibit quite low overpotentials of 0.415, 0.453 and 0.394 V. All the five active sites considered exhibit relatively high ORR activities.

Computational details

The spin-polarized density functional theory (DFT) method implemented in the Vienna Ab initio Simulation Package (VASP 5.4)^33–35 was employed to perform the calculations. The ionic cores were described by using the projector augmented wave (PAW) method.³⁶ The generalized gradient approximation (GGA)³⁷ in the formalism of the Perdew–Burke–Ernzerhof (PBE) functional was used to describe the electronic exchange–correlation energy in the energy calculations and the PBEsol³⁸ exchange–correlation functional was used in the optimization calculations. 1 × 1 × 1 Gamma centered grid k-points were used for non-periodic calculations. The convergence criterion of the electronic calculations was set to 10⁻⁵ eV and the force was set to be 10⁻² eV Å⁻¹. The energy cutoff of the plane-wave basis set was 500 eV. The thickness of the vacuum layer between two neighbouring fullerenes or fullerene fragments was set to be more than 20 Å so that the interaction between two neighbouring species can be neglected.

The ORR intermediates’ adsorption free energies were calculated based on the computational hydrogen electrode (CHE) model proposed by Nørskov et al.³⁸ relative to H₂O (g) and H₂ (g) according to the following equation: ΔG = Δ(E) + Δ(ZPE) − TΔS, where Δ(E) is the calculated adsorption energy, Δ(ZPE) is the change of zero-point energy and ΔS is the change of entropy between the adsorbed state and the gas phase. The adsorption energies were calculated based on the following formulas: ΔE(O*) = E(O*) − E(*) − [E(H₂O) − E(H₂)], ΔE(OH*) = E(OH*) − E(*) − [E(H₂O) − 1/2E(H₂)], and ΔE(OOH*) = E(OOH*) − E(*) − [2E(H₂O) − 3/2E(H₂)]. The temperature is 298.15 K. The gaseous entropies of H₂O (g) and H₂ (g) were taken from the NIST database.³⁹ The ZPE was derived from the calculated vibrational frequencies. Moreover, solvent corrections⁴⁰ were added to the adsorption free energies, in which the adsorption energies of OH* and OOH* were amended by ∼0.3 eV. Note that the adsorption free energy is relative to H₂O (g) and H₂ (g), which can be a positive value. A larger positive value represents weaker adsorption.

The ORR reaction was assumed to proceed through the 4-electron pathway in alkaline conditions, as shown in the following equations: (1) O₂* + H₂O(l) + e⁻ → OOH* + OH⁻, (2) OOH* + e⁻ → O* + OH⁻, (3) O* + H₂O(l) + e⁻ → OH* + OH⁻, and (4) OH* + e⁻ → OH⁻ + *, where * denotes the possible active sites on the catalysts; O*, OH* and OOH* are the adsorbed intermediates. The difference in free-energy change between the initial and final states in each step is defined as the reaction free energy ΔG. The reaction free energies in the four steps are directly related to the adsorption free energies of the intermediates: (1) ΔG₁ = ΔG(OOH*) − 4.92 eV + ΔG(pH) + eU, (2) ΔG₂ = ΔG(O*) − ΔG(OOH*) + ΔG(pH) + eU, (3) ΔG₃ = ΔG(OH*) − ΔG(O*) + ΔG(pH) + eU, and (4) ΔG₄ = −ΔG(OH*) + ΔG(pH) + eU. U is the applied electrode potential. The theoretical onset potential is U_onset = max{ΔG₁, ΔG₂, ΔG₃, ΔG₄}/e, and the theoretical overpotential is defined as U_over = max{ΔG₁, ΔG₂, ΔG₃, ΔG₄}/e + 1.23 [V].

Conclusions

The ORR activities of four kinds of C₂₀, C₂₄, C₃₆ and C₆₀ fullerenes and fullerene-based fragments are theoretically investigated by using DFT and computational hydrogen electrode (CHE) methods. Compared with perfect fullerenes, fullerene-based fragments exhibit much higher ORR activities. In general, the active sites associated with more pentagon rings show a stronger adsorption toward OH* and OOH* species. For the four C₆₀-based fragments, C₆₀-frag1, C₆₀-frag2, C₆₀-frag1l and C₆₀-frag2l, they possess similar active sites with one adjacent pentagon and two adjacent hexagon rings, but their adsorption behaviours and ORR activities are markedly different. C₆₀-frag1 and C₆₀-frag2l exhibit excellent ORR activities, with the theoretical overpotentials as low as 0.389 and 0.407 V, respectively. In contrast, the overpotentials of C₆₀-frag1l and C₆₀-frag2 are much higher (0.986, 1.377 V), suggesting poor ORR activities. In addition to the location of active sites, the overall degree of point-group symmetry of the fragment seems to correlate closely with the ORR activities. The two C₆₀-frag1 and C₆₀-frag2l fragments with a lower point-group symmetry exhibit a higher HOMO level, and are more likely to lose electrons, thereby resulting in a stronger adsorption of OH*/OOH* species and higher ORR activities. In contrast, C₆₀-frag2 exhibits the highest symmetry of C_5v, but the weakest adsorption of OH*/OOH* species and the lowest ORR activities among the four fragment models considered. Insights into the molecular mechanisms of ORR activities can provide theoretical guidance towards the rational design of metal-free carbon-based electrocatalysts for the ORR.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr. Haoxiang Xu for valuable discussions. KKM was supported by the National Natural Science Foundation of China (21803002) and a scholarship from the China Scholarship Council (CSC). XCZ was supported by the University of Nebraska Holland Computing Center.

References

1. W. Gao, Z. Zhang, M. Dou and F. Wang, ACS Catal., 2019, 3278–3288.
2. J. Liu, M. Jiao, B. Mei, Y. Tong, Y. Li, M. Ruan, P. Song, G. Sun, L. Jiang, Y. Wang, Z. Jiang, L. Gu, Z. Zhou and W. Xu, Angew. Chem., Int. Ed., 2019, 58, 1163–1167.
3. D. Zhou, S. Wang, Y. Jia, X. Xiong, H. Yang, S. Liu, J. Tang, J. Zhang, D. Liu, L. Zheng, Y. Kuang, X. Sun and B. Liu, Angew. Chem., Int. Ed., 2019, 58, 736–740.
4. Y. Zhu, B. Zhang, X. Liu, D.-W. Wang and D. S. Su, Angew. Chem., Int. Ed., 2014, 53, 10673–10677.
5. C. Bezerra, L. Zhang, K. Lee, H. Liu, A. Marques, M. Pereira, H. Wang and J. Zhang, Electrochim. Acta, 2008, 53, 4937–4951.
6. T. Palaniselvam, V. Kashyap, S. N. Bhange, J.-B. Baek and S. Kurungot, Adv. Funct. Mater., 2016, 26, 2150–2162.
7. K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764.
8. C. Zhang, N. Mahmood, H. Yin, F. Liu and Y. Hou, Adv. Mater., 2013, 25, 4932–4937.
9. X. Wang, G. Sun, P. Routh, D.-H. Kim, W. Huang and P. Chen, Chem. Soc. Rev., 2014, 43, 7067–7098.
10. I.-Y. Jeon, H.-J. Choi, S.-M. Jung, J.-M. Seo, M.-J. Kim, L. Dai and J.-B. Baek, J. Am. Chem. Soc., 2013, 135, 1386–1393.
11. S. Chen, J. Bi, Y. Zhao, L. Yang, C. Zhang, Y. Ma, Q. Wu, X. Wang and Z. Hu, Adv. Mater., 2012, 24, 5593–5597.
12. Z.-W. Liu, F. Peng, H.-J. Wang, H. Yu, W.-X. Zheng and J. Yang, Angew. Chem., Int. Ed., 2011, 50, 3257–3261.
13. R. Liu, D. Wu, X. Feng and K. Müllen, Angew. Chem., 2010, 122, 2619–2623.
14. J. Wang, H. Jin, Y. He, D. Lin, A. Liu, S. Wang and J. Wang, Nanoscale, 2014, 6, 7204–7208.
15. A. Aijaz, N. Fujiwara and Q. Xu, J. Am. Chem. Soc., 2014, 136, 6790–6793.
16. J. Y. Cheon, J. H. Kim, J. H. Kim, K. C. Goddeti, J. Y. Park and S. H. Joo, J. Am. Chem. Soc., 2014, 136, 8875–8878.
17. D. Guo, R. Shibuya, C. Akiba, S. Saji, T. Kondo and J. Nakamura, Science, 2016, 351, 361–365.
18. J. Zhang, Z. Zhao, Z. Xia and L. Dai, Nat. Nanotechnol., 2015, 10, 444.
19. K. Gao, B. Wang, L. Tao, B. V. Cunning, Z. Zhang, S. Wang, R. S. Ruoff and L. Qu, Adv. Mater., 2019, 31, 1805121.
20. X. Zou, L. Wang and B. I. Yakobson, Nanoscale, 2018, 10, 1129–1134.
21. D. Yan, Y. Li, J. Huo, R. Chen, L. Dai and S. Wang, Adv. Mater., 2017, 29, 1606459.
22. L. Tao, Q. Wang, S. Dou, Z. Ma, J. Huo, S. Wang and L. Dai, Chem. Commun., 2016, 52, 2764–2767.
23. Y. Jia, L. Zhang, A. Du, G. Gao, J. Chen, X. Yan, C. L. Brown and X. Yao, Adv. Mater., 2016, 28, 9532–9538.
24. L. Zhang, Q. Xu, J. Niu and Z. Xia, Phys. Chem. Chem. Phys., 2015, 17, 16733–16743.
25. C. Tang, H.-F. Wang, X. Chen, B.-Q. Li, T.-Z. Hou, B. Zhang, Q. Zhang, M.-M. Titirici and F. Wei, Adv. Mater., 2016, 28, 6845–6851.
26. J. Zhu, Y. Huang, W. Mei, C. Zhao, C. Zhang, J. Zhang, I. S. Amiinu and S. Mu, Angew. Chem., Int. Ed., 2019, 58, 3859–3864.
27. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
28. Y. Jiang, L. Yang, T. Sun, J. Zhao, Z. Lyu, O. Zhuo, X. Wang, Q. Wu, J. Ma and Z. Hu, ACS Catal., 2015, 5, 6707–6712.
29. F. Diederich and C. Thilgen, Science, 1996, 271, 317–324.
30. Z. Chen, H. Jiao, M. Bühl, A. Hirsch and W. Thiel, Theor. Chem. Acc., 2001, 106, 352–363.
31. W. An, N. Shao, S. Bulusu and X. C. Zeng, J. Chem. Phys., 2008, 128, 084301.
32. W. An, Y. Gao, S. Bulusu and X. C. Zeng, J. Chem. Phys., 2005, 122, 204109.
33. V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, ACS Catal., 2012, 2, 1654–1660.
34. J. Wang, Z. Huang, W. Liu, C. Chang, H. Tang, Z. Li, W. Chen, C. Jia, T. Yao, S. Wei, Y. Wu and Y. Li, J. Am. Chem. Soc., 2017, 139, 17281–17284.
35. M. Xiao, H. Zhang, Y. Chen, J. Zhu, L. Gao, Z. Jin, J. Ge, Z. Jiang, S. Chen, C. Liu and W. Xing, Nano Energy, 2018, 46, 396–403.
36. H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348.
37. K. Yuan, S. Sfaelou, M. Qiu, D. Lützenkirchen-Hecht, X. Zhuang, Y. Chen, C. Yuan, X. Feng and U. Scherf, ACS Energy Lett., 2018, 3, 252–260.
38. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
39. https://webbook.nist.gov/chemistry/ .
40. F. Calle-Vallejo, J. I. Martínez and J. Rossmeisl, Phys. Chem. Chem. Phys., 2011, 13, 15639–15643.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr05338g

‡ These authors contributed equally to this work.

---